Abstract
Simple deterministic models are still at the core of theoretical epidemiology despite the increasing evidence for the importance of contact networks underlying transmission at the individual level. These mean-field or ‘compartmental’ models based on homogeneous mixing have made, and continue to make, important contributions to the epidemiology and the ecology of infectious diseases but fail to reproduce many of the features observed for disease spread in contact networks. In this work, we show that it is possible to incorporate the important effects of network structure on disease spread with a mean-field model derived from individual level considerations. We propose that the fundamental number known as the basic reproductive number of the disease, R0, which is typically derived as a threshold quantity, be used instead as a central parameter to construct the model from. We show that reliable estimates of individual level parameters can replace a detailed knowledge of network structure, which in general may be difficult to obtain. We illustrate the proposed model with small world networks and the classical example of susceptible–infected–recovered (SIR) epidemics.
Keywords: random networks, small-world networks, mean-field models, epidemics, basic reproductive number
1. Introduction
Contact networks are increasingly recognized as central to the dynamics of infectious diseases and other transmission phenomena (Lloyd & May 2001; Barabási 2002; Newman et al. 2006). As a consequence of contact network structure, the vast majority of populations are heterogeneously mixed and therefore standard mass-action assumptions do not apply to the description of epidemic spread. Results on disease spread in networks have in fact challenged the still widely used formalism of epidemiological models based on the Kermack and McKendrik equations (1927; e.g. Morris 1995; May & Lloyd 2001; Eames & Keeling 2002; Newman 2002). These deterministic equations and their many descendants are known as ‘mean-field’, ‘compartmental’ or ‘mass-action’ models because they assume homogeneous mixing; every individual is in weak contact with any other in the population (Anderson & May 1992). However, in large populations, individuals typically contact only a small, clustered, subpopulation and the local correlations that result from transmission in such structured networks are not well captured by standard mean-field models (Keeling 1999a,b).
Despite this clear departure from homogeneous mixing, numerous contributions have been made by theory based on this assumption (see Anderson & May 1992; Smith et al. 2005). The simplicity of the resulting equations makes them both appealing and analytically tractable. Elegant extensions of the theory have been developed to address heterogeneous mixing within populations (or communities of species), by considering multiple host subgroups and a transmission matrix specifying ‘who acquires infection from whom’ (the WAIFW matrix; Anderson & May 1984; Schenzle 1984; Diekmann et al. 1990; Dobson 2004). In this framework, however, transmission within subgroups remains homogeneous. At a further extreme, transmission can be followed at the level of individuals in a contact network as a stochastic process. Network models add realism on the structure of contacts, but empirical information to completely describe the transmission pathways is often difficult if not impossible to obtain. Similar trade-offs are evident in models for transmission processes other than disease, including the spread of behaviour, rumours and computer viruses, and for the dynamics of ecological systems involving individual interactions. Owing to this trade-off, the proliferation in ecology and epidemiology of individual-based models has been accompanied by parallel and on-going efforts to develop simplifications that approximate the dynamics of complex systems at aggregated levels (e.g. Bolker & Pacala 1997; Levin & Pacala 1997; Keeling 1999a,b; Iwasa 2000; Law & Dieckmann 2000; Pascual 2005). For example, the empirical concept of a minimum effective neighbourhood has been developed to assess the importance of local correlations and demographic stochasticity, and the related performance of mean-field models in the invasion dynamics of epidemics (Keeling & Grenfell 2000).
In this work, we show that it is possible to approximate the main features of disease spread in networks with simple mean-field models by constructing the transmission rate from individual level parameters to implicitly include some effects of network structure on disease dynamics. Specifically, we propose that the basic reproductive number R0, which is typically derived from the model, be considered instead as a fundamental parameter to construct the equations from. We illustrate this idea with SIR dynamics (for susceptible–infected–recovered individuals) in a population of constant size for both (Poisson) random and small-world networks. A derivation of R0 for small-world networks is also presented. We end by asking how much information on the network itself is required to parameterize the proposed mean-field model and to capture main features of epidemic spread. Heterogeneous mixing does not appear to necessarily require detailed network models.
2. Networks models
In a network model, each of the N individuals in the population is represented by a vertex. Edges connecting a pair of vertices represent a contact between individuals. The number of edges of a given vertex is known as its degree. The network structure is described by the adjacency matrix Aij whose entries are 1 if individual i is in contact with individual j and 0 otherwise. Here, we consider bi-directional edges and therefore the adjacency matrix is symmetrical.
We simulate SIR stochastic epidemics in static networks. Two network structures are considered: Poisson (random) networks and small-world networks. The probability of disease transmission along an edge during an interval δt is where τ is the probability of transmission per contact per unit of time. To incorporate demography and maintain a constant population size and network structure, individuals ‘die’ at rate μ and are instantly replaced by susceptible individuals with the same contacts. The infectious period is assumed exponentially distributed with mean 1/γ. We also assume that the disease does not increase the mortality and therefore the removal rate is γ=r+μ in which r is the recovery rate. All the rates considered in this work are measured in units of the inverse of the recovery rate (i.e. we set r−1=1) and are therefore non-dimensional. The population is composed of S, I and R subpopulations of susceptible, infectious and recovered individuals, respectively.
3. Mean-field models for random networks: beyond homogeneous mixing
(a) Standard mean-field models
In a network of size N with homogeneous mixing, all the individuals are in ‘weak’ contact with each other. Thus, the degree of each individual is N−1. On an average, infections are produced at the rate τSI and therefore, the mean of the infected population evolves according to the ordinary differential equation . For large values of N, the threshold parameter Nτ/γ (derived from the equations of the model) coincides with the basic reproductive number (see electronic supplementary material) and at equilibrium the average susceptible proportion satisfies 〈S/N〉=1/R0, as expected. The mean-field model for networks with homogeneous mixing is therefore a mass-action model. However, homogeneous mixing may be realistic only for small populations. More typically, an average individual is in contact only with a small fraction of the population, and the mean of the degree distribution, n, is much smaller than the population size N (Keeling & Grenfell 2000; Newman 2002; Meyers et al. 2005).
In random networks (Erdős & Rényi; e.g. Bollobás 1995), the degree distribution is Poisson with mean n. Since an average infectious individual is in contact with n individuals (a random sample from the total population; see electronic supplementary material) but only the fraction S/N is susceptible, the average rate of infection becomes nτ(S/N)I and the mean-field model is given by
| (3.1) |
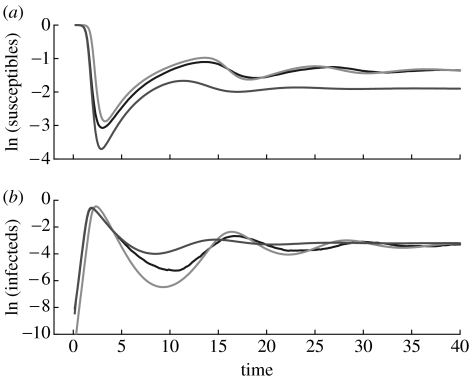
which, by construction, reproduces the initial rate of disease spread (Keeling & Grenfell 2000). However, the threshold parameter derived from this model is nτ/γ which does not coincide with the basic reproductive number R0=nτ/(τ+γ) (Andersson 1997; Aparicio et al. 2000; Diekmann & Heesterbeek 2000). In fact, according to this model, an average infectious individual may produce as many as nτ/γ secondary infections which may exceed the maximum number of available susceptible contacts, n. On the other hand, owing to the random nature of the network, it is expected that at equilibrium 〈S/N〉=1/R0, a fact that is confirmed by the stochastic simulations. Thus, this standard mean-field model fails to reproduce equilibrium values (figure 1) and the epidemic threshold parameter derived from its equations is not the basic reproductive number corresponding to the epidemiological setting. These failures are a direct consequence of the fact that n≪N.
Figure 1.
Comparison of the population dynamics of (a) susceptible and (b) infected proportions for the stochastic model of transmission in a Poisson random network and two mean-field models. The blue lines correspond to a stochastic simulation (with a total number of individuals N=90 000, a probability of transmission per contact per unit of time τ=1, and a mortality rate μ=0.05). The solution of the standard mean-field model 3.1 is in red and that of the modified mean-field model 3.2–3.5 is in green (natural logarithms were used).
(b) A modified mean-field model constructed from individual-level parameters
Although the standard mean-field model fails to capture the course of epidemics in random networks, we expect given this randomness that some mean-field model may successfully describe the average epidemic evolution. Next, we present a derivation of a mean-field model that takes into account implicitly the influence of network contact structure on disease spread. Key information on this influence is contained in the basic reproductive number.
The basic reproductive number is usually defined as the number of secondary cases produced by an average infectious individual placed in a completely susceptible population. This definition implicitly assumes homogeneously mixed populations. However, for other contact network structures, it does not incorporate the effect of local contact structure on the initial spread of the disease. An alternative definition is to consider the number of cases produced by an average infective at the beginning of the epidemic, i.e. when the depletion of susceptibles is negligible, but many generations of infectives have occurred, in order to ‘wash out’ the effect of initial conditions (e.g. Diekmann & Heesterbeek 2000, pp. 73–76). For the cases considered in this work, this last definition leads to rather complex computations for the basic reproductive number. As a useful alternative, we considered here an intermediate situation: the basic reproductive number was defined as the number of secondary cases produced by an average infectious individual in the second generation (Andersson 1997; Aparicio et al. 2000). This quantity can differ significantly from the first generation calculation for contact networks, particularly for small n and for networks with high clustering. The value of R0 estimated in the second generation better approximates the number of new cases produced per case at the beginning of an epidemic. This basic reproductive number can be computed from individual level considerations (e.g. Aparicio et al. 2000; Diekmann & Heestebeek 2000; Keeling & Grenfell 2000) and its expression will depend on the local structure of contacts and other individual level parameters, such as infectiousness and the distribution of the infectious period.
For example, in Poisson random networks with exponentially distributed infectious periods, the basic reproductive number is (Andersson 1997; Dieckmann & Heesterbeek 2000; see also electronic supplementary material). We propose a mean-field model whose central feature is a transmission rate built from this basic reproductive number instead of the phenomenological parameter, β=nτ.
At the beginning of the epidemic, an average infectious individual will produce R0 new infections during a mean effective infectious period (te) which is shorter than the mean infectious period, 1/γ. To approximate this pattern, we split the mean infectious period into two contributions where te≡1/γe. Infectious individuals produce infections only during the effective infectious period, 1/γe, remaining the rest of their infectious life (1/g) ‘inactive’. These individuals are still infected but owing to the stochasticity of the transmission process, the last infection they produce always occurs before complete recovery. In addition, infected individuals can deplete their local pool of susceptibles and no longer be able to transmit the disease. As the epidemic progresses, the number of infections caused by each infectious individual is reduced by the susceptible fraction because the cluster of contacts of any individual is a random sample of the population. Thus, an average infectious individual will produce R0(S/N) infections during a period 1/γe and will remain ‘inactive’ during a period 1/g.
The evolution of the active infectious population I is now given by . Individuals leaving the active class I are still infected and may be moved to a new class Y defined as containing infected but ‘no longer infectious’ individuals. The mean-field model becomes
| (3.2) |
| (3.3) |
| (3.4) |
| (3.5) |
The threshold parameter of this model is R0 and at equilibrium 〈S/N〉=1/R0. Neither of these two key properties depends on the value of γe which only affects the transients. Here, we choose γe=τ+γ in order to reproduce the initial rate of disease spread. Figure 1 shows the excellent agreement of the model with the time course of the stochastic simulations.
Owing to the random structure of these networks, we expected an appropriately defined mean-field model to work well. A more challenging case is considered next using small-world networks, for which local structure exists and individual contacts are no longer a random sample of the population.
4. Networks with high clustering
A drawback of Poisson random networks as models of social networks is their low clustering coefficient. Small-world networks (Watts & Strogatz 1998) have become a popular toy model for social networks because they exhibit both a high clustering coefficient, C, and a short mean path length, L. Thus, C corresponds to the probability that two neighbours of a node are themselves connected, while L is the average shortest distance between the two nodes in the network. We specifically consider small-world networks of mean degree n=8. The clustering coefficient and mean path length are determined by the disorder parameter (ϕ). When ϕ=0, the ordered network is a regular network where each individual is in contact with its eight nearest neighbours. The disorder parameter specifies the probability that an individual has a long-distance contact, i.e. a contact which is not among its local neighbours. We constructed the small-world networks (0<ϕ<1) using the algorithm of Watts & Strogatz (1998). In our implementation, the regular network (ϕ=0) is a two-dimensional lattice on a torus (see Roy & Pascual 2006 for details), a choice motivated by the spatial nature of local interactions in epidemiology. In the stochastic simulations, we consider a disorder parameter ϕ=0.1 for which the network is in the small-world regime (with a high C of approximately 0.75 but a short L of 0.08, both normalized by their respective values for ϕ=0 when the network is regular).
Next, we derive an expression for R0 for small-world networks (see further details in the electronic supplementary material) and examine whether the resulting mean-field system approximates the stochastic dynamics of the disease. For ϕ>0, an average individual has n contacts of which i≤n may be long-distance contacts with probability approximately given by
| (4.1) |
At the beginning of the epidemic, infected long-distance contacts may themselves produce R0rdm infections on average (and we make the approximation that R0rdm=nρ).
Consider now a source case with exactly i long-distance contacts that produce a secondary case. This secondary case may be one of its i long-distance contacts with probability i/n or one of its local contacts with probability (n−i)/n. In the first case, the secondary infection will produce, on average, R0rdm ternary cases. In the second, the secondary infection may have j long-distance contacts with probability approximately given by P(j,ϕ). This secondary case will therefore produce, on an average, (n−j)R0sp/n infections among its local contacts and jR0rdm/n among its long-distance contacts, where R0sp denotes the basic reproductive number of the regular ordered network. By averaging the over all values of j, we obtain the expected number of infections produced by a secondary case which is itself a local contact of a source case with exactly i long-distance contacts: . Finally, averaging for all the values of i, we obtain the following expression for the number of infections caused by an infected in the second generation
| (4.2) |
where ρ=τ/(τ+γ) is the probability of transmission per case and the expression of R0sp used to calculated equation (4.2) is (see electronic supplementary material for details):
| (4.3) |
The values obtained with equation (4.2) are in excellent agreement with empirical estimates of the basic reproductive number obtained from simulations (see Fig. 3 in the electronic supplementary material).
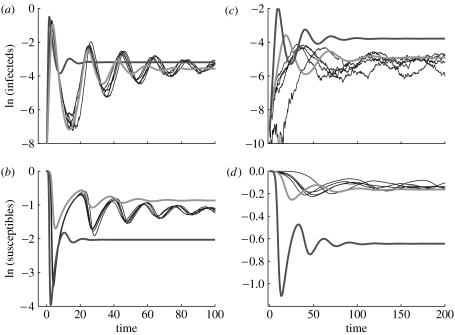
A high clustering coefficient greatly decreases the initial rate of disease spread but has a much less noticeable effect on equilibrium values. Two representative cases are shown in figure 2 for two different values of the transmission parameter, τ. For both the cases, model (3.2–3.5) performs much better than the standard mean-field model (3.1) which greatly overestimates the initial rate of disease spread because it ignores the local structure of the contacts (figure 2). This last deficiency could be corrected by defining an effective neighbourhood as ne≡R0sw/ρ. However, even with this correction, the threshold for this model would always overestimate the basic reproductive number, because . The modified mean-field model approximates both the initial growth, the turning point and the trough of the first epidemic, as well as the equilibrium level of susceptibles. These results are robust across a range of parameters of the stochastic simulations (see Fig. 4 in the electronic supplementary material). The model cannot, however, completely reproduce the exact phase and amplitude of the decaying oscillations to equilibrium.
Figure 2.
Comparison of the population dynamics of (a, c) infected and (b, d) susceptible proportions for two mean-field models and the stochastic model of transmission in a small-world network. Two different values of the transmission parameter were used: (a, b) τ=1 and (c, d) τ=0.25. A set of stochastic simulations are shown in blue (with network parameters ϕ=0.1 and N=90 000). Solutions for the standard mean-field model 3.1 are shown in red and those for the modified mean-field model 3.2–3.5 are shown in green (μ=0.05, r=1, γ=r+μ).
5. How much do we need to know about the networks? Empirical parameterization
A detailed knowledge of complete network structure, including the type of network and the mean number of contacts, allowed us to compute an appropriate expression for the basic reproductive number R0 and to construct from this quantity mean-field models that capture many of the main population-level features of the dynamics even for highly clustered networks. Unfortunately, in practice, such knowledge is not typically available, especially at the start of an epidemic. We therefore ask next how much information is required on the network itself to parameterize the model. We take the view that R0 when the network of contacts is unknown is an empirical parameter to be estimated.
The variable usually measured during the course of an epidemic is the number of new cases (reported) per unit of time, known as the incidence of the disease. We simulate the evolution of the incidence using the network model for different network structures. Typically, at the beginning of the epidemic, the incidence undergoes a phase of exponential growth whose parameter, λ, can be estimated from the linear regression of the logarithm of incidence versus time. The modified mean-field model for that initial phase can be written as . It follows that R0 can be estimated from the relation if γ and τ are assumed to be known (see electronic supplementary material for details). We also consider the case of the standard mean-field model because when the average number of contacts is unknown, its version (equation (3.1)) can be improved by introducing the effective number of contacts, ne (see also the definition of a minimum effective neighbourhood in Keeling & Grenfell 2000) which may be estimated from the initial growth rate of the incidence. Specifically, the standard mean-field model becomes where neτ may be estimated from the relation neτ−γ=λ if the value of γ is assumed to be known.
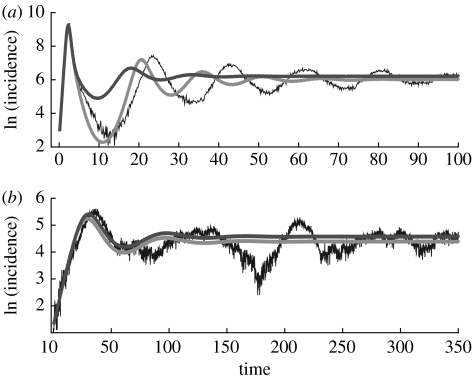
We simulated epidemics for a small-world network of 90 000 individuals and an initial infected population of size 9 with ϕ=0.1 and μ=0.05 (in all the cases r=γ−μ=1). For τ=0.25, the expected basic reproductive number (from equation (4.2) using the empirical estimation for R0sp; see electronic supplementary material) is 1.26 while for τ=1, it increases to 2.46. In the first case, the initial spread is greatly influenced by stochasticity while in the second, epidemics are almost deterministic (figure 3). With R0 and ne, respectively, estimated from the initial phase of exponential growth, both the mean-field models provide a good approximation to the time course of the disease for the first peak of the transients and for the average long-term incidence. The modified mean-field model (3.2–3.5) also captures the trough of the decaying epidemic (figure 3, τ=1). It is worth noticing that although the standard mean-field with an effective number of contacts works well when compared with the temporal course of the incidence, it still fails in an important way: the basic reproductive number resulting from the fitted equation overestimates its real value, more significantly for larger values of τ. This problem does not occur for the modified mean field. The following calculations demonstrate this point.
Figure 3.
Comparison of the time course of incidence for the stochastic disease model in a small-world network and two mean-field models parameterized from the initial phase of the first epidemic. Two different values of the transmission parameter are shown ((a) τ=1 and (b) τ=0.25). The blue lines correspond to the stochastic network simulations (ϕ=0.1, N=90 000, μ=0.05). We estimated λ from the initial phase of exponential growth of the realizations. From these values, we obtained the effective number of neighbours, , and the reproductive number , which in turn were used to parameterize the standard mean-field model 3.1 corrected with an effective number of neighbours (in red), and the modified mean-field model 3.2–3.5 (in green; see also section 2 in the electronic supplementary material). Natural logarithms were used.
We randomly selected 10 simulations undergoing an initial phase of exponential growth for both values of τ. From the estimated means and standard errors for , we obtained the following estimates for τne and R0, respectively: , (for τ=0.25) and , (for τ=1). For τ=0.25, R0∼neτ/γ, and there is little difference between both mean-field models. The threshold values of 1.12 and 1.14 are close to the expected value of R0=1.26. For τ=1, the threshold of the standard mean-field model overestimates the empirical value of R0=2.46, while the estimation obtained with the modified mean-field model is still in excellent agreement .
6. Discussion
The standard mean-field models are still at the core of theoretical epidemiology and ecology. In the epidemiological models, the fundamental parameter R0, the basic reproductive number of infectious diseases, plays a central role as an invasion threshold, of critical relevance to assess control measures. It is a standard procedure to derive expressions for the basic reproductive number, R0, from these models. Here, we have proposed to reverse the perspective on this key epidemiological quantity (in particular, when the fundamental assumption of these models, homogeneous mixing, does not hold): the basic reproductive number becomes a parameter from which a mean-field type model can be formulated. The resulting ‘modified’ mean-field model captures implicitly some important effects of heterogeneous mixing in contact networks, providing a better approximation to the population-level time course of the disease than the standard mean-field formulation. Thus, it is possible to use simple models to capture the temporal course of epidemics, even though transmission among individuals may occur in a complex network of contacts (see also Keeling & Grenfell 2000; Keeling 2005).
Of course, there are particular features of the dynamics that cannot be completely recovered with such a simple model, including the exact phase and amplitude of the transient cycles following the first epidemic and other oscillatory phenomena that result from spatial processes in networks (e.g. Roy & Pascual 2005; Verdasca et al. 2005). Evolutionary outcomes of network structure (e.g. Van Baalen 2002) will also require an explicit treatment of individual contacts. The applicability of the proposed approach is also dependent on spatial scale. One type of network has recently been proposed in which individuals belong to a nested hierarchy of levels, with random mixing applying within groups at the lowest level (Watts et al. 2005). Clearly, for such a network, when the deviations from random mixing involve transmission across levels of the hierarchy representing large spatial scales, our model would not apply. However, it would provide the basis to model transmission at the different levels of the hierarchy with a mass-action model, even when random mixing at that level is not warranted. Similarly, the model could be applied at the level of cities or schools as a building block of more complex formulations that explicitly represent the spatial network underlying disease propagation over larger geographical areas (Grenfell et al. 2001).
It has been shown before that individual level considerations, such as local structure and the number of contacts per individual, explain the discrepancy between the real value of R0 and standard estimates obtained at the population level from mean-field models (e.g. Keeling & Grenfell 2000). Our approach further underscores that the concept of basic reproductive number is model independent. Given an epidemiological setting, the basic reproductive number must provide the threshold parameter of any satisfactory model, but the reciprocal is not necessarily true. In some models, the derived threshold parameter does not provide R0. We have provided an example of this discrepancy when the individual-level effects are incorporated into a mean-field population model only through an effective neighbourhood size.
Another type of approximation for disease dynamics in networks has been proposed in the literature to account for individual-level effects, based on moment closure methods (or pair approximations; e.g. Keeling et al. 1997; Keeling 1999a,b; Eames & Keeling 2002). The resulting system has higher dimensionality than mean-field models, with equations not only for mean quantities but also for second-order moments (variances and covariances). Most of the disease applications are for networks with low clustering. Here, we focus on networks with high clustering and on approximations more closely related to the lower dimensional systems typical of epidemiological models. The next step is to consider other types of networks, including those related to the recently emphasized notion of superspreaders for which there is a skewed distribution of individual infectiousness (Galvani & May 2005; Lloyd-Smith et al. 2005).
At the beginning of the epidemic, an average infectious individual will produce R0 infections. As the epidemic progresses, this number is reduced because some of the contacts are already recovered (or infected). For a Poisson random network, this susceptible fraction is simply the population fraction S/N. For small-world networks, however, local processes are dominant and, therefore, the local susceptible fraction is in general different from the population fraction S/N. Most of the secondary cases will compete for many of the same susceptible contacts, while the few long-distance contacts infected will find almost completely susceptible neighbourhoods. In other words, epidemics in random and small-world networks are different even if their basic reproductive numbers are the same. In the extreme of a highly spatial network, the proposed model always predicts an initial phase of epidemic exponential growth which is not usually observed. However, even for small values of the disorder parameter, small-world networks exhibit an almost exponential growth phase (figure 3) and in such cases, the proposed model performs well. Further refinements of the functional form of transmission are possible that would capture the decrease in the availability of susceptibles. One possible candidate is a hybrid form that combines the use of R0 proposed here with the use of an empirical exponent on the susceptible fraction, previously proposed to modify the transmission rate at the population level (e.g. Severo 1969; Liu et al. 1987; Pascual et al. 2002; Roy & Pascual 2005).
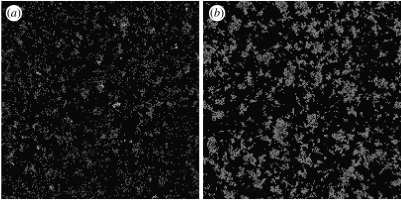
The effect of a local depletion in susceptibles is at the source of the discrepancy we see, for example, in the growth rate of the epidemic predicted by the modified mean-field model and the stochastic simulations in figure 2 (b,d). After a similar initial phase, the growth rate of the stochastic simulation is slower. This effect is more pronounced for low values of the transmission rate, τ, because the neighbourhoods of infected individuals are most affected by the formation of clusters of recovery (figure 4). By contrast, for high τ, the epidemic builds up as fronts of infection propagate through a sea of susceptibles (figure 4).
Figure 4.
Snapshots of the spatial grid for the stochastic model with the small-world network, for two different values of τ ((a) τ=0.25 and (b) τ=1). The red, blue and black sites correspond to infected, recovered and susceptible individuals, respectively. For initial conditions including a few foci of infection in a completely susceptible population, clusters develop quickly, after a short initial spread that appears exponential. For (a) the lower transmission rates, the clusters interfere most with the further propagation of the disease as most infected individuals are in close contact with recovered and other infected individuals. This difference is apparent by comparing the clusters of infection for the two transmission parameters.
Another refinement of the proposed model concerns the new class Y introduced for individuals that are still infected but no longer contribute to new infections. For simplicity, we have considered that the time individuals remain in this new class is exponentially distributed. Further theoretical work is warranted on the shape of this distribution and its effects on transient cycles. While it is theoretically possible to consider a more flexible distribution (like the gamma distribution used in epidemiology for the recovery process; Lloyd 2001), the empirical parameterization of the model from individual measurements would be more difficult.
The class Y takes into account the fact that an average infectious individual produces all infections in a time which is shorter than his infectious period. However, there is no physical distinction between the individuals in classes I and Y. We chose to include this class because it allowed us to compare model solutions with stochastic realizations. However, neither S nor I are typically measured in the course of an epidemic; only the number of new cases (incidence) is available. Therefore, for practical purposes like predicting the incidence or the size of epidemics, the class Y does not play a role. In other words, we may consider the Y individuals as recovered. In this case, model (3.2–3.5) reduces to a SIR model in which the infectious individuals are removed at a higher rate than the inverse of their mean infectious period γ, with a transmission rate given by the basic reproductive rate of the system, γeR0(S/N). The expression of R0 encapsulates our knowledge about the transmission process and includes implicitly the effects of contact network structure on transmission.
While network structure has a profound effect on disease spread, such structure is usually unknown and often unlikely to be completely elucidated. When complete knowledge of the network is not available but its degree distribution is known, a series of important probabilistic quantities characterizing epidemic behaviour can be obtained (Newman 2002; Meyers et al. 2005). This approach does not provide, however, a set of (ordinary differential) equations for predicting the time course of the disease. In a complementary approach, we have shown here that at least for the case considered, SIR dynamics in static small-world networks with exponentially distributed infectious periods, such a model is plausible without knowledge of either the degree distribution or any other aspect of network structure. Empirical parameterization of the model using data for the beginning of the epidemic is sufficient to accurately predict the main features of the time course of the epidemic, when reliable estimates of the individual level parameters are available. Future work should consider other types of networks, including non-static ones and other individual-based models of disease dynamics. Data on known networks and specific diseases can be used to further evaluate the forecasting ability of the proposed model. Extensions of similar ideas to other types of systems involving individual interactions in ecology are also possible.
Acknowledgments
We thank the Santa Fe Institute for its hospitality and for the stimulating environment it provided to conduct parts of this work. We also thank Lauren Ancel-Meyers for interesting discussions while at SFI and Manojit Roy for his network code. This research was supported by a Centennial Fellowship from the James S. McDonnell Foundation to M.P.
Supplementary Material
In this ESM we provide detailed derivations of the basic reproductive numbers for homogeneously mixed networks, regular networks, and small-world networks, and a description of how the estimations of the basic reproductive numbers are obtained for the network models. We further show how the mean field models are parameterized from data on incidence, and compare simulations of the network models to those of the mean-field formulations for a wide range of parameter values.
References
- Anderson R.M, May R.M. Spatial, temporal, and genetic heterogeneity in host populations and the design of immunization programmes. Institute of Mathematics and its Applications. J. Math. Appl. Med. Biol. 1984;1:233–266. doi: 10.1093/imammb/1.3.233. [DOI] [PubMed] [Google Scholar]
- Anderson R.M, May R.M. Oxford University Press; Oxford, UK: 1992. Infectious diseases of humans. [Google Scholar]
- Andersson H. Epidemics in a population with social structure. Math. Biosci. 1997;140:79–84. doi: 10.1016/s0025-5564(96)00129-0. doi:10.1016/S0025-5564(96)00129-0 [DOI] [PubMed] [Google Scholar]
- Aparicio J.P, Capurro A.F, Castillo-Chavez C. Transmission and dynamics of tuberculosis on generalized households. J. Theor. Biol. 2000;206:327–341. doi: 10.1006/jtbi.2000.2129. doi:10.1006/jtbi.2000.2129 [DOI] [PubMed] [Google Scholar]
- Barabási A.-L. Perseus; Cambridge, MA: 2002. Linked: the new science of networks. [Google Scholar]
- Bolker B, Pacala S.W. Using moment equations to understand stochastically driven spatial pattern formation in ecological systems. Theor. Popul. Biol. 1997;52:179–197. doi: 10.1006/tpbi.1997.1331. doi:10.1006/tpbi.1997.1331 [DOI] [PubMed] [Google Scholar]
- Bollobás B. Academic Press; London, UK: 1995. Random graphs. [Google Scholar]
- Diekmann O, Heesterbeek J.A.P. Wiley; New York, NY: 2000. Mathematical epidemiology of infectious diseases. [Google Scholar]
- Diekmann O, Heesterbeek J.A.P, Metz J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious-diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. doi:10.1007/BF00178324 [DOI] [PubMed] [Google Scholar]
- Dobson A. The population dynamics of pathogens with multiple hosts. Am. Nat. 2004;164:S64–S78. doi: 10.1086/424681. doi:10.1086/424681 [DOI] [PubMed] [Google Scholar]
- Eames K.T.D, Keeling M.J. Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl Acad. Sci. USA. 2002;99:13 330–13 335. doi: 10.1073/pnas.202244299. doi:10.1073/pnas.202244299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galvani A.P, May R.M. Epidemiology: dimensions of superspreading. Nature. 2005;438:293–295. doi: 10.1038/438293a. doi:10.1038/438293a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenfell B.T, Bjørnstad O.N, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature. 2001;414:716–723. doi: 10.1038/414716a. doi:10.1038/414716a [DOI] [PubMed] [Google Scholar]
- Iwasa Y. Lattice models in ecology and pair-approximation analysis. In: Dieckmann U, Law R, Metz J.A.J, editors. The geometry of ecological interactions: simplifying spatial complexity. Cambridge University Press; Cambridge, UK: 2000. [Google Scholar]
- Keeling M.J. The effects of local spatial structure on epidemiological invasions. Proc. R. Soc. B. 1999a;266:859–867. doi: 10.1098/rspb.1999.0716. doi:10.1098/rspb.1999.0716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J. Correlation equations for endemic diseases. Proc. R. Soc. B. 1999b;266:953–961. doi:10.1098/rspb.1999.0729 [Google Scholar]
- Keeling M.J. The implications of network structure for epidemic dynamics. Theor. Popul. Biol. 2005;67:1–8. doi: 10.1016/j.tpb.2004.08.002. doi:10.1016/j.tpb.2004.08.002 [DOI] [PubMed] [Google Scholar]
- Keeling M.J, Grenfell B.T. Individual-based perspectives on R0. J. Theor. Biol. 2000;203:51–61. doi: 10.1006/jtbi.1999.1064. doi:10.1006/jtbi.1999.1064 [DOI] [PubMed] [Google Scholar]
- Keeling M.J, Rand D.A, Morris A.J. Correlation models for childhood epidemics. Proc. R. Soc. B. 1997;264:1149–1156. doi: 10.1098/rspb.1997.0159. doi:10.1098/rspb.1997.0159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kermack W.O, McKendrick A.G. Contributions to the mathematical theory of epidemics, part I. Proc. R. Soc. A. 1927;115:700–721. [Google Scholar]
- Law R, Dieckmann U. Moment approximations of individual-based models. In: Dieckmann U, Law R, Metz J.A.J, editors. The geometry of ecological interactions: simplifying spatial complexity. Cambridge University Press; Cambridge, UK: 2000. pp. 252–269. [Google Scholar]
- Levin S.A, Pacala S.W. Theories of simplification and scaling of spatially distributed processes. In: Tilman D, Kareiva P, editors. Spatial ecology, the role of space in population dynamics and interspecific interactions. Princeton University Press; Princeton, NJ: 1997. pp. 271–295. [Google Scholar]
- Liu W, Hethcote H.W, Levin S.A. Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 1987;25:359–380. doi: 10.1007/BF00277162. doi:10.1007/BF00277162 [DOI] [PubMed] [Google Scholar]
- Lloyd A.L. Destabilization of epidemic models with the inclusion of realistic distributions of infectious periods. Proc. R. Soc. B. 2001;268:985–993. doi: 10.1098/rspb.2001.1599. doi:10.1098/rspb.2001.1599 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd A.L, May R.M. How viruses spread among computers and people. Science. 2001;292:1316–1317. doi: 10.1126/science.1061076. doi:10.1126/science.1061076 [DOI] [PubMed] [Google Scholar]
- Lloyd-Smith J.O, Schreiber S.J, Kopp P.E, Getz W.M. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. doi:10.1038/nature04153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- May R.M, Lloyd A.L. Infection dynamics on scale-free networks. Phys. Rev. E. 2001;64:066112. doi: 10.1103/PhysRevE.64.066112. doi:10.1103/PhysRevE.64.066112 [DOI] [PubMed] [Google Scholar]
- Meyers L.A, Pourbohloul B, Newman M.E.J, Skowronski D.M, Brunham R.C. Network theory and SARS: predicting outbreak diversity. J. Theor. Biol. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. doi:10.1016/j.jtbi.2004.07.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris M. In: Epidemic models: their structure and relation to data. Mollison D, editor. Cambridge University Press; Cambridge, UK: 1995. pp. 302–322. [Google Scholar]
- Newman M.E.J. Spread of epidemic disease on networks. Phys. Rev. E. 2002;66:016128-1–016128-11. doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
- Newman, M. E. J., Barabási, A.-L. & Watts, D. 2006 The structure and dynamics of networks Princeton, NJ: Princeton University Press.
- Pascual M. Computational ecology: from the complex to the simple and back. PLoS Comput. Biol. 2005;1:101–105. doi: 10.1371/journal.pcbi.0010018. doi:10.1371/journal.pcbi.0010018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual M, Roy M, Franc A. Simple temporal models for ecological systems with complex spatial patterns. Ecol. Lett. 2002;5:412–419. doi:10.1046/j.1461-0248.2002.00334.x [Google Scholar]
- Roy M, Pascual M. On representing networks heterogeneities in the incidence rate of simple epidemic models. Ecol. Complex. 2006;3:80–90. doi:10.1016/j.ecocom.2005.09.001 [Google Scholar]
- Schenzle D. An age-structured model of pre- and post-vaccination measles transmission. Institute of Mathematics and its Applications. J. Math. Appl. Med. Biol. 1984;1:169–191. doi: 10.1093/imammb/1.2.169. [DOI] [PubMed] [Google Scholar]
- Severo N.C. Generalizations of some stochastic epidemic models. Math. Biosci. 1969;4:395–402. doi:10.1016/0025-5564(69)90019-4 [Google Scholar]
- Smith K.F, Dobson A.P, McKenzie F.E, Real L.A, Smith D.L, Wilson M.L. Ecological theory to enhance infectious disease control and public health policy. Front. Ecol. Environ. 2005;3:29–37. doi: 10.1890/1540-9295(2005)003[0029:ETTEID]2.0.CO;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Baalen M. In: Adaptive dynamics of infectious diseases. Dieckmann U, Metz J.A.J, Sabelis M.W, Sigmund K, editors. Cambridge University Press; Cambridge, UK: 2002. pp. 85–103. [Google Scholar]
- Verdasca J, Telo da Gama M.M, Nunes A, Bernardino N.R, Pacheco J.M, Gomes M.C. Recurrent epidemics in small world networks. J. Theor. Biol. 2005;233:553–561. doi: 10.1016/j.jtbi.2004.10.031. doi:10.1016/j.jtbi.2004.10.031 [DOI] [PubMed] [Google Scholar]
- Watts D.J, Strogatz S.H. Collective dynamics of small-world networks. Nature. 1998;393:440–442. doi: 10.1038/30918. doi:10.1038/30918 [DOI] [PubMed] [Google Scholar]
- Watts D.J, Muhamad R, Medina D.C, Dodds P.S. Multiscale, resurgent epidemics in a hierarchical metapopulation model. Proc. Natl Acad. Sci. USA. 2005;102:11 157–11 162. doi: 10.1073/pnas.0501226102. doi:10.1073/pnas.0501226102 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
In this ESM we provide detailed derivations of the basic reproductive numbers for homogeneously mixed networks, regular networks, and small-world networks, and a description of how the estimations of the basic reproductive numbers are obtained for the network models. We further show how the mean field models are parameterized from data on incidence, and compare simulations of the network models to those of the mean-field formulations for a wide range of parameter values.