Coronary risk factors predicting early and late coronary deaths

Abstract

Objective: To study the time related association of a single measurement of coronary risk factors with coronary heart disease (CHD) deaths occurring during a very long follow up period in a population sample of middle aged men.

Design, setting, and methods: Age, systolic blood pressure, serum total cholesterol, physical activity at work, body mass index, and cigarette smoking were measured once in 1622 CHD-free men aged 40–59 belonging to the Italian rural cohorts of the seven countries study. During 35 years of follow up 214 men died from CHD (sudden death and definite myocardial infarction). Seven partitioned proportional hazards models were solved, one for each independent five year block of follow up, to predict the risk of CHD death.

Results: The seven, five year partitioned hazard functions were cumulated and smoothed for each risk factor. The resulting curves showed a regularly increasing time trend in risk for coronary deaths as a function of age, serum cholesterol, systolic blood pressure, and cigarette smoking and a regularly decreasing risk for physical activity. The curves fit straight lines, with large squared correlation coefficients ranging from 0.92–0.97. This suggests a relatively constant strength in the association of risk factor levels with events, which are predicted whatever the length of time after risk factors were measured. These findings were not altered by adding to the models risk factor changes preceding the quinquennium of death.

Conclusion: A single measurement of some coronary risk factors in middle aged men maintains a regular and almost monotonic relation with the occurrence of CHD deaths during 35 years of follow up.

In a previous article dealing with the Italian rural cohorts of the seven countries study,¹ it was shown that a single measurement of several cardiovascular risk factors was strongly and significantly associated with coronary heart disease (CHD) deaths during 35 years of follow up.

That preliminary analysis, however, was conducted on cumulated events and could not show the time trend in the strength of the association. In fact, when all events are used as the end point for the entire follow up, there is no way to identify the shape of the time related association. The relation may be regular and monotonic or strong in the early phases of follow up and then of lesser strength, or null or even negative, with all possible variations. The preliminary finding says only that, on average, there was a positive (or negative) overall association between risk factors and events.

Relatively simple statistical techniques can be used to describe the time trend of the association. In this analysis we hypothesised that six selected coronary risk factors were associated with 35 year CHD deaths in a monotonic fashion.

MATERIAL AND METHODS

The epidemiological material used for this analysis derives from the two Italian rural cohorts of the seven countries study of cardiovascular diseases, made up of men aged 40–59 years enrolled and first examined in 1960.² They represented 98.8% (n = 1712) of defined samples of the rural communities of Crevalcore in northern Italy and Montegiorgio in central Italy. Field surveys with measurement of risk factors and clinical evaluation were conducted at entry and then again on survivors every five years for 35 years. For the main purpose of this analysis only baseline measurement of risk factors taken at year 0 are considered, together with information on mortality during 35 years. For some analyses risk factor measurements taken in subsequent examinations were also considered.

Risk factors and their measurement techniques and units were the following:

• age, in years, was rounded off to the nearest birthday

• systolic blood pressure was measured in mm Hg in the right arm in the supine position at the end of a physical examination by trained physicians using mercury sphygmomanometers following the procedure described in the Cardiovascular survey methods manual³; two readings approximated to the nearest 2 mm Hg were made one minute apart and averaged

• serum cholesterol, in mmol/l, was measured on casual blood samples using the method described by Anderson and Keys⁴

• physical activity at work was graded in three levels by matching physical activity levels derived from a simple questionnaire with the reported profession (1 = sedentary activity; 2 = moderate activity; 3 = heavy activity)

• body mass index, in kg/m², was computed from height and weight measured following the procedure reported in the Cardiovascular survey methods manual³

• cigarette consumption, as the number of cigarettes smoked per day, was elicited from a questionnaire and the average number of cigarettes was estimated.

Collection of data on vital status and causes of death was complete for 35 years and no subject was lost to follow up. Causes of death were allocated by reviewing and combining information from death certificates, hospital and medical records, and interviews with physicians and relatives of the deceased and any other witnesses of fatal events. Causes of death were determined by a single reviewer (AM) following defined criteria, according to the International classification of diseases, 8th revision (ICD-8).⁵ In the presence of multiple causes, a hierarchical preference was adopted with violence, cancer in advanced stages, CHD, and stroke, in that order.

The end point of this analysis was CHD deaths occurring in subjects free from CHD at entry examination. Coronary deaths were those coded 410–414 by the ICD-8,⁵ plus cases of sudden coronary death occurring within two hours from onset of symptoms, after the exclusion of other possible causes.

Baseline data were collected in the 1960s before the era of the Helsinki Declaration. Subsequently, oral informed consent was obtained for collecting follow up data.

Data from coronary disease free subjects, were analysed excluding from the entry denominator those who already showed any clinical coronary manifestation.

Finally data were analysed from 1622 men free from CHD at entry and for whom all six risk factors measurements were available.

The analysis was conducted using the Cox proportional hazards model⁶ using the BMDP standard statistical package (BMDP Inc, Cork, Ireland) following two steps: firstly, a model was produced using all events that occurred during the 35 years of follow up, as a function of baseline risk factor measurements; and secondly, seven results were computed, each dealing with events occurring in subsequent and independent blocks of five years—for a total of 35 years—corresponding to the so called partitioned or segmented modelling approach.

In the first approach subjects who died from non-CHD causes were automatically dropped from the denominator at the time of the event, as censored cases. In the second approach those who died before the explored quinquennium of follow up were excluded from the denominator, while those who died in that quinquennium interval from causes other than CHD were treated as censored cases.

The coefficients for each risk factor and for each five year block of follow up were tested for heterogeneity.⁷ An approximated hazard function was estimated by subtracting 1 from the hazards ratios for one unit of measurement for each risk factor. Hazards functions were sequentially cumulated and plotted against time. They are not cumulative hazard functions but can be defined as cumulated hazard ratio scores. Confidence intervals around the hazard ratio scores were estimated from the standard errors of the coefficients and were also cumulated. Linear regression equations of cumulated hazards on time were computed, forcing the line at the origin of axes. The whole procedure imitates that suggested by Aalen, which uses linear modelling.⁸

To study the possible influence on the partitioned coefficients of risk factor changes occurring during the follow up and the derived functions, the analysis was run again, with the addition to the models of simple indicators of risk factor change. In particular, change was defined as the difference between the risk factor level at the beginning of each quinquennium of observation and at the baseline. This analysis was confined to the first three quinquennial periods, since measurements taken later were of limited reliability because of much lower participation rates. Many subjects and a sizable number of events would have been excluded from the analysis and altered the findings.

RESULTS

In 35 years of follow up 214 coronary deaths were recorded. Table 1 shows results of a proportional hazards model analysis with all CHD deaths in 35 years as end point and six risk factors as covariates. The coefficients for age, systolic blood pressure, serum cholesterol, and cigarette smoking were positive and significant. The coefficient for physical activity was negative and significant. The coefficient for body mass index was positive and non-significant.

Table 1.

Results of a proportional hazards model analysis predicting 214 coronary deaths among 1622 men in 35 years as a function of six risk factors

Risk factor	Coefficient	T Value	Delta for computing hazard ratios	Hazard ratios	95% CI
Age in years	0.0891	6.08	5 years	1.56	1.35 to 1.80
Systolic blood pressure in mm Hg	0.0181	5.18	20 mm Hg	1.44	1.25 to 1.65
Serum cholesterol in mmol/l	0.2668	4.25	1 mmol/l	1.31	1.15 to 1.48
Physical activity score (1, 2, 3)	−0.3218	−3.33	1 score unit	0.72	0.60 to 0.88
Body mass index in kg/m2	0.0025	0.13	3 kg/m2	1.01	0.90 to 1.13
Cigarettes/day	0.0204	2.96	10 cigarettes	1.23	1.07 to 1.40

CI, confidence interval.

Table 2 gives the results of the seven proportional hazards model analyses, each dealing with an independent quinquennium of follow up. In the seven models, the coefficients for systolic blood pressure were significant on four occasions; those for age and cholesterol on three occasions; those for physical activity and cigarette smoking on two occasions; and that for body mass index on no occasion.

Table 2.

Results of the partitioned proportional hazards model analysis for seven five year periods with coronary heart disease deaths as end point and six risk factors as covariates

Follow up period	Deaths/ sample	Factor	Coefficient	T Value	Delta for computing hazard ratios	Hazards ratios	95 % CI
Years 1–5	9/1622	Age	0.0229	0.32	5 years	1.12	0.56 to 2.26
		Systolic blood pressure	0.0096	0.63	20 mm Hg	1.21	0.67 to 2.20
		Cholesterol	0.8507	3.47	1 mmol/l	2.34	1.45 to 3.79
		Physical activity	–0.1081	–0.23	1 score unit	0.90	0.36 to 2.25
		Body mass index	–0.0274	–0.30	1 unit	0.97	0.81 to 1.16
		Cigarettes	0.0168	0.54	10 cigarettes	1.18	0.64 to 2.18
Years 6–10	16/1542	Age	0.1012	1.87	5 years	1.66	0.98 to 2.82
		Systolic blood pressure	0.0367	4.12	20 mm Hg	2.08	1.47 to 2.95
		Cholesterol	0.2630	1.15	1 mmol/l	1.30	0.83 to 2.04
		Physical activity	–0.8927	–2.89	1 score unit	0.41	0.22 to 0.75
		Body mass index	–0.1085	–1.49	1 unit	0.90	0.78 to 1.03
		Cigarettes	–0.0126	–0.43	10 cigarettes	0.88	0.50 to 1.57
		Systolic blood pressure*	0.0411	4.02	20 mm Hg	2.27	1.53 to 3.39
		Cholesterol*	0.4950	2.00	1 mmol/l	1.64	1.01 to 2.06
Years 11–15	28/1428	Age	0.1208	3.01	5 years	1.83	1.23 to 2.71
		Systolic blood pressure	0.0195	2.19	20 mm Hg	1.48	1.04 to 2.09
		Cholesterol	0.0193	0.11	1 mmol/l	1.02	0.72 to 1.44
		Physical activity	–0.1201	–0.42	1 score unit	0.89	0.51 to 1.55
		Body mass index	0.0173	0.33	1 unit	1.02	0.92 to 1.13
		Cigarettes	0.0669	3.75	10 cigarettes	1.95	1.38 to 2.77
		Systolic blood pressure*	0.0275	2.76	20 mm Hg	1.53	1.18 to 2.56
		Cholesterol*	0.0193	0.10	1 mmol/l	1.02	0.69 to 1.50
Years 16–20	33/1258	Age	0.0373	1.03	5 years	1.20	0.84 to 1.72
		Systolic blood pressure	0.0305	3.84	20 mm Hg	1.84	1.35 to 2.51
		Cholesterol	0.3171	2.01	1 mmol/l	1.37	1.01 to 1.87
		Physical activity	–0.2389	–0.96	1 score unit	0.78	0.48 to 1.28
		Body mass index	–0.0047	–0.09	1 unit	1.00	0.90 to 1.10
		Cigarettes	–0.0072	–0.36	10 cigarettes	0.93	0.63 to 1.38
Years 21–25	35/1063	Age	0.0657	1.88	5 years	1.39	0.99 to 1.96
		Systolic blood pressure	0.0045	0.47	20 mm Hg	1.09	0.75 to 1.59
		Cholesterol	0.1315	0.82	1 mmol/l	1.14	0.83 to 1.56
		Physical activity	–0.2272	–0.94	1 score unit,	0.80	0.50 to 1.28
		Body mass index	0.0785	1.62	1 unit	1.08	0.98 to 1.19
		Cigarettes	0.0300	1.86	10 cigarettes	1.35	0.98 to 1.85
Years 26–30	42/864	Age	0.0648	1.96	5 years	1.38	1.00 to 1.91
		Systolic blood pressure	0.0290	2.19	20 mm Hg	1.79	1.06 to 3.00
		Cholesterol	0.0075	2.09	1 mmol/l	1.01	1.00 to 1.01
		Physical activity	–0.6464	–3.17	1 score unit	0.52	0.35 to 0.78
		Body mass index	–0.0069	–0.15	1 unit	0.99	0.91 to 1.09
		Cigarettes	0.0302	2.06	10 cigarettes	1.35	1.01 to 1.80
Years 31–35	51/653	Age	0.1712	5.40	5 years	2.35	1.72 to 3.21
		Systolic blood pressure	0.0058	0.63	20 mm Hg	1.12	0.78 to 1.61
		Cholesterol	0.2591	1.97	1 mmol/l	1.30	1.00 to 1.68
		Physical activity	–0.0869	–0.36	1 score unit	0.92	0.57 to 1.47
		Body mass index	–0.0054	–0.11	1 unit	0.99	0.90 to 1.10
		Cigarettes	0.0061	0.39	10 cigarettes	1.06	0.78 to 1.44

*Derived from independent models with estimates adjusted for specific risk factor changes.

A test of heterogeneity applied to the coefficients of each risk factor of the results was never significant, suggesting that the hypothesis of heterogeneity among coefficients can be rejected (table 3).

Table 3.

Test of heterogeneity for coefficients from the seven models of table 2

Factor	χ2	p Value
Age	11.26	0.0806
Systolic blood pressure	10.80	0.0946
Cholesterol	8.46	0.2063
Physical activity	7.79	0.2537
Body mass index	5.06	0.5358
Cigarettes	11.43	0.0759

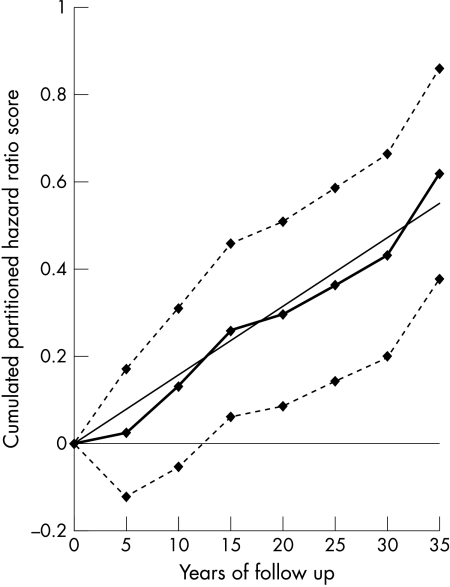
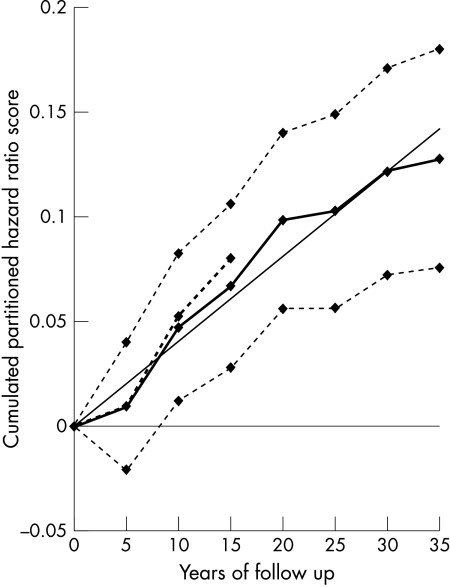
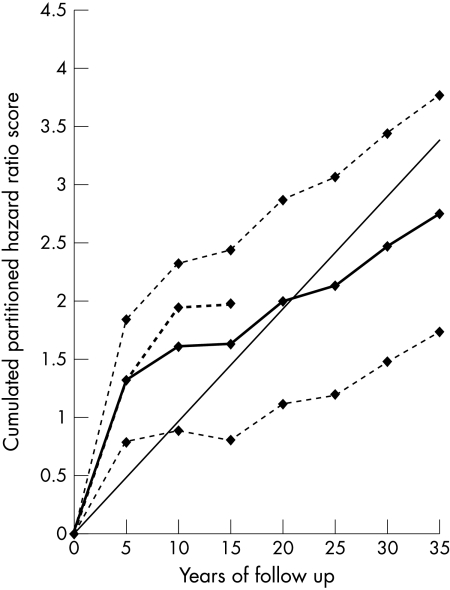
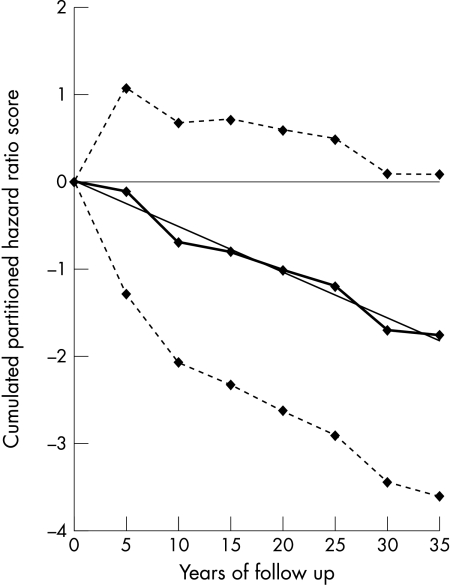
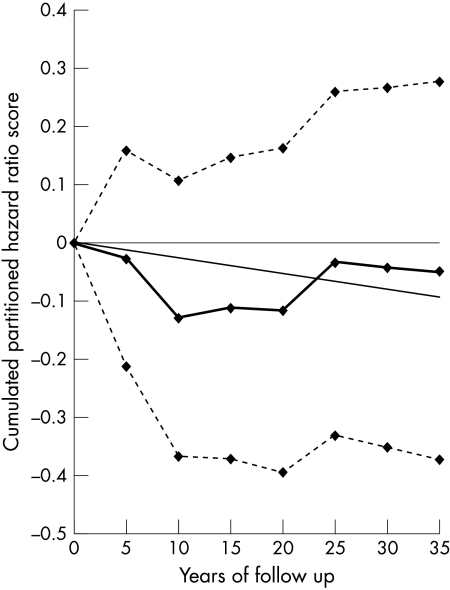
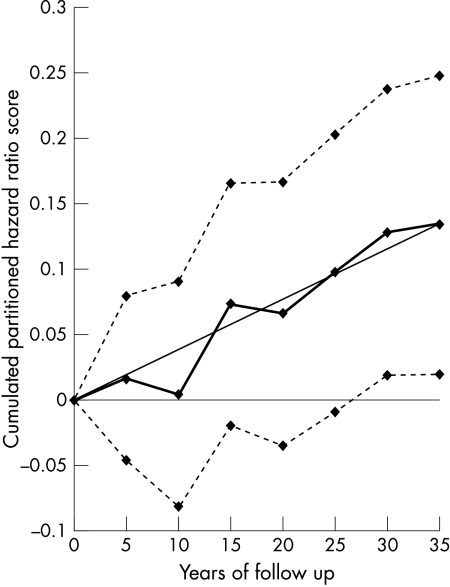
Figures 1, 2, 3, 4, 5, and 6 show graphically the cumulated hazard ratio scores for a unit of each risk factor, together with their 95% confidence intervals and a fitted straight line forced at the origin of axes. Table 4 lists the parameters of the fitted regression lines. Figures should be read considering that at each five year step the steepness of the slope describes the strength of the association of baseline risk factor levels with events for the subsequent five years, on average.

Figure 1.

Cumulated partitioned hazard ratio scores for age in the prediction of deaths from coronary heart disease (CHD) during 35 years. Thick line indicates cumulated partitioned hazard ratio scores; dotted lines indicate upper and lower confidence limits; straight line indicates fitted regression equation.

Figure 2.

Cumulated partitioned hazard ratio scores for systolic blood pressure in the prediction of CHD deaths during 35 years. Thick line indicates cumulated partitioned hazard ratio scores; thick dotted line indicates cumulated partitioned hazard ratio scores adjusted for previous risk factor change; dotted lines indicate upper and lower confidence limits; straight line indicates fitted regression equation.

Figure 3.

Cumulated partitioned hazard ratio scores for cholesterol in the prediction of CHD deaths during 35 years. Thick line indicates cumulated partitioned hazard ratio scores; thick dotted line indicates cumulated partitioned hazard ratio scores adjusted for previous risk factor change; dotted lines indicate upper and lower confidence limits; straight line indicates fitted regression equation.

Figure 4.

Cumulated partitioned hazard ratio scores for physical activity in the prediction of CHD deaths during 35 years. Thick line indicates cumulated partitioned hazard ratio scores; dotted lines indicate upper and lower confidence limits; straight line indicates fitted regression equation.

Figure 5.

Cumulated partitioned hazard ratio scores for body mass index in the prediction of CHD deaths during 35 years. Thick line indicates cumulated partitioned hazard ratio scores; dotted lines indicate upper and lower confidence limits; straight line indicates fitted regression equation.

Figure 6.

Cumulated partitioned hazard ratio scores for cigarette consumption in the prediction of CHD deaths during 35 years. Thick line indicates cumulated partitioned hazard ratio scores; dotted lines indicate upper and lower confidence limits; straight line indicates fitted regression equation.

Table 4.

Parameters of the regression lines forced at origin of axes, fitted in to seven quinquennial cumulated partitioned hazard ratio scores

Factor	Regression coefficient	SE	T Value	p Value	r2
Age	0.0157	0.0007	22.43	<0.0001	0.96
Systolic blood pressure	0.0040	0.0002	20.00	<0.0001	0.96
Cholesterol	0.0905	0.0077	11.77	<0.0001	0.88
Physical activity	−0.0525	0.0018	29.17	<0.0001	0.97
Body mass index	−0.0026	0.0010	2.60	0.0331	0.49
Cigarette smoking	0.0038	0.0003	12.67	<0.0001	0.92

Time trends of cumulated hazard ratio scores for age, systolic blood pressure, and cholesterol increased at each subsequent quinquennium of follow up suggesting a relatively regular and constant association of risk factors with events during the whole follow up period. The 95% lower confidence limits for age and systolic blood pressure become > 0 around year 10, while that of serum cholesterol was always > 0. The regression lines suggest good fits, corresponding to large values of r². However, the impression is that the curve for systolic blood pressure tended to flatten after year 20 and that for cholesterol became a little less steep after year 10.

The curve for physical activity had a negative and regular trend confirming its inverse long lasting association with CHD risk. However, the upper confidence limit approached zero only towards the end of follow up having been positive beforehand. The r² derived from the fitted regression line was large.

The curve for body mass index was irregular and closer, on average, to a flat shape than to an increasing or decreasing shape. This suggests a substantially null relation between body mass index and CHD deaths at any time of the follow up, confirmed by the fact that the two confidence limits always ran one above and the other below zero. The fitted regression coefficient was negative and the r² was the smallest among those of the six risk factors.

The curve for cigarette smoking increased during the 35 years of follow up but rather irregularly mainly during the first 20 years. The lower confidence limit became positive only after 25 years, while the correlation coefficient of the fitted regression was large.

We hypothesised that partitioned coefficients could be influenced by risk factor changes during the follow up. In fact, after the entry examination there were large average increases in mean levels of most risk factors. Systolic blood pressure increased from 143.6 mm Hg at baseline to 153.2 mm Hg at year 10 and 166.7 mm Hg at year 25.^2,9 Similarly serum cholesterol increased from 5.21 mmol/l (201.6 mg/dl) to 5.58 mmol/l (215.8 mg/dl) after 10 years and 5.84 mmol/l (225.8 mg/dl) after 25 years.^2,9 These two factors then stabilised or declined thereafter. On the other hand there was a steady decline in cigarette consumption and in the mean levels of physical activity. Slight changes were seen in body mass index.

The procedure has been tested only for systolic blood pressure and serum cholesterol because of the special influence they have on prediction of CHD. Their coefficients, adjusted for interim changes and derived from independent models, are also incorporated into table 2 for the second (years 6–10) and third (years 11–15) periods. Partitioned coefficients in models adjusted for risk factor changes were, on average, larger than disregarded changes, except for cholesterol during the third five year period. In general all the curves of the cumulated hazard ratio scores were set at a higher level. Curves of the hazard function adjusted for changes and limited to the first 15 years are also inserted in figs 2 and 3, dealing with systolic blood pressure and serum cholesterol. The shape of the curves was approximately the same.

DISCUSSION

This analysis shows that some classic risk factor baseline levels had a relatively constant relation with the occurrence of CHD deaths during a 35 year follow up. This is true for age, systolic blood pressure, serum cholesterol, and cigarette smoking directly and for physical activity inversely. Body mass index was never significantly related with the outcome and its time relation with an event but rather fluctuated around the level of no relation.

The curves are to be interpreted as the description of the strength and possible stability of the relation of risk factors with the occurrence of events at each subsequent time interval, although in this particular analysis, the interval is relatively long—five years. Among other things, this analysis tests the proportionality hazards assumption of the Cox model.

There were some irregularities in the curves describing the relation between risk factors and events during the follow up period, but they are partly justified by the small number of events in each five year block. On the other hand, the straight line fitted on data have large correlation coefficients, giving strength to the relatively monotonic and regular relation between risk factor levels and CHD deaths. Some relations are not linear along the whole time period. This can be interpreted as a non-linear relation or as the consequence of selection of cases due to the influence of risk factors potentially important also for non-coronary conditions.

There are technical alternatives to the partitioned Cox model, such as the Aalen model,⁸ which is based on a linear function and evaluates each single event, one by one, during the follow up and then uses a smoothing technique to cumulate the hazard functions. It can be shown that for relatively small effects, such as those of few events every five years, the two approaches produce similar results.

The strength of the association of baseline measurements with early and late events seems to be reinforced when changes of risk factor levels are added to the predictive models. However, the shapes of the plotted curves are unchanged, although their steepness is greater at least for systolic blood pressure and serum cholesterol, and for the first 15 years of follow up when data were reliable for the purpose.

The use of baseline measurements only in longitudinal studies tends to underestimate the associations between usual risk factors and CHD rates because of regression dilution effects.^10–12 In fact baseline measurements are often observed to be of lesser value in predicting long term events than they actually are, and adjustment for regression dilution can give a better estimate of their associations. The regression dilution effects can be due to random error, short term variation, and long term change. Our analysis with the inclusion of risk factor changes should be considered in the broader context of the regression dilution phenomenon, which can be used to improve the predictive ability of events after long periods of time.

In general, a single measurement in middle age retains its association with events and predicts events with similar strength for a long period of time. The strength of the association is somewhat improved by taking into account possible changes in risk factor levels due to aging or other reasons. The additional information of changes in risk factor levels has been described elsewhere for the first 25 years of follow up of this study² and there is no contradiction with these findings.

The problem of predicting early versus late events has been addressed in other studies, although using different techniques.

As mentioned above, by using the same data for a shorter follow up period, we have shown that the predictive power of coronary risk factors was similar for CHD incident events during the first 10 years and the subsequent 15 years of follow up.²

An analysis of the Honolulu heart study of middle aged men segregated early events from late events on the basis of age at the time of the event (< 60 years and 60 or older).¹³ Systolic blood pressure, alcohol intake, serum cholesterol, serum glucose, and cigarette smoking were independent predictors for early and late onset coronary events. On the other hand cigarette smoking had a smaller effect on late events, whereas serum triglycerides were predictors only of early events.

In the 25 year follow up of the Finnish cohorts of the seven countries study, the association of baseline cholesterol with coronary mortality was similarly strong during the first 10 years and the subsequent 15 years of follow up.¹⁴ The extension of the follow up to 30 years, with an analysis of three decades in the same cohorts, suggested that baseline serum cholesterol and smoking habits were strong predictors of CHD death occurring either early or late during the follow up, while baseline systolic blood pressure was no longer associated with CHD deaths after 20 years. Only after that time did baseline body mass index became directly associated with events.¹⁵ In our data the coefficients for systolic blood pressure become much smaller, and on two occasions non-significant, after 20 years of follow up.

In the Whitehall study in the UK, it was shown that, for a given age at death, the longer the gap between cholesterol measurement and death the more predictive the cholesterol concentration for CHD and all cause mortality, confirming that a single measurement taken earlier in life still holds predictive value after many years.¹⁶

In the Chicago Heart Association detection project in industry,¹⁷ late follow up events were predicted with the same strength as early follow up events by baseline measurements of blood pressure, cholesterol, and smoking habits.

Our findings and those reported in the literature help in interpreting some misunderstanding about the predictive power of risk factors in the elderly. The association of serum cholesterol concentrations with CHD events has been long debated and its interpretation is uncertain.¹⁸ The same applies to blood pressure with contrasting evidence about its ability to predict events when measured in old age.^19–21

Our findings clearly raise two entirely different questions: firstly, whether a single measurement in adulthood can predict events far in the future and even in to very old age; and secondly, whether measurements taken in the elderly can still predict the occurrence of events. It seems now that the first question can be answered by stating that some risk factors are associated for a very long time even with very distant events that occur in advanced ages. For example, in our sample, CHD deaths recorded during the last five years of follow up were strongly predicted among men aged 70–94 years whose risk factors were measured when they were aged 40–59 years.

The interpretation of this phenomenon is not clear. Personal characteristics in middle age may change over time, but at that age they are probable indicators of the degree of damage already done and maintain their strength and predictive value for long time. Again, this does not negate the possible benefits of changing levels of modifiable risk factors but is a warning that the association of past levels with the occurrence of events may last for life.