Divergent Evolution Within Protein Superfolds Inferred from Profile-based Phylogenetics

Abstract

Many dissimilar protein sequences fold into similar structures. A central and persistent challenge facing protein structural analysis is the discrimination between homology and convergence for structurally similar domains that lack significant sequence similarity. Classic examples are the OB-fold and SH3 domains, both small, modular β-barrel protein superfolds. The similarities among these domains have variously been attributed to common descent or to convergent evolution. Using a sequence profile-based phylogenetic technique, we analyzed all structurally characterized OB-fold, SH3, and PDZ domains with less than 40% mutual sequence identity. An all-against-all, profile-versus-profile analysis of these domains revealed many previously undetectable significant interrelationships. The matrices of scores were used to infer phylogenies based on our derivation of the relationships between sequence similarity E-values and evolutionary distances. The resulting clades of domains correlate remarkably well with biological function, as opposed to structural similarity, indicating that the functionally distinct sub-families within these superfolds are homologous. This method extends phylogenetics into the challenging “twilight zone” of sequence similarity, providing the first objective resolution of deep evolutionary relationships among distant protein families.

Introduction

Many dissimilar amino acid sequences adopt very similar protein structures, indicating that protein fold space is mapped redundantly onto sequence space.^1–3 While the wwPDB database currently represents over 20,000 different sequences of structural domains,⁴ only approximately 700–800 unique protein folds are known.^5–7 Elucidation of homologies among known protein domains and folds increases our understanding of protein function, structure, and evolutionary mechanisms.^6–10 A systematic and objective method for determining the evolutionary relationships between protein domains with low sequence similarity is needed to analyze this ever-growing wealth of data.

A long-standing and unresolved debate in structural biology concerns the demarcation of structural homology versus analogy for proteins in the “twilight zone” (i.e. < 25–40% sequence identity).^11–23 Proteins that have diverged from a common ancestor will preserve elements of this heritage in terms of function, structure, and sequence.^22–24 Because tertiary structures are relatively robust to sequence perturbations, protein folds are well conserved and evolve much more slowly than amino acid sequences.^{3,6,8,9,25–27} However, protein folds are more susceptible to evolutionary convergence than are amino acid sequences.

Unlike sequence-space, which is practically infinite, fold-space is finite and small. Many independent analyses predict that the earth’s biota likely contains under 10,000 distinct protein folds.^28–31 Furthermore, the majority of these protein domains belong to a small fraction of folds, the most common of which are known as the “superfolds”.³⁰ Thus, the likelihood of fold convergence is much greater relative to sequence convergence, since the number of possible folds to choose from is much smaller.^14,18 The significant probability of fold convergence has been confirmed recently by the structure determination³² of the first in vitro evolved protein domain,³³ which was found to be a member of a known natural fold.^34,35 If protein domains have evolved de novo more than a few thousand times since life began, then it is possible that each fold may have evolved independently many times.

When comparing two protein domains, significant sequence similarity by itself is strong evidence for common ancestry.^{13,17,26,36,37} In the absence of significant sequence similarity, similar protein function and structure is widely considered to be compelling evidence for common ancestry, based upon the improbability of convergence of both structure and function.^17,25 Nonetheless, unrelated protein domains may have the same fold solely due to protein-folding physical constraints, selection for similar functions, or chance.^18,38 Thus, highly dissimilar protein sequences that adopt the same protein fold may have independent origins or may be distantly homologous. Unlike the case of sequence similarity, we currently have no widely accepted, objective measure for the likelihood of convergence of tertiary structure.¹⁷

Here we outline an objective method for extending the detection of structural homology within the challenging twilight zone of sequence similarity. We chose three widely represented and structurally similar small β-barrel superfolds, well known for their great sequence heterogeneity: the OB-fold, SH3 fold, and PDZ fold (Figure 1). The similarities within and between these fold superfamilies have been credited alternatively to common origins or to evolutionary convergence.^6,21,39–45 Sequence profile-based E-values were calculated between protein domains belonging to these β-barrel superfolds. We derived a relationship between Karlin–Altschul sequence similarity E-values, similarity scores, and evolutionary distances and converted the E-values to evolutionary distances. Using this sensitive distance metric, we inferred distance-based phylogenies of these protein domains that indicate homologous, divergent evolutionary relationships for several large families of domains within a given superfold. The combination of sequence profile analysis and distance-based phylogenetic methods, a technique we term “profile-based phylogenetics”, extracts patterns in the data efficiently using a distance-based phylogenetic algorithm. The relationships determined from this phylogenetic analysis correlate remarkably well with biological function.

Figure 1.

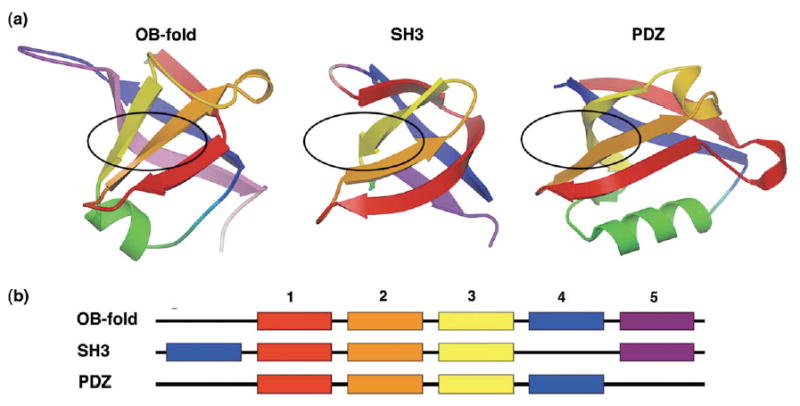
Topologies of the OB-fold, SH3 domain, and PDZ domain superfolds. (a) The OB-fold is shown with the five β-strands of the central barrel colour-coded: strand 1 is red, 2 is orange, 3 is yellow, 4 is blue, 5 is lavender. The SH3 and PDZ domains have corresponding β-strands coloured as in (a). The approximate canonical ligand-binding sites each fold are indicated by black ovals, (b) A schematic illustrating the relationships of the β-strand secondary structure among the three superfolds, coloured as in (a). SH3 doman β-strand 4 is permuted to the N terminus relative to the OB-fold, while the PDZ domain lacks β-strand 5.

Results and Discussion

Profile-based phylogenetic analysis

Sequence profiles provide a statistical summary of the collective information found in a family of related protein sequences.⁴⁶ Commonly used profile-based sequence analyses^46–48 significantly outperform pairwise methods in detecting remote homology.⁴⁹ Recent sequence profile–profile techniques, which score a profile against other profiles, give an additional increase in detection of weak sequence similarity.⁵⁰ For profile–profile analysis, we selected all protein domains in the SCOP database^6,51,52 with 40% or less sequence identity from within the OB-fold, SH3, and PDZ superfamilies. Selection based on structure enriches for likely homologues and greatly decreases sequence comparison noise,^53,54 since it is relatively improbable that two proteins with very different folds will be homologous. The average pairwise sequence identity for this set of protein domains is very low; after alignment with CLUSTAL, the pairwise sequence identity was 8(±4)% (mean ± standard deviation) between the OB-fold domain sequences and 10(±7)% between the SH3 domain sequences. After constructing sequence alignments with close homologs for each of these domains, we performed all-against-all profile–profile analyses with COMPASS,⁵⁰ scoring all alignments of the OB-fold domains against each other and all alignments of the SH3 domains against each other. The structurally characterized PDZ domains, all highly similar in sequence, were used as controls (described below).

Inspection of the complete matrix containing all possible pairwise E-values revealed many novel significant scores (i.e. E < 0.01) among 56 of the 93 OB-fold domains and 60 of the 82 SH3 domains. In addition to detecting significant similarities within known functional families of domains, we also found complex patterns of relationships between functional families within each superfold. To efficiently display and analyze this extensive set of data, the E-values were converted to evolutionary-based distances suitable for distance-based phylogenetic inference (see equation (3) in Theory and equation (4) in Materials and Methods).

Each phylogenetic analysis of statistically significant interrelationships produced two large trees, one for the OB-fold domains and one for the SH3 domains. The resulting weighted least-squares profile-based phylogenies for the OB-fold and for the SH3 domains are shown in Figures 2 and 3, respectively. After taxon jackknifing,^55,56 several clades are connected at unresolved midpoints of the trees. For clarity, each robust clade (i.e. ≥90% jackknife support (JS)) of three or more domains is shown as a separate unrooted tree, with arrows indicating the clade’s root as inferred from the original connection to the unresolved center node. In contrast to many conventional phylogenies displaying organismal relationships, these domain trees are built almost exclusively from paralogous proteins and are not expected to recapitulate species relationships. The most striking aspect of these trees is that the domains arrange in nested hierarchies primarily correlated with their biological functions rather than with their structural similarities.

Figure 2.

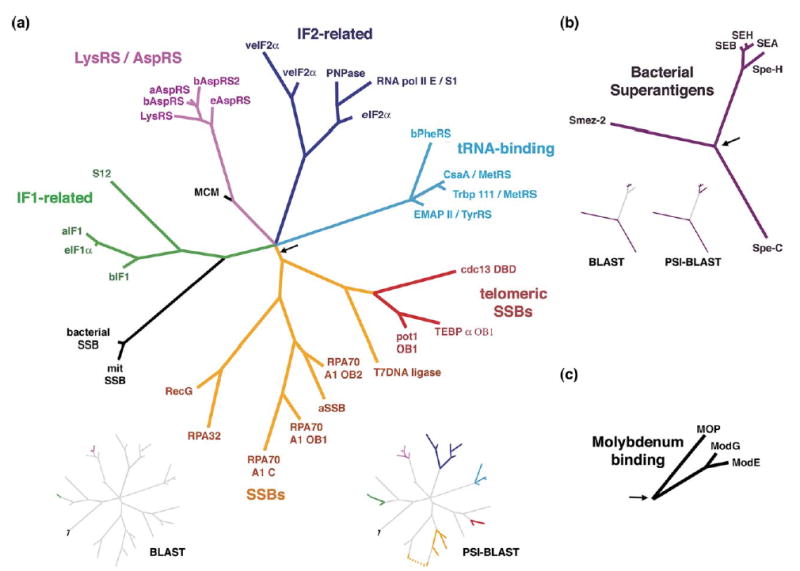
Profile-based phylogenies for the OB-fold domains. Branch lengths are proportional to evolutionary distances. Black arrows show tree rootings, based on the connection of these clades to the original center node, (a) The OB-fold nucleic-acid binding clade. (b) The superantigen enterotoxin clade. (c) The molybdenum-binding clade. Inset trees: relationships between the ASTRAL SCOP domain sequences that are detectable by BLASTP and PSI-BLAST searches of the NCBI non-redundant protein database (final E-values < 0.01) are highlighted in colour. While PSI-BLAST is able to detect many of these relationships, it has a much higher false positive rate than COMPASS.⁵⁰

Figure 3.

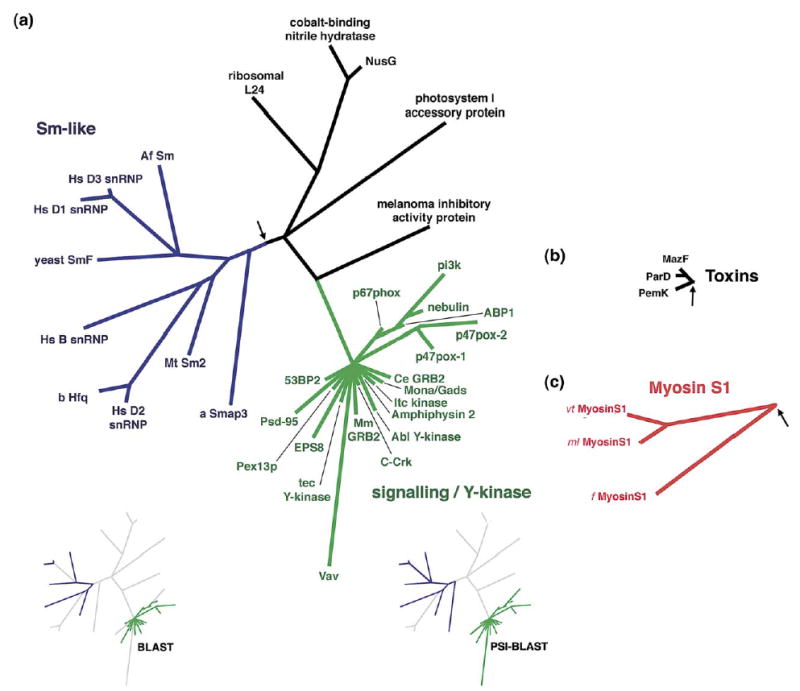
Profile-based phylogenies for the SH3 domains, (a) The RNA-binding Sm-like clade and signaling clade. (b) The plasmid-toxin clade. (c) The myosin-associated clade. Insets as in Figure 2.

The nucleic acid-binding OB-fold superfamily resolves by function

Thirty-one of the OB-fold domains in our database cluster in a superfamily of nucleic acid-binding OB-fold domains (100% JS; Figure 2(a)). This OB-fold superfamily contains five major clades: an ssDNA-binding (SSB) branch, a tRNA-binding branch, a tRNA-synthetase (RS) branch, and two translation initiation factor (IF) related branches (IF-1 and IF-2). The inferred root of this clade bisects the tree between the ssDNA-binding domains and the RNA-binding domains, near a large multifurcation that joins the RNA-binding domains. Statistical support for the majority of these relationships is novel, though similar, limited groupings have been postulated based largely upon structural and functional similarity alone.⁶ Conventional BLASTP searches with the SCOP domain sequences detect significant relationships between only a very few of these nucleic acid binding OB-fold domain families, while the profile searching program PSI-BLAST detects an additional limited number (see colored branches in the insets of Figure 2(a)).

The SSB clade includes an archaeal SSB OB-fold, several of the vertebrate replication protein A (RPA) OB-folds, T4 DNA ligase, and a subclade including three OB-folds from the known sequence-specific telomeric ssDNA-binding proteins. While conventional pairwise sequence comparisons fail to detect significant sequence similarity for the majority of these SSB domains, it has been suggested previously that they evolved by gene duplication.^44,57 For instance, RPA70 A1 contains four tandem, adjacent OB-fold domains. Three of these domains are represented in this profile-based SSB clade, providing evidence for the proposed gene duplication event. In contrast, the Oxytricha nova telomere end-binding protein (TEBP) α subunit also contains three tandem OB-fold domains, but these domains do not cluster together in our trees. Notably, the bacterial and mitochondrial SSBs are not found in this clade but rather cluster with IF1-related RNA-binding domains (see below).

Historically, the evolutionary relationships among telomere ssDNA-binding proteins have been controversial and difficult to ascertain, although recent weak sequence-profile similarity has indicated homology among these OB-fold domains.^45,58 Functionally, the telomeric OB-folds are most similar to the SSBs. Here the telomeric OB-fold domains cluster with the non-specific SSBs, revealing that this functional relationship has an evolutionary basis and suggesting that the sequence-specific telomere domains are derived, specialized SSBs.

The tRNA-synthetase OB-fold clade includes type IIb AspRS, AsnRS, and LysRS anticodon-binding domains. Sequence relationships among these synthetases are well-established for regions of the proteins outside of the OB-fold domain.^59,60 However, the OB-fold domains themselves are extremely divergent, and taken in isolation they lack detectable sequence similarity as probed by pairwise BLAST. Thus, the tRNA-binding clade is consistent with known synthetase evolutionary relationships and highlights the sensitivity of our method. Surprisingly, LysRS branches from within the AspRSs, raising the possibility that the AspRSs are polyphyletic and that LysRS was derived from eukaryotic AspRS.

A second clade of tRNA-associated OB-fold domains contains representatives from the EMAPII, Csaa, Trbp111, TyrRS, MetRS, and bacterial PheRS proteins (the SCOP “Myf” superfamily⁶). Unlike the OB-fold domain of the type IIb synthetases, these RS domains are spatially removed from the tRNA anticodon, and functionally they are sequence non-specific tRNA-binding domains. Assuming the inferred rooting for this tree, TyrRS (type Ic) and MetRS (type Ia) domains are derived from the PheRS B2 domain (type IIc). This may reflect a corresponding order of amino acid addition to the early genetic code apparatus, a hypothesis that has been offered previously based on independent criteria.^61,62 However, while it is widely recognized that TyrRS is closely related to TrpRS and that MetRS is closely related to LeuRS, IleRS, and ValRS,⁶⁰ we can find no evidence of bona fide OB-fold domains in these other synthetases. Thus, the evolution of RSs may be further complicated by heterogeneous origin or loss of independent RS domains.

The IF1-type clade includes bacterial, eukaryotic, and archaeal IF1 OB-fold domains, even though no statistically significant similarity can be found between bacterial IF1 OB-folds and the others via ordinary pairwise comparisons. Intriguingly, at the base of this clade is bacterial S12/eukaryotic S23, one of the most conserved proteins in the ribosome. S12 is also strongly implicated in translational initiation, and in a high-resolution structure of the ribosome IF1 binds on the outside of S12 relative to the RNA core.⁶³ Biochemical studies have shown that, in turn, IF2 interacts with IF1.^64,65 It has been hypothesized previously that IF1, IF2, and IF3 evolved via serial gene duplications.⁶⁶ According to the evolutionary principle of continuity,^67,68 new functions and their corresponding structures will tend to be added to the periphery of previously existing essential structures and systems. Our data are thus consistent with an evolutionary scenario in which the ancestral ribosome evolved the S12 protein cofactor, followed by gene duplication of the ancestral S12 domain resulting in the IF1 proteins. In this RNA-binding IF1 clade, bacterial and mitochondrial SSB OB-fold domains appear to be outliers. We note, however, that Escherichia coli SSB is also an RNA-binding protein and recognizes its own mRNA cooperatively with high specificity.⁶⁹

Two functionally distinct superfamilies of SH3 domains: Sm-like RNA-binding and signaling domains

SH3 domains and Sm-like domains share the same fold, and two prominent clades from our SH3 analysis are a cluster of RNA-binding Sm-like domains and a largely unresolved cluster of signaling domains (Figure 3(a)). The Sm-like superfamily includes several small nuclear ribonucleoparticle (snRNP) proteins that span all three domains of life: archaea, bacteria, and eukarya. Many of these domains are very divergent and previously limited interrelationships have only been found using sensitive sequence-profile methods.^70,71 It has been suggested that the ubiquitous eukaryotic Sm-like domains evolved from an earlier bacterial or archaeal ancestor.⁷¹ However, the bacterial domains and several archaeal domains appear derived given our inferred rooting, being nested within the eukaryotic domains, suggesting possible early horizontal transfer events between kingdoms.

Profile-based phylogenies differ from structure-based trees

Automated structure-based clustering methods, such as DALI,⁵ COMPARER,⁷² SSAP,⁷³ and STAMP,⁷⁴ are widely used, valuable tools for taxonomic analysis of protein domains based on structural similarity. For instance, the DALI and SSAP structure-based clustering methods have been used previously to classify the known OB-fold domains.^40,75 However, manual assessment is currently more successful than automated methods in detecting distant structural similarity between protein domains.²⁵ For this reason, the manually curated SCOP hierarchy is widely used as a standard for structure classification. The SCOP database is specifically intended to reflect the conformational similarities and evolutionary relationships among all structurally characterized protein domains, with the explicit consideration of their functions.⁶ With but one exception (the bacterial OB-fold SSBs), our profile-based phylogenies are entirely consistent with the SCOP hierarchy. In contrast, both the DALI⁴⁰ and SSAP⁷⁵ OB-fold structure-based dendrograms are considerably different from the SCOP classification at both the superfamily and family levels.

While the structure-based dendrograms correspond well with SCOP at the family level for most closely related domains, there are many exceptions. For example, in the DALI dendrogram,⁴⁰ tRNA-anticodon domains (RNA-binders) cluster with SSB DNA-binding domains, except for LysS RS, which clusters instead with a group of bacterial toxins (of a different SCOP superfamily). The cold shock domains (primarily ribosomal RNA-binders) cluster with a molybdenum-binding domain (of a different superfamily) and with two DNA-binding domains. Overall, the RNA-binding domains are polyphyletic, being interrupted by two clusters of bacterial toxins (different superfamily), a TIMP domain (another superfamily), and one cluster of ssDNA-binding domains. Similarly, DNA-binding domains are also polyphyletic, as there are two disjointed groups of DNA-binding domains interrupted by clusters of RNA-binding domains and domains from three other superfamilies. In their SSAP dendrogram, Kikugawa et al. identify four large clustered groups. RNA-binding domains are spread among groups 1, 2, and 4.⁷⁵ In group 4, RNA-binding tRNA-synthetase domains cluster with DNA-binding domains (including many ssDNA-binding SSBs). In group 1, other SSBs cluster with the RNA-binding Myf domains and with ribosomal RNA-binding IF1. In contrast, the bacterial and archaeal IF1s are found in group 2. Consequently, the most conspicuous pattern observed in the profile-based OB-fold phylogeny is absent in the structure-based dendrograms: domains do not cluster exclusively according to cellular function. Most notably, DNA-binding domains are found intermixed with RNA-binding domains and with domains from other families and superfamilies. Thus, the DALI and SSAP dendrograms are markedly different from our profile-based phylogeny and from SCOP at both the superfamily and the family level.

Profile-based phylogenetics may be expected to differ from purely structure-based methodologies for several theoretical reasons. First, the differences detailed above reinforce the principle that structural variation does not necessarily parallel sequence variation. Many heterogeneous protein sequences fold into similar structures, and significantly different structures may have similar sequences.²⁶ Second, due to the unsolved problem of the probability of structural convergence, pure structure-based methods cannot resolve homologous domains from analogous domains in the absence of additional information.^{13,15,17,18,22,26,76–80} Because a tree can always be constructed from non-homologous data, the existence of a structure-based dendrogram by itself does not provide necessary evidence for common ancestry.^81–83 Profile-based phylogenetics, on the other hand, provides evidence for domain homology from both statistically significant sequence-based E-values and by statistical jackknife support for stable clades. Third, an explicit, quantitative evolutionary model is necessary for specifying a legitimate evolutionary distance measure that is tree-additive and statistically consistent. Distance measures lacking these properties can result in misleading phylogenies.⁸¹ The phylogenetic interpretation of current structure-based clusterings is based on the qualitative principle that RMSDs may increase as domains diverge from each other over evolutionary time.^5,72 While several authors have proposed quantitative evolutionary models relating the change in RMSD with evolutionary time,^84–86 these models are currently not employed by structure-based clustering methods for inference of evolutionary distances. Thus, structure-based clustering methods produce dendrograms that generally reflect overall structural similarity rather than evolutionary relationships.

Support for divergent versus convergent evolution of domain superfamilies

The phylogenetic results reported here indicate that each stable clade of domain families, consisting of domains related by an interconnected web of statistically significant sequence-profile scores, is derived from a common ancestral domain. In principle, however, the functionally correlated clustering observed in our trees could be explained by convergent evolution. Convergence could produce the observed phylogenetic patterns if similar amino acid propensities are required for important structural features or if specific amino acid patterns are necessary for biochemical function.

Recent evidence from in vitro evolution studies, however, suggests that the sequence requirements necessary for specifying a given fold with a given function are extremely low. The high-resolution structure³² of a zinc-binding domain (the Keefe–Szostak domain) derived via directed protein evolution³³ has recently been solved. This artificial protein adopts a known, natural protein fold, the treble clef finger zinc-binding motif.^34,35,87 Thus, the natural treble clef domains and the artificial Keefe–Szostak protein are clearly bona fide examples of both structural and functional convergent evolution.³⁴ The SCOP structure database contains 34 known natural treble clef domains with less than 40% mutual sequence identity. Neither pairwise BLASTP nor COMPASS profile comparisons of the Keefe–Szostak protein sequence with these known treble clef finger sequences result in any significant E-values (all E-values are greater than 0.30 and 0.37, respectively). Thus, in this case of true fold convergence, structural and functional requirements have no detectable influence on sequence similarity, even using sensitive profile-based techniques.

To test specifically whether the domain clustering in our analysis could be due to structurally necessary residue frequencies, we performed an all-against-all profile–profile analysis among the SH3 domains, the OB-fold domains, and representatives of a similar small β-barrel fold, the PDZ domain (Figure 1(a)). Structurally, the SH3 fold is an OB-fold with a single β-strand permutation³⁹ (see Figure 1(b)). Similarly, the PDZ fold can be considered an OB-fold with the C-terminal β-strand 5 deleted. Notably, the β-strands of an SH3 domain can be permuted, in all possible combinations, with retention of tertiary structure,⁸⁸ indicating that the order of secondary structural elements does not obligatorily determine the protein fold. Thus, these different β-barrel folds should have largely similar structural requirements in terms of amino acid sequence and propensity, irrespective of their differences in connectivity. Nonetheless, we were unable to detect any significant profile sequence similarities among the domains from these three folds, and thus observed no stable cross-clustering between folds in the global phylogenetic analysis. In fact, over half of the domains included in this analysis have no significant relationships with any of the stable clades, even within the same fold (see Supplementary Data). Therefore, phylogenetic clustering with functionally or structurally similar domains is not a necessary result of sharing a similar protein fold.

Domain clustering in our analysis could also arise from functionally required residue propensities rather than from divergence. The OB-fold, SH3, and PDZ superfolds further share the biochemical function of binding oligomeric substrates, such as oligonucleotides, oligosaccharides, and oligopeptides. These folds bind their ligands with a similar interface on an analogous side of their respective β-barrels, primarily involving the three β-strands common to all three folds (corresponding to β-strands 1, 2, and 3 of the OB-fold,⁸⁹ shown in red, orange, and yellow, respectively, in Figure 1). If convergent evolution were responsible for the functionally correlated clustering that we observe, it might be anticipated, for example, that RNA-binding SH3 domains would cluster with RNA-binding OB-folds, or that peptide-binding PDZ domains would cluster with peptide-binding SH3 signaling domains. Nevertheless, as described above, this possibility is not observed. Moreover, the many domains that completely lack any significant relationships in fact have very similar functions to the domains found in the phylogenies (see Supplementary Data). As one example, only the N-terminal OB-fold domain of the α subunit of TEBP clusters with the telomeric domains (the red clade in Figure 2). In contrast, the other two ssDNA-interacting OB-fold domains in the TEBP complex, which specifically bind the same telomeric substrate, both lack significant relationships with any other domains. Thus, sharing a similar function and a similar fold does not assure functionally correlated clustering, providing further evidence that functional requirements are unlikely to be responsible for the stable clustering of domains in the phylogenies.

Functionally driven structural convergence, by definition, requires similarity of functional structures. However, other than adopting a small β-barrel fold, these domains differ markedly in the structural features that are necessary for performing their cellular function. This observation is highlighted by the DALI and SSAP OB-fold structure-based dendrograms discussed earlier,^40,75 which frequently cluster functionally dissimilar domains and segregate functionally similar domains.

The telomeric ssDNA-binding OB-fold domains provide a representative example of functionally similar structures that adopt very different conformations and that have different amino acid residue requirements (Figure 4). The Cdc13, Pot1, and TEBP proteins share many biochemical similarities. They all bind their respective G-rich, single-stranded telomeric DNA with high specificity and affinity, and they share common biological functions in mediating chromosome capping, end-protection, and telomere-length regulation.^90–92 However, the high-resolution structures of these proteins complexed with ssDNA show the telomeric substrates in very different relative conformations and interacting with different regions of the canonical binding interface of the OB-fold β-barrel.^93–96,115 The residue composition found at the protein–ssDNA binding interface is likewise dissimilar: predominantly aromatic in Cdc13,⁹⁴ hydrophilic in Pot1,^93,115 and hydrophobic in TEBP.^95,96 In nucleic acid-binding OB-fold domains, the β1-β2, β2-β3, and β4-β5, loops are functionally critical for substrate recognition,⁸⁹ yet in the telomeric domains these loops are some of the most variable features in sequence, length, and conformation⁹⁴ (Figure 4). In fact, the segment of strongest sequence-profile similarity common to each of the telomeric domains maps to a “scaffolding” region of the OB-fold β-barrel⁸⁹ that does not interact with the telomeric ssDNA (primarily the region of β-strand 4 opposite the ssDNA-binding interface; see Figure 4). Analogous arguments can be constructed for the other clustered OB-fold and SH3 domains, and the differences in functionally important structural details increase when considering broader functional families, such as all the ssDNA-binding, all the RNA-binding, or all the nucleic acid-binding OB-fold domains. Thus, the functionally important structural features of these domains have not converged, indicating that common ancestry is responsible for the significant sequence-profile similarity and consistent phylogenetic clustering of these protein domains.

Figure 4.

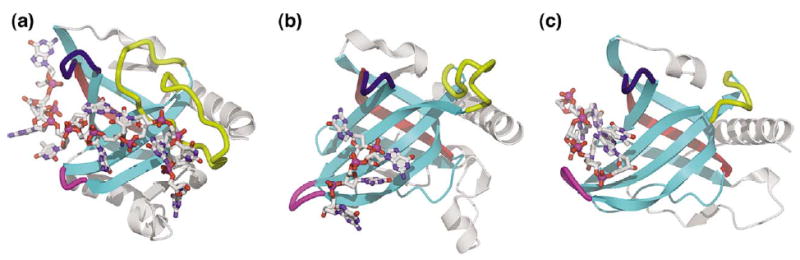
Comparison of the functionally critical telomeric ssDNA-binding OB-fold domains of three telomeric end-binding proteins: (a) Saccharomyces cerevisiae Cdc13-DBD,⁹⁴ (b) O. nova TEBP α OB1,⁹⁶ and (c) Schizosaccharómyces pombe Pot1 OB1.¹¹⁵ Proteins are displayed in the same orientation based upon structural superposition. The β-strands of the canonical OB-fold β-barrel are shown in cyan. The functionally important yet dissimilar β1-β2, β2-β3, and β4-β5 loops of the OB-folds are indicated in magenta, yellow, and blue, respectively. The telomeric ssDNA ligands, represented in ball-and-stick, adopt diverse conformations and interact with different regions of the canonical OB-fold binding cleft. OB-fold β-strand 4, the region of greatest statistically significant sequence-profile similarity common to the domains, yet distant from the telomeric ssDNA-binding site, is highlighted in red.

Profile-based phylogenetic methods provide an objective approach for detecting homology of protein folds in difficult cases of extreme divergence when domains cannot even be aligned with confidence, since the relationships depicted in the phylogenies are based only upon E-values. The predicted ancestral domain at the inferred root of most of these stable and significant clades must have been present in the last common ancestral population, since most of the branches span all three domains of life. For example, our analysis indicates that the large nucleic acid-binding OB-fold clade consists of homologous archaeal, bacterial, and eukaryotic domains, all derived from an original ancestral nucleic acid-binding OB-fold domain. In the absence of sequence similarity, earlier analyses of the nucleic acid-binding OB-fold domains had alternatively hypothesized various combinations of divergent and/or convergent evolutionary explanations for the structural and functional similarities.^21,39–45 These protein domains exhibit a twin, nested hierarchy of profile-sequence similarity recapitulated by functional similarity, which provides further evidence for the homology of the observed clusters. By extending phylogenetics into the twilight zone, profile-based phylogenetics deepens our foundation for understanding the function, structure, and evolutionary pathways of a fundamental unit of molecular evolution, the protein domain.

Theory

Our distance-based phylogenetic analysis is based on the principle that the expected Karlin–Altschul E-value for a comparison between two sequences or alignments increases monotonically with evolutionary distance. Our derivation of an E-value-based evolutionary distance metric proceeds according to the following steps. We first present a novel equation for the change in the expected similarity score of two homologous sequences as a function of evolutionary time, given an arbitrary BLOSUM-style scoring matrix and an arbitrary evolutionary amino acid rate matrix. However, because this formulation cannot be solved analytically for evolutionary time, an accurate exponential approximation is then proposed by assuming homogeneous amino acid transition rates. Combining this latter approximation with the Karlin–Altschul equation, which relates E-values to similarity scores, we obtain a simple transform of E-values which gives an evolutionary distance metric that is tree-additive and is a linear function of evolutionary time (see equation (3)), features required for consistent distance-based phylogenetic inference. Finally, we show that simulations support the use of this approximate distance metric in realistic cases even when our assumptions are relaxed, for instance, when amino acid transition rates are unequal, when rates vary between sites, and when sequences evolve insertions and deletions.

Evolutionary assumptions

We make several common, general evolutionary assumptions in the following derivation.^81,97,98 Substitutions at all positions in a protein sequence are mutually independent, and they change according to the same time-reversible, time-continuous Markovian model. Each amino acid has a constant instantaneous transition rate which is invariant with respect to its position in the sequence. While others have proposed models for sequence change involving insertions and deletions,^99,100 we do not explicitly consider indel evolution. The units of evolutionary time are arbitrary and may correspond to real time or to organismic generations. The evolutionary distance d_i,j between two sequences i and j is a linear function of evolutionary time and is proportional to the total number of actual amino acid substitutions which have occurred in both sequences since their divergence from a common ancestor.

Formulation of expected log-odds similarity score as a function of evolutionary time

First, we must obtain a relationship for how the similarity score for two aligned sequences will decrease with time as the sequences evolve. Given an instantaneous amino acid rate matrix A and its diagonal matrix of equilibrium amino acid frequencies Π, the expected log-odds similarity score 〈S(t)〉 for two sequences of length L that have diverged from a common ancestor over an evolutionary time t is given by:

$$\langle S(t)\rangle =L{1}^{\prime }[(S\mathrm{\Pi })\odot e^{At}]1$$ (1)

where 1 is an appropriately dimensioned column vector of ones, and X⊙Y denotes the Hadamard, element-wise matrix product of matrices X and Y (see Appendix A). It is useful to consider the special case in which the sequences evolve according to the instantaneous rate matrix implicit in the log-odds scoring matrix S (i.e. when S is a function of A).¹⁰¹ The expected log-odds score given an arbitrary BLOSUM scoring matrix and its implicit transition matrix is given by:

$$\langle S(t)\rangle =L{1}^{\prime }[(S\mathrm{\Pi })\odot {\{\mathrm{\Pi }\hspace{0.17em}exp(S)\}}^{t/t_0}]1$$ (2)

where exp(X) denotes the element-wise exponentiation of matrix X. The constant t₀ is characteristic for each scoring matrix and represents the time elapsed since the divergence from a common ancestor for the sequences used in the construction of the scoring matrix. The maximum likelihood estimate is given by:

$${\widehat{t}}_0=-\text{tr(}\mathrm{\Pi }\hspace{0.17em}ln\hspace{0.17em}[\mathrm{\Pi }\hspace{0.17em}exp(S)])$$

where tr X is the matrix trace of X.

The change in similarity score 〈S(t)〉 is well approximated by exponential decay

Given a known similarity score S(t) for two sequences, we wish to estimate the time since their divergence. However, the above relationships (equations (1) and (2)) are relatively complicated expressions that cannot be solved analytically for evolutionary time t. As a first approximation we make the Jukes–Cantor assumption that all amino acid transition rates are equivalent. In this case the expected similarity score 〈S(t)〉 given by equation (2) will decay exponentially, regardless of the specific log-odds matrix used (see Appendix B):

$$\frac{\langle S(t)\rangle }{L}=\beta e^{\alpha t_{i,j}}+\zeta$$

This equation can be solved readily for t_i,j, a result that echoes the well-known Poisson-correction method for calculating evolutionary distances from sequence identity first introduced by Zuckerkandl & Pauling.²³ To test the validity of this approximation, we fit an exponential decay to the change given by equation (2) with the unequal rates implied by a BLOSUM62 matrix. In fact, equation (2) can be approximated well by exponential decay (regression coefficient of 0.99972; Figure 5), and exponential fits for the entire range of available BLOSUM matrices (BLOSUM30 to BLOSUM100) are equally good.

Figure 5.

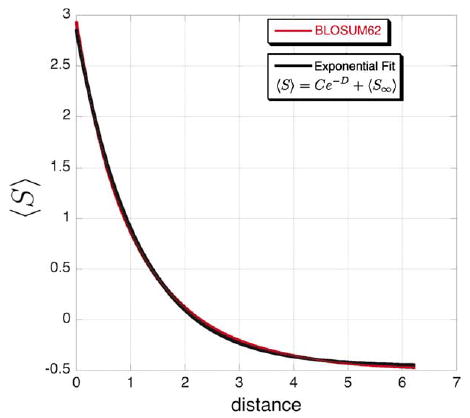
Exponential decay approximates the change in expected log-odds score with time. The red line is a plot of the exact change in the expected log-odds score using a BLOSUM62 matrix and its implicit instantaneous rate matrix as given by equation (2). The black line is a χ² best fit of equation (2) using a BLOSUM62 matrix to an exponential decay (〈S〉=3.31 e^−0.8906−0.460, R = 0.99972).

Evolutionary distances inferred from E-values

The change in expected E-value with evolutionary time can be obtained by combining the above exponential decay equation for similarity scores with the Karlin–Altschul equation,^36,102,103 which relates similarity scores to E-values (Appendix C). This leads to the following evolutionary distance metric as a function of the E-value:

$$\begin{array}{l}{d}_{i,j}=-ln\left(\frac{-ln\hspace{0.17em}{E}_{i,j}+ln\hspace{0.17em}{E}_{\infty }}{-ln\hspace{0.17em}{E}_{\text{self}}+ln\hspace{0.17em}{E}_{\infty }}\right)\\ =-ln\left(\frac{-ln\hspace{0.17em}{E}_{i,j}+\gamma }{-ln\hspace{0.17em}{E}_{\text{self}}+\gamma }\right)\end{array}$$ (3)

where E_∞ is the expected E-value after an infinite length of evolutionary time, E_self is the expected E-value for scoring a sequence or alignment against itself, and γ is the Euler-Mascheroni constant (γ ≈ 0.57722; see Appendix C). Our E-value-based distance metric is thus an extension of similar metrics previously proposed for similarity scores.¹⁰⁴

E-value evolution equations fit to simulated sequence data

Protein sequence data generated from simulated evolution was used to test the validity of the equations derived above. Protein sequences were evolved using the Seq-Gen¹⁰⁵ and Dawg¹⁰⁶ computer programs under various evolutionary models. For Seq-Gen, the evolutionary models included JTT, PAM, BLOSUM, WAG, and mtREV. Unlike Seq-Gen, Dawg implements several models of indel evolution and distributes indel lengths according to a biologically relevant power law. For Dawg simulations we evolved “coding sequences” under several evolutionary models (e.g. JC, K2P, HKY, and F84), restricting indels to be in-frame, and translated the resulting sequences (ignoring stop codons). We used parameters that specify a geometric distribution, which is approximately equivalent to the affine scoring model with gap-open and gap-extension penalties since each insertion or deletion event adds or removes a geometrically distributed number of bases.

For the pairwise sequence case, two sequences (initially 100 amino acid residues in length) were evolved for increasing amounts of time and were scored with BLASTP⁴⁷ using the NCBI bl2seq utility. For the profile (multiple sequence alignment) case, two families of sequences (initially 100 aa in length) were evolved along a given tree for increasing amounts of time and were scored with COMPASS.⁵⁰ In all cases, scoring was performed with the BLOSUM62 matrix, the default for COMPASS and BLASTP. Regardless of the particular evolutionary model, all simulation data fit equations (C3) and (3) well, with little overall difference (Figure 6). Transformed E-values scale approximately linearly with evolutionary distance, with the variance increasing dramatically at large evolutionary distances as expected from a Poisson process.¹⁰⁷ Since the simulations use various evolutionary models, including indel evolution, rate variation across sites, and unequal amino acid rates given by various instantaneous rate matrices, our theoretical treatment appears relatively robust to violations of our evolutionary assumptions.

Figure 6.

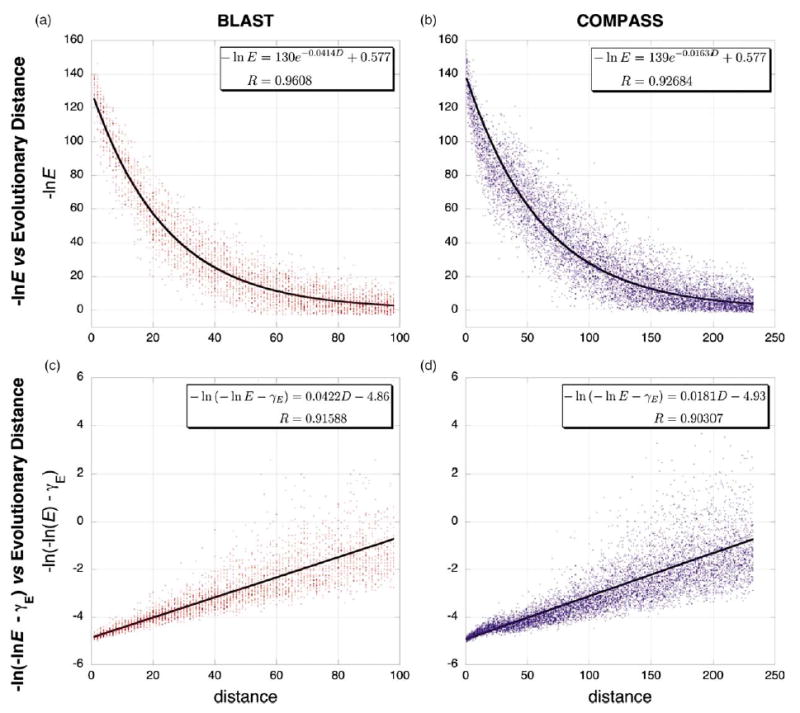
Theoretical fits of the E-value/distance relationship from simulated protein evolution data. Representative data from simulated protein evolution of pairwise sequences is shown at left in red (a) and (c) and of sequence alignments is shown at right in blue (b) and (d). (Dawg, JC nucleotide evolution model, gamma rate variation α=1, negative binomial model of indel evolution, relative insertion probability=deletion probability =0.04). The upper two graphs (a) and (b) plot ln(E) versus evolutionary distance and show data fit to equation (C3), where 〈S_cen〉 is given by equation (2) and 〈S_∞ 〉=γ. The lower two graphs (c) and (d) show the same data, plotted as ln(−ln E−γ) versus evolutionary distance and fit with equation (4). The constant ln C was not fit but was estimated as described in Materials and Methods. Because the variance increases with evolutionary distance in the latter two plots, these fits were weighted by the inverse of the evolutionary distance (analogous to weighting by the inverse of evolutionary distance in the phylogenetic least-squares analyses). In all graphs, the largest plotted distance corresponds to an E-value of 0.1.

Materials and Methods

Sequence profile construction and scoring

All structurally characterized OB-fold, SH3, PDZ, and treble clef finger³⁵ domains with 40% or less sequence identity were obtained from the ASTRAL SCOP 1.65 protein domain sequence database^†.⁵¹ A database of multiple sequence alignments of each of these domains was constructed as described.⁴⁵ The sequence of each domain was searched against the non-redundant protein database with BLASTP.⁴⁷ Sequences returned with BLASTP E-values <10⁻¹⁰ were aligned with CLUSTAL¹⁰⁸ or DIALIGN,¹⁰⁹ and the alignments were cropped to the limits of the original query domain. As listed in Supplementary Data, the final alignment database contains 93 OB-fold, 83 SH3, one PDZ, and 34 treble clef domain alignments. PSI-BLAST searches were performed with NCBI’s blastpgp 2.2.6^47,110 for five iterations using an the default E-value cut-off of 0.001 for inclusion of sequences in the profiles.⁴⁷ This less stringent cut-off biases the results in favour of PSI-BLAST relative to COMPASS in terms of detecting remote homologs, while also resulting in a much higher PSI-BLAST false positive rate.^50,111

For each fold we performed an all-against-all scoring of each domain alignment against all others using COMPASS⁵⁰ with default parameters, resulting in pairwise matrices of 4278 OB-fold and 3403 SH3 Bonferroni-corrected E-values. Each of the natural treble clef domain alignments were scored against the artificially evolved treble clef Keefe-Szostak domain^32,33 with both COMPASS and BLASTP.

E-value conversion to evolutionary distances

For converting E-values to evolutionary distances, we used the following version of equation (3):

$$d_{i,j}=-ln(-ln\hspace{0.17em}{E}_{i,j}-\gamma \text{)}+ln\mathrm{\hspace{0.17em} }C$$ (4)

We estimated the constant ln C as the arithmetic average of ln(−ln E_self−γ) for all sequences or alignments under consideration. To avoid negative pairwise distances, all rescaled values less than zero were set to zero. Equation (4) is undefined for E>e^−γ ≈ 0.561. To constrain distances to defined values and to minimize spurious clusters in the phylogenetic analysis due to noise, we set an effective maximum evolutionary distance corresponding to an E-value of 0.01 for all E-values greater than 0.01 (after a Bonferroni correction, vide infra^37,112), a point conventionally denoting lack of statistical significance.

In order to perform valid tests for statistically significant sequence similarity, the E-values must be corrected for multiple tests. In our all-against-all comparison, each profile is scored multiple times, once against every profile contained in our profile database. In some programs such as BLAST, this correction is performed by setting the target sequence length parameter (n in the Karlin-Altschul equation) equal to the total length of the database being searched (see equations (C1) and (C2)). However, we correct for multiple tests by application of a simple Bonferroni correction to the E-values,^37,112 independently of the m and n sequence length parameters. As opposed to setting n to the total database size, a Bonferroni correction is more appropriate here as the relevant null hypothesis is that all the single-domain profiles in our database are a priori equally unlikely to be homologous.¹¹² The Bonferroni correction also maintains the symmetry necessary for a distance metric, such that d_i,j=d_j,i for two sequences i and j.

Phylogenetic analysis

Weighted least-squares phylogenetic analyses of the transformed distance matrices were performed using PAUP*,¹¹³ weighting by the inverse of the distance. This weighting scheme approximates weighting by the inverse of the variance, as needed for heteroscedastic data. Other distance-based algorithms (including neighbour-joining, BIONJ, minimum evolution, and UPGMA) produced trees with similar topologies. Because bootstrapping of the data (the domain alignments) is inapplicable to profile analysis, first order taxon jackknifing ^55,56 was used to estimate the robustness of the inferred trees to data perturbation. Taxon jackknifing involves deleting a taxon, re-performing the phylogenetic analysis for all taxa, and calculating the consensus tree from all analyses. The jackknife support (JS) for a given clade is the percentage of all jackknifed trees displaying that clade, not counting the deleted taxon. We estimate the position of the root as the midpoint of each tree, which is dependent upon a rate constancy assumption weaker than the molecular clock assumption. All inferred trees have topologies similar to the ultrametric UPGMA trees. Because the UPGMA method assumes rate constancy, the molecular clock assumption has support in our analyses (somewhat surprisingly) as a rough approximation. Furthermore, simulations have shown that root inference using a molecular clock assumption is relatively accurate and insensitive to heterogeneous evolutionary rates.¹¹⁴

Scripts and programs for performing the all-against-all COMPASS analysis and for conversion of the resulting E-values to a PAUP*-formatted distance matrix file are available from authors upon request.

Appendix A

We consider an arbitrary BLOSUM-style log-odds matrix S,¹¹⁶ though the results can be modified easily to apply to PAM matrices. The entries in the BLOSUM-style log-odds matrix S have pseudo-units of unscaled natural logarithm nats (and not multiples of bits, as is common). For an alignment of two or more sequences, the log-odds score S is given by:

$$S=L{1}^{\prime }[S\odot F]1$$

where F is the matrix of pairwise amino acid frequencies in the alignment. Given our evolutionary assumptions (i.e. independent sites, no rate variation among sites, time-reversibility), the frequency matrix F is given by F=P(t)Π, where P(t) is an Markovian (stochastic) amino acid transition matrix at time t. An expected transition matrix can be calculated from its corresponding instantaneous rate matrix A by 〈P(t) 〉=e^At. Substitution then yields equation (1).

If we accept the implicit assumption that the sequence blocks used to construct a given BLOSUM matrix¹¹⁶ have each evolved from one ancestral sequence over a common evolutionary time t₀,¹⁰¹ then we can infer the corresponding instantaneous rate matrix.⁸¹ An amino acid transition matrix T = P(t₀) for a BLOSUM matrix can be calculated from:

$$\mathrm{T}=\mathrm{\Pi }\hspace{0.17em}exp(S)$$ (A1)

Then, the maximum likelihood estimates of A and t₀ are given by:

$$\widehat{A}=\frac{ln\hspace{0.17em}T}{t_0}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{t}}_0=-\text{tr}(\mathrm{\Pi }\hspace{0.17em}ln\hspace{0.17em}T)$$

where trX denotes the matrix trace of X. Substitution gives equation (2).

Appendix B

In the Jukes–Cantor model, where all amino acid transition rates are equivalent, there are only two different terms in the amino acid transition matrix P, one for the diagonal elements and one for the off-diagonal elements:⁸¹

$$p_{\text{D}}=p_{i,j}=\frac{1}{20}+\frac{19}{20}{e}^{-20\alpha t}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if\hspace{0.17em}}i=j$$

$$p_{\text{O}}=p_{i,j}=\frac{1}{20}-\frac{1}{20}{e}^{-20\alpha t}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if\hspace{0.17em}}i\ne j$$

The expected average score per amino acid then is given by:

$$\begin{array}{l}\frac{\langle S(t)\rangle }{L}=\sum _i{s}_{i,i}{p}_{i,i}{\pi }_i+\sum _i\sum _{j\ne i}{s}_{i,j}{p}_{i,j}{\pi }_i\\ =\sum _i{s}_{i,i}{p}_{\text{D}}{\pi }_i+\sum _i\sum _{j\ne i}{s}_{i,j}{p}_{\text{O}}{\pi }_i\end{array}$$ (B1)

Each element π_i, in the equilibrium frequency matrix Π is equal to 1/20, and p_D and p_O are constants for a given time. Thus, both can be removed from the summations. After rearrangement, equation (B1) can be reduced to an exponential decay:

$$\begin{array}{l}\frac{\langle S(t)\rangle }{L}=\frac{p_{\text{D}}}{\text{20}}\sum _i{s}_{i,i}+\frac{p_{\text{O}}}{\text{20}}\sum _i\sum _{j\ne i}{s}_{i,j}=\delta p_{\text{D}}+\varepsilon p_{\text{O}}\\ =\frac{\delta }{20}+\frac{19\delta }{20}{e}^{-20\alpha t}+\frac{\varepsilon }{20}-\frac{\varepsilon }{20}{e}^{-20\alpha t}\\ =\frac{\delta }{20}+\frac{\varepsilon }{20}+\left(\frac{19\delta }{20}-\frac{\varepsilon }{20}\right)e^{-20\alpha t}=\beta e^{-20\alpha t}+\zeta \end{array}$$

where:

$$\beta =\text{(19}\delta -\varepsilon )/20\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\zeta =(\delta +\varepsilon )/20$$

$$\delta =\text{tr\hspace{0.17em}}S/20\hspace{0.17em}=\sum _i{s}_{i,i}/20$$

$$\varepsilon =1^{\prime }S1/20-\delta =\sum _i\sum _{j\ne i}{s}_{i,j}/20$$

Appendix C

The relationship between E-values and the similarity score obtained from a alignment of sequences is given by the Karlin–Altschul equation:³⁶,¹⁰²,¹⁰³

$$E=kmn\hspace{0.17em}{e}^{-S}=e^{-(S-ln\hspace{0.17em}kmn)}$$ (C1)

where the individual scores in the sum score S are in units of nats, m is query sequence length, n is target sequence length, and k is the Karlin–Altschul constant. The negative natural logarithm of the E-value provides a centered similarity score, normalized for sequence lengths:³⁷

$$S_{\text{cen}}=S-ln\hspace{0.17em}(kmn)=-ln\hspace{0.17em}E$$ (C2)

Assuming that all amino acid transition rates are equivalent (as in the Jukes–Cantor approximation), the change in the expected similarity score 〈S_cen〉 with increasing evolutionary time t_i,j can be approximated by exponential decay:

$$\langle S_{\text{cen}}\rangle =C\hspace{0.17em}{e}^{-\alpha t_{i,j}}+\langle S_{\infty }\rangle$$ (C3)

$$d_{i,j}=\alpha t_{i,j}=-ln(\langle S_{\text{cen}}\rangle -\langle S_{\infty }\rangle )+lnC$$ (C4)

where d_i,j is in arbitrary units. 〈S_∞〈 is the expected centered score at an infinite evolutionary distance and corresponds to the average score of two random sequences. In equations (C1) and (C2), 〈S_∞〈 is equal to the Euler-Mascheroni constant γ, the mean of an extreme value distribution with location parameter = 0 and shape parameter = 1.¹⁰²,¹¹²,¹¹⁷ The constant lnC is the y-intercept, and can be found from a self score (〈S_self〈 = 〈S_i,i〈) and setting d_i,j = d_i,i = 0, giving:

$$ln\hspace{0.17em}C=ln(\langle S_{\text{self}}\rangle -\langle S_{\infty }\rangle )$$

Thus, substitution of equation (C2) and γ into equation (C4) yields equations (3) and (4).