Molecular dynamics simulations of unfolding and refolding of a β-hairpin fragment of protein G

Abstract

We have studied the unfolding and refolding pathway of a β-hairpin fragment of protein G by using molecular dynamics. Although this fragment is small, it possesses several of the qualities ascribed to small proteins: cooperatively formed β-sheet secondary structure and a hydrophobic “core” of packed side chains. At high temperatures, we find that the β-hairpin unfolds through a series of sudden, discrete conformational changes. These changes occur between states that are identified with the folded state, a pair of partially unfolded kinetic intermediates, and the unfolded state. To study refolding at low temperatures, we perform a series of short simulations starting from the transition states of the discrete transitions determined by the unfolding simulations.

Because straightforward molecular dynamics typically can examine trajectories only tens of nanoseconds in duration, the milliseconds needed to fold even small proteins are far too long to simulate directly. A clever stratagem that allows progress to be made in studying conformational changes in proteins is to instead simulate unfolding, under conditions (high temperature, acid pH, high denaturant) such that the unfolding reaction rate is accelerated into an accessible range (1–7). These simulations have yielded insights into the initial stages of unfolding to an expanded conformation, which is assumed to reflect the later stages of refolding (8, 9). The inferred transition state (TS) for this process is in agreement with experimental determinations of the folding TS under physiological conditions (10). Important open questions pertain to the relationship between extremely rapid unfolding at 500 K and the much slower refolding process at physiological temperatures, as well as the underlying physical reason for the surprisingly good agreement between high- and low-temperature TSs.

Here we address these questions by using high-temperature unfolding to study the C-terminal β-hairpin fragment of protein G, whose refolding kinetics have been well characterized by Munoz et al. (11, 12). This 16-residue peptide folds rapidly and cooperatively to a conformation with defined secondary structure and a packed hydrophobic cluster of aromatic side chains. Because the β-hairpin is small, its unfolding can be studied in much more detail (13, 14) than the larger proteins whose high-temperature unfolding have been examined previously (1–7). By using simulations a few ns in duration, we have studied complete unfolding events at temperatures as low as 400 K, and the initial stages of unfolding at 350 and 370 K (77°C and 97°C). The availability of many simulations over a range of temperatures permits the determination of the complete unfolding pathway. We find that unfolding occurs in discrete steps, as discussed below.

By using this unfolding pathway, we can test the hypothesis that refolding under physiological conditions can occur by the reverse of the high-temperature unfolding mechanism. Although a complete simulation of refolding is not possible, we instead can simulate each step of the refolding reaction at 27° C, starting from a TS conformation as determined from high-temperature unfolding. We use analysis techniques that allow us to identify the TSs for the various transitions of the unfolding pathway (17–19). Even for slow kinetic processes, the actual passage through the TS can be hundreds to thousands of times faster than the overall folding rate; most of the folding time therefore is spent waiting for the fluctuations to reach the TS (20). By identifying candidate TS conformations from fast high-temperature simulations, we can bypass this time-consuming part of the simulation.

Methods

Molecular Dynamics Method.

We simulate unfolding of the C-terminal domain (GEWTYDDATKTFTVTE) of protein G by using namd2 (21) with charmm19 potentials (22). The initial state of the peptide is taken from the first model conformation of the full protein G in Protein Database entry 1GB1. The hairpin is placed in a 60-Å diameter spherical box, surrounded by tip3p (23) water at a density of 0.87 g/cm³ (2, 3) that has been pre-equilibrated at 300 K. Simulation time steps are 2 fs, with shakeh (21, 24) constraints used for protein and water hydrogens. Each run is started with a 50-ps equilibration step starting from a Maxwell velocity distribution at 300 K, followed by an instant temperature jump through velocity rescaling to a higher temperature; rescaling was continued at this temperature every 10 time steps (20 fs). To verify that the native state is stable in our simulation method, we simulated 1 ns at 300 K and 3 ns at 350 K. We found that the hairpin remained in a native-like fold (with frayed ends; refs. 11 and 12) with an rms deviation from the native state of 1.5 Å at 300 K and 1.7 Å at 350 K.

Order Parameters: Definition of N_HB and R_core.

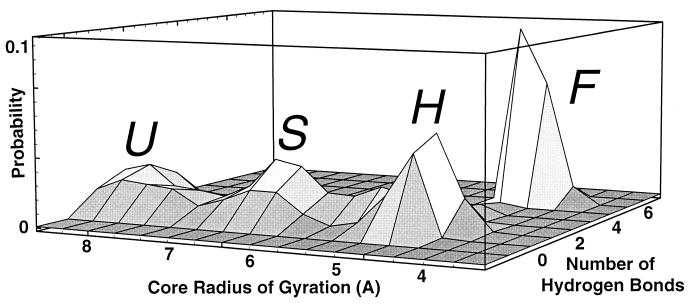
To classify a given conformation one must choose some order parameter(s) that can differentiate the states of the peptide. Natural choices involve descriptors of the secondary and tertiary structure, such as the number of hydrogen bonds N_HB and the size of the hydrophobic core R_core, respectively. Here, we define a hydrogen bond to exist if the carbonyl oxygen and amide hydrogen of the peptide backbone are within 2.5 Å. N_HB is defined as the number of backbone-backbone hydrogen bonds, excluding the two at the frayed end of the hairpin. R_core is the radius of gyration of the heavy atoms in the three aromatic side chains that make up the hydrophobic cluster and reflects the compactness and hence solvation of this cluster. A contact is defined to exist if the α carbons are with 6.5 Å. States are defined based on the probability distribution of conformations vs. the order parameters N_HB and R_core (see discussion below and Fig. 4).

Figure 4.

Probability distribution of conformations sampled from six 400-K unfolding trajectories, plotted vs. number of hydrogen bonds (N_HB) and core radius of gyration (R_core). The four distinct maxima correspond to the states F, H, S, and U. States were chosen to correspond to the probability maxima in the cumulative probability distribution shown here. For Fig. 3, the U, S, and H states were discriminated from each other by the core radius of gyration R_core:U if R_core > 7 Å; S if 6 Å ≤ R_core ≤ 7 Å; H if R_core < 6 Å and less then six native contacts (equivalent to three native hydrogen bonds); and F if R_core < 6 Å and greater than or equal to six native contacts (equivalent to N_HB ≥ 4).

Unfolding Trajectories

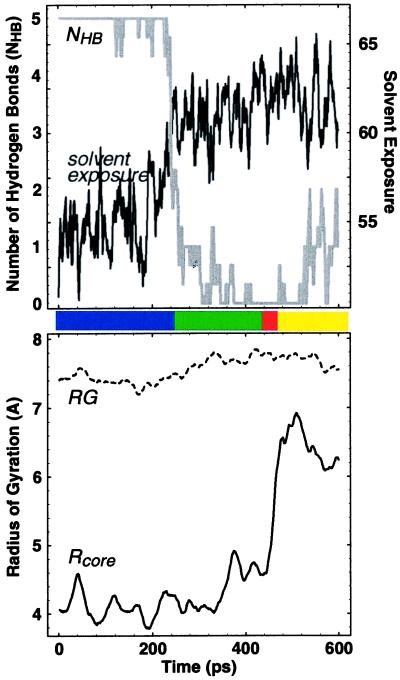
To explore the unfolding pathway of the β-hairpin, we have computed 22 unfolding trajectories at temperatures ranging from 350 K to 900 K, of up to 3 ns in duration. Each trajectory is an all-atom molecular dynamics simulation with explicit solvent (21) (see Methods for details). The initial conformation of the peptide is its native structure in the full protein G as determined by NMR (25), which is characterized by a hydrophobic cluster of three aromatic residues [tryptophan (W43), tyrosine (Y45), and phenylalanine (F52)] packed against each other, and a valine (V54) that is buried below the tryptophan side group. At temperatures above 450 K, few-ns trajectories typically reach a completely unfolded state; at lower temperatures only partial unfolding typically is observed during a few ns. Taking all of the simulations together, we find that unfolding always occurs as a reproducible series of discrete events (shown for a single trajectory in Figs. 1–3) that define a high-temperature ünfolding pathway, which we describe next.

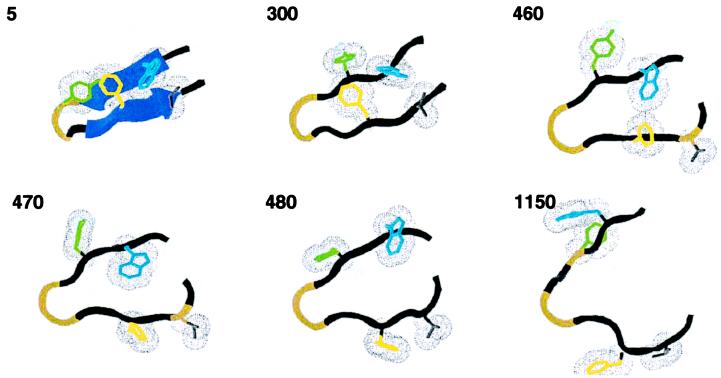
Figure 1.

A typical unfolding trajectory at 400 K demonstrates discrete unfolding steps. β-sheet hydrogen bonds (if formed) are shown as sheets, and the hydrophobic core is shown in wire frame with van der Waals radii (Trp red, Phe blue, Tyr purple, Val gray). The time in ps is given in the upper left of each frame.

All simulations begin with a rapid fraying of the ends of the hairpin, which occurs within a few ps of the start of each trajectory. The hydrophobic cluster remains well packed, and the secondary structure between the core and the turn remains intact. This frayed state persists for approximately half a ns (533 ± 444 ps at 400 K, see Table 1 for 500-K data), and for a few ns or more at 350 K (see Fig. 3 for a summary of all of the trajectories). We identify the ensemble of such conformations with the folded state F of the peptide, consistent with NMR evidence (25) and theoretical results (11, 12) that the native state includes such fluctuations. Here and below, we use the term “state” to refer to a rapidly interconverting population of conformations with specific conformational attributes.

Table 1.

Mean first passage time (±SD) for the unfolding reactions at 400 K and 500 K

Transition	Time at 400 K in ps	Time at 500 K in ps
F → H	533  ±  444 (4)	408  ±  336 (8)
H → S	177  ±  87 (7)	87  ±  66 (7)
S → U	54  ±  45 (4)	51  ±  38 (11)

The number of transitions in the data set is given in parenthesis. 

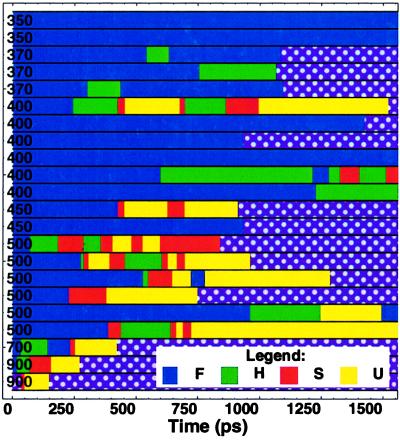
Figure 3.

Summary of the 22 unfolding trajectories. The color denotes the state (F blue, H green, S red, and U yellow). See Fig. 4 caption for details of the classification of conformations into these four states. The 400-K trajectory used in Figs. 1 and 2 is the first 400-K trajectory in this chart.

The first discrete event in unfolding is the complete loss of hairpin secondary structure (i.e., backbone-backbone hydrogen bonding), which occurs after a variable period of time spent in the frayed state. Interstrand hydrogen bonds suddenly break and are replaced by hydrogen bonds with the surrounding water. The valine side group is released from the core. Despite these changes, the hydrophobic cluster remains intact. Conformations with this character typically persist for hundreds of ps at the temperatures we studied (177 ± 87 ps at 400 K) and define the H (hydrophobic core) state.

The second conformational change observed is the dissolution of the hydrophobic core, which occurs as two discrete steps that occur in rapid succession. First, in a process that takes only a few ps, several water molecules infiltrate the hydrophobic core, coating the originally unexposed hydrophobic surfaces with a layer of water molecules (26–28). The core then remains in a partially solvated state with one or two water molecules trapped between the side chains for about 50 ps (54 ± 45 ps at 400 K). This defines the S (partially solvated cluster) state. A final sudden step is the complete breakdown of the hydrophobic cluster. After this event, the peptide fluctuates among a large set of essentially unstructured conformations (the unfolded state U) and unfolding is complete.

The Unfolding Pathway Consists of Discrete Steps

The consistent observation of these discrete steps in our collection of 22 unfolding runs can be summarized by a four-state unfolding mechanism

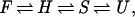1

where F is the frayed, folded state, H is the state without secondary structure but with a packed core, S is the state with partially solvated core, and U is the completely unfolded state.

Each step in Eq. 1 is written as a reversible reaction, because in our simulations we occasionally observe the back reactions (particularly H → S), especially at the higher temperatures (see also the discussion of TSs below). We have not observed direct F → U transitions, but on several occasions (twice at 500 K and once at 450 K) observed direct F → S transitions, without an intervening H state. These rare events either indicate a direct F → S transition, or a difficulty discriminating the H and S states based only on the core radius of gyration R_core. The states H and S appear as obligatory but transient kinetic intermediates in high-temperature unfolding. Their short lifetimes are consistent with the observed two-state equilibrium (11, 12, 25, 29). The 22 simulations are summarized according to this scheme in Fig. 3. We support this pathway with three complementary analyses.

Distinct Peaks in the Cumulative Probability Distribution.

The existence of four discrete states of the peptide (F, H, S, and U) is consistent with four corresponding maxima in the observed cumulative probability distribution vs. the number of hydrogen bonds N_HB and core size R_core (see Methods for definitions of N_HB and R_core), shown in Fig. 4. The cooperative nature of the transitions between states is demonstrated by the probability minima between states.

Dwell Times Within States Are Much Longer Than Transit Times Between States.

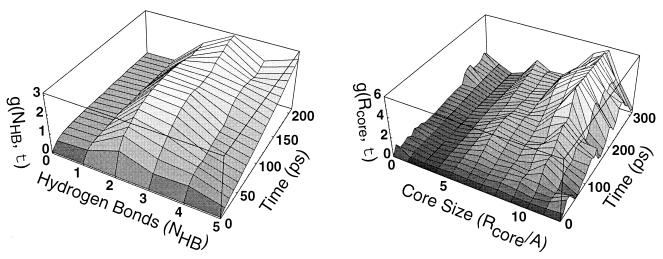
Each peak in Fig. 4 represents a population of conformations that are rapidly interconverting on ps time scales. The dwell and transition times can be calculated from the fluctuation correlation functions of N_HB and R_core, as detailed in Fig. 5. At 400 K, the typical dwell time within each peak is longer than 100 ps. By contrast, the transitions between states occur as rapid, discrete jumps that are complete within tens of ps (as shown in Figs. 2 and 4). These jumps are the cooperative transitions indicated in the pathway (1).

Figure 5.

Dwell time within a state vs. transit time between states. We consider the fluctuations of a dynamical quantity x(t) over the course of an unfolding trajectory. Here x can be either the number of hydrogen bonds (N_HB) or the core radius of gyration (R_core). The correlation function g(τ;X) ≡ 〈[x(t + τ) − x(t)]²〉_x(t)=X measures the mean square variation of x over a time interval τ, given that x took the value X at the start of the interval. The average is taken over all six 400-K simulations (total time = 10.2 ns). For X in the vicinity of a metastable free energy minimum, fluctuations in x(t) will remain small during the characteristic lifetime of the state. For X near a free energy barrier, however, fluctuations in x will grow rapidly as the polymer quickly moves into one of the adjacent free energy minima. From this correlation function we can extract (a) the location of the metastable states, (b) the characteristic dwell-time within a state (typically 100 ps at 400 K), and (c) the characteristic transit time across free energy barriers (typically 10–20 ps at 400 K).

Figure 2.

Quantitative characterization of the 400-K trajectory shown in Fig. 1. Both the number of hydrogen bonds (N_HB; see Methods) and the “solvent exposure” (the number of protein atoms within 3.0 Å of a solvent atom; our results did not change qualitatively for values ranging from 1.5 to 4.5 Å) sharply change around 250 ps, signaling the F → H transition. Because N_HB does not discriminate between the H, S, and U states, these transitions can be studied by using the core radius of gyration R_core. A sharp transition in R_core signal the H → S transition around 450 ps, which is followed rapidly by the S → U transition around 475 ps. The radius of gyration R_G of all the α-carbons typically does not exhibit any features near these transitions. The plots shown are results of box car averaging over a 10-ps window for R_G and R_core and a 2-ps window otherwise. General features are insensitive to the nature of this averaging.

Fast Refolding from Putative TSs.

As reactions in their own right, each step of Eq. 1 is expected to have a TS that corresponds to a free energy barrier that must be surmounted. The conformations at the peak of this barrier comprise the TS ensemble. Because TSs are inherently unstable with respect to either the “product” or “reactant” states, one expects that (a) a simulation started from a TS conformation will rapidly encounter a product or reactant conformation, and (b) the product and reactant will be equally likely outcomes. These properties of the TS suggests a computational method (15, 16, 18, 19) for identifying TS conformations by simulating a collection of short test trajectories beginning from a candidate conformation, and computing the probability that these trajectories proceed in the forward direction. For a TS conformation, this probability will be near 1/2.

To determine TS conformations for each transition in the reaction (1), we examined conformations selected at ps intervals from a high-temperature unfolding trajectory during a time when the character of the conformation is changing from one state to another, as measured by the relevant order parameter. For example, to obtain candidate TS conformations for the F ⇌ H transition, we look near the time at which the number of hydrogen bonds N_HB changes sharply. To test whether a given conformation C is in the TS ensemble, we run 40 more test simulations. Each of these test simulations has the same initial conformation C for peptide and solvent atoms, but differing initial velocities chosen from a Maxwell-Boltzmann velocity distribution at the temperature of interest. Because from the TS the forward and reverse states are reached relatively rapidly, these test simulations can even be carried out at temperatures relevant for refolding, as we show below.

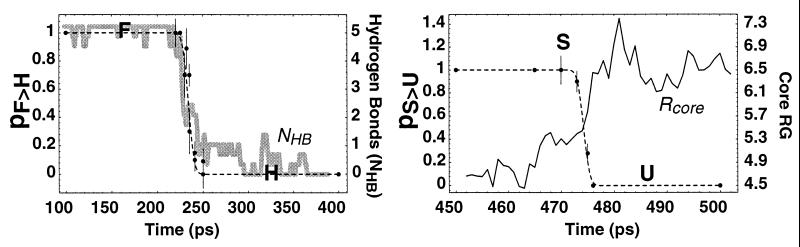
Each test trajectory is terminated when a conformation is reached that is in the F or H state, as determined by the value of N_HB (see Fig. 4). The transition probability P_F⇌H(C) then is given by the fraction of these short trajectories that end at H, shown in Fig. 5, Left. TS conformations are by definition equally likely to fold or unfold (15, 16) and therefore will have transition probabilities of P ≈ 1/2. Fig. 5, Right shows a similar calculation for the S ⇌ U transition.

Transition probability calculations can be easily done at low temperatures, because the time it takes for a conformation to diffuse away from the top of a free energy barrier can be orders of magnitude faster than the rate at which the barrier is crossed starting from the initial or final states (20, 30). The ratio of the “commitment time” for a TS trajectory to the rate constant is the probability that the peptide finds itself at the TS. For high barriers, this probability can be quite small.

We have determined members of the TS ensembles for the F ⇌ H and S ⇌ U transitions by using this approach. As expected, the typical time for proceeding in either the folding or unfolding directions from the TS was very short (221 ± 124 ps at 300 K and 25 ± 12 ps at 400 K, respectively, for the F ⇌ H transition), reflecting the inherent instability of the TS ensemble (see Fig. 6). This calculation confirms the difference between dwell and transit times and supports the conclusion that unfolding of this β-hairpin proceeds by a series of cooperative events.

Figure 6.

The transition probability P calculated at 300 K vs. time along the 400-K trajectory shown in Figs. 1 and 2 for the (Left) F ⇌ H and (Right) S ⇌ U transitions for conformations in the transition region. The solid line is the order parameter used to discriminate states, i.e., (Left) hydrogen bonds N_HB and (Right) core size R_core. The dashed line is a fit to P = (erf[(t-t_TS)/t_trans]+1)/2, where t is time, t₀ is the time at which P = 1/2 (that is, near the TS) and t_trans is the duration of the transition region. We see that P_F⇌H(C) and P_S⇌U(C) change sharply from 0 to 1 over a few ps time interval (with t_trans = 7.0 and 1.3 ps, respectively, at 400 K). Transition probabilities for this 400-K run calculated at 400 K are indistinguishable within error from the 300-K probabilities presented here.

Comparison with Experiments and Theory

By using our collection of trajectories, we can estimate the rates in the unfolding direction for each transition in pathway (1) by averaging the respective mean-passage times. The rate-limiting step for unfolding appears to be the F → H transition. The existence of a single rate-limiting step in the unfolding pathway implies that unfolding will be observed with two-state kinetics, even though there are transient kinetic intermediates, (i.e., H and S). The transient nature of these intermediates suggests that their free energy relative to the native and unfolded states are relatively high and thus will not be relevant in a thermodynamic sense, rendering the hairpin two-state in equilibrium measurements as well.

To estimate the unfolding rates at 300 K based on high-temperature simulations, we examined the mean first passage times from one state to another. The temperature dependence of these times was fit to an Arrhenius plot, yielding enthalpic barriers of ΔH_F→H = 9 ± 8 and ΔH_H→S = 5 ± 4 kcal/mol. We did not have sufficient data to estimate ΔH_S→U, although we find that the S → U rate is much faster than the others and is not rate limiting. To estimate the unfolding rate, we must account for both the enthalpic barrier and the diffusion constant. The unfolding time can be written in general as t_U(T) = τ(T) exp(ΔH/T), where τ is the diffusion constant. The ratio τ(T = 300)/τ(T = 400) can be estimated by calculating the ratio of the diffusion constants of water at these temperatures. We find that τ(T = 300)/τ(T = 400) ≈10. Thus, our extrapolation yields t_u = 10 × τ(400 K) exp(ΔH/300 K) ≈ 0.1 μs, which, considering the logarithmic accuracy of our extrapolation, is reasonably close to the observed rate of 3.5 ± 0.5 μs (11, 12).

We note that experimentally, negative enthalpic barriers were measured for folding (11, 12). Although our method cannot directly measure barriers for folding, a positive enthalpic barrier in unfolding is consistent with a negative barrier for folding if the enthalpy decreases as the protein becomes more native (i.e., E_unfolded > E_TS > E_native).

Our calculations suggest that folding of the hairpin occurs by forming the core first and the β-sheet hydrogen bonds second. This mechanism also was noted in refs. 11 and 12. An alternative model for β-hairpin refolding also has been proposed by Munoz et al. (11, 12), which provides a phenomenological picture that is quantitatively consistent with experiments. In this model, a turn with a fluctuating “zipper” of interstrand hydrogen bonds positions the aromatic residues so that they are poised to pack into a hydrophobic cluster. The TS for the two-state refolding transition consists of conformations with a short, unstable hairpin held together by approximately three hydrogen bonds (11, 12). When the hydrophobic cluster forms, the hairpin is stabilized in a transiently populated intermediate (a local minima in the free energy landscape of refs. 11 and 12), and then finally the F state is reached.

In both our model and that of Munoz et al., the critical rate-limiting step in refolding is the positioning of the aromatic groups so that the hydrophobic cluster can form. The primary difference between the two models is whether the interstrand hydrogen bonds near the turn appear before or after the core is formed. If refolding occurs by the reverse of high-temperature unfolding, then our results suggest that the hydrophobic cluster would form without assistance from interstrand hydrogen bonds near the turn, i.e., by a U → S transition followed by a S → H transition. This behavior is expected to depend on the flexibility of the turn region in the unfolded state as well as the specific turn type (31) that appears in the folded state.

This distinction between the two models of the refolding pathway could in principle be tested by engineering a peptide with a modified backbone that is incapable of forming interstrand hydrogen bonds near the turn. For the pathway derived from unfolding simulations presented here, the tryptophan fluorescence quench rate should be unchanged, because the hydrophobic cluster of the H state still should form at the same rate. For the Munoz et al. model (12), however, fluorescence quenching would be expected to occur more slowly.

Discussion

At high temperatures, where refolding events are rare, the principle of microscopic reversibility guarantees that refolding will occur by the reverse of the unfolding pathway (20). It is natural to conjecture that the nature of this refolding pathway is preserved at lower temperatures (1). Here we have tested this hypothesis for a small peptide by determining the unfolding pathway for a 16-residue β hairpin by using a collection of molecular dynamics trajectories at high temperatures (370 K to 900 K), and then systematically simulating, at low temperatures (300 K), the rapid crossing of the TSs for each of the steps in the pathway. The determination of the full unfolding pathway is made possible by the small size of the hairpin, which allows us to simulate complete unfolding at 400 K.

Although one cannot simply simulate refolding starting from an unfolded conformation, we have shown that barrier crossings between the metastable states of β-hairpin peptide can be studied by using all-atom molecular dynamics. Our computational strategy is first to identify these metastable states by using high-temperature unfolding simulations, and then to perform a series of short molecular dynamics runs from putative TSs between them. This approach allows a refolding event to be pieced together from many quick calculations (tens of ps) and avoids simulations of long dwell times (hundreds of ps and up) in the metastable states. It is the rapid increase of these dwell times with decreasing temperature that prevents straightforward simulation of a folding event.

The principal caveat of this method is that states (or transitions) that are relevant at low temperatures may not appear in high-temperature unfolding trajectories. We therefore cannot exclude the possibility of other parallel folding pathways that might compete (or even dominate) at lower temperatures with the reversed unfolding pathway we have found. This scenario could occur, for example, because of the temperature dependence of hydrophobicity and hydrogen bonds. While hydrogen bonds get effectively weaker at temperatures greater than 300 K, hydrophobicity first gets stronger and then weakens with temperature. Such effects are a general limitation of the high-temperature methodology.

By using this approach, we have reconstructed a refolding pathway of the protein G β-hairpin under physiological conditions. According to our simulations, the β-hairpin can refold by a caricature of the “hydrophobic collapse” scenario (32), with secondary structure appearing after the native topology first is established by hydrophobic interactions. It is striking that even for this small fragment of a protein, folding and unfolding are evidently cooperative events that proceed by pathway of discrete steps between metastable partially structured intermediate states, as observed by several groups (33, 34), suggesting that short-lived metastable states of proteins play an essential role in folding pathways.

ABBREVIATION

TS

transition state