Evaluation of Elastic Properties of Atomistic DNA Models

Abstract

A number of intriguing aspects in dynamics of double-helical DNA is related to the coupling between its macroscopic and microscopic states. A link between the elastic properties of long DNA chains and their atom-level dynamics can be established by comparing the worm-like chain model of polymer DNA with the conformational ensembles produced by molecular dynamics simulations. This problem is complicated by the complexity of the DNA structure, the small size of DNA fragments, and relatively short trajectory durations accessible in computer simulations of microscopic DNA dynamics. A careful study of all these aspects has been performed by using longer DNA fragments and increased durations of MD trajectories as compared to earlier such investigations. Special attention is paid to the necessary conditions and criteria of time convergence, and the possibility to increase the sampling by using constrained DNA models and simplified simulation conditions. It is found that dynamics of 25-mer duplexes with regular sequences agrees well with the worm-like chain theory and that accurate evaluation of DNA elastic parameters requires at least two turns of the double helix and ∼20-ns duration of trajectories. Bond length and bond-angle constraints affect the estimates within numerical errors. In contrast, simplified treatment of solvation can strongly change the observed elastic parameters of DNA. The elastic parameters evaluated for AT- and GC-alternating duplexes reasonably agree with experimental data and suggest that, in different basepair sequences, the torsional and stretching elasticities vary stronger than the bending stiffness.

INTRODUCTION

The flexibility and internal dynamics of DNA are known to play an important role in its biological function. Biologically relevant dynamics of DNA spans a broad range of length scales starting from a subnanometer level of single basepairs and continues to macroscopic lengths where the double helix can be considered as a continuous flexible rod. All these motions are evidently coupled. For instance, the macroscopic elastic properties of DNA depend upon the basepair sequence, while external torsional stress applied to long chains affects the local rates of basepair opening. The corresponding molecular mechanisms are only partially understood and disclosing them represents a challenging task.

Long DNA double-helix behaves as a continuous elastic rod with harmonic bending, torsional, and stretching deformability. Its equilibrium shape is described by the worm-like chain (WLC) model (1,2), whereas the torsional and stretching fluctuations can be treated with the standard formalism of the classical statistical mechanics. This model accurately describes experimental data by using only a few adjustable parameters, which have been measured since the 1960s with progressively improved accuracy (3). More recently, single molecule nanomanipulations (4–10) became the major source of information on the DNA elasticity, and the WLC theory is successfully used for extracting information from such data (11–18). The validity of the WLC description of long DNA is corroborated by the success of Monte Carlo simulations of the WLC model with experimentally measured parameters. In many cases, such simulations demonstrated remarkable agreement with experiment and made predictions confirmed later (19–22).

Owing to important methodological advances made approximately 10 years ago (23–25), the local atom-level DNA properties are now reasonably well reproduced in classical molecular dynamics (MD) simulations of small duplexes in explicit aqueous environment (26,27). MD simulations are based upon empirical force fields that are parameterized by using experimental data for small molecules as well as quantum mechanics calculations (26,28). The experimental information about DNA elasticity is not used for parameterization; therefore, comparison of atom-level MD models with the WLC theory present significant fundamental interest. To establish this link between the microscopic MD and the WLC theory, we need to extract the effective WLC parameters from atom motions in short DNA fragments observed during relatively short times. This problem is not simple, because the DNA structure is complex, the duration of MD trajectories is limited by computer resources, and because we cannot exclude that the WLC theory works well for DNA only starting from prohibitively long fragments.

The first attempt to evaluate the elastic parameters of DNA from atom-level data was made by Olson et al. (29), who studied statistics of fluctuations in x-ray DNA structures assuming that the perturbations due to the crystal environment and proteins bound to DNA are equivalent to the heat bath effect. MD simulations of DNA were first analyzed from the same perspective by Bruant et al. (30), and later by Lankas et al. (31), who specifically targeted the sequence-dependent DNA elasticity. The obtained estimates of the WLC parameters reasonably agreed with other data. These studies, however, did not consider important issues concerning the overall agreement of DNA dynamics with the WLC theory, statistical convergence, and the accuracy of the final estimates. These aspects are crucial for probing relatively small modulations of DNA elasticity, for instance, due to small external stress. Here we study in detail the problems involved in the interpretation of MD trajectories of DNA in terms of the WLC theory by using longer DNA fragments and increased durations of MD trajectories. Special attention is paid to the necessary conditions and criteria of time convergence, and the possibility to increase the sampling by using constrained DNA models and simplified simulation conditions. It is found that dynamics of 25-mer duplexes with regular sequences agrees well with the WLC theory and that accurate evaluation of DNA elastic parameters requires at least two turns of the double helix and ∼20-ns duration of trajectories. Bond length and bond-angle constraints affect the estimates within numerical errors. In contrast, simplified treatment of solvation can strongly change the observed elastic parameters of DNA. The elastic parameters evaluated for AT- and GC-alternating duplexes suggest that, in different basepair sequences, the torsional and stretching elasticities vary stronger than the bending stiffness.

THEORETICAL BACKGROUND AND METHODS

The persistence lengths of the WLC model

The persistence length (PL) is a convenient measure of statistical flexibility of polymer chains that can be estimated experimentally. The advantage of the WLC model is that all its properties, including the local ones, are fully determined by the bending, torsional, and stretching PLs, which gives a theoretical possibility of evaluating the DNA elasticity from the MD of relatively short chains.

The standard definition of the bending PL is as follows. Consider a chain fragment of the contour length L placed in a thermal bath. We connect the two chain-ends by a vector and compute its projection upon the local chain direction measured at its origin. The Boltzmann average of this projection characterizes the internal molecular flexibility. The bending PL is defined as the limit of this projection with L → ∞.

We assume that the polymer can be approximated by a continuous flexible rod and try to compute its bending PL from local elastic properties. Statistical mechanics of flexible rods was first analyzed by Bresler and Frenkel in the 1930th (2). For an isotropic rod of length L, its bending energy in the first approximation is

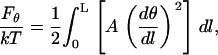(1)

where θ(l) is the bend angle of fragment (0, l) and A is a constant. The Boltzmann average of the bending angle 〈cosθ〉 is computed by using the general theory of fluctuations (2)

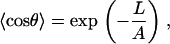(2)

and it follows that

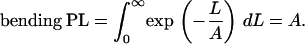(3)

Equation 2 can be rewritten in a linear form suitable for data processing

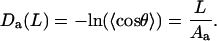(4)

The D_a values estimated for DNA fragments of increasing lengths should grow linearly and the rate of this growth gives an estimate of the bending PL. Several similar functions will be introduced below and, for convenience, they are all referred to as “deviations.” Subscript a indicates that D_a and A_a are obtained from average bend angles.

The WLC bending PL can be also estimated from the average end-to-end distance. Vector R joining the chain-ends is

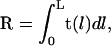(5)

where t(l) is a unit tangential vector. The average square distance 〈R²〉 is obtained by straightforward integration using Eq. 5 together with Eq. 2, which gives (2)

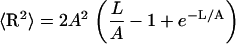(6)

For DNA fragments used in MD, we always have L ≪ A, therefore Eq. 6 is approximated as

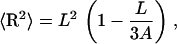(7)

which gives a linear relationship similar to Eq. 4,

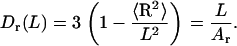(8)

The D_r value can be computed from MD trajectories and used for evaluating A_r.

If the DNA molecule behaves as an elastic rod, the values of A_a and A_r must be equal. Even though Eqs. 4 and 8 are not independent, comparison of A_a and A_r appears useful in practice. A serious difficulty inherent in this type of computation is in the unknown rate of convergence. Both 〈cosθ〉 and 〈R²〉 are positive and there is no other parameter that would have a standard limiting value. Therefore, it is not easy to judge how complete the sampling is at a given stage of simulation. In the course of MD, the values of A_a and A_r can approach the same limiting value differently. For instance, local bending dynamics may be fast with respect to translational motion of the chain ends. In this case the rapid bending dynamics should be dominated by correlated fluctuations that leave the chain-ends fixed. As a result, A_a and A_r measured for finite trajectories may differ significantly. Comparison of A_a and A_r provides a valuable additional check of convergence and consistency of the data. Moreover, it is desirable to select a procedure that allows obtaining accurate estimates from possibly short MD trajectories. From this prospect, an appealing possibility for testing resides in using fluctuations of R² and cosθ rather than their averages. Here, we test this idea for cosθ. Its standard deviation Δcos_θ is

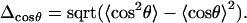(9)

The WLC theory does not offer an analytical relationship for Δcos_θ(L), but the angle distributions obtained by MC simulations of a genuine WLC model reasonably well agree with

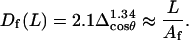(10)

For WLC chains of ∼10-nm length and the bending PL of 20–60 nm, this equation gives an estimate of the persistence length with an error ∼2%.

An additional complication in the DNA bending dynamics lies in the possibility of static curvature. Certain DNA sequences are known to induce stable bends and, probably, many more such sequences exist but are not known. Moreover, static and metastable bending components are indistinguishable in the course of a finite MD simulation; therefore it is important to have a monitoring procedure to check whether the DNA bending observed in an MD trajectory contains such components. Here we apply the following approach. A reference Cartesian frame is placed at the chain origin, with the unit vector e_z looking along the helical axis, and vectors e_x and e_y being perpendicular to it. The unit vector of the helical axis at the opposite chain-end is denoted h. For true WLC dynamics we should have 〈h_x〉 = 〈h_y〉 = 0, and 〈h_z〉 = cosθ > 0. If 〈h_x〉 ≠ 0, or 〈h_y〉 ≠ 0, the DNA fragment under consideration is curved, on average. Let us define a unit vector 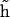with components

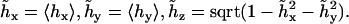(11)

Vector 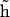gives an approximate direction of a helical axis of the average DNA conformation. Now we can measure the angle 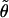between vectors h and 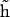and compute its average cosine as

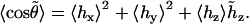(12)

Just by analogy with Eq. 4, we can write

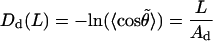(13)

and

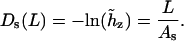(14)

The last two equations do not have a rigorous justification. Intuitively, one can expect that the left-hand values in Eqs. 13 and 14 both grow with L; therefore, these formulae can be considered as first approximations of more complex functions. Below, parameters A_d and A_s are referred to as dynamic and static PL, respectively. In the course of MD of a true WLC model one should observe that A_s → ∞ and A_d → A_a; therefore, the closeness of A_d and A_s to the limiting values serve as additional criteria of convergence. The distinction between the static and dynamic PL is usually used in the framework of the wedge theory of DNA curvature (32–34). Here, we use the same terms in the context of dynamics of a single DNA molecule; therefore, the above definition of A_s and A_d is adapted for processing MD data. The physical meaning of A_s and A_d is not the same as in the wedge theory. Notably, no simple additivity rules exist that connect A_s and A_d with the total PL.

The classical WLC model can be extended to take into account fluctuations of the overall winding angle and the chain length. To this end, the total elastic energy is written as

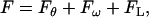(15)

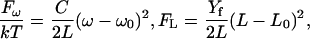(16)

where ω(L) is the total winding angle while ω₀ = 〈ω〉 and L₀ = 〈L〉 denote minimum energy values. Parameter C in Eq. 16 is called torsional PL (by analogy with A in Eq. 1) and Y_f is Young's stretching modulus. Equation 15 is the first approximation of the elastic energy, with the possible coupling between bending, torsional, and stretching motions neglected. In contrast to the bending-angle θ, the winding and the length of consecutive DNA stretches are simply additive; therefore, expressions similar to Eq. 1 for torsional and stretching energies readily give Eq. 16. The Boltzmann averaging of Eq. 16 gives expressions similar to Eq. 4,

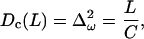(17)

and

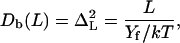(18)

used for estimating the values of C and Y_f from MD results. The stretching PL, B, is usually defined as (15)

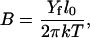(19)

where l₀/2π is a scaling coefficient, with l₀ = 3.4 nm (the length of one helical turn in B-DNA).

Despite the apparent similarity of Eqs. 4, 17, and 18, the bending PL is clearly distinguished from the other two because it is determined from the average bending angle rather than the standard deviation. This difference is due to the nontrivial additivity of bending angles along the chain that requires a special treatment (the WLC model), and it does not depend upon the chain length. For instance, if both L and θ are very small, the bending energy of a flexible rod can be approximated as

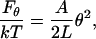(20)

and expansion of both sides of Eq. 2 gives

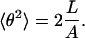(21)

If we replace θ² on the left in Eq. 21 by 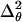(by analogy with Eq. 17), the bending PL A on the right must be replaced by a larger value 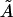because 〈θ〉 ≠ 0 for the WLC model. Parameter 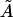also characterizes the bending rigidity, but it can significantly differ from A even with L → 0. Therefore, evaluation of the bending PL from standard deviations rather than averages of bending angles is possible only by approximate empirical relationships like Eq. 10.

Construction of helical axes

To compare an ensemble of DNA conformations with the WLC model, every DNA structure should be replaced by an oriented space line. This issue would be unimportant if one could run MD simulations for very long double helices, which is hardly possible even in long-term prospect. Following earlier similar studies (30,31), we decided to employ the Curves algorithm by Lavery and Sklenar (35) to construct the DNA helical axes and measure bending, torsional, and stretching fluctuations. To this end, the algorithm was reimplemented and verified against the original Curves program for selected DNA conformations and also by processing intervals of MD trajectories by the two implementations in parallel. The Curves algorithm starts by constructing a local Cartesian frame at every base, with the frame orientation depending only upon the coordinates of N1/N9 atoms and the base plane. The optimal helical axis consists of a new sequence of Cartesian frames, one for each basepair, that we call axis frames. They are positioned in space by numerical optimization of a target function that can be written as

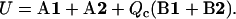(22)

The exact definition of the four terms denoted A1, A2, B1, and B2 are given in the original article (35). Qualitatively, conditions A1 and A2 require that orientations of base coordinate frames with respect to the axis frames of the same level were possibly similar for neighboring levels. Conditions B1 and B2 do not consider the DNA structure and only require that the optimal helical axis be locally close to a straight line. Essentially, the axis is modeled as a flexible rod with elastic properties determined by conditions B1 and B2, and the numerical optimization of function (22) is used to fit it to the DNA structure. In the original version of the algorithm, factor Q_c was absent (Q_c = 1). Here it was added to vary the bending elasticity of the axis rod.

MD simulations

We study dynamics of 25-mer double-helical DNA fragments with AT- and GC-alternating sequences (AT25 and GC25, respectively). AT25 is modeled in three simulation regimes that differ by hydration conditions as well as the number of degrees of freedom in the DNA duplexes. In all cases, the AMBER98 force-field parameters (23,36) were used with the rigid TIP3P water model. Molecular dynamics simulations of rigid and partially fixed molecules were carried out with the ICMD method (37,38) adapted for DNA (39,40). In the first regime (trajectory AT25a, 16 ns, time-step 0.002 ps), the duplex was modeled with all degrees of freedom in a rectangular water box with a neutralizing number of sodium ions. In the second regime (trajectory AT25b, 28 ns, time-step 0.01 ps), the hydration conditions were the same as in AT25a, but the duplex was modeled with all backbone torsion degrees of freedom, free bond angles in sugar rings, and rigid bases and phosphate groups. In the third regime (trajectory AT25c, 120 ns, time-step 0.01 ps), the minimal B-DNA model was used, with semi-implicit treatment of solvent as described earlier (39,41,42). Duplex GC25 was modeled in conditions corresponding to AT25b (trajectory GC25 20 ns, time-step 0.01 ps). Trajectories AT25a, AT25b, and GC25 were run with periodical boundaries, in NVT ensemble conditions with water density at ∼0.997. The electrostatic interactions were treated by the SPME method (25), with the common values of Ewald parameters; that is, 9 Å truncation for the real-space sum and β ≈ 0.35. In all cases, the fiber canonical B-DNA model (43) was used as the starting state. The starting states of trajectories AT25a and AT25b were prepared as follows. The DNA fragment was immersed in a rectangular water box 110 × 46 × 46 Å, with a higher water density of 1.04. The box was neutralized by placing Na⁺ ions at random water positions at least 5 Å from the solute. The system was energy-minimized and dynamics were initiated with the Maxwell distribution of generalized momenta at low temperature. The system was next slowly heated to 293 K and equilibrated during 0.6 ns. After that, the water density was adjusted to 0.997 by removing the necessary number of water molecules selected randomly at least 5 Å from DNA and ions, and the simulations were continued with NVT ensemble conditions. In all simulations, the temperature was maintained by the Berendsen algorithm (44) with a relaxation time of 10 ps. In all trajectories the DNA structures were saved every 2.5 ps. These conformations were later processed with the Curves algorithm to accumulate the data for the statistical analysis according to the WLC model. To increase the sampling, all possible internal fragments of the 25-mer duplexes were considered; for example, averaging for dimers involved 24 times more conformations than for 25-mer.

RESULTS

Artifacts of elasticity of helical axis

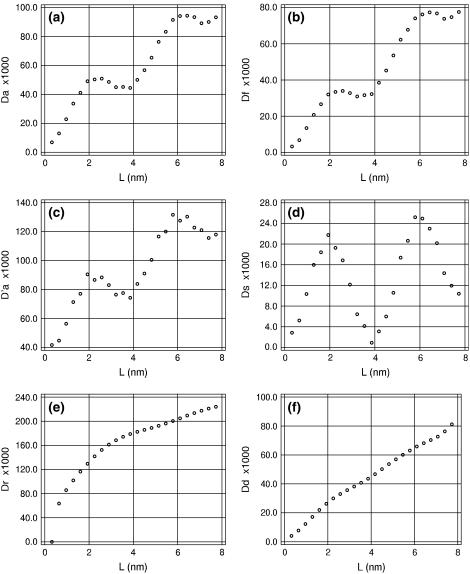
Fig. 1 displays the apparent chain-length dependence of different bending deviations for trajectory AT25b when the helical axes of DNA structures are computed with the original parameterization of the Curves algorithm; that is, with Q_c = 1 in Eq. 22. According to the WLC theory described above, all plots in this figure except D_d and D_s must be linear with the same slope. Instead, they all display strong deviations. The most striking are evident regular oscillations of D_a with a period close to that of DNA. Their origin becomes evident if we compare the traces of D_s and D_d. It is apparent that the helical axis exhibits static bending that regularly changes with the chain length. The corresponding DNA conformations, however, are quite straight and show no deformations that could have been responsible for such effects. The apparent static bending reaches maxima for DNA lengths of 0.5 and 1.5 helical turns, but is close to zero for full turns, which means that the axis is helical itself, with the winding period identical to that of the double helix.

FIGURE 1.

Chain-length dependences of bending deviations measured by different methods. Results of trajectory AT25b were processed by the Curves algorithm with Q_c = 1.

The D_r plot is also nonlinear, but it appears quite differently. The Curves algorithm treats centers of the axis frames and their unit vectors separately. The local direction of the axis rod is given by one of these vectors and it is considered as tangential to the curved axis. The apparent qualitative difference between D_a and D_r plots in Fig. 1 suggests that only the tangential vectors rotate together with the helical winding, while the axis itself is free from this artifact. To check this suggestion, the same analysis was carried out by measuring bending angles in the broken line that passes through the centers of the axis frames. The corresponding plot is also shown in Fig. 1 (D′_a), and it exhibits the same oscillations as the D_a plot. Thus, the optimized axis really involves artificial modulations that are small and almost invisible by eye, but revealed in Fig. 1 due to averaging. The concave shape of the D_r trace probably has the same origin.

In the earlier studies based upon the Curves analysis of DNA structures these artifacts were not noticed (30,31). To check if they are specific to our implementation of Curves the same data were processed with the original program, but the results did not change. Moreover, this effect is not specific to the Curves algorithm. Similar features persist with the alternative procedure (41,45) that also uses numerical optimization, but finds a common axis of coaxial cylindrical surfaces passing through different atoms of DNA backbone. Therefore, the origin of the artifact helicity is in the very principle of fitting an elastic axis rod to a DNA structure. This may be a problem of local minima because the initial axis trace usually has some degree of helicity. It is also possible that the artificial helicity appears spontaneously during fitting because this is the lowest-energy deformation of a straight rod. In any case, evaluation of the WLC parameters of DNA from the data shown Fig. 1 is hardly justified. Fortunately, it appears that these artifacts can be reduced by adjusting the stiffness of the axis rod.

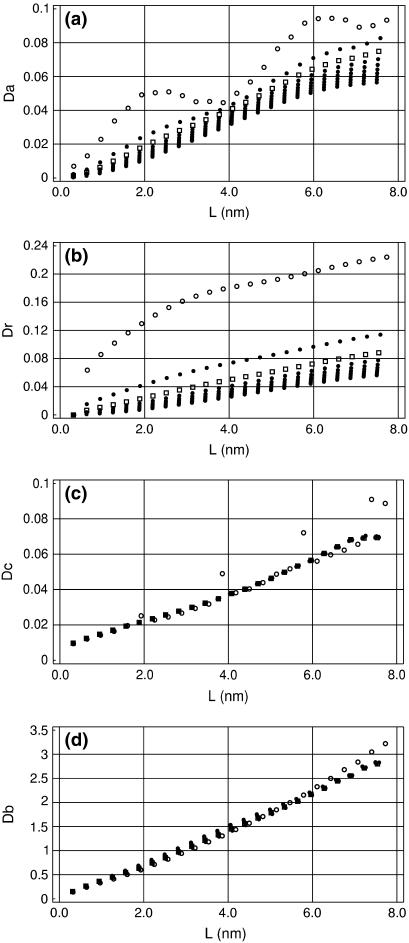
Fig. 2, a and b, shows how the artificial stiffness of the axis rod affects the measured bending deviations. The original Curves parameterization (Q_c = 1) gives a relatively soft axis that, for short DNA fragments, bends excessively in response to local conformational fluctuations. With the stiffness increased, the artifact oscillations in the D_a traces are reduced as well as the short length burst in the D_r traces, and for Q_c = 10 the chain length dependences demonstrate good agreement with the WLC theory. With the stiffness further increased, the initial artifacts change their sign. Notably, the bending looks smaller for short DNA fragments as well as near chain-ends, because in these cases, the fitted axis is less loaded by the DNA structure and it is easier for it to straighten.

FIGURE 2.

Chain-length dependences of deviations D_a, D_r, D_c, and D_b with increased stiffness of the axis rod in Curves. The multiple plots in all plates were obtained by increasing Q_c in Eq. 22, Q_c = 1, 5, 10, 15, 20, 25, 30, 35, and 40. Traces for Q_c = 1 and 10 are shown by ○ and □, respectively. Other traces are shown by •. The initial data were the same as in Fig. 1.

The apparent torsional and stretching deviations are less dependent upon Q_c. As seen in Fig. 2 c, with the default Curves stiffness Q_c = 1, D_c exhibits periodical bursts in phase with the oscillations in Fig. 1, but they disappear with Q_c = 5. The torsional stiffness looks higher for fragments shorter than one helical turn as well as the longest, but this effect is not significant. The apparent stretching deviations, D_s, shown in Fig. 2 d, are almost independent of Q_c. The trace obtained for Q_c = 1 is concave, but it straightens for Q_c = 5 and does not change with further increase of the helical stiffness.

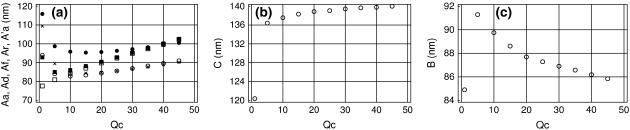
The results in Fig. 2 suggest that reasonably good estimates of DNA elastic parameters can be obtained from the slopes of linear fits of D(L) obtained with increased artificial stiffness of the helical axis. It is understood that as Q_c in Eq. 22 is gradually increased, the helical axis becomes more and more straight, and the question arises as to whether the elastic parameters we measure refer to DNA rather than to the artificial stiffness of the axis rod. Fig. 3 shows, however, the contribution of the artificial stiffness is not large and can be accounted for. The corresponding persistence lengths were obtained by linear regression analysis of D(L) dependences evaluated for trajectory AT25b. It is seen that, as expected, different estimates of the bending PL in Fig. 3 a all grow with Q_c. With Q_c > 5 this growth is small, so that an order-of-magnitude increase in Q_c gives only ∼10% increase in A_a. Moreover, the plots in Fig. 3 a are nearly linear when Q_c > 10; therefore, they can be extrapolated to Q_c = 0 to give asymptotic values. Interestingly, all estimates of the bending PL linearly extrapolated to Q_c → 0 from Q_c > 10 converge to ∼80 nm.

FIGURE 3.

Dependence of the estimated DNA elastic parameters upon the artificial stiffness of the helical axis. (a) Bending PL. A_a, ○; A_d, •; A_r, □; A_f, ▪; and A′_a, +. (b) Torsional PL. (c) Stretching PL.

The torsional and stretching PL shown in Fig. 2, panels b and c, respectively, are only weakly dependent upon Q_c. In fact, the Q_c factor in Eq. 22 directly affects only the bending stiffness of the axis rod. Therefore, the weak dependences seen in Fig. 2, b and c, result from compensations during numerical optimization of the target function Eq. 22. Notably, with Q_c increased, the soft stretching degree of freedom is increasingly involved in the fitting, which gives larger stretching fluctuations and smaller stretching PL. The torsional PL is almost constant, suggesting that different compensation factors approximately cancel out.

Fig. 2 indicates that the artificial stiffness Q_c = 10 represents a reasonable compromise because, on the one hand, it scales down the artifacts displayed in Fig. 1, and, on the other hand, it is relatively low and gives estimates of elastic parameters close to the Q_c = 0 asymptotic intercepts.

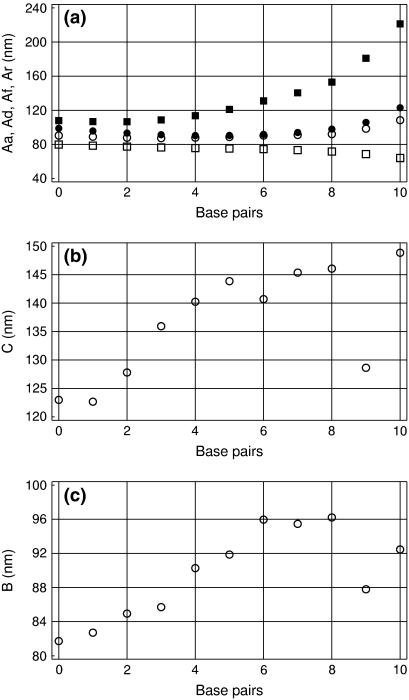
Chain-end effects

In analysis of DNA structures, a few terminal basepairs are commonly excluded. This is reasonable because the DNA ends may be physically more flexible and also because fitting of helical axis near chain ends is less reliable. Fig. 4 shows how the estimated persistence length changes when terminal basepairs are excluded from analysis. With 10 basepairs excluded, only the central 5-mer is considered, and so forth. The four different estimates of the bending PL shown in Fig. 4 a were obtained by linear regression analysis of the corresponding D(L) plots, with the helical stiffness Q_c = 10. It is seen that the end effects are small. A descending trend in A_a and A_r is larger for short trajectories, but it reduces with time. Certainly, long chains need longer time for sampling configurations corresponding to a given persistence length. However, a much more noticeable trend observed in Fig. 4 a consists of the divergence of the four estimates of the bending PL, which becomes dramatic when the length of the remaining part of DNA approaches one helical turn. With the reduced DNA length, the amplitudes of bending fluctuations are reduced and the above-discussed artifacts of Curves become more pronounced. In addition, the sampling is reduced due to the smaller number of DNA conformations analyzed and also due to a smaller number of points for the linear regression analysis. As seen in Fig. 4, b and c, these factors affect the estimates of the torsional and stretching PLs only when <1 helical turn remains for analysis. In contrast to bending, however, here the expected strong chain-end effects are evident. The DNA ends look softer than its inner part as regards both winding and stretching. As noted already, factor Q_c directly affects only the bending stiffness. With Q_c = 10 the chain-end effects seem to be significantly reduced for bending, whereas for stretching and torsional deformations they are still distinguishable.

FIGURE 4.

Bending, torsional, and stretching PL measured for the central part of the 25-mer fragment. The number of basepairs excluded from both ends is shown on the x axis. (a) Different estimates of the bending PL. A_a, ○; A_d, •; A_r, □; and A_f, ▪. (b) Torsional PL. (c) Stretching PL.

Based upon the foregoing considerations, the following procedure was used in the further data processing:

1. The helical stiffness Q_c = 10 is used as optimal, but the analysis is repeated for a series of Q_c values to check its effect upon the results.

2. Three basepairs from both ends are excluded from analysis in correspondence with the earlier studies (31).

3. Based upon the results shown in Fig. 2, the persistence lengths are estimated by linear regression analysis of the D(L) plots over L > 6 for bending-angle deviations (except D_s(L)), L > 12 for D_r, and L > 3 for torsional and stretching deviations. The D_s(L) plots remain oscillating with high Q_c values; therefore, the static PL is estimated by simple averaging of A_s(L). Every point on D(L) plots is weighted by the corresponding number of sampled DNA conformations.

Time-convergence

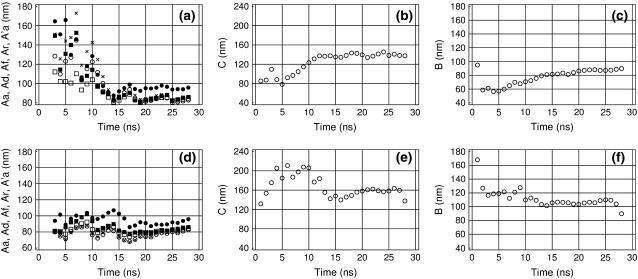
Perhaps the most difficult issue concerns the duration of MD trajectories necessary for reliable estimates of the DNA elastic parameters. Recent experimental reports suggest that the conformational relaxation times can be hopelessly long even in short DNA fragments (46–48). In contrast, certain structural parameters of DNA seem to converge very rapidly during MD; for example, the average helical parameters and the average fraction of B_II conformations (49). Fig. 5 shows the time-dependence of the measured DNA elastic parameters for trajectory AT25b. When MD trajectories start from canonical structures, DNA commonly exhibits a conformational drift at the beginning. The duration of this initial phase cannot be known a priori because it depends upon the specific conformational parameter considered and because it is difficult to distinguish between slow drift and a slow equilibrium fluctuation. If the data with such drift are interpreted as fluctuations, statistical parameters measured during the first nanoseconds can be strongly biased, and it takes a long time before they reach their true values. For torsional and stretching PL, this effect is always seen as very slow growth, because these are computed from standard deviations of the winding angle and the length of DNA, respectively. The corresponding manifestations in the measured bending PL may vary.

FIGURE 5.

Time-convergence of the measured DNA elastic parameters in trajectory AT25b. (a,d) Bending PL with normal and inverted time directions, respectively. A_a, ○; A_d, •; A_r, □; A_f, ▪; and A′_a, +. (b,e) Torsional PL with normal and inverted time directions, respectively. (c,f) Stretching PL with normal and inverted time directions, respectively.

Fortunately, this problem can often be clarified by carrying out the trajectory analysis in two opposite time directions, as shown in Fig. 5 for trajectory AT25b. With the normal time direction, both torsional and stretching PLs exhibit slow growth, as expected. Comparison with the corresponding plates in the lower row indicates that the most probable convergent values are 160 and 105 nm for the torsional and stretching PLs, respectively, which is somewhat higher than the corresponding maxima obtained in the normal time direction. The bending PL shown in Fig. 5, a and d, also behaves differently when the trajectory is analyzed in the two opposite time directions. The initial straight conformation induces a slow decreasing trend in Fig. 5 a which is absent in Fig. 5 b. Comparison of these two plates suggests that the bending PL is somewhat below 80 nm.

These figures show also that different estimates of the bending PL become closer with time, which is very important because this feature can be used as a unique necessary criterion of convergence. The rate of convergence is similar for all five estimates of the bending PL so that none of them generally give better estimates for short trajectories. Nevertheless, all of them are useful because, as seen in Fig. 5, a and d, only comparison of all these values gives a correct appreciation of convergence. The discrepancy between A_d and the total PL falls down initially, but eventually stabilizes at a non-zero level. Simultaneously, the static PL, A_s, grows and stabilizes around ∼10^3.5 (data not shown). Even though A_s ∼ 10^3.5 seems large, it can result in a nonnegligible deviation of A_d from the total PL due to specific combinations of bending directions. This residual divergence between A_d and the total PL is mainly due to insufficient sampling of curved conformations with alternative bending directions, although it also involves a contribution from artifacts in the construction of the helical axis that are reduced, but not completely suppressed, with Q_c = 10.

Fig. 5 shows that all the measured elastic parameters are characterized by similar relaxation times. The convergence of the torsional and stretching PLs was expected to be somewhat faster because the corresponding fluctuations require relatively small atom displacements and they should be also much less hindered by water. Moreover, in the course of MD simulations, the average twist and rise normally reach stationary values after 1–2 ns. Surprisingly, Fig. 5 clearly shows that the convergence is similar for all elastic parameters. This may indicate that all these motions are significantly coupled, which should have been taken into account in Eq. 15, as earlier suggested by some groups (31). Accurate analysis of this issue requires further studies.

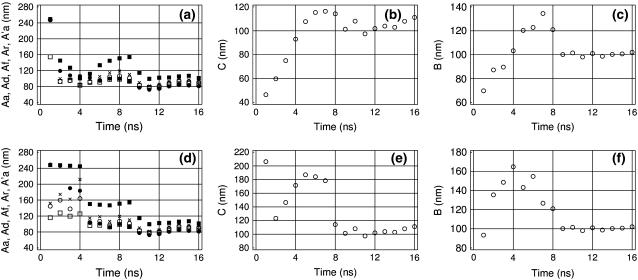
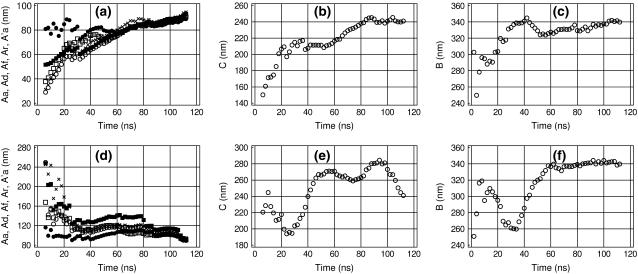
Alternative DNA models

Figs. 6 and 7 show the time dependence of the measured elastic parameters for the two alternative representations of the AT-alternating 25-mer duplex. The three models we consider strongly differ in performance. Model AT25a (Fig. 6) is most detailed, but also most computationally demanding. Model AT25b (Fig. 5) is five times less expensive computationally and may represent a reasonable compromise for practical computations. Model AT25c (Fig. 7) is computationally much faster than the former two, but its approximations may affect DNA dynamics. Trajectory AT25a was continued to 16 ns, which, according to Fig. 5, is the necessary minimum for convergence. Comparison of Figs. 5 and 6 suggests that the standard geometry fixations used in model AT25b do not significantly affect the elastic properties of DNA. The only significant difference concerns the lower apparent torsional PL for AT25b, but it appears to be due to a more pronounced chain-end effect. The behavior of the torsional PL for AT25a is qualitatively similar to that shown in Fig. 4, but the plateau at ∼150 nm is reached only when six basepairs from both ends are excluded. We conclude, therefore, the elastic parameters can be measured with reasonable accuracy by using the partially fixed DNA model. MD trajectories for the third model, AT25c, can be run for much longer durations, but as seen in Fig. 7, the absolute rate of convergence in this case is also the lowest. This was expected since the distance scaling of electrostatic interactions is known to increase artificially the strength of all polar contacts including hydrogen bonds (50). The same effect can also be responsible for the generally higher stiffness of the AT25c model compared to the other two.

FIGURE 6.

Time-convergence of the measured DNA elastic parameters in trajectory AT25a. The same notations as in Fig. 5.

FIGURE 7.

Time-convergence of the measured DNA elastic parameters in trajectory AT25c. The same notations as in Fig. 5.

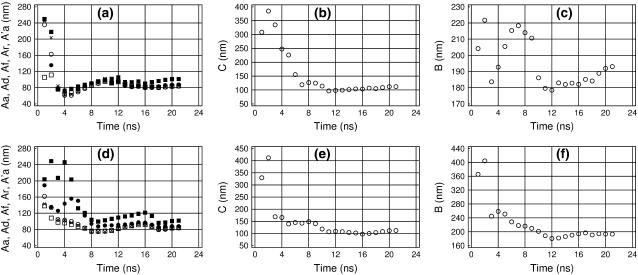
GC-alternating 25-mer fragment

The sequence-dependence of the elastic DNA parameters is very important because many proteins are believed to recognize specific DNA sites by testing their deformability. Fig. 8 shows the results of similar analysis carried out for the GC-alternating 25-mer DNA duplex. Qualitatively, these results are similar to those in Fig. 5; notably, the two molecules exhibit similar bending stiffness. Nevertheless, a significant difference is observed in the measured values of the torsional and stretching PLs. The GC-alternating duplex is significantly stiffer for stretching, but somewhat softer for twisting. The bending deformations of DNA result in large atom displacements and strongly affect the overall shape of the molecule, therefore the bending flexibility of DNA is generally recognized as a key factor in protein-DNA recognition. The torsional and stretching deformations cause smaller atom displacements. However, this does not exclude the possibility of recognition of specific DNA sequences according to their torsional and stretching stiffness. For instance, the amplitudes of relative atom displacements at the opposite ends of the 25-mer duplex estimated from the data in Fig. 2 are ∼1.7 Å and 2.8 Å, respectively, for stretching and twisting. These values are not negligible and the sequence effect upon twisting and stretching observed here can cause a difference in interaction energies sufficient for recognition.

FIGURE 8.

Time-convergence of the measured DNA elastic parameters in trajectory GC25. The same notations as in Fig. 5.

DISCUSSION

In these studies we were looking for a reliable procedure for evaluation of macroscopic elastic properties of the DNA double helix from atom-level MD simulations. Representative ensembles of conformations were studied for 25-mer double-helical DNA fragments in three different approximations for two regular alternating basepair sequences. The conformational statistics of ensembles generated by MD simulations demonstrates good qualitative agreement with the WLC theory and allows reasonably accurate estimates of the bending, torsional, and stretching PLs. The duration of trajectories necessary for acceptable convergence is significant, but accessible with the currently available computational resources. The measured values of DNA elastic parameters differ form the best experimental estimates, but the differences appear within the range of variations observed with different experimental approaches and solvent conditions. This is very encouraging since MD simulations are based upon the force field generated independently without any prior knowledge of experimental DNA stiffness. Therefore, even with the current accuracy, this MD approach can be used for probing various effects upon the DNA elasticity produced by external factors like solvent conditions or external stress.

Much of our efforts were spent on sorting out different factors that hinder interpretation of the atomic-level DNA dynamics in terms of the WLC theory. The major such factor is related with the necessary reduction of a detailed DNA conformation to an oriented axis rod (optimal helical axis). The Curves algorithm was proposed approximately 20 years ago (35), and since then became a standard instrument for treating this problem (30,31). Here it was found that the helical axes computed by Curves generate systematic artifact deviations from the WLC theory that can be reduced by adjusting the internal parameters of the algorithm. This does not mean that the earlier usage of Curves was biased by artifacts. Real double-helical DNA conformations do not have strict helical symmetry; therefore, the concept of optimal helical axis is relative and valid for a certain choice of criteria and parameters. Any such axis is good for comparisons if it is chosen as a conventional standard. The axes computed with the standard Curves parameterization deviate from the WLC theory, but those computed with increased axis stiffness may be inadequate for other purposes.

One might suggest that the Curves algorithm should be corrected to suppress the observed deviations from the WLC theory without increasing the artificial axis stiffness. In our view, this can only hide the problem and complicate interpretation of the results. The oscillating character of angular deviations in Fig. 1 varies with the basepair sequence of the DNA fragment, and sometimes it is not that obvious. In contrast, our earlier experience shows that, with the standard Curves algorithm, the A_r trace always has a concave shape. Such pattern can be misinterpreted as if short DNA fragments experience strong local bends that are anticorrelated along the sequence and cancel out in longer stretches. The oscillations shown in Fig. 1 in fact represent a fortunate feature that immediately reveals their nonphysical nature. Any improved axis-fitting algorithm will still be prone to local artifacts because the problem is inherent in the very fitting principle. For instance, the Curves algorithm assumes that base orientations with respect to the optimal helical axis change smoothly along DNA. This certainly contradicts the zigzag character of DNA with alternating sequences and perhaps results in the regular oscillations in Fig. 1. Unfortunately, it is hardly possible to propose a simple alternative algorithm free from such defects. We believe that accurate evaluation of DNA elasticity in MD simulations must, in any case, include systematic variation of the parameters employed by the axis-fitting algorithm and extrapolation to zero artificial stiffness. From this perspective, the Curves method is advantageous because it is rather rapid.

Earlier estimates of elastic parameters of MD models of DNA were made with the same force field and similar simulation conditions (30, 31), but with double helices of 15–16 basepairs and the duration of trajectories of 1–5 ns. We believe that the relatively small DNA length in these earlier studies explains why the Curves effect discussed above was not noticed. Instead, the apparent chain-length dependences of elastic parameters were interpreted as physical effects (31). In addition, unlike these earlier reports, we did not take into account the coupling between different elastic deformations because we were not sure if the accuracy of our data justifies a more sophisticated analysis. It is not surprising, therefore, that some of the values reported in Table 1 significantly differ from earlier estimates. Nevertheless, the qualitative trends are well reproduced—notably, the AT-alternating duplex exhibits higher torsional, but lower stretching stiffness than the GC-alternating DNA, which was also observed by Lankas et al. (31).

TABLE 1.

Parameters of DNA fragments measured in the course of MD

Trajectory	A	C	B	RMSD-B	RMSD-A	Twist	Rise
AT25a	∼80	∼150	∼100	4.01	6.38	32.7	3.21
AT25b	75	160	105	5.71	4.72	32.0	3.10
AT25c	115	270	340	3.05	8.45	34.2	3.43
GC25	80	105	190	2.78	6.53	34.4	3.2

Columns A, B, and C contain the estimated bending, stretching, and torsional PL, respectively. The RMSD values were measured with respect to the fiber canonical A- and B-forms (43) for DNA conformations averaged over the last nanosecond. Twist and Rise are evaluated for the same conformations by the Curves program (35). All distances are in nanometers and angles in degrees.

According to Table 1 the best MD elastic parameters obtained for realistic DNA models somewhat differ from the recent estimates (12,13,17,18,51). However, the differences are comparable to those between various experimental estimates of the same values (3,52). The bending PL is overestimated and it appears close to experimental data reported for low salt conditions (11). Interestingly, its value is very similar for AT- and GC-alternating duplexes even though the helical parameters of the former are strongly shifted toward the A-form due to the known force-field bias (36,53). This observation suggests that the shift in the bending PL may be due to insufficient screening of DNA charges in the standard hydration conditions used here, although relatively high stretching PL values argue against such interpretation (11). The torsional and stretching PLs strongly differ for these two DNA sequences, but still remain close to the recent experimental estimates (51). It should be stressed that this good general agreement with experiment is obtained without any fitting, by using force-field parameters adjusted with small molecule data only (23,36). The accuracy of the MD method will certainly be improved and, in the future, this approach can become one of the standard procedures along with experiment. Even in its present state, however, it can lead to useful insights in certain unclear aspects of DNA elasticity, such as its sequence-dependence and the coupling between different deformations, as well as effects of external stress. Simulations aimed at these objectives are in progress.