Microtubule Organization in Three-Dimensional Confined Geometries: Evaluating the Role of Elasticity Through a Combined In Vitro and Modeling Approach

Abstract

Microtubules or microtubule bundles in cells often grow longer than the size of the cell, which causes their shape and organization to adapt to constraints imposed by the cell geometry. We test the reciprocal role of elasticity and confinement in the organization of growing microtubules in a confining box-like geometry, in the absence of other (active) microtubule organizing processes. This is inspired, for example, by the cortical microtubule array of elongating plant cells, where microtubules are typically organized in an aligned array transverse to the cell elongation axis. The method we adopt is a combination of analytical calculations, in which the polymers are modeled as inextensible filaments with bending elasticity confined to a two-dimensional surface that defines the limits of a three-dimensional space, and in vitro experiments, in which microtubules are polymerized from nucleation seeds in microfabricated chambers. We show that these features are sufficient to organize the polymers in aligned, coiling configurations as for example observed in plant cells. Though elasticity can account for the regularity of these arrays, it cannot account for a transverse orientation of microtubules to the cell's long axis. We therefore conclude that an additional active, force-generating process is necessary to create a coiling configuration perpendicular to the long axis of the cell.

INTRODUCTION

The organization of cytoskeletal filaments such as actin filaments and microtubules plays an important role in cell morphogenesis (1,2). One of the features determining the behavior of the cytoskeleton is that it is naturally confined by the cell boundaries. Although the plasma membrane itself is quite flexible, the confinement is in many situations similar to a rigid box, due to the intracellular actin-cortex or extra-cellular limitations on membrane deformations. Examples of this are animal cells embedded in a tissue or in a confluent layer, or plant and fungal cells that are naturally surrounded by a rigid cell wall (3). To investigate the influence of rigid confinement on the organization of microtubules, in vitro experiments have been performed focusing on the positioning of microtubule (MT) nucleation centers (4,5) or the role of motor proteins in quasi two-dimensional flat geometries (6). Here, we consider free-growing filaments confined in three-dimensional (3D) elongated boxes in the absence of a fixed nucleation center or molecular motors. Although this problem is of general relevance for semiflexible filaments growing in rigidly confined geometries (including actin filaments (7)), we discuss our results in the particular context of the cortical microtubule organization in growing plant cells. For this system, the possible influence of microtubule elasticity on the ordering of microtubules has been discussed in a heuristic fashion before (see, e.g., (8–11)), but an actual quantitative estimate of the ordering effect, based on physical modeling, seems lacking.

Our approach involves a), quantitative theoretical modeling based on bending energy minimization of the coiling microtubules, and b), in vitro experiments, in which the complex biological system is partially reconstructed in a controlled way, starting from purified components. In the mathematical models, microtubules are represented as inextensible filaments with an elastic resistance to bending. The local bending energy associated with this resistance is proportional to the filaments' inverse radius of curvature squared, and is characterized by a single parameter, the so-called “bending stiffness”, κ. In the in vitro experiments, microtubules grow from nucleation seeds in microfabricated chambers. These chambers are prepared with sizes chosen to be similar to typical plant cells. In this model system, filament elongation is due to microtubule polymerization. The advantage of working with artificial systems that imitate certain cellular functions (4–6) is that the experiment provides an intermediate description of the system, bridging the living cell and the necessarily oversimplified mechanical theory. On one hand, compared to the simple theoretical picture, we are including all the degrees of freedom of real microtubules. On the other hand, the experimental environment is much simpler than a living cell. Most importantly, it does not include regulation by other proteins.

Cortical microtubules in plant cells

During interphase, intercalary growing plant cells contain a specialized cortical pattern of aligned microtubules that is closely related to the direction of cell growth, and that has no equivalent in other eukaryotes (12–16). Typically, in elongating cells, microtubules are organized perpendicular to the direction of growth, which mostly coincides with the long axis of the cell. It has been suggested that the orientation of the cortical microtubules directly determines the orientation of the cellulose microfibrils during their deposition into the cell wall (15–17). These cellulose microfibrils in turn play an important role in the mechanical integrity of the cell. Although doubts have been raised on the literal validity of this assumption (18–21), and cellulose synthases also move in ordered arrays when the cortical microtubules are not present (17), it is likely that the microtubules do play a role in determining where new wall deposition takes place (22,23). In nonelongating cells, microtubules are never transverse to the cell's long axis but instead random, oblique, or longitudinal.

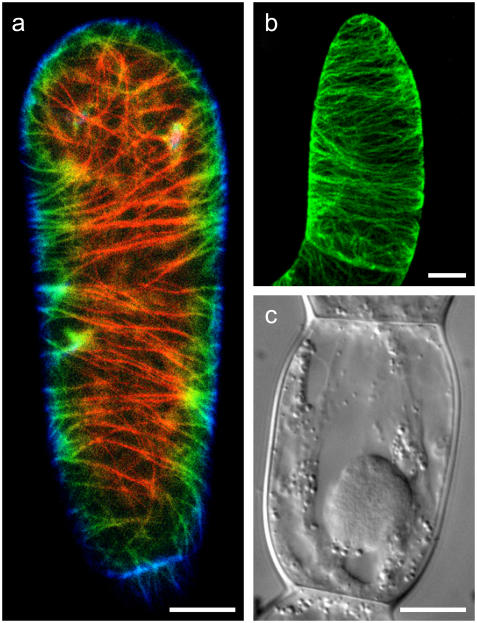
In plant cells, there is evidence that the microtubules, which individually are short (∼10 μm) compared to the cell size, form cross-linked bundles that appear to be many cell sizes long. Evidence for the existence of these bundles comes from transmission electron microscopy showing aligned short microtubules close to each other and the plasma membrane, and multiple cross-links between them (24,25). Additional indirect evidence comes from 3D reconstructions of confocal microscopy images with fluorescently labeled microtubules (see, e.g., Fig. 1, a and b). From time-course fluorescence and bleaching experiments, it is apparent that these bundles, although being stable as a whole, are dynamic in their microtubule content (27–29). These microtubule bundles arrange in long coils that wind around the cell cortex (30) (Fig. 1, a and b, and Supplementary Fig. 1). In this situation, the length of a MT bundle may be regulated by growth/shrinkage of the individual MTs and cross-linking between them, but one can also imagine that the length of these bundles is regulated through, for example, a motor-dependent microtubule sliding mechanism.

FIGURE 1.

Living plant cells with typical interphase microtubule organization and dimensions. (a) Confocal laser scanning microscopy image of a tobacco BY-2 suspension culture cell expressing GFP-TUA (green fluorescent protein linked to α-tubulin (25)). Nine images, 1 μm apart along the z-axis, were color coded from red to blue to represent the depth of the image (totaling 8 μm). In (b), a projection of a full confocal stack (totaling 21 μm) is shown of a tobacco BY-2 cell that was chemically fixed and immuno-labeled for α-tubulin (55). In both panels, the microtubules and microtubule bundles that wrap transversely around the cell are clearly visible. 3D reconstruction movies of these cells are available as Supplementary Material. (c) Example of a young T. virginiana stamen hair cell whose length and diameter were the basis of the dimensions and sizes of the theoretical boxes and the in vitro experiments in microfabricated chambers. This cell is part of the multicellular trichome on the stamen. Bars indicate 10 μm.

The cortical microtubule array can change its organization under a number of different circumstances. Microtubules are, for example, able to change their orientation in response to stimuli from plant growth regulators (31), blue light (32), electric fields (33), and gravity (34). Also, tubulin tyrosination (35), indirect microtubule-microtubule interactions (26), and the activity of the microtubule associated proteins, such as MOR1 (36), can influence the organization.

Despite a wealth of observations, an explanation for the formation of the cortical microtubule array, and its ability to change, is still lacking. In trying to understand the physics behind cortical array organization, one can distinguish between passive mechanisms, related to the mechanical properties of cytoskeletal filaments, and possible contributions from active processes such as treadmilling (27), dynamic instability (24,28,29), microtubule and γ-tubulin dependent nucleation (37), and motor proteins (38,39).

Earlier, we explored the theoretical possibility that thin hard rods, like microtubules, confined in a quasi two-dimensional space, can undergo an entropy-driven transition from a random (isotropic) organization to an ordered (nematic) state with increasing concentrations (40). In experiments in vitro, we indeed found that, for high enough concentrations, microtubules aligned in patches of ∼30–100 μm². The relatively high concentration that was required for the onset of this ordering suggests that, although excluded volume effects may influence the organization of cortical microtubules in the plant cell, they are most likely not the main driving force behind the formation of the aligned cortical array. Here, we examine the role of microtubule elasticity, and ask what to expect for the ordering behavior of (bundles of) microtubules confined in a 3D geometry that mimics the shape of an elongating plant cell.

We find that growing microtubules in a chamber assume coiling shapes above a critical length. Although these configurations are very similar to those found in plants, in almost all cases microtubules wrap longitudinally or obliquely along the chamber walls, and not transversely as observed in elongating plant cells. The modeling confirms this result, and shows that, although transverse coiling is a theoretical possibility for short microtubule lengths in relatively large and square confining boxes, this is not the case for parameter values that apply to plant cells. This leads us to conclude that elastic properties do have the ability to organize microtubules into coiled shapes in a confined space with cellular dimensions, but also that the combination of only active elongation and passive coiling by itself cannot lead to the specific organization of microtubules observed in plant cells. Thus, additional mechanisms are necessary for a plant cell to form and rearrange a transverse cortical microtubule network.

MATERIALS AND METHODS

Theory

Model

The representation of a microtubule, or a bundle, is a filament having length l, whose shape is described by a curve r(s), assigning a point in space for any value of the arc length parameter s. A given shape corresponds to a single configuration. In the model, the following functional specifies the value of the bending energy:

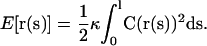(1)

Here, C(s) = |∂²r/∂s²| is the local curvature and κ the bending rigidity of the filament, i.e., the microtubule. In the model, the value of κ is considered as a fixed parameter. Furthermore, we impose the condition that the filament is unstretchable.

Energy estimates for longitudinal versus transverse helical coiling

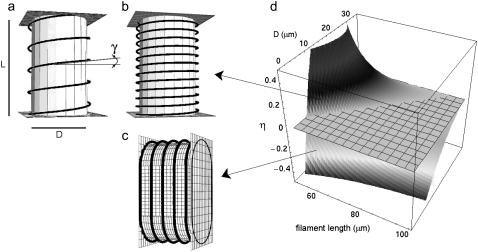
The energy estimates were calculated for two types of configurations, transverse and longitudinal helices on cylindrical surfaces. We imposed both the shape of the filament and that of the confining surface, and then calculated the corresponding energies. To construct the transverse helix, we used a cylinder where the filament could wrap only in the side walls (end caps were not present), and a length L that was larger than its base diameter D (see Fig. 2, a and b). For the longitudinal helix, we either used an elliptical box or an elongated box with rounded edges (see Fig. 2 c). This last case is particularly simple to tackle analytically, as the helix is constructed by piecewise connecting straight (zero curvature) filament stretches with filament stretches on the constant curves of two half-cylinders. The dimensions of the confining surfaces (Fig. 2, a–c) are D × L for the cylinders or D × D × L for the other boxes, where L > D (the box is elongated), and, calling l the filament length, l > L (necessary geometrical condition for the filament to be able to form a helix). The result for the ratio of E_Lo, the energy of a longitudinal coil, to E_Tr, the energy of a transverse one, was computed as

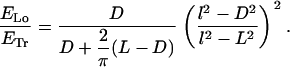(2)

FIGURE 2.

Filament configurations and bending energy estimates. The confining surface for the transverse helical coil is a cylinder with length L and diameter D and inaccessible end caps (a). The filament wraps around the cylinder and has a helical shape. The longer the filament, the lower the helical pitch (b). The transverse helix is compared with a longitudinal helix wrapped around an elongated box with rounded edges that has the same dimensions (length L and width D) (c). (d) Relative ratio η of the bending energy of a longitudinal (E_Lo) and a transverse coil (E_Tr) as a function of filament length l and box width D, for a fixed box length L of 35 μm. When this quantity is higher than zero, a transverse coil is favored; below zero, a longitudinal coil is favored. The intersection with the zero plane yields the critical filament length as a function of D. For the experimental value of 25 μm for the box's width D, the critical value for the filament length (l) is 80 μm.

This leads to the expression 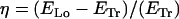, which is plotted in Fig. 2. A brief derivation of Eq. 2 is given in Appendix B.

Minimum energy configuration for a filament in a confined cylinder

To find the minimum energy configuration for a fixed shape of the confining surface, we evaluated the functional (1) for all possible configurations of the filament. The favored configuration is the one that minimizes elastic energy, i.e., for which δE = 0. For a filament on a cylinder with fixed boundary conditions at the end walls (clamped or torque-free, see Appendix A and Fig. 3 a), this leads to the Euler-Lagrange equation

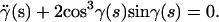(3)

FIGURE 3.

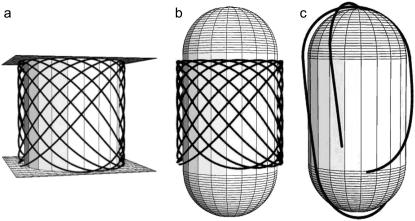
Euler-Lagrange minimal bending energy solutions. (a) Solution for a cylinder with inaccessible end walls is a wave-like configuration that loops around the cylinder several times. (b) On a spherocylinder with accessible caps, the minimal energy solution of the Euler-Lagrange equation is again an oscillating configuration, but only when the filament ends are fixed perpendicular to the length of the cylinder. (c) When one of the two ends is released, the minimum energy configuration is always a longitudinal coil.

In this equation, γ(s) is the angle between the tangent vector t = dr/ds of the filament and the horizontal axis, which is defined by the unit vector ê_ϕ, associated to the angular cylindrical coordinate ϕ (see Appendix A for a complete derivation of this equation). This equation is formally similar to the one that describes the motion of a pendulum. From the solution for the cylinder with inaccessible end walls, the minimum energy configuration of an elastic filament confined to a spherocylinder is computed by extending the solution with maximal circumferences on the constant-curvature sphere (see Fig. 2, b and c).

Experiments

Determination of plant cell-like aspect ratios

Tradescantia virginiana stamen hair cells were prepared from young flower buds in culture medium (5 mM Hepes, pH 7.0, 1 mM KCl, 1 mM MgCl₂, 0.1 mM CaCl₂) and observed in parafilm lined chambers on glass slides with differential interference contrast microscopy (Fig. 1 c). Lengths and diameters of 74 barrel shaped, nontip cells were measured and averaged. Data were not divided according to the cell cycle state, although cells just before division are generally larger then ones that have just finished division.

Tubulin and nucleation seeds

Tubulin was purified from pig brains as described earlier (41) and resuspended in MRB80 buffer (80 mM K-Pipes, 1 mM EGTA, 4 mM MgCl₂, pH 6.8). The protein concentration was measured by ultraviolet absorption. Lyophilized rhodamine-labeled tubulin was purchased from Cytoskeleton (Denver, CO) and resuspended in MRB80. Nucleation seeds were grown from free tubulin at 5 mg/ml in MRB80 with 2 mM GMPCPP for 45 min at 35°C. The batch of GMPCPP was generously provided by Tim Mitchison (Harvard Medical School, Cambridge, MA). The seeds were flash-frozen in liquid nitrogen after being extended in the presence of 0.4 mg/ml rhodamine-labeled tubulin and 5 mM guanosine triphosphate (GTP). The addition of the rhodamine-labeled tubulin allowed for easy detection of the seeds.

Microfabricated chambers

Microscope coverslips were cleaned for 1 day in chromosulfuric acid and briefly in 2M KOH in ethanol. After being rinsed, the slides were sonicated three times 10 min in dH₂O, rinsed in ethanol, and dried in an oven at 100°C. Photoresist SU-8 (micro resist technology, Berlin, Germany) was spun on the coverslips in layers of 25 or 40 μm. After a preexposure bake, the coverslips were illuminated with ultraviolet light at 1.75 mW/cm² through a quartz mask with chromium patterns, consisting of arrays of 25 × 35 or 40 × 80 μm rectangles and ellipsoids. The patterns were developed for five minutes in a micro resist SU-8 developer, rinsed, and hard baked. The caps to seal the microfabricated chambers were made from the silicon rubber polydimethylsiloxane (PDMS). The silicone elastomer precursor and a curing agent (Sylgard 184, Dow Corning, Seneffe, Belgium) were mixed in a 10:1 ratio (w/w), and brought under a low pressure with a small vacuum pump for 15 min to remove air bubbles. Uniform layers of ∼1–2 mm thick were cross-linked for 1 h at 100°C on top of flexible plastic sheets. The resulting rubber-like sheets were cut in circular disks to fit on the patterned coverslips. Patterned coverslips and PDMS disks were cleaned by sonication in ethanol, 5% soap in dH₂O, and dH₂O sequentially (1 min each).

Sample preparation

All the surfaces were coated with 2.5 mg/ml casein in MRB80 for 3 min to avoid aspecific binding of tubulin to the chamber walls, and dried with nitrogen. Thereafter, a), the nucleation seeds in MRB80, and b), 1 mg/ml tubulin (10% rhodamine-labeled), 2.5 mM GTP and an oxygen scavenging system (75 mM glucose, 0.6 mg/ml glucose oxidase, 0.3 mg/ml catalase, 7mM dithiothreitol) in MRB80 were introduced in the chambers in two sequential steps on a cold metal block. After each step, the patterned coverslips were incubated in a low-vacuum chamber for 3 min to avoid the trapping of air bubbles in the chambers. The chambers were sealed with PDMS disks (Fig. 4 c). By using a solution of fluorescein isothiocyanate silica beads (1 μm diameter, courtesy of Dirk Vossen, Utrecht University, The Netherlands) in water, it was possible to test that the chambers were filled and sealed. The beads were imaged with video-enhanced fluorescence microscopy, and showed diffusive motion.

FIGURE 4.

Scanning electron microscopy images of the microfabricated chambers, arranged in arrays of rectangular boxes and elliptical cylinders. A sample consists of a few thousand chambers on a microscope coverslip. The elongated base of the boxes defines the dimensions D and L. The depth is made equal to D. (a) Top view of an array of 35 × 25 × 25 μm boxes. (b) Tilted view of an array of boxes sized 80 × 40 × 40 μm (detail). (c) Sketch of the chamber assembly with indication of the imaging direction, i.e., the location of the objective lens (side view; not to scale).

Fluorescence and confocal microscopy, and image reconstruction

Fluorescent microtubules in chambers were observed using an inverted Leica DM-IRB fluorescence microscope equipped with a 100×, 1.3 numerical aperture, oil immersion objective and a Kappa Opto-Electronics (Gleichen, Germany) charge-coupled device with variable integration time, connected to a computer and an S-VHS VCR. The samples were imaged from the side of the patterned coverslip and taped while moving the microscope stage manually at random through different regions. We checked for diffusive motion of short microtubules in early stages of polymerization to discard a possible role for convection. The orientation of the microtubules was established from visual examination of the video tapes. Z-stacks of images were acquired using a Leica TCS-SP2 confocal microscope with a 63×, 1.4 numerical aperture, oil immersion objective and analyzed to reconstruct the shape of the polymerized microtubules in the chambers. Due to the scattering from the walls, there was a decrease in fluorescence intensity from the coverslip side (bottom) to the PDMS side (top) of the chambers. Images of chambers filled with an aqueous solution of 0.05 mg/ml fluorescein verified that this was inherent to the technique (Supplementary Fig. 2). To compensate for this artifact, a linear gradient contrast mask in the z direction was applied to 3D image reconstructions with the program ImageJ (http://rsb.info.nih.gov/ij/). Isosurfaces were visualized using the program MayaVi (http://mayavi.sourceforge.net/). Manual filament tracking was carried out using ImageJ, and the coordinate files were analyzed with the program Xmakemol (http://www.nongnu.org/xmakemol/). Due to the flexibility of PDMS, sometimes the caps of the chambers were slightly bent inward. This problem was enhanced after incubating the samples at 35°C to increase microtubule polymerization. In all the relevant cases for the analysis, deformation was checked at the confocal microscope and was <5%.

RESULTS

In our model systems, dynamic (bundles of) microtubules are represented theoretically as unstretchable filaments with variable length and resistance to bending confined to a two-dimensional surface (see Materials and Methods section), and in our in vitro experiments as single microtubules polymerizing from nucleation seeds in a microfabricated chamber. Clearly, in setting up these models we are making a number of assumptions: a), that the bending elasticity is a sufficient mechanical characterization of microtubules; b), that the passive behavior of a bundle of microtubules in vivo can be qualitatively represented by that of a single microtubule in vitro, and c), that the elongation mechanism does not matter, so that polymerization can, for example, represent relative sliding in vivo. The implications of these choices will be discussed along with the results. To avoid misunderstandings, throughout the article we use the word “filament” for the theoretical counterpart of a single microtubule or a bundle thereof.

To help us choose the geometry and size of the theoretical and in vitro “cells”, we measured the diameter and length of growing T. virginiana stamen hair cells (Fig. 1 c). For the cell diameter, we found a mean value of 25.7 μm (standard deviation 1.7 μm; n = 74) ranging from a minimum value of 22.7 μm to a maximum of 30.5 μm. For the cell length, the mean value was 35.9 μm (standard deviation 6.4 μm; n = 74), with minimal value 18.4 μm and maximal value 48.7 μm. Based on these results, a cell diameter of 25 μm and a length of 35 μm were considered as representative dimensions for the theoretical surfaces and the microfabricated chambers.

Theoretical model

In our theoretical model, the cell cortex is idealized as a two-dimensional closed surface, typically represented by the surface of a cylinder with or without accessible caps. Microtubules (or microtubule bundles) are represented by elastic inextensible filaments that are confined to this two-dimensional surface. The resistance to bending of the filaments is the only parameter responsible for their shape. In particular, there is no intrinsic chirality (a filament, at rest, does not have any structural signature that makes it prefer a helical shape). This is justified by experimental observations of the mechanical properties of microtubules polymerized in vitro (42). Thus, the organization at the cylindrical surface is determined only by the interplay between the length of the elastic filament and the constraint forces that confine it to a two-dimensional surface. To enable the comparison with the in vitro model system (and the living cell), the specific parameters of the microtubule, the filaments' stiffness and length, need to be specified. The bending stiffness of a single microtubule is known experimentally to be of the order of 10 pN·μm² (42,43). The stiffness of a microtubule bundle of N filaments can be estimated as N times that of a single microtubule (if they are free to slide past each other, even in the presence of friction caused by the cross-links). The microtubule length in the experiments varied, up to a maximum of 100–120 μm.

Energy estimates of a transverse versus a longitudinal coiling helix

Filaments want to be straight, and relatively short ones (shorter than the length of the cell) will therefore align with the long axis of the cell. When filaments become longer, one possibility is that they form a transverse helix with a helical pitch that depends on the filaments' length (Fig. 2 a) (8,9). The longer the filament, the lower the helical pitch, so that microtubules are more and more transverse (Fig. 2 b). However, next to this transversal coil another configuration is possible: a longitudinal coil, in which the filament is wrapped around the long axis of the cell. To establish which way of coiling is energetically more favorable, we compared the bending energies between the above transversal (Fig. 2, a and b) and various longitudinal coil configurations. This was achieved by limiting the coiling to one of the two directions and imposing two walls at the extremities of the curved surface that prevent the filament from spanning the caps. We considered longitudinal coils on elongated boxes with rounded edges (Fig. 2 c) as well as elliptical cylinders (not shown), both with comparable aspect ratios (length L to diameter or width D) as the cylinders that were used for the transverse coils. The bending energies were calculated for increasing cylinder diameters (or box widths), and increasing filament lengths. For example, a 100 μm long and transversely coiled filament on a cylinder with a diameter of 25 μm and a length of 35 μm, the size and aspect ratio of a typical T. virginiana stamen hair cell, has a bending energy that is a factor of 1.25 higher than the bending energy of the same filament, coiled longitudinally on an elongated box with the same dimensions. The main result is that there is a trade-off in energy cost for the filament between doing a smaller number of high-curvature turns, as in the longitudinal coil, and a higher number of low-curvature ones, as in the (tilted) transverse coil. As the box or cylinder gets longer, fewer and fewer high-curvature turns are needed in the longitudinal configuration, which will eventually always be more favorable.

The results are summarized in Fig. 2 d, where we plot the relative ratio of the bending energy of a longitudinal over a transverse coil (η = (E_Lo − E_Tr)/E_Tr) for a cylinder or box with a length of 35 μm as a function of the cylinder's diameter (or box's width) and the filament's length (see Eq. 2 in Materials and Methods). In this estimate, we assumed an integer number of coils to calculate E_Lo. Note that η is independent of the bending rigidity of the filament, since κ affects E_Lo and E_Tr in the same way. η is positive when the transverse coil is favored, negative when the longitudinal coil is favored, and zero when the two configurations have equivalent bending energies. The graph shows that a transverse helix is energetically favored only for shorter filaments, whereas a longitudinal coil is the dominant shape for longer filaments. For a cylinder with a diameter of 25 μm and a length of 35 μm, we can expect a threshold filament length (above which longitudinal coiling is energetically favored) of ∼80 μm. This crossover filament length depends only slightly on the exact shape of the box. The bending energy for a 100 μm long filament coiling longitudinally on an elliptical cylinder (not shown) with above-mentioned dimensions differs only a few percent from the longitudinal coil on an elongated box with rounded edges. Most importantly, the crossover filament length depends on the box's aspect ratio, decreasing as the box becomes narrower.

Minimal energy configuration

Although the above energy estimates of imposed configurations can be useful to understand the influence of aspect ratio on preferred orientation, they do not tell us what the real minimum energy configuration of the system is. Therefore, we again considered a cylinder on which the filament was confined between two end walls. The solution given by a true minimization of the energy functional (see Materials and Methods) is not a helix as considered before, but an oscillating configuration in which the filament crosses back and forth between the two end walls (Fig. 3 a). Comparing this configuration with a helix of equivalent length (Fig. 2 b), it is easy to understand why the repeated traversing between two walls should be favored: the hoops of a long helix become close to transverse circles, whose curvature is the highest on the surface of a cylinder, whereas the oblique hoops maintain a constant, intermediate, curvature, regardless of the filament length.

Taking away the end walls and replacing them with accessible semispherical caps, allows the filament to explore more configurations, including a longitudinal coil. To answer if a longitudinal, transverse, or oscillating coil is favored when the filament is longer than the cell length, the procedure to find minimum energy solutions was repeated for a cylinder with accessible spherical caps (44). In the solutions, the filament wraps into an oscillating configuration when both filament ends are fixed in a transverse direction (Fig. 3 b). In other words, the oscillating arrangement is only possible if there is some extra force to keep the filament ends in place. When one or both ends are released, the filament always wraps longitudinally (Fig. 3 c).

From these theoretical considerations, we conclude that i), assuming that the configurations are helices, longitudinal coils are energetically favored for long filaments and large aspect ratios of the cell; ii), transverse helices may be favored for shorter filaments; and iii), the minimization of the energy functional gives no solutions that are simply helical or completely transverse even in the limiting case of fixed boundary conditions on the sides of the cylinder (that render the end caps inaccessible).

In vitro experiments

In the experiments, microtubules were polymerized from nucleation seeds in microfabricated chambers (Figs. 4 and 5). In these samples, the confinement is not two-dimensional as in the theoretical model, because filaments shorter than the cell's longest diagonal are free to move in the internal volume of the microchambers. However, two-dimensional confinement to the side walls is effectively accomplished when the growing filaments become long and are forced to bend against the side walls.

FIGURE 5.

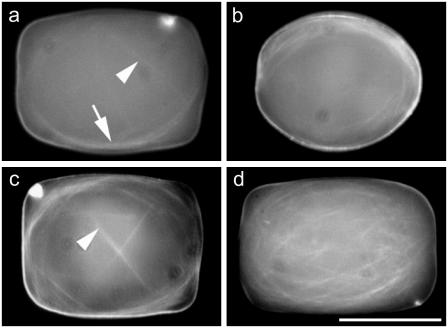
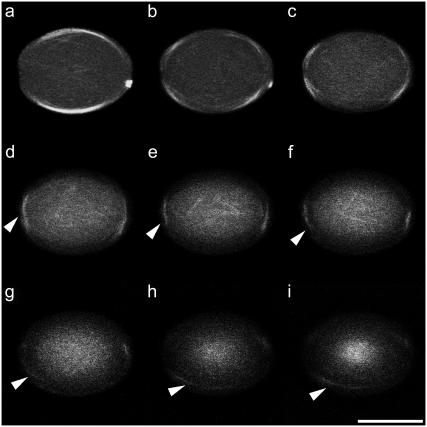
Microchambers imaged with conventional fluorescence microscopy. Rhodamine-labeled microtubules were imaged in the focal plane at the coverslip side (bottom) of small microchambers (25 × 25 × 35 μm). (a) Microtubule buckling was visible after 10 min of incubation at room temperature. The arrow points to a group of microtubules coiling longitudinally, whereas the arrowhead points to an individual microtubule coiling transversely. (b) After 1 h of incubation at room temperature, microtubules coiled longitudinally in most of the cases (71%). (c) Although the dominant coil was always longitudinal, transverse coils were sometimes (16%) visible (arrowhead). (d) Occasionally, marked longitudinal coiling was visible that was not strictly in the plane of focus, but looped around perpendicular to it. Bar is 20 μm.

The chambers were built on microscope coverslips using lithographic techniques. They had the shape of elongated boxes with elliptical or rectangular bases. We used chambers of two sizes, 35 × 25 × 25 μm and 80 × 40 × 40 μm (Fig. 4, a and b). The chambers were filled with a solution containing microtubule nucleation seeds, free tubulin and GTP and then sealed with a rubber-like material (PDMS). Microtubules polymerized at room temperature from the nucleation seeds in the sealed chambers and reached lengths greater than the long axis of the box (Fig. 4 c). Each chamber contained roughly a few tens of microtubules. The length of the individual microtubules was not under control, since microtubules polymerizing from seeds have, due to the dynamic instability process, a wide steady-state length distribution (41). The tubulin was partly labeled with the fluorescent dye rhodamine, so that the growing microtubules could be imaged with conventional fluorescence and confocal microscopy techniques. This involved a few technical difficulties: a), the background of free labeled tubulin reduced the signal/noise ratio, especially at the beginning of the polymerization reaction, b), the damage due to photobleaching limited the amount of time we could image our samples, and c), the scattering from the side walls affected the image quality (see below).

Transverse versus longitudinal coiling

The microtubule configurations were imaged with conventional fluorescence microscopy, in many chambers simultaneously, to have a global indication of the statistical occurrence of the different coiling configurations. With this technique, only the microtubules close to the bottom of the chambers (i.e., close to the coverslip surface and objective lens on the inverted microscope; Fig. 4 c) could be visualized. Nevertheless, transversal coils could be distinguished from longitudinal ones. In the larger (80 × 40 × 40 μm) chambers, microtubules were too short to form coils, and only the longest ones were observed to buckle, without bending around the side walls, after having positioned themselves along the longest available diagonal in the boxes (not shown). Thus, we estimate that the microtubules had a maximal length of ∼100–120 μm (slightly longer than the longest diagonal of the chambers). This length is about three times the longest axis of the smaller chamber, so that coiling is expected there. Indeed, in the smaller chambers (35 × 25 × 25 μm), and with the same conditions, the microtubules were long enough to bend around the side walls and form coils (Fig. 5).

In the early stages of polymerization, after 10 min of incubation at room temperature in the small chambers, individual microtubules were only long enough to coil in a small fraction of the chambers (Fig. 5 a). Thus, only few observations of coiled microtubules were possible, because the shorter polymers were not yet immobilized. Of 54 buckled microtubules observed in 200 chambers across three experiments, 36 were judged longitudinal and 18 transverse. In the later stages (after 30 min to 1 h incubation at room temperature), more microtubules had polymerized (Fig. 5, b–d) and it was now possible to collect data from a larger number of chambers. After counting the configurations for 148 chambers over three experiments, we found that 71% of the chambers showed only longitudinal coils (Fig. 5 b); ∼16% showed mostly longitudinal coils in addition to some transverse (Fig. 5 c), whereas <1% contained only transversely coiled filaments (not shown). The remaining chambers had random or nondefinable coil orientations. Most of the longitudinal coils we observed coiled around the direction of observation of the chambers (i.e., in the horizontal plane), as in Fig. 5 b. Only few longitudinal coils were oriented perpendicular to the horizontal plane (Fig. 5 d).

We conclude that during the early stage of polymerization, there is still a balance between the number of longitudinal and transverse coils. When the microtubules become longer, the balance is shifted to more longitudinal coils. The greater frequency of transverse coils early on in the polymerization reaction is consistent with the theoretical prediction that such coils are favored for shorter filaments.

3D reconstruction

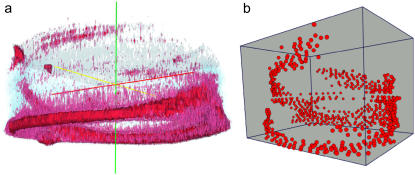
Confocal imaging of the chambers allowed the reconstruction of the full shape of the buckled microtubules in individual chambers (Figs. 6 and 7). It was not possible to image single filaments early on in the polymerization reaction, due to thermal vibrations, image integration time, and light scattering from the chamber walls. After 1 h of incubation, when most of the free tubulin in the chamber had polymerized and the configurations were more stationary, the dominant configurations appeared as helices that coiled around in longitudinal arrangements, i.e., parallel to the bottom of the chamber and slightly spiraling up toward the PDMS lid on the chamber (Fig. 7, a and b). It should be noted that we mostly observed longitudinal coils in the bottom part of our chambers. One could argue that the relative lack of coils higher up in the chambers might be due to geometric asymmetries, caused by a slight concaveness of the PDMS cap (<5%, see Materials and Methods) or by differences in the material properties of the chamber faces (glass versus photoresist versus PDMS; see Materials and Methods). However, our observations were most likely biased due to problems with light scattering from the side walls, which causes a loss of signal intensity farther away from the objective lens. To test this last possibility, we filled the chambers with freely diffusible fluorescein in water and made optical sections from top to bottom (and vice versa). The fluorescence intensity in yz-projections of these chambers has a conical shape, clearly showing that not the whole chamber could be imaged with the same intensity (Supplementary Fig. 2).

FIGURE 6.

Montage of confocal xy-sections showing microtubules in a 25 × 25 × 35 μm chamber, from the coverslip side (bottom) to the PDMS lid (top). Microtubules can be followed through the sections to form a coil (see arrowheads). The distance between two subsequent sections is ∼2.5 μm. Bar is 20 μm.

FIGURE 7.

3D image reconstructions of coiling microtubules. (a) Reconstruction produced from a confocal z-stack of microtubules coiling in a small oval chamber (25 × 25 × 35 μm) using intensity isosurfaces. The red/purple isosurfaces show the bundle of microtubules. The light blue isosurface shows the shape of the chamber. (b) 3D image reconstruction of the same coil using a position tracking method (see Materials and Methods). The spheres indicate points with clearly visible microtubule groups, which where manually tracked from confocal xy-stacks.

DISCUSSION

In this work, we studied the organization of microtubules growing in microfabricated chambers having box-like elongated shapes. We compared the results with the theoretical predictions for a confined filament with finite bending elasticity. In the experiments, we examined the coiling configurations of the filaments obtained by fluorescence and confocal microscopy, and analyzed the statistical occurrence of different kinds of coiling in relation with the polymerization stage (and thus the length) of the filaments. Experiment and theory agree quite well in the prediction that longitudinal coiling is favored compared to transverse coiling. In fact, for the aspect ratios and sizes analyzed, the favored configuration in our elongated box is almost always a longitudinal coil (Figs. 2–7), Only in the early stage of polymerization do we observe transverse, or rather, oblique configurations. Our energy estimates predict that longitudinal coiling is energetically favored over transverse coiling if the filament is longer than a threshold length and assuming that the configurations are helices whose pitch is dependent on filament length (see Eq. 2). Looking for configurations that truly minimize the bending energy, purely transverse coils were not found at all. Instead, the longitudinal coil was the only solution in a cylinder with accessible caps (Fig. 3 c), and an oscillating coil was found in the presence of restricting end walls or transversely fixed filament ends (Fig. 3, a and b). In our experiments, microtubules were too short to test this prediction in a stringent way. However, our fluorescence images (e.g., Fig. 5 c) do show some spirals in opposite directions that resemble the theoretically predicted oscillating coils (Fig. 3, a and b). Consistent with the theoretical predictions, we found a balance between longitudinal and transverse (oblique) coils in the early stages of polymerization, when microtubules were still relatively short, and a decided preference for longitudinal coils in later stages, when microtubules were longer (with an estimated length of 100–120 μm; Figs. 5–7). Indeed, our comparison of the bending energy of longitudinal and transverse coils for the experimental box size of 35 × 25 × 25 μm gave a theoretical threshold filament length of ∼80 μm (thus ∼2.5 times the long axis of the chamber), above which longitudinal coiling is energetically favored.

In principle, microtubule bundles in vivo could have a quite different stiffness from individual microtubules in vitro. How robust are our predictions with respect to variations in filament stiffness? Both our estimates and solutions are independent of κ, thus the limit of validity of our conclusions is set by the main hypothesis of the model—that filament stiffness is the only relevant feature. This would cease to be true when the persistence length becomes of the order of the chamber size, which in terms of κ happens at ∼1 order of magnitude below the stiffness of one microtubule in vitro. It seems unlikely that microtubules in vivo would be that weak. Our work thus suggests that confinement and bending elasticity together are in principle sufficient to organize long microtubules in coiling configurations. For this, the only relevant features are filament length, resistance to bending, and the size and aspect ratio of the confining box.

The relevance of our results for microtubules in plant cells relies on the hypothesis that the microtubules in the cortical array cross-link to form bundles that have mechanical integrity. Although we argued in the Introduction that this is likely the case, there is no direct experimental evidence for this. Granted this fact, our findings imply that in the live plant cell, additional mechanisms other than elasticity are necessary to form and maintain the typical transverse microtubule arrangement in the cortex. This is not surprising, as the situation in vivo is quite complex. Our simple analysis based on elasticity might be useful to estimate the magnitude of the passive drives that need to be overcome. In fact, assuming a cell radius of the order of 10–15 μm and given the stiffness of a single microtubule (which has a persistence length of the order of a few millimeters), one readily estimates a stored energy of the order of 1 pN μm, or ∼250 kT, for a single transverse loop that spans the circumference of the cell.

The additional mechanisms needed to organize a cortical array against the dictates of elasticity could be kinetic and/or physical constraints, or active forces arising from the internal dynamics of the bundles. Short transverse microtubule coils that, compatible with our theoretical and experimental findings, are formed in the beginning of the cell growth might not be able to transform into minimum bending energy longitudinal coils and might thus get trapped in a metastable state. This kinetic trapping could have a variety of microscopic origins, ranging from steric hindrance between microtubules to the presence of cross-linking molecules connecting the microtubules to the plasma membrane. Proteins like MAP65 (15,45,46), or phospholipase-D (16,47) could perform these tasks. As for active forces, the activity of molecular motors could be involved in forcing the microtubule array to be transverse (38). Systems of purified microtubules and molecular motor complexes have been show to exhibit a remarkable number of self-organized spatial patterns (6,48,49). In addition, motor proteins could generate forces that change the shape of the microtubule bundles, such as torque or torsion, which are not inherent to the single microtubules. We note that, from the point of view of our model, when a force is present (e.g., from motors or cross-linkers), the bending rigidity κ does not drop from the equations (see Eqs. A2 and A13). This means that an additional length scale could appear in the system, and therefore different configurations from those discussed here are possible. Experimentally, little is known about the activity of microtubule motors during interphase in plants (50,51), except that motors are involved in cell shape generation of trichomes (52,53). On the other hand, no axial or lateral transport of microtubules was observed in living Arabidopsis thaliana or tobacco BY-2 cells during interphase (27,29). The in vitro system we adopted could be adapted to pose questions on the role of molecular motors in the organization of freely nucleated microtubules in 3D-confined geometries. Preliminary experiments with purified motor proteins in this direction indicate the presence of configurations that are indeed different from those found without motors (54).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX A: DERIVATION OF EQ. 3

We consider the case of an elastic filament with length l and bending rigidity κ, which is confined on a cylindrical sheet with radius r. The shape of the filament is given by the position vector r(s), where s is the arc length. The optimal shape r(s) of this filament corresponds to the minimum of the elastic energy,

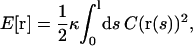(A1)

where C(r(s)) is the curvature at position r(s). To derive the shape equation of the filament, we use the variational principle

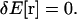(A2)

Roughly, Eq. A2 means that there is no change of the elastic energy for any different shape r(s), which is arbitrarily close to r(s). To use Eq. A2, we derive an explicit form of Eq. A1 with the use of cylindrical coordinates (r, ϕ, z) and the corresponding orthogonal system of axes (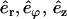). The curvature can be expressed as the derivative of the tangent vector t(s), C(r(s))² = (dt/ds)². The tangent vector is given by

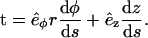(A3)

The derivative of the tangent vector with respect to the arc length s is

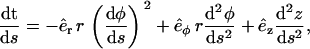(A4)

where we used the relation 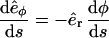. We now use the inextensibility condition, which can be realized imposing that the length of the tangent vector is constant, |t(s)| = 1, i.e., (see Eq. A3)

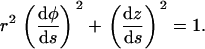(A5)

Using Eq. A5 to eliminate the second derivative of z(s) from Eq. A4, one obtains

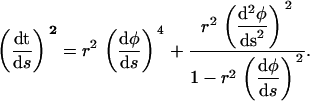(A6)

Equation A6 can be simplified introducing the ascending angle γ(s), which is defined by the relations

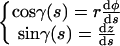(A7)

With the help of definition A7, Eq. A6 becomes

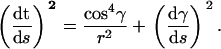(A8)

Then the elastic energy functional E[r] becomes:

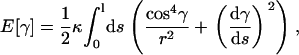(A9)

and the shape of the filament is fully defined by the equation of its ascending angle γ(s).

One can use Eq. A9 to apply the variational principle A2. Suppose the curve γ(s) is the true physical shape of the filament that minimizes the elastic energy. Considering a small deviation from this curve, which is defined by a slightly different shape γ′(s), we are interested in the “variation”

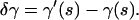(A10)

We consider the variation A10 by keeping fixed conditions at the ends of the filament. These conditions depend on whether the ends are clamped or torque free:

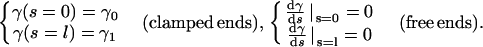(A11)

Given an arbitrary variation A10, we obtain from Eq. A9 after integration by parts:

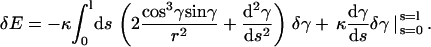(A12)

Now it is important to realize that with the use of boundary conditions (A11), the boundary terms in Eq. A12 vanish. Since δγ is arbitrary, the condition δE = 0 is satisfied if and only if the integrand is zero, i.e.,

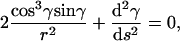(A13)

which is Eq. 3 from the main text.

APPENDIX B: DERIVATION OF EQ. 2

Transverse coil

We refer to Fig. 2, a and b. If we denote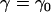 the constant ascending angle, then from the second equation from Eq. A7 we have

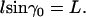(B1)

With the use of Eq. B1, we derive from Eq. A9 the elastic energy for the transverse coil

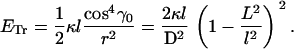(B2)

Longitudinal coil

For this case, we refer to Fig. 2 c. We denote the constant ascending angle in this case as 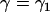. From Eq. A7 we have

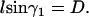(B3)

We now consider a piece of the filament that coils around the chamber only once. A part of this piece is bent on the round sides of the chamber and it has a length

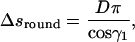(B4)

which can be derived after integrating around a full circle the first condition in Eq. A7. Another part of this coil is sitting on the flat sides of the chamber, and the length of this is calculated in the same way:

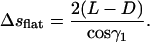(B5)

The ascending length along the transverse direction of such a coil is 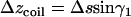, where 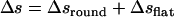is the total length of this coil. The number of coils around the chamber is 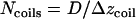, i.e.,

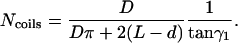(B6)

The total elastic energy is

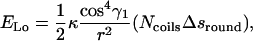(B7)

as only the bent parts of the filament contribute. With the use of Eqs. B3, B4, and B6, the energy of the longitudinal coil is written as

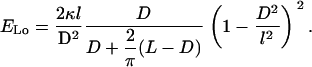(B8)

Finally, calculating the energy ratio from Eqs. B8 and B2, one obtains Eq. 2.