Soil nutrients influence spatial distributions of tropical tree species

Abstract

The importance of niche vs. neutral assembly mechanisms in structuring tropical tree communities remains an important unsettled question in community ecology [Bell G (2005) Ecology 86:1757–1770]. There is ample evidence that species distributions are determined by soils and habitat factors at landscape (<10⁴ km²) and regional scales. At local scales (<1 km²), however, habitat factors and species distributions show comparable spatial aggregation, making it difficult to disentangle the importance of niche and dispersal processes. In this article, we test soil resource-based niche assembly at a local scale, using species and soil nutrient distributions obtained at high spatial resolution in three diverse neotropical forest plots in Colombia (La Planada), Ecuador (Yasuni), and Panama (Barro Colorado Island). Using spatial distribution maps of >0.5 million individual trees of 1,400 species and 10 essential plant nutrients, we used Monte Carlo simulations of species distributions to test plant–soil associations against null expectations based on dispersal assembly. We found that the spatial distributions of 36–51% of tree species at these sites show strong associations to soil nutrient distributions. Neutral dispersal assembly cannot account for these plant–soil associations or the observed niche breadths of these species. These results indicate that belowground resource availability plays an important role in the assembly of tropical tree communities at local scales and provide the basis for future investigations on the mechanisms of resource competition among tropical tree species.

The high local diversity of tropical tree communities poses a unique challenge for testing niche assembly theories based on resource competition (1). In these species-rich communities, hundreds of tree species can coexist in a single site (2), which renders assessment of the outcome of pairwise competitive interactions intractable. Conversely, the high diversity and relative rarity of most species also means that species seldom encounter each other in ecological neighborhood interactions (3), which suggests that competitive differences among species might not have a predictable effect on community structure. In fact, neutral theories of community assembly assume that there are no competitive differences among species and that ecological communities are assembled by random dispersal. Under neutral community assembly, alpha diversity would be governed by metacommunity diversity and speciation–extinction at macroecological scales (4, 5).

Despite the contrasting mechanisms of community assembly proposed by neutral and niche theories, several lines of evidence support each of these perspectives. Tropical tree species differ in their light requirements for regeneration (6) because of a tradeoff between growth rate under high light and survival in the shade (7–9). Seedlings and saplings of different species differ in their resistance to pests, resulting in a frequency-dependent advantage when species are locally rare (10, 11). And species are known to assume different positions along a competition–colonization tradeoff axis that allows competitively inferior species to persist, because they are better colonizers (12, 13). Nevertheless, there are aggregate properties of communities such as population size and range size distributions that are also well explained by neutral models that do not invoke species differences in life history traits (14–16).

The clearest evidence for the effects of habitat and soil factors on species distributions comes from studies conducted at mesoscales (≈1–100 km²) (17, 18) and landscape scales (10² to 10⁴ km²) (19–24). At these scales, tropical forest landscapes are a mosaic of edaphic types (25, 26), with levels of heterogeneity and spatial segregation that allow the effects of dispersal and habitat factors on species distributions and community structure to be relatively easily quantified. At local scales (<1 km²), however, the spatial aggregation patterns of species that result from both limited dispersal and habitat heterogeneity coincide in ways that make it difficult to disentangle their relative importance to local community structure (27, 28). Although the importance of edaphic factors in maintaining local diversity has long been recognized (29, 30), a thorough, quantitative assessment of the importance of soil resources on tropical tree distributions for entire communities has not been undertaken. Typically, studies have either focused on a small fraction of the tree species in any community (31–33) or related community-wide tree species distributions to topographical variables whose relationships with underlying soil resources are unknown (28, 34, 35). To test relationships between species distributions and soil resource availability, soil resources and species distributions need to be mapped at high spatial resolution for entire communities in plots large enough to span substantial spatial heterogeneity in soil factors.

In this study, we conduct such community-wide analyses and present evidence that the spatial distributions of large numbers of tree species in three diverse Neotropical forest plots are strongly associated with the distributions of soil resources. We use data on tree distributions for all free-standing trees ≥1-cm diameter at breast height in large permanent plots in lowland forest at Barro Colorado Island (BCI), Panama, and Yasuni National Park, Ecuador, and in montane forest at La Planada Forest Reserve, Colombia. At each site, we used identical methods to measure extractable soil cations, available N, nitrogen mineralization (N_min) rates, and extractable phosphorus at 0- to 10-cm depths at high spatial resolution. We then generated maps of estimated soil resource availability at the 10 × 10-m scale for each plot, using geostatistical methods (36).

We first used exploratory unconstrained ordination analyses, using nonmetric multidimensional scaling (NMDS) to test whether species composition was related to soil nutrient variation. Next, we tested associations between species distributions and soil nutrient distributions. To do this, we needed to account for the spatial covariation among the multiple soil resources and the spatial aggregation patterns of species that are in part due to limited dispersal. We also expected that testing several individual soil nutrients would result in a large number of comparisons overall and thereby an inflated type I error. To account for spatial covariation among variables and minimize overall type I error, we computed principal components (PCs) of soil nutrient values and used only the first three components to test species–soil associations. To model the spatial aggregation pattern of each species, we fitted the Poisson cluster model (PCM) by using the Ripley's K function as the summary statistic (27). We then compared the associations between observed species distributions and PCs with null expectations derived from using artificial species distributions simulated by using the PCM. Finally, we explored whether individual soil nutrients have differing effects on community structure by analyzing species nutrient niche breadths. Niche breadth values indicate the fraction of each available soil nutrient gradient occupied by a species (37).

Results and Discussion

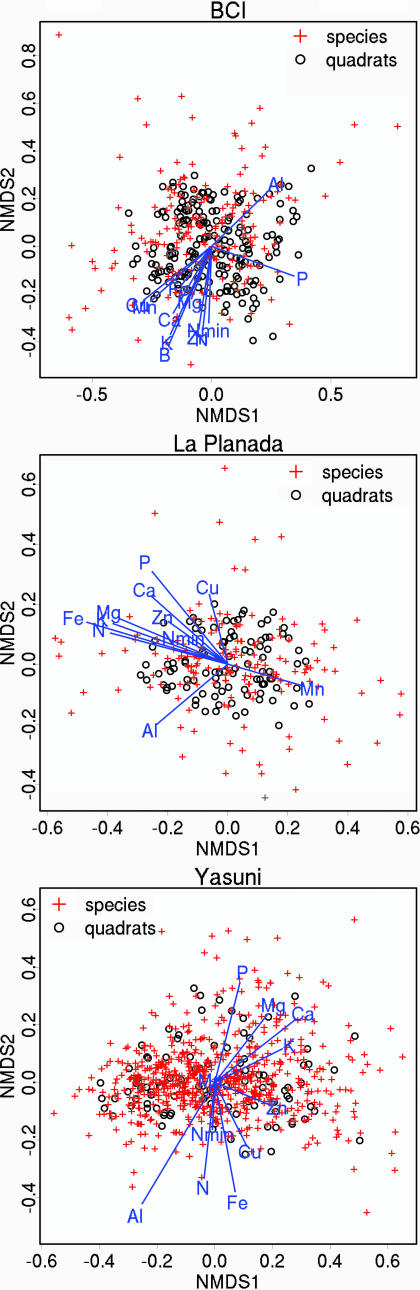
At all three sites differences in species composition among 50 × 50 m quadrats were significantly related to differences in the mean levels of soil nutrients in quadrats. We fitted soil nutrient vectors to NMDS ordinations of species abundance (38, 39) in 50 × 50 m quadrats and found that most soil variables were significantly correlated to the NMDS ordination axes [Fig. 1, and supporting information (SI) Fig. 4 and SI Table 3]. However, as the directions and the lengths of the soil nutrient vectors indicate (Fig. 1), several soil nutrients show similar effects, particularly at BCI and La Planada. Soil variables are correlated with each other at all sites, but more so at BCI and La Planada (SI Tables 4–6). A surprising finding from all three sites, however, is that N and P do not show stronger effects than Ca, Mg, and Fe. Another notable finding is that the influence of Al is comparable in strength, although different in direction, with that of some major nutrients.

Fig. 1.

NMDS ordinations for the three sites: BCI (Top), La Planada (Middle), and Yasuni (Bottom). Species abundances in 50 × 50 m quadrats were used to compute the ordinations in four dimensions. Both species scores and quadrat scores for the first two ordination axes are plotted. Mean concentrations of soil nutrients in 50 × 50 m quadrats were fitted to the ordinations to test the relationships between species composition and soil nutrients. The orientation of arrows indicates the direction in ordination space in which the soil variables change most rapidly and in which they have maximum correlation with the ordination configuration, whereas the length of the arrows indicates the rate of change.

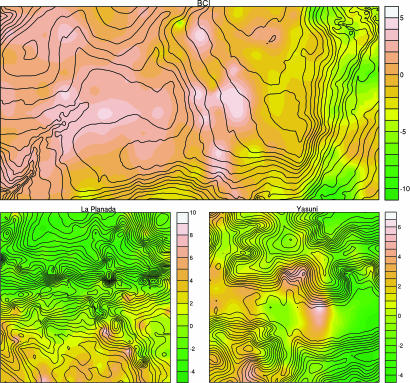
At all three sites, soil nutrients show nonuniform patchy distributions that are often correlated with topographical features such as slope and elevation (SI Table 7). Typically, soil nutrient distributions show strong spatial structure with significant spatial autocorrelation out to 80–150 m. Parameter values of the fitted variogram models used to generate soil maps are given in SI Tables 8–10. Soil nutrients were also correlated with each other (see SI Tables 4–6); we therefore derived orthogonal composite soil nutrient variables by using PC analysis (Fig. 2). The first three PCs (PC1, PC2, and PC3) were uncorrelated with each other and together accounted for ≈75–78% of the variation in soil nutrient concentrations at all three sites.

Fig. 2.

Contour maps of PC1 values for BCI (Upper), La Planada (Lower Left), and Yasuni (Lower Right). The abscissa of all plots is oriented in the east-west direction. The lines are elevation contour lines at 5-m intervals. Soil sample data were subjected to variogram modeling, which was then used in block kriging to estimate mean nutrient concentrations in 10 × 10 m blocks. PCs were computed by using z scores of these mean block estimates. The color scales on the right of each map indicate PC1 values. See SI Figs. 5 and 6, respectively, for maps for PC2 and PC3.

The PCM test was designed to test whether species distributions show affinities to soil nutrient distributions represented here as PCs. Using the PCM test, we found that 104 of 258 species at BCI (40%), 72 of 199 species at La Planada (36%), and 479 of 943 species at Yasuni (51%) were significantly associated to at least one of the first three PC axes of soil nutrient values (Table 1). We limited the number of tests of plant–soil associations by considering only three PC axes instead of testing individual soil nutrients. Nevertheless, hundreds of species at each site were tested for associations to these PC axes, so we had to account for false rejections of the null hypothesis. Here, we estimated the extent of this type I error by running the PCM tests for each plot after swapping its soil PC maps with maps from the other plots. The species in each plot were tested for associations to PC1 and PC2 maps from the other sites where plot size permitted such swapping. Using this approach, we consistently found that ≈9–13% of species show significant associations to a soil map from a different site. This yields an average of 11% type I error rate. Applying this error rate decreases the percentages of species with significant associations to 29% at BCI, 25% at La Planada, and 40% at Yasuni. We also tallied species–soil associations after excluding rare species (n < 50) from our analyses. Excluding rare species resulted in only marginal changes in the proportions of species with significant associations (Table 1).

Table 1.

Soil variable loadings on the three PCs at the three sites

Soil variable	BCI			La Planada			Yasuni
	PC1	PC2	PC3	PC1	PC2	PC3	PC1	PC2	PC3
Al	0.152	−0.504	0.560	0.039	−0.665	0.028	0.051	−0.503	−0.154
B	−0.351	−0.129	−0.172	—	—	—	—	—	—
Ca	−0.368	0.019	−0.032	0.367	0.015	0.198	0.347	0.415	0.153
Cu	−0.330	−0.034	0.225	0.285	0.272	0.152	0.454	−0.064	0.005
Fe	−0.296	−0.028	0.350	0.317	0.107	−0.376	0.321	−0.222	0.105
K	−0.362	0.004	−0.027	0.386	−0.123	−0.107	0.166	0.261	−0.495
Mg	−0.345	0.032	−0.059	0.389	−0.040	0.054	0.318	0.394	0.126
Mn	−0.276	−0.108	0.320	−0.026	0.584	0.316	−0.012	0.108	−0.623
P	0.030	−0.740	−0.108	0.370	0.116	−0.073	−0.295	−0.416	0.122
Zn	−0.330	−0.089	−0.108	0.340	0.015	0.309	0.415	0.057	0.264
N	−0.120	−0.356	−0.588	0.343	−0.240	0.095	0.361	−0.310	−0.054
Nmin	−0.268	0.178	0.088	0.105	0.204	−0.756	−0.222	−0.116	0.454
Variance, %	55.0	12.2	10.9	51.9	13.6	11.2	38.3	19.3	17.4
Species (n ≥ 5)	56	47	19	32	26	31	141	341	98
Species (n ≥ 50)	35	35	12	26	16	22	64	217	42

Variance values indicate the percentage of the total variance in soil properties accounted for by each PC. PCs > 3 explained <10% of the variation at all three sites. The last two rows indicate the numbers of species with significant associations by the PCM test to each of the PCs for species with n ≥ 5 and n ≥ 50 (see text). At all three sites some species showed significant associations to more than one PC; hence, the sum of significant associations to the three PCs is greater than the total numbers of species.

We interpret these plant–soil associations as directional responses of plants to variation in soil properties. However, tree species may both influence and respond to soil properties through litterfall inputs and effects on microbial communities and decomposition rates (40, 41). We suggest that these feedback effects are less likely to influence spatial variation in soil nutrient availability in species-rich tropical forests, where high local tree and liana diversity homogenize litter inputs at the spatial scale at which plant–soil associations are observed. In support of this view, Powers et al. (42) found no significant differences in soil nutrient concentrations underneath crowns of four large emergent tree species compared with a common (control) tree species in a rainforest in Costa Rica, even though leaf litter nutrient concentrations were different in these species compared with the control. Moreover, it is well known that the physical and chemical processes that determine soil formation cause variation in soil characteristics at local spatial scales (43). Geological processes bring different rock layers to the surface within a given area, which results in differences in the nature of parent material that have a significant effect on soil characteristics. Finally, topographic variation also causes soil catena formation, which results in spatial variation in the chemical properties of soils derived from the same parent material. The significant correlations between topography (slope, elevation, and convexity) and soil nutrients at all three sites suggest that such physical processes are important in determining spatial variation in soil characteristics. Nevertheless, the possibility that plants reinforce or oppose the physically derived patterns of soil nutrient variation remains, and the relative contributions of plant effects compared with other processes cannot be assessed by using our data.

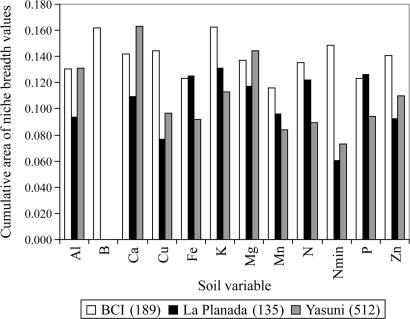
Some soil variables are strongly correlated with each other (see Fig. 1), so we cannot undertake a quantitative assessment of the relative importance of individual soil nutrients to community structure. We therefore used a qualitative approach to assess the rank-order importance of the different elements on community structure. To do this, we first computed a standardized niche breadth value for each species along each soil nutrient gradient. This niche breadth value indicates the fraction of each available resource gradient used by each species (37). We then computed the area under the cumulative distribution of species niche breadth values for each soil nutrient to indicate the community-level specialization to that soil nutrient gradient. Larger cumulative areas indicate narrower niche breadths and greater specialization among species in the community. Using niche breadth analyses, we found that at BCI, B and K appear to have the strongest effect on community structure, followed by N_min, Cu, Ca, Zn, and Mg. Al and P had relatively weaker effects on community niche structure at BCI (Fig. 3). At Yasuni, Ca and Mg had the strongest effects, followed by Al, K, and Zn, whereas P and N showed relatively weak effects compared with the other sites. Finally, at the montane site, La Planada, K, P, Fe, and N, in that order, showed the strongest effects on niche structure.

Fig. 3.

The influence of soil nutrients on niche structure in the three forest dynamics plots. The values on the y axis are areas under the cumulative curves of species niche breadth values for each soil variable. The greater the area for a given soil variable, the greater the effect of that variable on niche structure. The values in parentheses are the total number of species analyzed at each site.

Interpreting cross-site patterns on the relative importance of different soil nutrients is difficult. Mean levels and spatial variation need to be considered, but more importantly the relative importance of a given element in a site is likely to be determined by the relative availability of the other essential elements in that site. Nevertheless, some generalizations exist in the literature. Previous studies of nutrient limitation to plant growth have argued that P is more limiting than N in mature lowland tropical forests, whereas the reverse is held to be true for montane forests (43–47). Based on this, we expected that the relative importance of P would be greater at BCI and Yasuni, and that the influence of N would be greater at La Planada. However, our findings do not support any general pattern. At La Planada, N and P had similar effects on community niche structure, whereas N_min had the smallest effect. At the lowland sites, the rank-order of the importance of N and P were reversed between BCI and Yasuni. Thus, N_min and N had a greater effect than P at BCI, whereas P showed a marginally greater effect than N or N_min at Yasuni. This is surprising, given that the mean levels of P relative to mean levels of N and N_min rates at BCI were substantially lower than those at Yasuni (Table 2).

Table 2.

Soil nutrient concentrations and pH values in the three forest dynamics plots

Site	Al	B	Ca	Cu	Fe	K	Mg	Mn	N	Nmin	P	Zn	pH
BCI	1,013.8	0.944	1732.5	8.08	178.5	171.8	298.9	370.7	25.92	17.84	2.90	5.66	5.66
	(233.3)	(0.536)	(743.2)	(2.04)	(46.2)	(74.7)	(128.0)	(155.6)	(7.96)	(12.82)	(1.62)	(4.14)	(0.34)
La Planada	3,732.4	—	168.6	2.20	562.2	62.5	26.1	3.9	22.71	−5.91	20.20	1.28	4.46
	(234.3)	(63.78)	(0.43)	(219.1)	(18.0)	(7.5)	(5.5)	(4.2)	(7.11)	(12.89)	(0.48)	(0.29)
Yasuni	1,796.7	—	409.9	1.06	284.1	99.8	112.5	139.8	10.84	−0.21	6.34	1.44	4.63
	(278.8)	(275.4)	(0.49)	(82.4)	(112.0)	(65.2)	(95.0)	(3.01)	(4.08)	(2.35)	(0.55)	(0.31)

For each plot, the top row gives plot-wide mean values (mg/kg) of 10 × 10 m quadrats, and the values in parentheses are standard deviations. N_min, N mineralization rates (mg/kg per 28 days).

At all sites, base cations had the greatest rank importance effect for species distributions. A striking difference between Yasuni and the two other sites was the dominant influence of Ca, Mg, and K. We found that Ca, Mg, and K had greater influence on PC2 at Yasuni, and PC2 accounted for only approximately half as much variation in soil nutrients as PC1 (Table 1). Yet there were many more species associated with PC2 than with PC1. Between the two lowland sites BCI and Yasuni, the mean levels of Ca, Mg, and K relative to the mean levels of N and P were lower at Yasuni than at BCI. In particular, the mean Ca to mean P ratio was almost an order of magnitude lower at Yasuni compared with BCI (Table 2). These PCM test results for Yasuni are also consistent with results from niche breadth analyses that show the dominant role of these elements in this site (Fig. 3). Nutrient effects on community structure therefore appear determined both by the magnitude of their variation across the plot and by specific nutrients that might be particularly limiting to plant growth relative to other nutrients within each site.

Low pH values result in reduced availability of Ca, Mg, K, and P, whereas cations such as Al, Cu, Mn, and Zn become more soluble and available for plant uptake, particularly at pH <5 (43). At both La Planada and Yasuni, pH values were <5 in >75% of the measured sample locations, compared with BCI, where pH values were <5 in only 7% of measurements. The differences in the mean availability of the base cations Ca, Mg, and K, and also of Al, between the three plots were consistent with these differences in pH (Table 2). Because pH values were often <5 and Al concentrations relatively high at La Planada and Yasuni, Al toxicity could play an important role in these sites. Strongly acidic (pH <5) soils also show low B availability because of B sorption to Fe and Al₂O₃ surfaces of soil minerals (43). B is an essential plant nutrient, and we found a strong influence of B at BCI, but our soil extractions did not yield detectable concentrations at La Planada and Yasuni. Low pH and relatively high Al and Fe concentrations are probably responsible for the very low levels of B at these sites. These patterns suggest that, by influencing the availability of several plant nutrients, soil pH indirectly exerts strong influence on species distributions in these tropical forests.

Our results show that spatial distributions of a substantial fraction of species in each site are related to the spatial heterogeneity in soil resource distributions in ways that suggest specialization to different levels of essential resources. However, our finding that all three forests show significant structuring due to soil resource variation is somewhat surprising, because the three sites were originally chosen in part so that habitat variation was minimal (44, 45). The BCI and La Planada plots occupy relatively flat plateaus above otherwise steeply dissected hill and mountain tops, whereas the Yasuni plot is relatively more dissected and topographically heterogeneous and occupies one of two soil types that occur within the park (20, 34). Yet we find that even these levels of heterogeneity in soil characteristics influence the distributions of large numbers of tree species at each site. Differences in the proportion of apparent habitat specialist species among plots may in part be attributed to differences in the levels of habitat heterogeneity. And this might in part explain why Yasuni has the greatest proportion and numbers of apparent habitat specialist species among the three sites.

Conclusions

Here we have shown strong and consistent relationships between tree distributions and soil nutrient distributions for more than one-third of the tree species in three diverse neotropical forests. Our estimates of the prevalence of soil resource-based niche differentiation among tree species are conservative on at least one count. Our test is based on differences in tree densities among quadrats along single environmental (soil) gradients, and therefore, it is not sensitive to resource-ratio differences at fine spatial scales down to the level of individual trees. Yet, such differentiation based on resource ratios is in principle a powerful mechanism for niche differentiation in a plant community (46). Focused experimental tests are needed to evaluate the importance of limiting resources and identify the differences in resource requirements among species. The patterns of species distributions with respect to resources that we identify allow us to make testable predictions on the resource requirements for large numbers of species at each study site. The species–soil nutrient relationships that we report therefore constitute the necessary first step in designing feasible experimental studies to identify the soil resource-based niche structure of these highly diverse forests.

Methods

We conducted research at three sites: (i) The 50-ha plot on BCI, in central Panama, which supports lowland semideciduous moist forest with 301 species and 229,049 individuals ≥1 cm diameter at breast height; (ii) the fully censused western 25 ha of the Yasuni 50-ha plot, which supports lowland evergreen forest with 1,104 morphospecies and 152,353 individuals; and (iii) the 25-ha plot at La Planada, which supports evergreen montane forest at 1,800 m above sea level with 228 species and 115,129 individuals. The topography is gentle in all plots with the exception of a small part of the La Planada plot. The soils at BCI are mostly well weathered kaolinitic Oxisols; at La Planada they are mostly acidic Andisols developed from volcanic ash; and at Yasuni they are mostly clayey, acidic, Udult Ultisols (for detailed site descriptions, see ref. 45).

We sampled soils by using a regular grid of points every 50 m. Each alternate grid point was paired with an additional sample point at 2, 8, or 20 m in a random compass direction from the grid to capture variation in soil properties at finer scales. We thus sampled 300 points in 50 ha at BCI and Yasuni but placed a higher density of 253 points for the 25-ha plot at La Planada (soil analyses were carried out for the full 50 ha at Yasuni, even though tree data were available only for the western 25 ha). At each sample point we collected 50 g of topsoil (0- to 10-cm depth) and used 20 g to measure moisture content gravimetrically. We extracted available cations and P from 2.5 g of fresh soil, using the Mehlich III extractant solution (47). Elemental analysis for the cations (Table 2) and P was done on the Mehlich-III extracts by using atomic emission–inductively coupled plasma (AE–ICP) spectroscopy at Cornell University Laboratories. We extracted N as NH₄⁺ and NO₃⁻, using 2.0 M KCl on 2 g of soil (48). Nitrogen was estimated colorimetrically on the KCl extracts, using an auto analyzer OI FS 3,000 (OI Analytical, College Station, TX). To measure in situ N mineralization rates, we drove 3-in (1 in = 2.54 cm) diameter poly(vinyl chloride) pipes 15 cm into the ground, covered the tops with lateral slits to prevent rainwater from entering while allowing gas exchange, and allowed the tubes to incubate for 28 days. At the end of the incubation period, the tubes were removed from the ground, and 2 g of the soil in the tubes were collected and analyzed for N as described above.

NMDS ordinations were done at the scale of 50 × 50 m by using the statistical software package “vegan” version 1.9-6 [by J. Oksanen, R. Kindt, and R. B. O'Hara (2005), available at http://cc.oulu.fi/∼jarioksa/softhelp/softalist.html] in the R programming environment version 2.1.1 [by the R Development Core Team (2005), available at www.R-project.org]. After several trials, noting the stress values obtained in the ordinations, we chose the number of dimensions equal to four to yield optimal ordinations. Block averages of soil nutrient values for 50 × 50 m quadrats were obtained by using geostatistical methods described below. By using vegan, these soil nutrient vectors were then fitted to NMDS ordination axes scores such that the projections of points onto vectors have maximum correlations with corresponding environmental variables.

To obtain spatial predictions, using geostatistical methods, we first Box–Cox transformed (lambda restricted to 0, 0.5, or 1.0) the soil nutrient data (mg/kg), performed polynomial trend-surface regressions, and computed empirical variograms, using the residuals from the regressions. Because the data were relatively sparse, we assumed isotropy. We fitted variogram models to the empirical variograms, and obtained spatial predictions for 10 × 10 m blocks, using ordinary kriging. The trend was then added back to the kriged means, and the values were back-transformed to the original scale. We estimated prediction errors, using 100 conditional simulations for each soil variable. Prediction errors were <15% in most cases, but because kriging tends to smooth variation, errors of up to 50% were obtained at a few locations where our soil measurements yielded extreme low or high values. Geostatistical analyses were carried out mainly by using the R package “gstat” (49).

We anticipated that using individual soil variables for species–soil association tests would result in a large number of comparisons and severely inflate type I error. Moreover, quadrat mean estimates of some soil nutrients were significantly correlated with each other [these correlations were strongest at BCI, but considerably weaker at Yasuni and weakest at La Planada (see SI Tables 4–6)]. We therefore derived orthogonal composite variables by computing PCs on the block-kriged values of all soil nutrients and limited the number of PCs used for species–soil association tests. We chose only the first three PCs because PCs greater than PC3 individually accounted for <10% of the variation in soil nutrients at each site. We finally tested for associations between species distributions and soil nutrient distributions described by these principle components (PCs), using a Monte Carlo simulation test that accounts for the spatial structure in both data sets.

Our test procedure involves modeling the spatial aggregation pattern for each species by using a spatial point process model and by using the fitted model to simulate species distributions (27). Simulating such artificial distributions that maintain the observed spatial aggregation patterns of species allowed us to construct expectations of species–soil associations under dispersal assembly alone. We first measured the spatial aggregation of populations, using Ripley's K, and used toroidal randomization to test for deviations from complete spatial randomness. We then modeled spatial aggregation of species distributions, using the PCM with Ripley's K as the summary statistic (27, 50). The PCM captures small-scale spatial aggregation in species distributions that are mostly due to aggregated dispersal (37). For species that were not significantly aggregated by Ripley's K, we used the homogeneous Poisson process to simulate spatial distributions. For each combination of a species map and a PC map, we computed the mean and standard deviation of an index of association between the two maps. The mean value for the index of association is simply

where N is the total number of trees in the plot, n_i is the number of trees in quadrat i, and x_i is the value of the soil variable in quadrat i. Similarly, the standard deviation of the index of association is

.

We also computed the same indices between 1,000 simulated species maps (constructed by using the PCM) and each PC map. We used these simulated means and standard deviations to construct the expectations under dispersal assembly for each species–PC combination. Significant deviations of the observed values of the index of association from the values that were expected under dispersal assembly indicate nonrandom effects related to soil nutrient distributions. Statistical significance was assessed by a two-tailed test (α = 0.025 for each tail) for species means, and a one-tailed test (α = 0.05) for standard deviations (observed values smaller than the distributions of values expected under dispersal assembly).

We calculated species niche breadth, using a standardized measure (K-S), which indicates the fraction of each available resource gradient used by each species (37). For niche breadth analyses we included only those species with at least 50 individuals. We computed niche breadth by comparing the predicted values of soil variables at observed tree locations to the predicted soil values at 1,000 randomly chosen locations in the plot. We assessed the overall influence of each soil variable on the niche structure of each community by assembling cumulative distributions of species niche breath values for each soil variable and computing the area under the curve. The stronger the effects of a soil variable on community niche structure, the greater the area under the curve.

Abbreviations

BCI

Barro Colorado Island

PCM

Poisson cluster model

NMDS

nonmetric multidimensional scaling

N_min

nitrogen mineralization

PC

principal component