Monte Carlo Study of Substrate-Induced Folding and Refolding of Lattice Proteins

Abstract

Many proteins can switch from one conformation to another under the influence of an external driving force, such as the binding to a specific substrate. Using a simple lattice model we show that it is feasible to design protein-like lattice proteins that can have two different conformations, depending on whether or not they are bound to a substrate. We give three different examples of such substrate-induced refolding. In addition, we have explored substrate-induced folding of lattice proteins that do not fold when free in solution. We show that such proteins can bind with the same high specificity as prefolded protein, but have a considerably lower binding free energy. In this way proteins can bind to a substrate in a way that is highly specific, yet reversible.

INTRODUCTION

Proteins can change their conformation when exposed to different environments. The simplest example of this phenomenon is the protein folding or unfolding that can be induced by a change in temperature, pressure, or solvent conditions. In addition, there are many examples of proteins that undergo a transition from one ordered structure to another under the influence of an external agent. Motor proteins (1–3) are an example of this class of proteins. The structural transformation in motor proteins is driven by the chemical reaction with a molecular fuel (often ATP). However, there are also proteins that undergo structural rearrangements when they bind reversibly and selectively to a particular substrate. The substrate acts as a switch to activate or deactivate some function of the protein. A particularly interesting class of proteins are those that are disordered in solution but fold when brought into contact with a substrate. Such “natively unfolded” or “intrinsically unstructured” proteins are known to play a key role in many cell regulatory processes and it has been argued that the ability to fold upon binding provides high specificity coupled with low affinity to the binding process (4). Schoemaker et al. (5) have proposed that such a mechanism could considerably speed up the binding of a protein to its target substrate. This hypothesis, called “fly-casting”, has been tested for several models (6–8). Clearly, the ability to fold or refold upon binding to a substrate puts severe constraints on the amino-acid residue sequence of the protein, as it must be compatible with one stable structure in the absence of the substrate, yet must refold to another structure when bound to the substrate. In this article, we explore the design of protein-like lattice polymers that can refold upon binding to a substrate. In addition, we show that it is possible to design lattice proteins that are disordered (natively unfolded) in solution, but fold when in contact with a specific substrate. As fully atomistic simulations of the design process would, at this stage, be prohibitively expensive, we use a lattice model for hetero-polymers that, although simple, exhibits many of the features of proteins. The interaction between the monomeric units (“residues”) of the lattice proteins are described by the interaction matrix proposed by Miyazawa and Jernigan (9). The substrate is constructed from the same set of monomeric units as the protein, and the interactions between the protein and substrate are therefore also given by the parameters of Miyazawa and Jernigan (9). The same “toy” protein model was used by Borovinskiy and Grosberg (10) who studied the design of a simple molecular motor.

The aim of our study is twofold: first we wish to investigate under what conditions the substrate can induce a conformational change of the protein from the native state in solution to a different native state in the bound condition. Secondly, we investigate under what conditions a substrate can induce the folding of a protein that is unfolded in solution.

As the results of such simulations might depend on the specific sequence of the designed protein and substrate, we repeat the calculations for four different protein-substrate pairs.

The remainder of this paper is organized as follows: after a brief review of the simulation techniques (details are given in the Appendix), we present the simulations of the binding of our model proteins to the substrates. We conclude with a discussion of some of the implications of these simulations.

METHODS

The system that we consider consists of a lattice protein that is free to move inside a finite box. The substrates are small, rigid, objects built from residue-like units. The conformational energy of the system is given by

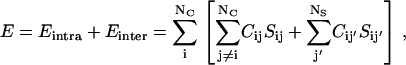(1)

where the indices i and j run over the residues of the protein (N_C), while j′ runs over the elements of the substrate (N_S), C is the contact matrix, defined as

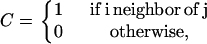(2)

while S is the interaction matrix. For S we use the 20 × 20 matrix determined by Miyazawa and Jernigan (9) on the basis of the observed frequency of contacts between each pair of amino acids.

Sequence design

A given lattice polymer can form a large number of compact conformations, each one of them characterized by a different contact map. Through its contact map, the energy of the polymer depends on its conformation (see Eq.1). The density of states as a function of energy determines a conformational entropy S(E). The mean-field approximation for this conformational entropy is (11)

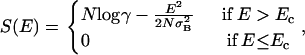(3)

where N is the number of monomers in the chain, σ_B is the standard deviation of the interaction matrix, and γ is the coordination number for fully compact structures on the lattice. In the definition of the entropy the constant 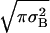is ignored as explained by Derrida (11). The lower root of the equation S(E) = 0 is denoted by E_c. It is given by 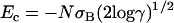. The “native state” corresponds to the lowest energy conformation for a given sequence. The energy of the native state is lower than E_c. If the native state is nondegenerate, this lowest-energy conformation has zero entropy, which leads to the well-known funnel-shape free-energy landscape (12). The width of the distribution of energies of the nonnative states depends on the heterogeneity of the lattice protein. A limiting case is the homopolymer where all compact conformations with the same overall shape have the same energy. Obviously, such a homopolymer does not have a unique native state. Heterogeneity is essential for the designability of specific native structures.

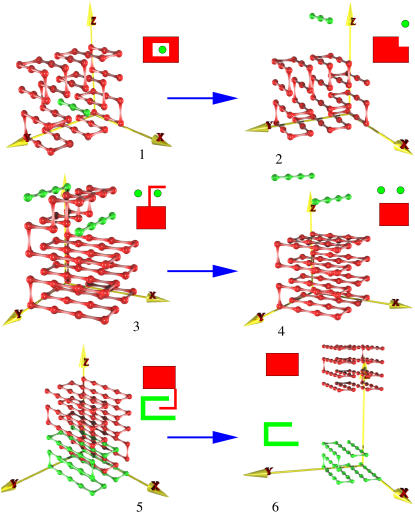
There are several ways to “design” the sequence of lattice proteins such that they fold into a specific, predetermined conformation. We reported one such strategy in Coluzza et al. (13). This method is briefly reviewed in the Appendix. Sequences are generated by minimizing the energy of the target configuration(s) and, at the same time, by maximizing the number of letter permutations to increase the sequence heterogeneity. In this study we use this scheme to design a protein-substrate system. In particular, we design our lattice proteins such that they have different native states in solution and when in contact with the substrate. A similar approach can be used to design a residue sequence that will fold in different structures when bound (Fig. 1 (1, 3, and 5)) and unbound (Fig. 1 (2, 4, and 6)) (see Appendix). Once the best sequences are chosen according to our design scheme, we can proceed to test if the desired folding properties have been achieved and then to compute the free-energy landscape associated with the binding process. Note that to get good “refolding”, we did not need to control explicitly the free-energy landscape for refolding, as was done in Borovinskiy and Grosberg (10).

FIGURE 1.

Spatial arrangement of the chain in the structures used to explore configurational changes induced by the binding. The conformation on the left corresponds to the native structure in solution. In contact with a substrate, the model protein folds into the structure shown on the right. In particular, the free and bound native structures of sequence A (Table 1) are denoted by 1 and 2, respectively. Similarly the free (bound) native structures of sequences B and C are denoted by 3 (4) and 5 (6), respectively.

Folding

To study the folding of a particular model protein, we use a Monte Carlo simulation with four basic moves: corner-flip, crankshaft, branch rotation, and center of mass translation. The corner-flip involves a rotation of 180° of a given particle about the line joining its neighbors along the chain. The crankshaft move, is a rotation by 90° of two consecutive particles. A branch rotation is a turn, around a randomly chosen pivot particle, of the whole section starting from the pivot particle and going to the end of the chain. With these moves we expect to have a good balance between collective and local moves.

During the simulation we measure the free energy as function of three order parameters. The first is the conformational energy (Eq. 1) of the chain. The second is the number of native contacts Q in a given conformation, which is a commonly used order parameter in the study of protein folding. However, as we are considering also a model with two native structures, it is better to define as an order parameter the difference in the number of contacts that are “native” to the two target structures (e.g., 1 and 2) i.e.,

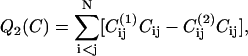(4)

where 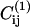and 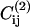are the contact maps of the two target structures, and C_ij is the contact map of the instantaneous configuration. To be more precise: as we consider two distinct native states (1 and 2), we assign a value +1 to every contact that belongs to structure 1 and a value −1 to every native contact of structure 2. Contacts that appear in both 1 and 2 do not contribute to this order parameter. It is important to notice that some of the native contacts can correspond to intramolecular interaction. To quantify binding it is useful to use a third order parameter Q_S that measures the number of contacts between the protein and the substrate regardless of whether they are native or not.

The free energy, as a function of an order parameter Q (Eq. 4) is defined by

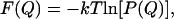(5)

where 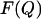is the free energy of the state with order parameter Q and 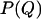is the equilibrium probability to observe conformations with order parameter Q. In a simulation, we determine 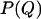by accumulating a histogram of the number of conformations as a function of the order parameter Q. Direct (brute force) calculation of this histogram is not very efficient as the system is often trapped in local minima, especially at low temperatures. To solve this sampling problem, we employ Virtual-Move Parallel Tempering (VMPT) (14) a parallel-tempering algorithm based on the sampling of rejected states (13,15).

The VMPT scheme is particularly useful for the study of conformational changes induced by a substrate, as the lowest free-energy state of the free protein will become a relatively high free-energy state after binding to the substrate. For more details about the VMPT scheme, we refer the reader to Coluzza and Frenkel (14).

RESULTS

To study the influence of a substrate on the equilibrium properties of our model protein we considered three different conformational changes induced by substrates of different sizes. In Fig. 1 we show the target structures between which the transitions occur: 1 ⇔ 2, 3 ⇔ 4, and 5 ⇔ 6. Because the same procedure is applied in every case, we focus our explanation on the conformational change from structure 1 (Fig. 1, left) to structure 2 (Fig. 1, right). Following the procedure explained in section 2 we optimize the conformational energy of the chain in both structure 1 (see Fig. 1, left) and 2 (see Fig. 1, right). After eight simulations with different random numbers, each of the order of 10⁹ steps long, we collect all the sequences with the lowest energy for the two structures. In Table 1 we show the sequences selected for the different conformational changes.

TABLE 1.

Sequences generated for the test structures (Fig. 1)

R H F S Y T R R G M D D R C W V C D A C V M C T P H W L E Y N K I L E N P K I M E Q R K W G E D P K F A E Q N K I M S Q	Sequence A
L E A S P S K I R E G Y P G R T R D F Y W C K D L E C M N C K I L E C N W C K I R E C M H F R D P D F Y W C K Q V E C M N C K V V A T G Q H Q H	Sequence B
P R D G L W G R D Q P R D F M I F R D Y M K D C L W C K E W N K E C M I C R E N N K D C L W C K E N M K E C M I C K E W F K D C L W C K E F N K E C M I C R E N P R Q F M I G H Q H H H P G L V T S T Y A V V A A V T S Y Y P S Q A H V G S T Q	Sequence C

Each letter represents a different amino acid (9). The letters in bold are the amino acids of the substrate.

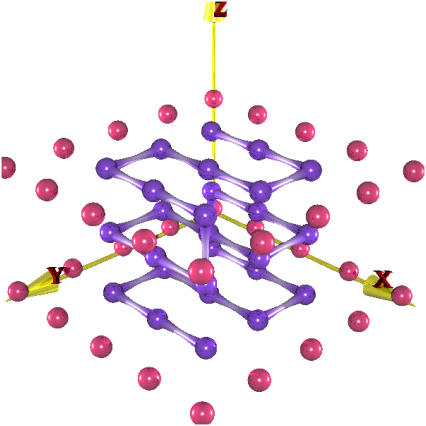
The study of the folding mediated by binding to a substrate is done by considering the equilibrium properties of the protein in Fig. 2. Following the procedure explained in the Appendix we designed the protein in the bound state with different percentages of “random” amino-acid residues ranging from 0% to 60%. The results are a group of sequences D0-D60. The effect of randomly chosen residues is to introduce noise in the design process, which the other amino acids have to compensate for during the optimization. When the noise exceeds a certain threshold, the interactions between the residues in the chain are insufficient to stabilize the native structure. However, the native conformation is favored when the chain is brought into contact with the substrate.

FIGURE 2.

Spatial arrangement of the protein of the protein-substrate system used to study the binding-induced folding process. In purple we have represented the protein whereas the red spheres constitute a substrate frozen in the middle of the simulation box.

Free-energy calculations

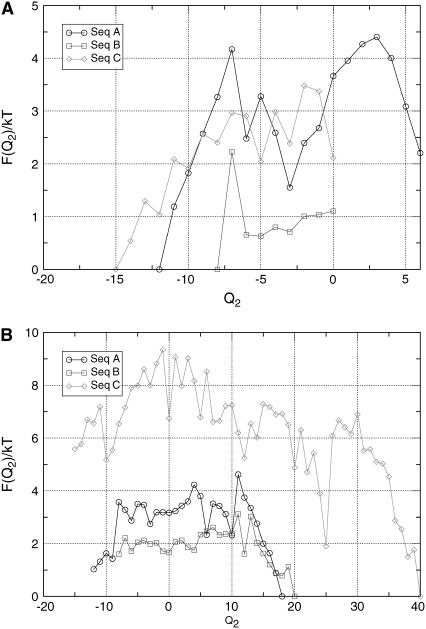
As a first check, we verified that the generated sequences do indeed fold into the respective target structure according to whether or not they are bound to the substrate. We start with a random coil not touching the substrate. In Fig. 3, A–C, we plot the free energy of sequence A,B,C, respectively, as function of the number of native contacts Q (Eq. 4) at the temperature of T = 0.1. In each plot we distinguish between conformations that do and do not touch the substrate. A common feature of the three proteins is that they fold into the designed structure that corresponds to the bound state. For example, for sequence A, the equilibrium conformation in the bound state corresponds to structure 1 (Q₂ = 18), while the unbound state is most stable in structure 2 (Q₂ = −12). Similar behavior is observed for sequences B and C, designed to undergo the refolding transitions 3 ⇔ 4 and 5 ⇔ 6, respectively. In other words, our design algorithm allows us to generate lattice proteins that undergo a major conformational change upon binding to a substrate. Although these results are limited to simple lattice proteins, this qualitative behavior should also be present in more realistic protein models.

FIGURE 3.

Plots of the free energy 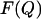of the different sequences as a function of the number of native contacts Q₂ (Eq. 4), at T = 0.10. States that touch the substrate (A) have been plotted separately from those that do not (B). The curve corresponding to the touching states is longer, because in the definition of the order parameter we take into account also the native contacts with the substrate. All data were obtained with a combined parallel tempering and umbrella sampling simulation.

To investigate the temperature dependence of the different conformational changes, we raise the temperature until we reach a regime where the native unbound state is in equilibrium with the native bound configuration. For all cases it is possible to reach a temperature where the protein detaches from the surface without denaturing the protein. However, this is not always the case in real proteins. In fact, it is well known experimentally (16) that random domains of proteins can fold into well-defined structures upon binding.

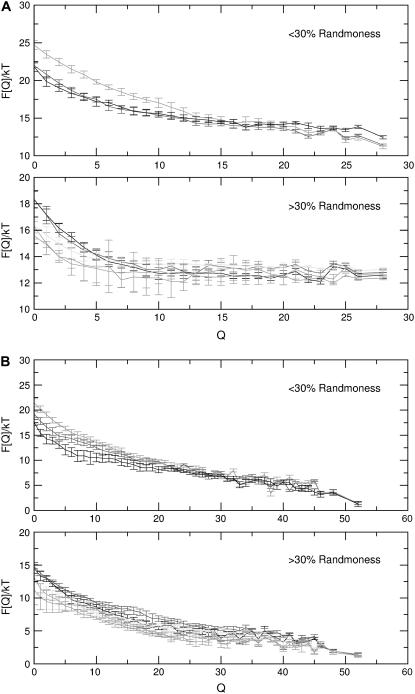
Let us consider in more detail the case of protein D (Fig. 2) that folds when it binds to a substrate. In Fig. 4, A and B, we plot the free energy of the free and bound states, respectively, of sequences D as function of the number of native contacts Q (Eq. 4). It is important to remember that the order parameter Q measures the number of native contacts with respect to only one reference structure. Above a certain threshold of “randomness” (30%) the unbound chain no longer has a stable native conformation. Yet, in the bound state, the protein still folds. We found that, even for 60% randomness, bound proteins can still fold. Although the details of the competition between randomness-induced disorder and substrate-induced order depend on the size of the substrate and the protein, these results do show that proteins that are disordered in solution, can become ordered (and hence functional) under the influence of a substrate. Moreover, all the sequences show a strong specificity in the binding; this can be seen in the plots of the free-energy landscape as a function of both Q and Q_s (supplemental Fig. S2, Supplementary Material). For the extremes D0 and D60 the surface has a funnel shape that indicates a strong preference for specific binding (15).

FIGURE 4.

Plots of the free energy 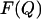of sequences D0–D60 (0–60% of random amino acids) as a function of the number of native contacts Q (Eq.4), at T = 0.10. States that touch the substrate are plotted separately (A) from those that do not (B). The curve corresponding to the touching states is longer, because in the definition of the order parameter we take into account also the native contacts with the substrate. We have further divided the curves according to percentage of random amino acids in the sequence. On top we plotted the folding free energies for sequences with <30% of random residues. The curves show that proteins free in solution fold only when the number of random amino acids is below the threshold, whereas all sequences fold when they are bound to the substrate. All data were obtained with a combined parallel tempering and umbrella sampling simulation.

Proteins that fold under the influence of a substrate have interesting binding properties. In particular, their binding constants depend very strongly on temperature. Intuitively, the reason for this dependence is easy to understand: the strength of binding is determined by exp(−Δf/k_BT), where Δf is the difference in free energy of a molecule in contact with the substrate and in solution. This free-energy difference contains an energetic and an entropic contribution. When a molecule folds upon binding to the substrate, there is a large entropy loss Δs associated with the binding process. To obtain a given binding strength, this entropy loss must be compensated by a correspondingly large gain in Δe/k_BT, where Δe is the energy gain upon binding. The binding strength itself provides no direct information about the entropic and energetic contributions to Δf. However, the temperature dependence of exp(−Δf/k_BT) is determined exclusively by the binding energy. As Δe must be large for chains that fold upon binding, the substrate-binding constant for such chains tends to be much more sensitive to temperature than that of chains that are also folded in solution. Within the context of our lattice model, this phenomenon can be studied in some detail.

In particular, we can compute the free-energy difference between a protein that is bound to a substrate and a protein that is in solution. In the free energy of the latter, we do not include the translational contribution (as it depends on the simulation-box size). If we define Q_b as the partition sum of all protein conformations that have at least on contact to the substrate, and Q_f as the partition sum of a “free” protein in the bulk (the distance between the protein and the substrate is such that no contacts are possible), then we can define Δf ≡ −k_BT ln(Q_b/Q_f). If we assume that the number density ρ_f of proteins in solution is so low that we can ignore interactions between different proteins, then we can relate the concentration-dependence of X_b, the fraction of substrates that are bound to a protein, to the binding free energy Δf:

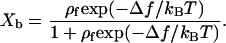(6)

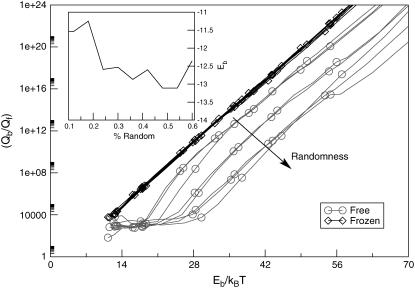
In Fig. 5 we show the temperature dependence of the binding strength (determined by exp(−βΔf) ≡ Q_b/Q_f) between the bound and the free native state for protein D, as a function of the degree of randomness. In the figure we compare the binding strength both for the situation where the internal degrees of freedom of the protein are “frozen” in the native structure and for the fully flexible case (for which the protein is disordered in solution). The open diamonds denote the result for the artificially stabilized native structure: it exhibits perfect Arrhenius behavior. Our choice of the temperature scale ensures that all curves connecting the diamonds collapse. The open circles denote the results for the fully flexible proteins. As can be seen from the figure, the binding strength at constant E_b/k_BT is now strongly reduced compared to the case of the rigid proteins: the greater the disorder, the lower the binding strength. However, the slopes of the curves are approximately the same as before. This indicates that the binding energy, which determines the slope of the Arrhenius plot, is the same as in the rigid case. This result illustrates that this simple model allows us to vary the specificity with which proteins bind to a substrate without changing the binding strength itself.

FIGURE 5.

The binding strength of a protein is determined by the ratio Q_b/Q_f (see text). In this figure, we show the temperature dependence of this ratio as a function of the degree of randomness of the protein. When the protein is frozen in its native state (diamonds), the conformational entropy does not change upon unbinding. The frozen proteins (diamonds) bind at a higher temperature than proteins that disorder upon unbinding (circles) or, equivalently, at a fixed (reduced) temperature, proteins that fold upon binding are less strongly bound than ordered proteins with the same binding strength. Note that each sequence D has a different binding energy E_b (plotted in the inset). To facilitate comparison of the different curves, we express the temperature in units E_b/k_BT.

This is presumably an important advantage of proteins that fold upon binding: it makes it possible to have very strong energetic interactions, without causing the protein to bind irreversibly (4).

There can be several reasons why a large binding strength is useful: one is simply to make the binding strength strongly temperature dependent. The other is to make the binding highly specific (using a large number of “bonds” at the binding site) without causing the protein to stick irreversibly to the substrate. Finally, there is also the possibility that a single natively unfolded protein can fold into different ordered structures, depending on the nature of the substrate. We did not explore this scenario. One can envisage also the opposite case where a protein gets more disordered upon binding to a substrate. In that case, the binding energy could be made lower without decreasing the binding strength. Such a strategy might be useful for binding processes that should be relatively insensitive to temperature. We have not explored this latter scenario.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: DESIGN ALGORITHM

The basic design moves are single point mutations. As in the conventional Metropolis scheme, the acceptance of trial moves depends on the ratio of the Boltzmann weights at temperature T of the new and old states. However, if this were the only criterion, there would be a tendency to generate homo-polymer chains with a low energy, rather than chains that fold selectively into the desired target structure. To ensure the necessary heterogeneity, we impose the following additional acceptance criterion

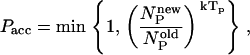where T_p is an arbitrary parameter that plays the role of a temperature, and N_P is the number of permutations that are possible for a given set of amino acids. N_P is given by the multinomial expression

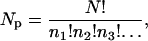(7)

where N is the total number of monomers and n₁, n₂, etc. are the number of amino acids of type 1,2,…. While sampling the sequence space with a Monte Carlo scheme, we keep the temperature (T_P) associated with this quantity high. In doing so we generate a heterogeneous composition of amino acids. A large amino-acid alphabet helps to reduce the degeneracy of the ground state, and so mimic the folding behavior of a real system. During a Monte Carlo run of several million cycles, a large number of distinct sequences are generated. The sequence S* with the lowest energy is assumed to be the best candidate to fold into the native state.

(8)

We found that, for these chain lengths (60–80), the set of values and T = 1/20 yielded good sequences, in the sense that the native state that was both stable and nondegenerate.

A similar approach can be used to design a sequence that will fold into different conformations when bound and unbound. To achieve this, we start with an arbitrary initial sequence. The design program then randomly changes the sequence of amino acids and accepts or rejects the trial move according to the following acceptance rules:

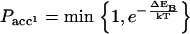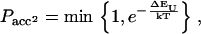where E_B and E_U are the conformational energy of the bound state and the unbound state, respectively. The next objective is to design a protein that folds to a native structure only when bound to a substrate. To create such a protein we start from a configuration where the protein is bound to the substrate as in Fig. 2. We then design the sequence of amino acids of the chain and of the substrate using the same scheme as in references (13,17,18), with the extra condition that a certain number of amino acids will be ignored in the mutation moves, or in other words they will remain random. In this way the intramolecular contact alone will not be strong enough to keep the protein in native state, but it will need the intermolecular bonds with the substrate.