Law and order: Assessing and enforcing compliance with ontological modeling principles in the Foundational Model of Anatomy

Abstract

The objective of this study is to provide an operational definition of principles with which well-formed ontologies should comply. We define 15 such principles, related to classification (e.g., no hierarchical cycles are allowed; concepts have a reasonable number of children), incompatible relationships (e.g., two concepts cannot stand both in a taxonomic and partitive relation), dependence among concepts, and the co-dependence of equivalent sets of relations. Implicit relations—embedded in concept names or inferred from a combination of explicit relations—are used in this process in addition to the relations explicitly represented. As a case study, we investigate the degree to which the Foundational Model of Anatomy (FMA)—a large ontology of anatomy—complies with these 15 principles. The FMA succeeds in complying with all the principles: totally with one and mostly with the others. Reasons for non-compliance are analyzed and suggestions are made for implementing effective enforcement mechanisms in ontology development environments. The limitations of this study are also discussed.

1. Introduction

Ontology modeling principles—specifying syntactic and semantic rules and constraints—are designed to ensure the soundness and consistency of the representation, conditions under which ontologies can serve the purpose of knowledge sharing and reuse. While some principles are general and therefore applicable to most ontologies, others are specific to the domain being represented. In some systems (e.g., description logic-based systems), axioms are used to implement such principles, thus enabling automatic classification and consistency checking. More generally, however, principles can be stated in natural language and used as guidelines by ontology developers.

Unlike concepts and relationships, the principles followed by ontology developers are rarely specified explicitly. Most ontology authoring tools do not even offer such capability. For example, an anatomical entity such as Lobe of lung may subsume Lobe of left lung and Lobe of right lung, but the classification criterion used here—laterality—is not represented explicitly. As a consequence, other developers contributing to the development of the same ontology may use a different spatial criterion—equally valid—for classifying Lobe of lung into Upper lobe of lung and Lower lobe of lung. This simple example illustrates that the lack of explicit articulation for classification criteria and, more generally, for modeling principles is likely to lead to inconsistent representations, especially in large ontologies. From the perspective of applications, consistent representations are required for tasks such as ontology integration and ontology mediation, crucial to the Semantic Web.

The objective of this study is to assess the degree to which an ontology complies with modeling principles and to investigate methods whereby compliance with these principles can be enforced. In practice, we first outline ontology modeling principles for which we provide operational definitions. Then, using these definitions, we assess the compliance of an ontology with these principles. Finally, we analyze reasons for non-compliance and suggest possible solutions for better enforcement.

The ontology under investigation is the Foundational Model of Anatomy (FMA). We selected the anatomical domain because it is central to biomedicine. While macroscopic anatomy is required for the representation of diseases and procedures, subcellular anatomy has become increasingly important for molecular biology. The FMA is a large-scale ontology of anatomy comprehensive enough to support clinical applications.

Several approaches to assessing consistency in ontologies have been suggested. Jones and Paton [1] presented five types of problems in the formal representation of hierarchical knowledge. The OntoClean methodology evaluates the nature of properties involved in taxonomic relationships based on a set of meta-properties originating from philosophical notions: identity, essence, unity, and dependence [2,3]. In the biomedical domain, we recently investigated how the description logic-based terminology SNOMED CT complies with principles of classification [4]. In another study of SNOMED CT, Ceusters et al. [5] used ontological and linguistic information to identify missing relations and improper assignment of relationships. As one of the few large-scale ontologies of anatomy, the FMA has been investigated from various perspectives. Relevant to our study is the work of Schulz et al. who transformed the FMA into a description logic-based representation (“Structure-Entirety-Part triplets”), by which some taxonomic and partonomic cycles were identified [6,7].

The major contribution of this study is to provide an operational definition of 15 principles related not only to classification, but also to various aspects of dependence (both among concepts and among sets of relations). As a case study, we investigate the degree to which the FMA complies with these principles. The algorithms we implemented for assessing and enforcing these principles are independent of the system in which the FMA was developed. However, validation mechanisms derived from these principles could be built in ontology development environments (e.g., as plug-ins in Protégé or axioms and rule extensions in description logic-based systems).

2. Materials

The FMA¹ is an evolving ontology that has been under development at the University of Washington since 1994 [8,9]. Its objective is to conceptualize the physical objects and spaces that constitute the human body. The FMA was developed around 10 foundational principles:

• Unified context principle: Structural anatomy is the only perspective considered (as opposed to functional or clinical anatomy).

• Abstraction level principle: The FMA represents canonical (not instantiated) anatomy.

• Species specificity principle: While currently focusing on human anatomy, high-level classes in the FMA are defined to represent the anatomy of vertebrates in general.

• Definition principle: Aristotelian definitions are provided for high-level classes.

• Dominant concept principle: Each class in the FMA is defined in reference to the dominant class (Anatomical structure).

• Organizational unit principle: Cell and Organ are the two organizational units and every other anatomical structure either constitutes or is constituted by cells and organs.

• Content constraint principle: The largest anatomical structure represented in the FMA is the whole organism; the smallest is Biological macromolecule.

• Relationship constraint principle: The three types of relationships among anatomical entities represented in the FMA are (1) class subsumption, (2) static physical relationships and (3) relationships indicating transformations between developmental stages.

• Coherence principle: The anatomy taxonomy is organized as a tree (single-inheritance class subsumption hierarchy), with Anatomical entity as its root.

• Representation principle: In addition to being an ontology of anatomy, the FMA is also concerned with terminology and collects the names (mostly in English and Latin) of the entities it represents.

The version of the FMA under investigation in this paper (February 9, 2004 version) comprises 69,889 classes covering the entire range of macroscopic, microscopic, and subcellular canonical anatomy. Concept names in the FMA are pre-coordinated, and, in addition to preferred names (one per concept), 40,683 synonyms are provided (up to 6 per concept).

The FMA is implemented in Protégé,² a frame-based ontology editing and knowledge acquisition environment developed at Stanford University [10]. Ontologies developed in Protégé are composed of classes and instances, classes being organized in taxonomic hierarchy. Slots and facets are another important component of frame-based systems: slots specify relationships between classes and describe class properties; facets express constraints on slots.

The FMA is modeled by the taxonomic relationship, is-a. Additionally, seven kinds of partitive relationships are used part of, general part of, clinical part of, constitutional part of, regional part of, systemic part of, and 2D part of. All the partitive relationships have inverses: part, general part, clinical part, constitutional part, regional part, systemic part, and 2D part, respectively [11].

There are also 74 associative relationships, e.g., branch of, contained in and nerve supply of, of which 38 have inverses (e.g., branch/branch of and contains/contained in). continuous with is its own inverse, and 35 associative relationships do not have inverses (e.g., fascicular architecture and has wall).

Taxonomic, partitive, and associative relationships link concepts to other concepts. In addition to such relationships, there are 121 slots in the FMA describing atomic properties of concepts, whose types are Boolean, Integer, Symbol, String and Instance.³ For example, the slot has mass accepts a Boolean value (true or false).

In addition to the properties represented through relations and slots, the classification principles defining the higher-level classes of the anatomy taxonomy are made explicit through textual definitions for these classes. In practice, each subdivision in the tree is motivated by a single property (e.g., has mass). The number of subclasses for a given class is determined by the possible values for the corresponding property (e.g., has mass: yes/no). The top-level of the anatomy taxonomy is represented in Fig. 1 along with the classification criteria for these classes.

Fig. 1.

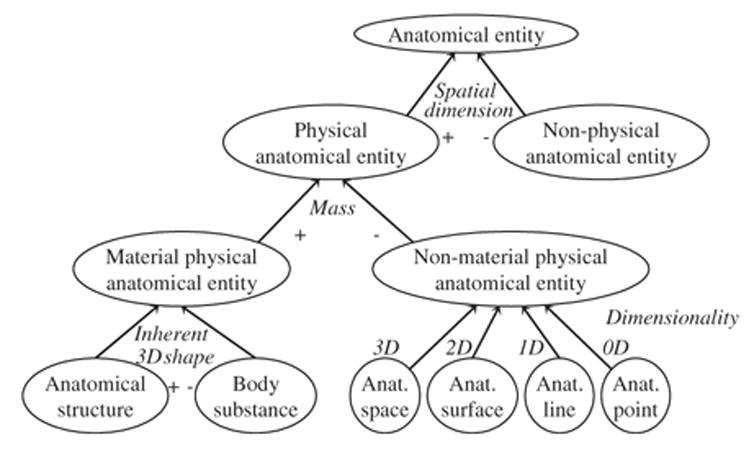
Top-level classes of the anatomy taxonomy of the FMA.

3. Definitions

An ontology is defined as a theory of reality (in philosophy) or a conceptualization of what exists (in artificial intelligence). In practice, an ontology consists of categories of individuals organized in taxonomies and connected by various other relationships. This is the reason why a graph structure is often used for representing ontologies. In order to be able to assess and enforce the modeling principles for ontologies, we start by defining the following notions: graph structure, taxonomy, and ontology. Definitions of these notions focus on structural aspects and are not intended to capture all aspects of ontologies (for a formal definition of biological classes and ontological relations, see [12,13]).

A graph G consists of two sets N and E. N is a non-empty set of nodes, and E is a set of edges, an edge being a pair of nodes from N. G is directed if its edges are directed. The node from which a directed edge originates is called the source and the one in which it terminates is the target. A path in a directed graph is a sequence of nodes 〈x₀, x₁, … , x_n〉(n > 0) where every two adjacent nodes x_i and x_i+1(0 ≤ i ≤ n − 1)are source and target, respectively, of some edge. The path is direct if n = 1; indirect otherwise. The path is called a cycle if x₀ and x_n are the same node. A graph is acyclic if it has no cycles.

A taxonomy is a directed acyclic graph satisfying the following conditions:

1. The nodes in the graph are concepts (or classes or categories⁴ ).

2. An edge between x and y represents a direct taxonomic (is-a) relationship from x to y. x is called a child (or subclass or subcategory) of y and y a parent (or superclass) of x. A concept–relationship–concept triple 〈x, is-a, y〉, called a relation, can also be used to represent the edge between x and y.

3. A taxonomic (is-a) relationship holds between concepts x and y (i.e., 〈x, is-a, y〉) if (a) x is a child of y, or (b) there exists a concept z such that the two relations 〈x, is-a, z〉 and 〈z, is-a, y〉 hold. If 〈x, is-a, y〉 holds, x is called a descendant of y and y an ancestor of x; in such cases, x is more specific than y (or is subsumed by y) and y is more general than x.

4. There is one and only one concept, called the root of the taxonomy, which has no parents. Every concept except the root has at least one parent.

5. The concepts x₁, x₂, … , x_n (n > 1) are called siblings if they all have the same parent.

A concept is called a leaf if it has no children in the taxonomy. Single inheritance characterizes a taxonomy where every concept except the root has one and only one parent. Conversely, multiple inheritance characterizes a taxonomy where at least one concept has more than one parent.

An ontology is composed of at least one taxonomy and may comprise several distinct taxonomies. Concepts across taxonomies do not stand in a taxonomic relation. Concepts in an ontology represent categories of things existing in reality or abstractions generated for classification purposes. Each category or abstraction is represented exactly by one concept. Additionally, an ontology may satisfy the following:

1. In addition to the is-a relationship, partitive (meronomic) relationships may hold between concepts, denoted by part-of. Every part-of relationship is irreflexive, asymmetric and transitive. is-a and part-of are also called hierarchical relationships.

2. In addition to hierarchical relationships, associative relationships may hold between concepts. Some associative relationships are domain-specific (e.g., the branching relationship between arteries in anatomy and rivers in geography).

3. Relationships r and r′ are inverses if, for every pair of concepts x and y, the relations 〈x, r, y〉 and 〈y, r′, x〉 hold simultaneously. A symmetric relationship is its own inverse. Inverses of hierarchical relationships are called inverse-is-a and has-part, respectively.

4. Every non-taxonomic relation of x to z, 〈x, r, z〉, is either inherited (〈y, r, z〉) or refined (〈y, r, z′〉 where z′ is more specific than z) by every child y of x. In other words, every child y of x has the same properties (z) as it parent or more specific properties (z′).

5. In addition to inter-concept relationships, concepts may have various properties, some of which are constrained by type (e.g., Boolean and integer), value range, cardinality, etc.

Hierarchical relationships are generally considered to be partial ordering relationships, i.e., reflexive, antisymmetric, and transitive [14]. In practice, however, the convention used in most ontologies is that the is-a relationship is irreflexive. Hence we define a taxonomy as acyclic. Similarly, irreflexive partitive relationships define the so-called proper parts in some systems or theories [15]. In this paper, we refer to is-a and part-of as hierarchical relationships.

4. Ontological principles

In addition to the structural aspects of ontologies defined earlier, there are principles of good ontology modeling. In this section we discuss such principles related to taxonomy, relationships, and dependence. Some of these principles are independent of the domain and others are specific to anatomy, the domain under investigation in this paper. The compliance of the FMA with the principles presented in this section will be investigated in the next section.

4.1. Principles related to taxonomy and relationships

We use x₀ − r₁ → x₁ − r₂ → x₂ … − r_n → x_n to denote a path between the concepts x₀ to x_n in the graph structure of an ontology, where n > 0 and r₁, r₂, … and r_n are relationships (hierarchical or associative). According to the definition given for a taxonomy, there should be no is-a cycles in an ontology. Analogously, according to the definition of part-of relationships, there should be no part-of cycles in an ontology. This means that for every concept x, there should be no paths such as x − is-a →… −is-a → x or x − part-of →… −part-of → x, where part-of represents any partitive relationship. Cycles containing a mix of is-a and part-of relationships are not allowed either.

In addition to concepts, relationships can be organized in taxonomies. Relationship r₁ being a child of relationship r₂ implies that for every pair of concepts x and y, 〈x, r₂, y〉 holds if 〈x, r₁, y〉 holds. Some relationships are incompatible with other relationships. If relationships r₁ and r₂ are incompatible, there is no pair of concepts x and y for which 〈x, r₁, y〉 and 〈x, r₂, y〉 hold simultaneously. For example, is-a (representing class subsumption relationship) and part-of (representing part-whole relationship) are incompatible and should be clearly distinguished within an ontology [16]. Incompatibility can also occur among various kinds of partitive relationships. The FMA, for example, defines seven different partitive relationships, four of which are incompatible with each other (constitutional part of, systemic part of, regional part of and 2D part of) [11]. Finally, incompatibility can also occur between hierarchical and associative relationships, or among associative relationships themselves. For example, the relationships branch of and tributary of in the FMA describe the spatial connections (subdivision and confluence) of linear portions of tree-like structures such as veins, arteries, and nerves. These two associative relationships are therefore incompatible with both is- a and part-of relationships.

Taxonomies can be thought of as the backbone of an ontology. Each taxonomy is organized according to classification principles. A classification criterion defines the difference between a given concept and its children. The classification criteria associated with top-level classes in the anatomy taxonomy of the FMA (spatial dimension, mass, inherent three-dimensional shape, dimensionality) have been presented in Fig. 1. Other major criteria in the anatomical domain include the presence of a cavity (cavitated vs. solid organ), the internal architecture (parenchymatous vs. non-parenchymatous), the organizational pattern (lobar, corticomedullary, etc.) Additional criteria used to further classify anatomical entities include spatial criteria (e.g., right/left, upper/lower, anterior/posterior), temporal criteria (e.g., permanent/deciduous), shape (e.g., long/short), and size (e.g., large/small). Ideally, a classification satisfies the so-called “jointly exhaustive and pairwise disjoint” rule. This implies that every concept should be classified by only one criterion, although several classification criteria may be used at different levels in the classification. Additionally, every child should differ from its parent by at least one difference (e.g., different values for a given slot). Moreover, each non-leaf concept should have at least two children. All children of a given parent have distinct characteristics (differentiae) compared to their parent (genus) and all differ from one another.

4.2. Principles related to dependence

In an ontology, some entities are dependent on other entities. For example, concept x is dependent on concept y when x cannot exist unless y exists. The multiple aspects of dependence among concepts in an ontology include physiological, causal, logical, functional, and practical dependence [17]. Ref. [18] investigated the ontological, lexical and statistical dependence relations in Gene Ontology. In the following, we discuss two types of dependence relations: concept dependence and concept–relation dependence, both deriving from terms (i.e., concept names). Unlike terminology, ontology is not directly concerned with naming entities. In practice, however, terms often reflect dependence relations among concepts. Concepts generally have at least one name. Multiple names for a concept are synonyms and concepts may be identified by one unique preferred name.

Concept dependence reflects the necessary co-existence of entities in reality. For example, in anatomy, any entity whose name contains the word “wall” (e.g., Thoracic wall) indicates an ontological dependence on the entity bounded by this wall (here, the Thorax). Similarly, Nail wall is not expected to be present if Nail is not defined in the ontology. More generally, terms such as Subdivision of x or Organ component of x should not exist in an ontology unless x exists. Analogously, entities such as Primary x and Secondary x are not expected to exist independently of each other or independently of x.

Beyond dependence relations, terms may also embed various relations, of which concept dependence is the byproduct. We call this kind of dependence between concept names and relations concept–relation dependence. In anatomy, concept names such as Thoracic wall not only reflect the dependence of Thoracic wall to Thorax, but also indicate that the Thorax has Thoracic wall as one of its parts. Other types of relationships (e.g., is-a) can be embedded in concept names. For example, Sweat gland indicates that Sweat gland is a kind of Gland.

4.3. Principles related to co-dependence of equivalent relations

Relation equivalence is exemplified by the reification of part-of relationships. It consists of using a concept named Part of W to subsume a concept P instead of using a part-of relationship between the concept P (the part) and W (the whole). The two representations 〈P , is-a, Part of W 〉 and 〈P , part-of, W 〉 are equivalent for most purposes. In addition, these two relations are co-dependent, i.e., they cannot be modified or removed independently of each other. Concept names reifying part-of relationships in the FMA include Subdivision of W and Organ component of W, where W is a concept present in the ontology. For example, Subdivision of hand suggests that all of its descendants, e.g., Hand proper, stand in part of relation with Hand. 〈Hand proper, regional part of, Hand〉 is also present in the FMA. Therefore, the two relations 〈Hand proper, is-a, Subdivision of hand〉 and 〈Hand proper, regional part of, Hand〉 are equivalent and co-dependent.

Relation dependence reflects logical or semantic connections among relations. For example, the two relations 〈x, is-a, y〉 and 〈y, part-of, z〉 can be combined logically and their combination 〈x, is-a, y〉 ∧ 〈y, part-of, z〉 implies 〈x, part-of, z〉 [16]. In other words, the relation 〈x, part-of, z〉 is equivalent to the combination of relations 〈x, is-a, y〉 ∧ 〈y, part-of, z〉 and the two sets of relations {〈x, part-of, z〉} and {〈x, is-a, y〉, 〈y, part-of, z〉} are co-dependent. When the three co-dependent relations are explicitly represented in an ontology, the modification of anyone of them requires that the other two be checked for validity.

In a previous study [19,20], we noted that relations are not always explicitly present in the FMA, and we proposed methods for making such relations explicit for the purpose of aligning anatomical ontologies. More precisely, we investigated augmentation methods for acquiring relations embedded in concept names (i.e., reified relations) and inference methods for generating new relations from a combination of existing relations.

Examples of relations acquired by augmentation include 〈Finger, part-of, Hand〉. Unlike Hand proper, Finger does not have an explicit part-of relation to Hand. Instead, Finger is a child of Subdivision of hand. Therefore, we created the relation 〈Finger, part-of, Hand〉 from 〈Finger, is-a, Subdivision of hand〉, where Subdivision of hand reifies a partitive relation to hand. Relations can also be captured by various other linguistic phenomena such as nominal modification and prepositional attachment. The former often represents a hyponymic relation involving the head of the noun phrase (e.g., Sweat gland is a kind of Gland). In anatomical terms, prepositional attachment using “of” (P of W) often denotes a partitive relation between P and W (e.g., Neck of femur is part of Femur).

Inference consists of generating new relations from combinations of existing relations. The inference rules we used generate a partitive relation between a specialized part and the whole and between a part and a more generic whole. For example, the relation 〈Atrioventricular valve, part-of, Heart〉 can be inferred from 〈Atrioventricular valve, is-a, Cardiac valve〉 (explicitly represented) and 〈Cardiac valve, part-of, Heart〉 (generated by augmentation).

Augmentation and inference can be seen as a corollary of the dependence relations presented above. In both cases, the implicit relations are expected to be consistent with the relations explicitly represented. In what follows, we take advantage of the methods developed for identifying implicit relations for checking the consistency of dependence relations.

5. Operational definition of ontological principles

We want to study the degree to which the FMA complies with 15 principles selected from the ontological principles presented in Section 4. The 15 principles listed in Table 1 are related to hierarchical cycles, classification, incompatible relationships and dependence. Additionally, some principles are applied to relations represented implicitly.

Table 1.

Operational definition of the principles

Principle		Definition
Hierarchical cycles	H1	No is-a hierarchical cycles are allowed.
	H2	No part-of hierarchical cycles are allowed.
Classification	T1	Every non-leaf concept has at least two children.
	T2	Every concept has a reasonable number of children (relative to other concepts in the same ontology).
	T3	In every group of siblings, each concept has specific properties or relations to other concepts.
	T4	Every non-leaf concept is classified according to a single criterion.
Incompatible relationships	R1	For every pair of concepts x and y, x and y do not have both is-a and part-of relationships.
	R2	For every pair of concepts x and y, x and y have at most one kind of the four part-of relationships: constitutional part of, systemic part of, regional part of and 2D part of.
	R3	For every pair of concepts x and y, x and y do not have both branch of (or tributary of) and hierarchical relationships (is-a or part-of).
Dependence	D1	Concept Subdivision of x (or Organ component of x) does not exist unless concept x exists.
	D2	Term containing the word “wall” indicates that the corresponding concept has part-of relationship to some larger concept.
Co-dependence of equivalent relations	C1	The co-dependence between equivalent relations 〈x, is-a, Subdivision of y〉 (or 〈x, is-a, Organ component of y〉) and 〈x, part-of, y〉 must be identified.
	C2	The co-dependence between equivalent sets of relations {〈x, is-a, y〉, 〈y, part-of, z〉} (or 〈x, part-of, y〉, 〈y, is-a, z〉}) and 〈x, part-of, z〉} must be identified.
Implicit relations	I1	The implicit relations are consistent within themselves.
	I2	The implicit relations are consistent with explicit relations.

6. Methods and results

In order to study the degree to which the FMA complies with the principles in Table 1, we first acquire the terms, concepts, and relations explicitly represented in the FMA. In addition, we extract implicit relations and study their consistency.

6.1. Acquiring terms, concepts, and explicit and implicit relations

Acquiring terms consists of extracting both the preferred name and synonyms (if any) of every concept. Acquiring relations consists of extracting the relations explicitly represented. Then, these relations are complemented with missing inverse relations. For example, 〈Right lung, clinical part, Apex of right lung(viewed clinically)〉 is an explicit relation in the FMA but its inverse relation is missing. In order to make the relations extracted from the FMA complete in terms of inverse relations, we generated the missing ones (e.g., 〈Apex of right lung(viewed clinically), clinical part of, Right lung〉), but still consider them as explicit relations. As shown in the upper part of Table 2, 367,224 relations are explicitly represented between concepts in the FMA, 93% of which are hierarchical relations. After complementation, the number of relation increased by about 25%.

Table 2.

Number of explicit and implicit relations in the FMA

Explicit relations (direct)	Explicitly represented	367,224
	Complemented	92,480
	Total	459,704
Unique implicit relations	Augmented	198,330
	Inferred	11,581,584
	Total	11,779,914

As mentioned earlier, many relations are not explicitly represented in the FMA. Instead, the FMA-based applications such as OQAFMA [21], Emily [22] and GAPP [23] communicate directly with the FMA knowledge base and explore paths among classes dynamically. We are not suggesting that all possible relations should be represented explicitly. However, we argue that all relations FMA-based applications generate should be compatible among themselves and with the relations represented explicitly. Implicit relations can be acquired, for example, by augmentation and inference (see Section 4.3). As shown in the bottom part of Table 2, 198,330 hierarchical relations were created by augmentation in the FMA (excluding the relations represented explicitly), 39% of which came from reified part-of relations and 61% from other linguistic phenomena (prepositional attachment and nominal modification). A total of 11,581,584 relations were generated by inference (excluding the relations represented explicitly or acquired by augmentation) [20]. Inference resulted in many more relations because the inference rules we applied perform like the transitive closure of the combination of is-a and part-of.

6.2. Hierarchical cycles (H₁ and H₂)

Principle H₁

For every concept x, we created the set of all the concepts reachable from x through the is-a relationship, directly or indirectly. This set constitutes the is-a transitive closure for x, denoted by isaTransClosure(x). If x ∈ isaTransClosure(x), an is-a hierarchical cycle is identified. No is-a cycles were found in the FMA.

Principle H₂

Similarly, we created the part-of transitive closure⁵ for every concept x, i.e., the set of all the concepts reachable from x through part-of relationships, directly or indirectly, denoted by partofTransClosure(x). If x ∈ partofTransClosure(x), a part-of hierarchical cycle is identified. Thirty-two part-of cycles were identified. One such cycle is direct (〈Skeletal muscle, systemic part of, Skeletal muscle〉), while the others are indirect (e.g., Right conjunctival sac − part of → Right conjunctiva − systemic part of → Right conjunctival sac).

6.3. Number of children per concept (T₁ and T₂)

We counted the number of children of every concept, which ranged from 0 (for leaf nodes) to 221. There are 23,368 non-leaf concepts in the FMA, accounting for about 33% of all FMA concepts. Of these non-leaf concepts, a vast majority (23,111) have at least two children, i.e., comply with principle T₁. For example, Limb has two children, Upper limb and Lower limb. However, 257 of non-leaf concepts (about 1%) have a single child. Examples of such concepts include Alveolus (single child: Pulmonary alveolus), Intercostal artery (single child: Supreme intercostal artery), and Organ component of rectum (single child: Non-striated muscle fiber of rectum).

The distribution of the number of children per concept having more than one child is shown in Fig. 2 (cumulative frequency). About 79% of these concepts have two children, 18% have between 3 and 10 children, and 2.7% have between 11 and 50 children. Only 0.1% of these concepts have more than 50 children. Overall, 95% of the concepts have seven children or less. Principle T₂ does not specify precisely the higher bound for the number of children per concept [24]. Intuitively, however, an unusually large number of children—relatively to other concepts in the same ontology—is likely to reflect inadequate classification. Table 3 shows some examples of concepts with a large number of children.

Fig. 2.

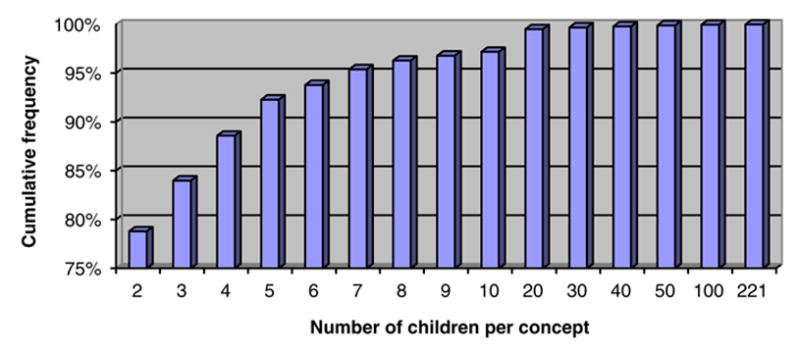
Distribution of the number of children per concept (cumulative frequency).

Table 3.

Examples of concepts with a large number of children (#)

Concept name	#	Children (partial list)
Set of arteries	221	Ventral branches of aorta Set of short posterior ciliary arteries Set of long posterior ciliary arteries	Set of arteries of brain Set of muscular arteries
Organ component of muscle (organ)	218	Fascia of muscle Organ component of muscle of arm	Organ component of diaphragm Intertubercular tendon sheath
General anatomical term	186	Right side of jaw Left side of jaw Muscle Ocular muscle	Body space General anatomy Blood cell
Set of veins	164	Set of veins of heart Set of right ventricular veins Set of left ventricular veins	Set of temporal veins Set of deep temporal veins Set of superficial veins
Anatomical line	125	Groove Groove for transverse sinus Crest of round window	Anterior border of testis Posterior border of testis Border of uterus

6.4. Existence of differences among siblings (T₃)

For every concept having more than one child, we created a list of all the relations in which each child was involved, and we identified the children having exactly the same sets of relations. In other words, siblings sharing identical relations with other concepts were grouped together.

Eleven thousand three hundred and nineteen such groups of siblings were identified, corresponding to 11,199 distinct parent concepts. As illustrated in Fig. 3, 48% of the 23,111 concepts having more than one child have at least two children sharing identical relations to other concepts. For example, Ligament of right wrist and Ligament of left wrist are siblings (children of Ligament of wrist) and exhibit no differences in their relations to other concepts. In practice, the two siblings—as represented in the FMA—differ only by their names.

Fig. 3.

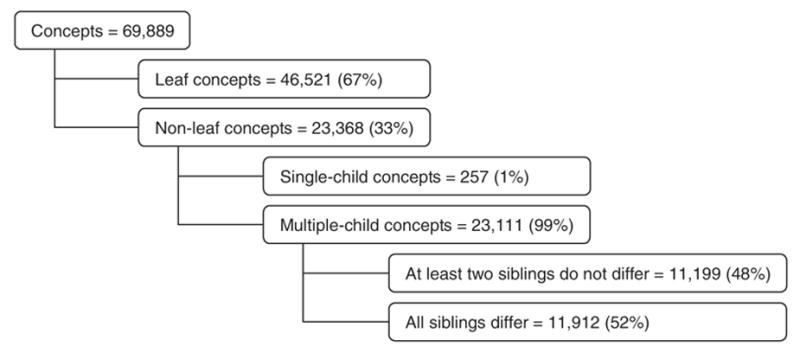
Existence of differences among siblings.

Not surprisingly, this phenomenon is more frequent in the children of concepts having a large number of children. Among the 31 concepts having from 50 to 221 children, there is only one (Set of joints) whose children can be distinguished from each other by their relations to other concepts. In contrast, the children of the other 18 concepts exhibit no differences among most of their siblings.

6.5. Existence of a single classification criterion for each concept (T₄)

Unlike many other biomedical ontologies, the FMA uses explicit classification criteria for its top-and mid-level concepts. These criteria are expressed through textual, Aristotelian definitions (e.g., Material physical anatomical entity: physical anatomical entity which has mass) and, sometimes, properties (e.g., has inherent 3D shape is true for anatomical structure and false for body substance). However, when present, classification criteria are not systematically identifiable through properties in the FMA. Moreover, no classification criterion is recorded for concepts close to the leaf level. Therefore, checking compliance with principle T₄ cannot be systematic and automatic. In a limited number of cases, however, a classification criterion can be identified from the names of the children of a given concept. Laterality (right/left) offers an example of such criterion, where a concept x has children Left x and Right x. In this case, according to principle T₄, x should have no other children than these two.⁶ For simplicity reasons, and because it is a frequent feature in anatomy, we limited our study to laterality.

Sixteen thousand one hundred and eighty-one concepts in the FMA have children whose names exhibit a laterality marker (right/left), accounting for 70% of the 23,111 concepts with multiple children in the FMA. For example, Base of patella has two children: Base of right patella and base of left patella, and the two children of cardiac chamber are Right cardiac chamber and Left cardiac chamber. Laterality is the single classification criterion for nearly 95% of the 16,181 concepts, including, for example, Base of patella. Such cases are in compliance with principle T₄.

Eight hundred and fifty-eight (5%) of the 16,181 concepts exhibit multiple classification criteria. For example, as illustrated in Fig. 4, in addition to Right cardiac chamber and Left cardiac chamber, children of Cardiac chamber also include Cardiac atrium and Cardiac ventricle. Cardiac chamber is classified by two criteria: laterality (Right cardiac chamber and Left cardiac chamber) and morphology⁷ (Cardiac atrium and Cardiac ventricle). Interestingly, the two children classified by laterality are further classified by morphology (e.g., Right atrium and Right ventricle for Right cardiac chamber). Similarly, the two other children of Cardiac chamber corresponding to the morphology criterion should be further classified by laterality (dotted lines in Fig. 4). However, this would make concepts such as Left ventricle hybrid concepts, inheriting from both Cardiac ventricle and Left cardiac chamber, which is not allowed in the FMA where single inheritance is the rule.

Fig. 4.

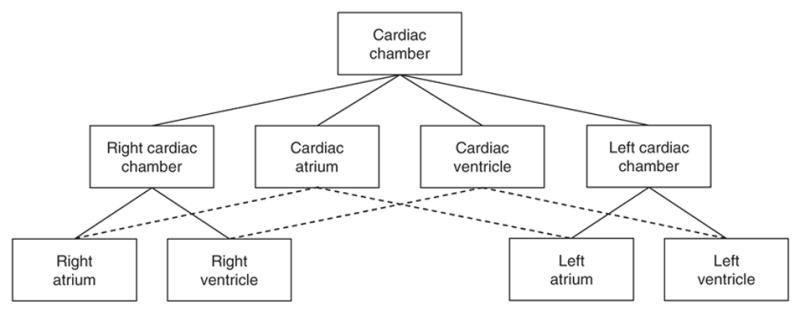
Classification of Cardiac chamber in the FMA.

6.6. Incompatible relationships (R₁, R₂, and R₃)

Principle R₁

The transitive closure created for is-a and for part-of (see Section 6.2) is used to check the presence of incompatible relations 〈x, is-a, y〉 and 〈x, part-of, y〉. For every pair of concepts x and y, the presence of both y ∈ isaTransClosure(x) and y ∈ partofTransClosure(x) is checked.

Among the 1,105,164 is-a relations and 972,612 part-of relations—direct and indirect—in the FMA, only 309 pairs of concepts stand in both is-a and part-of relation. For example, Auricle of atrium has is-a and regional part of relationships to Auricle of heart. Thirty concepts include all their children also as parts (e.g., Auricle of heart). Fig. 5 shows an example where the incompatible is-a and part-of relations are both indirect and therefore more difficult to detect by manual review.

Fig. 5.

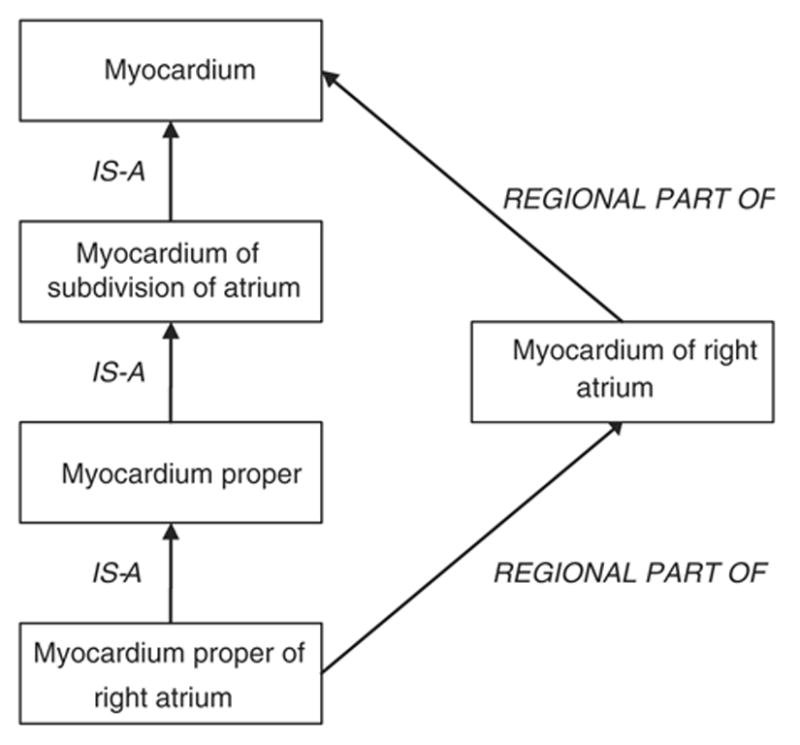
Indirect is-a and part of incompatible relations in the FMA.

Principle R₂

For each concept x, a set of all concepts having a path to x—direct or not—through the relationship constitutional part of is created. A similar set of concepts is created for each of the three other relationships: systemic part of, regional part of, and 2D part of. The presence of a concept in more than one set indicates incompatible relations.

Among the 222,994 pairs of concepts standing in at least one of the four kinds of incompatible part of relations, 123,353 (about 55%) stand in more than one kind of part of relation. For example, Prostatic lobule stands in constitutional part of, systemic part of, and regional part of to Prostatic gland. The large number of incompatible partitive relations in the FMA comes from the strategy adopted during the modeling.⁸

Principle R₃

For each pair of concepts x and y standing in either branch of or tributary of relation, the transitive closure created for is-a and for part-of is used to check the presence of incompatible relations (e.g., 〈x, branch of, y〉 and 〈x, is-a, y〉). Since branch of and tributary of are not transitive, only direct branch of and tributary of relations need to be searched.

Among the 6989 pairs of concepts linked by direct branch of or tributary of relationships, 21 were identified as also standing in is-a relation. For example, Lingual branch of vagus nerve has is-a and branch of relationship to Pharyngeal branch of vagus nerve. Four hundred and thirty pairs of concepts linked by direct branch of or tributary of relationships (about 6%) were identified as also standing in part-of relation. For example, Internal iliac artery is in both part of and branch of relationship with Common iliac artery.

6.7. Dependence (D₁ and D₂)

Principle D₁

For each term in the form of Subdivision of x or Organ component of x, a systematic check was made for a concept with name x. Preferred names and synonyms were both used in this process.

One thousand nine hundred and eighty terms in the FMA contain either “subdivision of” or “organ component of”. In 1809 cases (91%), the concept on which they depend was present in the FMA, e.g., Temporal part of head for Subdivision of temporal part of head. However, in 171 cases (9%), this concept was not defined in the FMA. For example, the concept Upper premolar tooth is absent although Subdivision of upper premolar tooth exists.

Principle D₂

The existence of a direct part-of relationship is checked between each concept whose name contains “wall” and some other concept. Again, both preferred names and synonyms were used in this process.

There are 1321 terms containing “wall” in the FMA, corresponding to 1068 concepts. Six hundred and eighty-two of these (64%) exhibit the expected part-of relation, e.g., 〈Wall of gut, regional part of, Gut〉. For the remaining 386 (36%), however, there is no explicit part-of relationship to any other concept (e.g., Nail wall). This is precisely what the techniques we developed for acquiring implicit relations are meant to address. In all but three cases (1%), these techniques were able to generate the missing partitive relations. In 75% of the cases, the missing relation was obtained by augmentation (i.e., by analyzing concept names). For example, 〈Nail wall, part-of, Skin〉 can be created from 〈Nail wall, is-a, Organ component of skin〉 (reified part-of relation). In 24% of the cases, the missing relation was generated by inference. For example, the relation 〈Wall of portal vein proper, part-of, Portal vein〉 can be inferred from 〈Wall of portal vein proper, is-a, Wall of portal vein〉 and 〈Wall of portal vein, part-of, Portal vein〉.

6.8. Co-dependence of equivalent relations (C₁ and C₂)

Some relations in the FMA are redundant, such as 〈x, is-a, subdivision of y〉 and 〈x, part-of, y〉, when both are explicitly represented. A relation which is explicitly represented may also be redundant with a combination of other explicit relations. As mentioned earlier, it is important that the co-dependence between these equivalent relations (principle C₁) or sets of relations (principle C₂) be clearly identified.

Among the 147,077 direct part-of relations explicitly represented in the FMA, we identified 5546 relations (4%) equivalent to some is-a relations. For example, 〈Fascia of muscle, part-of, Muscle (organ) 〉 is equivalent to 〈Fascia of muscle, is-a, Organ component of muscle (organ) 〉. We also identified 45,800 relations (31%) equivalent to some combinations of relations. For example, 〈Upper lobe of lung, part-of, Lung〉 is equivalent to 〈Upper lobe of lung, is-a, Lobe of lung〉 and 〈Lobe of lung, part-of, Lung〉.

6.9. Consistency of implicit relations (I₁ and I₂)

A large number of implicit relations were made explicit by the augmentation and inference techniques presented earlier. These relations are expected to be consistent with themselves (principle I₁) and with the relations explicitly represented (principle I₂). The technique used to check the consistency of implicit relations is similar to that used for principles H₁ and H₂, (i.e., checking the transitive closures of is-a and part-of relationships, respectively, for each concept), with the difference that the sets of relations now include implicit relations.

The implicit relations are generally consistent with themselves except in two cases. For example, the explicit relation 〈Surface of umbilicus, is-a, Subdivision of surface of umbilicus〉 implicitly represents a direct part-of cycle 〈Surface of umbilicus, part-of, Surface of umbilicus〉. Combining is-a and part-of relations contributed to the identification of 37 cycles. Examples include Cardiac muscle of atrium − is-a Cardiac muscle(tissue) − constitutional part of → Cardiac muscle of atrium, and Smooth muscle − systemic part of → Muscularis mucosae of stomach − is-a → Muscularis mucosae − is-a → Smooth muscle.

In all but two cases, the implicit relations are consistent with the relations represented explicitly. For example, the explicit relation 〈Apex of urinary bladder, is-a, Subdivision of urinary bladder〉 implicitly represents 〈Apex of urinary bladder, part-of, Urinary bladder〉. This conflicts with the explicit relation 〈Apex of urinary bladder, regional part, Urinary bladder〉. Note that when implicit and explicit relations conflict, a human review is needed to determine which relation is valid. In this particular case, the explicit relation 〈Apex of urinary bladder, regional part, Urinary bladder〉 is wrong.⁹

7. Discussion

7.1. Limitations of this study

The 15 principles presented in Section 5 for which we provide an operational definition are not always theoretically sound, are far from complete, and rely in part on terminological features.

Soundness issues

As mentioned in Section 6.2, one obvious limitation of this approach is the use of a transitive closure of part-of where several kinds of partitive relationships are mixed, some of which are not transitive.¹⁰ As a consequence, some of the partitive relations present in such a transitive closure may not hold and conflicts detected between such relations and other relations may be false positives. In practice, however, most of the partitive relations generated in this process are indeed valid and the benefit of over-generating relations outweighs the risk of falsely identifying conflicts. Analogously, some relations generated from a combination of is-a and part-of relations may not hold. For example, 〈Left eyeball, part-of, Eye〉 is not true (not every Eye has a Left eyeball as its part), although it was generated from 〈Left eyeball, is-a, Eyeball〉 and 〈Eyeball, part-of, Eye〉. Therefore, the practical limitation of this approach is the need for a human review of the problems identified. In other words, when implemented in an ontology development environment, such mechanisms should be used to draw the attention of ontology developers, not for the automatic resolution of conflicts.

Completeness issues

To some extent, a similar objection can be made about taxonomic relations. Although there is only one is-a relationship in the FMA, the relations 〈Right cardiac chamber, is-a, Cardiac chamber〉 and 〈Cardiac atrium, is-a, Cardiac chamber〉 actually exhibit different kinds of is-a (topological and morphologic is-a, respectively). The uncontrolled use of is-a to signify different sorts of relations results in what Guarino has called “is-a overload”, which is often associated with examples of incorrect subsumption [25]. In contrast, the use of explicit subsumption links would enable a large taxonomy such as the FMA to be subdivided in partitions—in this example, a topological (left/right) partition and a morphologic (atrium/ventricle) partition—within which taxonomic reasoning can be more reliably performed. The various partitions would yield complementary views on different aspects of one and the same reality. The formal theory underlying such partitions is presented in [26].

In addition to explicit subsumption links, additional principles could be based on concepts properties not expressed through inter-concept relationships (e.g., constraints on slot values); the incompatibility among some associative relationships could also be exploited. More generally, the principles defined in this study largely rely on the structural features of an ontology. Formal-ontological principles defined, for example, in [12] would of course constitute a powerful complement to our approach.

Terminology issues

Our method for assessing the dependence among concepts in an ontology mostly relies on the lexico-syntactic features of concept names. However, collecting the names of entities is the objective of terminology, not ontology. Although the FMA provides a rather extensive list of names for each concept, other ontologies of anatomy do not (e.g., GALEN¹¹ ). Therefore, the applicability of our dependence principles is likely to vary among ontologies.

7.2. Why do ontologies fail to comply with modeling principles?

In this analysis, the FMA complies overall with all 15 principles to a large extent. However, the compliance is complete only with principle H₁: the absence of is-a cycles; non-compliance with the other principles ranges from a few occurrences (e.g., for principle I₂: consistency between implicit and explicit relations) to about 50% (e.g., for principle T₃: presence of explicit differences among siblings). There are many reasons why compliance of the FMA with the other 14 principles is less than complete. The most obvious is that the FMA is considered by its authors and curators to be incomplete and still evolving, with large segments of the ontology awaiting population with relationships. We believe, however, that the single most important factor is the lack of support for modeling principles in ontology development environments. This is the case not only in frame-based systems such as Protégé—used for developing the FMA—but also, as noted by Golbreich et al. [27] in description logic-based systems, including OWL editors.

In the absence of built-in mechanisms for enforcing consistency, the burden of assessing it lies with the developers of the ontology. In a large ontology such as the FMA, maintaining consistency without automatic mechanisms is a considerable challenge and the relatively small number of conflicts identified in this study reflects the careful work of its team of developers. Although ontology development environments such as description logic-based systems provide some support for checking consistency, their use does not necessarily ensure compliance with all principles [4]. The approach proposed in this paper, although limited, is independent of any formalism or environment and is therefore applicable to (or adaptable by) most ontologies.

7.3. Explicit articulation of modeling principles and dependence relations

Making explicit the classification criterion used in a subsumption link—as suggested earlier—would result not only in reliable reasoning, but also in more consistent ontologies. Labeling is-a relations with the underlying classification criterion would, for example, enable the identification of gaps along hierarchical paths for a particular criterion. By representing some classification criteria through slots (e.g., has mass), the FMA exposes the most salient properties of anatomical entities. However, other classification criteria are described solely in textual definitions, preventing computers from reasoning automatically about these criteria.

Similarly, we believe that the explicit representation of dependence relations among concepts and co-dependence between sets of equivalent relations constitutes an important step towards more consistent ontologies. Such a representation would make it possible to alert the developers of ontologies when any of the dependent concepts or co-dependent relations are about to be modified. Additionally, the ability to establish equivalence between relations across ontologies constitutes a key factor for aligning ontologies developed under different principles.

These measures would of course be complementary to existing techniques such as OntoClean and other formal ontological approaches to assessing and enforcing consistency.

8. Conclusions

The creation and maintenance of large ontologies require not only the appropriate domain expertise but also well-defined organizational principles. In addition, maintaining ontologies in a consistent state also requires that such principles be actually enforced in the editing environments used to develop ontologies. Few environments, however, currently provide such capabilities. We proposed a set of 15 general principles based on classification, dependence and co-dependence of equivalent relations, for which we provide operational definitions. These definitions can be used as quality assurance tools for ontologies.

In the domain of anatomy, the Foundational Model of Anatomy (FMA) offers a good example of a large ontology (about 70,000 classes) based on a set of modeling principles. We investigated the degree to which the FMA complies with our 15 principles. The FMA succeeds in complying with all the principles: totally with one and mostly with the others. While demonstrating the effectiveness of our principles for detecting inconsistency in ontologies, we also offer suggestions for implementing effective enforcement mechanisms in ontology development environments.