Polymerization and mechanical properties of single RecA–DNA filaments

Abstract

The polymerization of individual RecA–DNA filaments, containing either single-stranded or double-stranded DNA, was followed in real time, and their mechanical properties were characterized with force-measuring laser tweezers. It was found that the stretch modulus of a filament is dominated by its (central) DNA component, while its bending rigidity is controlled by its (eccentric) protein component. The longitudinal stiffness of DNA increases 6- to 12-fold when the DNA is contained in the protein helix. Both the stretch modulus and the bending rigidity of a fiber change in the presence of various nucleotide cofactors—e.g., [γ-thio]ATP, ATP, and ADP—indicating a substantial re-arrangement of spatial relationships between the nucleic acid and the protein scaffold. In particular, when complexed with ATP, a fiber becomes twice as extensible as a [γ-thio]ATP fiber, suggesting that 32% of the DNA-binding sites have been released in its core. Such release may enable easy rotation of the DNA within the protein helix or slippage of the DNA through the center of the protein helix.

The RecA protein from Escherichia coli (352 amino acids; M_r 37,842) plays a central role in the processes of homologous recombination, recombinational DNA repair, and chromosomal segregation during cell division. RecA is an ancient, ubiquitous, multifunctional enzyme in all bacteria, with structural and functional homologues in eukaryotes ranging from yeast to humans (1–3).

RecA is also an allosterically regulated DNA-binding protein. Fundamental to all its activities is the ability to interact with nucleotide cofactors such as ADP or ATP, which modulate the stability and structure of the RecA–DNA complex (4). Upon binding ATP or a nonhydrolyzable analog such as [γ-thio]ATP (ATP[γS]), RecA undergoes an allosteric transition into a high-affinity DNA-binding form. This form of the protein is capable of binding cooperatively to single-stranded (ss)− and double-stranded (ds)DNA in a stoichiometric ratio of 1 RecA molecule per 3 nucleotides or base pairs, respectively, thus forming a right-handed helical filament that is the active species in the DNA-strand exchange and repressor cleavage reaction. Under the electron microscope (2, 3) this filament appears as a long-pitched (85–100 Å) spring formed on either ss− or dsDNA. This filament contains about 6 protein monomers per turn, with the DNA in a stretched configuration displaying an axial rise of 5.1 Å per nucleotide or base pair, respectively (5). Electron microscope studies (6) have also revealed that the DNA lies deep along the axis of the protein helix. This form of the complex is referred to as the active filament. RecA can still polymerize on ss− and dsDNA in the presence of ADP even though the protein is in its low-DNA-affinity form. Electron microscope studies of these complexes revealed shorter-pitch springs (60–75 Å). These complexes will not initiate recombination and are called inactive filaments.

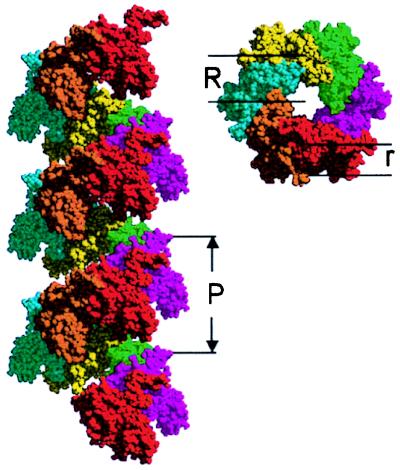
Even in the absence of DNA, RecA can polymerize to form a helical structure (1). The crystal structure of this protein helix has been solved to 2.3 Å in the presence of ADP (7, 8). Here, each protein monomer shows a major domain believed to be involved in the binding of ssDNA and dsDNA. In addition, the highly conserved region of the protein directly associated with DNA binding is arranged in two loops that are disorganized in the crystal. Two smaller subdomains at the N and C termini extend from the protein and participate in the stabilization of the 6₁ helical polymer of protein subunits and interpolymer bundles, respectively. A figure of the spring-like protein helix formed out of 19 individual subunits is shown in Fig. 1.

Figure 1.

A RecA filament built from 19 individual subunits, showing three complete turns of the RecA helix. (Left) Side view. (Right) Top view. The software package midas 2.1 (Univ. of California, San Francisco) was used to form the electronic model structure according to the crystal structure published by Story et al. (7, 8). P is the pitch of the filament, R indicates the mean radius of the helical spring, and r indicates the mean radius of the protein “wire.”

During homologous recombination, two DNA sequences must be compared over a distance of many bases to ensure the specificity of the match. The polymerized RecA protein must stretch, orient, and stiffen the polynucleotide to facilitate the register between homologous sequences. The persistence length of dsDNA–RecA–ATP[γS] filament determined from an electron microscope study (9) is ≈600 nm, indicating that it has a bending rigidity 12 times higher than dsDNA alone. However, the stretch modulus (elongation stiffness or spring constant) of the fiber has not been determined, nor it is known how the mechanical properties of the DNA and protein components are modified through their interaction. Is the excess filament stiffness, over that of DNA, provided entirely by the protein scaffold, or does the protein coating modify the stiffness and flexibility of the DNA? What are the nature and extent of the interactions between the protein scaffold and the DNA? How do the various cofactors modify the bending rigidity and the stretch modulus of the fiber? What protein–nucleic acid interactions are modified by various cofactors? Is ATP hydrolysis coupled to the mechanical properties of the filaments?

The kinetics of polymerization of RecA on DNA remains also a subject of much interest. Pugh and Cox (10) showed that polymerization of ATP[γS] RecA onto dsDNA occurs by a three-step process at physiological pH. The first step involves the weak binding of isolated protein molecules to the DNA. The second, and rate-limiting, step involves the isomerization of a prebound RecA molecule to a form that locally stretches and unwinds the DNA, thus forming a stable polymerization nucleus. This process is followed by a third and rapid propagation step in which the initial nucleation sites grow by the addition of new RecA. Leger et al. (11) followed the polymerization of RecA on individual dsDNA molecules in the presence of ATP[γS] and showed that the polymerization rate varied with the applied force on the DNA. However, no distinction between the activation energies for nucleation and propagation nor estimation of their values was made.

To address these questions, the polymerization kinetics of RecA on individual DNA molecules was examined, and the bending rigidity and stretch modulus of RecA–DNA filaments were measured in the presence of various cofactors by using force-measuring laser tweezers (12).

MATERIALS AND METHODS

A 10416-bp fragment was cut from a 12-kbp plasmid by using two restriction enzymes which left different 4-base overhangs. Two short dsDNA linkers (20 bp) with complementary overhangs were ligated to the ends of this fragment. These linkers had different chemical modifications on their outboard ends, one end being biotinylated on the 5′ blunt end while the other end was either amino-modified or thiol-modified on the 3′ blunt end, yielding a 10.4-kbp dsDNA modified on both ends of the same strand. By means of heterobifunctional crosslinkers [i.e., EDC and sulfo-NHS or sulfo-SMCC (Pierce)] and using standard protocols, the amino- or thiol-modified DNA end was coupled to the surface of a carboxyl- or amino-functionalized polystyrene bead, respectively (Bangs Laboratories, Fishers, IN). A polystyrene bead with the coupled DNA was held in the laser trap, while the other end of the molecule was attached by a streptavidin-biotin linkage to a polystyrene bead held at the end of a micropipette by suction. The center-to-center distance between the beads was measured by capturing the beads’ images in a video frame-grabber. Moving the pipette relative to the trap extended the DNA molecule. Reference force–extension curves for single dsDNA or ssDNA molecules were obtained in assembly buffer [33 mM Hepes, pH 7.2/50 mM NaCl/5 mM Mg(OAc)₂]. RecA–DNA filaments were formed on either dsDNA or ssDNA molecules tethered between the beads by flowing a solution of 2 μM RecA (New England Biolabs) in polymerization buffer [33 mM Hepes, pH 7.2/100 μg·ml⁻¹ BSA/50 mM NaCl/5 mM Mg(OAc)₂/2 mM DTT/1.5 mM nucleotide cofactor] through the fluid chamber. When ATP was used as a cofactor, an additional ATP-regenerating system was added to the polymerization buffer (5 mM phosphoenolpyruvate, 5 units·ml⁻¹ pyruvate kinase from Sigma–Aldrich). All experiments were performed at room temperature (20–25°C).

RESULTS AND DISCUSSION

Following the Polymerization of a Single Fiber.

The polymerization of RecA on a dsDNA molecule tethered between two beads (12) was followed in real time with laser tweezers. In the presence of ATP or ATP[γS], RecA polymerization increases the contour length of dsDNA and therefore its end-to-end distance x at a given force F. The number of DNA base pairs covered with RecA is then given by

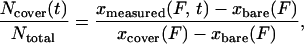1

where N_total is the total number of base pairs in the DNA molecule, x_bare(F) is the extension of the free DNA molecule, and x_cover(F) is the extension of the DNA molecule when it is fully complexed with RecA at a give force. The rate of RecA polymerization is then dN_cover/dt (for the active filament).

In contrast to a recent study (11), no RecA polymerization was observed for at least 10 min on dsDNA, unless the molecule was first placed under high tension. In the present study, it was necessary to set the force on the dsDNA at >60 pN—i.e., close to the force at which the overstretching of dsDNA occurs, ≈65 pN (12). In these conditions, polymerization was invariably observed within a few seconds. Overstretching may be required to observe prompt polymerization if the dsDNA is devoid of nicks or single-strand gaps as in the present study. To determine which step in the polymerization reaction is force dependent, two different polymerization kinetics experiments were performed.

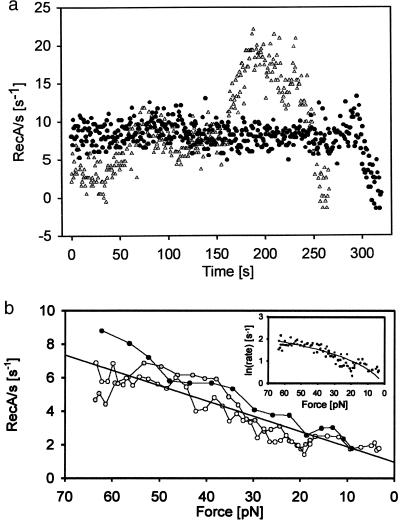
In the first type of experiment, the force applied to the DNA molecule was kept constant at 65 pN by moving the pipette away from the trap as the polymerization ensued. Interestingly, the rate of polymerization was not constant but varied from molecule to molecule as the polymerization proceeded (see Fig. 2a). These variations may express a dependence of polymerization rate on the DNA sequence or, alternatively, they may reveal that the polymerization at constant force occurs from multiple nucleation sites. According to this interpretation, keeping the force constant generates various nucleation sites that propagate simultaneously through the dsDNA molecule. Increases in polymerization rate would then correspond to the addition of new nucleation sites, whereas decreases in this rate would correspond to propagating fronts ceasing to grow as they run into adjacent ones. As shown in Fig. 2a, the rate of polymerization is seen to increase or decrease in a somewhat discrete manner in multiples of 4 s⁻¹. This value is also the smallest rate detected among the molecules studied, suggesting that it may correspond to the rate of propagation of a single nucleation site at 65 pN.

Figure 2.

Polymerization of RecA on dsDNA with or without force feedback. (a) Polymerization speed of two different RecA dsDNA fibers (●, ▴) polymerized at constant force of 64 pN in the presence of ATP[γS]. The time between points is 0.8 s, and a running average of 30 points was applied. Frame-grabber jitter of ≈20 nm probably causes the fast fluctuations. Both experiments shown, eventually covered the full length of the DNA. (b) Polymerization speed of three different RecA fibers without force feedback (see text). The figure shows the polymerization rate vs. the force applied to the growing DNA RecA fiber. (Inset) ln(rate) vs. force analysis of the slope allows one to extract the step size of the polymerization.

In the second type of experiment, the distance between the pipette and the center of the trap was kept constant. Therefore, as the polymerization ensued, converting the dsDNA into longer dsDNA–RecA filament, the bead moved toward the trap center and the tension in the molecule dropped. The result of this experiment is illustrated in Fig. 2b, where it is seen that polymerization, once initiated at high force (≈65 pN), continues despite the tension drop in the molecule. The rate of polymerization, however, decreases at lower forces.

These observations, taken together, suggest that a significant activation barrier exists for the nucleation of RecA on dsDNA and that this barrier can be overcome by overstretching the DNA molecule. Moreover, overstretching is required only for the nucleation step of RecA polymerization on dsDNA and not for the subsequent propagation steps. Assuming that each RecA binds to 3 base pairs, extending each of them by 50%, an activation energy value for nucleation E_a = 3 × 65 pN × 0.5 × 0.34 nm = 33 pN⋅nm, or about 8 k_BT, is obtained for the formation of the strained nucleation intermediate. Here it has been assumed that the molecule must be extended by the full 3 × 0.5 × 0.34 nm to attain the intermediate state from the reacting species. A better estimate for this length can be obtained by analysis of the force dependence of the propagation (see below).

Because RecA polymerization continues even as the tension in the molecule drops during propagation (Fig. 2b), the RecA molecules at the growing end of the filament must catalyze the addition of subsequent RecA monomers on the dsDNA, possibly by orienting them in the appropriate fashion on the DNA molecule and by stabilizing their transition states through the binding energy associated with protein–protein interactions. Thus the activation energy E_a would be lowered by the protein–protein interaction an amount E_I, and by the applied force an amount FΔx, where Δx is the activation length to the transition state. The polymerization rate could be written as dN_cover/dt = A₀exp[−(E_a − FΔx − E_I)/k_BT], where A₀ is an attempt frequency, k_B is the Boltzmann constant, and T the absolute temperature. The observed variation in rate with force (Fig. 2b) permits us to compute a value for Δx. But a plot of the logarithm of the elongation rate versus the force is not linear, as shown in the Inset of Fig. 2b. This observation suggests that extension of the chain and, therefore, the application of force, is the rate-limiting step for propagation only at low forces. Taking the value of the slope (0.064) of the low-force regime (<20 pN) of the polymerization gives a 2.6-Å step size, about half the width of the full elongation step for a single RecA molecule.

Pugh and Cox (10) determined that the rate constant for the isomerization step (the rate-limiting step of the nucleation process) is k₂ = 0.25 ± 0.02 min⁻¹ at 25°C and 50 mM NaCl. Thus, the application of external mechanical force to the filament is an efficient way to speed up the nucleation process. Assuming k₂(F) = k₂e^FΔx/k_BT and using FΔx = 4 k_BT, k₂(65 pN) = 0.25 min⁻¹ × 54.6 = 13.65 min⁻¹. This result is consistent with the observation that applying high tension on dsDNA induces polymerization within a few seconds.

Polymerization of RecA on ssDNA occurred spontaneously, and its rate was too fast to follow it in these assays. The ssDNA was prepared in situ by two methods—either the naked dsDNA was exposed to a 50 mM NaOH solution or the dsDNA was pulled with forces higher than 140 pN (see asterisk in Fig. 3)—both of which released the second strand into solution, leaving a single DNA chain tethered between the beads to interact with RecA monomers.

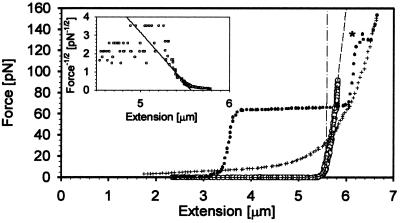
Figure 3.

Force vs. extension plot for a ssDNA–RecA filament in the presence of ATP[γS] (shown in empty circles). The dotted curve shows the F vs. extension curve for bare dsDNA, and the crosshair curve shows the bare ssDNA. To convert the dsDNA to ssDNA the dsDNA fragment was pulled to forces higher than 140 pN. At this force the second strand was released into the surrounding buffer. The dash-dotted curve displays the inextensible WLC model for a molecule with contour length 5.57 μm and a persistence length of 923 nm, whereas the dashed curve shows the extensible WLC model including a stretch modulus of 2210 pN. (Inset) F^−1/2 vs. extension plot for the ssDNA–RecA filament in the presence of ATP[γS]. At forces close to 5 pN, the end-to-end distance of a WLC approaches its contour length as F^−1/2, therefore, extrapolation to infinite force in an F^−1/2 vs. extension plot yields the contour length at the abscissa intercept, while extrapolation to zero extension gives an ordinate intercept equal to (4A/k_BT)^−1/2. The line indicates the mean value of the persistence length of all the ssDNA–RecA–ATP filaments measured.

Extracting the Mechanical Properties of RecA Fibers.

Force–extension data were used to characterize the intrinsic elasticity of the individual fibers. All the active RecA filaments displayed an entropic elasticity of an inextensible worm-like chain (WLC) at low forces. That is, the end-to-end distance, x, is controlled by the local bending of the filament caused by thermal fluctuations. x is related to the external force (F) by FA/k_BT = x/L + ¼(1 − x/L)⁻² − ¼, where A the molecule’s persistence length and L is its contour length (14, 15). At forces near 5 pN, the end-to-end distance of a WLC approaches its contour length as F^−1/2. As shown in the Inset of Fig. 3, the extrapolation to infinite force in an F^−1/2 vs. x plot yields the contour length at the abscissa intercept, while extrapolation to zero extension gives an ordinate intercept equal to (4A/k_BT)^−1/2.

At forces greater than 10 pN, the elastic behavior of the filaments deviates noticeably from that predicted by the inextensible WLC model. In this regime, the molecule behaves as a stretchable solid as shown by the deviation of the data from the WLC function. The inflection point in a plot of extension vs. ln(F) demarcates roughly the entropic elastic vs. enthalpic elastic regimes. This force F* is given by (16)

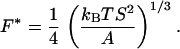2

Here S is the stretch modulus of the molecule. An equation that describes this extensible WLC regime is

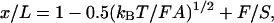3

where the first two terms give the entropic elasticity and the third term gives the enthalpic elasticity of the chain. By measuring x at forces <5 pN and fitting to WLC and by measuring x at forces >5 pN and fitting to Eq. 3, both the persistence length and the stretch modulus of the filaments were obtained.

The Mechanical Properties of ATP[γS] RecA Fibers.

Typical force–extension data from a ssDNA–RecA filament in the presence of ATP[γS] are shown in Fig. 3. The figure shows the same molecule in three different forms. First the bare dsDNA was pulled (dotted curve); this dsDNA was then converted to ssDNA by exposing the dsDNA to one high-force cycle (force >140 pN; see asterisk in Fig. 3). This process released one of the strands into solution, yielding a naked ssDNA (crosshair curve). In the subsequent step the molecule was complexed with RecA–ATP[γS] monomers, forming the active ssDNA–RecA filament. Both dsDNA– and ssDNA–RecA filaments were pulled in the presence of ATP[γS]. These filaments were formed on the DNA in polymerization buffer. RecA–ATP[γS] formed filaments on both ssDNA and dsDNA that were very stable and could be stretched with forces up to 150 pN without changing their characteristics. To confirm that two DNA chains were present at the core of dsDNA–RecA filaments and that upon binding RecA did not displace one of the chains nor did the force melt the dsDNA, the filaments were deproteinated with a solution of 1% SDS/5 mM EDTA. At the end of this process the elasticity of the remaining DNA was characterized in assembly buffer. These experiments invariably recovered the characteristic curve of bare dsDNA, including the overstretching transition.

Below 5 pN (F* in Eq. 2), the RecA filaments display the entropic elasticity of an inextensible WLC. By measuring force vs. extension for the fibers at forces below 5 pN and fitting the data to the extensible WLC model (Eq. 3), the persistence lengths of the RecA–ATP[γS] active filaments on dsDNA and ssDNA were extracted (see Inset of Fig. 3). The values for ds− and ssDNA filaments are 962 ± 57 nm and 923 ± 46 nm, respectively. Significantly, the persistence length of the filament is insensitive to whether one or two DNA chains are present at its core. Smaller persistence lengths were determined for incompletely covered RecA–DNA filaments. The values shown in Table 1, correspond to fully covered filaments. Persistence length values previously determined by electron microscopy may be artificially lower because of “conformational trapping effects” during deposition. Next, the stretch moduli of the filaments were extracted by analyzing the data above 5 pN. The values extracted for ds− and ssDNA are 4,900 ± 800 pN and 2,210 ± 580 pN, respectively. Noticeably, the dsDNA–RecA filament differed from the ssDNA–RecA filament formed with ATP[γS] in its stretch modulus by a factor of 2. The mechanical properties of the ssDNA or dsDNA covered with RecA in the presence of nucleotide cofactors are summarized in Table 1.

Table 1.

Mechanical parameters of DNA–RecA filaments

Parameter	dsDNA	ssDNA	dsDNA–RecA–ATP[S]	ssDNA–RecA–ATP[S]	dsDNA–RecA–ATP	ssDNA–RecA–ATP
Length, μm	3.55	7.11	5.40 ± 0.14	5.57 ± 0.08	5.29 ± 0.16	5.30 ± 0.14
Pitch, nn	3.4		9.57*	9.87*	9.38	9.39
Persistence length, nm	53	0.75	962 ± 57 (WLC)	923 ± 46 (WLC)	936 ± 120 (WLC)	860 ± 130 (WLC)
Stretch modulus, pN	13†	210†	4,900 ± 800 (WLC)	2,210 ± 580 (WLC)	2,280 ± 600 (WLC)	960 ± 120 (WLC)

^*Assuming 6.18 RecA subunits per turn (3). 

^†Here S = (ΔF/ΔL) × L taken at L = 1.5 times the B-form of dsDNA, so 13 pN comes from the overstretch force plateau of B-form DNA. The stretch modulus of two ssDNA molecules in parallel is 2 × 210 pN = 420 pN. 

Mechanical Properties of ATP RecA Fibers.

Filaments of RecA on ssDNA were formed in the presence of 1.5 mM ATP (see Materials and Methods). The persistence length of these filaments was comparable to that of the filaments formed on ssDNA in the presence of ATP[γS] (see Table 1). Surprisingly, however, the stretch moduli of these filaments were only half the value of the moduli of filaments formed in the presence of ATP[γS]. These filaments were very stable and showed no measurable signs of exchanging RecA molecules with the solution, which would be detected as changes in the contour length of the filaments with different forces or different concentrations of free protein in solution.

Substantially more protein exchange took place when the filament was formed on dsDNA in the presence of ATP (17). A force–extension plot in Fig. 4 shows the behavior of a typical dsDNA–RecA–ATP filament. Hysteresis is obvious, and the filament changes its contour length repeatably by ≈3% as the force is cycled between high and low values. Depleting the source of RecA molecules by passing only assembly buffer through the chamber revealed an intermediate state of the dsDNA–RecA filament that displayed the plateau characteristic of the overstretching dsDNA transition. Thus, under these conditions, some of the dsDNA between the beads was uncomplexed. Flowing RecA (with ATP) past the filament reproduced once again the force–extension hysteresis shown in Fig. 4 (circles). The persistence length of these complexes is 936 ± 120 nm (ATP), but its stretch modulus is again half the value of the dsDNA–RecA filament in the presence of ATP[γS] (see Table 1).

Figure 4.

F vs. extension plot for dsDNA–RecA ATP filaments. Fully coated dsDNA–RecA ATP form (empty circles correspond to the extension cycle and filled circles indicate the relaxation cycle). After RecA was depleted from the surrounding buffer an intermediate dsDNA–RecA ATP filament (triangles) that did not show any hysteresis as in the fully coated version showed up. The small dots correspond to dsDNA, shown here for reference.

Mechanical Properties of ADP RecA Fibers.

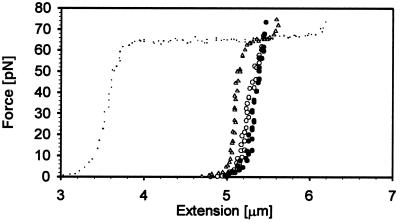
When RecA protein was polymerized on ssDNA in the presence of 24 μM ADP (18) the shape of the curve changed drastically, as shown in Fig. 5. The elasticity curves of ssDNA–RecA filaments in the presence of ADP were neither reversible nor reproducible in successive cycles, but several features were characteristic and repeatable. The force–extension–release curves display hysteresis. When a certain extension of the filament is reached (arrows, Fig. 5) the force rises quickly, indicating a contour length is reached. Then the curve follows a monotonically varying force–extension curve (almost plateau), which could correspond to gaps opening up in the protein filament. During the release cycle, the filament displays a longer contour length, indicating that RecA binding to ssDNA can be enhanced by external force. The higher the force attained during the stretching part of the cycle, the greater the amount of protein that bound to the DNA. In fact, at high forces, the inactive filament can reach up to 98% of the contour length of an active filament in the presence of ATP (see Table 1), suggesting that monomers from the solution may have bound to the gaps. Thus, the DNA/RecA ratio of the inactive filament (5 bases/monomer) may be modified by force. After relaxation at zero force for 10–60 s, the filaments lost most of their extra RecA monomers, since they have shortened again but appeared somewhat longer than in the previous stretching.

Figure 5.

Inactive ssDNA–RecA ADP filament. The first time the filament is pulled (shaded circles), the force remains very low until a length of 2.5 μm is reached, a value very close to its predicted inactive contour length of 2.6 μm (3). The force rises rapidly but flattens (first arrow) at about 10 pN. In the release half of the cycle (empty circles), the force drops at a contour length that is longer than its contour length during the stretching half. The curve composed of circles has a force maximum set at 20 pN, whereas the curve of triangles has a value of 55 pN. Curves of small dots show the F vs. extension properties of bare dsDNA (left) or ssDNA (right). The dashed line shows the WLC model for a ssDNA–RecA–ATP filament according to the values shown in Table 1.

It was not possible to fit the experimental data to a WLC model with the values indicated for the inactive filament in the literature (3). The features displayed by the force–extension curves of inactive filaments might reflect force-dependent reversible association of inactive type monomers. Alternatively, the complex behavior shown in Fig. 5 could reflect a force-induced allosteric transition of a number of monomers in the filament from the inactive to the active form in the presence of ADP. Additional monomers from solution could bind in the forced-induced active conformation to achieve an active filament stoichiometry of 3 bp per monomer. The experiments performed in this study were not able to distinguish between these two alternative explanations.

Finally, the force–extension behavior of dsDNA filaments formed in the presence of 24 μM ADP was also investigated. As with dsDNA filaments formed in the presence of ATP or with ATP[γS], when the molecule is cycled back and forth before entering the overstretch transition, no filaments are formed and the force extension curve is that of the naked dsDNA. It is reproducible and displays no hysteresis. If the overstretch plateau is reached, however, the molecule displays hysteresis, the release curve no longer following the stretch curve. Thus, overstretching is required for the binding of RecA to dsDNA in the presence of ADP as well. However, unlike the case of filaments formed in the presence of ATP, the bound RecA molecules depolymerize during the release part of the cycle at forces around 20 pN so that the molecule behaves again like naked dsDNA in the following stretch cycle (data not shown).

Mechanical Properties of the Protein and Nucleic Acid Components.

To gain insight into the organization of the nucleic acid in complexes formed between RecA and ss− and dsDNA, it is convenient to determine the degree to which the mechanical properties of the protein and nucleic acid components are modified by their interaction with each other.

Because of their parallel orientation, the stretch modulus of the filament can be thought of as the sum of a protein component and a DNA component. Because the stretch modulus of the protein component is not directly accessible in the experiments, this parameter is estimated from the dimensions of the helix (Fig. 1) and known properties of protein. To this end, the protein helix is modeled as a wire with circular cross section of radius r whose centerline traces a helix of radius R with pitch P and inclination angle α such that tan(α) = P/2πR. Assuming R > r, the stretch modulus of such a helix is given by (19)

4

where L is the total rise of the helix (L = nP) for n helical turns and L_c is the helix contour length, L_c = n[(2πR)² + P²]^1/2. The factors B_w and C_w are the bending and twisting rigidity, respectively, of the protein wire. The bending rigidity of a wire is given by B_w = Eπr⁴/4, where here E is the Young’s modulus of the material, about 3.4 × 10⁹ N/m² for protein (20). The twisting rigidity of a wire is related to its bending rigidity through Poisson’s ratio (σ) such that C_w = B_w/(1 + σ). For most polymeric materials, such as protein, σ = 0.5. Thus C_w = 0.67 B_w.

To determine r, the 2.3-Å resolution structure of Story et al. (7, 8) (Fig. 1) was electronically cut perpendicular to the cross section of the protein spring, and the various values obtained for different cross sections were averaged, yielding a value r = 1.5 nm. Similarly, the average distance of the center of mass of each cross section to the helical axis gave R = 3.1 nm. Then, using P = 9.5 nm (3), a value of S_RecA = 440 pN is obtained for the stretch modulus of the RecA helix. Furthermore, the stretch modulus of the bare ssDNA and dsDNA molecules obtained at 150% extension of dsDNA B-form contour length are 210 pN and 13 pN, respectively (Table 1). The measured S for RecA filaments is 2,210 pN for ssDNA RecA filaments, which is much greater than the sum of the individual components. Therefore the DNA, the protein, or both are highly stiffened by their interaction. To make a change in the protein solely responsible for the increased filament stiffness would require its Young’s modulus to become 17 GPa, an unusually large value for a biopolymer. The DNA, however, is the central member of the spiral fiber, giving it a larger effect on the fiber’s stretch modulus. To make the DNA account solely for the increased filament stiffness requires the DNA Young’s modulus to increase to 1.1 GPa, assuming the DNA has the same cross-sectional area as in B-form. This value is consistent with the stiffness of many biopolymers (21) and could be accounted for by the formation of a complex between the DNA and the disordered RecA loops. Therefore the element that accounts for most of the filament’s stretch modulus is probably the nucleic acid–protein complex located at its central core.

The persistence length and the entropic elasticity of the RecA fiber are determined by its bending rigidity. The bending rigidity of the fiber may be the sum of independent DNA and protein bending rigidities if the DNA can slip through the protein helix. Alternatively, if the DNA is stuck to the helix and increases the radius of the protein wire, then it affects the bending rigidity as r⁴. What then is the bending rigidity of a helix with the dimensions shown in Fig. 1? Suppose a bending moment (torque-couple) τ is applied to a helix with n turns, causing its axis to deflect through an angle θ. This total angle is the sum of n subangles Δθ from the individual turns. Each helical turn can be further subdivided into components Δx, Δy, and Δz, which are parallel to the x, y, and z axes. Suppose τ is parallel to the y axis. Then the component Δy contributes to Δθ by twisting, whereas the components Δx and Δz contribute by bending. Thus

5

But the torque-couple is also related to the deflection angle by the relation τ = B_hθ/L, where L is the end-to-end length of the relaxed helix and B_h is its bending rigidity. Thus

6

Because the persistence length is related to the bending rigidity by A = B_h/k_BT (22), a value of A = 784 nm for the protein helix is obtained. This value is similar to the persistence length of both the ssDNA–RecA and dsDNA–RecA filaments obtained from the force–extension curve data (see Table 1).

Several conclusions can be drawn from these analyses:

First, the stretch modulus of the filament is largely dominated by the nucleic-acid/RecA-loop hybrid running through its core. The calculated stretch modulus of the protein spring alone (440 pN from Eq. 4) accounts for only a small part of the measured stretch modulus.

Second, the stretch modulus of dsDNA in the filament is very nearly twice that of ssDNA (see Table 1 for ATP[γS] and ATP). The fact that the two strands contribute independently to the stiffness of the filament suggests that each strand adopts a similar structure without affecting the structure of the other strand.

Third, the stretch modulus of RecA filaments formed on ssDNA and dsDNA in the presence of ATP[γS] is ≈12 times higher than can be accounted for by the normal (entropic) elasticity of either one or two strands of bare ssDNA, respectively, at 150% extension. Thus, association with RecA not only extends ssDNA but also stiffens it, probably by preventing the rotation of the bonds in the backbone and greatly reducing its degrees of freedom.

Fourth, in the presence of ATP, these stretch moduli drop to a value which is only ≈6 times higher than the values of the corresponding ssDNA strands. Thus, upon ATP hydrolysis, some of the protein interactions that stiffen the ssDNA are removed. Perhaps bases are released from the inner protein surface and thus the chain backbone bonds regain rotational freedom. Such a process may be required for detachment of the protein from the final product of recombination. The stretch modulus of a ssDNA chain containing both free (soft) and attached (stiff) segments arranged in series is [(1 − X_free)/S_attached + X_free/S_free]⁻¹, where X_free is the mole fraction of soft segments and S_attached and S_free are stretch moduli for the two segment types. Using the value of 1,770 pN [2,210 pN (S_{ssDNA–RecA-ATP[γS]}) − 440 pN (S_RecA)] for S_attached from ssDNA–RecA–ATP[γS] fibers, and 210 pN for S_free from a free ssDNA fiber stretched to the length of a RecA fiber (see note at the bottom of Table 1) yields the 520 pN [960 pN (S_{ssDNA–RecA-ATP}) − 440 pN (S_RecA)] stretch modulus for ssDNA–RecA–ATP only if X_free is set to ≈32%. For 2 single strands at the core of a dsDNA–RecA filament, this figure is ≈15%. This method of analysis sets a lower limit on the fraction of released bases, since only part of the bond rotational freedom may be regained on segment release, and therefore 210 pN underestimates S_free. Also, stretching a soft segment should deform the protein spring because of lateral attachments through the remaining stiff segments, thus increasing S_soft. The low fraction of sites involved in this process may simply reflect the equilibrium between ATP hydrolysis by RecA and ADP phosphorylation by the ATP-regeneration system present in solution (17). Consistent with this interpretation and with previous observations (17), no significant depolymerization was observed in the ssDNA–RecA filament upon ATP hydrolysis. A small amount of depolymerization was observed upon hydrolysis in filaments formed on dsDNA (17).

Fifth, unlike the stretch modulus, the bending rigidity of the filament is almost independent of the cofactor used or the number of DNA strands at its core. Its value is largely dominated by the protein component as shown by the predicted persistence length of 784 nm. Because the bending rigidity of the protein varies as the fourth power of its radius r, adding even 1 Å in this quantity through interaction with the DNA chain increases its persistence length by 200 nm, yielding a value of ≈980 nm, the same as the experimentally observed value. However, on addition of the second strand the bending rigidity of the filaments increased only ≈50 nm, indicating that the second strand does not adhere tightly to the RecA helix and that it is able to slide past the protein component during bending.

One of the primary functions of RecA may be to lengthen and stiffen DNA chains to facilitate the pairing of homologous sequences. The values of the stretch modulus and bending rigidity of these filaments and their dependence on the number of DNA chains at their core, or the cofactors used, are consistent with these requirements (see Table 1). Single-molecule experiments involving active ssDNA–RecA filaments interacting with a bare dsDNA to perform strand exchange are now within reach. These experiments will provide further insights into the molecular mechanism involved in homologous recombination. Further investigation on inactive ssDNA–RecA filaments may give additional insights into the conversion of the active to the inactive filament.

ABBREVIATIONS

ATP[γS]

[γ-thio]ATP

ss- and dsDNA

single-stranded and double-stranded DNA

WLC

worm-like chain