The propagation of binding interactions to remote sites in proteins: Analysis of the binding of the monoclonal antibody D1.3 to lysozyme

Abstract

The interaction of a ligand with a protein occurs at a local site (the binding site) and involves only a few residues; however, the effects of that interaction are often propagated to remote locations. The chain of events initiated by binding provides the basis for fundamental biological phenomena such as allosterism, signal transduction, and structural-stability modification. In this paper, a structure-based statistical thermodynamic approach is presented and used to predict the propagation of the stabilization effects triggered by the binding of the monoclonal antibody D1.3 to hen egg white lysozyme. Previously, Williams et al. [Williams, D. C., Benjamin, D. C., Poljak, R. J. & Rule, G. S. (1996) J. Mol. Biol. 257, 866–876] showed that the binding of this antibody affects the stability of hen egg white lysozyme and that the binding effects propagate to a selected number of residues at remote locations from the binding epitope. In this paper, we show that this phenomenon can be predicted from structure. The formalism presented here permits the identification of the structural path followed by cooperative interactions that originate at the binding site. It is shown that an important condition for the propagation of binding effects to distal regions is the presence of a significant fraction of residues with low structural stability in the uncomplexed binding site. A survey of protein structures indicates that many binding sites have a dual character and are defined by regions of high and low structural stabilities. The low-stability regions might be involved in the transmission of binding information to other regions in the protein.

Because of its ability to measure individual residues, the technique of NMR-detected hydrogen exchange has become the most important technique in the study of protein-folding equilibria (1–14). Hydrogen-exchange measurements performed under native conditions have revealed significant heterogeneity in the magnitude of the protection factors observed for different residues within the same protein. These observations are inconsistent with the notion of a dominant two-state equilibrium under native conditions. If a single event (e.g., global unfolding) were responsible for exposing all the buried amide groups to the solvent, it would be expected that all of them would have the same protection factor. However, this situation is not observed experimentally (1–14). Analysis of the observed heterogeneity indicates that a large fraction of the amino acid residues in a protein become exposed to the solvent as a result of local rather than global unfolding reactions. In fact, under native conditions, the predominant equilibrium is not between the native and the unfolded state but between a large number of states generated by the occurrence of local unfolding reactions within the native structure. These local unfolding reactions involve only a few residues, occur independently of each other, and define, to a large extent, the native-state ensemble.

The above observations have called into question the traditional view, in which proteins behave as all-or-none cooperative entities, because small regions are able to undergo folding/unfolding in an independent manner. At the same time, these experiments have brought to light new fundamental questions. If the native state is a structure in which multiple regions are able to undergo small, independent, local unfolding events, then cooperativity is regional rather than global. If cooperative interactions are regional, how can the effects of local perturbations be propagated from one region to another? How is the binding of a ligand able to induce changes in regions far away from the binding site? If cooperative interactions do not extend uniformly throughout the entire protein molecule, then some residues may have a more important role than others in the development of cooperative responses. In fact, molecular communication must occur through cooperative pathways that involve only a subset of residues within the protein molecule. The identification and characterization of those pathways will have important consequences to our understanding and engineering of protein function.

Recently (13), we introduced a computational technique (single-site thermodynamic mutation) aimed at characterizing the structural distribution of the response caused by energy perturbations originating at different locations in a protein. This algorithm has been extended recently to situations in which the perturbation originates by ligand binding (Core_Bind; ref. 15). For the current study, the analysis was applied to the binding of a specific monoclonal antibody (D1.3) against hen egg white lysozyme (HEWL). The crystallographic structure for this complex has been determined at high resolution (16), and hydrogen-exchange data for both free HEWL and its complex with D1.3 are available (17). It is shown that the high-resolution structure of a protein can be used to derive the structural path followed by the stabilizing interactions induced by binding.

RESULTS AND DISCUSSION

The Absence of Global Cooperativity in the Native State.

The existence of local unfolding reactions under native conditions gives rise to an ensemble of conformational states in which each state is defined by the presence of one or more locally unfolded regions. The relative probability of those states is given by the Gibbs energy of the defining local unfolding reaction(s). Previously, we have shown that the high-resolution structure of a protein can be used as a template to generate a large number of states with varying degrees of unfolding and that the probabilities of those states, calculated by using an empirical energy function, quantitatively account for the observed protection factors (13, 18–20). This approach has been applied successfully to HEWL, equine lysozyme, bovine pancreatic trypsin inhibitor, turkey ovomucoid third domain, staphylococcal nuclease, T4 lysozyme, λ repressor, and the SH3 domain from α-spectrin (13, 14, 18–20).

Fig. 1 illustrates the most probable states calculated for HEWL under native conditions. For these calculations, a total of 98,286 states with degrees of unfolding varying from 7% to 100% were generated with the computer. The experimental pattern of hydrogen-exchange protection is well approximated by this approach (18). After sorting all the states in the ensemble in ascending Gibbs-energy order, it was found that 787 states (0.8% of the total) had Gibbs energies lower than the Gibbs energy of the unfolded state (12 kcal/mol relative to the native state). Of those 787 states, only 54 states (those shown in Fig. 1) had Gibbs energies lower than ≈6 kcal/mol. Those states are the ones that have the highest probabilities and define, to a large extent, the experimental pattern of hydrogen-exchange protection. It is noteworthy that all of these states are characterized by very low degrees of unfolding (<15%) in agreement with the notion that they are created by local unfolding events. It is also clear from these results that, under native conditions, the probability of the unfolded state is not only much lower than that of the native state, but also much lower than that of many conformations in which certain residues undergo unfolding. Thus, under native conditions, the dominant equilibrium is between the large number of states created by those local unfolding reactions.

Figure 1.

The most probable conformations in the native ensemble of HEWL. Only the states with Gibbs energies lower than 6.2 kcal/mol have been included. A total of 98,286 states were generated with the corex algorithm by using a window of 10 amino acids. In this figure, red represents native regions, and yellow represents unfolded regions. The states represented have been ordered according to their Gibbs energies: first row, from 0 to 2.5 kcal/mol; second row, up to 3.7 kcal/mol; third row, up to 4.5 kcal/mol; fourth row, up to 5.3 kcal/mol; fifth row, up to 5.7 kcal/mol; and sixth row, up to 6.2 kcal/mol. Under the simulation conditions, the Gibbs energy of the unfolded state (not shown) is 12 kcal/mol.

As shown in Fig. 1, there are some regions of HEWL that are more likely to undergo unfolding than others. In particular, residues 119–125 corresponding to the 3₁₀ helix (F helix) have very low stability constants. Most of the states in the first row in Fig. 1 have this region unfolded, and some of them are only 0.5–0.7 kcal/mol higher than the native state. Other regions characterized by low stability constants are the β-sheet region of the β-domain (residues 42–46 and 50–54), the region between residues 66–80 in the β-domain, and the region defined by helix D (residues 108–115). The most important consequence of these observations is the lack of global cooperativity in the native state. The yellow regions in Fig. 1 are able to undergo folding/unfolding reactions without the remaining parts of the protein being affected. A similar situation has been observed for other proteins (1–14). If this situation is the case and if global cooperativity is absent, how are the effects of interactions with ligands transmitted to distal sites during the course of biological function? Does the binding of ligands to relatively unstable parts of the molecule affect other regions of the protein? In the case of HEWL, these questions can be answered experimentally and theoretically, because the binding of an antibody that specifically targets the F helix region has been characterized structurally and thermodynamically, as well as by NMR-detected hydrogen exchange (17, 21).

Ligand-Induced Redistribution of the Native-State Ensemble.

The most probable distribution of states under a given set of conditions may not be the most probable distribution under another set of conditions. Consequently, from a statistical standpoint, conformational changes or other protein processes need to be understood as changes in the most probable distribution of states (22). Changes in the most probable distribution can be elicited by changes in the physical or chemical environment and can be expressed formally by a set of linkage equations that relate the effective Gibbs energy of each state with changes in those conditions (ref. 23; see also refs. 22 and 24). In the presence of a ligand X, the Gibbs energy of an arbitrary state (ΔG_i) is given by

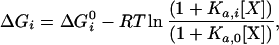1

where K_a,0 is the binding constant to the native state, K_a,i is the binding constant to state i, R is the gas constant, and T is the absolute temperature. The Gibbs energy of each conformational state will be affected in a manner dependent on the magnitude of the binding constant for that state. Accordingly, those states that are able to bind the ligand will be stabilized with respect to those states that are not able to bind the ligand, causing a change in the probability distribution of states.

In general, those protein conformational states in which the critical determinants of the binding site are formed will be able to bind the ligand with full or almost full affinity and will be preferentially stabilized with respect to those states in which the binding site is not formed. These ligand-induced changes in the probability distribution of conformational states will be reflected in the magnitude of the stability constants per residue (see ref. 22 for a general discussion). In the presence of a ligand, the probability of any arbitrary state of the protein will be given by the equation:

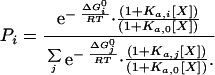2

The above ideas have been incorporated into the Core_Bind algorithm (15). This algorithm calculates the expected changes in the probability distribution of different protein states induced by the presence of a ligand. Core_Bind generates a large ensemble of partially folded conformations and calculates the intrinsic Gibbs energy (ΔG_i⁰) of each state by using procedures described previously (13, 18–20, 22). For each state, Core_Bind evaluates whether the binding site is structurally intact and, according to that criterion, determines whether the conformation is able to bind the ligand or not. In our calculations, it is assumed that those states in which the binding site is intact will have a binding affinity similar to that found experimentally.

The antibody D1.3 binds to the F helix region of HEWL with an affinity constant of 3 × 10⁸ M⁻¹ (16). The binding epitope for this antibody is defined primarily by the F helix and by some individual residues neighboring this region that are predicted to contribute significantly to the binding affinity, notably Asp-18, Asn-19, and Gly-22 in the loop connecting the A and B helices, Asn-27 in the B helix, and Gly-102 and Asn-103 in the loop connecting helices C and D (PDB ID code 1vfb). Furthermore, it has also been shown that, within the crystallographic resolution, the structure of HEWL is not affected by the binding event (17). Fig. 2 shows the most probable states in the conformational ensemble of HEWL that are binding competent toward D1.3. In the presence of D1.3, these states will be preferentially stabilized with respect to those states that are unable to bind D1.3. For example, in all the states shown in Fig. 2, the F helix is formed. Because the F helix is not intrinsically stable, the selection by the ligand of those states in which the F helix is formed implicitly includes the selection of those states in which the regions that contribute to the stabilization of that helix are also formed. This process results in a large redistribution of the native-state ensemble in the presence of the ligand.

Figure 2.

The most probable states in the conformational ensemble of HEWL that are binding competent toward the monoclonal antibody D1.3. In all these states, the binding site (corresponding mainly to the F helix) is structured, and the molecules can be recognized by the antibody even if other regions are unfolded. The states represented have been ordered according to their Gibbs energies: first row, from 0 to 5.3 kcal/mol; second row, up 6.4 kcal/mol; third row, up to 7.2 kcal/mol; fourth row, up to 7.8 kcal/mol; fifth row, up to 8.1 kcal/mol; and sixth row, up to 8.7 kcal/mol.

Because the ligand-induced redistribution of the native-state ensemble affects not only those regions in direct contact with the ligand but also regions linked by cooperative interactions, the potential exists for the occurrence of effects at distal sites from the binding site. These distal effects may include functional alterations (allosteric effects), modulation of the binding of a second ligand at a distal site, or stability effects at the residue level as seen by NMR-detected hydrogen exchange.

Effects of D1.3 Binding on Hydrogen Exchange.

The amide hydrogen protection factors obtained experimentally by NMR can be related to an important descriptor of the ensemble: the stability constants per residue (18). The stability constants per residue, κ_f,j, are the quantities that one would measure if it were possible to determine the stability of the protein experimentally by monitoring each individual residue. They are defined as the ratio of the summed probabilities of all states in which a residue is folded to the summed probabilities of all states in which that residue is not folded (18):

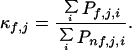3

For a significant number of residues in a protein, the hydrogen-exchange protection factors provide good estimates of κ_f,j (13, 14, 18–20). The apparent Gibbs energy per residue is given by ΔG_f,j = −RTlnκ_f,j. If a residue becomes exposed to solvent only as a result of global unfolding, then ΔG_f,j is equal to the global Gibbs energy (ΔG_U). If local unfolding processes are also able to expose a residue to solvent, then ΔG_f,j < ΔG_U.

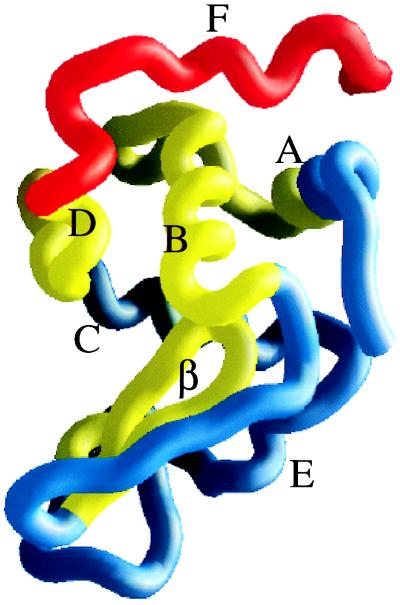
Fig. 3 illustrates the calculated effects of D1.3 binding on the residue stability constants for HEWL. In this figure, the residues in direct contact with the antibody are shown in red. These residues are expected to show enhanced protection to exchange for thermodynamic (increased stability) as well as steric (burial from solvent as a result of direct interaction with D1.3) reasons. Shown in yellow are residues that are not in contact with the antibody but are predicted by the Core_Bind algorithm to show enhanced protection because of the redistribution of the native-state ensemble. Finally, shown in blue are those residues not expected to have significant changes in their protection factors. As shown in Fig. 3, the effects of D1.3 binding extend through most of the stable core of the HEWL molecule. The effect propagates from the origin (F helix) to the immediately adjacent B helix (residues 24–37) and neighboring residues, parts of the A helix (residues 8–15) and the loop connecting them, parts of the D helix (residues 108–115), the central loop of the β-domain (residues 55–65), and the adjacent strand (residues 50–54). These results are in excellent agreement with the experimental protection factors measured for the D1.3–HEWL complex (see figure 3 and table 1 in ref. 17). There were 23 residues remote from the binding site for which enhanced protection could be measured. These residues are distributed throughout the regions predicted to show enhanced protection, except for two residues in helix C (Cys-94 and Lys-97), two residues in the loop connecting the β-domain and helix E (Cys-76 and Ile-78), and one residue (Leu-84) in helix E, all of which fall outside the regions predicted to show enhanced protection. The yellow regions in the figure define the path of cooperative interactions initiated by D1.3 binding. This path extends to regions remote from the binding site and to a significant portion of the HEWL molecule, despite the fact that the main binding determinant is one of the least stable parts of the molecule. In fact, in a previous analysis, we established that cooperative interactions were not bidirectional and that perturbations originating in regions characterized by low stability had longer-range effects than similar perturbations originating in more stable regions (13, 22). Another anti-HEWL antibody (D44.1) that binds to the primarily β-sheet region of HEWL on the opposite side of the D1.3 epitope also elicits long-range effects in the hydrogen-exchange protection factors (17). In this case also, the antibody binds to a region with low stability as indicated by the high probability of conformations in which this region is unfolded (Fig. 1).

Figure 3.

The structure of HEWL is color coded according to the magnitude of the effect of D1.3 binding on the stability constants per residue. In this figure, red denotes the region of HEWL in direct contact with D1.3. Yellow indicates the regions that are predicted to have enhanced stability constants, even though they are not in contact with the antibody. Blue denotes the regions predicted not to be affected by binding. The helices and β-domain have been labeled on the structure. The stability constants were calculated with the Core_Bind algorithm (15), and the figure was made with the program grasp (28).

Because the states stabilized by binding may have different functional properties or different binding affinities toward a different molecule, it is clear that the general process of ligand-induced redistribution of the native ensemble might have important functional implications. Another structural consequence of D1.3 binding to HEWL is a reduction in the magnitude of the conformational fluctuations in the native-state ensemble of the free protein. This effect manifests itself as a negative contribution to the heat capacity of binding. The probability distribution of states in free HEWL is broader than it is in the presence of D1.3. This tightening of the probability distribution of protein states on binding has been discussed (25).

Binding Sites.

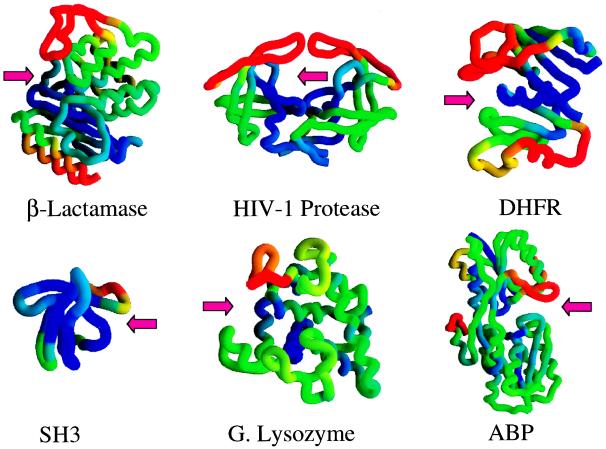
As discussed above, a significant portion of the binding site for the D1.3 antibody is defined by one of the least stable parts of the HEWL molecule (the F helix), and this characteristic is responsible for the extent of the propagation of the effects originating at the binding site. Previously, we studied the distribution of residue stabilities in the binding site of the HIV-1 protease (26, 27). It was concluded that it had a dual character, being defined simultaneously by regions of high stability and by regions of low stability. Examination of other proteins indicates that this might be a common structural characteristic of binding sites as shown in Fig. 4. In this figure, the structures of six proteins have been color coded according to the magnitude of their residue stability constants. It is evident that, in all these cases, the binding sites are defined simultaneously by regions with high structural stability (blue) and regions with low structural stability (red). As in the case of the binding of the D1.3 antibody to HEWL, the interactions of ligands with the proteins shown in Fig. 4 will cause a redistribution in their native-state ensemble and a concomitant change in the residue stability constants of residues distal to the binding site. The magnitude of these effects is related to the stability of the residues defining the binding site. If the binding site were formed by high stability residues only, all the states in the ensemble would be binding-competent, and ligand binding will induce only an energy shift without an internal reordering in the ensemble. In that case, the propagation of the effects would be limited to the immediate neighborhood of the binding site. A ligand-induced redistribution in the probabilities of conformational states requires that only a subset of the native ensemble is binding-competent. This condition is satisfied when part of the residues that define the binding site have low structural stability or exist in a non-binding-competent conformation in the unligated protein.

Figure 4.

The structures of β-lactamase, HIV-1 protease, dihydrofolate reductase, SH3 domain, goose lysozyme, and arabinose binding protein are color coded according to the value of their residue stability constants. In this figure, blue denotes the most stable regions, and red indicates the least stable regions. In each case, the arrow denotes the location of the binding site. The figure was made with the program grasp (28).

CONCLUSIONS

The studies presented here provide a look at the way in which stabilizing perturbations initiated by binding propagate throughout a protein molecule. It is clear that, under native conditions, the stabilizing effects do not propagate to all residues, even though they are able to propagate to regions far away from the binding site, as evidenced in the hydrogen-exchange protection factors measured by Williams et al. (17). As expected from the ensemble view of the native state, the transmission of cooperative interactions involves only a subset of residues within the protein molecule. This selective stabilization might be required from a functional perspective, because it is linked to the redistribution in the conformational ensemble and the preferential stabilization of those states that have a desired set of functional characteristics.

ABBREVIATION

HEWL

hen egg white lysozyme