A genetic network for the clock of Neurospora crassa

Abstract

A diverse array of organisms from bacteria to humans may have evolved the ability to tell time in the presence or absence of external environmental cues. In the lowly bread mould, Neurospora crassa, biomolecular reactions involving the white-collar-1 (wc-1), white-collar-2 (wc-2), and frequency (frq) genes and their products constitute building blocks of a biological clock. Here we use genetic network models to explain quantitatively, from a systems perspective, how these building blocks interact, and how a complex trait like clock oscillation emerges from these interactions. We use a recently developed method of genetic network identification to find an ensemble of oscillating network models quantitatively consistent with available RNA and protein profiling data on the N. crassa clock. Predicted key features of the N. crassa clock system are a dynamically frustrated closed feedback loop, cooperativity in frq gene activation, and/or WC-1/WC-2 protein complex deactivation and substantial posttranscriptional enhancement of wc-1 RNA lifetime. Measuring the wc-1 mRNA lifetime provides a critical test of the genetic networks.

Biomolecules arranged in a chemical reaction network provide a comprehensive view of how living systems function (1) and are at the heart of a new systems approach to biology (2). The biological clock (3) provides a prototypical and biologically ubiquitous example of how a complex trait can emerge from the interaction of even a small number of gene regulatory elements. In an experimentally well studied example, the filamentous fungus, Neurospora crassa, and the biomolecular reactions involving the white-collar-1, white-collar-2, and frequency genes and their products constitute building blocks of a biological clock (4). A central open question of systems biology is whether these building blocks are necessary and sufficient to define a circuit or genetic network that oscillates, and how, in quantitative detail, such oscillations emerge from the interactions among these building blocks. Here we use a recently developed method of genetic network identification (5) to find an ensemble of oscillating network models, constituted from wc-1, wc-2, and frq and their products, which is quantitatively consistent with available RNA and protein profiling data on the N. crassa biological clock. The use of genetic networks to integrate diverse experimental information and to predict the behavior of a complex trait, such as the biological clock, provides a new paradigm for quantitative genetics at the molecular level (6).

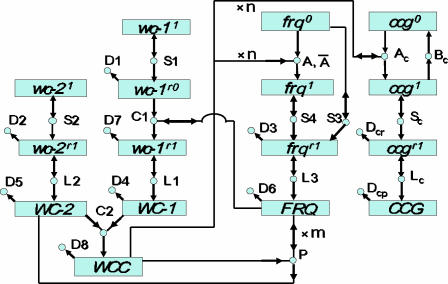
Key features of the genetic network that permit oscillations are: (i) the presence of functional wc-1, wc-2, and frq genes, generating protein products WC-1, WC-2, and FRQ, and the white collar complex (WCC) formed by WC-1 and WC-2; (ii) a closed-feedback loop of the biomolecular reactions in the genetic network, with WCC activating the frq gene → the activated frq gene producing frq mRNA → frq mRNA producing FRQ protein and → FRQ protein deactivating WCC; (iii) dynamical frustration arising in the feedback loop because of WCC's stimulation of the production of FRQ, whereas FRQ induces the deactivation of WCC; and (iv) a minimal level of cooperativity in the activity of WCC in activating the frq gene and/or in the activity of the frequency protein FRQ in deactivating WCC. The observed positive feedback of the FRQ protein on WC-1 synthesis (4) is predicted not to be a topologically essential element for oscillations to occur in the network. Rather, the prediction is that FRQ acts to increase the lifetime of wc-1 mRNA by an as-yet-unexplained mechanism, thereby enhancing wc-1 translational efficiency to a level required for sustained oscillations.

A genetic network for the biological clock in the dark, consisting of 25 reactions and 16 participating biomolecular species, is shown in Fig. 1. The experimental basis for each reaction in the network will now be described. There is strong evidence that the proteins WC-1 and WC-2 form a complex (WCC), which acts as a transcription factor for the frq and clock-controlled genes ccg (7, 8). In turn, the oscillator protein FRQ provides negative feedback by the phosphorylation-dependent inactivation of the transcription factor WCC (9) and positive feedback through the posttranscriptional control of WC-1 synthesis (4). The band (bd) gene is hypothesized to be one of these ccg genes in the circuit (7, 10).

Fig. 1.

A genetic network for the biological clock. Molecular species in the network are represented by boxes. The white-collar-1 (wc-1), white-collar-2 (wc-2), frequency (frq), and clock controlled gene (ccg) gene symbols can be superscripted 0, 1, r0, and r1, indicating, respectively, a transcriptionally inactive (0) or active (1) gene or a translationally inactive (r0) or active (r1) mRNA. Associated protein species are denoted by uppercase letters. Reactions in the network are represented by circles. Arrows entering circles identify reactants, arrows leaving circles identify products, and bidirectional arrows identify catalysts. The labels on each reaction, such as S4_, also denote the rate coefficients for each reaction. Reactions without products, such as D8, are decay reactions. Reactions A and P have cooperative kinetics: (A) n WCC + frq⁰ → frq¹ and (P) WCC + m FRQ → WC-2 + m FRQ. n and m are Hill coefficients or cooperativities. Only for the A reaction, a back reaction, (Ā) frq¹ → n WCC + frq⁰, is included, with nonzero rate coefficient Ā.

The dynamical behavior of this network is then described in terms of kinetic rate equations (11), with assumed standard mass action kinetics forming a system of coupled ordinary differential equations (ODEs). A unique solution of these coupled ODEs that can be directly compared with experimental time-dependent profiling data requires as input a knowledge of the initial (starting) concentrations of all molecular species and of the rate coefficients of all reactions (such as those given in Table 1, from an ensemble fit to the experimental data), which describe gene activation, transcription, protein synthesis, complex formation, and mRNA and protein decay. Some of these reactions (i.e., A, Ā, C₁, P, and A_c) involve the participation of the clock proteins FRQ and WCC. As uncovered by a mathematical analysis of this rate equation model [see supporting information (SI) Text], the genetic network in Fig. 1 can display a diversity of dynamical behaviors, including regular circadian oscillations and damped oscillatory transients to a stable stationary state.

Table 1.

Rate coefficients in the genetic network model of the biological clock (n = m = 4) predicting its observed oscillations (Fig. 2)

X	k	〈X〉	σ(X)
A	5	0.5717	0.145
Ā	1	0.338	0.032
S1	1	24.4	9.85
S2	1	0.077	0.535
S3	1	0.000529	0.001599
S4	1	8.34	0.99
D1	1	0.14	0.061
D2	1	0.001736	0.000560
D3	1	0.440	0.0489
C1	2	0.0519	0.03159
L1	1	79.2	12.8
L2	1	20.2	2.49
L3	1	5.76	2.08
D4	1	0.352	0.0600
D5	1	0.349	0.0356
D6	1	0.241	0.0200
D7	1	0.0717	0.0158
D8	1	0.00609	0.00752
C2	2	7.34	1.273
P	5	10.45	10.22
Ac	5	2.26	2.02
Bc	1	0.19	0.01
Sc	1	0.002	0.003
Lc	1	9.21	10.21
Dcr	1	4.83	2.64
Dcp	1	5.663	2.252

Ensemble mean 〈X〉 and ensemble SD σ(X): = [〈X²〉 − 〈X〉²]^1/2 for rate coefficients (X) in the n = m = 4 biological clock model of Fig. 1. For a k th order reaction (with k = 1, 2, or 5), the rate coefficient is given in units of 1/(h × cu^k−1), where cu represents the arbitrary but common model unit of concentration for all species. The estimated value of 1/〈D₆〉 ≈ 4 h is consistent with the FRQ protein life time of ≈4–7 h, estimated from the FRQ-decay data of Liu et al. (18). Equilibration of ensemble method is shown in SI Fig. 5.

Results and Discussion

Comparison to Profiling Experiments.

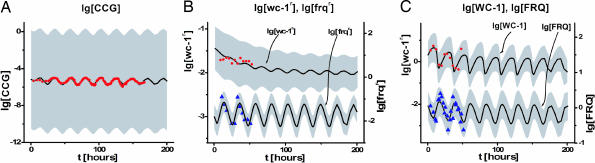
Predictions by the model ensemble using the ensemble averages ± 2 SD are shown in Fig. 2 and are quite in accord with the experimental data on the clock in the dark. The conclusion is that the genetic network in Fig. 1 is sufficient to explain published profiling data on the biological clock. The ensemble means and SDs for the 26 rate coefficients of the model are given in Table 1. Although a plethora of models have been proposed to explain biological rhythms (12), there needs to be a tighter linkage between theory and experiment, as noted by Winfree (13). This is beginning to happen for the Mus and Arabidopsis clocks (14, 15). In Fig. 2, we present detailed experimental support for the model in Fig. 1.

Fig. 2.

Comparison of experiments. A model ensemble for the genetic network in Fig. 1, with cooperativities n = m = 4, predicts various profiling data on the biological clock of N. crassa in the dark. In each image, predictions of the model ensemble for the decadic log (lg) of concentration (in model concentration units, cu; see Methods) are shown with ±2 ensemble SDs (shaded areas) about the ensemble mean (continuous lines). The points are the experimental log data. (A) Levels of conidiation for a bd mutant, hypothesized to be a measure of a CCG protein, over a 7-day interval. (B) Levels of wc-1^r = wc-1^r0 + wc-1^r1 and frq^r RNA over time t. (C) Levels of FRQ and WC-1 protein over time t.

The model ensemble makes a number of predictions consistent with experimental observations. The WC-1 protein is predicted to lag the FRQ protein with close to an 8-h phase difference in Fig. 2C, consistent with the experimentally observed 8-h phase difference (4). The FRQ protein and frq RNA are predicted to oscillate with a 4- to 6-h phase difference in Fig. 2 B and C, as observed (10). The derepression of FRQ takes 14–19 h of the circadian cycle, as observed in Fig. 2C (16). The range of log [wc-1^r1] oscillations implies a <2-fold induction of the wc-1^r1 mRNA (compared with >12-fold induction of frq RNA) during the cycle in the model in Fig. 2B; indeed, only limited oscillations in wc-1 RNA are observed, if any (4). The level of WC-2 (presumptively in the nucleus) is predicted to be in great excess of other proteins, as observed (17). Finally, the rate of translational synthesis of FRQ (L₃ in Fig. 1) is relatively rapid (with translation coefficients on the order of L₃ ∼ 6/h, in Table 1) compared with the posttranslational degradation of WCC mediated by FRQ in decay reaction P (with a cycle-maximum decay coefficient on the order of P× [FRQ]^m ∼ 1.2/h) (17). The model also trivially concurs with experiments, in that knocking out the wc-1, wc-2, or frq genes is predicted to eliminate oscillations, as observed (7). Our estimated value of 〈D₆〉⁻¹ ≈ 4 h is consistent with the FRQ protein lifetime of ≈4–7 h, obtained directly from the FRQ-decay data of Liu et al. (18), independent of our model ensemble. Models and data, together with plots of all species on varied scales (including linear) of parameter estimates vs. sweep number and of one parameter against another (including correlations), can be found at http://gene2.csp.uga.edu.

Minimal Requirements for a Ticking Clock.

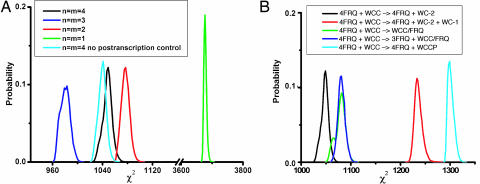
Having identified a circuit in Fig. 1 that is simple and explains observations on the biological clock in the absence of external environmental stimuli, it is natural to ask what features of the clock are essential for oscillations. A key feature to obtain oscillations in the genetic network has been the introduction of cooperative kinetics in the activation of frq (A) and/or the deactivation of WCC (P), with cooperativity exponents or Hill coefficients n and m, respectively, as defined in Fig. 1. From the mathematical analysis described in SI Text for a slightly simplified version of the model, with WC-2 set to a time-independent constant, it can be seen that some minimal amount of cooperativity, namely n m > 4, is required for the model to exhibit undamped oscillations regardless of initial conditions. There is some evidence that FRQ acts as a dimer (19), which would suggest m = 2. Four model ensembles were identified with varying Hill coefficients, with n = m and n = 4, 3, 2, or 1 (11). From Fig. 3A, it can be seen that the ensemble without cooperativity (n = m = 1) has χ² values substantially larger than those of the three ensembles with cooperativity. The χ² values of the remaining three model ensembles, with cooperativity, significantly overlap, and the best fits are achieved with Hill coefficients of n = m = 3, substantially less than postulated in some previous models (20) and in correspondence with the most robust version of a simplified stochastic model with the same Hill coefficient n = 3 (21). On the basis of the limited-duration data available, we cannot at present discriminate between truly oscillatory (undamped) models and weakly damped oscillatory models, such as the n = m = 2 model shown in Fig. 3A.

Fig. 3.

Comparison of model fits. Some model ensembles, using modified or simplified versions of the model in Fig. 1, outperform the original model in terms of χ² values. A histogram of values of χ² = −2 lnQ + const (see Methods) is shown for varying model ensembles. (A) The number of molecules of WCC (n) or FRQ (m) working together cooperatively (i.e., the Hill coefficients) in reactions A and P are varied with n = m. Also, the histogram of χ² values for a model ensemble without posttranscriptional regulation of wc-1 by FRQ is reported. Some models with less cooperativity in the action of WCC or FRQ (e.g., n = m = 3, dark-blue curve) or without posttranscriptional regulation (light-blue curve) have smaller χ² values on average than the n = m = 4 model. We have explored in detail models with n ≠ m (for n, m = 2,…, 4) with additional Monte Carlo runs as in Fig. 4; it was unnecessary to consider n = 1 and m = 1,…,4 or m = 1 and n = 1,…,4 because these cases do not satisfy the condition nm > 4 necessary for oscillations (see SI Text). The best model ensemble (histogram most shifted to the left) to date remained n = m = 3. (B) The deactivation reaction (P) is varied, allowing five different deactivation mechanisms (including the one in Fig. 1, in black) to be compared for their goodness of fit. Each deactivation reaction is defined in B Inset.

The exact mechanism by which the FRQ protein deactivates WCC complex is beginning to be understood (9). Smolen et al. (22) propose that the FRQ protein simply sequesters WCC complex in contrast to the model in Fig. 1, in which FRQ degrades WC-1 in the P reaction. Is it necessary that the P reaction be a degradation reaction? To answer this question, the ensemble method was used to reconstruct the likelihood functions under four distinct hypotheses about WCC deactivation with four slight modifications in the P reaction, defined in Fig. 3B. Two of these hypotheses are variants on Smolen's sequestering hypothesis, supplemented with cooperativity (involving an interaction between FRQ and WCC), and another simply assumes that FRQ catalytically triggers WCC complex falling apart into its constituents, WC-1 and WC-2. Schafmeier et al. (9) present evidence that it is unlikely that FRQ and WCC interact. Their final model includes FRQ acting as a cyclin to recruit a kinase to inactivate WCC by phosphorylation to WCCP. A simplified lumped circuit version of this model is tried as well with the following P reaction: WCC + 4 FRQ → WCCP + 4 FRQ. As can be seen in Fig. 3B, these alternative deactivation mechanisms are reasonably competitive with the proposed degradation mechanism in Fig. 1. At this point in time, the data used in Fig. 3B (4, 7, 10, 23) do not strongly support a particular deactivation mechanism, although the original deactivation mechanism in Fig. 1 appears to outperform the four other mechanisms proposed in Fig. 3B.

Reaction networks with both positive- and negative-feedback elements have been proposed to explain the dynamics of the biological clock (24, 25). The network in Fig. 1 has both kinds of elements. One positive-feedback element in the clock appears to be the posttranscriptional control of WC-1 synthesis (4) by FRQ in reaction C₁ of Fig. 1. In Fig. 3A, we also show the results for a model without this positive posttranscriptional feedback of FRQ on WC-1 synthesis, i.e., assuming a modified C₁ reaction, wc-1^r0 → wc-1^r1, without participation of FRQ. As can be seen, the two ensembles overlap substantially in their likelihood (χ²) values, and they do not differ significantly with regard to fit to available profiling data on the N. crassa clock. The FRQ positive feedback in reaction C₁ is evidently not an essential element of the network topology for the biological clock to function, as concluded elsewhere (22, 26).

So, why is there posttranscriptional control of WC-1 by FRQ (22, 26, 27)? A possible answer is suggested by the predicted lifetime of the translationally active wc-1^r1 mRNA, 〈D₇〉⁻¹ ≈ 14 h (from Table 1), which is comparable to a full (≈24-h) oscillation period and ≈2 times longer than the predicted lifetime of the inactive wc-1^r0 species, 〈D₁〉⁻¹ ≈ 7 h. We thus hypothesize that the primary function of the C₁ reaction is not to control WC-1 production but simply to enable it by conferring sufficient longevity to the wc-1 mRNA. Without this mRNA stabilization, the clock system would be relegated to a nonoscillatory region of its parameter space, i.e., the wc-1 mRNA would decay too fast for the clock to tick. One might ask how a fit to the data can be achieved without the positive feedback by FRQ on wc-1 mRNA, as shown by the light-blue curve in Fig. 3A. The answer is that, in our circuit without posttranscriptional regulation of wc-1 mRNA, the modified C₁ reaction (without FRQ participation) still serves to lengthen the lifetime of the wc-1 mRNA, i.e., 〈D₇〉, is still substantially reduced relative to 〈D₁〉. The problem is that, without FRQ participation, we are lacking a biochemical explanation for the lifetime increase.

The fact that, compared with its FRQ regulator (Fig. 2C), wc-1^r1 has a much weaker oscillation amplitude (Fig. 2B) is then an immediate consequence of FRQ-induced mRNA stabilization. For long wc-1^r1 lifetimes, comparable to the oscillation period, [wc-1^r1] tends to time average over the oscillations in its FRQ-controlled production rate. If the wc-1^r1 mRNA lifetime were much shorter than the oscillation period, it would be difficult to reconcile the two experimental observations that, on the one hand, FRQ is a critical translational activator, yet, on the other hand, the resulting activation, as measured by [wc-1^r], oscillates much more weakly than the activator itself. We caution, however, that our simulations and the underlying data strongly support only a very long wc-1^r1 mRNA lifetime; the evidence for a much shorter wc-1^r0 mRNA lifetime is far weaker, because the D₁ rate coefficient is only very poorly constrained by the data. The existence of the FRQ-induced mRNA stabilization and its detailed biochemical mechanism thus needs to be explored further experimentally.

A central feature of the genetic network representing the biological clock in Fig. 1 is its closed dynamically frustrated feedback loop (28), where WCC activates the frq gene, and where its FRQ protein turns around to deactivate WCC. Visualization of the model ensemble provides insights into how clock oscillations emerge in the genetic network in a way consistent with the data in Fig. 2. Key parameters of this feedback loop in Fig. 1 are the rate of activation (A) of frq by WCC, the rate of spontaneous frq deactivation (Ā), and the rate of deactivation of WCC by FRQ (P). In the mathematical stability analysis given in SI Text, a function R has been identified that partitions the 47-dimensional parameter space into one domain, where only undamped oscillations occur (red), and another where damped oscillations are possible (blue), as shown in SI Fig. 6.

In SI Fig. 6, the n = m = 4 model ensemble is projected into the (A′, P′, Ā′) volume, where the rate constants (A, P, Ā) have been rescaled to be dimensionless quantities. As can be seen, these rescaled ensemble rates represent a cylinder (red) containing ≈57% of the ensemble that satisfy the Routh–Hurwitz criterion for instability (R > 0 at all fixed points; see stability analysis in SI Text), which is necessary and sufficient for the model to exhibit sustained oscillations. The remaining 43% of the ensemble (blue), which are scattered, do not have sustained oscillations. If this subset of damped oscillators (blue) is trimmed from the ensemble, the remaining models (red) form a tight cylindrical droplet of rescaled model parameters. Similar plots in which the z axis Ā′ is replaced with the other rescaled rate coefficients that control transcription and translation of frq in the closed feedback loop (S₄, L₃) are not as constrained and can take a broader spectrum of values on the vertical axis (plots not shown). The values of the rescaled rates (A′, P′, Ā′) of activation and inactivation of frq and decay of WCC are thus key quantitative elements for sustained oscillations. The plot in SI Fig. 6 emphasizes that the data in Fig. 2 are consistent with a genetic network with sustained oscillations (in red) but do not eliminate some genetic networks with damped oscillations (in blue).

Robustness of the Biological Clock.

Perturbation of the ensemble shown in SI Fig. 6 also allows examination of the robustness of the biological clock (21, 26). One of the key predictions of the model ensemble is that the lifetime (1/D₇) of the translationally active wc-1 mRNA is long (≈14 h). To examine robustness of the model, we varied this key parameter for each ensemble member from its estimated value of ≈14 h (〈D₇〉 = 0.07/h, in Table 1) down to 1.0 h (or D₇ = 1.0/h), keeping all other rate coefficients fixed at their ensemble-generated values. As indicated in Table 2 by the percentage of stable oscillators in the so-perturbed ensemble, the cyclical dynamics is robust against an ≈15-fold decrease of lifetime, but then the ensemble becomes arrhythmic at a lifetime of ≈1.33 h (or D₇ = 0.75/h) or shorter. The actual distribution of D₇ values (not shown here) in the unperturbed ensemble of SI Fig. 6 imposes a much tighter constraint of D₇ < 0.10/h (i.e., the experimental data, through the ensemble likelihood, support only a lifetime of translationally active wc-1 mRNA longer than 10 h).

Table 2.

As the lifetime of the translationally active wc-1 messenger RNA, wc-1, decreases (or equivalently, its decay rate coefficient D₇ increases), the model ensemble predicts that the system becomes arrhythmic

D7 (1/h)	Posc, %
0.07	71
0.10	66
0.15	61
0.20	57
0.25	54
0.50	46
0.75	42
0.90	40
1.00	37
1.10	36
1.25	33
1.50	28
2.00	14
2.50	3
3.00	0

The percentage of stable oscillators, P_osc, in the model ensemble from SI Fig. 6 (for the n = m = 4 model in Fig. 1 with WC-2 constant) perturbed by the decay rate coefficient D₇ for each ensemble member being varied from 0.07 (approximately the mean estimate in Table 1) to 3.00, while keeping all other rate coefficients fixed at ensemble-generated values. This percentage monotonically decreases as the lifetime of the translationally active wc-1 mRNA decreases (or equivalently, as its decay rate coefficient D₇ increases).

Critical Test of the Biological Clock Model by Measuring the Lifetime of the wc-1 mRNA.

An essential element for the genetic networks to produce oscillations is the long lifetime of the wc-1 mRNA. If the measured wc-1 mRNA lifetime were too short (Table 2), then the proposed genetic networks that are consistent with the published data would be incorrect. The lifetime of the wc-1 mRNA was measured by introducing a quinic acid (QA) inducible copy of the wc-1 gene qa-2:wc-1 (26) into the his-3 locus of a strain, which is descended from a wc-1 mutation (Fungal Genetics Stock Center 3914), as a critical test of the models proposed (Table 1). The strain was shifted from QA (0.0192% or 0.3%) to glucose (2%) or galactose (2%) at the light/dark (L/D) transition to turn off production of wc-1 mRNA, and wc-1 mRNA levels were measured relative to those of rRNA by real-time PCR (see SI Fig. 7). As a control to verify the function of the switch, wc-1 mRNA levels were measured under induced and noninduced conditions (see SI Fig. 7 Inset). Two glucose transporters were found to be light-responsive (unpublished results), and galactose uses a different transporter system (29). Therefore, a switch to an alternate carbon source (galactose) was tried as well, eliminating the precipitous drop in wc-1 mRNA shortly after the L/D transition. The estimated lifetime of wc-1 mRNA behaves as predicted and has a long measured lifetime (128 h or D₇ = 0.0072 ± 0.0078), consistent with the prediction of the genetic networks (〈D₇〉 = 0.07 ± 0.02, in Table 1); moreover, the model ensemble (Table 1) was able to predict the drop in levels of wc-1 mRNA over time as shown in SI Fig. 7. As we shall see below, by introducing a light response into the model the ensemble prediction (〈D₇〉 = 0.019 ± 0.003) comes even closer to the experimental value.

Testing the Biological Clock Model by Its Light Entrainment Response.

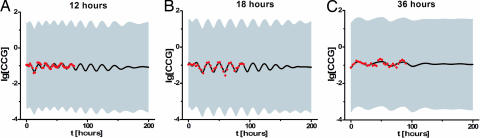
As a final test of the genetic network in Fig. 1 and to reduce the variation in the parameters (Table 1) by the addition of an additional 205 new data points on the CCG species, the biological clock was entrained with a varying artificial day [12-, 18-, and 36-h period (23)]. The model was modified to allow a light response by introducing one new species, the photon, that assists in the formation of WCC complex. The C₂ reaction (Fig. 1) is complemented by C₃: WC-1 + WC-2 + photon → WCC. Froehlich et al. (8) have shown that FAD is a cofactor to WC-1 light sensitivity in vitro. This simple extension of the model correctly predicts the light entrainment response in Fig. 4, because the artificial day is varied from 12 to 36 h and produced a more precise prediction of the wc-1 mRNA lifetime = (1/D₇) (〈D₇〉 = 0.019 ± 0.003), which is closer to the measured value of 0.0072 ± 0.0078. Inclusion of the light-entrainment data reduces the ensemble standard errors (Table 1) for a majority of the rate constants.

Fig. 4.

The biological clock of N. crassa and its model entrain to an artificial day of 12-, 18-, and 36-h duration. (A) Six hours of light followed by 6 h of night and repeating. (B) Nine hours of light followed by 9 h of night and repeating. (C) Eighteen hours of light followed by 18 h of night and repeating. Dots indicate data points (23), and shaded regions are the predictions of the model ensemble supplemented with one new reaction, C₃, to allow a light response: WC-1 + WC-2 + photon → WCC. The solid line is the mean of the ensemble predictions. The model ensemble here was initialized from an earlier accumulation run using published data (see Methods).

Concluding Remarks.

The usual modus operandi for quantitative genetics is to narrow progressively the search for quantitative trait loci (QTLs) to explain a complex trait in terms of a position on a chromosome (30). The ultimate expression of this approach is the Human HapMap (31). Once the QTLs are in hand from the use of the HapMap, the end goal is the discovery of what the QTLs do. Here we have introduced a different but complementary paradigm for explaining a complex trait. A genetic network is introduced as a precise hypothesis to explain how genes and their products control the biological clock (as in Fig. 2). The resulting genetic network provides quantitative and testable predictions about how biomolecules interact to determine such a complex trait.

Methods

Clock Data on the Band (bd) Mutation and Sources of Profiling Data on the N. crassa Biological Clock.

The wc-1 RNA data are digitized from figure 1A of ref. 4, and the frq RNA are digitized from figure 1C of ref. 10; the WC-1 protein data are digitized from figure 1 of ref. 4, and the FRQ protein are digitized from figure 1B of ref. 4. The physiological bd data are from figure 2 of ref. 7 and figure 4 of ref. 23.

Measuring the Lifetime of the wc-1 mRNA.

A bd his3 a N. crassa strain (87-84), kindly provided by J. C. Dunlap and J. J. Loros (Department of Biochemistry, Dartmouth Medical School, Hanover, NH), was crossed with a wc-1 met-7 A strain (FGSC 3914). Offspring 87-84-6 was confirmed to be his-3 wc-1 at 34°C and was transformed with a plasmid pDE3dBH-qa-2:wc-1 (targeting the his-3 locus), kindly provided by Y. Liu (26), by using the spheroplast method and histidine selection (32). In each lifetime experiment, transformant 87-84-6-8 was grown in ≥16 replicate 500-ml flasks with 120 ml of quinic acid (0.0192% or 0.3%) plus Fries Medium liquid culture for 4 h at 25°C in a shaker (New Brunswick Scientific, Edison, NJ, Series 25) at 150 rpm under 70 μm/s per m² light source and then shifted to 2% galactose (or 2% glucose) plus Fries in the dark (or light); other conditions were the same. For each time point, a culture was harvested by vacuum filtration and frozen at −70°C for later RNA isolation by using the High Pure RNA isolation kit (Roche, Indianapolis, IN). RNAs were analyzed by real-time PCR on an ABI-Prism 7500 (Applied Biosystems, Foster City, CA) by using Taq Man probes against an rRNA standard. Details are described in SI Text.

Ensemble Identification of Genetic Networks.

Ensemble identification was carried out as described in refs. 5, 33, and 34 and in SI Text and SI Fig. 5.

Abbreviation

ODE

ordinary differential equation.