Extended random sequential adsorption model of irreversible deposition processes: From simulations to experiments

Abstract

An experimental study of the irreversible deposition of colloidal particles of various radii R on a solid surface is presented over a wide range of the Péclet number, Pe, or reduced radius R* (Pe = R*⁴). The experimental data are analyzed by means of a new generalized random sequential adsorption model that takes explicitly the diffusion of the particles during the deposition into account. It allows description of the continuous transition from a random sequential adsorption-like to a ballistic-like deposition behavior. It depends on three parameters: d_s, related to the diffusion of the particles before adhesion; n_s, related to the number of allowed adhesion trials of a particle; and R_e, representing the effective particle radius. The model allows accounting for all of the experimental observations relative to the radial distribution functions and the number density fluctuations over the whole coverage range and all investigated values of R*. In addition, it is found that d_s/R is proportional to R*⁻² as expected for a diffusional process. Moreover, the parameters d_s and n_s appear to be connected through the empirical relation (d_s/R)n_s^2/3 = C, where C is found to be of the order of 50. This unique statistical model allows an accurate description of the irreversible deposition process, whatever the influence of gravity with respect to diffusion.

The structure of an assembly of particles deposited or adsorbed on a solid surface depends on the ability of the particles to diffuse along the surface: when they can diffuse on the surface, the laws of statistical mechanics predict the properties of the system. In the case of irreversible deposition processes in which, once adsorbed, the particles can neither move along the surface nor desorb from it, the structure depends on the particle interactions and on a parameter R*, related to the Péclet number by Pe = R*⁴, which characterizes the relative importance of the gravitational field with respect to the Brownian motion of the particles during the deposition process (1). Large values of R* (R* > 3) correspond to deposition processes in which gravity plays a dominant role, whereas small values of R* (R* < 1) characterize purely diffusional deposition processes.

Over the last few years, our understanding of these irreversible deposition processes has evolved from both the experimental and the theoretical point of view, and a great effort toward modeling has been undertaken. For the case of large R*, the ballistic-deposition (BD) model has been developed (2, 3). It has been shown experimentally that this model describes accurately such deposition processes (4). For the case of small R*, the random sequential adsorption (RSA) model has been introduced (5). Its validity for describing adsorption processes is less clear. Although it seems to predict quite accurately the radial distribution function, g(r), of the assembly of the adsorbed particles (6, 7), it leads to contradictory results as far as the density fluctuations of adsorbed particles is concerned. This latter is measured by the reduced variance (ratio of variance σ² to mean 〈n〉) of the distribution of the number of particles deposited on a great number of subsurfaces of equal size that are part of the deposition plane (6, 8).

For particles characterized by intermediate values of R*, the interplay between diffusion and gravity during the deposition process becomes the dominant feature. To model these processes, the generalized BD model, which allows a continuous transition from the RSA to the BD model, has been introduced (9). Unfortunately, it does not incorporate the diffusional aspect of the deposition process. On the other hand, models in which the diffusion in the gravitational field is directly simulated have also been proposed (10). It is, however, difficult to compare experimental results to their predictions because of the extensive computer power needed to cover large surfaces.

The present article is aimed at the elaboration of a new statistical model that is less computer time-consuming, while also allowing a continuous transition from the RSA model to the BD model. In addition, the model takes the diffusion during the deposition process into account, while avoiding its explicit simulation. We compare the results of this model to experimental data obtained for a series of particles covering a large R* domain (Table 1). The measured quantities are the radial distribution function g(r) and the reduced variance σ²/〈n〉. Whereas g(r) gives information on the local correlation between deposited particles, σ²/〈n〉 contains information on the ability of a deposited particle to hinder a new one to deposit on the same subsurface (11). If, after having interacted with a deposited particle, an incoming particle can diffuse away from the subsurface, it is lost for this subsurface and thus influences σ²/〈n〉. We exploit this property with a method by analyzing the evolution of σ²/〈n〉 as a function of the size of the subsurfaces to obtain information on the importance of the diffusion during the deposition process. Both the model and the analysis method are original.

Table 1.

Characteristics of the particles (mean radius and SD given by the manufacturer), size of the pictures, and fitting parameters derived from the ERSA model

System name	Mean radius R ±SD, μm	R*	Pe	Zeta potential, mV	Picture size, Ap/R2	Re/R	ds/R	ns	(ds/R) ns2/3
P07	0.7940  ±  0.0080	0.666	0.197	−56.8	42.88  ×  36.59	1.10	10  ±  2	40  ±  10	117.0  ±  42.9
P08	1.0065  ±  0.0110	0.845	0.509	−59.5	38.53  ×  32.68	1.10	7  ±  1	20−5+10	51.6−16.0+24.6
P11	1.2250  ±  0.0130	1.03	1.12	−36.4	49.58  ×  42.53	1.10	5  ±  1	30  ±  10	48.3  ±  20.4
P13	1.5315  ±  0.0150	1.29	2.73	−33.5	40.54  ×  34.77	1.05	3  ±  0.2	80  ±  20	55.7  ±  13.0
P17	2.0000  ±  0.0200	1.68	7.94	−32.7	42.62  ×  36.35	1.05	1.5  ±  0.2	200  ±  20	51.3  ±  10.3
P21	2.4955  ±  0.0300	2.09	19.2	−37.1	34.16  ×  29.13	1.05	1.3  ±  0.2	220  ±  20	47.4  ±  10.2

EXTENDED RSA (ERSA) DEPOSITION MODEL

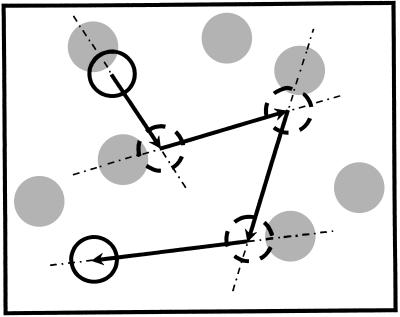
The irreversible deposition model presented here (ERSA) is an extension of the RSA model in which monodispersed particles, considered as hard spheres, are deposited sequentially on the surface. It contains two parameters: the maximum diffusion distance d_s during one deposition attempt, and the maximum number of deposition attempts n_s of a particle. These parameters depend on the radius R and buoyancy Δρ of the particles. An adsorption trial consists of the following steps (illustrated in Fig. 1). (i) A position is randomly chosen over the surface. If the particle does not overlap with any of the already adsorbed spheres, it is irreversibly fixed to the surface, and the trial is finished. One could also introduce an adsorption probability, as was done by Luthi et al. (12). There was, however, no strong motivation to do so because in our experiments, the surface was coated with fibrinogen (see below). (ii) Otherwise, a new position is selected on a line joining the centers of the depositing particle with the fixed one that was hit. This position is defined by the radial distance chosen randomly between 0 and d_s, starting at the center of the depositing particle, taken in the direction going from the center of the deposited particle to the center of the depositing one. If, in this new position, the particle does not overlap with any of the adsorbed spheres, it is irreversibly fixed on the surface; otherwise, a deposition attempt is repeated, following rule ii. If, after n_s attempts, the particle cannot find a location to deposit, it is removed from the system and the deposition procedure is repeated with a particle starting from a new random position on the plane.

Figure 1.

Schematic representation of the diffusing trajectory of a depositing particle (○). represents the deposited particles, and the dashed circles represent the intermediate positions of the trial particle.

The parameter d_s describes the diffusion of the particles during the sedimentation process: the smaller the Péclet number, the larger the d_s value. In fact, it is expected that d_s/R ∝ R*⁻², as follows from a crude analysis based on the Langevin equation accounting for the diffusion in a gravitational field (13). It appears therefore that the usual RSA model is not a limiting case of the ERSA model, basically because the RSA model does not account explicitly for the diffusion of the particles. It can, however, be recovered when n_s is preset to unity. Any overlap then produces the immediate rejection of the trial particle, whatever the value of d_s. On the other hand, when R* increases, it is known that the rolling mechanism over deposited particles becomes increasingly important. This mechanism is imitated in the ERSA model by decreasing d_s and increasing n_s. In the limit of a virtually infinite R*, the BD model is recovered when n_s → ∞ and d_s → 0, the product d_s × n_s being on the order of magnitude of some R. Thus, in contrast to the RSA model, the BD model is actually a limiting case of the ERSA model. Finally, it may be stressed that the values of d_s and n_s corresponding to a particular value of R* must also account for the possibility a particle has to escape from a trap formed by at least three deposited spheres, as is observed experimentally. The comparison of the ERSA model predictions to experimental results will reveal that the model correctly reflects the physical mechanisms governing the adsorption process.

In addition to the parameters d_s and n_s, an effective particle radius, R_e, is introduced in the model. This supplementary degree of freedom is necessary on the one hand to account for the electrostatic interactions (7, 14) and on the other hand to correct for the fact that the particle radius is never known exactly, its measured value being in addition partially dependent on the determination technique.

It may also be emphasized that the ERSA model, which covers the entire range of Péclet numbers, includes the diffusion in the bulk and in the vicinity of the adsorbing surface. This means that it includes de facto the influence of the lubrication forces, as expressed by the nonisotropic friction tensor in more theoretical approaches (13).

MATERIALS AND METHODS

Experiments.

The experimental procedure has been described extensively in previous publications (4, 6, 15) and will thus be only briefly outlined here. The experiments were performed by depositing polystyrene particles of radii ranging from ≈0.8 up to 2.5 μm and of density 1.05 g⋅cm⁻³ on a cover glass slide on which fibrinogen, a plasma protein, is first adsorbed. This coating is performed to render the adsorption irreversible. The particles of six different sizes (Table 1) were purchased from Duke Scientific (Palo Alto, CA) and used after dilution in an aqueous HCl solution at pH 4.

After deposition of the particles, 900 mutually independent pictures, each covering the same area A_p of the surface (Table 1), were taken with a charge-coupled device video camera with 256 × 256 picture elements. Such a large number of pictures is required to reduce the scattering of σ²/〈n〉. These pictures were subsequently treated by an image analysis software (visilog, Noesis, Orsay, France) to determine on each picture the position of the centers of the deposited particles and then the number of particles. The radial distribution function g(r) and the reduced variance of the distribution of the number of particles in the pictures were derived from these data. To determine the dependence of σ²/〈n〉 on the area A_p covered by a picture, each picture was subdivided into 4^ℓ identical rectangles (1 ≤ ℓ ≤ 6). One thus creates a new assembly of subsurfaces of equal area A_p/4^ℓ, characterized by a new value of σ²/〈n〉. Finally, for each experiment, which corresponds to a given surface coverage θ, we obtained the radial distribution function g(r) and a series of σ²/〈n〉 values related to the values of the integer ℓ, including ℓ = 0 for which the original area is recovered. This provides an additional information that can be exploited when these experimental data are compared with the predictions of the model obtained by computer simulations.

Computer Simulations.

For each experimental system (i.e., each particle size) computer simulations were performed in which a large surface was covered by particles according to the deposition model described above. The size of this surface, to which periodic boundary conditions were applied, was chosen such that it corresponds to the area covered by 900 experimental pictures. The ratio of the area of each of the 900 subsurfaces to the projected area of a particle in the simulation was equal to its experimental counterpart. Moreover, the aspect ratio of the surface was also the same. It should be emphasized that the (x, y) coordinates defining the position of the adsorbed particles were pixelized as were those from the experimental pictures. The particle radius was first set equal to the particle radius given by the manufacturer, and the parameters (d_s, n_s) were adjusted so as to obtain the best possible agreement between the computed σ²/〈n〉 and the one derived from the experiments for all the seven subsurface areas. Once this was achieved, the radial distribution function predicted by the simulations usually had a shape quite similar to the experimental one, but a homothetic transformation of the interparticle distance, r, had to be carried out to bring them in closer agreement. This is equivalent to changing the radius of the particles to an effective radius R_e. However, because both effects are embodied in a unique parameter, it is not possible to quantify their respective importance. In any case, R* given in Table 1 is calculated by using R. Even whether R_e was to correct only for the geometrical size of the particles, their R* would not be affected by >10% for the particles considered here, because R_e/R ≤ 1.10. The simulations were then repeated to optimize the triplet of parameters (d_s, n_s, R_e) with respect to the reduced variances as well as to the radial distribution functions.

RESULTS AND DISCUSSION

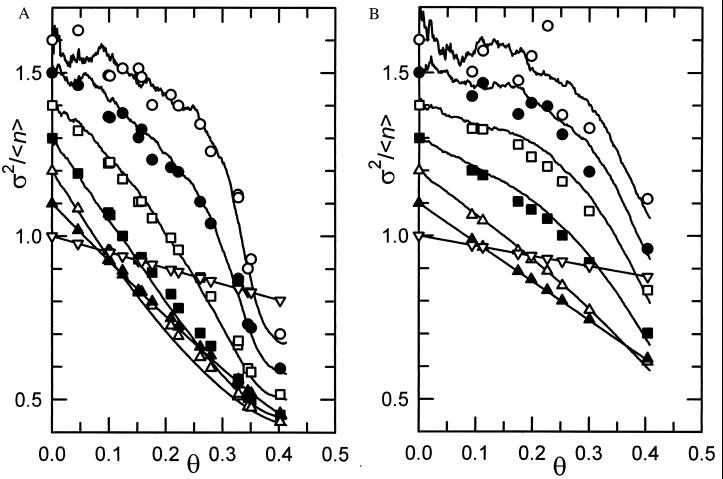
Figs. 2 and 3 represent, respectively the comparison of the experimental reduced variance σ²/〈n〉 for the two extreme particle radii investigated experimentally (systems P07 and P21) and of the radial distribution function g(r) for the six systems (from P07 to P21), with the computer simulation results corresponding to the optimized parameters (d_s, n_s, R_e). The agreement between experimental results and model predictions for σ²/〈n〉 are very satisfactory for both the P07 (Fig. 2A) and P21 (Fig. 2B) systems for all of the subsurface sizes and over the full coverage range. These results are typical for the entire series of investigated systems. The ideal agreement for the smallest subsurface size comes from the fact that in this case, each subsurface contains the center of at most one particle so that the limiting Bernoulli law is recovered. On the other hand, the area covered by the initial pictures (which represent the largest subsurface area considered) is large enough for the limiting law, in which σ²/〈n〉 becomes insensitive to the size of the subsurfaces to be reached. This has been verified by direct comparison between simulation results with the known expressions for σ²/〈n〉 as a function of the coverage for the RSA and the BD models in the limit of infinitely large subsurfaces (15). One can thus state that the experimental results and those derived from the ERSA model, as far as σ²/〈n〉 is concerned, are in good agreement for all the subsurface sizes and over the full coverage range.

Figure 2.

(A) Reduced variance σ²/〈n〉 as a function of the coverage θ for the P07 system. The symbols correspond to the experimental values, and the lines correspond to the simulations. The results corresponding to the different subsurface areas considered have been successively shifted by 0.1 for the sake of clarity. The symbols appearing on the y axis are ranked in order of decreasing size of the subsurfaces from top (ℓ = 0) to bottom (ℓ = 6). (B) Same as A, except that σ²/〈n〉 corresponds to the P21 system.

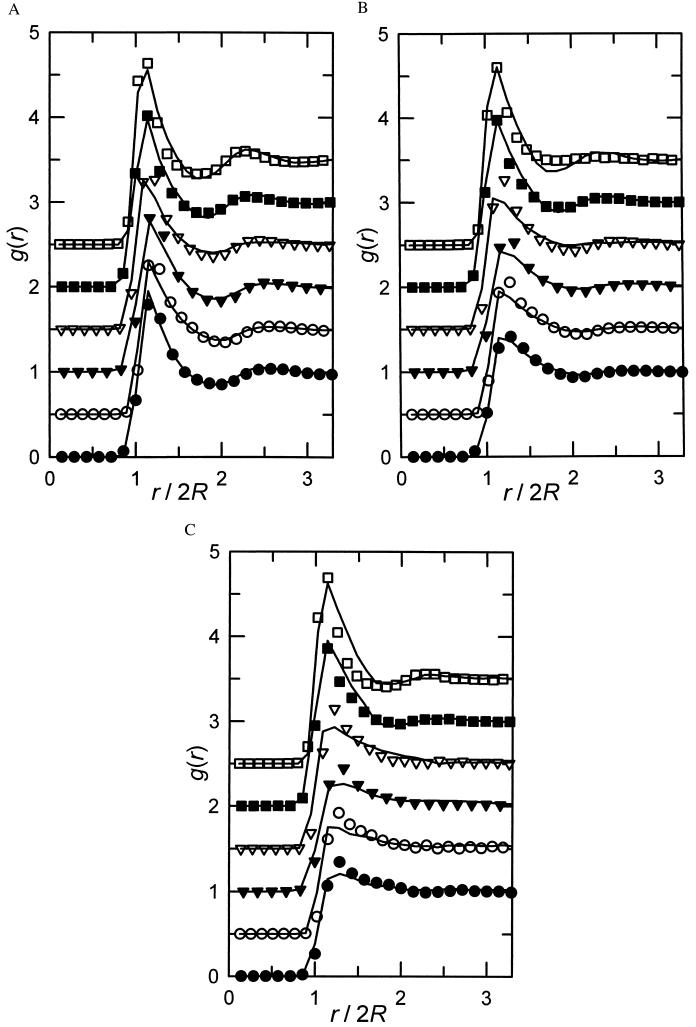
Figure 3.

(A) Radial distribution functions g(r) for the six particle systems investigated as a function of the interparticle distance r, at θ on the order of 0.4. The symbols correspond to the experimental results, and the lines to the model results. The data have been successively shifted by 0.5 for the sake of clarity. From top to bottom: P21 (θ = 0.404), P17 (θ = 0.381), P13 (θ = 0.381), P11 (θ = 0.388), P08 (θ = 0.366), and P07 (θ = 0.403) particle systems. (B) Same as A, except that θ is on the order of 0.25. From top to bottom: P21 (θ = 0.253), P17 (θ = 0.267), P13 (θ = 0.267), P11 (θ = 0.250), P08 (θ = 0.258), and P07 (θ = 0.261) particle systems. (C) Same as A, except that θ is on the order of 0.1. From top to bottom: P21 (θ = 0.113), P17 (θ = 0.126), P13 (θ = 0.126), P11 (θ = 0.116), P08 (θ = 0.130), and P07 (θ = 0.124) particle systems.

As to the radial distribution function g(r), an excellent agreement is reached at high coverage (θ on the order of 0.4, Fig. 3A) for all particle sizes between the experimental results and our model predictions. The agreement is still very good for intermediate coverage (θ on the order of 0.25, Fig. 3B), and some deviations only appear at low coverage (θ on the order of 0.1, Fig. 3C). These deviations in g(r), which seem not to appear in σ²/〈n〉, can be due to the fact that the particles are assumed to be hard spheres with an effective radius. This is certainly an oversimplification that might affect more strongly g(r), which is a direct measure of the very local particle interactions, than σ²/〈n〉, which depends more directly on the ability of particles to hinder new ones to adhere. It may be noted that the computed g(r) values do not vanish at r < 2R merely because the coordinates were pixelized, as already indicated.

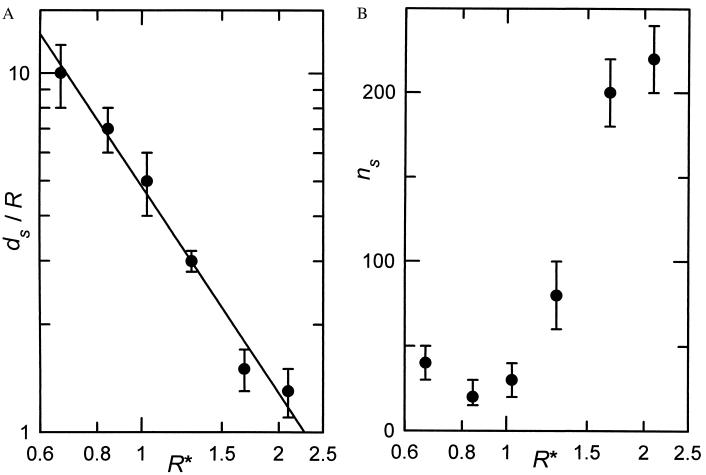
The values of d_s and n_s corresponding to the best agreement between experiments and simulations are given in Table 1 and represented in Fig. 4 A and B as a function of R*. From Fig. 4A it is revealed that d_s/R varies as βR*^−α, with α = 1.92 ± 0.13 and β = 4.88 ± 0.28. This result confirms our expectation that d_s characterizes the distance over which a particle can diffuse during the deposition process and that d_s/R should vary as R*⁻², as suggested above. Fig. 4B shows that the parameter n_s first remains stable for R* smaller than or near 1 and then increases rapidly with R*. In fact, the two parameters d_s and n_s cannot be fully independent: for large values of R*, once the depositing particle interacts with an already adsorbed one, it diffuses closely along the deposited particle toward the surface. In the ERSA model, because d_s becomes small when R* is large, this movement requires a larger number of steps, which leads to an increase in n_s (Fig. 4B). On the other hand, n_s is also related to the escape probability of a particle from a trap: the larger n_s, the higher is this escape probability provided that d_s remains larger than R/√3. The connection between d_s and n_s seems to be confirmed by the fact that the product (d_s/R)n_s^2/3 determined experimentally is constant (within the experimental uncertainties) with respect to R* except for the smallest value of R*. In this case one can, however, expect electrostatic interactions to come into play and thus to add new features to the process not taken into account in the model. Because traps form only at high coverage, it is expected that the model becomes more sensitive to n_s at large coverage, as was indeed observed during the adjustment procedure. It was also observed that the model is more sensitive to n_s for the larger subsurfaces, whereas it is more sensitive to d_s for the smaller subsurfaces and over the entire coverage range; in fact, it becomes more sensitive to d_s already in the small coverage domain for the smaller particles. This observation has greatly facilitated the adjustment procedure and can be explained as follows: for small particles, the diffusion distance of a particle during the deposition process is large. This result implies that after interaction with an already deposited particle, the depositing one can diffuse over a long distance before finally reaching the deposition surface. If, during this process, it diffuses over such a distance as to leave of the subsurface over which it had originally landed, it is lost for this subsurface. This is equivalent to a new particle landing randomly over the deposition plane, as far as σ²/〈n〉 is concerned. Thus, this latter becomes very sensitive to d_s for subsurfaces having a characteristic size of the order of d_s and less sensitive for larger subsurfaces. Moreover, this effect should appear over the whole coverage range. Finally, it was also noticed that σ²/〈n〉 is not very sensitive to the effective radius of the particle, whereas g(r) depends critically on this parameter.

Figure 4.

(A) Representation of the diffusion distance d_s as a function of the reduced radius R*, corresponding to the six particle systems investigated (●). The solid line is the least-squares fit to the experimental data. (B) Representation of the maximum number of attempts n_s as a function of the reduced radius R*, corresponding to the six particle systems investigated.

CONCLUSION

We have introduced in this study a statistical model that takes into account irreversible deposition processes under the influence of gravity. This model depends on three parameters: d_s, which proves to be essentially a maximum diffusion distance; n_s, the maximum number of deposition attempts of a given particle; and R_e, the effective radius of the particles considered as hard spheres. Many experiments, at various surface coverages, have been performed for six particle sizes covering the transition region from a BD-like to an RSA-like behavior. It has been shown that it is possible to adjust these three parameters to account for all of the structural parameters that were determined experimentally (radial distribution function and reduced variance over the full coverage range and for different subsurface sizes). This is a very strong indication for the general validity of this model aimed at describing such irreversible processes.

In addition, it has been shown that d_s/R seems to scale as R*⁻², as expected from the Langevin equation. Moreover, the experiments also seem to indicate that both d_s and n_s are connected through the relation (d_s/R)n_s^2/3 ≈ 50, for which no theoretical explanation has been found so far by the authors. Further experiments performed in the low-R* domain would be necessary to validate this relation.

The usually undesirable finite size effects were thoroughly exploited here to “measure” the power of the model. This method should be very useful as a complement to the radial distribution functions to characterize other systems like adsorbed protein monolayers by atomic force microscopy or electron microscopy.

ABBREVIATIONS

RSA

random sequential adsorption

ERSA

extended random sequential adsorption

BD

ballistic deposition