Establishing the entatic state in folding metallated Pseudomonas aeruginosa azurin

Abstract

Understanding how the folding of proteins establishes their functional characteristics at the molecular level challenges both theorists and experimentalists. The simplest test beds for confronting this issue are provided by electron transfer proteins. The environment provided by the folded protein to the cofactor tunes the metal's electron transport capabilities as envisioned in the entatic hypothesis. To see how the entatic state is achieved one must study how the folding landscape affects and in turn is affected by the metal. Here, we develop a coarse-grained functional to explicitly model how the coordination of the metal (which results in a so-called entatic or rack-induced state) modifies the folding of the metallated Pseudomonas aeruginosa azurin. Our free-energy functional-based approach directly yields the proper nonlinear extra-thermodynamic free energy relationships for the kinetics of folding the wild type and several point-mutated variants of the metallated protein. The results agree quite well with corresponding laboratory experiments. Moreover, our modified free-energy functional provides a sufficient level of detail to explicitly model how the geometric entatic state of the metal modifies the dynamic folding nucleus of azurin.

The entatic state occurs in proteins when a group, metal or nonmetal, is forced into an unusual, energetically strained geometric or electronic state (rack-induced state) (1–4). Through the polypeptide's folding-induced rigidity, the protein fails to provide the expected geometry of ligating groups that would occur with freely mobile ligands in solution, thereby tuning the ligand's redox characteristics. In metalloproteins, the metal ions are typically bound to the protein through one or more lone pair donors, endogenous biological ligands (e.g., the imidazole moiety of histidine, the carbonyl oxygen of the main chain or the side chain of an asparagine residue). In several cases the ligands are arranged such that an optimal geometry is precluded (1–4). The resulting entatic state in a given metalloprotein is determined by the entire rigid protein scaffold in concert with the hydrogen-bonding network proximal to the coordination sphere (5, 6). The particular geometry of the rack-induced state influences the electronic structure of the metal site. Moreover, the resulting forced electronic structure, at least in certain cases, becomes essential for the protein's biochemical function in electron transport (7). We should remember the entatic hypothesis is in some respects still controversial. Results from some quantum calculations have suggested that the geometry of metal–ligand complexes identified as being rack-induced are not necessarily highly strained (8), whereas other theoretical studies suggest that the rigidity of the protein may in fact be much more significant than initially thought (9).

Cupredoxins, a family of electron-transfer metalloproteins, are believed to adopt such a rack-induced state by way of a distorted tetrahedral (type I) copper site. The geometry of the ligand set provided by the protein in this so-called entatic state is neither optimal for Cu¹⁺ nor Cu²⁺. As a result, redox interconversion does not result in dramatic structural changes. Consequently, the overall reorganization energy for the electron transfer, including the inner coordination sphere, of the type I copper site is relatively small (10–13), speeding the electron transfer process. The architecture of a typical type I copper sites involves four canonical ligands; specifically, a strongly coordinating thiolate of a cystine residue, the imidazole nitrogens of two histidines, and a weakly coordinating thioether sulfur on a methionine residue.

Pseudomonas aeruginosa azurin is a small (128 aa) cupredoxin, i.e., a blue copper protein, composed of eight β-strands arranged in a double-wound Greek key topology, which forms a rigid β-barrel (14). Interestingly, the redox-active copper is coordinated to the protein via five ligands instead of four. In addition to the four canonical ligands (i.e., H46, C112, H117, and M121 to a lesser extent), a secondary weak-axial ligand, the main-chain carbonyl of G45, completes the active site, resulting in a trigonal bipyramidal geometry rather than the canonical distorted tetrahedral arrangement often found.

Upon unfolding of metallated azurin, the copper remains bound to the denatured polypeptide in a trigonal coordination composed of the native ligands C112, H117, and possibly M121 (15). In the denatured state the slow irreversible redox coupling between the C112 thiol and Cu²⁺ promotes sulfur oxidation. As a result, Cu²⁺ metallated azurin does not fold reversibly in the laboratory (16); thus, a thorough investigation of how the metal center influences the protein's stability and folding dynamics is very difficult. Fortunately, Zn²⁺ can be exchanged for copper without significant change to the rigid structure of azurin (14, 17). Because zinc is essentially redox inactive, a more detailed assessment of the metal's role in the folding landscape can be performed for this system. Moreover, the main properties of the entatic state at least from the geometrical point of view still hold; the first coordination sphere and the intricate hydrogen-bonding network that constitutes the second coordination sphere is largely unperturbed by the substitution and like copper its geometry is not optimal for zinc coordination [see supporting information (SI) Fig. 6].

Experiments on Zn²⁺-metallated azurin revealed a significant nonlinear free-energy relationship for the kinetics under both folding and unfolding conditions. The curvature in the so-called “chevron plot” appears to result from transition-state movement. Recently, the protein engineering method (i.e., φ-value analysis) pioneered by Fersht and coworkers (18, 19) was used to obtain snapshots of zinc-substituted azurin's dynamic folding nucleus with residue specific resolution. Analysis of several point mutated variants (typically involving hydrophobic-to-alanine transformation) of zinc-metallated azurin, covering all of the secondary structure elements, revealed that the folding nucleus is spatially delocalized and gradually becomes more native-like around an epicenter situated on residue L50 (20). The dramatic difference in kinetic folding behavior between apo-azurin, which has a fixed and rather polarized folding nucleus (21, 22), and the malleability exhibited by the zinc form was rationalized in terms of a minor change on a common broad activation barrier. This article studies the folding landscape for Zn²⁺-metallated azurin by using a free-energy functional scheme appropriately modified to treat metal coordination events to shed light on how the dynamic folding nucleus is involved in forming the so-called entatic state.

The Theoretical Foundation

The Basis of the Variational Approach.

Our study of the dynamic folding nucleus and free-energy profile of zinc-metallated azurin uses a variational approach that explicitly incorporates the metal coordination reactions. The current approach starts with a functional developed by Portman, Takada, and Wolynes (23–25). Their variational method is based on a coarse-grain free-energy functional that only considers native contacts consistent with the dominance of native interactions required by the principle of minimal frustration (26–29). The Hamiltonian for the polymeric assembly is comprised of two terms, a pairwise contact interaction, H_int, and a backbone scaffold term, H_chain, modeling a collapsed stiff chain of monomers each representing a residue in the protein's primary sequence (Eq. 1):

Here a is a microscopic length taken to be the mean square distance between adjacent monomers in the chain, B is an energy term conjugate to the radius of gyration of the chain, r_i is the position of monomer i in the polymer chain, and the correlations between any two C_α positions are given by Γ⁻¹ (25). The term H_int in the energy functional contains a pairwise potential u(r_ij) with an interaction strength coefficient ε_ij. We parameterized the ε_ij coefficients by using Miyazawa–Jernigan contact energies. The interaction potential u(r_ij) is a sum of three Gaussian potentials representing short-range (s), intermediate-range (i), and long-range (l) parts, where α_l < α_i < α_s are the long-, intermediate-, and short-range widths, respectively. The long-range term is attractive, whereas the intermediate- and short-range terms are repulsive (i.e., γ_l < 0, γ_i > 0, and γ_s > 0, respectively) (25).

Modeling the Coordination Reaction.

To model the metallated form of azurin, the cofactor was explicitly incorporated into the functional, and the corresponding coordination event during the folding process was considered. First, the appropriate metal–ligand interactions were simply treated as contacting positions carrying electrostatic interactions during the folding event, and as a separate step these ligands were allowed to undergo coordination reactions to the Zn²⁺, which confer the appropriate binding stability. Separating, these two steps resemble the differentiation between forming contact pairs and inner-shell reorganization in inorganic solution reactions. For some metals there may be barriers for the coordination step, but these are small for Zn²⁺. To describe the ligand–cofactor interactions, the C112 and H117 ligands were modeled as permanent constituents of the backbone connections, while cofactor interactions with residues G45 and H46 were allowed to form or break during the folding and unfolding process. The methionine at position 121 was classified as a weakly interacting ligand in the folded copper-metallated protein with an interaction distance of ≈3.2 Å, whereas zinc-substituted azurin's interaction distance was approximated at 3.3 Å (14, 17, 30, 31) (see SI Fig. 6). Considering that the resolution provided by x-ray crystallography for the Cu²⁺- and Zn²⁺-metallated azurin structures is presently limited to 1.5 Å, the thioether's sulfur interactions with the cofactor are geometrically indistinguishable in practice. Moreover, the role of M121 as a coordinating residue in the unfolded state is still not settled (10, 15, 20, 32). Accordingly, this particular residue was not explicitly modeled as a coordinating residue, only as a contacting residue. Furthermore, the limited resolution provided by our current model restricts our assessment to a given geometric structure; as a result, the detailed effects of changing the metal cofactor geometry on the folding landscape do not directly enter, but instead only the overall energetics of the coordination process enter the model. To treat electronic structure effects on the folding landscape explicitly would require extensive ab initio quantum mechanical calculation, or at the very least, a highly refined semiempirical quantum treatment.

The Coordinating Stiff Chain.

To model the C112 and H117 residues as constituents of the stiff chain, we introduce an additional term to the usual polymer backbone term H_chain. A fixed angle θ between adjacent bonds, based on the molecular structure, is assumed and explicitly modeled in the inverse of the monomer correlation Γ (Eq. 2). The usual backbone scaffold term H_chain has a Γ matrix form as follows:

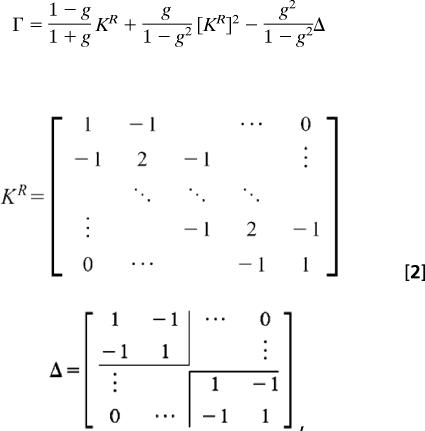where g = −cos θ, (π/2 ≤ θ ≤ π), and K^R is Γ in terms of a Rouse matrix, and Δ accounts for the polymer boundaries of the respective termini, based on the stiff chain model (33). To account for the cofactor's interaction with the native ligand set, the correlation matrix is modified to be Γ_holo:

where C_[112,129] and C_[117,129] describe the position correlations between the zinc ion and C_α atom of residues 112 and 117. The resulting backbone scaffold is represented by:

Modeling the Noncovalent Ligand Interactions.

Experimentally, one finds the cofactor–ligand interactions confer an additional 7 kcal·mol⁻¹ of stability to the folded protein (20). The microscopic rates of the individual metal–ligand association reactions are significantly larger than the overall folding rate. This finding suggests the ligand cofactor interactions are most probably not rate-limiting during the folding process and can be treated as representing a quasi-equilibrium. To model the folding in the absence of the coordination reactions, the metal–ligand interactions with H46 imidazole and the carbonyl of G45 were first treated by using a pairwise potential that would reflect only intramolecular charge–charge interactions within the protein. To approximate the electrostatics effects alone the weight of a given metal–ligand-charged interaction was given by a strength coefficient ε_ij (Eq. 1), based on the Miyazawa–Jernigan scale (34) with well depths set to 3 and 5 kcal·mol⁻¹ for glycine–Zn²⁺ and histidine–Zn²⁺, respectively. These electrostatic well depths were chosen based on those for glycine or histidine interacting with singly positively charged residues, which we take to approximate the strength of the corresponding metal–ligand interactions, when there is no specific coordination.

To accurately fit the thermodynamics of the coordination in the context of the folded protein a different metal–ligand interaction H_{int_coord} was used. When the residues become coordinated the contact interactions are increased in strength to have coefficients with well depths of 13 and 15 kcal·mol⁻¹ for glycine–Zn²⁺ and histidine–Zn²⁺ coordination, respectively. The ligation term when coordination occurs is written as:

where ε_[45,metal] and ε_[46,metal] are termed the coordinate contribution of the histidine and glycine metal–ligand interactions, respectively. The difference between ε_[45,metal] and ε_{[46, metal]} reflect the expected difference between histidine nitrogen and carbonyl oxygen coordination. The overall magnitude of the binding results in a stability change at T = 1.91 caused by the coordination event that is approximately −7 kcal·mol⁻¹. Thus, the coordination strength fits the experimental thermodynamics (20). Notice that this finding is consistent with the entatic state hypothesis; the expected additional thermodynamic stability based solely on the coordination energies would be considerably higher (i.e., 28 kcal·mol⁻¹) than the experimental value. This quantitative difference reflects the entropic cost of forming the coordination sphere in the context of the folded protein.

Approximating the Free-Energy Surface.

The free-energy surface of the zinc-metallated protein is obtained by using a variational scheme based on a reference Hamiltonian H₀, which constrains the biopolymer chain and the Zn²⁺ ion to fluctuate to varying extents about their location in the native state (Eq. 6):

Here C_i is a set of constraining variables that reflects the local Debye–Waller factors for main-chain motions, thereby monitoring the fluctuation of each residue about its native position r_i^N. The Feynman–Gibbs–Peierls–Bogoliubov variational principle is based on the reference Hamiltonian H₀, which yields variational free energy values as extrema of

Here, Z₀ is the partition function of the reference Hamiltonian and 〈H-H₀〉₀ denotes the average with respect to H₀. Using this relation, energies and entropies were computed for the metallated wild type and several variants as described (35).

Results and Discussion

The Folding Free-Energy Landscape of Metallated Azurin: Qualitative Connection Between Experiment and Theory.

Fig. 1 exhibits the predicted folding free-energy profile, when modified to incorporate ligation effects, as a function of a single reaction coordinate. Although, a priori the precise energetic consequences of the ligation events requires extensive quantum calculations, the available experimentally measured stabilities of azurin with and without the zinc cofactor provides a reasonable parameterization of the energies (20, 21, 36). In Fig. 1 we show the free-energy profile of zinc-metallated azurin first when the noncovalent ligands (i.e., G45 and H46) are treated as having electrostatic interactions H_int alone (●) and the profile when the residues become coordinated H_{int_coord} (□). Coordination confers an additional ≈7 kcal·mol⁻¹ of stability at T = 1.91. Very significant stabilization in the free-energy profile arising from the coordination contribution already occurs at the early transition-state and native-state ensembles. We see that the entatic state forms concomitantly with the folding nucleus.

Fig. 1.

The free-energy profile of zinc metallated azurin at temperature T = 1.91. The bold line represents the free-energy profile when the metal–ligand interactions were simply treated as contacting positions carrying electrostatic interactions during the folding event (●). Dashed lines connect the corresponding positions of the free-energy profile of the metallated enzyme treated with the coordinate contribution of the histidine and glycine metal–ligand interactions H_{int_coord} (□). (Inset) The primary coordination sphere: the coordinating ligands, His-46 (orange) and Gly-45 (green) are shown relative to the canonical loop (gray).

The predicted folding routes and the position of the folding barrier of Zn²⁺-substituted azurin are shown as a function of temperature in Fig. 2. This collection of folding profiles reveals a stark difference between the apo-azurin (22) and holo-azurin system (Fig. 2); specifically, for the Zn²⁺ form the position of the rate-limiting step in a given folding route varies as a function of temperature. In contrast to what is found for the apo-enzyme, the folding barrier for the Zn²⁺-metallated protein progressively moves toward the native structure as temperature increases, in good agreement with experimental observation (20). Interestingly, as the temperature increases, the ligation intermediate also becomes more stable relative to the metal–ligand interactions approximated by the electrostatics effects alone; thus, the two differently interacting conformational ensembles probably can coexist under some thermodynamic conditions (e.g., T ≈ 1.91) (Fig. 1). At higher temperatures the ligation intermediate becomes more stable than the native state based only on the charge–charge interaction; thus, the formation of the entatic state makes a greater contribution to the folding reaction at higher temperatures.

Fig. 2.

The free-energy profile for metallated-azurin (A) and apo-azurin (B) (adapted from ref. 22) as a function of temperature. The dashed line in A follows the trajectory of the metallated folding nucleus as function of temperature. From right to left the corresponding temperatures for the folding barriers are ∼1.86 (‡_early), ∼1.96 (‡_middle), and ∼2.06 (‡_late).

The Structural Interpretation of the Folding Dynamics: The Rise of the Entatic State.

Fig. 3 shows the predicted mean square deviations of each residue from its native location in the transition-state ensemble both as a function of sequence and temperature, based on our modified variational scheme. This plot provides a detailed structural interpretation of how the folding routes change with temperature. As the mean square deviation of a residue i becomes smaller, the more native-like that position becomes. This plot clearly shows that the folding nucleus becomes less diffuse (more native-like) with increasing temperature, which is consistent with the free energy folding routes shown in Fig. 2. Fixing our attention on the primary coordination sphere, residue C112 shows the smallest fluctuations throughout the dynamic transition, whereas H117 exhibits a progressive decrease in variability relative to its mean position as the temperature increases, finally assuming a near native-like fluctuation at T = 2.06. Interestingly, M121, which was not explicitly modeled as a coordinating residue, but simply as a contacting position, demonstrates the most dramatic change in relative position early in the transition (i.e., from 1.86 to 1.96). Conversely, the noncovalent coordination ligands G45 and H46 simultaneously experience a marked change only later in the dynamic transition (i.e., 1.96 to 2.06) (Fig. 3).

Fig. 3.

The local fluctuations around the native structure of members of the transition-state ensemble as measured by the mean square deviation (MSD) of residues as function of temperature [i.e., T = 1.86 (‡_early), 196 (‡_middle), and 2.06 (‡_late) represented as black, red, and blue, respectively] and residue sequence number. The fluctuation of a given residue constituting the fold barrier is given by the convariance matrix B, where B_ij = a⁻²〈(r_i − 〈r_i〉)(r_j − 〈r_j〉)〉 and a is a scaling factor equal to 3.8 Å. The cofactor is represented by the set of triangles in the right lower corner. (Inset) Formation of the primary coordination sphere: the five copper ligands, His-46 (orange), Gly-45 (green), Cys-112 (cyan), His-117 (red), Met-121 (purple), and the cofactor (yellow).

How does the geometric entatic state develop relative to the formation of the complete scaffold? In the early transition state of the metallated protein, aggregation of the C-terminal region (residues 85–128 or β-strands 5, 6, 7, and 8) provokes a more native-like geometry at the coordinating loop; in turn, the residues of the N terminus (residues 1–85 or β-strands 1, 2, 3, and 4, and the α-helix) experience a significant reduction in their fluctuations, completing the ligand set and the proper geometry of the entatic state (Fig. 3). A majority of the residues in the primary coordination sphere are formed very close to their final location very early in the moving transition state. This phenomena reflects a considerable degree of topological frustration in the system giving a large entropic penalty as a result of forming this early conformation of residues distant in sequence from each other. Concisely, the canonical loop forms and establishes native-like geometry for residues C112, H117, and possibly M121 but precedes the native interactions with ligands 45 and 46 that complete the entatic state. In our model, we have not explicitly included a term for nonnative interactions or misligations; therefore, we do not explicitly show any possible energetic frustration around the coordination sphere that might result from these factors. However, the entropic factor caused by the stringent distance and geometry requirement by itself provides sufficient destabilization in accord with the entatic mechanism.

A Comparison of the Experimentally Inferred and Predicted Folding Dynamics: A Detailed Explication and Reconstruction of the Nonlinear Free-Energy Relationship.

The calculated free-energy profiles already provide a correct qualitative description of the folding event likewise they also give quantitative predictions. The apparent activation free energy determined by the natural logarithms of the observed (un)folding rates as a function of denaturating conditions often generate linear, or in our case, more interestingly, nonlinear, extrathermodynamic free-energy relationships with stabilization free energies. These free-energy relationships yield the so-called chevron plots. Each chevron plot provides an overview of the energetic consequences of mutations on the folding barrier and the relative position of the folding barrier along the reaction coordinate. Reconstruction of a nonlinear (curved) chevron plot is not trivial, requiring accurate prediction of absolute folding and unfolding rates. In the theoretical calculations, the balance of folding reaction is altered by changing the temperature, whereas in the laboratory the balance is changed by using chemical denaturants.

To calculate the folding rate at a given temperature T, first one identifies the folding barrier position at E^‡ on the free-energy profile (Fig. 2). E^‡ is the sum of the contact energies with the highest free energy.

The sum of the contact energies is an order parameter paralleling the more commonly used Q, which is appropriate for funneled landscapes. This choice of coordinates is sensible if nonnative interactions are neglected. In the solvent-denatured situation nonspecific collapse also probably contributes to E^‡. Once the rate-limiting step (i.e., the highest folding barrier) is identified, the corresponding free-energy changes to the folding barrier ΔG_u,f^‡ = −(G^‡ − G_u,f) can be calculated. The rate coefficients for folding k_f and unfolding k_u follow using the Arrhenius equation (8):

where A the prefactor is be calculated microscopically (25); we fit the parameter A in the present analysis. At last, the observed relaxation rate k_obs is the sum of k_f and k_u. To simplify the analysis, the rate coefficients at different temperatures were fit by using a second-order polynomial in the exponent (9):

The parameters a and c give the linear dependence of folding and unfolding, respectively, and the observed curvature of the folding and unfolding arms are reflected by the parameters b and d, respectively. The resulting in machina chevron plots (Fig. 4), i.e., for wild type along with 14-point mutated variants, allow for a more thorough assessment of the transition state as a function of temperature. In the fits the parameters a, b and c, d satisfy the stability requirement. So there are only two independent degrees of freedom in the fitting.

Fig. 4.

Nonlinear extrathermodynamic free-energy relationships. (Upper) Experimental, ln k_obs versus GuHCl (M); adapted from ref. 20. (Lower) Theoretical chevron plots, ln k_obs versus temperature, for 14 metallated-azurin variants provide an overview of the energetic consequences of mutations on the folding barrier along with the relative position of ‡. An expanded view of the individual theoretical chevron plot is shown in SI Fig. 7.

The calculated chevrons allow one to compare the relative stability of the folded protein, ΔΔG_{N_D} and the folding barrier, ΔΔG_{‡_D} for each variant compared with those of the wild type. Combining the relative changes of the folding barrier and protein stability yields theoretical φ-values φ_T = ΔΔG_{‡_D}/ΔΔG_{N_D}, which can then be directly compared with experimentally determined φ-values φ_E (Fig. 5). A recent experimental study that used φ-value analysis, as a function of discrete denaturant concentrations, gave snapshots of the zinc-metallated azurin's dynamic folding nucleus with residue-specific resolution (20). Fig. 5 provides a direct comparison of the theoretically and experimentally derived φ-values, at discrete temperatures and GuHCl concentrations with corresponding stabilities, respectively. This comparison clearly shows a solid correlation between the experimentally and theoretically derived φ-values at each condition (i.e., GuHCl concentration or temperature, respectively). Moreover, this correlation clearly shows that the present variational scheme is quite robust and accurately predicts the zinc-metallated azurin's dynamic folding nucleus with residue-specific resolution that is at least on par with that provided by the experimental study.

Fig. 5.

A direct comparison of theoretical and experimental φ-values. x represents φ_experimental at 0 M and φ_theoretical at T = 1.86 (‡_early), ○ represents φ_experimental at 2 M and φ_theoretical at T = 1.96 (‡_middle), and ▵ represents φ_experimental at 4 M and φ_theoretical at T = 2.06 (‡_late). The correlation coefficient between the calculated and experimental values is 0.77.

The Effects of the Entatic State on the Dynamic Folding Nucleus.

Although the detailed electronic structure aspects, i.e., the quantum mechanical features, of forming the entatic state throughout the folding reaction (specifically with regard to the redox active copper site) cannot be addressed explicitly with the model Hamiltonian we use, our current approach would provide a crude prediction of the effects of tuning the reduction potential through metal substitution. Specifically, we can examine the redox phenomenon during folding by varying the relative coordinate contribution in the model Hamiltonian. Unfolded copper-metallated azurin has a reduction potential of ≈0.5 V, which can be ascribed to the electron-donating properties of the C112 thiolate moiety. As the protein folds, the progressive dehydration of the metal's milieu (i.e., hydrophobic encapsulation proximal to the active site) lowers the redox potential (11, 16, 37). Thus, as the metallated protein folds the redox active copper becomes less susceptible to reduction. That is to say, the ligand interactions cooperatively change as the molecule becomes more native-like. Our calculations show the most dramatic changes caused by ligation occur early in the resulting free-energy profile.

Conclusions

In this study, the folding dynamics of zinc-metallated P. aeruginosa azurin was investigated via a free-energy functional, which models the coordination reaction explicitly. Both the qualitative form for the free-energy profile and the quantitative predictions of the energetic consequences of mutations derived from our modified variational scheme agree very well with experimental observation (20). The calculations show that the progressive movement of the folding barrier toward the native state reflects the effects of topological frustration in forming the geometric entatic state and results in a nonlinear free-energy relationship (i.e., a curved chevron plot). The calculation clearly shows that at high temperature the activation energy required to break the bonds between the cofactor and respective ligands (i.e., resides G45 and H46) is much larger than the barrier to simply unfold the polypeptide. This additional rate-limiting event results in a kinetic bottleneck which in turn changes the pattern of the overall free-energy relationship for zinc metallated-azurin from that of the apo-protein (see SI Fig. 8). By combining theoretical modeling and experimental studies in the laboratory we can see how forming the entatic state is coupled to the dynamics of folding the metallated azurin at a level of detail that cannot be currently achieved by experiments alone.