‘Simplification’ of responses of complex cells in cat striate cortex: suppressive surrounds and ‘feedback’ inactivation

Abstract

In mammalian striate cortex (V1), two distinct functional classes of neurones, the so-called simple and complex cells, are routinely distinguished. They can be quantitatively differentiated from each other on the basis of the ratio between the phase-variant (F1) component and the mean firing rate (F0) of spike responses to luminance-modulated sinusoidal gratings (simple, F1/F0 > 1; complex, F1/F0 < 1). We investigated how recurrent cortico-cortical connections affect the spatial phase-variance of responses of V1 cells in the cat. F1/F0 ratios of the responses to optimally oriented drifting sine-wave gratings covering the classical receptive field (CRF) of single V1 cells were compared to those of: (1) responses to gratings covering the CRFs combined with gratings of different orientations presented to the ‘silent’ surrounds; and (2) responses to CRF stimulation during reversible inactivation of postero-temporal visual (PTV) cortex. For complex cells, the relative strength of the silent surround suppression on CRF-driven responses was positively correlated with the extent of increases in F1/F0 ratios. Inactivation of PTV cortex increased F1/F0 ratios of CRF-driven responses of complex cells only. Overall, activation of suppressive surrounds or inactivation of PTV ‘converted’ substantial proportions (50 and 30%, respectively) of complex cells into simple-like cells (F1/F0 > 1). Thus, the simple–complex distinction depends, at least partly, on information coming from the silent surrounds and/or feedback from ‘higher-order’ cortices. These results support the idea that simple and complex cells belong to the same basic cortical circuit and the spatial phase-variance of their responses depends on the relative strength of different synaptic inputs.

Following seminal papers by Hubel & Wiesel (1959, 1962) a degree of consensus has emerged that the so-called simple (cf. S cells of Henry, 1977) and complex cells (cf. C cells of Henry, 1977) represent two principal functional classes of neurones in the mammalian cytoarchitectonic cortical area 17 (striate cortex, area V1; for reviews see Henry, 1977; Gilbert, 1977; Movshon et al. 1978a, b, c; Orban, 1984; Skottun et al. 1991; Mechler & Ringach, 2002; Bair, 2005; cf. also Mata & Ringach, 2005). Classical receptive fields (CRFs) of simple cells, like RFs of most neurones in the dorsal lateral geniculate nucleus (LGNd), are characterized by the presence of spatially distinct, adjacent subregions each excited by either light ‘on’ or light ‘off’ with antagonistic ‘push–pull’ effects on each other. However, unlike LGNd neurones (cf. Shou & Leventhal, 1989), simple cells tend to exhibit a high degree of orientation selectivity (Hubel & Wiesel, 1959, 1962; Henry et al. 1974; cf. Martinez et al. 2005). Complex cells are also orientation selective; however, the ‘on’ and ‘off’ subregions within their CRFs tend to overlap spatially (Hubel & Wiesel, 1962; cf. for review Martinez et al. 2005).

Maffei & Fiorentini (1973) were probably the first to report that, as in the case of LGNd neurones, optimally oriented luminance-contrast-modulated sine-wave gratings drifting across their CRFs strongly modulate firing rates of simple cells. Indeed, Fourier transform of the firing rates of simple cell's responses to drifting gratings optimized for orientation and spatial and temporal frequencies shows that most of the energy is concentrated at the temporal frequency of stimulation (F1), with comparable or smaller changes in the mean firing rate (F0), hence their F1/F0 ratios are > 1 (cf. Movshon et al. 1978a; De Valois et al. 1982; Skottun et al. 1991). Overall, simple cells tend to sum linearily the light intensities falling on their receptive fields (Hubel & Wiesel, 1962; Movshon et al. 1978a; Tolhurst & Dean, 1987; Carandini et al. 1999). Complex cells, by contrast, exhibit substantial non-linearities of spatial summation (Hubel & Wiesel, 1962; Movshon et al. 1978b; Palmer & Davis, 1981; Dean & Tolhurst, 1983; Spitzer & Hochstein, 1985) and, although the luminance-contrast-modulated gratings drifting across their CRFs increase their average firing rates, the passage of single bars of the sine-wave gratings optimized for orientation and spatial and temporal frequencies hardly or only weakly modulates their firing rates (Maffei & Fiorentini, 1973; Movshon et al. 1978b), hence their F1/F0 ratios are < 1 (De Valois et al. 1982; Skottun et al. 1991).

Hubel & Wiesel (1962) proposed that the functional relationship between simple and complex cells is a hierarchical one in which the structure of simple cell CRFs is determined by the excitatory convergence of a number of LGNd neurones and the structure of complex cell CRFs is derived from the excitatory convergence of a number of simple cells (cf. for reviews Ringach, 2004; Martinez et al. 2005). In contrast, recently developed non-hierarchical models propose that simple–complex distinction depends mainly on the strengths and integrative properties of cortico-cortical connections rather than the ‘synaptic distance’ from the LGNd. In particular, Chance et al. (1999) proposed that area 17 neurones exhibit phase-variant, simple-like responses when their recurrent excitatory cortico-cortical inputs are weak and phase-invariant, complex-like responses when their recurrent excitatory cortico-cortical inputs are stronger. Along similar lines, an ‘egalitarian network model’ developed by Tao et al. (2004) proposes that while most cortical cells (both simple and complex) receive LGNd drive, it is an overall balance between the cortico-cortical and LGNd drive which ‘determines whether individual neurons in this recurrent circuit are simple or complex.’ In the present study, we examined to what extent manipulating the strengths of recurrent excitatory and, to a lesser extent, inhibitory drives to neurones in the cat striate cortex indeed differentially affects the magnitudes of the phase-variant F1 component and mean firing rate F0 and hence changes the F1/F0 ratios of spike responses. In particular, we investigated whether the F1/F0 ratios of spike responses to sinusoidal gratings (and hence presumably the simple–complex distinction) are affected by: (1) stimulation of their silent (usually suppressive) RF surrounds outside the CRFs (cf. Li & Li, 1994; Walker et al. 2000; Akasaki et al. 2002; Ozeki et al. 2004), and (2) reversible inactivation of the predominantly excitatory ‘feedback’ signals from the ‘higher-order’ postero-temporal visual cortex (PTV cortex; Huang et al. 2002), the presumed homologue of primate infero-temporal cortex (Lomber et al. 1996a,b).

In most complex cells and in some simple cells, the reductions in the response magnitude induced by coactivation of the CRFs and silent surrounds were accompanied by substantial increases in the F1/F0 ratios, that is, greater phase-variance. The reductions in the magnitude of responses induced by reversible inactivation of PTV cortex were also usually accompanied by substantial increases in the phase-variance of complex cells. Our results have already been presented in the form of abstracts (Bardy et al. 2006; Dreher et al. 2006).

Methods

Domestic cats (Felis catus) bred by Laboratory Animal Services of the University of Sydney were used. The animal preparation and recording procedures followed the guidelines of the Australian Code of Practice for the Care and Use of Animals for Scientific Purposes and were approved by the Animal Care Ethics Committee of the University of Sydney.

Animals, anaesthesia and surgical procedures

Ten adult cats of either sex weighing 2–5 kg were initially anaesthetized with a gaseous mixture of 2.5–5.0% halothane in N₂O–O₂ (67:33%). Throughout the surgical procedures, the percentage of halothane was maintained at 1.5–2.0%. Neuromuscular transmission was abolished with an i.v. (via cephalic vein in a forelimb) infusion of a 2 ml bolus of gallamine triethiodide (40 mg ml⁻¹) solution followed by a continuous i.v. infusion (7.5–10 mg kg⁻¹ h⁻¹). Residual eye movements, not blocked by the gallamine, were largely eliminated by bilateral cervical sympathectomy (Rodieck et al. 1967). A broad-spectrum antibiotic, amoxycillin trihydrate (75 mg, Amoxil, Beecham), and atropine sulphate (0.3 mg, to reduce mucous secretion) were administered i.m. on a daily basis. Craniotomies were performed over the left ventral posterior suprasylvian region (Horsley-Clarke or HC co-ordinates: lateral 20 mm, posterior 3–8 mm) and left area 17 (HC co-ordinates: lateral 0–5 mm, posterior 0–10 mm).

Throughout the experiment, the animals were artificially ventilated via a tracheal cannula with peak expired alveolar CO₂ maintained at 3.7–4.0% by adjusting stroke volume and/or rate of the pulmonary pump. The body temperature, monitored by subscapular probe, was maintained automatically at ∼37.5°C with a servo-controlled heating blanket. The heart rate was monitored continuously and maintained in the range 180–220 beats min⁻¹ (depending on the weight of the animal) by adjusting the halothane level in the gaseous mixture between 0.4 and 0.7%. The electroencephalogram recorded with a metal screw touching the dura mater over the contralateral frontal cortex and a reference electrode clamped onto the cat's skin was also monitored continuously. A ‘deep sleep’ state characterized by δ waves (∼0.5–4.0 Hz) was maintained by adjusting when necessary the level of halothane in the gaseous mixture.

The corneas were protected with zero-power, air-permeable contact lenses. Pupils were dilated, accommodation blocked and nictitating membranes retracted with application of an aqueous solution of atropine sulphate (1%) and 0.128% phenylephrine hydrochloride (Bausch and Lomb, NSW, Australia) on alternate days. Artificial pupils (3 mm in diameter) and corrective lenses appropriate to focus the eyes on a tangent screen located 57 cm away, were positioned in front of the eyes. The optic disc of each eye was back projected at least twice daily on the tangent screen using a fibre-optic light source and the positions of the areae centrales plotted directly and/or by reference to the optic discs (cf. Bishop et al. 1962; Sanderson & Sherman, 1971).

Recording neuronal activity from area 17

A plastic cylinder around the craniotomy was glued with dental acrylic to form a well, and a small opening was made in the dura mater directly above the recording site. A stainless-steel microelectrode of relatively high impedance (7–12 MΩ; FHC, Bowdoinham, ME, USA) was positioned above the appropriate recording site; the well was then filled with 4% agar in physiological saline and sealed with warm liquid wax (melting point ∼40°C). The microelectrode was then slowly (20–60 μm min⁻¹) advanced vertically into area 17 using a hydraulic micromanipulator (David Kopf's Instruments Tujunga, California, USA). To assist with reconstruction of electrode tracks (see ‘Localization of recording sites’) the microelectrode was coated with fluorescent dye DiI (DiCarlo et al. 1996). Action potentials from single neurones were recorded extracellularly, conventionally amplified and monitored both visually (on an oscilloscope) and acoustically (over a loudspeaker). Triggering was continuously monitored on an oscilloscope and set in such a way that only the action potentials of single neurones (identified by their unique shape and amplitude) triggered standard pulses, which were then fed into a computer for data collection.

Assessment of receptive field structure in relation to ‘on’ and ‘off’ discharge regions

The excitatory discharge field is defined here as an area in visual space from which hand-held visual stimuli evoked neuronal discharges at a rate exceeding that of the background (or ‘spontaneous’) activity (as determined subjectively by monitoring the response over a loudspeaker; cf. minimum discharge field, Barlow et al. 1967). The excitatory discharge fields of recorded neurones were plotted separately through the ipsilateral and contralateral eyes (with the other eye covered) using elongated light bars (generated by a hand-held ophthalmoscope) and hand-held elongated dark bars.

Based on the spatial arrangement of their excitatory discharge regions revealed by the stationary flashing light slits and moving light or dark bars, the cells were classified as either simple (or S) or complex (or C). Thus, the cells which had spatially distinct ‘on’ and ‘off’ discharge regions and/or spatially separate discharge regions for the light and dark bars were identified as simple, while cells which had spatially overlapping ‘on’ and ‘off’ discharge regions and/or spatially overlapping light bar and dark bar discharge regions were identified as complex (Gilbert, 1977; Henry, 1977; Burke et al. 1992). The ocular dominance class was determined by listening to the audio-monitor and by subjective assessment of the relative magnitude of responses to the optimally orientated stimuli presented separately via each eye. For binocular cells, the excitatory discharge fields were plotted for each eye. However, quantitative assessment of other features of RFs was conducted only with stimuli presented via the dominant eye.

Assessment of classical receptive field (CRF) properties and CRF–surround interactions

Luminance contrast-modulated sine-wave drifting gratings (Fig. 1, left) were generated by a visual stimulation system, VSG 2/3 (Cambridge Research System, UK) and presented on a CRT monitor (BARCO, Kortrijk Belgium) placed 57 cm from the cat's eyes. To ensure that the gratings indeed had a sinusoidal luminance profile, linearizing of the luminance of the display on the CRT monitor based on the Look-Up-Tables was conducted every 2–3 months.

Figure 1. Location of recording sites and cortical inactivation site.

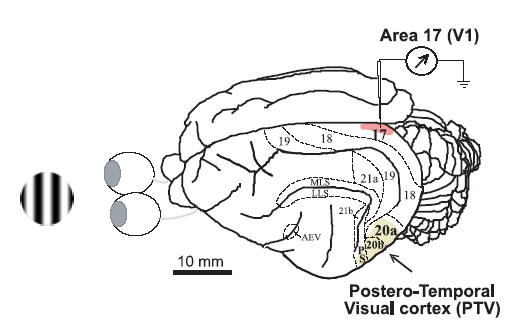
On the left is an example of a patch of sine-wave luminance-modulated drifting grating used as a visual stimulus. On the right is a dorsolateral view of the left cerebral hemisphere of the cat showing the locations of visual cortical areas. The locations of cytoarchitectonic and functional areas 17, 18, 19, 21a, 21b, 20a and 20b, as well as those of the anterior ectosylvian visual area (AEV), posterior suprasylvian area (PS) and several areas in the medial lateral suprasylvian (MLS) region and the lateral lateral suprasylvian (LLS) region are indicated (after Burke et al. 1998). The shaded part of area 17 (striate cortex, area V1) indicates the general location of all our electrode penetrations. The area labelled as ‘Postero-Temporal Visual cortex (PTV)’ represents the cortical surface that was in contact with the cooling probe.

After mapping the excitatory discharge fields with hand-held stimuli (see above) we quantitatively determined the tuning curves of the cell for orientation and spatial and temporal frequencies to 100% contrast luminance-modulated sine-wave drifting gratings by varying each parameter. Once the optimal orientation, direction, and spatial and temporal frequencies were determined, we assessed the extent of the spatial summation field (cf. Bringuier et al. 1999) using optimized gratings of 100% contrast. Subsequently, we derived a contrast sensitivity function of the cell using the grating patch and determined the contrast at which the response saturated. Then contrast was reduced to 80% of that at which the response saturated. With this contrast, we reassessed the extent of the spatial summation field. The diameter of the classical receptive field (CRF) was defined as the size of the circular patch of optimized (orientation, direction as well as spatial and temporal frequencies) sine-wave driftings grating evoking the maximal response while stimulation of its surround itself did not evoke discharges above the level of background (‘spontaneous’) activity. In most cases, that is, in cells in which the silent surround was not facilitatory in respect to responses evoked from the CRFs, the diameter of CRFs determined in this way corresponded closely to the smallest diameter of a circular patch of optimized drifting gratings which evoked the maximal response. The CRFs determined by this method were, however, almost invariably substantially larger than the excitatory discharge fields determined with hand-held stimuli (see above). The responses to optimized CRF stimulation and to combined CRF + surround stimulation were tested with a series of visual stimuli; each stimulus was presented as a stationary grating for 1 s, then drifted for 3 s and then separated from the next presentation with a 1 s blank. Only the spike responses to the drifting parts of the stimulus cycles were analysed. For all but two cells in our sample, the optimal temporal frequency exceeded 0.7 Hz (see Results). Thus, this procedure allowed us to analyse the responses to more than one stimulus cycle for almost all cells. Each series comprised a patch of drifting grating centred and restricted to the CRF. This stimulus, referred to as ‘CRF stimulus’, was set to optimal orientation, direction, and spatial and temporal frequencies. The CRF stimulus was then combined with a series of surrounding sinusoidal drifting gratings (extending to a diameter of 28 deg) of the same spatial and temporal frequencies as those presented at the CRF. However, orientations of the surround stimuli varied in four distinct steps relative to orientation of stimuli covering the CRF (0, 45, 90 and 135 deg). The surround stimuli drifted in both directions orthogonal to their orientations (see items in Fig. 3B). Then, the ‘CRF + surround’ stimuli were followed by the same surround gratings with no grating in the CRF, which allowed us to confirm that during the tests the surround stimuli alone did not evoke any discharge activity. To compensate for variability of responses due to stimulus history, the stimuli in this set were interleaved and presented in a pseudo-randomized fashion. Each series of visual stimuli was repeated eight times.

Figure 3. Frequency histograms of optimal parameters for CRF stimuli in the present sample of area 17 cells.

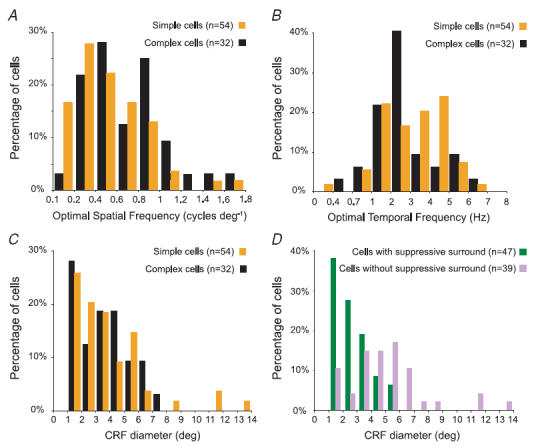
A, frequency histograms of optimal spatial frequencies for the present sample of area 17 cells. The median (0.5 cycles deg⁻¹) and the mean optimal spatial frequencies (0.5 ± 0.3 cycles deg⁻¹) for the simple cells were slightly lower than those (median, 0.6 cylces deg⁻¹; mean, 0.7 ± 0.4 cycles deg⁻¹) for the complex cells. B, frequency histograms of optimal temporal frequencies for the present sample of area 17 cells. Both the median (3.5 Hz) and the mean optimal temporal frequencies (3.5 ± 1.5 Hz) for the simple cells were higher than those (median, 2.5 Hz; mean, 3 ± 1.6 Hz) for the complex cells. C, frequency histogram of CRF sizes of simple and complex cells in the present sample. The median (4 deg) and the mean diameter (4.2 ± 2.7 deg) of the CRFs of simple cells were slightly larger than the median (3.8 deg) and the mean (3.9 ± 1.9 deg) of CRFs of complex cells. D, frequency histogram of CRF sizes of cells (both simple and complex) with or without significant suppressive surrounds when CRF + surround gratings of optimal orientation were used. The median (2.5 deg) and the mean diameter (2.9 ± 1.3 deg) of the CRFs of cells with suppresive surrounds were substantially smaller than the median (5 deg) and the mean diameter (5.5 ± 2.8 deg) of the CRF of complex cells.

Inactivation of postero-temporal visual cortex

Once the craniotomy had been performed, a specially shaped silver probe was positioned over the intact dura mater above PTV cortex. The area covered by the probe included virtually all cytoarchitectonic areas 20a and 20b (Tusa & Palmer, 1980) and the part of posterior suprasylvian area (PS; Updyke, 1986) behind the posterior suprasylvian gyrus. The probe and the opening were sealed with vacuum grease, which also acted as a thermal insulator. The correct positioning of the probe was confirmed post mortem for each cat. The temperature of the probe attached to a Peltier element (9 W; Marlow, Dallas, TX, USA) was controlled by a laboratory-built device. The responses of single neurones recorded from area 17 were first tested when PTV cortex was maintained at 36°C, i.e. control condition, and then 2–3 min after PTV cortex had been cooled to 10°C, thus allowing the temperature of the cortex to stabilize. The series of visual tests performed before and during inactivation of PTV cortex as well as after rewarming PTV cortex to physiological temperature consisted of standard presentations of optimized sine-wave gratings restricted to the CRFs as well as the usual combination of ‘CRF + surround’ stimuli. The effects of inactivation of the PTV cortex on the CRF–silent surround interactions are beyond the scope of the present paper and will be described elsewhere. The control runs before inactivation of the postero-temporal (PTV) cortex were repeated at least twice (16 repeats or more). In order to minimize the risk of irreversible damage (presumably due to the interference of cooling with circulation in the superficial blood vessels), the PTV cortex was kept at 10°C for the minimum period necessary to perform one series of standard tests (8 repeats; ≤ 16 min) and then rapidly (∼2 min) rewarmed back to physiological temperature. The same set of visual tests was repeated 10, 30 and 60 min after the cortex was rewarmed to normal temperature (recovery runs).

Consistent with several previous studies (e.g. Wang et al. 2000), the temperature gradient measured from the centre of the cooling probe was ∼5–6°C mm⁻¹, and when we cooled the dorsolateral part of the surface of area 20 to 10°C, the temperature of deep (infragranular) layers of area 20 and the temperature of the parts of the neighbouring cortical areas within 2 mm from the edge of the cooling probe were in the range of 10–20°C. Both the background and visually evoked activity in the striate cortices of anaesthetized cats (Michalski et al. 1993) or the cortex around the middle suprasylvian sulcus of behaving cats (Lomber et al. 1994) ceases completely when the local temperature is in the 10–20°C range. Thus, it appears that in the present experiments cooling of PTV cortex to 10°C resulted in silencing of neuronal discharges and hence feedback signals originating in areas 20a and 20b and area PS. In addition, the virtual inactivation (temperature in 10–20°C range) of the regions within a 2 mm radius from the cooling probe resulted in silencing parts of areas 21b, 18 and 19 immediately adjacent to area 20 (Fig. 1).

Consistent with the remoteness of the recording sites from the edge of the cooling probe (Fig. 1), our control data indicate that there was no direct spread of cooling to area 17. Indeed, the lowest temperature recorded in area 17 (monitored with a pair of microthermocouples, 25-μm-thick wires inserted 1 mm below the cortical surface) when area PTV cortex was cooled to 10°C was ∼35.5°C, that is, ∼0.5°C below the set temperature of 36°C.

Data analysis and statistics

The responses to the CRF stimuli in the control condition were used to classify the cell as simple (F1/F0 > 1) or complex (F1/F0 < 1). In the analysis, the firing rate of each cell was referred to either as the first Fourier phase-variant component F1 for simple cells or as the mean maintained firing rate F0 component for complex cells. In view of the very low ‘spontaneous’ activity of most cells (see Results), the background activity was not subtracted from F0 used in data analysis. To evaluate the unimodality of the frequency distribution of F1/F0 ratios we used the dip test of unimodality (Hartigan & Hartigan, 1985).

The CRF–surround interactions (or surround modulations) were measured as the mean firing rate of responses to the ‘CRF + surround’ stimuli versus the mean firing rate of responses to stimulation of CRF alone. The mean F1/F0 ratio presented in the Results is the average of the F1/F0 ratios of each trial accumulated. Statistical evaluation was performed using two non-parametric tests: Mann–Whitney U test and Wilcoxon matched-pairs signed-ranks test (Siegel, 1956). They will be referred to as Mann–Whitney test and Wilcoxon test, respectively. Only cells which did not show significant differences during successive control tests have been included in the sample. Statistical significance of the differences between two sets of data was accepted if the associated probability (P) value was 0.05 or less at the two-tailed criterion. The ± values in the text are either the standard errors of the means (s.e.m.) or the standard deviations (s.d.).

Localization of recording sites

At the end of each experiment, the animal was deeply anaesthetized by i.v. injection of sodium pentobarbitone (100 mg kg⁻¹) and perfused transcardially (descending aorta clamped) with 500 ml of warm (37°C) saline followed by 1000 ml of 4% paraformaldehyde in phosphate buffer (0.1 m at pH 7.4). The brain was stored in 30% sucrose in phosphate buffer, then coronally sectioned (at 50 μm) on a freezing microtome. Sections were mounted onto gelatinized slides, air-dried and viewed under the fluorescent microscope to locate the tracks made by electrodes coated with DiI. Subsequently, the sections were counterstained for Nissl substance with cresyl violet. In most cases, DiI marked the entire length of the track (cf. DiCarlo et al. 1996), and we were able to reconstruct laminar locations of the majority of the recorded cells using computer-assisted drawing programs and information about the location of cells in relation to the cortical surface.

Results

Stable extracellular recordings were obtained from 86 single neurones which responded reliably to optimally orientated drifting gratings. The CRFs of all units were located within 10 deg from the areae centrales and no more than 6 deg from the zero horizontal meridian (Tusa et al. 1978; Payne 1990). Most cells (60/86) were binocular, and their eye dominance distribution was not significantly different from those of our previous samples of area 17 cells with minimum discharge fields within 10 deg from the areae centrales (e.g. Burke et al. 1992).

Identification of simple and complex cells

We identified area 17 cells as either simple or complex based on the presence or absence of spatially distinct ‘on’ (light bar) and ‘off’ (dark bar) discharge regions in their excitatory discharge fields (see Introduction) and compared this identification with that based on the F1/F0 ratios in their responses to optimal sine-wave gratings covering their CRFs.

The cell whose responses are illustrated in the upper peristimulus time histogram (PSTH) in Fig. 2A had spatially separate ‘on’ and ‘off’ discharge regions in its CRF and thus was identified as a simple cell. Consistent with this, the phase-variant F1 component of the response to drifting gratings is much greater than overall mean firing rate, F0. By contrast, the lower PSTH in Fig. 2A illustrates responses to an optimal drifting grating of a cell which had spatially overlapping ‘on’ and ‘off’ discharge regions in its CRF and, consistent with its identification as a complex cell, the phase-variant F1 component of the response is smaller than the mean firing rate, F0.

Figure 2. Identification of simple and complex cells.

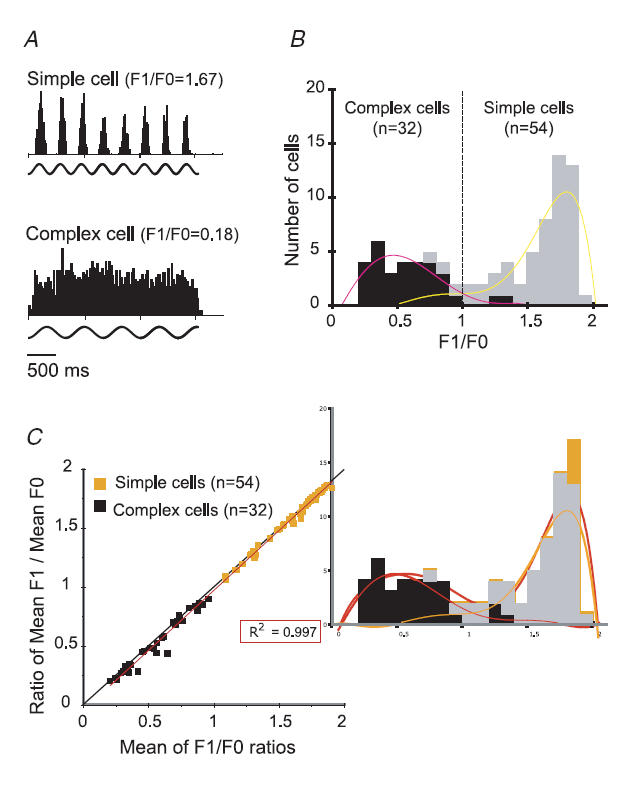
A, PSTHs of responses of a typical simple (upper PSTH) and a complex cell (lower PSTH) in area V1. The action potentials of the cells were generated in response to the presentation of optimized gratings covering their CRFs. The sinusoidal lines below each PSTH represent the temporal frequency modulation of the visual stimulus energy. The PSTH of the simple cell (F1/F0 = 1.65 ± 0.02, mean ±s.e.m.) and that of the complex cell (F1/F0 = 0.18 ± 0.03) are based on the accumulation of 8 trials. The optimal spatial and temporal frequencies and optimal orientation were: 1 cycle deg⁻¹, 2.7 Hz and 169 deg for the simple cell and 0.5 cycles deg⁻¹, 1.5 Hz and 79 deg for the complex cell. B, frequency histogram of F1/F0 ratios for our sample of V1 neurones. The cells were qualitatively identified as simple (shaded columns) or complex (filled columns) on the basis of the presence or absence, respectively, of spatially separated light ‘on’ and light ‘off’ discharge subregions in their CRFs. The polynomial trend-lines illustrate the overall links between qualitatively identified complex cells and lower F1/F0 ratios (left curve) and between qualitatively identified simple cells and higher F1/F0 ratios (right curve). C, F1/F0 ratios calculated by averaging F1/F0 ratios for each cell in response to each stimulus presentation versus the F1/F0 ratios calculated from the same cell's mean F1/mean F0 for all trials. The linear trend-line calculated for the entire sample (r²= 0.997) corresponded closely to the diagonal axis.

The frequency histogram distribution of cells with different F1/F0 ratios in their responses to non-saturating optimally orientated drifting gratings of optimal spatial and temporal frequencies covering their CRFs, which on a mean background evoked 80% of the maximal response, is presented in Fig. 2B. In view of the relative paucity of unequivocal complex cells (F1/F0 ratios, 0.2–0.7), the frequency distribution of F1/F0 ratios is skewed strongly in favour of simple cells. Although there were rather few cells (6/86; 7%) with ‘fuzzy’ F1/F0 simple–complex classification ratios in the 0.9–1.2 range, the commonly reported bimodality of the frequency distribution of F1/F0 ratios of cells in primary visual cortices of anaesthetized cats and macaques (Movshon et al. 1978a,b; De Valois et al. 1982; Skottun et al. 1991) is far from obvious in the present sample (cf. Dean & Tolhurst, 1983). Indeed, the distribution is not significantly different from unimodality (dip value, 0.041; 0.1 < P < 0.5; Hartigan's dip unimodality test).

In the present sample (Fig. 2B), all but three (52/55; 94.5%) cells identified as simple on the basis of the spatial distinctness of their ‘on’ and ‘off’ discharge regions were also identified as simple on the basis of their F1/F0 ratios of over 1. Similarly, all but two cells (29/31; 93.5%) identified as complex on the basis of their F1/F0 ratios below 1 were identified as complex on the basis of the apparent spatial overlap of their ‘on’ and ‘off’ discharge regions were also identified as complex on the basis of their F1/F0 ratios < 1 (Fig. 2B).

The F1/F0 ratios presented in Fig. 2B are based on the mean of the F1/F0 ratios taken in each of the trials (see Methods). Although this practice might have disproportionately amplified the errors in the denominator, it allowed us to calculate the s.e.m. of F1/F0 ratios. As indicated in Fig. 2C and consistent with expectations, the ratios calculated on the basis of the ratios of the means tended to be lower than those based on the mean of the F1/F0 ratios taken in each of the trials. Indeed, for the entire sample of 86 cells, or for 54 simple cells and 32 complex cells analysed separately, the ratios calculated on the basis of the ratios of the means were significantly (P < 0.001; Wilcoxon test) lower than those based on the mean of the F1/F0 ratios taken in each of the trials. Nevertheless, it is apparent from Fig. 2C that for most cells the amplified errors in the denominator did not lead to a great overestimation of the mean. Overall, the correlation between the ratios of the means of F1 and F0 and mean of F1/F0 was very high (r²= 0.997), and identification of cells as simple (F1/F0 > 1) or complex (F1/F0 < 1) was not affected by the way in which we have calculated the F1/F0 ratios.

General properties of simple versus complex cells identified on the basis of the F1/F0 ratios in response to optimized gratings

Consistent with numerous previous studies (see for review Orban, 1984) most cells (79/86) exhibited very little (< 2 spikes s⁻¹) background (‘spontaneous’) activity. Small proportions of both simple (2/54) and complex cells (4/32) exhibited background activities in the range of 2–10 spikes s⁻¹, and one simple cell had high ‘spontaneous’ activity of ∼30 spikes s⁻¹.

For the entire sample, the mean contrast that evoked 80% of the maximal response was 57% (±23%). The mean contrast that evoked 80% of maximal responses in the simple cells was lower (53%s.d.; ±23%) than that for complex cells (64%s.d.; ±21%).

The frequency histograms of the optimal spatial and temporal frequencies for our sample of cells for stimuli presented via the dominant eye are illustrated in Fig. 3A and B, respectively. The optimal spatial frequencies ranged from 0.1 to 1.7 cycles deg⁻¹, and there was a complete overlap between the distribution of optimal spatial frequencies of simple and complex cells (cf. Movshon et al. 1978c). However, unlike in the sample of cat area 17 cells recorded by Movshon et al. (1978c), the spatial frequencies preferred by simple cells were overall lower than those preferred by complex cells.

Although there was a complete overlap between the optimal temporal frequencies of simple and complex cells (range 0.3–6.5 Hz), consistent with the fact that simple cells preferred slightly lower spatial frequencies, temporal frequencies preferred by simple cells were overall slightly higher than those preferred by complex cells.

As indicated in Fig. 3C, the CRF diameters of over a quarter of both simple and complex cells were in the 1–2 deg range, the diameters of a clear majority did not exceed 4 deg, and the diameters of CRFs of almost 95% of all cells did not exceed 7 deg. However, consistent with slightly lower mean optimal spatial frequencies and slightly higher mean optimal temporal frequencies of simple cells, the CRFs of simple cells tended to be larger than the CRFs of complex cells.

The differences in the sizes of the CRFs between simple and complex cells appear to be largely related to the facts that: (1) cells that did not exhibit clear suppressive surrounds (Effects of co-stimulation) when optimally orientated gratings extended outside the CRFs tended to be simple; and (2) the CRFs of cells with no clear suppressive surround tended to be larger than the CRFs of cells with clear suppressive surrounds (Fig. 3D).

Laminar location

The laminar location of most cells (77/86; 89.5%) was reconstructed. Most cells (32/49 simple, 15/28 complex) were located in the geniculo-recipient layers, that is, the granular layer 4 (32 cells: 20 simple, 12 complex) or the infragranular layer 6 (15 cells: 12 simple, 3 complex). The remainder of the sample was located in the supragranular layers 2/3 (simple, 15/49; complex, 10/28) or the infragranular layer 5 (simple, 2/49; complex, 3/28).

Effects of co-stimulation of CRFs and silent surrounds on magnitudes of F1 and F0 and F1/F0 ratios

In the clear majorities of both simple (42/54) and complex cells (25/32), when the sine-wave luminance-contrast-modulated drifting gratings of different orientations were presented in the silent surrounds, the magnitude of response evoked by optimally oriented gratings restricted to the CRFs was significantly and often substantially reduced (Fig. 4A; cf. Maffei & Fiorentini, 1976; Nelson & Frost, 1978; Li & Li, 1994; Sengpiel et al. 1997; Akasaki et al. 2002; Ozeki et al. 2004). Indeed, for simple cells the mean magnitude for the phase-variant F1 component when CRFs were co-stimulated with silent surround was ∼50% (s.d.± 32%) of the F1 component when the CRFs were stimulated alone (50; ±33% for F0).

Figure 4. Effects of stimulation of silent surround on the CRF-driven responses of neurones in area 17.

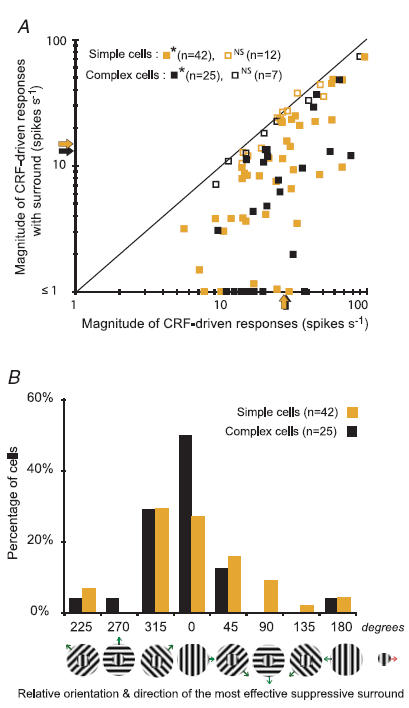
A, the magnitudes of responses of each cell (F1 component for simple cells; F0 for complex cells) to optimized gratings restricted to their CRF versus the magnitudes of responses to co-stimulation of CRF and the silent surround. Except for orientations and directions which were varied, the parameters of the gratings presented in the surrounds were identical to those optimized for the CRFs. Here we illustrate only the effects of the surround configuration that maximally reduced the CRF-driven response. The shaded arrows indicate for simple cells the mean magnitude of the F1 component of CRF-driven responses (27.3 spikes s⁻¹; s.e.m.± 2.5 spikes s⁻¹) and that of CRF + surround responses (15.3 spikes s⁻¹; s.e.m.± 2.1 spikes s⁻¹). The black arrows indicate for complex cells the mean firing rate, F0, of CRF-driven responses (27.8 spikes s⁻¹: s.e.m.± 3.5 spikes s⁻¹) and that of CRF + surround responses (13.3 spikes s⁻¹; s.e.m.± 2.9 spikes s⁻¹). In the majority of cells the maximal reduction in the magnitude of responses induced by stimulation of the surrounds was significant (Mann–Whitney test, *P≤ 0.05 and non-significant (NS) for P > 0.05). In over 15% (9/54) of simple cells and in over 20% (7/32) of complex cells, stimulation of the surround suppressed the CRF-driven response to < 1 spike s⁻¹. B, percentage frequency histogram of cells in which given orientations and directions of drifting of the surround gratings, relative to optimized orientation and direction of drifting of the CRF gratings, resulted in the greatest reduction in the response magnitude. The arrow attached to the icon on the right indicates the direction of the drift of the grating restricted to the CRFs. The arrows attached to the icons representing optimally oriented gratings restricted to the CRFs + gratings of different orientations presented in the surround indicate the directions of the drifts of the surround gratings.

Consistent with previous findings (cf. Akasaki et al. 2002), the reduction in the magnitude of responses was somewhat greater in the case of complex cells. Thus, for complex cells the mean magnitude of F0 evoked by stimulation of the CRFs + silent surround was ∼44% (±35%) of that evoked by stimulation of the CRFs alone (55; ±40% for F1). However, in the present sample, unlike in the sample of area 17 cells recorded by Akasaki et al. (2002), the difference between the simple and complex cells in the magnitude of reduction of responses when the CRFs and silent surrounds were co-stimulated was not statistically significant (P = 0.34; Mann–Whitney test; cf. Walker et al. 2000).

In both simple and complex cells, the extent of the reduction in the magnitude of responses depended on the orientation of the surround gratings in relation to the orientation of the gratings restricted to the CRF (cf. Maffei & Fiorentini, 1976; Nelson & Frost, 1978; Li & Li, 1994; Sengpiel et al. 1997; Akasaki et al. 2002; Ozeki et al. 2004). The frequency histogram in Fig. 4B is consistent with previous findings (cf. Li & Li, 1994; Sengpiel et al. 1997; Akasaki et al. 2002; Ozeki et al. 2004) that in a high proportion of cells (both simple and complex), the relative reduction in the magnitude of responses was greatest when the orientation and direction of movement of the CRF and silent surround gratings were the same (iso-orientation and iso-direction). However, in about 45% of our sample, iso-orientation gratings in silent surround did not produce significant suppression of the CRF-driven responses. Furthermore, in over 40% of the cells, the greatest reduction in the magnitude of responses was observed when the orientations and/or directions of movements of gratings restricted to the CRF and those in the silent surround were 45 deg apart (Fig. 4B; cf. Sengpiel et al. 1997).

Figure 5 illustrates the responses of several exemplary simple and complex cells to drifting optimal gratings covering their CRFs, as well as their responses to drifting gratings co-stimulating CRFs and the silent surrounds. The cell whose PSTHs are illustrated in Fig. 5Aa was a typical simple cell (spatially distinct ‘on’ and ‘off’ discharge regions in its CRF), and when its CRF was stimulated with a drifting grating the response was strongly phase-variant, that is, the F1 component of the response was much greater than the mean firing rate, F0. When the CRF and silent surround were co-stimulated, both the F1 and F0 components of the CRF-driven response were substantially and proportionally reduced (see Fig. 5Ba). The CRF of the cell whose PSTHs are illustrated in Fig. 5Ab contained only an ‘on’ discharge region. Although the mean firing rate (F0) of the response was relatively greater than that of the cell whose responses are illustrated in Fig. 5Aa, typically for the simple cell, it was smaller than the phase-variant F1 component. Co-stimulation of CRF and silent surround either increased (second PSTH) or decreased (third and fourth PSTHs) the magnitude of the CRF-driven responses, depending on the orientation and/or direction of movement of the surround gratings. When the orientations of the CRF and surround stimuli were the same, the magnitude of F0 was increased while F1 was unchanged. Hence, the F1/F0 ratio was decreased and the cell became complex-like (F1/F0 ratio < 1). In contrast, when CRF + surround stimuli induced a reduction in the overall magnitude of the responses, both F1 and F0 were reduced. The phase-variant component, F1, remained slightly greater than F0 and the F1/F0 ratio became greater (more simple-like; third and fourth PSTHs in Fig. 5Bb).

Figure 5. Effects of stimulation of silent surrounds on the firing patterns of simple and complex cells in area 17.

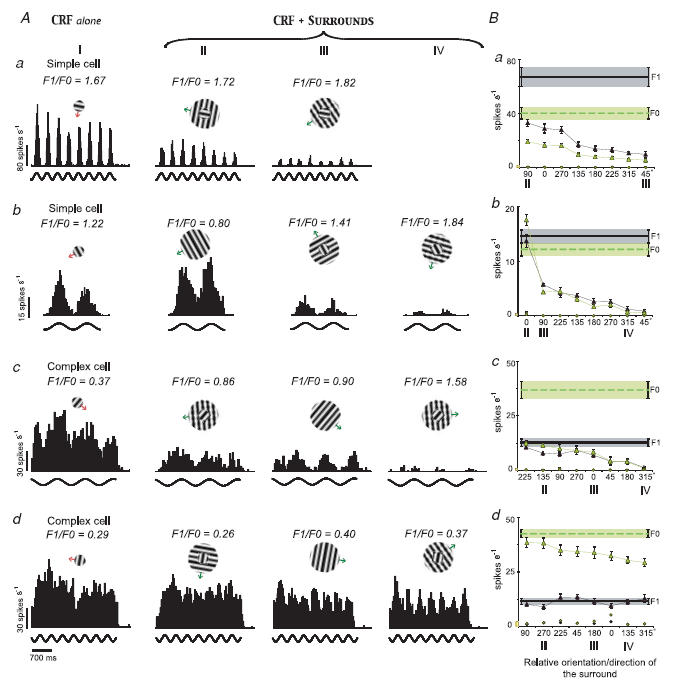
A, column I illustrates the PSTHs of 4 cells (a, b, c and d) to stimulation of their CRFs alone. Cells whose responses are illustrated in a, c and d were recorded from layers 6, 2 and 4, respectively. Columns II, III and IV illustrate the PSTHs of the cells' responses to stimulation of the CRF + surround. Stimulus configurations are shown at the top of each PSTH. Note that the CRF + surround PSTHs are ordered from left to right according to the strength of the surround-induced reduction in the magnitude of responses. B, tuning plots of the mean phase-variant F1 (filled triangles) and the mean firing rate, F0 (open triangles), of responses of the same 4 cells as a function of the orientation/direction incongruity between the CRF and the surround stimuli. Continuous and dashed horizontal lines indicate, respectively, the magnitude of F1 and F0 when CRFs were stimulated alone with optimized gratings. Shaded areas and error bars are the s.e.m. The filled and open circles indicate, respectively, the magnitudes of F1 component and F0 when the surrounds were stimulated alone. Bars on the abscissas next to 0 indicate the level of the background (‘spontaneous’) activity.

The cells whose responses are illustrated in Fig. 5Ac and Fig. 5Ad had spatially overlapping ‘on’ and ‘off’ discharge regions in their CRFs. Consistent with this, the F1 components of their responses were smaller than the mean firing rates, F0, and hence, the F1/F0 ratios were < 1. In both cells, co-stimulation of CRFs and silent surrounds resulted in overall reduction of the response magnitude. However, in the case of the cell whose responses are illustrated in Fig. 5Ac, at all surround orientations the mean firing rate, F0, was reduced considerably more than the F1 component (Fig. 5Bc). In the case of the cell whose responses are illustrated in Fig. 5Ad, only the F0 was substantially reduced when the CRF and silent surround were co-stimulated. Thus, the responses of both complex cells became much more phase-variant (simple-like) when their CRFs and silent suppressive surrounds were co-stimulated.

In Fig. 6, we have plotted for the entire sample the effects of co-stimulation of CRF and silent surround on: (1) the changes in magnitudes of F0 and phase-variant F1 component of responses (Fig. 6A); and (2) on the F1/F0 ratios (Fig. 6B).

Figure 6. Effects of stimulation of silent surround on F1 and F0 firing rates and F1/F0 ratios.

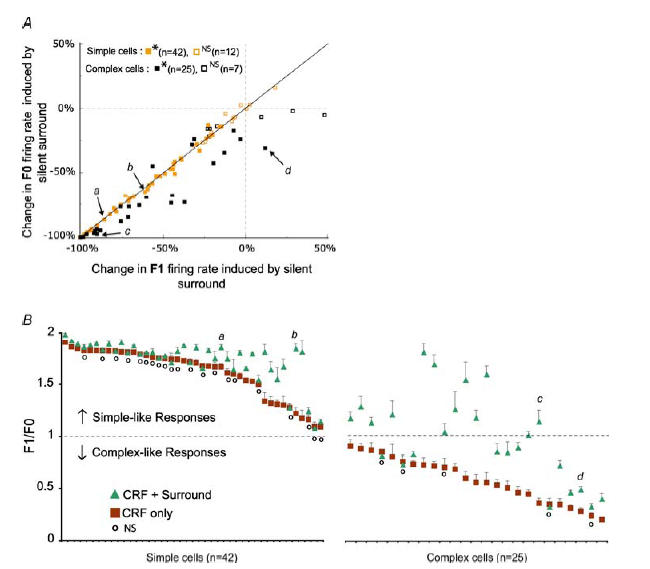
A, plot of percentage changes in the magnitude of the F1 component of responses against the percentage changes in the magnitude of the F0 induced by activation of silent surrounds. For simple cells the significance of changes is calculated on the basis of changes in the magnitude of F1 components, while for complex cells the significance of changes is calculated on the basis of the changes in the magnitude of F0 components (Mann–Whitney test, *P < 0.05; non-significant, NS for P > 0.05). The letters a, b, c and d refer to the 4 examples illustrated in Fig. 5. B, the graph shows F1/F0 ratios for 67 cells in which at least one surround orientation evoked a significant (P < 0.05; Mann–Whitney test) reduction in the magnitude of responses. The F1/F0 ratios are not plotted for cases where the magnitude of response was reduced by surround stimulation to less than 1 spike s⁻¹ and/or by more than 90%. The squares indicate the mean F1/F0 ratios (±s.e.m.) of responses to CRF stimuli alone, while the triangles indicate F1/F0 ratios of responses for the combination of CRF + surround that showed the maximum reduction in the magnitude of responses. The small circles indicate the cells without significant changes (NS) to the F1/F0 ratios of responses to CRF stimulation versus CRF + surround stimulation (P > 0.05; Wilcoxon test). Again, the letters a, b, c and d refer to the 4 examples illustrated in Fig. 5.

It is apparent from Fig. 6A that in virtually all simple cells in which co-stimulation of CRFs and silent surrounds had a significant effect (mostly reduction) on the magnitude of responses, the percentage changes in the magnitude of F0 and phase-variant F1 component were either identical or fairly similar. Nevertheless, in most simple cells (6/11) with F1/F0 ratios in the range of 1.0–1.5, the strongest surround-induced response reduction was accompanied by a substantial and significant (P < 0.05, Wilcoxon test) increase in the F1/F0 ratios (Fig. 6B; cf. also Fig. 5Ab and Bb and 7Ab). Overall, however, for simple cells the percentage changes in the magnitude of F0 induced by co-stimulation of CRFs and silent surrounds were not significantly different (P = 0.28; Wilcoxon test) from those in the magnitude of F1 component, and therefore surround-induced reduction in response magnitudes did not result in significant changes in F1/F0 ratios.

Figure 7. Relationship between the strength of suppression and charges in F1/F0 ratios.

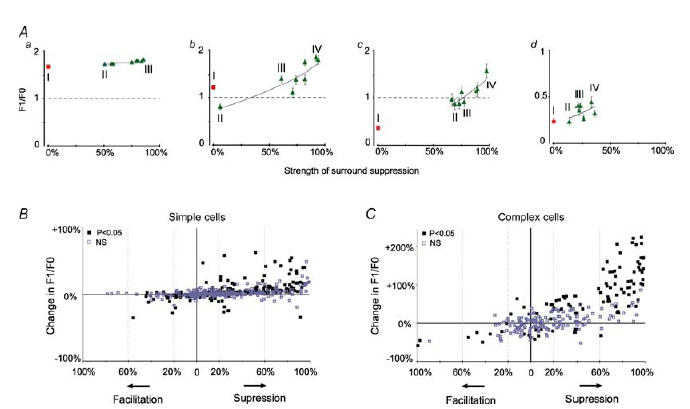
A, graphs showing the F1/F0 ratios in relation to the strength of the surround-induced ‘suppression’ of the responses of 4 example cells (a, b, c and d) whose PSTHs are illustrated in Fig. 5. The F1/F0 ratios of responses to stimulation of CRFs alone are indicated by the squares while the F1/F0 ratios of responses to co-stimulation of CRFs + surrounds are indicated by triangles. B and C, relationship between the relative strengths of silent surround and percentage changes in the F1/F0 ratios induced by co-stimulation of CRFs and silent surrounds. Each point on the graphs indicates changes induced by one of 8 combinations of CRF + surround in each of 86 cells. The significance of the changes between the F1/F0 ratios of the responses to the stimulation of CRF alone and the F1/F0 ratios of responses to co-stimulation of CRF + surround was determined with the Wilcoxon test.

By contrast, as indicated in Fig. 6A, in most complex cells the stimulation of the suppressive surround affected (mostly reduced) the magnitude of the phase-variant F1 component of the response to a lesser extent than it affected the mean maintained firing rate, F0 (cf. Fig. 5Ac,Bc, Ad and Bd). The differences were apparent even in the cells in which the co-stimulation of CRFs and silent surrounds did not significantly affect F0. Overall, for complex cells the percentage reductions in the magnitude of F1 component induced by co-stimulation of CRFs and silent surrounds were significantly lower (P < 0.001; Wilcoxon test) than reductions in the magnitude of F0. Furthermore, as indicated in Fig. 6B, in almost 50% (12/25) of complex cells, the most effective surround-induced suppression pushed their F1/F0 ratio above 1, that is, they became more spatial phase-variant or simple-like (cf. Figure 5Ac and Bc; cf. also Fig. 7Ac). The laminar location of seven of these complex cells was reconstructed, and most of them were located in the granular layer (3 cells) or infragranular layer 6 (2 cells).

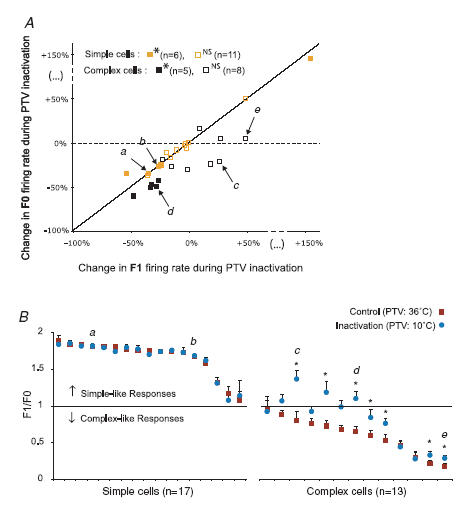
As indicated in Fig. 7, the increases in the F1/F0 ratios were, overall, positively correlated with the strengths of the surround-induced reduction in the magnitude of responses. However, very occasionally, in both simple and complex cells, the surround-induced reduction or increase in the overall magnitude of responses resulted in a reduction of F1/F0 ratios (Fig. 5Ab and 7B, C).

Effects of inactivation of postero-temporal visual cortex on magnitudes of F1 and F0 and on F1/F0 ratios of cells in ipsilateral area 17

The effect of reversible inactivation (cooling to 10°C) of ipsilateral PTV cortex was examined in 17 simple and 13 complex V1 neurons. As in case of all other V1 cells recorded in the present study, the cells had their CRFs located in the part of the visual field well represented in reversibly inactivated PTV cortex (Tusa & Palmer, 1980; Updyke, 1986).

As indicated in Fig. 8, inactivation of ipsilateral PTV cortex resulted in a reduction in the magnitude of responses of most cells in our sample (cf. Huang et al. 2002; see also Wang et al. 2000 for a similar effect of reversible inactivation of cat cytoarchitectonic area 21a). In over a third of the sample (11/30), the changes in the response magnitude were significant (P < 0.05; Mann–Whitney test). Within this group of 11 cells, in all but one simple cell (5/6), and in all (5/5) complex cells there was a reduction, rather than an increase, in the response magnitude during inactivation of PTV cortex. Overall, as indicated in Fig. 8, the extent of the reduction in the magnitude of responses of complex cells (mean F0 ±s.d., 60 ± 14% of the control response) was rather similar to that of simple cells (mean F1 ±s.d., 65 ± 12% of the control response). Indeed, as far as the extent of response reduction is concerned, the difference between simple and complex cells was not statistically significant (P = 0.31; Mann–Whitney test).

Figure 8. Effects of inactivation of PTV cortex on the magnitude of responses of V1 neurones to optimized sine-wave gratings restricted to the CRFs.

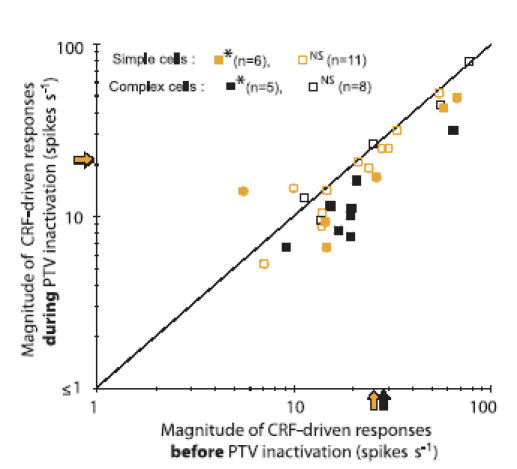
The magnitudes of responses (F1 for simple cells, F0 for complex cells) before inactivation of PTV cortex (PTV kept at 36°C) are plotted against the corresponding magnitudes of responses during inactivation of PTV cortex (temperature of PTV lowered to 10°C). The shaded and black arrows on the axes indicate, respectively, the mean F1 for simple and mean F0 for complex cells. Significance of changes between the two states was determined with Mann–Whitney test (*P < 0.05 and NS for P > 0.05).

The effects of inactivation of PTV cortex on the F1/F0 ratios of responses of simple and complex cells were, however, quite different. In simple cells, the F1/F0 ratios remained essentially unchanged during inactivation of PTV cortex (Fig. 9Aa and b). This constancy was due to the fact that when PTV cortex was inactivated, the magnitudes of both phase-variant F1 components and the mean firing rate, F0, decreased proportionally (Fig. 9Ba and b). Indeed, for simple cells overall, there were no significant differences (P = 0.33; Wilcoxon test) between the changes in the magnitudes of F1 and changes in the magnitude of F0 (cf. Fig. 10A) and so there were no significant changes in F1/F0 ratios (Fig. 10B, left panel).

Figure 9. Effects of PTV cortex inactivation on the firing pattern of area 17 neurones.

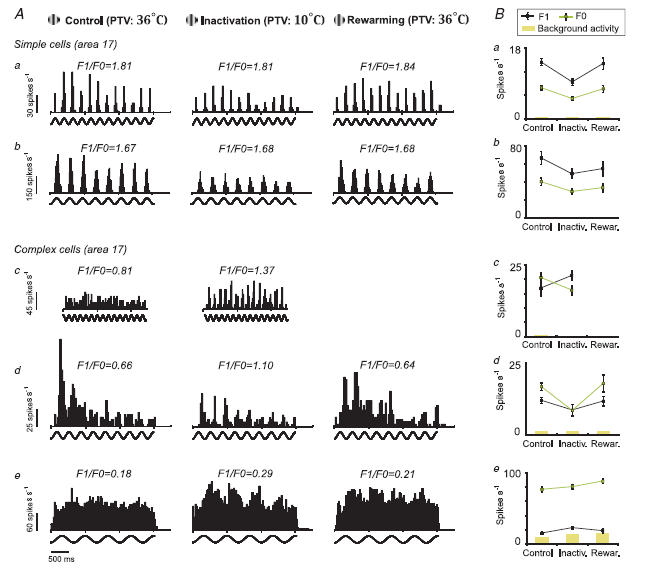
A, PSTHs of responses of 5 V1 cells stimulated with optimized gratings restricted to their CRF. Responses were recorded during three different states: PTV cortex kept at 36°C (left column, control); PTV cortex inactivated by cooling it to 10°C (middle column, inactivation); and within an hour after rewarming of PTV cortex to 36°C (right column, rewarming). Each PSTH represents an average of 8 trials. Due to deterioration of responses 10 min after rewarming, the ‘postrewarming’ PSTH of cell c is not presented. Cells a, b, d and e were recorded from layers 4, 6, 3 and 6, respectively. B, the mean F1 and F0 of the same 5 cells during control conditions, inactivation and after rewarming of PTV cortex. Error bars are s.e.m.

Figure 10. Effects of inactivation of PTV cortex on F1 and F0 firing rates and F1/F0 ratios.

A, percentage changes in the magnitude of phase-variant F1 components induced by reversible PTV inactivation versus the percentage changes in the mean firing rates, F0. The letters a, b, c, d and e refer to the 5 examples illustrated in Fig. 9. The significance of changes was determined with the Mann–Whitney test (*P≤ 0.05 and NS for P > 0.05). B, graph illustrating the F1/F0 ratios of area 17 cells tested before and during inactivation of PTV cortex. The squares and corresponding circles indicate, respectively, the mean ratio F1/F0 ±s.e.m. of the responses before and those during inactivation of PTV cortex. Again, the letters a, b, c, d and e refer to the 5 examples illustrated in Fig. 9. The asterisks indicate cells with significant changes in the F1/F0 ratios during inactivation of PTV cortex (P < 0.05; Wilcoxon test).

By contrast, in complex cells during inactivation of PTV cortex, there were often (Fig. 9Ac, d and e) substantial changes in the F1/F0 ratios. The changes in the F1/F0 ratios were due to the fact that during inactivation of PTV cortex the F1 components of the responses were usually reduced less than F0 (Fig. 9Bd and 10A). Occasionally during inactivation of PTV cortex, the magnitude of the F1 component increased while that of F0 decreased (Fig. 9Bc and 10A). Surprisingly, very occasionally, an increase in F1/F0 ratios during inactivation of PTV cortex was associated with substantial increases in background activity. Overall, for complex cells, the percentage reductions in the magnitude of F1 component induced by inactivation of the PTV cortex were significantly lower (P < 0.003; Wilcoxon test) than those in the magnitude of F0. Consistent with this, in a majority of complex cells (10/13; 77%) inactivation of the PTV cortex resulted in increases in F1/F0 ratios (Fig. 10B), and in most of them (7/13; 54%) the increases were significant (P < 0.05; Wilcoxon test).

The ‘recovery’ of responses after rewarming PTV cortex to 36°C was tested in most (12/19) of the cells in which cooling of PTV cortex did not significantly affect the magnitude of responses. In 10 of these there were no changes in the magnitude of responses within 60 min after rewarming PTV cortex to 36°C.

For most of the 11 cells (5/6 simple, 3/5 complex) in which inactivation of PTV cortex resulted in significant changes in response magnitude, rewarming PTV cortex to 36°C resulted in a return, within 10–60 min of rewarming, of the magnitude of responses to levels not significantly different from the precooling levels (Fig. 9Aa, b and d and Ba, b and d). Of the remaining three cells (1 simple, 2 complex), although there was some recovery in response magnitude, the magnitude of responses did not return to the precooling level within 30 min after rewarming PTV, by which time they were lost.

In 14 simple and 10 complex cells, we were able to compare the F1/F0 ratios of their responses before and during inactivation of PTV cortex with those after rewarming PTV cortex (cf. Fig. 9a, b, d and e Fig 9Ba, b, d and e). For all simple cells, the F1/F0 ratios were not affected by inactivation or rewarming of PTV. For the whole group of 10 complex cells, we paired F1/F0 ratios of each cell before, during and after rewarming of PTV cortex. The differences between control and cooling runs were significant (P = 0.012, Wilcoxon test). Similarly, the differences in F1/F0 ratios between cooling and rewarming runs were also significant (P = 0.038, Wilcoxon test). By contrast, the differences in F1/F0 ratios between control and rewarming runs were not significant (P = 0.10; Wilcoxon test).

Overall, during inactivation of PTV cortex, in nearly a third of complex cells (4/13; 30%) the F1/F0 ratios exceeded 1 (Fig. 9Ac and d and 10B, right panel). In other words, ‘shutting down’ feedback signals originating from PTV cortex made complex cells in area 17 more phase-variant, that is, more simple-like. When PTV cortex was rewarmed, the F1/F0 ratios of responses of these cells dropped back to complex-like ratios below 1.

Discussion

Changes in F1/F0 ratios during co-stimulation of CRF + silent surround

In most area 17 cells with F1/F0 ratios within the range of 0.4–1.5 (this includes most complex cells but only a small minority of simple cells in our sample), surround-induced reduction in the response magnitude was accompanied by substantial and significant increases in the F1/F0 ratios. The increase in the F1/F0 ratio was positively correlated with the relative magnitude of the surround-induced reduction in the response. In about 50% of cells that exhibited F1/F0 ratios < 1 (complex cells) when CRF was stimulated alone, the substantial surround-induced reduction in the mean firing rate, F0, was accompanied by a lesser reduction in the phase-variant F1 component and therefore an increase in the F1/F0 ratio to over 1. The reverse was also true, that is, in a limited number of cases when stimulation of the silent surrounds resulted in an increase rather than a decrease in the response magnitude, F1/F0 ratios of responses of simple cells tended to decrease (F1/F0 ratio < 1; second PSTH in Fig. 5Ab; cf. Fig. 7B and C).

It is worth noting that the increase in phase-variance of complex cells (recorded from the supragranular layers 2/3 of area 17 of anaesthetized cats), presumably resulting in their ‘conversion’ into simple cells when both the CRF and suppressive surround were stimulated simultaneously, is also apparent (but not commented upon) in Fig. 1A and 4A of a study by Akasaki et al. (2002).

The relatively large surround-induced increases in F1/F0 ratios in complex cells and in simple cells with F1/F0 ratios < 1.5 and no substantial changes in the ratio for simple cells with F1/F0 close to 2 are largely expected from the nature of the ratio, which is theoretically bounded from above.

The fact that in a proportion of simple cells there are substantial increases in F1/F0 ratios when the silent suppressive surrounds are co-stimulated with the CRF appears to be consistent with the idea that local intracortical inhibition is an important mediator of the ‘push–pull’ reciprocal opponency between ‘on’ and ‘off’ discharge subregions characterizing CRFs of simple cells (cf. Glezer et al. 1980; Palmer & Davis, 1981; Tolhurst & Dean, 1987; Ferster, 1988; Borg-Graham et al. 1998; Hirsch et al. 1998; Carandini et al. 1999; Anderson et al. 2001). It is also consistent with the idea that non-linear cortico-cortical inhibition contributes to the linearity of spatial summation of simple cells (cf. Wielaard et al. 2001; Tao et al. 2004).

However, the idea that the local intracortical inhibition is the principal mediator of surround suppression has been challenged in a recent study in which the iso-orientation surround suppression in cat area 17 was reduced but not abolished when GABA_A receptors were blocked with bicuculline methiodide (Ozeki et al. 2004). Overall therefore, the increase in the F1/F0 ratio accompanying the reduction in the magnitude of responses when the CRFs and silent surrounds are coactivated appears to be mainly related to a reduction in non-phase-specific excitation rather than a substantial increase in inhibition. This is entirely consistent with the model of Chance et al. (1999), in which both simple and complex cells constitute components of the same neural circuit, and the reduction in the strengths of recurrent excitation ‘simplifies’ complex cells.

Changes in F1/F0 ratios during inactivation of PTV cortex

Reversible inactivation of the ‘higher-order’ visual areas in the PTV cortex resulted in a significant reduction in the magnitude of CRF-driven responses in a substantial proportion of cells recorded from the visuotopically corresponding part of ipsilateral area 17. Furthermore, in most complex cells, but not simple cells, the reduction in the mean firing rate, F0, was accompanied by lesser reductions of the phase-variant F1 component and hence increases in F1/F0 ratios. Overall, in about 30% of complex cells, the F1/F0 ratios increased to over 1.

In both macaque monkeys and cats, the cortico-cortical ‘ feedback ’ from the ‘higher-order’ visual areas to area 17 is predominantly excitatory (cf. Hupé et al. 1998; Wang et al. 2000). Thus, the fact that during reversible inactivation of PTV cortex, complex cells behave in a more spatial phase-variant, simple-like fashion is again consistent with the prediction of Chance and colleagues' model (Chance et al. 1999) that: ‘any manipulation that weakens the effects of intracortical excitation will make complex cells act more like simple cells’. It is likely that the proportion of complex cells that become simple-like would be much greater if we ‘shut off’ the feedback signals not only from PTV cortex but also from most other ‘higher-order’ visual areas (cf. for review Burke et al. 1998).

Mechanisms underlying changes in spatial phase-variance when the response magnitude is reduced

Rivadulla et al. (2001) reported that in the superficial layers of cat area 17, selective blockade of either α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid (AMPA) glutamate receptors or N-methyl-d-aspartate (NMDA) glutamate receptors decreased the firing rate of both simple and complex cells. However, while selective blockade of AMPA receptors did not change F1/F0 ratios of simple cells, it increased the modulation of responses of complex cells to gratings, turning complex cells into simple-like cells. By contrast, decreases in firing rate of simple and complex cells following selective blockade of NMDA receptors were not accompanied by changes in the F1/F0 ratios of either cell type (Rivadulla et al. 2001). Thus, overall there is a substantial similarity between: (1) the effects of local selective blockade of AMPA receptors; (2) reduction in the magnitude of responses induced by activation of suppressive surrounds; and (3) reversible inactivation of ipsilateral PTV cortex. The similarity of these effects strongly suggests that when CRFs and silent suppressive surrounds are coactivated, or when the feedback signals are ‘shut off’, the excitatory signals have limited access to the AMPA receptors, and the excitation is mainly conveyed via the NMDA receptors. The fact that inactivation of PTV cortex strongly affects the F1/F0 ratios of complex cells but not simple cells suggests that feedback synapses on complex cells might be located predominantly in the vicinity of AMPA receptors.

A number of studies (e.g. Rose & Blakemore, 1974; Jagadeesh et al. 1997; Bringuier et al. 1999; Carandini & Ferster, 2000) report that the spike threshold contributes substantially to the sharpening of tuning of many RF properties (e.g. orientation, direction, receptive field size) of cells in the primary visual cortices of anaesthetized cats. It is postulated that this phenomenon, often called ‘the tip of the iceberg effect’, could explain how the sharply tuned spike responses of the cells would emerge from broadly tuned synaptic inputs (Carandini & Ferster, 2000). Priebe et al. (2004) reported that in anaesthetized cats a proportion of area 17 cells, identified as simple on the basis of their spike responses (spatially distinct ‘on’ and ‘off’ discharge regions within their CRFs), showed almost complete spatial overlap of the ‘on’ and ‘off’ discharge regions when the subthreshold membrane potential responses were analysed. Following the key proposal made by Mechler & Ringach (2002), Priebe et al. (2004) argued that the threshold non-linearity is required to make simple and complex cells into two distinct classes identifiable from the distribution of a single parameter, F1/F0. Indeed, they have shown that the distinction between responses of simple and complex cells to drifting gratings based on their spiking F1/F0 modulation ratios does not arise directly from a bimodal distribution in the membrane potential modulation ratios. It is possible that the decrease in excitatory input and/or increase of inhibition, induced by silent surround stimulation or inactivation of feedback signals, results in an increase of the distance between the resting membrane potential and the threshold. Assuming that most cells show at least some phase-modulated F1 response component, the ‘tip of the iceberg effect’ could sharpen the modulated firing rate of the cells, making their responses to gratings look ‘simpler’.

Is there a correlation between the F1/F0 ratios and presence or absence of spatially distinct ‘on’ and ‘off’ discharge subregions in the CRFs?

So far, it remains unknown whether the increases in F1/F0 ratios induced either by stimulation of the silent surround or by inactivation of PTV cortex are accompanied by the emergence of spatially distinct ‘on’ and ‘off’ discharge regions in their CRFs. A number of observations suggest it might be so. Thus, in the present study, there was a good match between identification of simple and complex cells based on qualitatively assessed spatial organization of their excitatory discharge fields and identification based on the F1/F0 ratios of their responses to optimized drifting gratings restricted to their CRFs (cf. Movshon et al. 1978a,b; Skottun et al. 1991). Similarly, Dean & Tolhurst (1983) and Priebe et al. (2004) reported good matches between the F1/F0 ratios in spike responses to gratings and quantitative measures of ‘on’/‘off’ overlap in area 17 cells of anaesthetized cats, while Mata & Ringach (2005) reported significant correlations between the two measures for V1 cells in anaesthetized macaque monkeys. However, as mentioned earlier, Priebe et al. (2004) found in anaesthetized cats, a proportion of area 17 cells that, based on the subthreshold membrane potential responses, appeared to be complex (almost complete spatial overlap of the ‘on’ and ‘off’ discharge regions in their CRFs), but could be regarded as simple because their spiking responses revealed spatially separate ‘on’ and ‘off’ discharge regions within their CRFs. Furthermore, in simple cells recorded from cat primary visual cortices, the transient blockade of GABA_A- mediated intracortical inhibition results in a substantial increase in the magnitude of responses and background activity which are accompanied by a significant transient enlargement of spatially distinct adjacent ‘on’ and ‘off’ regions in their CRFs (Sillito, 1975; Borg-Graham et al. 1998; Pernberg et al. 1998). Indeed, in these studies, the blockade of GABA-mediated intracortical inhibition resulted in a conversion of simple cells in area 17 (Sillito, 1975; Borg-Graham et al. 1998) or area 18 (Pernberg et al. 1998) into complex cells, since enlarged ‘on’ and ‘off’ discharge regions completely or largely spatially overlapped.

One has to notice, however, that despite presumed transient partial or complete spatial overlap of ‘on’ and ‘off’ discharge regions in CRFs of simple cells in area 17 of anaesthetized cats (see above), following iontophoretically applied bicuculline methiodide, Rivadulla et al. (2001) did not observe substantial reductions of the F1/F0 ratios in the responses of simple cells to gratings. Furthermore, Kagan et al. (2002) reported that in the primary visual cortex of alert macaque monkeys, the relative modulation of F1/F0 ratios of responses derived from spike rates of single neurones to drifting sinusoidally modulated luminance gratings did not correlate well with the degree of spatial overlap of ‘on’ and ‘off’ subregions, and complex cells with strongly overlapping ‘on’ and ‘off’ discharge subregions had F1/F0 ratios which ranged from 0.6 to 1.1.

Simple and complex classes: a dynamic continuum

The present findings, indicating that the simple and complex categories represent a continuum of properties rather than rigidly distinct categories, are consistent with conclusions reached previously by others (e.g. Henry, 1977; Dean & Tolhurst, 1983; Mechler & Ringach, 2002; Mata & Ringach, 2005). Furthermore, as mentioned earlier, the reported bimodality of the F1/F0 ratios derived from spike rates of responses of cat V1 neurones to sine-wave drifting gratings is not apparent when the modulation ratio is derived from changes in subthreshold membrane potentials (Priebe et al. 2004). Thus, the emergence of distinct categories of simple and complex cells appears to depend on a non-linear spiking mechanism. At least as far as phase-variance (F1/F0 ratios) is concerned, categorization of cells as simple or complex at any given moment reflects the underlying dynamic interaction of cortical processes.

Our data do not challenge the idea proposed by Hubel & Wiesel (1962) that the structure of CRFs of simple cells is determined by excitatory convergence of LGNd neurones whose RFs are aligned along a line of optimal orientation for the simple cell they innervate. However, the ‘conversion’ observed by us of apparent complex cells into putative simple cells (F1/F0 ratios > 1) is consistent with the idea that at least some complex cells receive strong input from the LGNd and the ‘complexity’ of their responses does not necessarily indicate a strictly hierarchical nature of visual information processing in V1, i.e. LGNd relay cells > simple cells > complex cells. Indeed, not only simple but also some complex cells receive monosynaptic excitatory inputs from the LGNd (e.g. Hoffmann & Stone, 1971; Stone & Dreher, 1973; Toyama et al. 1973; Singer et al. 1975; Tanaka, 1983, 1985; see for reviews Stone et al. 1979; Henry, 1986), and complex cells often generate action potentials in response to visual stimuli to which simple cells do not respond (cf. for reviews Stone et al. 1979; Orban, 1984). Furthermore, to a substantial extent, complex-like responses of neurones in area V1 appear to depend on excitatory feedback signals originating in higher-order visual areas, rather than on the excitatory convergence of signals from a number of orientation-selective simple cells with CRFs slightly displaced from each other, as proposed by Hubel and Wiesel's (1962) model.

The proportion of complex cells which could ‘convert’ into putative simple cells when the excitatory signals become weaker might depend on their laminar location, that is, their ‘synaptic distance’ from the LGNd input. In contrast, the cells, especially the complex cells, in which the magnitude of the responses to stimulation of the CRF is strongly reduced by stimulation of the silent suppressive surround, predominate in supragranular layers 2 and 3, that is, in layers which do not receive direct LGNd input (Akasaki et al. 2002; cf. Gilbert, 1977; Martinez et al. 2005). At present we are not able to examine such a correlation since most of the complex cells recorded by us (including most of the cells which ‘converted’) were located in cortical layers which receive direct input from LGNd. The correlation between the morphological (e.g. spiny stellate, pyramidal cells) and functional classes (simple versus complex) of neurones in mammalian primary visual cortices is rather poor (cf. Gilbert, 1983; Martin & Whitteridge, 1984; Martinez et al. 2005), and other factors (e.g. the distribution of AMPA and NMDA receptors; cf. Rivadulla et al. 2001) might play important roles in determination of simple and complex categories.

Implications of dynamic ‘switching’ between less phase-invariant (complex) and more phase-variant (simple) modes of operation

The present results indicate that the ‘simpleness’ (or phase variance measured by the modulation ratio) of area 17 neurones strongly depends on influences originating from outside the CRFs and/or in ‘higher-order’ visual cortices. The fact that a high proportion of spatial phase-invariant cells ‘convert’ into phase-variant, putative simple cells, appears to be quite advantageous for information processing efficiency. Thus, at least in striate cortices of anaesthetized macaque monkeys, spatial phase-variant simple cells carry on average twice as much edge-like and line-like feature-related information (Mechler et al. 2002) and ‘transmit information at higher rates and over a larger range, than do complex cells’ (Reich et al. 2001). Indeed, simple cells in striate cortices of anaesthetized cats respond reliably to oriented bars embedded in visual noise at much lower signal-to-noise ratios than complex cells (Hoffmann & Von Seelen, 1978).

The finding that inactivation of ‘higher-order’ PTV cortex results in increasing the F1/F0 ratios of most complex cells suggests to us that at any given moment, the proportions of V1 cells working in a simple or complex manner might be related to excitatory ‘attention state-dependent’ modulatory feedback signals from the ‘higher-order’ visual areas (for reviews see Lamme et al. 1998; Vidyasagar, 2001; Hochstein & Ahissar, 2002; cf. Guo et al. 2004).