Mathematical modeling of cell population dynamics in the colonic crypt and in colorectal cancer

Abstract

Colorectal cancer is initiated in colonic crypts. A succession of genetic mutations or epigenetic changes can lead to homeostasis in the crypt being overcome, and subsequent unbounded growth. We consider the dynamics of a single colorectal crypt by using a compartmental approach [Tomlinson IPM, Bodmer WF (1995) Proc Natl Acad Sci USA 92:11130–11134], which accounts for populations of stem cells, differentiated cells, and transit cells. That original model made the simplifying assumptions that each cell population divides synchronously, but we relax these assumptions by adopting an age-structured approach that models asynchronous cell division, and by using a continuum model. We discuss two mechanisms that could regulate the growth of cell numbers and maintain the equilibrium that is normally observed in the crypt. The first will always maintain an equilibrium for all parameter values, whereas the second can allow unbounded proliferation if the net per capita growth rates are large enough. Results show that an increase in cell renewal, which is equivalent to a failure of programmed cell death or of differentiation, can lead to the growth of cancers. The second model can be used to explain the long lag phases in tumor growth, during which new, higher equilibria are reached, before unlimited growth in cell numbers ensues.

The large intestine is one of the most frequent sites of carcinogenesis due, at least in part, to its continual self-renewal and the large numbers of daily cell divisions (1). There are millions of invaginations in the lining of the colon, called crypts, and it is widely believed that colorectal cancer is initiated when mutations or relatively stable epigenetic changes occur in the single layer of epithelial cells that line the crypt. Consequently, much work has been directed toward understanding the mechanisms involved in the dynamics of the cells in healthy and neoplastic (abnormally growing) crypts.

Stem cells are believed to reside near the bottom of the colorectal crypt (2), and these are capable of producing a variety of cell types that are required for tissue renewal and regeneration after injury (3). The stem cells divide to produce transit cells that migrate up the crypt wall toward the luminal surface. As the cells proceed up the crypt they differentiate into colonocytes, enteroendocrine cells, and Goblet cells (1). Once at the top, the cells either undergo apoptosis and/or are shed into the lumen and transported away (4, 5).

In the murine small intestine, the journey of the cells from the base of the crypt to its apex has been estimated to take between 2 and 3 days (6), and all the cells in the crypt, apart from the stem cells, will be renewed over this period. The stem cells are assumed to have a cycle time of between 12 and 32 h with an average of 24 h (7, 8). The transit cell population has an estimated cycle time of ≈11–12 h (4, 9).

The crypt is homeostatic with an equilibrium maintained between cell proliferation and cell loss due to death and shedding. If this balance is shifted toward proliferation by, for example, mutations that promote proliferation or inhibit apoptosis, then neoplasia results (10–13). In the colon, such upregulated cell proliferation is the first step toward adenoma formation and subsequent carcinogenesis (14, 15). Here we present some simple mathematical models of the colorectal crypt with the aim of identifying the key processes that may initiate and accelerate tumorigenesis.

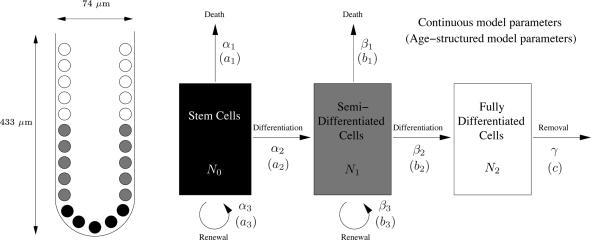
There have been a number of models that have studied cell population dynamics in the crypt, including the computational models by Paulus et al. (16, 17), Gerike et al. (18), and Meineke et al. (19), and the deterministic models by Boman et al. (20) and Hardy and Stark (21). One of the earliest and most influential models is that of Tomlinson and Bodmer (22), which we use as the starting point for our study. That model assumes that the cells in the crypt can be assigned to one of three different compartments: stem cells, semidifferentiated cells (transit-amplifying cells), and fully differentiated cells (Fig. 1). At the end of each cell cycle, stem cells and semidifferentiated cells are assumed to die (through apoptosis), differentiate, or renew with constant probabilities a₁, a₂, a₃, and b₁, b₂, b₃, respectively, where a₁ + a₂ + a₃ = 1 and b₁ + b₂ + b₃ = 1. These probabilities can also be interpreted as the proportions of each cell population dying, differentiating, and renewing. The fully differentiated cells are assumed to be removed from the system (through death or shedding) with probability (or proportion) c in a given time.

Fig. 1.

Schematic representation of a colonic crypt. (Left) A schematic diagram of a crypt, with stem, semidifferentiated (transit-amplifying), and fully differentiated cell populations. The dimensions given are for a human colonic crypt according to Halm and Halm (23). (Right) A diagram showing the compartmental structure used in the model by Tomlinson and Bodmer (22). The stem cells differentiate into semidifferentiated cells, which in turn differentiate into fully differentiated cells. Each cell population can die, and the stem cells and semidifferentiated cells can renew. The parameters for the age-structured model are the proportions of the populations a_i, b_i, and c that are leaving the compartments, and the parameters for the continuous model are rates of conversion α_i, β_i, and γ.

To formulate equations for the population of stem cells (denoted N₀), semidifferentiated cells (denoted N₁), and fully differentiated cells (denoted N₂) after each cell division, Tomlinson and Bodmer (22) implicitly assumed that the cell divisions in each population were synchronous, which requires the cell cycle time of stem cells (denoted t₀) to be an integer multiple of the cell cycle time of semidifferentiated cells (denoted t₁). The equations in ref. 22 are, however, not completely accurate, as they neglect the asynchronicity induced if t₀/t₁ is not an integer, as well as the compounding effect of semidifferentiated cells cycling more frequently than stem cells. Despite this, Tomlinson and Bodmer were able to predict that failure of apoptosis, or of differentiation, could lead to either exponential growth or a new equilibrium at higher cell numbers, and that failure of these processes was sometimes sufficient but not necessary for tumorigenesis, as this could also be achieved by a proliferative advantage. These observations can be used to explain premalignant growths, and the stepwise growth of tumors that occurs between long lag phases.

Our first aim in this paper is to remove the requirement of synchronicity from the model of Tomlinson and Bodmer, taking careful account of the different cell cycle times of stem and semidifferentiated cells. This requires a more complicated set of equations, in which we keep track not only of the number of cells but also of their age distribution. Since we are interested in the development of cell populations over timescales much longer than the cell cycle time, we also formulate a much simpler model in which growth occurs continuously rather than in discrete multiples of cell cycles. Such a model is much easier to analyze, and we show how the parameters in it may be related to those in the more detailed age-structured model.

If the transition probabilities of the process described in Fig. 1 are constant [as assumed by Tomlinson and Bodmer (22)], then the resulting equations are linear, and the model is structurally unstable, that is, a small change in some of the parameters can lead to a qualitative change in the solution. For example, unless exactly half the stem cells renew (a₃ = 1/2), the stem cell population will exhibit either exponential growth (a₃ > 1/2) or exponential decay (a₃ < 1/2).

To achieve homeostasis in any physical or biological system, some degree of feedback is necessary to maintain stability in the face of infinitesimal parameter changes. One approach to modeling homeostasis in the crypt is to allow the proportions of death, differentiation, and renewal to vary as the cell population sizes change. A step in this direction was taken by d'Onofrio and Tomlinson (24), who extend the model of Tomlinson and Bodmer (22) by allowing b₁ and b₃, the dying and renewing transit cell proportions, to depend on the size of the transit population N₁ and differentiated cell population N₂. Our second aim in this paper is to introduce two alternative forms of feedback that are able to maintain homeostasis in the crypt, and to use these to provide a possible explanation for the long lag phases of tumor growth after successive mutations before unregulated cell division occurs.

Generalizing the Modeling Approach

The Age-Structured Model for Asynchronous Cell Division.

To remove the constraint of synchronous cell division, we need to keep track of the distribution of cell age in each population, that is, we need an age-structured model [see, for example, Murray (25)].

We denote by N_i = N_i(t, a), for i = 0, 1, 2, the age distribution function for cells of population N_i at time t, so that there are N_iδa cells in the age range [a, a + δa]. We assume that each cell is committed to dying, differentiating, or renewing only at the end of its cell cycle, and that this process is instantaneous. Recall that we denote the cell cycle times of stem and semidifferentiated cells by t₀ and t₁, respectively, and because the fully differentiated cells are not progressing through the cell cycle, we follow Tomlinson and Bodmer (22) in introducing a corresponding reference time t₂ for fully differentiated cells after which they may die or be shed. Since cells are assumed not to die, divide, or differentiate during their cell cycle, conservation of cell numbers implies

for i = 0, 1, 2, which has the general solution N_i(t, a) = f(t − a) for some function f, corresponding to cells simply aging in time. The renewal, death, or differentiation of the cells at the end of the cell cycle gives the following conditions:

Taking N_i(0, a) = n_i(a), 0 < a < t_i, as the initial age profiles for the cell populations N_i, for i = 0, 1, 2, we can solve for the stem cell population immediately as

where n is the unique integer such that (n − 1) t₀ < t − a ≤ nt₀, corresponding to the number of times cells of age a have been through the cell cycle at time t.

To solve for N₁ we need to make some assumption about the initial distribution of cell ages. The simplest case to consider is that in which the cells all start at age zero, so that n_i(a) = n̂_iδ(a), where n̂_i is the initial total population of cells of type i, and δ is the Dirac δ-function. In this case

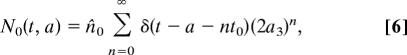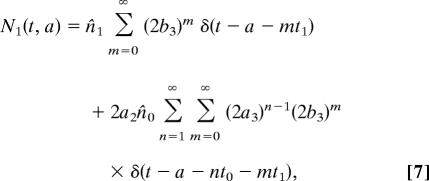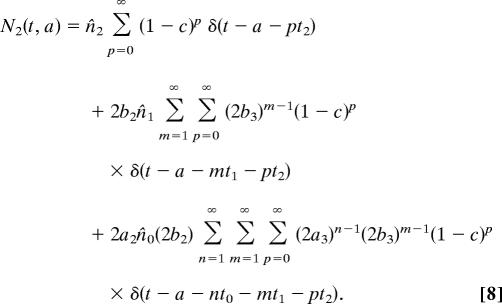Note that while the stem cells remain synchronous, the semidifferentiated and fully differentiated cells become asynchronous if t₀ is not an integer multiple of t₁.

Another relatively simple case to consider is a uniform initial distribution of ages, so that n_i(a) = n̂_i/t_i. A closed form solution is possible whenever t₀/t₁ is rational, and is given in the supporting information (SI) Text. In the biologically realistic case of, for example, t₀ = 2t₁, the solution for N₁ at the points where t − a = 2nt₁ satisfies

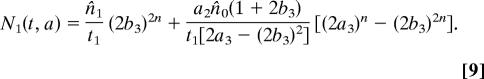Combining like terms in the double summation in 7 when t₀ = 2t₁ gives

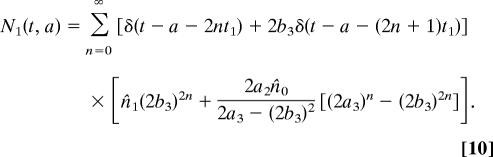The similarity between expressions 9 and 10 indicates that the distribution of cell ages, while necessary for consistency when modeling on the time scale of the cell cycle, is not crucial in determining the long-time behavior of the solution, and can make the solutions overly complicated. We therefore now develop a much simpler ordinary-differential equation (ODE) model which allows for continuous cell division.

The Continuous Model.

Here we assume that we are interested in times much greater than the cell cycle time, and that the cell populations are large enough that we can assume that they vary continuously with time, rather than taking only integer values.

Denoting the per-capita rate of stem (respectively semidifferentiated) cell proliferation by α₃ (respectively β₃), differentiation by α₂ (respectively β₂), and death by α₁ (respectively β₁), and the per-capita removal rate of fully differentiated cells by γ, the ODE model is

Note that these rates are analogous but not equivalent to the corresponding proportions of the cell populations in the age-structured model; the relationship between the two sets of parameters will be determined in the following section.

Eqs. 11–13 are much easier to solve than their age-structured equivalents. Given initial cell populations N_i = n̂_i, we find

where α = α₃ − α₁ − α₂ and β = β₃ − β₁ − β₂ are the net stem and semidifferentiated cell per-capita growth rates, respectively, and the constants A, B, and C are given by

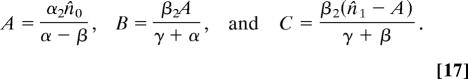Comparing the Age-Structured and Continuous Models.

In the age-structured model, we consider proportions of the cell populations dying, differentiating, or renewing at discrete time intervals, whereas in the continuous model, we assume that these processes occur continuously and we work with the rates at which they occur. To compare the models, it is important to be able to relate the two sets of parameters, which is the goal of this section.

In the age-structured model, for the case where all the cells in each population are initially synchronous in their cell cycles, we have the general solution 6–8. The total population of each cell type is given by integrating over all possible ages

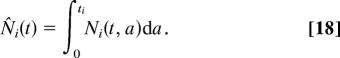It is shown in the SI Text that integrating 6–8 over all ages gives

for constants Â, B̂, and Ĉ that can be determined. Comparing 14–16 and 19–21, we see immediately that the renewal proportions and proliferation rates are related by

The remaining proportions a₂ and b₂ can be determined from the condition that A = Â, B = B̂ (because we have only two constants left to determine, we cannot also impose the condition C = Ĉ). The approximation of the age-structured model by the continuous model assumes that the cell populations are varying on a timescale much longer than that of the cell cycle, that is, that the renewal proportions are close to 1/2. In this case the relations 22 can be approximated by

and the conditions A = Â, B = B̂ lead to

with b₁ = 1 − b₂ − b₃, a₁ = 1 − a₂ − a₃. In this case the condition C = Ĉ is automatically satisfied.

Steady States and Structural Instability.

It is clear from 14–16 and 19–21 that both the age-structured and continuous models are very sensitive to the cell population renewal proportions a₃ and b₃ or net proliferation rates α and β. A nontrivial steady state can occur only if a₃ = 1/2, corresponding to α = 0. If a₃ > 1/2 (α > 0), the model exhibits exponential growth, whereas if a₃ < 1/2 (α < 0), the model exhibits exponential decay. When a model requires a parameter to take a particular value for its solutions to have the required behavior, the model is said to be structurally unstable. In biological systems, we expect there to be noise, and so such a model will be unrealistic. There is a similar but less stringent requirement on b₃ and β. For b₃ < 1/2 (β < 0), there is a nontrivial steady state, whereas for b₃ > 1/2 (β > 0), there is exponential growth. We will modify the model to include feedback in the following section, which will stabilize the model structurally.

First, we briefly examine the steady state of the continuum model. With α = 0, β < 0 (and of course γ > 0), the solution 14–16 approaches the steady state

as t → ∞, where the stem cell population is equal to its (undetermined) initial value, n̂₀, and the other populations are determined in terms of this. The results of Tomlinson and Bodmer (22) essentially correspond in this model to observing that altering the value of β (or indeed α₂, β₂, or γ) while keeping α = 0 can lead to a new steady state in the size of the populations, without necessarily leading immediately to exponential growth so long as β stays negative.

Modeling Homeostasis in the Crypt

We discussed above the need for some form of feedback to stabilize the model to infinitesimal changes in the parameters. This has been recognized by d'Onofrio and Tomlinson (24), who extended the difference equation model by Tomlinson and Bodmer (22), by allowing density dependence in the proportion parameters to model homeostasis in the crypt.

Here we present two possible feedback mechanisms that could maintain the equilibrium in the crypt. With the first mechanism, we find that the feedback is strong enough to preclude unlimited growth whenever it is present, so that cancerous growth can only occur if the feedback is assumed to have been knocked out by a genetic alteration. With the second mechanism, we find that unlimited growth in cell numbers can occur even in the presence of feedback if changes in the other parameters in the model drive the net growth rates above a critical value.

Feedback Model 1: Linear Feedback.

One way in which the cells could act to maintain homeostasis is by altering the proportion of cells differentiating in response to changes in the cell population sizes. We assume that when the population of stem or semidifferentiated cells increases the (per-capita) rate at which they differentiate increases in proportion. Thus we replace α₂ and β₂ in Eqs. 11–13 by, respectively, α₂ + k₀N₀ and β₂ + k₁N₁, where k_i > 0 are constants, giving

Thus the stem cells exhibit logistic growth, with a carrying capacity of N*₀ = α/k₀, where, as before, α = α₃ − α₁ − α₂. If α > 0 all solutions of 26 are attracted to this stable steady state; if α < 0 all solutions are attracted to N₀ = 0. We see that there are no values of the parameters (providing k₀ > 0) that allow unbounded growth in N₀.

For the semidifferentiated cells, there is one positive, stable, steady state given by

where, as before, β = β₃ − β₁ − β₂, which exists for all values of the parameters. Again, no value of the parameters leads to exponential growth.

Thus this model predicts that, providing the renewal rate of stem cells, α₃, is bigger than some critical size α₁ + α₂, the stem cell population is able to sustain itself and reaches a nonzero steady state. A change in the parameters of the model (corresponding to a genetic hit) will change the value of the steady state cell populations, but only a genetic hit which removes the feedback in the model will lead to unbounded growth.

Feedback Model 2: Saturating Feedback.

Here we again assume that when the population of stem or semidifferentiated cells increases, the rate at which they differentiate increases, but instead of assuming a linear dependence of per-capita rate on population size, we assume that there is a maximum per-capita rate of differentiation. Thus we replace α₂ and β₂ in Eqs. 11–13 by, respectively, α₂ + k₀N₀/(1 + m₀N₀) and β₂ + k₁N₁/(1 + m₁N₁), where m_i > 0 are constants. This gives

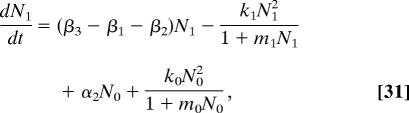Denoting α = α₃ − α₁ − α₂ as usual, we find that the extinct state N₀ = 0 is unstable for α > 0 and globally attracting for α < 0; thus we require α > 0 for the crypt to be viable. A further steady state of stem cells, corresponding to homeostasis, exists when α lies in the range 0 < α < k₀/m₀, and is given by N*₀ = α/(k₀ − m₀α). If α > k₀/m₀, then no steady state exists, and the cell population grows unboundedly. Thus we see the possibility of successive genetic hits increasing α (either by increasing the proliferation rate, or decreasing the differentiation or death rates) moving the crypt through increasing steady state cell populations, until finally α exceeds the critical value and unbounded growth occurs.

When the stem cell population is steady, the behavior of the semidifferentiated cell population depends on whether β = β₃ − β₁ − β₂ is greater or less than the critical value k₁/m₁. If β < k₁/m₁, there is a single, real, positive steady state for the semidifferentiated cell population given by

where D = α₂N*₀ + k₀N*₀²/(1 + m₀N*₀) = (α₃ − α₁)N*₀ is the stem-cell differentiation rate. If β > k₁/m₁, then the transit cells exhibit unbounded growth. Here again we have the possibility of successive genetic hits increasing β (either by increasing the proliferation rate, or decreasing the differentiation or death rates) moving the crypt through increasing steady state cell populations, until finally β exceeds the critical value and unbounded growth occurs.

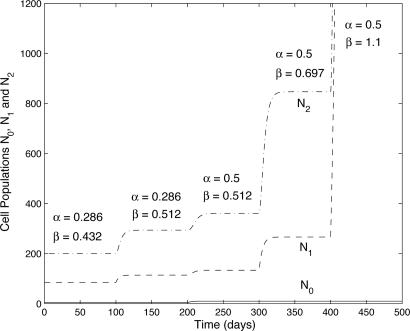
We demonstrate this process with the following example, illustrated in Fig. 2. Consider the initial parameter set α = 0.286, β = 0.432, γ = 0.323, α₂ = 0.3, β₂ = 0.3, k₀ = 0.1, m₀ = 0.1, k₁ = 0.01, and m₁ = 0.01. This produces critical threshold values α = k₀/m₀ = 1 and β = k₁/m₁ = 1; the population is therefore stable, with N*₀ = 4, N*₁ = 85, N*₂ = 200. Suppose a first mutation (in either β₁ or β₃) raises β to 0.512; then N*₀ is unchanged, but N*₁ = 114, N*₂ = 294. A second mutation making α = 0.5 produces a new steady state of N*₀ = 10, N*₁ = 134, N*₂ = 361. A third mutation making β = 0.697 produces a steady state of N*₀ = 10, N*₁ = 266, N*₂ = 847.If a fourth mutation causes β = 1.1, there is no steady state for the semidifferentiated cell population, and consequently both it and the fully differentiated cell population grow exponentially.

Fig. 2.

An illustrative sequence of mutations (occurring every 100 days) in the saturating feedback model (feedback model 2). The initial parameters are taken to be α = 0.286, α₂ = 0.3, β = 0.432, β₂ = 0.3, γ = 0.323, k₀ = 0.1, m₀ = 0.1, k₁ = 0.01, and m₁ = 0.01. The mutations cause, successively, β = 0.512, α = 0.5, β = 0.697, β = 1.1. For β = 1.1 there is no steady state and unbounded growth occurs.

This process simulates the widely assumed multistage process of carcinogenesis. Successive mutations could cause parameter changes which incrementally raise the size of the steady state. However, once the mutations have accumulated to a certain degree, and the parameters are raised above a certain threshold, unregulated cell population growth occurs and the tumor grows exponentially.

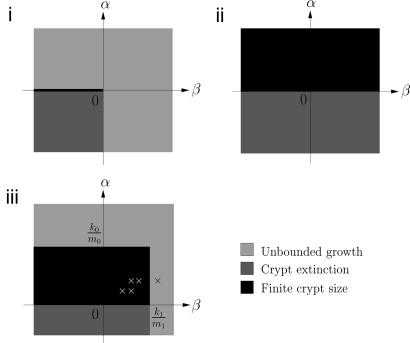
We conclude this section by summarizing the behavior of the three different models in different regions of the (α, β)-parameter space. For the model without feedback, the line α = 0, β < 0 corresponds to finite crypt size, the region α < 0 and β < 0 corresponds to crypt extinction, and the regions α > 0 and β > 0 correspond to unbounded growth. For the model with linear feedback, the region α > 0 corresponds to finite crypt size, and the region α < 0 corresponds to crypt extinction. Finally, for the model with saturating feedback, the region α < 0 corresponds to crypt extinction, the region 0 < α < k₀/m₀ and β < k₁/m₁ corresponds to finite crypt size, and the regions α > k₀/m₀ and β > k₁/m₁ correspond to unbounded growth. These regions are illustrated in Fig. 3.

Fig. 3.

Plots of the regions of stability of the cell population models for no feedback (i), linear feedback (ii), and saturating feedback (iii). In the case of no feedback, there are only stable solutions on the line α = 0, β < 0; otherwise, there is either extinction or unbounded growth. In the case of the linear feedback, there is never unbounded growth in cell numbers, and there is a steady state if α > 0, and extinction if α < 0. For the saturating feedback, there is a strip of the parameter space that permits stable solutions, when 0 < α < k₀/m₀ and β < k₁/m₁, and outside this region there is either extinction or unbounded growth. The crosses correspond to the five states in the (α, β)-parameter space from Fig. 2.

Discussion

We have presented some mathematical models that try to capture the behavior of the cell populations in a healthy crypt in the colon. We have corrected and extended the Tomlinson and Bodmer model (22) by producing two different types of models to capture the asynchronous division of cells. The age-structured model is able to keep track of all cells regardless of when they are generated in their cell cycles, and the continuous model is easier to analyze mathematically. We have shown that the continuous model is a good approximation to the age-structured model when the cell populations vary on a timescale that is much longer than that of a cell cycle.

Both of these models are very sensitive to small changes in the parameters, so we introduced two different types of feedback to make the continuous model structurally stable and to capture the regulation of cell numbers that occurs in the crypt. The first feedback controlled the system growth so that there was always a stable equilibrium and exponential growth in cell numbers could not occur unless mutations were able to knock out the feedback. The second form of feedback allowed stable equilibria in a certain range of parameters but also permitted uncontrolled growth in the cell populations if the parameters were pushed above a critical threshold. These different ranges of stability are illustrated in Fig. 3.

The key parameters are the net per-capita growth rates of the stem and transit cell populations, which represent renewal minus death and differentiation. So, in particular, the failure of programmed cell death or differentiation could lead to tumor growth, as concluded from the model by Tomlinson and Bodmer (22), as well as an increased proliferation rate.

The second form of feedback could help explain the observed lag phases after mutations occur, and thus the existence of benign tumors or adenomas before carcinogenesis takes over. Early mutations in the adenoma-carcinoma sequence could raise the net per-capita growth rates but keep them below their critical values, which will create new, higher steady states. Later stage mutations could push the net per-capita growth rates above their critical values, ensuring that unregulated cell population growth occurs. However, if no genetic changes occur that take a tumor out of the range corresponding to finite size in Fig. 3, then it remains benign. Although the evidence supports the view that essentially all colorectal cancers go through an adenoma, or benign phase, by no means do all adenomas develop into carcinomas.

In conclusion, mutations in any of the key parameters (death, differentiation, or renewal rates for the stem cells or transit cells) can initiate tumorigenesis, and eventually exponential growth in cell numbers leading to a carcinoma, but it is only changes in the net per-capita growth rates that are important, and then only with a suitable feedback model.