Kinetic diversity in G-protein-coupled receptor signalling

Abstract

The majority of intracellular signalling cascades in higher eukaryotes are initiated by GPCRs (G-protein-coupled receptors). Hundreds of GPCRs signal through a handful of trimeric G-proteins, raising the issue of signal specificity. In the present paper, we illustrate a simple kinetic model of G-protein signalling. This model shows that stable production of significant amounts of free Gα^GTP (GTP-bound Gα subunit) and βγ is only one of multiple modes of behaviour of the G-protein system upon activation. Other modes, previously uncharacterized, are sustained production of βγ without significant levels of Gα^GTP and transient production of Gα^GTP with sustained βγ. The system can flip between different modes upon changes in conditions. This model demonstrates further that the negative feedback of receptor uncoupling or internalization, when combined with a positive feedback within the G-protein cycle, under a broad range of conditions results not in termination of the response but in relaxed oscillations in GPCR signalling. This variety of G-protein responses may serve to encode signal specificity in GPCR signal transduction.

INTRODUCTION

GPCRs (G-protein-coupled receptors) constitute one of the biggest protein families in animals: more than 800 GPCR genes have been identified in the human genome, far outnumbering genes for other receptor types [1]. GPCRs recognize a vast array of extracellular signals, ranging from quanta of light to small nucleotide molecules and peptides to huge glycoproteins. They govern a multitude of cellular and organismal responses, such as receiving of sensory information, neurotransmission, immunity and development. More than half of all marketed therapeutic agents target GPCRs [2]. Our understanding of the mechanisms of GPCR functioning is crucial for biology and medicine.

GPCRs signal through activation of trimeric G-proteins. These proteins in the resting state exist as heterotrimers of α, β and γ subunits, where the α-subunit is bound to GDP. The Gα^GDPβγ complex can associate with GPCRs. Biochemical analysis provides a wealth of information about the G-protein cycle [3–5]. Activated GPCRs function as GEFs (guanine-nucleotide-exchange factors) for trimeric G-proteins, catalysing the exchange of GDP on Gα for GTP. This leads to dissociation of the complex into Gα^GTP and βγ, which can signal independently to various downstream effectors. Over time, GTP on Gα is hydrolysed back to GDP by the intrinsic GTPase activity of Gα, with the aid of GAPs (GTPase-activating proteins). GAP activity can be exerted by some effectors, such as PLCβ (phospholipase Cβ), or by specialized RGS (regulator of G-protein signalling) proteins [5]. Upon conversion into the Gα^GDP state, Gα can bind βγ and re-constitute the original complex, ready for a new round of signalling.

A generally accepted view of GPCR signalling is that receptor activation leads to a large increase in steady-state concentrations of free Gα^GTP and βγ, proportional to the ‘strength’ of GPCR activation. High concentrations of free Gα^GTP and βγ trigger intracellular signalling cascades, and fall back as a result of removal of the ligand from the extracellular space (signal termination), removal of the receptor from the cell surface (internalization) or covalent uncoupling of the receptor from G-proteins. This view is based on biochemical observations, such as the stable rise of GTP incorporation into and hydrolysis by G-proteins upon receptor stimulation [3], as well as stable receptor-induced dissociation of βγ from Gα in cell populations, terminated only by ligand washout [6] or receptor internalization [7]. These observations have been reproduced using kinetic simulations [7–11].

The uniformity in G-protein activation by GPCRs raises the issue of specificity in GPCR signalling. Indeed, hundreds of GPCRs have to signal through a limited set of G-proteins: only 16 genes for Gα subunits exist in humans [12] (six in Drosophila [13]). This issue is aggravated further by the promiscuity in the GPCR signalling: receptors and effectors usually do not discriminate between different βγ subunits [4]; moreover, receptors can activate G-proteins containing different Gα subunits [14], and genetic ablation of a Gα subunit often results in no or limited phenotypes, as other Gα subunits step up to fulfil the disrupted function [12].

In the present paper, we describe a novel kinetic model of trimeric G-protein signalling. Its simplicity is combined with careful examination of the reactions governing the G-protein cycle, as well as extensive parameter estimation from experimental data. This model challenges the conventional view of trimeric G-protein signalling and predicts a large variety of G-protein kinetic responses to receptor activation.

MATERIALS AND METHODS

Modelling equations

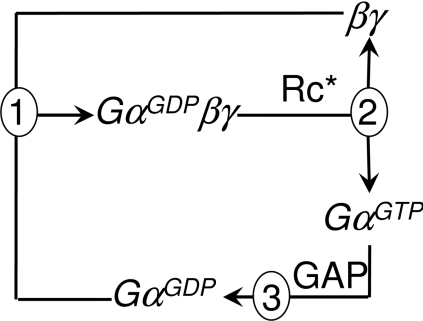
The kinetic model of the trimeric G-protein cycle (Figure 1) contains as variables concentrations of the trimeric G-protein complex ([Gα^GDPβγ]) and its derivatives ([βγ], [Gα^GTP] and [Gα^GDP]), and as constants concentrations of the activated GPCR ([Rc*]) and the GAP ([GAP]).

Figure 1. Trimeric G-protein cycle.

The cycle contains four dependent variables (Gα^GDPβγ, Gα^GTP, βγ and Gα^GDP) and two independent variables [Rc* (activated receptor) and GAP]. Three reactions (labelled ➀–➂ respectively) govern the cycle: association of βγ and Gα^GDP into the trimeric complex, Rc*-catalysed dissociation of the trimeric complex into βγ and Gα^GTP, and GAP-catalysed hydrolysis of GTP on Gα^GTP with formation of Gα^GDP. The rates of these reactions, V₁, V₂ and V₃, are described in eqns (2)–(4) in the Materials and methods section.

Changes in molar concentrations of the components of the cycle are described through rates of production and destruction of the respective components; it becomes apparent that only three rates (designated as V₁, V₂ and V₃) govern the behaviour of this simple cycle:

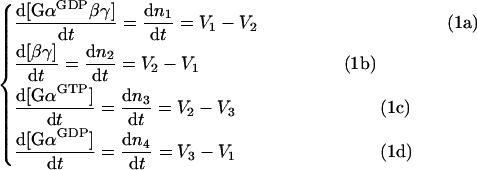where V₁ is the rate of re-association of the trimeric G-protein complex, V₂ is the rate of dissociation of the trimeric complex, and V₃ is the rate of hydrolysis of GTP on Gα. The respective reactions are depicted as ➀, ➁ and ➂ in Figure 1.

As one Gα subunit and one βγ heterodimer make one trimeric complex, and their association is not enzyme-catalysed, the rate V₁ is described simply as:

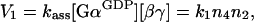2

where k_ass (≡k₁) is the association rate constant. In contrast, reactions described by rates V₂ and V₃ are enzymatic, with activated receptor (Rc*) catalysing dissociation of the trimeric complex, and GAP catalysing the GTP hydrolysis by Gα (Figure 1). Thus the Michaelis–Menten rate equations have to be used:

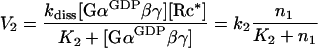3

where k_diss is the dissociation rate constant, K₂ is the Michaelis–Menten constant for the receptor-catalysed dissociation of the trimeric complex, and k₂≡k_diss[Rc*]. Similarly:

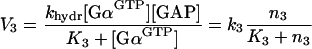4

where k_hydr is the hydrolysis rate constant, K₃ is the Michaelis–Menten constant for the GAP-accelerated GTP hydrolysis, and k₃≡k_hydr[GAP].

Mass conservation requires that:

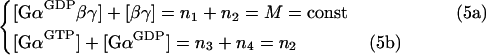where M is the total (trimeric-complexed plus free) concentration of the G-protein.

Thus the four dependent differential equations (eqns 1a–1d) can be rewritten as a system of two independent differential equations:

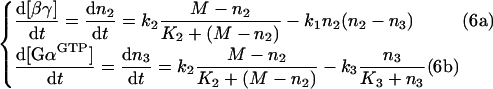having [Gα^GTP] and [βγ] as the two variables. After solving eqns (6a) and (6b), concentrations of Gα^GDPβγ and Gα^GDP are determined using eqns (5a) and (5b).

Alternative modelling equations (resulting in the same characteristics of the trimeric G-protein system) are given in the Supplementary Materials section at http://www.BiochemJ.org/bj/401/bj4010485add.htm.

Obtaining parameters for kinetic modelling

Published data (summarized in Supplementary Tables 2–5 at http://www.BiochemJ.org/bj/401/bj4010485add.htm) were used to obtain the rate constants and the Michaelis–Menten constants, as well as to find the range of trimeric G-protein, receptor and GAP intracellular concentrations. To convert the published data on the number of molecules per cell, cell volume estimates were used as shown in Supplementary Table 1 (http://www.BiochemJ.org/bj/401/bj4010485add.htm).

The obtained values (see Supplementary Table 2) show that the intracellular concentrations of trimeric G-proteins vary in the range 200 nM–3 μM, those of GPCRs vary in the range 1–500 nM, and those of GAPs vary in the range 10–300 nM.

It should be noted that local plasma membrane concentrations of the components of the trimeric G-protein cycle may be much higher than the total intracellular concentrations shown above. However, kinetic modelling at much higher concentrations reproduces the phenomena presented in the Results section, as with increased concentrations of the components of the cycle all three reactions speed up.

The k_ass value for re-association of the trimeric complex from Gα^GDP and βγ varied in different experiments (see Supplementary Table 3): k_ass for the trimeric G-protein G_i using two different methods was found to be 4×10⁴ M⁻¹·s⁻¹ [15] or 0.7×10⁶ M⁻¹·s⁻¹ [16], with respective dissociation constant, K_d=100 or 3 nM. Later K_d measurements [17] yielded even lower value of 0.2 nM for G_i, and 17–27 nM for the trimeric G-proteins G_o and G_s. It is thus likely that the k_ass value for G_i is fairly high (approx. 10⁶ M⁻¹·s⁻¹), whereas other G-proteins such as G_o and G_s have an k_ass value of approx. 10⁵ M⁻¹·s⁻¹ or lower.

Published k_diss values for receptor-driven trimeric G-protein dissociation vary widely (see Supplementary Table 4), from approx. 1 to 300 s⁻¹. The low values of k_diss were obtained in reconstituted systems and are likely to be underestimations, while the extremely high values obtained for rhodopsin/transducin may not be transferable to other receptor/G-protein systems. Likely in vivo k_diss values were estimated to be 20 s⁻¹ [18] and were varied in 5–25 s⁻¹ intervals for the present analysis.

From a general biochemical standpoint, the Michaelis–Menten constant for the receptor-driven trimeric G-protein dissociation (K₂ in eqn 3) is likely to be in the range of physiological G-protein concentration [19], which is indeed the case for transducin activation by rhodopsin [20]. Thus, although direct measurements for the Michaelis–Menten constant for other G-proteins are unavailable, we set K₂ at 500 nM.

GAPs were found to accelerate the GTP hydrolysis by orders of magnitude with a low Michaelis–Menten constant (K₃ in eqn 4) of approx. 2 nM [21]. Specific k_hydr values differ depending on the Gα–GAP pair (see Supplementary Table 5) and were varied in the 1–20 s⁻¹ interval in the present modelling.

Steady-state analysis

Numerical solutions to the system of non-linear equations (eqn 6a and 6b) are shown in the Results section. Here we present approximate solutions allowing us to estimate analytically the steady-state concentrations of the trimeric G-protein components.

The trimeric G-protein system reaches the steady-state when the derivatives in eqns (6a) and (6b) become zero and the rates V₁, V₂ and V₃ become equal. Attempts to solve eqns (6a) and (6b) directly produce cumbersome equations of the fourth order. However, the Michaelis–Menten equations for the rates V₂ and V₃ eqns (3) and (4) approach constants at substrate concentrations greatly exceeding the Michaelis–Menten constant (K₂ and K₃ in eqns 3 and 4). This is easily the case for V₃, as K₃ is low (see above). So, we separately analysed two different steady-state situations: with high steady-state [Gα^GTP] (>K₃), and low steady-state [Gα^GTP] (<K₃). Under conditions of high [Gα^GTP], V₃ becomes:

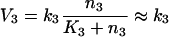7

Eqns (6a) and (6b) for the steady-state can now be rewritten as:

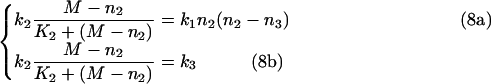Solving eqns (8a) and (8b) produces:

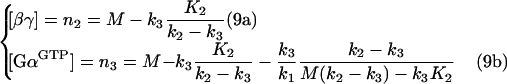Eqns (9a) and (9b) have been obtained by approximating K₃=0. This approximation is only valid for the set of parameters resulting in high steady-state [Gα^GTP]. In a different set of parameters, one or both solutions of eqns (9a) and (9b) can become ‘non-biological’, i.e. <0 or >M. It appears that if n₂>0 and n₃>0, the conditions n₂<M and n₃<M will apply. As a result, the following inequalities follow from eqns (9a) and (9b):

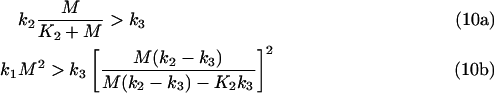Inequalities (eqns (10a) and (10b)) describe relationships between the maximal values of the rates V₁, V₂ and V₃, as:

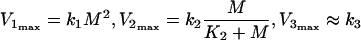11

From the consideration that K₂≈M (see above), it follows that V_2max≈k₂/2, and the inequalities (eqns (10a) and (10b) become:

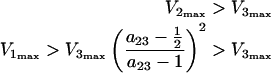12

where a₂₃=V_2max/V_3max. Inequalities (eqns 10a, 10b, 12a and 12b) describe the relationships between the V_max values required to obtain high steady-state [Gα^GTP]. Violation of these inequalities results in low steady-state [Gα^GTP].

If the steady-state [Gα^GTP] is low (<K₃), V₃ is no longer constant, but can be rewritten in a linear form. We decided to simplify V₂ into the linear form as well, as in the steady-state situation of trimeric G-protein activation, the concentration of the undissociated trimeric G-protein complex, Gα^GDPβγ, is low (<M≈K₂). Thus V₂ and V₃ become:

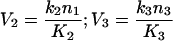13

Rewriting eqns (6a) and (6b) and solving them for the steady-state gives the following solutions:

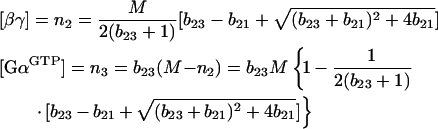14

where b_ij≡W_i/W_j, such that W₁=k₁M²=V_1max, W₂=k₂M/K₂, and W₃=k₃M/K₃. Here W₂ and W₃ are maximal rates for V₂ and V₃ written in the linear form (eqn 13). In eqn (14), solutions with a negative square root are discarded as being ‘non-biological’.

The steady-state analysis should be started with analysis of inequalities (eqns 12a and 12b). If they are fulfilled, the steady-state concentrations can be estimated using eqns (9a) and (9b). If not, eqn (14) should be used.

Modelling feedback reactions in the trimeric G-protein cycle

To model the positive feedback of Gα^GTP-enhanced GPCR activity, the V₂ rate equation (eqn 3) can be rewritten in the following form, after [22]:

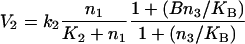15

where B and K_B are kinetic constants. In Figure 7, B is set as 100, and K_B is set as 500 nM.

Figure 7. Feedback loops can produce oscillations in the trimeric G-protein cycle.

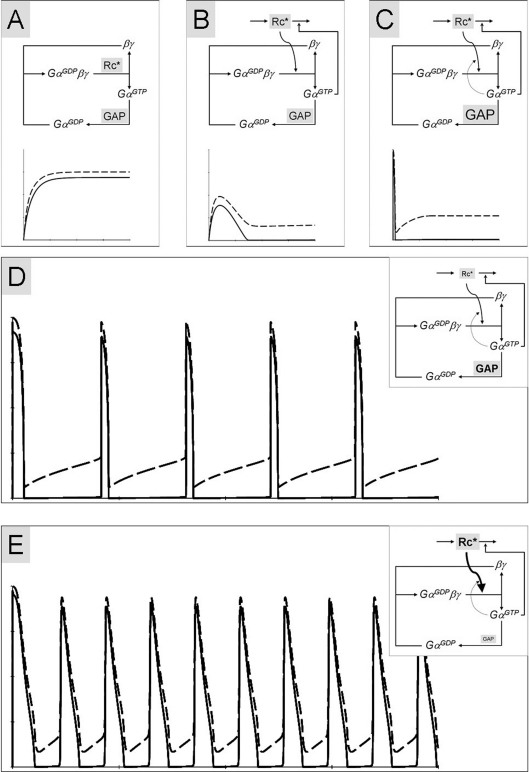
Mode 2 trimeric G-protein signalling (A) becomes transient upon incorporation of the negative-feedback loop of Gα^GTP-stimulated receptor internalization (B). Further addition of the positive-feedback loop of Gα^GTP-mediated stimulation of receptor activity induces oscillations in the trimeric G-protein cycle (D, E). The frequency and shape of oscillations depend on properties of the system: lower receptor/GAP activity ratio produces lower frequency (D) than does the higher receptor/GAP activity ratio (E). Strong off-balance activity of one enzymatic component prevents oscillations (C). Curve presentation is as in Figure 3. Kinetic parameters, other than in Figure 3, are: k_ass=0.01 nM⁻¹·s⁻¹; k_diss=20 s⁻¹ (in A–C and E) and 18 s⁻¹ (in D); k_hydr=3 s⁻¹ (in A–C and E) and 6 s⁻¹ (in D); [Rc*]=50 nM (in A–C and E) and 20 nM (in D); [GAP]=40 nM (in A, B, D and E) and 100 nM (in C). Time scale is 15 s in (A) and (B), and 300 s in (C–E).

To model the negative feedback of Gα^GTP-induced receptor internalization (removal from the cell surface), [Rc*] was set as a variable rather than as a constant:

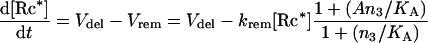16

where V_del is the rate of receptor delivery to the cell surface, k_rem is the rate constant for receptor removal, and A and K_A are kinetic constants (set as 0.3 nM⁻¹·s⁻¹, 0.01 s⁻¹, 180 and 400 nM respectively in Figure 7).

Computer modelling

Kinetic modelling was performed with the PLAS (Power Law Analysis and Simulation) software [19] (http://www.dqb.fc.ul.pt/docentes/aferreira/plas.html) using two numerical solvers: the BDF stiff integrator for rate-law systems and Taylor series method for power-law systems.

RESULTS

Description of the four kinetic modes in the trimeric G-protein system

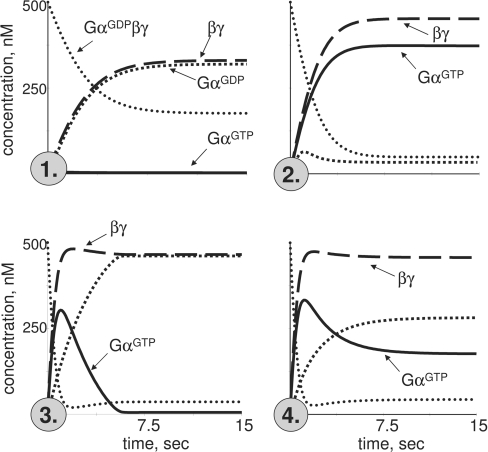
The kinetic model of the trimeric G-protein cycle (Figure 1) is described in the Materials and methods section. Kinetic modelling of this simple trimeric G-protein cycle yields surprising diversity in the signalling responses (Figure 2) in the range of parameters, quantified from experimental data (see the Materials and methods section). This diversity is largely manifest as the Gα responses, represented as predominant production of Gα^GTP over Gα^GDP, or vice versa; furthermore, these responses can be transient (Figure 2). In contrast, βγ production is mostly sustained and uniform in response to receptor activation, and varies mostly in its level. We operationally define levels of components of the trimeric G-protein cycle (Gα^GDPβγ, Gα^GTP, Gα^GDP and βγ) as ‘high’ if they exceed K₃ (the Michaelis–Menten constant for the GAP-accelerated GTP hydrolysis on Gα^GTP; set as 2 nM or <1% of the total G-protein concentration) and ‘low’ if they do not.

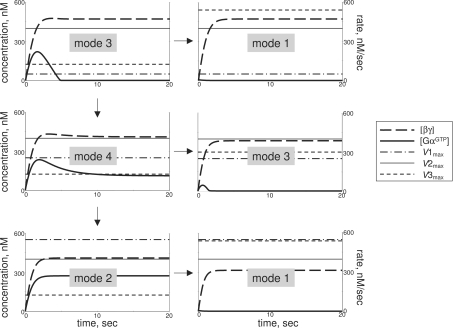
Figure 2. Four signalling modes predicted from kinetic modelling of the trimeric G-protein cycle.

Receptor activation starts at zero time. Mode 1 is sustained production of high levels of βγ and Gα^GDP, but not Gα^GTP, upon receptor activation. Mode 2 is production of high levels of βγ and Gα^GTP. Mode 3 is a sustained production of high levels of βγ, with Gα^GTP produced transiently and then falling to low levels, while mode 4 stabilizes Gα^GTP at high levels after the original overshoot. The kinetic parameters in all four modes are: starting [Gα^GDPβγ]=500 nM, and starting [βγ], [Gα^GDP] and [Gα^GTP]=1 nM; K₂=500 nM; K₃=2 nM. Other parameters are: k_ass=0.001 nM⁻¹·s⁻¹ (modes 1, 3 and 4), and 0.01 nM⁻¹·s⁻¹ (mode 2); k_diss=15 s⁻¹ (mode 1), 20 s⁻¹ (mode 2) and 25 s⁻¹ (modes 3 and 4); k_hydr=15 s⁻¹ (mode 1) and 5 s⁻¹ (modes 2–4); [Rc*]=30 nM (modes 1 and 2), 100 nM (mode 3) and 60 nM (mode 4); [GAP]=25 nM (modes 1 and 4), 20 nM (mode 2) and 52 nM (mode 3).

The observed diversity in G-protein responses can then be categorized into four distinct signalling modes (Figure 2): sustainable production of high concentrations of βγ and Gα^GDP with low levels of Gα^GTP (mode 1); sustainable production of high concentrations of Gα^GTP and βγ (mode 2); transient production of high concentrations of Gα^GTP with sustained high βγ (mode 3); and sustainable production of high concentrations of Gα^GTP and βγ with an initial overshoot in Gα^GTP production (mode 4). This categorization has a biological rather than mathematical meaning: ‘high’ concentrations are implied to induce signal transduction, whereas ‘low’ are not. Furthermore, modes 3 and 4 are close to the mathematical description, but are vastly different biologically, as only in mode 4 can the stable activation of Gα^GTP-dependent responses be expected.

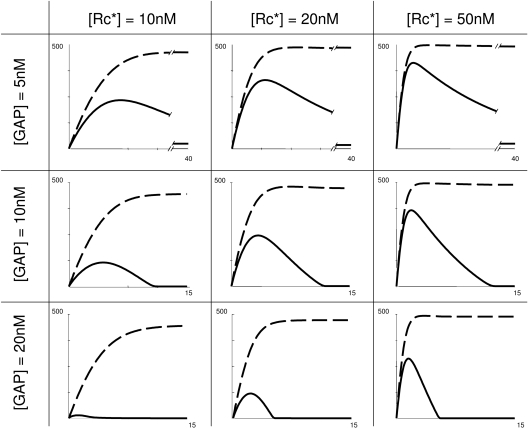
The conventional view of GPCR signalling implies that steady-state concentrations of Gα^GTP and βγ rise to high upon receptor stimulation. It is apparent from modelling presented here that this type of G-protein response is just one of multiple kinetic modes of G-protein activation (mode 2). The other three modes have not been previously characterized. The four modes of the trimeric G-protein cycle predicted here will probably produce a wider range of intracellular responses than just a sustainable production of Gα^GTP plus βγ. Specifically, Gα^GTP-dependent cellular responses cannot be expected in mode 1, and can only be transient in mode 3. Numerical analysis shows that the duration of the Gα^GTP transient in modes 3 and 4 is mostly under the negative control by the efficiency/concentration of the GAP, while the amplitude is largely determined by the efficiency/concentration of the activated receptor (Figure 3).

Figure 3. Transient Gα^GTP production in mode 3.

In conditions when Gα^GTP transient is produced, its amplitude is largely under GPCR control, while its period is largely under the negative GAP control. Only [βγ] (broken line) and [Gα^GTP] (continuous line) are shown. Curve presentation, starting concentration of the components, and the Michaelis–Menten constants are as in Figure 2. Kinetic parameters, other than those shown, are: k_ass=0.0001 nM⁻¹·s⁻¹; k_diss=20 s⁻¹; k_hydr=5 s⁻¹.

Steady-state analysis

The four kinetic modes can be placed in two separate groups: modes 2 and 4 showing high steady-state concentrations of both βγ and Gα^GTP; and modes 1 and 3 showing high steady-state concentration of βγ and low steady-state concentration of Gα^GTP. To assess whether the steady-state [Gα^GTP] is high or low, inequalities (eqns 12a and 12b) should be used to compare the maximal levels of the V₁–V₃ rates. If V_2max > V_3max and V_1max>V_3max, [Gα^GTP] will be high in the steady-state. In this situation, to calculate the steady-state concentrations of [Gα^GTP] and [βγ], eqns (9a) and (9b) should be used. For low steady-state [Gα^GTP], eqn (14) should be used instead.

Prediction of the kinetic modes

Three rates determine the behaviour of the trimeric G-protein cycle: the rate of dissociation of the trimeric complex (V₂), the rate of GTP hydrolysis on Gα^GTP (V₃), and the rate of re-association of the trimeric complex (V₁). The choice between the four signalling modes is determined by the maximal values of these three rates. Numerical analysis reveals that:

mode 1 (low Gα^GTP production) is achieved if V_3max>V_2max;

mode 2 (sustained high Gα^GTP production) is achieved if V_1max>V_2max>V_3max;

mode 3 (transient Gα^GTP production) is achieved if V_2max>V_3max>V_1max;

and mode 4 (Gα^GTP production with overshoot) is achieved if V_2max>V_1max>V_3max (17)

where V_max values are as defined as in the Materials and methods section (eqn 11). Figure 4 illustrates the dependence of kinetic modes on the V_1max, V_2max and V_3max parameters.

Figure 4. The kinetic mode can be determined based on comparison of the maximal levels of the three rates.

Top left: mode 3 occurs if V_2max>V_3max>V_1max. Increase in V_1max, so that V_2max>V_1max>V_3max, leads to mode 4 (middle left). Further increase in V_1max, so that V_1max>V_2max>V_3max, leads to mode 2 (bottom left). Increase in V_3max, so that V_3max>V_2max, leads to mode 1, regardless of whether V_1max is high (bottom right) or low (top right).

Let us consider the situation when V_3max>V_2max. This situation is one of the two conditions implying low steady-state [Gα^GTP] (see inequalities in eqns 12a and 12b). As V₃ approaches V_3max if [Gα^GTP]>K₃, the situation of V_3max>V_2max also means that, for all noticeable concentrations of Gα^GTP, the rate of its destruction through hydrolysis will be higher than the rate of its production through dissociation of the Gα^GDPβγ trimer. Thus [Gα^GTP] will always be low (mode 1), and [βγ] will depend on V_1max. In essence, [βγ] can be considerably below M only in mode 1. All other modes require V_2max>V_3max, and have high [βγ] close to M.

Kinetic mode 3 describes the situation when [Gα^GTP] first rises to high but then falls back to low. Numerical and analytical calculations show that mode 3 occurs when the maximal rates relate as V_2max>V_3max>V_1max. The condition V_2max>V_3max initially leads to fast dissociation of the Gα^GDPβγ trimers, forming high concentrations of free βγ and Gα^GTP. Later, the system adopts the steady-state in which the G-proteins will mostly exist in the form of βγ and Gα^GDP owing to low association rate V_1max. Indeed, the condition V_3max>V_1max is the other situation when the steady-state [Gα^GTP] cannot be high (see inequalities in eqns 12a and 12b).

Similar analysis shows that mode 2 exists if V_1max>V_2max>V_3max, and mode 4 exists if V_2max>V_1max>V_3max.

Flips between modes

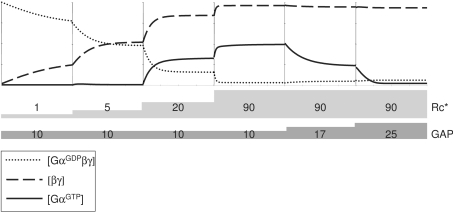
The multimodal behaviour of the trimeric G-protein cycle implies that the system can flip from one mode to another upon changes in concentrations of the components of the trimeric G-protein system. Such changes may arise from, e.g. increasing the concentration of the extracellular stimulus, reducing the plasma membrane levels of the receptor or changing the total receptor, GAP or G-protein levels. Figure 5 shows an example in which a system is predicted to flip from mode 1 (low Gα^GTP production) to mode 2 (sustained high Gα^GTP production) and back owing to changes in the levels of activated receptor and GAP. First, stimulation of a cell with low levels of a ligand yields relatively low concentrations of the activated receptor, which nevertheless elicits significant mode 1 responses (Figure 5). An additional increase in the ligand concentration stimulates the cell further, forcing the system to flip into mode 2. Cellular responses in these two modes would obviously be different. With time, a negative-feedback loop leading to enhanced production of the GAP protein can be activated; a 2.5-fold increase in the GAP concentration forces the system in Figure 5 back to mode 1, which would lead to termination of Gα^GTP-mediated responses. Importantly, changes in intracellular GAP concentration similar to those used in the modelling of Figure 5 have been observed experimentally upon prolonged stimulation of yeast cells with the mating hormone [10].

Figure 5. Flips between signalling modes.

The trimeric G-protein signalling system can flip from one mode to another and back upon changes in conditions. At zero time, the system is stimulated with 1 nM activated GPCR, and later with 5 nM; both stimulations result in increasing activation of the system in mode 1. Further increase in the GPCR activation (20 nM and then 90 nM) results in a switch to mode 2 of system activation. Concentration of the GAP is originally modelled at 10 nM; stepwise increases in GAP concentration lead to reduction and then loss of the Gα^GTP levels, switching the system back to mode 1; importantly, the system is still activated, and levels of βγ remain high. Kinetic parameters, other than those shown, are as in Figure 3, except for k_ass which is 0.0005 nM⁻¹·s⁻¹.

The steady-state flux

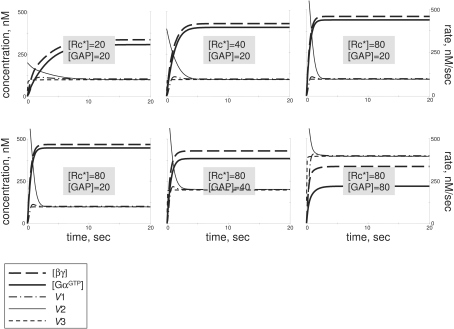
At the steady state, the three rates governing the G-protein system equalize. The resultant steady-state flux rate determines the velocity of turnover of the trimeric G-protein through the trimeric, active and monomeric inactive conformations. We have found that the steady-state flux rate is determined by the smallest of the V_max values in eqn (17). For example, mode 2 occurs if V_1max>V_2max>V_3max and the steady-state flux rate is determined by V_3max, but is practically independent of V_1max or V_2max. Figure 6 illustrates this feature. The steady-state flux rate is approximately linearly proportional to the lowest V_max value, while steady-state concentrations of βγ and Gα^GTP are affected to a considerably lower degree. For example, a 4-fold increase in GAP concentration (and thus V_3max) on Figure 6 leads to a 4-fold increase in the steady-state flux rate, but only a 2-fold decrease in the steady-state [Gα^GTP], and an approx. 50% decrease in the steady-state [βγ]. It is possible that certain intracellular responses to the trimeric G-protein activation might be determined not only by the absolute concentrations of βγ and Gα^GTP, but also, or rather, by the steady-state flux rate.

Figure 6. The steady-state flux rate is under the control of the smallest of the three V_max values.

The steady-state flux rate is achieved when the rates V₁–V₃ (thin lines) equalize. In mode 2, which occurs if V_1max>V_2max>V_3max, the steady-state flux rate is independent of the concentration of the activated receptor and thus V_2max (upper row), but is increased proportionally to the increase in the concentration of GAP and thus V_3max (bottom row). The steady-state concentrations of βγ and Gα^GTP are affected only moderately by changes in [GAP], as compared with the effect on the flux rate. Parameters are as in Figure 3, except for those shown, and k_ass=0.01 nM·s⁻¹.

Oscillations

It is well established that GPCR-elicited signalling over time stimulates uncoupling of the GPCR from G-proteins, either through the action of protein kinases A or C, or through the action of GRKs (GPCR kinases) and β-arrestins [24]. The GRK/β-arrestin signalling can lead further to receptor internalization. This regulation serves as a negative feedback terminating the response, with uncoupling being a faster acting, and internalization being a slower-acting negative feedback. Kinetic modelling confirms response termination by the negative feedback (Figures 7A and 7B). Similar modelling results are obtained for βγ- or Gα^GTP-initiated negative feedback on GPCRs, and both can operate in cells [25].

Existence of the negative-feedback loop in the trimeric G-protein cycle makes the system highly sensitive to incorporation of additional feedback regulation. For example, experiments and modelling show that coexistence of a positive- and a negative-feedback loop can result in oscillations in concentrations of system components [22,26,27]. In agreement with this, we show here that addition of a positive feedback to the trimeric G-protein cycle with signal-mediated receptor uncoupling or internalization leads not to termination of the response, but to stable oscillations in the trimeric G-protein cycle activation in a broad range of conditions (Figures 7D and 7E). The nature of the positive-feedback loop shown in Figure 7 is Gα^GTP-mediated activation of the GPCR-catalysed dissociation of the trimeric Gα^GDPβγ complex. Similar results are obtained by the βγ-mediated positive-feedback loop. Such stimulation of the GPCR by Gα^GTP or βγ can be either direct or indirect. The frequency and shape of the predicted oscillations in the trimeric G-protein cycle depend on the initial conditions (Figures 7D and 7E), such as the enzymatic potency of the receptor, or the nature of the GAP protein utilized.

Possible implications of the described variability in trimeric G-protein responses are elaborated in the Discussion.

DISCUSSION

The main result of the present study is a prediction of an unappreciated diversity in kinetic and steady-state responses of the trimeric G-protein system upon activation. Specifically, four distinct kinetic modes of the system behaviour are predicted: sustained production of βγ and Gα^GDP with only low levels of Gα^GTP (mode 1); sustained production of both βγ and Gα^GTP (mode 2); transient production of Gα^GTP with sustained βγ (mode 3); and sustained production of both βγ and Gα^GTP with an initial overshoot in Gα^GTP production (mode 4) (Figure 2). We performed extensive analysis of the experimentally measured parameters, such as kinetic constants and concentrations of components (see the Materials and methods section). The four kinetic modes exist in the identified range of parameters, and the choice between the four modes depends on the exact combination of parameter values. Once activated, the system can flip from one mode to another if parameters change (Figure 5). The prediction of choice of the kinetic mode by the G-protein system can be made by comparing the maximal values the three rates governing the trimeric G-protein cycle (eqn 17), these rates being the rate of formation of the trimeric G-protein complex (V₁), the rate of GPCR-catalysed dissociation of the complex (V₂) and the rate of GAP-accelerated hydrolysis of GTP on Gα-subunits (V₃).

The typically assumed way of trimeric G-protein activation is production of high steady-state concentrations of both βγ and Gα^GTP in response to cell stimulation – mode 2 in our classification. Although several models for GPCR–trimeric G-protein activation have been proposed previously [7–11,28], the three other kinetic modes that we describe here have not been predicted before. Our kinetic modelling shows that mode 2 can only be achieved if among the three rates governing the G-protein cycle, V_1max is the highest, and V_3max is the lowest (eqn 17). Previous models strongly overestimate V₁ and/or strongly underestimate V₃, thus being biased towards mode 2 and omitting the other modes. Several models are built implying V₁ to be not rate-limiting and the reaction of re-association of the trimeric G complex from βγ and Gα^GDP to be essentially instantaneous [8,10,11,28]. In other cases [7,9], the k_ass rate constant describing formation of the trimeric complex is set at approx. 30 nM⁻¹·s⁻¹, which is several orders of magnitude higher than that measured experimentally or used in our modelling (see the Materials and methods section). The kinetic modes 3 and 4, which require that V_1max is not the highest of the three rates, thus could not be predicted by the previous models.

Some earlier models were built without any consideration of the role of GAP proteins, thus underestimating V_3max by orders of magnitude [11,28]. In other models [7,9], the k_hydr constant for the Sst2p (yeast GAP)-catalysed GTP hydrolysis on Gpa1p (yeast Gα) was set at 0.11 s⁻¹ which rather corresponds to the basic GAP-independent GTP hydrolysis rate for mammalian and also yeast Gα subunits (0.05 s⁻¹ [3] and 0.21 s⁻¹ [10] respectively). Such underestimations of V_3max make the previous models unable to predict the kinetic mode 1, which requires that V_3max>V_2max (eqn 17).

The form of equations used to model the GPCR-catalysed dissociation of the trimeric complex (V₂) and the GAP-catalysed hydrolysis of GTP (V₃) are usually not of the Michaelis–Menten form in previous models. For example, both reactions are modelled as linear in [7,9]. The Michaelis–Menten reactions V₂ and V₃ can only be reduced to the linear form if the concentration of the substrate is much lower than the respective Michaelis–Menten constant. As shown in the Materials and methods section, V₃ can be reduced to the linear form only for the kinetic modes 1 and 3. In contrast, in kinetic modes 2 and 4 with high steady-state [Gα^GTP], V₃ is not linear but constant.

Thus the main difference between our kinetic model and those published previously is a more careful assignment and description of the rates governing the trimeric G-protein cycle, which allowed us observe the unexpected diversity in kinetic responses of this system.

Current experimental techniques used to monitor trimeric G-protein activation in vitro or in cell populations can hardly detect the kinetic diversity in G-protein responses predicted here. First, these techniques analyse activation of the G-protein system normalized for a population of cells. As a result, the kinetic aspects of individual cell behaviour, such as transient Gα^GTP production or oscillations in the G-protein cycle, become overlooked. Secondly, current methods do not measure the concentrations of the components of the trimeric G-protein cycle, but rather the steady-state flux rates of the system. For example, activation of GTP hydrolysis on trimeric G-proteins upon cell stimulation is often taken as a sign of formation of high concentrations of free Gα^GTP and thus activation of Gα^GTP-dependent responses. However, such accelerated GTP hydrolysis shows only that the G-protein system is active and constantly goes through the trimeric G-protein cycle, while the concentration of Gα^GTP can in fact be minuscule (as in kinetic modes 1 and 3). Other techniques, focusing on concentrations of individual components, should be developed to monitor kinetic behaviour of the trimeric G-protein system in individual cells.

As current techniques measure the steady-state flux rates, rather than concentrations of the components of the G-protein system, some unexpected experimental observations become apparent. For example, under some conditions, increase in the concentration of the GAP proteins enhances not only the rate of GTP hydrolysis in GPCR-stimulated cell membranes (V₃), but also the rate of GPCR-induced incorporation of GTP into trimeric G-proteins (V₂) [8]. As our modelling shows (see the Results section and Figure 6), in kinetic modes 2 and 4, the steady-state flux rate is directly proportional to V_3max. Thus an increase in the concentration of GAP, increasing V_3max, will increase the steady-state flux rate and, as a result, all three rates governing the cycle, including the rate of GTP incorporation (V₂).

Analysis of the steady-state flux rates offers explanations for the paradoxical experimental observations that certain GPCR-triggered cellular responses are enhanced by addition of a GAP [29,30]. We propose that certain cellular responses are under the influence of the flux rate of G-protein turnover through the trimeric G-protein cycle, rather than solely on the absolute concentrations of active components of the trimeric G-protein system. A similar hypothesis was put forward for the small GTPase Rab5-controlled vesicular trafficking, where it was not the concentrations of the GTP- compared with GDP-bound forms of Rab5 that activated trafficking, but rather the speed of Rab5 cycling between the GTP- and GDP-bound forms [31]. In the case of trimeric G-proteins, when kinetic modes 2 or 4 are in place, increasing [GAP] will increase the flux rate and thus stimulation of some intracellular read-out mechanisms.

The four modes of the trimeric G-protein cycle predicted here will produce a wider range of intracellular responses than a sustainable production of Gα^GTP plus βγ. For example, mode 1 (production of high βγ with low Gα^GTP) will elicit βγ-dependent, but not Gα^GTP-dependent, responses, and might be used in βγ-activated signalling in yeast mating [32] or leucocyte chemotaxis [33]. Mode 1 might also be involved in responses controlled by free Gα^GDP (e.g. in the GPCR-mediated control of asymmetric cell divisions [34]). Modes 3 and 4 (transient production of Gα^GTP) are attractive for explaining transient cellular responses to stimuli. So far, negative-feedback loops have been implicated in explaining such transient responses. In the present study, we show that such transience may be a result of intrinsic properties of the trimeric G-protein cycle.

Kinetic modelling shows that the duration of the Gα^GTP transient in modes 3 and 4 is determined largely by the efficiency/concentration of the GAP, while the amplitude is mostly determined by the efficiency/concentration of the activated receptor (Figure 3). As different signalling complexes comprising the activated receptor, trimeric G-protein complex and the GAP protein can emerge [5,35,36], they may result in production of different Gα^GTP transients decoded differently by the downstream signalling components.

The four kinetic modes arise in the experimentally measured kinetic and concentration range of parameters. For example, k_ass values for different Gα subunits vary by one or two orders of magnitude [17], which leads to a prediction that trimeric G-proteins with higher k_ass (such as G_i) can be found with more likelihood in mode 2 than trimeric G-proteins with lower k_ass (such as G_s or G_o) for which modes 3 and 4 are more likely.

GRK- and β-arrestin-dependent desensitization/internalization of GPCRs after prolonged stimulation is a well-known feedback mechanism of adaptation and signal termination [24]. Interestingly, a body of evidence shows that the GPCR desensitization pathway is also required for obtaining certain cellular responses and not just termination of cell activation. For example, leucocyte chemotaxis is defective in mice lacking GRK6 or β-arrestin 2 [37]. Chemotactic leucocytes exhibit short- and long-scale oscillatory behaviour (with periods of approx. 10 and 45 s) necessary for chemotaxis [38]. One might speculate that repetitive termination of the GPCR response, mediated by the GRK6/β-arrestin 2, directs this oscillatory chemotactic behaviour. Similarly, some GPCR-stimulated oscillations in intracellular Ca²⁺ are dependent on protein kinase C-mediated GPCR uncoupling [39,40], supporting the hypothesis that cyclic GPCR activation translates into Ca²⁺ oscillations [41].

However, kinetic modelling of the G-protein cycle with the negative feedback does not produce oscillations, but a single transient response (Figure 7B). [Under some marginal conditions, damped oscillations can be obtained (results not shown).] However, addition of a positive feedback to such modified G-protein system produces oscillations under a broad range of conditions. The nature of the positive-feedback loop in our modelling is Gα^GTP- or βγ-mediated activation of the GPCR-catalysed dissociation of the trimeric Gα^GDPβγ complex. Such stimulation of the GPCR by Gα^GTP or βγ can be either direct or indirect, and may include enhancement of the enzymatic activity of the receptor or increase in the affinity of ligand–receptor interaction. Potentially, the positive feedback could be achieved by substrate inhibition of the GAP-catalysed GTPase reaction [22]. Free βγ has been found to inhibit the GAP-catalysed GTPase reaction [5,42]. However, the mechanism of this inhibition appears to be competitive, with βγ increasing the apparent Michaelis–Menten constant of the reaction, without changing V_max [43]. Incorporation of such inhibition into the kinetic modelling did not significantly change the behaviour of the system and was not sufficient to induce oscillations (results not shown).

The frequency and shape of the predicted oscillations in the trimeric G-protein cycle depend on the initial conditions (Figures 7D and 7E), such as the properties of the receptor and the GAP. They also depend on other receptor properties, such as dephosphorylation/trafficking rates. Thus a plethora of kinetic responses can be elicited within a cell by activation with different stimuli, even if the same or similar trimeric G-protein complexes are used to transduce them. The downstream signalling components are then predicted to read different oscillations of the G-protein cycle differently, which would then elicit different cellular responses.

Several experimental observations are explained by the kinetic modelling of oscillations presented here. For example, it has been shown that a large increase in GAP concentration turns GPCR-induced Ca²⁺ oscillations into a sustained Ca²⁺ increase [44]. This is in a good agreement with the cessation of trimeric G-protein oscillations predicted to result from a large increase in GAP concentration (Figure 7C).

Experimental demonstration of the positive feedback in the trimeric G-protein system is lacking so far, but is a frequent phenomenon in a variety of chemical, metabolic, genetic or signalling cascades (see, e.g., [27,45,46]). Such a positive feedback is known to exist in the endocytic traffic controlled by the small G-protein Rab5. There, membrane-bound GTP-loaded Rab5 molecules recruit a complex of the Rab5 effector Rabaptin-5 and the Rab5-specific GEF Rabex-5, thus amplifying the activation of membrane-bound Rab5 molecules [47]. We predict the existence of a similar positive-feedback loop in the trimeric G-protein cycle. Oscillation in the G-protein cycle would be able to convey a wealth of information (encoded in the form of oscillation frequency, shape and amplitude) to the downstream signalling components. Such G-protein oscillations can translate into oscillations in the activation of downstream signalling intermediates, demonstrated for cAMP [48], inositol 1,4,5-trisphosphate [40] and Ca²⁺ [39]. They may also be decoded by non-oscillating read-outs, perhaps similarly to the way different calcium oscillations translate differently into transcriptional responses [49].

The simple kinetic modelling shown in the present paper predicts an unappreciated diversity in G-protein responses, highlighting that behaviour of even simple systems can be far more complicated than intuitively expected. The diversity of G-protein responses comes in the format of four different kinetic modes and flips between them, as well as two different steady-state conditions (with high or low [Gα^GTP]). Furthermore, steady states with different flux rates can be produced. The model further serves as a framework to incorporate positive- and negative-feedback loops, predicting oscillations in the trimeric G-protein cycle. The following features (and their various combinations) of the trimeric G-protein cycle are predicted to determine specific activation of the downstream signalling: (i) the concentration of free βγ; (ii) the steady-state concentration of Gα^GTP; (iii) the amplitude and duration of the Gα^GTP transient; (iv) the steady-state flux rate; and (v) in the oscillatory mode, the frequency and the amplitude of the βγ and Gα^GTP peaks.

This wealth of kinetic and steady-state responses produced by the simple trimeric G-protein system may serve to encode signal specificity in GPCR signalling.