First-spike latency information in single neurons increases when referenced to population onset

Abstract

It is well known that many stimulus parameters, such as sound location in the auditory system or contrast in the visual system, can modulate the timing of the first spike in sensory neurons. Could first-spike latency be a candidate neural code? Most studies measuring first-spike latency information assume that the brain has an independent reference for stimulus onset from which to extract latency. This assumption creates an obvious confound that casts doubt on the feasibility of first-spike latency codes. If latency is measured relative to an internal reference of stimulus onset calculated from the responses of the neural population, the information conveyed by the latency of single neurons might decrease because of correlated changes in latency across the population. Here we assess the effects of a realistic model of stimulus onset detection on the first-spike latency information conveyed by single neurons in the auditory system. Contrary to expectation, we find that on average, the information contained in single neurons does not decrease; in fact, the majority of neurons show a slight increase in the information conveyed by latency referenced to a population onset. Our results show that first-spike latency codes are a feasible mechanism for information transfer even when biologically plausible estimates of stimulus onset are taken into account.

The first-spike latency has been shown to carry information in several sensory modalities, including the auditory (1, 2), visual (3, 4), and somatosensory (5–7) systems. However, most studies quantifying first-spike latency information assume that the brain has an independent reference for stimulus onset from which to extract latency. In the majority of situations, this independent onset reference does not exist; the need for a timing reference has caused some to question the ultimate feasibility of first-spike latency codes (8).

A number of authors have suggested possible alternative latency measures (1, 3, 5, 6), but few have actually compared the information contained in different onset references. Stecker and Middlebrooks (9) computed the information contained in the relative spike timing of pairs of simultaneously recorded neurons in auditory cortex, and Furukawa et al. (10) compared the median errors from neural-network estimates of location with similar data. In both cases, performance with relative-latency measures was worse than with an independent onset reference, presumably because using a single neuron as the onset reference increases the overall measurement jitter. Other authors (11–13) have investigated rank order codes, where information is conveyed by the relative order in which neurons fire. Jenison (14) has shown by using modeling and maximum likelihood techniques that correlation can, in principle, increase the information available in first-spike latency, provided the decoder knows the correlation structure. However, such location estimates get noisier when stimulus onset is estimated at the same time (15).

This work addresses how latency information estimates change when measured relative to a stimulus onset time derived from the neural population. Using a coincidence-detector model, we estimate stimulus onset time from a pseudopopulation consisting of all of the neurons recorded with the same set of stimuli. We then take as the neural responses only the first spikes after this population onset time and compute the mutual information between the stimuli and these responses.

We find that correlated changes in first-spike latency across the population actually do not decrease the information contained in first-spike latency. Instead, using the population reference decreases the information in some neurons but increases it in others. On average, neurons show a slight increase in the information contained in population-referenced first-spike latencies.

Results

We presented frozen, broadband noise to decerebrate cats, with cues for sound localization added by using virtual-space techniques (16). The rationale for the design of these experiments is explained elsewhere (17, 18). Two sets of 25 stimuli were used, varying in two binaural sound localization cues each. In the first set, interaural time differences (ITDs) and interaural level differences (ILDs) were each varied over five values (for a total of 25 stimuli); in the second set, ILD and average binaural intensity (ABI; the average dB sound level in the two ears) were varied. The range of ILDs and ITDs was equally spaced across azimuths from −60° to 60°. Standard surgical and electrophysiological techniques were used to obtain single-neuron recordings in the central nucleus of the inferior colliculus (IC) of decerebrate cats, a nucleus known to show latency variation to sound localization cues (19, 20).

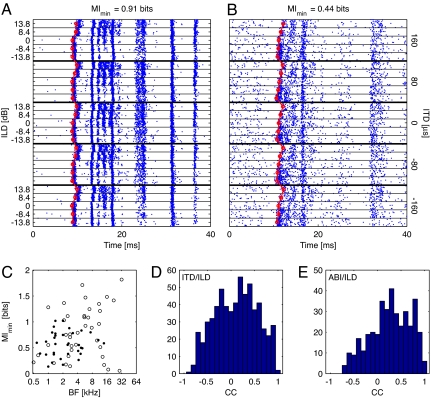
Spike rasters of responses to one set of virtual-space stimuli are shown for two example neurons in Fig. 1 A and B. Although these neurons respond robustly throughout the stimulus presentation, there is a marked latency difference during the first few response bursts that rapidly decays away. Later spike bursts do not show consistent latency differences. Consistent with this difference in behavior, there is often independent information about the stimulus in latency and ongoing spike timing (unpublished results).

Fig. 1.

Examples of first-spike latency functions and information. (A and B) Spike rasters in response to the ITD/ILD stimulus set for two example neurons. Each box shows the first 40 ms of response to a particular stimulus, with multiple repetitions displaced vertically. (A) BF = 1.3 kHz; 109 repetitions. (B) BF = 4.1 kHz; 120 repetitions. (Left) Thin lines separate different ILDs. (Right) Thick lines separate different ITDs. The first-spike latencies are shown in red. First-spike latency information assuming an independent onset reference at the minimum latency of 5 ms (MI_min) is given above each plot. (C) MI_min is plotted as a function of BF for all neurons with >20 stimulus repetitions. Filled circles, ITD/ILD stimuli; open circles, ABI/ILD stimuli. (D and E) Histograms of all pairwise cross-correlations between first-spike latency functions for ITD/ILD stimuli (D) and ABI/ILD stimuli (E).

First-spike latency was estimated by an algorithm that detects the first significant deviation of spike rate from spontaneous rate (explained in Materials and Methods). Latency estimates are shown for the example neurons in Fig. 1 A and B as the red lines in the spike raster plots.

The mutual information (MI) between first-spike latency and stimulus identity was computed with Victor's binless method (21), described in Materials and Methods, by using all first spikes falling within a window of 5–50 ms after stimulus onset. We refer to this information, which assumes a constant onset reference at the minimum latency of 5 ms, as MI_min. The results are plotted as a function of the best frequencies (BFs) of the whole population of neurons in Fig. 1C. On average, the first-spike latency variation contains 0.70 ± 0.41 (SD) bits of information about the stimuli, somewhat less than the information in spike count or ongoing spike timing (17, 18).

To test the extent of correlation in latencies across the population, cross-correlation coefficients were computed for the latencies of every pair of neurons recorded with the same stimulus set (Fig. 1 D and E). Although many neurons have correlated first-spike latency functions, a number of neurons have uncorrelated or even anticorrelated responses. There is substantial variation in the first-spike latency functions across the population.

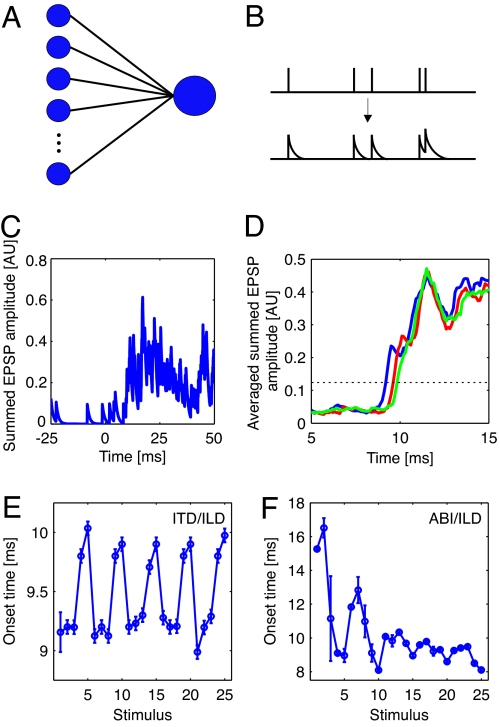
To estimate an internal reference for stimulus onset, we grouped all of the neurons from all experiments into a pseudopopulation and used this population as input into a biologically plausible coincidence detector model, outlined in Fig. 2 and described in Materials and Methods. The stimulus onset was taken as the time at which the membrane potential of this model neuron crossed a threshold (Fig. 2D). In the auditory system, such a model could mimic the activity of onset neurons in the ventral cochlear nucleus (22, 23). There is considerable variation in the estimate of onset time with stimulus identity (Fig. 2 E and F), thus calculations based on such a population reference for stimulus onset will differ from those derived by assuming an invariant stimulus onset reference.

Fig. 2.

Coincidence detector model. (A) Schematic of the model, where one coincidence detector neuron receives input from every cell in the population. (B) Every spike from the presynaptic neurons is convolved with an exponential tail (with 1-ms decay time) to mimic the excitatory postsynaptic potential (EPSP) it would induce on the coincidence detector. (C) The summed EPSP amplitude from one randomly chosen set of spike trains for one stimulus in the ITD/ILD stimulus set. (D) The average summed EPSP amplitude in the coincidence detector from 500 randomly chosen sets of spike trains. Traces from three different ITD/ILD stimuli are shown. The dotted line represents the threshold for stimulus onset detection. (E and F) Population-derived stimulus onset times from the coincidence detector model for the ITD/ILD stimulus set (E) and the ABI/ILD stimulus set (F). Results are means ± means ± 1 SD of 50 runs of the model (in some instances, the error bars are smaller than the symbol size).

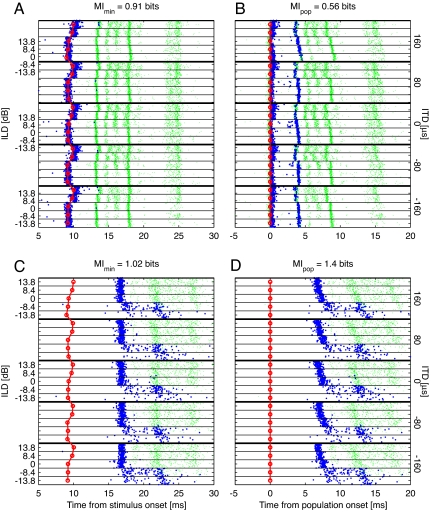
We recomputed the MI carried in first-spike latency about stimulus identity by using the stimulus onset time derived from the coincidence detector. To do so, spike times for each stimulus were measured relative to the population onset to that stimulus. Spikes occurring before the population onset signal were discarded. If an individual neuron's first-spike latency function is correlated with the population reference, then using the population reference will make the stimuli less distinguishable and decrease the information conveyed by first-spike latency, which indeed is the case for some neurons (Fig. 3 A and B). However, neurons whose first-spike latency functions are not correlated with the population onset response should have spike bursts that overlap less when measured relative to the population onset time, making the stimuli more distinguishable and increasing the information conveyed by first-spike latency. This behavior is also seen in some neurons (Fig. 3 C and D).

Fig. 3.

Measuring first-spike latency relative to the population onset. (A) Spike raster plot of the first 30 ms of one neuron's response to the ITD/ILD stimulus set (the same neuron as in Fig. 1A). All spikes are shown as small green dots, the first spikes within the 50-50 ms window are overlaid with a larger blue dot. The population-derived onset time is shown in red. (B) Same rasters as in A, but the spike times are given relative to the population-derived stimulus onset. The blue dots represent the first spikes in a 45-ms window starting at the population onset. The full MIs for each condition are shown above the plots. (C and D) Same as A and B, for a different example neuron (BF = 2 kHz; 100 repetitions).

The correlation of a neuron's first-spike latency function with the population onset time is not the only factor determining whether information will increase or decrease. Often, the latency variation of the first burst of spikes is different from that of subsequent bursts, as evidenced in Fig. 1 A and B. Because the neurons do not necessarily fire a spike in the first burst, the next few bursts can also play a role in first-spike latency information transfer. Thus, even when the first bursts of spikes overlap more when corrected for the population estimate of stimulus onset, reducing information, the second bursts often overlap less, increasing the information.

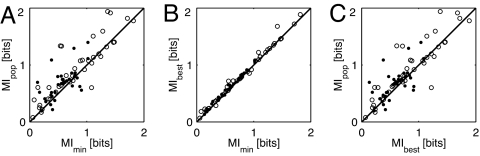
Across the population of neurons, these competing processes work against each other. Fig. 4A compares the MI values estimated under the assumption of an invariant stimulus onset reference (MI_min) with those estimated by using the coincidence detector (MI_pop). The majority of neurons (53 of 73) show a slight increase in information for the population onset (P < 1e-5, signed-rank test). The mean value of MI_pop is 0.82 ± 0.43 bits compared with 0.70 ± 0.41 bits for MI_min.

Fig. 4.

Comparing information contained in first-spike latencies with different onset references. MI_pop, information contained in first-spike latencies referenced to the variable population onset. MI_min, information contained in first-spike latencies referenced to a constant onset at 5 ms. MI_best, information contained in first-spike latencies referenced to the best delayed constant-onset reference of 8.2 ms for ITD/ILD stimuli and 7.6 ms for ABI/ILD stimuli. (A) MI_pop as a function of MI_min. (B) MI_best as a function of MI_min. (C) MI_pop as a function of MI_best.

Spontaneous spikes add noise to the first-spike latency measurements, reducing the overall information. One possible reason for the increase in population-referenced latency information is that fewer spontaneous spikes contaminate the measurement because the onset time is delayed. To test this hypothesis, we measured the information contained in first-spike times measured relative to a number of different constant-onset references, ranging from 5 to 15 ms (in 0.2-ms increments). For the ITD/ILD stimulus set, the delay that gives the maximum average information is 8.2 ms; for ABI/ILD stimuli it is 7.6 ms. The information carried in first-spike latencies measured relative to the best delayed constant-onset reference (MI_best) is increased slightly over the information from the minimum latency reference of 5 ms (MI_min), as shown in Fig. 4B (mean MI_best = 0.72 ± 0.41 bits). However, the majority of neurons still carry more information when latency is measured relative to the population onset reference as opposed to the best constant delay (Fig. 4C; P < 0.001, signed-rank test). Thus, the information increase with the population reference is not the result of eliminating spontaneous spikes.

Discussion

First-spike latency is a clear and robust cue for a variety of sensory features. Here we show that it remains a reliable cue in the absence of an external reference to stimulus onset. Using a coincidence detector model to generate an internal reference for stimulus onset, we show that latencies relative to this reference carry as much if not more information than latencies relative to an external reference.

An interesting aspect of the latency data shown here is that neurons show a shift in first-spike latency but not a shift in the timing of subsequent spikes (Figs. 1 and 3). This behavior has been noted previously (24) and has been explained by assuming that the driving potential of the neuron is well below threshold before stimulus onset but is never far from threshold during stimulus presentation (25).

The coincidence detector mechanism used to derive the population reference (Fig. 2) is similar to conceptual and functional models for onset neurons in the auditory system (26–28). Two types of onset neurons, octopus cells (29, 30) and large (D-type) multipolar neurons (31), are found in the cochlear nucleus. These neurons are characterized by broad-frequency tuning and short latencies with very small jitter. They respond strongly to modulated stimuli and thus mark temporal features of sounds, such as the syllables of speech. Octopus cells project to an area of the contralateral ventral nucleus of the lateral lemniscus (VnLL) that also contains onset neurons (32–34); the VnLL, in turn, projects to the IC, often making inhibitory terminals (35). Both sets of onset cells have properties consistent with a population marker for stimulus onsets.

To compute latency, the auditory system could use circuits like those used for echo-delay sensitivity (36–38) or duration tuning (39). Analogous to the mechanism suggested for duration tuning, a latency-sensitive neuron could respond to the coincidence between the rebound excitation at the end of an inhibitory input and a second subthreshold excitatory input (the one with the latency being measured). At coincidence, the excitatory input would be suprathreshold. Short-latency inhibitory inputs to the IC are necessary for this model, and such inputs have been described previously (39, 40). Neurons of this type could convert particular latencies relative to an onset neuron reference to a burst of spikes in the cell, i.e., to a rate code. However, such neurons would also inevitably retain some latency information because of the time delays inherent in the postulated responses. Thus, they would provide information in more than one form, which could be used by other neurons according to their input configuration. It will take specific experiments to explore the possibilities inherent in these ideas.

It should be stressed that the results here are based on responses of populations of neurons recorded nonsimultaneously and thus reflect only latency variations induced by the stimuli. Given this limitation of our data, we are not able to investigate the impact of so-called noise correlations, i.e., trial-to-trial variations in first-spike latency that are correlated across neurons. If strong, such noise correlations would counteract the effects shown here and could change the results. However, such an outcome requires noise correlation on a massive scale and seems inconsistent with the precise first-spike timing shown by auditory onset neurons in the cochlear nucleus and lateral lemniscus, which often have first-spike latency standard deviations of 1 ms or less, similar to the error bars in Fig. 2 E and F.

Materials and Methods

The surgical procedure, recording protocol, and stimulus design are described fully in ref. 17.

Surgical Procedure.

Acute recording experiments were performed on adult cats with clean external ears (from Liberty Labs, Waverly, NY). Animals were anesthetized for surgery with 1 mg/kg xylazine and 40 mg/kg ketamine (i.m.). Decerebration was achieved by transecting the brain between the superior colliculus and the thalamus, after which anesthesia was discontinued. The IC was exposed by aspirating the occipital cortex and removing part of the bony tentorium. The bullae on both sides were vented with 30 cm of PE 90 tubing. All procedures were performed in accordance with the guidelines of the Institutional Animal Care and Use Committee of The Johns Hopkins University.

Recording Protocol.

Recordings were made in a sound-attenuating chamber. Sounds were presented on speakers placed on hollow ear bars inserted into the ear canals. In situ speaker calibrations show responses that are uniform (±4.6 dB sound pressure level) between 40 Hz and 35 kHz. Platinum/iridium microelectrodes were used for single-neuron recording. Electrodes were advanced dorsoventrally through the IC to sample neurons with various BFs. Once a neuron was isolated and its BF determined, one of two stimulus sets (described below) was presented multiple times to build up statistics sufficient to characterize the MI. These results include data from 73 neurons, including 35 recorded with the ITD/ILD stimulus set and 38 with the ABI/ILD stimulus set.

Stimuli.

Two sets of virtual-space stimuli were created; each set was manipulated to vary independently in two parameters, and each parameter was adjusted in five steps, for a total of 25 stimuli per set. The stimulus sets were based on a token of frozen noise (330 ms, sampled at 100 kHz) filtered through an average head-related transfer function [averaged over spatial location; from Rice et al. (ref. 41)]. In the first stimulus set, the noise was split into two streams that were delayed relative to one another to impart an ITD and attenuated relative to one another to impart an ILD. ITD and ILD were varied over values typical of azimuths from −60° to 60°: the ITDs were −160, −80, 0, 80, and 160 μs, whereas the ILDs were −13.8, −8.4, 0, 8.4, and 13.8 dB, where negative values refer to ipsilateral locations. In the second set, the ABI (dB sound intensity averaged across the two ears) was set, and then the noise was split into two streams, which were attenuated relative to one another to impart an ILD. ABI was varied in 4-dB steps from −8 to 8 dB (relative to the average system attenuation), and ILD was varied in 8-dB steps from −16 to 16 dB, applied in such a way as to preserve the ABI.

First-Spike Latency Functions.

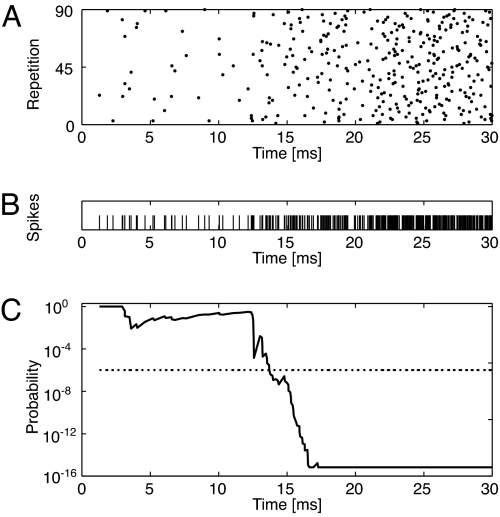
To compute the correlation coefficients in Fig. 1, the following binless algorithm was used to distinguish spontaneous from stimulus-driven spikes. The algorithm compares the observed response over several time windows with the expected response under the assumption that the neuron is firing spontaneously, with Poisson statistics. First, spikes from all N repetitions of a stimulus are collapsed into a single response (Fig. 5 A and B). Under the Poisson assumption, the probability of observing a response of at least n spikes in a window t_n is:

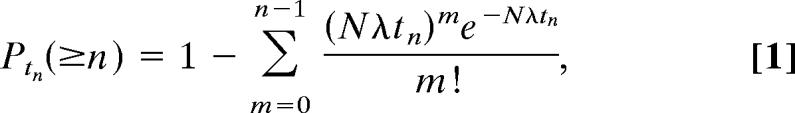where λ is the spontaneous rate of the neuron. Proceeding from stimulus onset, the possibility that each spike is the result of a stronger than chance deviation of the driving rate from the spontaneous rate is considered by computing the probability that the spontaneous rate would have produced this spike as the last of n spikes in a window t_n, where n ranges from 5 up to all of the spikes observed so far, and t_n is the width of the observed window containing these spikes. The first time at which any of these probabilities exceeds a threshold of 10⁻⁶ is marked as the latency of the neuron to that stimulus (Fig. 5C). If this threshold is not exceeded within 50 ms of stimulus onset, the latency is left undefined. Examples of the first-spike latency functions for several neurons are shown in supporting information (SI) Fig. 6.

Fig. 5.

Algorithm for detecting first-spike latency in the presence of spontaneous discharges. (A) Spike raster plot of the first 30 ms of one neuron's response to one stimulus. (B) The spikes from A are combined into a single spike train. (C) The probability that the spike trains ending at time t result from Poisson spontaneous activity is plotted versus t.

Mutual Information.

First-spike latency information is contained in two independent mechanisms (2): first, the information contained in the probabilities that each stimulus leads to at least one spike (MI_cnt); and second, the information contained in the probability densities of the timing of that first spike, should it occur (MI_tim). If p_spike represents the probability that the stimulus set elicits at least one spike, the first-spike latency information, MI_FSL, can be written by using the chain rule for information (42) as:

MI_cnt was estimated directly by counting the number of times a stimulus elicited at least one spike for each stimulus. MI_tim was estimated by using a binless method (21), in which the probability density functions of spike timing are estimated from the distance between neighboring samples. This method avoids bias problems associated with binning the time axis, and in simulations it is nearly bias free when >20 repetitions of each stimulus are collected (see SI Methods and SI Fig. 7). The median number of stimulus repetitions collected for these data was 65.

Coincidence Detector.

To generate the internal reference for stimulus onset time, the coincidence calculation in Fig. 2 was used. For each stimulus, one spike train was selected at random for each neuron and convolved with an exponential (Fig. 2B); the trains were summed, to mimic the postsynaptic potential of a coincidence detector neuron (Fig. 2C). This procedure was repeated 500 times, with a different random set of spike trains each time, and the resultant postsynaptic potentials were averaged (Fig. 2D). The threshold for stimulus onset detection was defined as halfway between the mean summated EPSP for spontaneous activity (defined as the average activity over the last 100 ms of the silent interval between stimuli) and the mean summated EPSP for driven activity (defined as the activity in a window between 50 and 300 ms after stimulus onset), where the mean is taken over all 25 stimuli in the set.

Abbreviations

ABI

average binaural intensity

BF

best frequency

EPSP

excitatory postsynaptic potential

IC

inferior colliculus

ILD

interaural level difference

ITD

interaural timing difference

MI

mutual information.