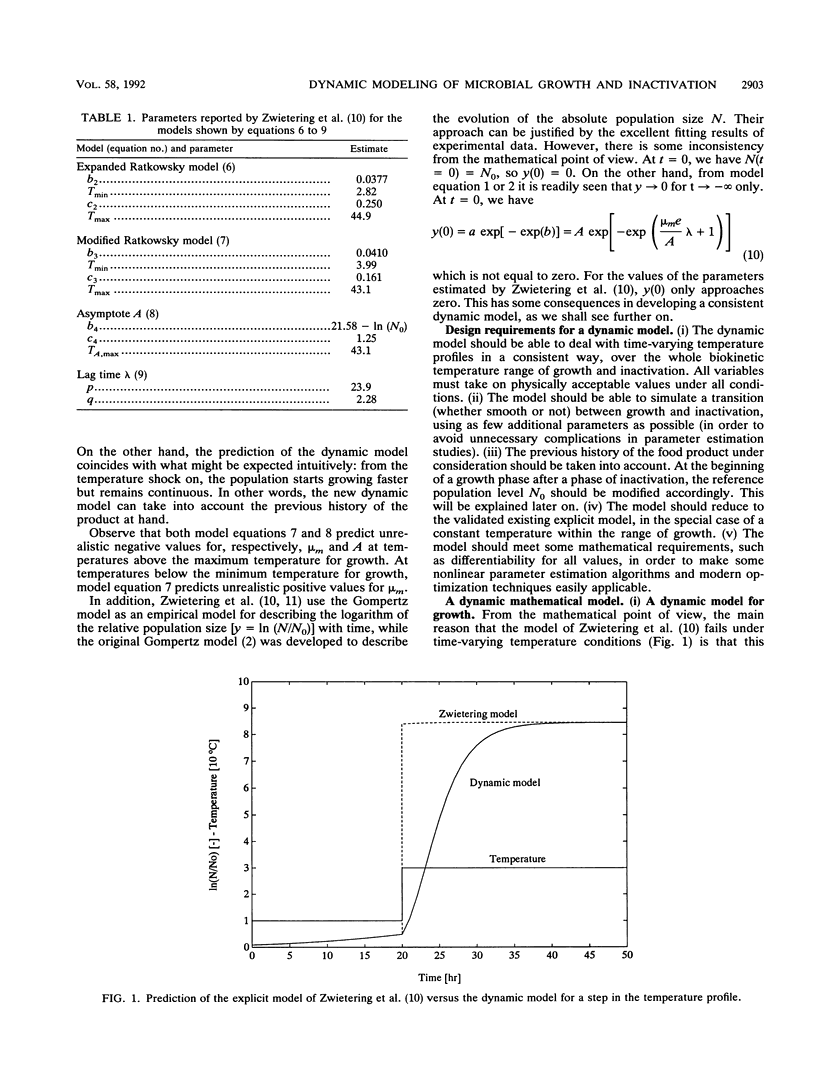
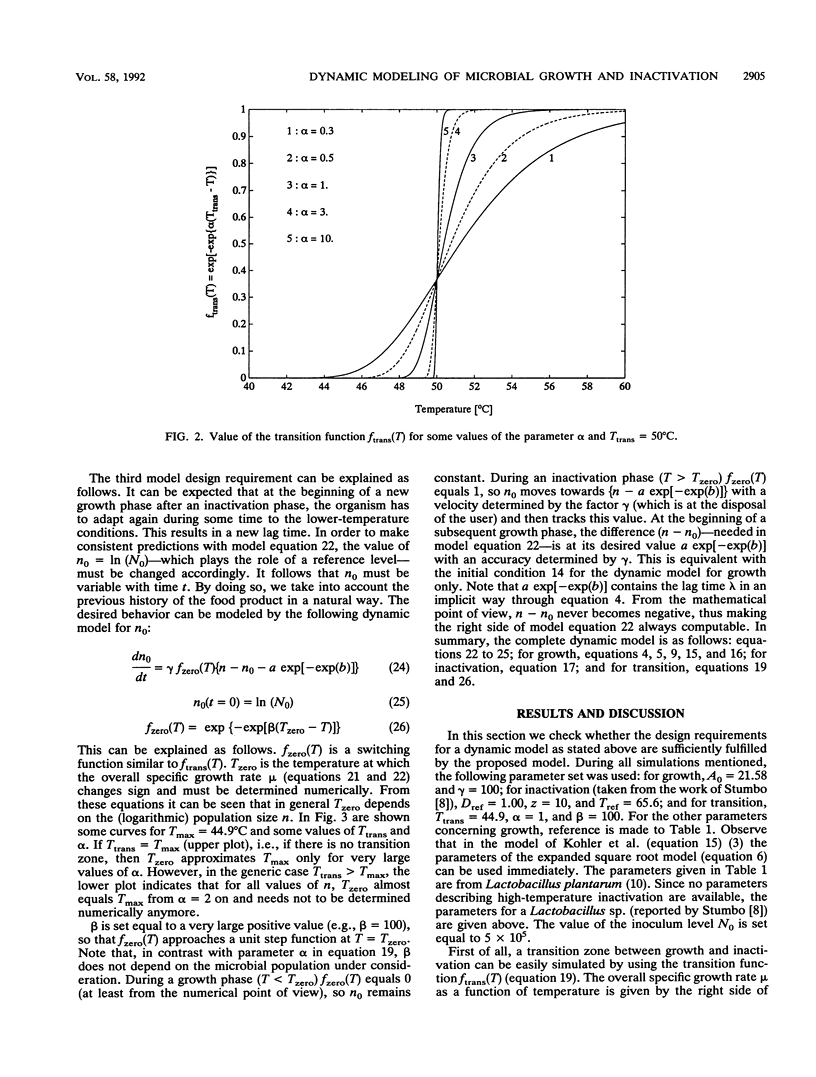
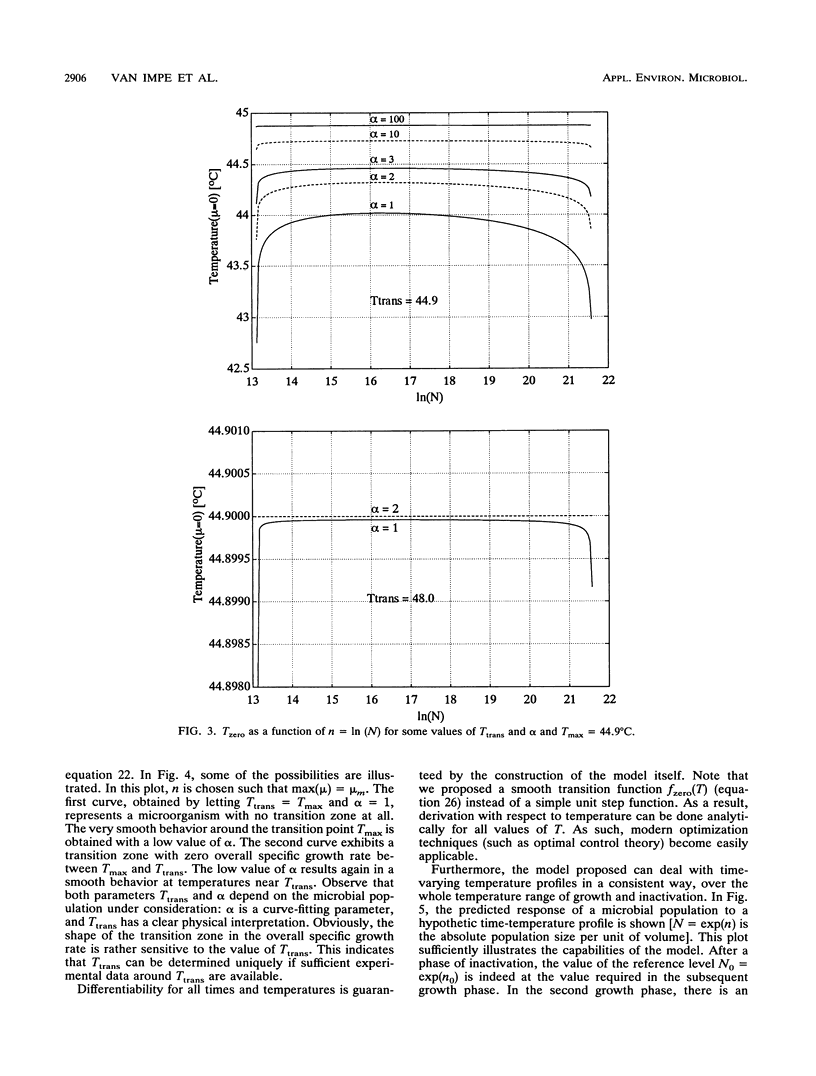
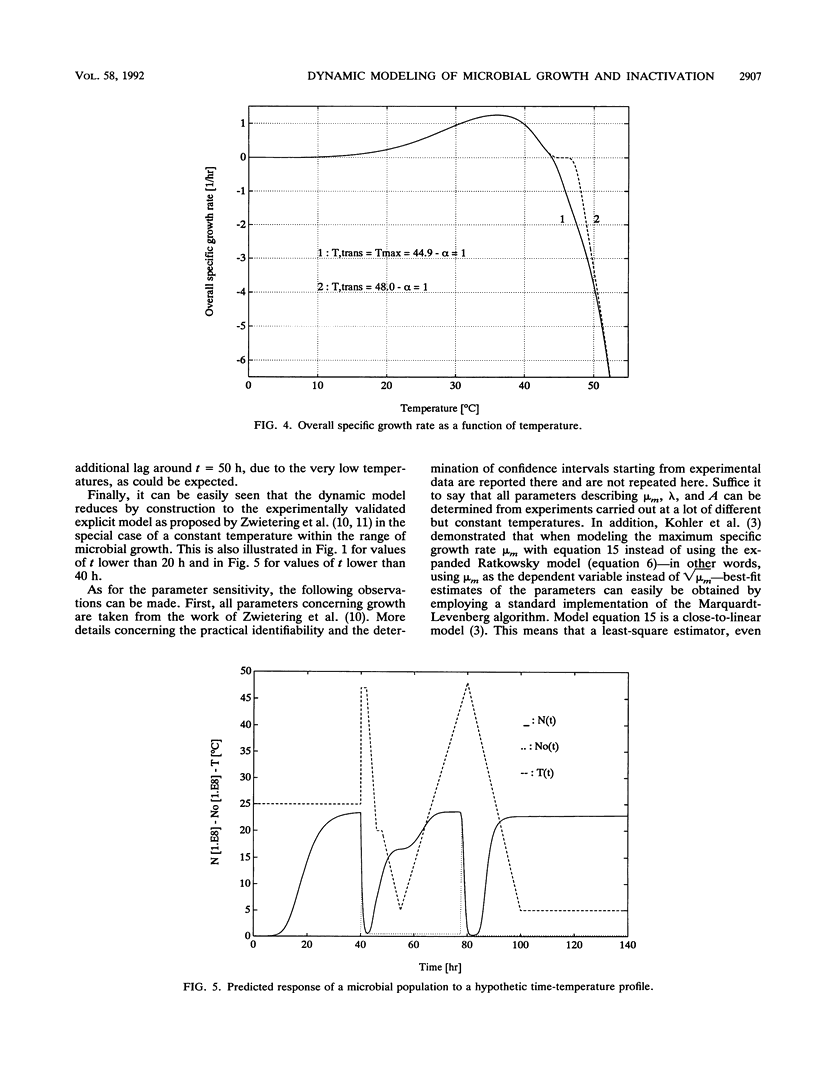
Abstract
Many sigmoidal functions to describe a bacterial growth curve as an explicit function of time have been reported in the literature. Furthermore, several expressions have been proposed to model the influence of temperature on the main characteristics of this growth curve: maximum specific growth rate, lag time, and asymptotic level. However, as the predictive value of such explicit models is most often guaranteed only at a constant temperature within the temperature range of microbial growth, they are less appropriate in optimization studies of a whole production and distribution chain. In this paper a dynamic mathematical model--a first-order differential equation--has been derived, describing the bacterial population as a function of both time and temperature. Furthermore, the inactivation of the population at temperatures above the maximum temperature for growth has been incorporated. In the special case of a constant temperature, the solution coincides exactly with the corresponding Gompertz model, which has been validated in several recent reports. However, the main advantage of this dynamic model is its ability to deal with time-varying temperatures, over the whole temperature range of growth and inactivation. As such, it is an essential building block in (time-saving) simulation studies to design, e.g., optimal temperature-time profiles with respect to microbial safety of a production and distribution chain of chilled foods.
Full text
PDF



Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Ratkowsky D. A., Lowry R. K., McMeekin T. A., Stokes A. N., Chandler R. E. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J Bacteriol. 1983 Jun;154(3):1222–1226. doi: 10.1128/jb.154.3.1222-1226.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratkowsky D. A., Olley J., McMeekin T. A., Ball A. Relationship between temperature and growth rate of bacterial cultures. J Bacteriol. 1982 Jan;149(1):1–5. doi: 10.1128/jb.149.1.1-5.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwietering M. H., Jongenburger I., Rombouts F. M., van 't Riet K. Modeling of the bacterial growth curve. Appl Environ Microbiol. 1990 Jun;56(6):1875–1881. doi: 10.1128/aem.56.6.1875-1881.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwietering M. H., de Koos J. T., Hasenack B. E., de Witt J. C., van't Riet K. Modeling of bacterial growth as a function of temperature. Appl Environ Microbiol. 1991 Apr;57(4):1094–1101. doi: 10.1128/aem.57.4.1094-1101.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]


