Evidence of Cholesterol Accumulated in High Curvature Regions: Implication to the Curvature Elastic Energy for Lipid Mixtures

Abstract

Recent experiments suggested that cholesterol and other lipid components of high negative spontaneous curvature facilitate membrane fusion. This is taken as evidence supporting the stalk-pore model of membrane fusion in which the lipid bilayers go through intermediate structures of high curvature. How do the high-curvature lipid components lower the free energy of the curved structure? Do the high-curvature lipid components modify the average spontaneous curvature of the relevant monolayer, thereby facilitate its bending, or do the lipid components redistribute in the curved structure so as to lower the free energy? This question is fundamental to the curvature elastic energy for lipid mixtures. Here we investigate the lipid distribution in a monolayer of a binary lipid mixture before and after bending, or more precisely in the lamellar, hexagonal, and distorted hexagonal phases. The lipid mixture is composed of 2:1 ratio of brominated di18:0PC and cholesterol. Using a newly developed procedure for the multiwavelength anomalous diffraction method, we are able to isolate the bromine distribution and reconstruct the electron density distribution of the lipid mixture in the three phases. We found that the lipid distribution is homogenous and uniform in the lamellar and hexagonal phases. But in the distorted hexagonal phase, the lipid monolayer has nonuniform curvature, and cholesterol almost entirely concentrates in the high curvature region. This finding demonstrates that the association energies between lipid molecules vary with the curvature of membrane. Thus, lipid components in a mixture may redistribute under conditions of nonuniform curvature, such as in the stalk structure. In such cases, the spontaneous curvature depends on the local lipid composition and the free energy minimum is determined by lipid distribution as well as curvature.

INTRODUCTION

There have been speculations that lipids of high spontaneous curvature might play important roles in membrane fusion since the event requires the lipid bilayers to go through intermediate structures of high curvature (1–11). A recent experiment found an increased concentration of high-curvature lipids in the membrane regions between fusing Tetrahymena (12). In another experiment, a mixture of lysophospholipids and fatty acids, the hydrolysis products of snake presynaptic phospholipase A2 neurotoxins, mimicked all of the biological effects of this same neurotoxin (13). Both lysophospholipids and fatty acids are high-curvature lipids and their biological effects were consistent with the lipid mixture promoting the fusion of synaptic vesicles with the presynaptic membrane. Although it seems obvious that lipids of high curvature would promote monolayer bending, some fundamental questions remain. Two possible scenarios have been envisioned. In one, high-curvature lipid components modify the average spontaneous curvature of the relevant monolayer, thereby facilitate its bending (6–9); in another, the high-curvature lipid components localize and become the major component in the bending region (14). In general terms, one may ask, are lipid components of different spontaneous curvatures redistributed upon bending? Does bending alter the relative importance between the mixing entropy and the lipid-lipid interactions? The answer would greatly influence the free energy landscape for a membrane process involving local bending such as fusion and pore formation. More fundamentally, the free energy of bending (15) for multicomponent membranes may need to be reconsidered for configurations of nonuniform curvature.

In this article, we will discuss this issue by studying the lipid distribution in a monolayer of a binary lipid mixture before and after bending. We are interested in whether there is a differential lipid distribution as a result of nonuniform bending. Therefore, we choose to compare the distribution between the lamellar phase and the distorted hexagonal phase (16). In an earlier study (17), we have obtained low-resolution results from a mixture of deuterated di18:1-phosphocholine (DOPC) and nondeuterated di18:1-phosphoethanolamine (DOPE) by neutron diffraction. We saw a homogeneously distributed lamellar phase transformed to an inhomogenously distributed distorted hexagonal phase with a higher concentration of DOPE at the high-curvature region. The resolution of neutron diffraction was limited by relatively large energy spread (∼2%), poor collimation (0.01 radian divergence), and low flux. All these factors can be improved by many orders of magnitude, and therefore one can expect a much better resolution, if a similar experiment can be performed with x-ray (synchrotron radiation), instead of neutron. Recently we have developed a procedure for applying the x-ray method of multi-wavelength anomalous diffraction (MAD) to lipid systems (18) and demonstrated its application to a regular hexagonal phase (19). This method can single out the distribution of label atoms attached to one lipid component in the mixture, and also simplify the phase problem for the reconstruction of electron density distributions. Here we will use this method to study the possible role of cholesterol as a curving agent.

Cholesterol is a major lipid component in the plasma membrane of animal cells (20). It has been known that addition of cholesterol to phospholipids tends to induce the formation of the inverted hexagonal phase (21,22), and in general imparts a negative curvature to the lipid monolayer (23). This property has been suggested as the reason for its ability to promote membrane fusion (11,14,24). In this study, the lipid mixture consists of cholesterol and di18:0(9,10dibromo)PC in 1:2 molar ratio. The spontaneous curvature of di18:0(9,10dibromo)PC is comparable to that of di18:1PC (DOPC). At 25°C, DOPC transforms from the lamellar phase to the rhombohedral (R) phase below ∼45% relative humidity (RH) (16), whereas di18:0(9,10dibromo)PC transforms to the R phase below ∼60% RH (19). This means that di18:0(9,10dibromo)PC requires a smaller osmotic pressure to transform to a curved phase, indicating a slightly higher negative spontaneous curvature than DOPC. However, di18:0(9,10dibromo)PC does not transform to a hexagonal phase even if the hydration is reduced to the equivalent of 40% RH. When cholesterol is added to di18:0(9-10dibromo)PC (in this experiment at the 2:1 PC/cholesterol molar ratio), two additional phases appear in low hydrations. From high RH to low RH, the mixture changes from the L_α phase to the R phase at 70% RH and then to a distorted hexagonal (H_IIδ) phase at 60% RH and finally to an inverted hexagonal (H_II) phase below 44% RH.

Our experiment shows that cholesterol and di18:0(9-10dibromo)PC are homogenously mixed in the lamellar phase and in the H_II phase. But in the H_IIδ phase, cholesterol almost entirely concentrates in the high-curvature regions. We will discuss the implications of this result.

EXPERIMENTAL METHODS

Materials and sample preparation

1,2-Distearoyl(9-10dibromo)-sn-glycero-3-phosphocholine (abbreviated as di18:0(9,10Br)PC) and cholesterol were purchased from Avanti Polar Lipids (Alabaster, AL). Silicon wafers (〈100〉 surface, P-doped), 300-μm thick, were purchased from Virginia Semiconductor (Fredericksburg, VA). The materials were used as delivered.

Our method of diffraction used oriented samples deposited on a flat substrate. The oriented lipid samples were first prepared in a fully hydrated lamellar phase, then transformed to the distorted hexagonal phase for investigation (25). The procedure for preparing the 2:1 mixture of di18:0(9,10Br)PC and cholesterol has been described previously in Pan et al. (19), where the same system was studied in the inverted hexagonal phase. Before the lipid preparation, silicon wafers were cleaned abrasively and then soaked in a heated bath of sulfuric acid and chromic acid mixture for 15–20 min, followed by repeated washing with distilled H₂O and ethanol. The lipid mixture was first dissolved in a 1:1 trifluoroethanol-chloroform solvent and then uniformly deposited onto a cleaned silicon substrate. The organic solvent was evaporated in vacuum or open air for ∼1 h. The deposit was then hydrated with saturated water vapor and incubated in an oven at 35°C overnight. The result was 0.4 mg of lamellar phase lipid spread over an area of 10 × 10 mm², with an average thickness of 4 μm. To transform the lipid to the distorted hexagonal phase, the sample was kept inside a humidity-temperature chamber (26). The substrate was attached to a temperature-controlled aluminum mount by heat-sink paste. Inside the chamber, there was a water reservoir, whose temperature was adjusted to vary the relative humidity within the chamber. A temperature transducer (AD590, Analog Devices, Norwood, MA) and a relative humidity sensor (HC-600, Ohmic Instruments, Easton, MD) were mounted close to the sample to monitor the sample condition. The outputs from the sensing elements were fed to PID feedback control circuits, which in turn powered two sets of Peltier modules (Melcor, Trenton, NJ), one for heating or cooling the sample and another for heating or cooling the water reservoir. The chamber was covered by a double-layered insulating wall with kapton windows for the passage of x ray. Between the two layers, a resistive heating coil maintained the surface temperature of the chamber above that of the sample so as to prevent water condensation on the kapton windows.

X-ray experiment

The sample was first examined by the x-ray diffractometers at Rice (25), where the phase diagram of the lipid was determined. Anomalous x-ray experiment was performed at the beamline X21 of the National Synchrotron Light Source, Brookhaven National Laboratory (Upton, NY). The setup was similar to that described in Yang and Huang (26). The x-ray beam was collimated by two sets of slits before the sample chamber, resulting in a beam size of 0.5 × 0.5 mm² at the sample. The sample maintained at 25°C and 58% RH in the temperature/humidity chamber was oriented at a grazing incident angle. Diffraction patterns were recorded on a MarCCD detector (Mar USA, Evanston, IL) vertical to the incident beam. A schematic of the diffraction geometry is shown in the inset of Fig. 1. A helium beam path between the sample chamber and the detector was used to reduce air scattering. A niobium attenuator was used to keep strong reflection orders from saturating the detector. The intensity of the incident beam was monitored by a Bicron scintillation detector (Saint-Gobain Crystals, Newbury, OH) that measured the elastic scattering from a 0.9-μm thick polyethylene film inserted in the incident beam—the detector measured the 90° scattering from the incident beam in the direction perpendicular to the incident polarization.

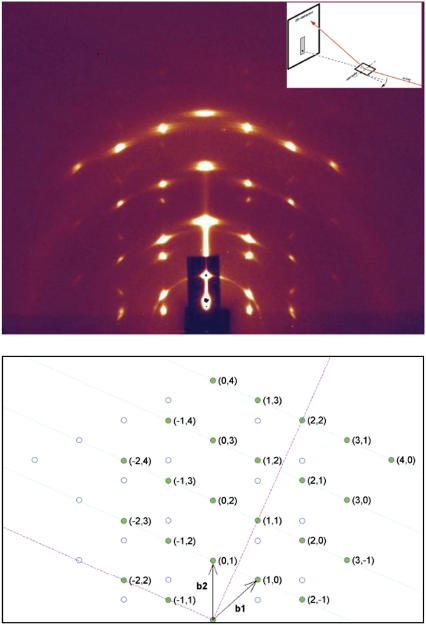
FIGURE 1.

(Top) The detector image of x-ray reflection from a 2:1 mixture of di18:0(9,10Br)PC and cholesterol in the H_IIδ phase. The inset shows a schematic of the diffraction geometry. (Bottom) The diffraction pattern was translated to the reciprocal space according to the diffraction geometry. The two reciprocal vectors are b₁ = (0.1314 Å⁻¹ sin 48.2°, 0.1314 Å⁻¹ cos 48.2°) and b₂ = (0, 0.1314 Å⁻¹). The solid green dots are the lattice defined by b₁ and b₂. The open circles are the mirror image of the lattice reflected by the mirror plane along the q_z and perpendicular to q_x—this left-right symmetry is due to the sample being a two-dimensional powder on the plane of the substrate. Due to the equality |b₁| = |b₂|, there are two mirror planes (purple lines) in the crystal lattice, one bisecting b₁ and b₂, another bisecting −b₁ and b₂.

The technical detail for MAD measurement has been described in a previous article (18). The initial steps included measuring the wavelength dependence of the detectors, and the absorption spectrum of bromine in the actual sample. By a standard procedure described in Wang et al. (18), both the real f′_λ and imaginary f″_λ parts of the bromine atom's anomalous scattering factor were obtained from the measured absorption spectrum. The results were shown in Fig. 1 of Pan et al. (19). The energy of the bromine K-edge is 13.474 keV. Eight sub-edge x-ray energies were chosen such that the values of f′_λ at successive energies differ by Δf′_λ = 0.5 in the unit of electron (Table 1 of (18)). The diffraction patterns of the sample were recorded at each of these chosen x-ray energies.

TABLE 1.

Results of MAD analysis (symmetry-related peaks are grouped as one independent peak)

(h,k) Index	|F2|2	F0/F2	|F0|2	r	ɛ(Std of |F2|)	Initial phase (F2)	Final phase (F2)
(3,−1), (−1,3)	546.2	0.50	139.2	0.9728	2.27	1	1
(3,0), (0,3)	405.2	0.69	190.7	0.9167	3.58	1	−1
(3,1), (1,3)	1317.7	1.04	1429.7	0.9453	5.12	−1	−1
(2,−1), (−1,2)	1146.5	1.20	1648.4	0.9469	4.70	−1	−1
(−2,2)	192.4	−0.93	165.6	−0.8860	2.96	−1	−1
(2,0), (0,2)	65.6	3.10	629.8	0.5872	4.56	1	1
(2,1), (1,2)	6599.9	0.46	1412.9	0.9850	5.81	1	1
(2,2)	9179.6	0.73	4865.4	0.9858	6.66	−1	−1
(−1,1)	1723.1	−0.99	1673.3	−0.8460	10.68	1	−1
(1,0), (0,1)	5529.4	−0.74	3031.2	−0.9749	6.94	−1	−1
(1,1)	7227.7	0.82	4829.3	0.9945	3.65	−1	−1

As previously described in our method article (18), we took precaution to avoid radiation damage to the sample. The x-ray beam was blocked between scans so the sample was exposed to radiation only during data collection. After the completion of eight energy recordings, the diffraction pattern of the first energy was recorded again to compare with the initial recording. Then we displaced the substrate to a previously unexposed sample position to repeat the same measurement in the reversed order of the x-ray energies. We made sure there was no change in the diffraction pattern by this double-checking procedure, indicating no deterioration effect from radiation damage. More extensive tests on radiation damage were established in previous experiments (18).

Separately, the lamellar phase of the sample was examined by ω–2θ scan on an x-ray diffractometer at Rice that had 0.1° angular resolution. This diffractometer was previously described in Weiss et al. (27). The result showed that the lamellar phase was homogeneous.

RESULTS AND ANALYSIS

Diffraction patterns and data reduction

Fig. 1 shows a reflection pattern produced by the 2:1 mixture of di18:0(9,10Br)PC and cholesterol in the H_IIδ phase. The bottom figure shows the translation to the reciprocal (q) space. The normal to the substrate (vertical in Fig. 1) is labeled q_z. Because the in-plane orientations of the sample domains are random, each lattice point is a Bragg ring parallel to the substrate and centered around q_z. The Ewald sphere of reflection at a grazing incidence intercepted most of the Bragg rings (see below) and registered each ring with a diffraction peak on the detector at a distance from q_z corresponding to the ring radius 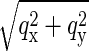(26).

The symmetry of the H_IIδ pattern is two-dimensionally oblique. In this case the horizontal axis of the reciprocal space in Fig. 1 is q_x. All of the diffraction peaks can be accounted for by the two reciprocal vectors b₁(0.1314 Å⁻¹ sin 48.2°, 0.1314 Å⁻¹ cos 48.2°) and b₂ (0, 0.1314 Å⁻¹), expressed in (q_x, q_z). The angle between the two basis reciprocal vectors is 48.2°, which substantially deviates from the hexagonal angle of 60°. However, we believe that the H_IIδ lattice possesses a mirror plane bisecting the two reciprocal vectors b₁ and b₂ (the dotted line bisecting b₁ and b₂ in Fig. 1 B). This is because the lengths of b₁ and b₂ are the same, both 0.1314 Å⁻¹ as determined by a linear fit to all orders. The same mirror symmetry has been noted for all H_IIδ phases we have measured so far, including mixtures of DOPC/DOPE at various ratios (16), with or without deuteration (17). Hence the space group for the H_IIδ phase is p2m (28). In the following, the data will be analyzed assuming the p2m symmetry.

In general a complete diffraction pattern requires more than one diffraction geometry (26). A grazing-angle reflection correctly measures all the diffraction peaks except for those on the q_z axis and those with the q_z component equal to zero (26). As one can see from Fig. 1, each of these missing peaks has its symmetry counterpart recorded by the grazing-angle reflection. Therefore the complete diffraction pattern for a H_IIδ phase requires only the grazing-angle reflection measurement.

From the reflection patterns measured at eight x-ray energies, the data were first corrected for the wavelength dependence of the detectors (18). The integrated peak intensities were then extracted from the raw data following the method described in Yang and Huang (26) and Ding et al. (17). The steps included background removal and two ways of peak integration (18), and corrections for x-ray polarization, the Lorentz factor, diffraction volume, and absorption. Also, for multi-wavelength measurements, one needs to correct the intensities for their wavelength dependence, i.e., the measured intensity is proportional to the cubic wavelength (29). Eleven independent peaks, listed in Table 1, have integrated intensities substantially above the background. The symmetry-related peaks are grouped as one independent peak and their intensities averaged. Other visible but weak diffraction peaks were not included for analysis.

MAD analysis

The diffraction amplitude of a system containing atoms with anomalous scattering factor 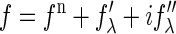is written as

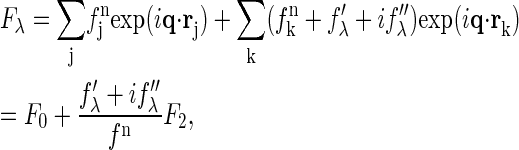(1)

where 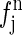is the normal scattering factor of atom j at position r_j. The index j includes all atoms except for the anomalous atoms, and the index k includes only the anomalous atoms. 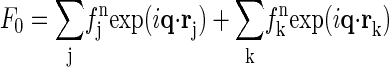is the normal diffraction amplitude of the whole system; 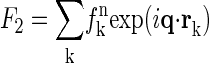is the normal diffraction amplitude of the anomalous atoms alone; and F₀ and F₂ are functions of q, independent of the x-ray wavelength.

The molecular distribution in the structure under consideration is fluidlike. Its average molecular distribution in the unit cell is most likely centrosymmetric. We will assume this is the case. Then the amplitudes F₀ and F₂ are real quantities, and Eq. 1 is absolute-squared to a simple expression 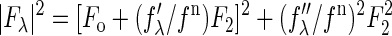. On the right-hand side of this equation, the second term is ∼1% of the first term, due to the fact that, at energies below the absorption edge, the values of f″_λ are ∼10% of |f′_λ| (see Table 1 of (18)). Therefore, we obtain the approximate relation

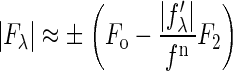(2)

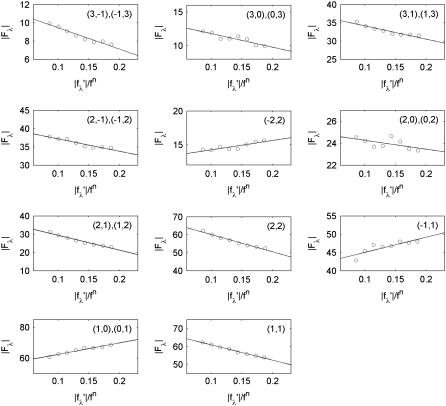
for our system. For each independent peak listed in the first column of Table 1, the values of |F_λ| are plotted as a function of |f_λ′|/fⁿ in a panel of Fig. 2. The data in all the panels appear to follow a linear relation, confirming the linear approximation made for Eq. 2. From the straight-line fit in each panel, the intercept of the fitted line gives |F₀|; the magnitude of the slope gives |F₂|; and the sign of the slope gives the sign of −F₀/F₂. In Table 1, we have listed for each of the 11 independent peaks the values of |F₀|² and |F₂|², the ratio F₀/F₂, the linear-correlation coefficient r for the straight-line fitting, and ɛ the standard deviation for |F₂|.

FIGURE 2.

MAD analyses for the detected peaks. For each independent peak, the square-root of the integrated intensity |F_λ| is plotted as a function of |f′_λ|/fⁿ. The data are fit with a straight line, from which |F₀|², |F₂|², and the ratio F₀/F₂ are obtained. The results are in Table 1.

Bromine distribution

The MAD method has achieved two purposes. First, the difficult problem of determining the phases for F₀ (30) is simplified to that of determining the phases for F₂. Second, the resolution of molecular distribution is improved by visualizing the label atoms alone.

From the magnitudes of the amplitudes 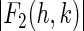we construct the Patterson function of the Br distribution

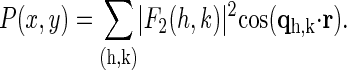(3)

The result is shown in Fig. 3. The Patterson function is equivalent to the density-density correlation function

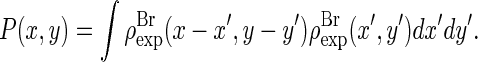(4)

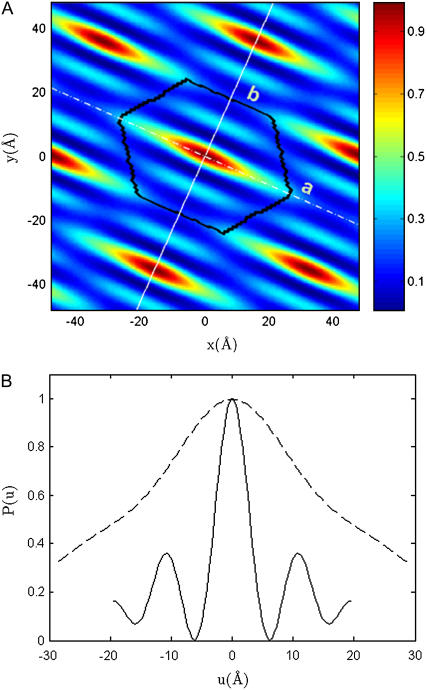
Note that since the density is a periodic function of the lattice, so is the Patterson function. To analyze Fig. 3, it is useful to compare it with the corresponding Patterson map in the H_II phase (see Fig. 5 of (19)), where the Patterson function is a circularly symmetric peak at the center. It was shown in Pan et al. (19) that the circularly symmetric Patterson peak corresponds to a bromine distribution on a circular ring. Similarly, the ellipselike Patterson in Fig. 3 A is consistent with a bromine distribution on an ellipselike ring. Very importantly we note that (in Fig. 3, bottom) the Patterson profile, along the minor axis, has a central peak and two strong symmetric side peaks at ±10.7 Å. (For the discussion of the dominant features, we ignore the small peaks at ∼20 Å.) In a Patterson map, the peak at the origin is due to the self-correlation whereas a peak off the origin is due to the intercorrelation, in this case, between two sides of the ellipse (see a model analysis in Eqs. 5 and 6 of (18)). This is confirmed by a Gaussian fitting that found that the central peak and the side peaks have the identical width 4.57 Å. In contrast, the Patterson profile along the major axis has no side peaks. These features of the Patterson function indicate that the ellipselike distribution of Br has high density along the two sides parallel to the major axis, but has small or vanishing density near the vertices of the ellipse. These features derived from the Patterson map are model-independent. They provide a basis for building a model that can be used to determine the phases of the amplitudes F₂(h,k).

FIGURE 3.

(Top) The Patterson function of Br amplitude |F₂|. The black line is the boundary of a unit cell. The dashed and solid lines indicate the direction of the major and minor axis, respectively. (Bottom) The Patterson profile along the minor axis (solid line) and along the major axis (dashed line) of a unit cell.

FIGURE 5.

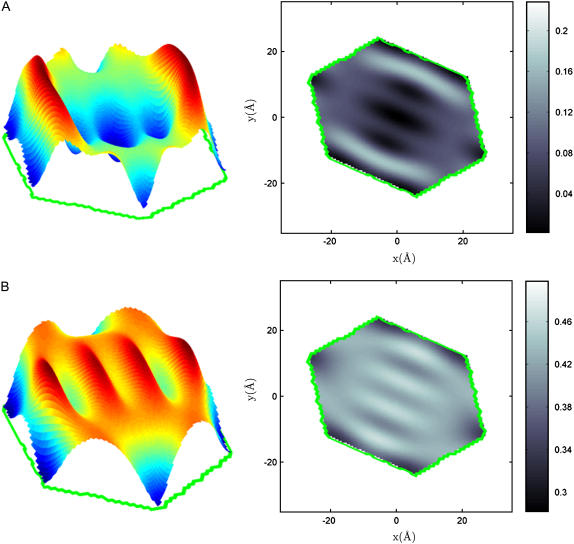
The electron density distributions of Br and the whole lipid mixture shown in pairs, top and bottom, respectively. Each panel was constructed for one of 16 possible combinations of positive or negative phases for the four peaks (2,−1), (2,2), (−1,1), and (3,0). Panels 0 and 7 are based on the initial model phases and the final phases shown in Table 1, respectively. Out of all 16 combinations, only one, panel 7, satisfies the congruent condition between the bromine and the lipid distributions.

We can also infer the structural relation between the H_II phase and the H_IIδ phase from the transformation of the diffraction pattern during the phase transition. As the system crossed the phase boundary from H_II to H_IIδ, every hexagonal peak except the ones on the q_z axis gradually split into two. For example, referring to Fig. 1, in the H_II phase up to the phase boundary (44% RH), the peak (1,0) and the mirror image of the peak (−1,1) (i.e., the circle below (1,0)) coincided with the reciprocal vector b₁ at 60°. As the humidity of system increased above 44% RH into the H_IIδ phase, the peak split into two, one moving upward and another moving downward, ended up as Fig. 1 when the RH reached 58%. Thus the lipid structure in the H_IIδ phase was continuously deformed from the lipid structure in the H_II phase. The circular distribution of the H_II phase was compressed in one direction and extended in the perpendicular direction in the H_IIδ phase. After the analysis for the H_II phase (19), we built a model as an elliptical ring of Br distribution centered at the origin of a unit cell, similar to Eq. 9 of Pan et al. (19):

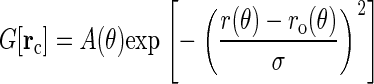(5)

In Eq. 5, r_o(θ) is an ellipse centered at r_c with a major axis 2a and a minor axis 2b, respectively, parallel to the two mirror-symmetry planes (shown in Figs. 1 and 3). The exponential function describes a Gaussian distribution along the radial direction with respect to the ellipse r_o(θ). The prefactor A(θ) expresses a nonuniform angular distribution. The width σ can be obtained from the Patterson function Fig. 3. It is easy to show (see a model analysis Eqs. 5 and 6 in (18)) that the width of a Patterson peak is 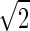times that of the corresponding peak in real space. Therefore from the Patterson peak width 4.57 Å, we have the width σ = 3.23 Å. Equation 5 describes the Br distribution in an isolated unit cell. To describe the Br distribution in a lattice, we need to include the density contribution from the six adjacent unit cells. Therefore the electron density measured by x-ray diffraction in the unit cell centered at the origin is calculated from

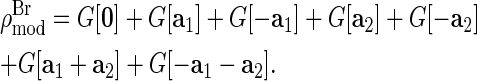(6)

The model amplitudes are calculated from

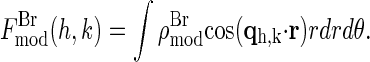(7)

According to the features deduced from the Patterson map in Fig. 3, we built a model by letting 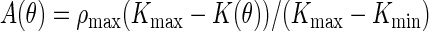, where K(θ) is the curvature of the ellipse, 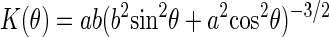, i.e., a bromine density distribution that is large where K(θ) is small and small where K(θ) is large. We then vary the values of a and b (the sizes of the major and minor axes) to maximize the T function (19)

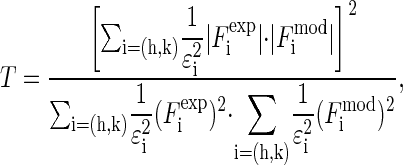(8)

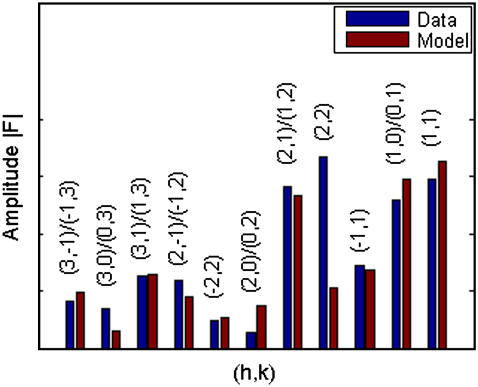
that measures the degree of agreement between the model and the experimental values |F₂(h,k)| (written as 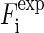in Eq. 8). We found that the best fit was obtained at a = 21.0 Å, b = 14.4 Å with the T value = 91.7%. The amplitudes of the model are compared with 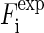in Fig. 4. The value for the minor axis 2b = 28.8 Å from the model fitting is remarkably close to the distance given by the Patterson profile. (The distance between the two side peaks is 21.4 Å. The length of the unit cell along the minor axis is 39.0 Å. This gives the minor axis of the Br ellipse, 39.0 – (21.4/2) = 28.3 Å.) We used this model to calculate 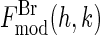. The phases of 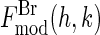were then used as the phases of the experimental |F₂(h,k)|, listed in Table 1 as the initial phases. From the sign of F₀/F₂ determined from the MAD analysis, we also have the corresponding phases for the experimental |F₀(h,k)|. The amplitudes with phases produced the electron density distributions for the Br distribution and for the entire lipid distribution:

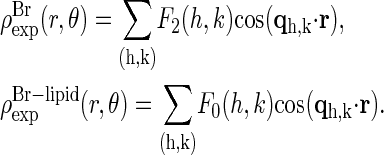(9)

However, the results produced by the initial model phases given in Table 1 are not consistent with each other—see panel 0 of Fig. 5. We know that the electron density distribution of the entire lipid mixture determined by F₀ values should be dominated by the high-density region of the phosphate headgroups and the high-density region of bromine labels. Since the phosphate group and bromines both belong to the PC molecule, their distributions must be congruent to each other, with the former around the central water region and the latter consistent with the Br distribution determined by F₂ values. The 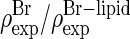pair shown in panel 0 of Fig. 5 clearly does not satisfy the congruency condition.

FIGURE 4.

Comparison of the magnitudes of the diffraction amplitudes between the model and data. They are mutually normalized by the condition .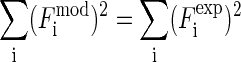

In the hexagonal case where we were able to refine the model until its agreement with data reached T > 97% (19), the phases determined by the model can be confidently used as the phases of the experimental amplitudes 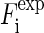. Here, at the level of agreement shown above, we can reasonably assume that the majority of the phases determined from the model are likely correct, but probably not all. However, unlike the case for the H_II phase (19), there is no apparent way of refining the model—there are simply too many possibilities. Therefore we resorted to modeling the other high-density region of the lipids, i.e., the headgroup region of the PC. The amplitude of the lipids without bromine is

(10)

where the index j includes all atoms except for the anomalous atoms. Even though the signs for F₀ and F₂ are still undetermined, since the sign of F₀/F₂ is known we can calculate |F₁(h,k)| from |F₀(h,k)| and |F₂(h,k)|. The electron density of the lipids without bromine is dominated by the PC headgroups. The distribution of the PC headgroups must be congruent with the distribution of Br atoms. Therefore we used the same model for Br, Eq. 5, but with smaller major and minor axes a and b to match the amplitudes |F₁(h,k)|. From the result of the hexagonal phase (19), we found that the headgroup to Br distance is 10.7 Å. Accordingly we deduced from the model Br ellipse (a = 21.0 Å, b = 14.4 Å) a model headgroup ellipse of a = 10.3 Å, b = 3.7 Å. We used this model to calculate the phases of F₁(h,k) and the corresponding phases for F₂(h,k). We compared the phases determined this way with the initial model phases for F₂(h,k) shown in Table 1: the phases agree for seven peaks, but disagree for four peaks (2,−1), (2,2), (−1,1), and (3,0).

We then examined all the possible combinations of positive or negative phases for each of the four peaks (2,−1), (2,2), (−1,1), and (3,0). Out of the 16 possible combinations, only one gives a congruent pair of Br and whole lipid distributions. We accept the result shown in the panel 7 of Fig. 5 as the correct electron density distributions. These phases of F₂(h,k) are listed in the last column of Table 1 as the final phases. For comparison, Fig. 5 also shows seven 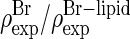pairs that do not satisfy the congruency condition; eight other pairs whose incongruency is similar or worse are not shown (but can be easily constructed from Table 1).

Fig. 6 shows the details of bromine and whole lipid distributions in a unit cell.

FIGURE 6.

The details of the bromine (left) and the lipid mixture (right) distributions in one unit cell.

Normalized lipid distribution

Normalization of the electron densities is difficult because of the lack of information about the water content. However, a schematic distribution of the two lipid components can be obtained by considering the chain region alone where there is no water. From the whole lipid distribution (Fig. 6), the positions of the PC headgroups can be determined. The ridgeline of the headgroup density is defined as the phosphate trajectory. It is known that the distance from the phosphate to the first methylene of the hydrocarbon chains is close to 5 Å (31–33). We define the interface such that the principal normal to the phosphate trajectory intersects with the interface at 5 Å. The space between the interface and the unit cell boundary is the chain region. After the analysis of the hexagonal phase (19), we take a unit cell cylinder of 8.9 Å in height (called a unit block that contains ∼1 layer of PC molecules). (There was a slight numerical error in the chain volume used in (19).) The chain volume of an average molecule made of two-thirds di18:0(9,10Br)PC and one-third cholesterol is 946.1 ų (34). We found that there are ∼7.6 di18:0(9,10Br)PC, 3.8 cholesterol molecules and 61.2 water molecules in a unit block. Next we assume that the Br density at the center of the unit cell is zero. Then from the amplitude of the Br distribution we know how the Br, and therefore its associated PC, distributed in the unit block.

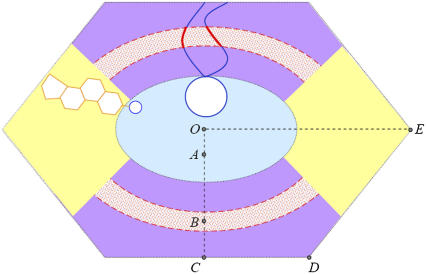
We schematically divide the unit cell into regions according to the Br distribution: the high Br regions (purple in Fig. 7) and the low Br regions (yellow in Fig. 7). The volume ratio of the high Br regions to the low Br regions is 2:1. We found 80% of di18:0(9,10Br)PC and 13% of cholesterol in the high Br regions, and 20% of di18:0(9,10Br)PC and 87% of cholesterol in the low Br regions. It is clear that the great majority of cholesterol molecules are accumulated in the vertex regions.

FIGURE 7.

Schematic of the lipid distribution. The light blue region includes headgroups, glycerol backbones, and water molecules, bound by the interface. The chain region is divided into high Br regions (purple) and low Br regions (yellow). The volume ratio of the high Br region to the low Br region is 2:1. We found 80% of di18:0(9,10Br)PC and 13% of cholesterol in the high Br regions, and 20% of di18:0(9,10Br)PC and 87% of cholesterol in the low Br regions. The symbols of the majority molecule, PC in the purple region and cholesterol in the yellow regions, are depicted. Dotted red belts represent the high Br distribution. Point A is the peak position of PC headgroup density; the interface is defined to be 5 Å away from A. Point B is the peak position of Br distribution. The measured distances are OA = 4.5 Å, OB = 14.4 Å, OC = 19.5 Å, OE = 29.2 Å, and CD = 14.6 Å.

DISCUSSION

Distribution of lipid components in the L_α, H_II, and H_IIδ phases

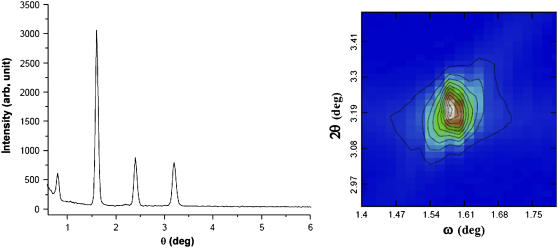
In the lamellar phase, the two components, cholesterol and di18:0(9,10Br)PC, are homogenously mixed. This is proven by the diffraction pattern (Fig. 8) that exhibits only one lamellar series. Also the two-dimensional ω-2θ scan around the second Bragg peak showed a single sharp maximum. If there were two types of domains—for example, a cholesterol-rich domain and a cholesterol-poor domain—there would be two series of lamellar peaks, and an asymmetrically broadened maximum or two peaks in the two-dimensional ω-2θ scan (unpublished results).

FIGURE 8.

(Left) Lamellar diffraction pattern of 2:1 mixture of di18:0(9,10Br)PC and cholesterol in the lamellar phase, measured by ω–2θ scan at 25°C and ∼90% RH. (Above ∼90% RH, the lamellar peaks began to broaden, similar to pure di18:0(9,10Br)PC as reported in (18).) Only one single lamellar series appears in the pattern. (Right) A two-dimensional ω-2θ scan around the second order indicates the peak has a single maximum. These data indicate the uniformity of the lamellar phase.

The question of lipid distribution in the H_II phase is more interesting. This is because in a hexagonal unit cell the radial distance from the center to the boundary is not constant. In the Wigner-Seitz unit cell, the lipid headgroups surround a central water core. The lipid chains are anchored at the lipid-water interface and extend radially (in average) toward the cell boundary. Apparently the lipid chains extend farther toward a vertex as compared to the chains extended perpendicularly to a side. Since a lipid chain has a thermodynamically favored mean length at the free energy minimum, an isothermal extension or shortening of the mean length is expected to incur an energy penalty. If the lipid is of single-component, it is obvious that the hydrocarbon region is packed by chains extended at different mean lengths. The extra energy for filling a hexagonal tube relative to the energy for filling a hypothetical circular tube is called the hydrocarbon packing energy (35,36) or hydrophobic interstice energy (3). It seems possible that, in the case of a binary mixture, the lipid components might be differentially distributed to lessen the hydrocarbon packing energy even though the entropy of mixing would be lowered.

The bromine distribution in the H_II phase of di18:0(9,10Br)PC/cholesterol 2:1 mixture was measured previously (Fig. 7 of (19)). Its density is undulated around the hexagonal unit cell with high points at the vertices. At first sight, this might be seen as an indication of undulating distribution of the di18:0(9-10dibromo)PC density with a complementary distribution for cholesterol. However, a simple analysis showed that the undulation of bromine density is entirely consistent with the variation of the chain cross section according to the length of chain extension, if the chain volume is constant. Thus we concluded that the lipid distribution in this H_II phase is homogenous with uniform density, with no detectable effect of hydrocarbon packing stress. However, this should not be taken as a disproof of hydrocarbon packing energy. As noted by Gruner (36), the hydrocarbon packing energy decreases with the radius of curvature. And the radius of curvature of this H_II phase is very small (lattice constant 44.933 Å) compared with those studied at full hydration (lattice constants 64–90 Å) (35,36). Nevertheless, it is such small radii of curvature that are relevant to the intermediate states of membrane fusion (37).

It was noted when the H_IIδ phase was first discovered (16) that this phase appears only in lipid mixtures, never in a single-component lipid. This fact alone strongly suggests that lipid demixing is the key feature of the H_IIδ phase. Now the direct measurement of the electron density in unit cell clearly showed a nonuniform distribution of the lipid components, with the cholesterol component concentrated in the high curvature vertex regions. This finding is consistent with the previous neutron diffraction result on the distribution of DOPC/DOPE 1:1 mixture in the H_IIδ phase (17). Although the neutron diffraction was of much lower resolution compared with the present x-ray measurement, the result nonetheless showed a higher concentration of DOPE in the high curvature vertex regions. Both cholesterol and DOPE are the high curvature components in their respective mixtures. Based on the H_II phase result, we do not expect the hydrocarbon packing energy to play any significant role in influencing the lipid distribution in the H_IIδ phase. Clearly the nonuniform lipid component distribution in the H_IIδ phase is correlated with the nonuniform curvature of the monolayer.

We have not yet succeeded in solving the diffraction phase problem to resolve the lipid distribution in the R phase.

Phase diagram and hydration dependence

Membranes in physiological conditions are often said to be in full hydration. However, in cells, especially eukaryotes that have intracellular membranes, it is quite possible that patches of membranes subject to local osmotic pressure gradients because of the presence of a very high total concentration of macromolecules (38). In the process of membrane fusion, the water molecules between membranes must be removed for the membrane leaflets to merge. The removal of the water molecules adjacent to the lipid bilayers creates a locally dehydrated condition. Indeed fusion of lipid vesicles is routinely induced by introducing polyethylene glycol in the suspension to create local osmotic pressure in between vesicles (39). Correspondingly, fusion intermediate states (the stalk structures) can be induced in multilamellars as a rhombohedral phase under osmotic pressure (26,37).

The phases induced by osmotic pressure favor the negative curvature, consistent with the reduction of water molecules in the headgroup region. For single-component lipids, such as diphytanoyl phosphatidylcholine, three phases in the order of increasing osmotic pressure have been observed: L_α, R, and H_II. For two-component lipids, such as DOPC/DOPE and di18:0(9,10Br)PC/cholesterol mixtures, four phases have been observed: L_α, R, H_IIδ, and H_II in the order of increasing osmotic pressure. So far the stalk phase has not been observed in full hydration. This seems to be consistent with the hypothesis that membrane fusion takes place in a locally dehydrated condition. It is not clear if the H_IIδ phase can exist in excessive water, like the H_II phase does.

The H_IIδ phase investigated here was induced by an osmotic pressure corresponding to 58% RH. The H_IIδ phase of DOPC/DOPE mixtures has been observed from ∼45% RH to ∼75% RH, depending on the mixing ratio and temperature (16). These are based on very limited investigations (16). The possible range of RH for the H_IIδ phase is unknown at the moment. Water is an important component of a lipid monolayer. The properties of lipid molecules are undoubtedly affected by osmotic pressure.

Curvature elastic energy for lipid mixtures

One of the most important characteristics of lipid membranes (monolayers or bilayers) of uniform and fixed composition is that their shapes are governed by Helfrich's curvature-elastic energy (per unit area) (15):

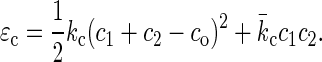(11)

c₁ and c₂ are the two principal curvatures of the membrane surface. c_o is the spontaneous curvature. k_c is the bending modulus and 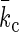the Gaussian elastic modulus. The spontaneous curvature c_o naturally depends on the lipid composition (23,40). Now we have found that the lipid components may redistribute under the condition of nonuniform curvature. In such circumstances the free energy minimum is determined by the curvature as well as the lipid distribution. Even if the shape of the membrane is known, it is not simple to calculate its energy if the membrane is of multiple components and if the shape is of nonuniform curvature, such as in pore formation or membrane fusion.

A simple model for the distribution of lipid components A and B can be described by an energy term E consisting of neighboring-pair interactions, E = ɛ_AAp_AA + ɛ_ABp_AB + ɛ_BBp_BB, and an entropic term −TS. The value ɛ_AA represents the energy of association between a pair of A-lipid molecules, and so on. The p_AA represents the number of neighboring pairs consisting of two A-lipid molecules, and so on. When A and B are randomly (or homogenously) distributed, the entropy S is maximum: S_max = −k_BN(a ln a + b ln b) (a and b are the mole fractions of A and B, respectively; N is total number of the lipid molecules and k_B the Boltzmann constant). To a good approximation, a redistribution of lipid molecules in a monolayer can be expressed by a change of energy ΔE that is a multiple of ω_AB = (ɛ_AA + ɛ_BB)/2 − ɛ_AB and a change of the entropic term −TΔS (41). Our experiments have shown that cholesterol and di18:0(9,10Br)PC are randomly distributed in the L_α phase, implying that the entropic term dominates in this phase. Indeed, the estimate of ω_AB for most lipid molecules in large unilamellar vesicles is negative and only ∼k_BT/2 or smaller (41). In other words, in planar bilayers, demixing is slightly favored by the interaction energy, but the entropic penalty for demixing is larger.

However, it is reasonable to expect the energy of association between lipid molecules to depend on the curvature of the monolayer: ɛ_AA(c), ɛ_AB(c), and ɛ_BB(c), where c is the mean curvature of the monolayer. Furthermore, the curvature dependence of the association energy may be different for different lipid molecules. Then the total free energy of a curved monolayer, consisting of the free energy of lipid distribution and Helfrich's curvature-elastic energy, is a function of both the distribution (p_AA, p_AB, p_BB) and c. The spontaneous curvature is position-dependent, depending on the local lipid composition. Depending on the external conditions, it is possible that the free energy reaches minimum when both the lipid distribution and curvature are not uniform. A reasonable explanation for the differential distribution of cholesterol and di18:0(9-10dibromo)PC in the H_IIδ phase is that the association energy of a lipid component is most negative (most stable) when the local curvature matches the spontaneous curvature of the lipid molecule. Since the spontaneous curvature of cholesterol is more negative than that of di18:0(9,10Br)PC) (as evidenced by cholesterol's induction of the hexagonal phases), it is most stable for cholesterol to reside in the highest curvature region. Note that the degree of hydration will influence the headgroup-headgroup interaction as well as the spontaneous curvature of a lipid molecule, so the energy of association also depends on the degree of hydration. This could explain why the H_IIδ phase transformed to the H_II phase upon further dehydration.

Cholesterol and membrane fusion

Approximately 90% of cholesterol in animal cells is confined to the plasma membrane. Only small pools of cholesterol are in intracellular membranes, including endoplasmic reticulum, nuclear membranes, Golgi apparatus, mitochondria, lysosomes, and peroxisomes (42,43). This is despite the fact that cholesterol transports rapidly and in both directions between the plasma membrane and internal membranes. (It has been estimated that it takes ∼1 h for the entire pool of plasma membrane cholesterol to pass through the endoplasmic reticulum and returns to the cell surface (43,44).) This nonuniform distribution of cell cholesterol is considered physiologically specified and functionally important. The homeostatic system that maintains the cellular cholesterol distribution has been described (43,45,46). However, the function of cholesterol in each membrane is not clear. Commonly speculated functions of cholesterol include enhancing the rigidity and permeability-barrier properties of the membrane, inhibiting possible phase transitions of lipid bilayers, and participating in the formation of lipid rafts which, in turn, have been implicated in many biological functions (20,47).

As mentioned earlier, cholesterol has been known to impart a negative curvature to the lipid bilayer (21–23). This property has been correlated to its ability to promote membrane fusion (11,14,24). The hypothesis is that cholesterol would lower the formation energy of the fusion intermediate state called a stalk (2,3,6–8,10,48), hence facilitating the fusion. Cholesterol is, for example, required for the generation of high-curvature clathrin-coated buds in vivo—cholesterol-depleting compounds prevent maturation of a bud past a shallow level of curvature (49,50).

There is now a substantial body of evidence supporting the stalk-pore model (1–9) for the fusion of viruses with cells (48,51) and for soluble n-ethylmaleimide-sensitive factor attachment protein receptors (SNARE)-mediated fusion (52–55). All fusion reactions of lipid bilayers appear to proceed via an intermediate state in which the outer (proximal) leaflets of two contacting membranes merge into an hourglass-like structure (a stalk). This structure was found in the unit cell of the rhombohedral (R) phase of diphytanoyl phosphatidylcholine (26,37). It is reasonable to expect that the unit cell of the R phase of the cholesterol/di18:0(9-10dibromo)PC mixture is also a stalk structure, but the phase problem of diffraction from this phase has not been solved. According to the experimental result presented above, we expect cholesterol to concentrate in the high-curvature region of the stalk. Compared with pure di18:0(9,10Br)PC, which transforms to the stalk phase at 60% RH, the addition of cholesterol facilitates the transition to the stalk phase at a smaller osmotic pressure 70% RH. Thus we speculate the roles of high-curvature lipids in the stalk-pore membrane fusion as follows.

It has been proposed that a heterogeneous distribution of lipids might be a precondition for fusion (12). Our results imply that such a precondition may be unnecessary. Starting with two homogenously mixed bilayers, the negative-curvature lipid components might facilitate the formation of the first intermediate state of fusion by aggregating toward the high negative-curvature region of the stalk structure. The participation of the negative-curvature lipids would thus lower the energy of the stalk formation although paying a relatively small price of decreasing the entropy of mixing. In the final step of fusion pore formation, it is not clear whether the mean curvature of the distal leaflet is positive or negative. Nevertheless, since the most highly curved structure during fusion is the stalk structure, lipids of high negative spontaneous-curvature such as cholesterol will play the most important role.