Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2007 Apr;17(4):520–526. doi: 10.1101/gr.6023607

Recent human effective population size estimated from linkage disequilibrium

Albert Tenesa 1,2,3, Pau Navarro 3, Ben J Hayes 4, David L Duffy 5, Geraldine M Clarke 6, Mike E Goddard 4,7, Peter M Visscher 3,5,8
PMCID: PMC1832099  PMID: 17351134

Abstract

Effective population size (Ne) determines the amount of genetic variation, genetic drift, and linkage disequilibrium (LD) in populations. Here, we present the first genome-wide estimates of human effective population size from LD data. Chromosome-specific effective population size was estimated for all autosomes and the X chromosome from estimated LD between SNP pairs <100 kb apart. We account for variation in recombination rate by using coalescent-based estimates of fine-scale recombination rate from one sample and correlating these with LD in an independent sample. Phase I of the HapMap project produced between 18 and 22 million SNP pairs in samples from four populations: Yoruba from Ibadan (YRI), Nigeria; Japanese from Tokyo (JPT); Han Chinese from Beijing (HCB); and residents from Utah with ancestry from northern and western Europe (CEU). For CEU, JPT, and HCB, the estimate of effective population size, adjusted for SNP ascertainment bias, was ∼3100, whereas the estimate for the YRI was ∼7500, consistent with the out-of-Africa theory of ancestral human population expansion and concurrent bottlenecks. We show that the decay in LD over distance between SNPs is consistent with recent population growth. The estimates of Ne are lower than previously published estimates based on heterozygosity, possibly because they represent one or more bottlenecks in human population size that occurred ∼10,000 to 200,000 years ago.

Effective population size (Ne) is an important population parameter that helps to explain how human populations evolved and expanded, and to improve the understanding and modeling of the genetic architecture underlying complex traits (Reich and Lander 2001). Traditionally, Ne has been estimated by comparing DNA sequences (i.e., from the distribution and divergence of polymorphisms). However, Ne is unlikely to have been constant during the evolution of humans, and so DNA sequence heterozygosity estimates some average Ne over a long period of time. Ne can also be estimated from linkage disequilibrium (LD) data (Hill 1981). This approach will estimate Ne over more recent history than DNA sequence heterozygosity (Hayes et al. 2003) and can therefore complement evolutionary studies of human populations. Until recently it has not been possible to estimate Ne from LD due to the large number of closely linked markers required to do so.

In this study we estimated genome-wide Ne from LD using data from ∼1,000,000 SNPs (HapMap project [The International HapMap Consortium 2003], data release #16 [http://www.hapmap.org/genotypes/2005-03_16a_phaseI/]) in four different human populations of African, Asian, and European ascent. Ours is the first example of using LD to estimate the effective population size of human chromosomes.

LD between each pair of SNPs depends on both Ne and the recombination rate between the SNPs. The distances between SNPs that we used (5–100 kb) are too small to estimate recombination rate using pedigree-based linkage analysis, so we have used other methods. Since errors in estimates of recombination rates from population data might bias the estimate of Ne, we have used three different methods to estimate these recombination rates. Each method resulted in very similar estimates of effective population size.

Methods

All our analyses were based on the known approximate relationship between LD, as measured by r2, the squared correlation of allele frequencies at a pair of loci, and Ne. In particular, we used E(r2) ≈ 1/(α + 4Nec) + 1/n for markers on the same autosome, where c is the recombination rate between the SNPs and n is the chromosome experimental sample size. The constant α = 1 in the absence of mutation (Sved 1971) and α ≈ 2 if mutation is taken into account (Hill 1975; Weir and Hill 1980; McVean 2002). We first describe how these formulae were derived and then how this theory was applied to the estimation of Ne from SNP data from multiple population samples. Although formulae for the expectation of r2 have been published, for completeness we include succinct derivations.

Relationship between Ne and E(r2) without mutation

Given the correlation of the frequency of alleles at two autosomal loci at generation t (rt), the mean and variance of the correlation at generation t + 1 is

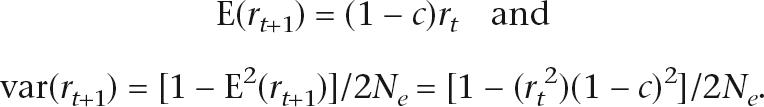graphic file with name 520equ1.jpg

The latter expression uses the general expression for the sampling variance of an estimate of a correlation coefficient r with sample size n; i.e., var(r) = [1 − E2(r)]/n. Using E(x2) = E(x)2 + var(x) for a random variable x (for example, see Lynch and Walsh 1998) results in

graphic file with name 520equ2.jpg

At equilibrium, E(rt+12) = E(rt2) = E(r2), so E(r2) = (1 − c)2E(r2) + [1 − E(r2)(1 − c)2]/2Ne. Rearranging and approximating (1 − c)2 by (1 − 2c) gives E(r2) = 1/(1 + 4Nec). This result was first reported by Sved (1971).

For the X chromosome, recombination occurs only in females. The X chromosome in males may have recombined (since it is a maternal chromosome), and only the maternal X chromosomes in females may have recombined. Hence, two-thirds of X chromosomes may have recombined and one-third may not. The sample size for the disequilibrium (correlation) coefficient is (3/2)Ne because females produce Ne X gametes and males produce (1/2)Ne gametes. Hence,

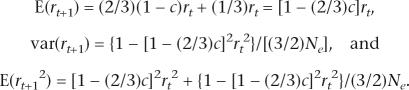graphic file with name 520equ3.jpg

At equilibrium, and ignoring the smaller terms, E(r2) = 1/(1 + 2Nec).

Relationship between Ne and E(r2) with mutation

For autosomal loci, Hill (1975) showed that, in the presence of mutation, E(r2) ≈ (10 + ρ)/(22 + 13ρ + ρ2), with ρ = 4Nec. Since (22 + 13ρ + ρ2) factors into (11 + ρ)(2 + ρ), a further approximation is E(r2) ≈ 1/(2 + ρ) ≈ 1/(2 + 4Nec). For the X chromosome, following the same logic as before, E(r2) ≈ 1/(2 + 2Nec).

Chance LD due to finite experimental sample size

Weir and Hill (1980) showed that experimental sampling introduces chance disequilibrium of var(r) = 1/n and they suggested the adjustment of E(r2) for chromosome sample size. Taking both experimental and evolutionary sampling effects into account, we can summarize the relationship between LD and Ne in the general expression

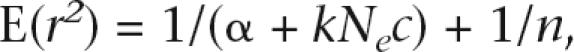graphic file with name 520equ4.jpg

where α = 1 in the absence of mutation, α = 2 if mutation is taken into account, k = 4 for autosomes, and k = 2 for the X chromosome. In data applications, we observe r2 and, assuming that we know c or have a good estimate thereof, Ne can be estimated for autosomes and the X chromosome.

Data

HapMap samples from four different populations were available (http://www.hapmap.org/genotypes/2005-03_16a_phaseI/). Samples were 30 trios from CEPH (CEU) families; 30 trios from Yoruba in Ibadan, Nigeria (YRI); and 45 unrelated Japanese (JPT) and Han Chinese (HCB) individuals. Chromosome sample size (n) was ∼120 for the CEU and YRI samples and 90 for the JPT and HCB samples. For more information, refer to The International HapMap Consortium (2003).

To compare LD across two samples from approximately the same population, data generated by Perlegen Sciences for European Americans (n = 46) were also obtained (http://genome.perlegen.com/browser/download.html).

Haplotype frequency and r2 estimation

For each chromosome, pairwise r2 was calculated (Hill and Robertson 1968) only for SNP pairs between 5 kb and 100 kb apart both to avoid the influence of gene conversion on observed LD at SNPs that are closer (Frisse et al. 2001) and to minimize the effect of a very recent expansion of the effective population size on LD (Hayes et al. 2003). A combined EM/Lander-Green algorithm to estimate pairwise haplotype frequencies (as implemented in Haploview; Barrett et al. 2005; http://www.broad.mit.edu/mpg/haploview/) was used to estimate r2 for all autosomes for the HapMap data. For the X chromosome, an EM algorithm combining phase known and unknown data was used. The software for the X chromosome calculations is freely available at http://homepages.ed.ac.uk/eanv63/. SNPs were rejected if their P-value for Hardy-Weinberg equilibrium (HWE) was <0.001 (the default setting in Haploview) or if their minor allele frequency (MAF) was <0.05.

For the Perlegen data, standard EM algorithms were applied to estimate haplotype frequencies and these used to estimate r2 for all autosomes. We filtered out markers with a minor allele frequency <0.05 and estimated r2 for all pairs of markers formed by markers that were between 5 kb and 100 kb apart. A total of 866,949 pairwise r2 estimates were in common with the CEU HapMap sample.

Estimation of recombination rates using three methods

The estimation of the recombination rate for pairs of markers is important because given the value of the recombination rate, effective population size can be estimated from the relationship between r2 and Nec. To verify the robustness of our estimates of Ne, we estimated recombination rates using three different methods.

Method 1

We obtained estimates of recombination rate from LD and the known map length of the chromosome. For each chromosome the pairwise r2 was calculated for all pairs of SNP in sliding windows of 100 kb with a 50 kb overlap. The average recombination rate for each 100 kb window was estimated from the average LD within that window. These average recombination rates were scaled so that over a whole chromosome they add up to the known map length of the chromosome. The recombination rate for any pair of SNPs within a 100 kb window was estimated to be proportional to the physical distance between the SNPs and the average recombination rate over the window. This approach ignores variation in recombination rate within a 100 kb window.

More specifically, to obtain estimates of the recombination rate for any pair of SNPs, we fitted for each window the nonlinear model yij = 1/(αi + βidij) + eij with yij = (r2 − 1/n), that is, r2 adjusted for chromosome sample size, for SNP pair j in window i at physical distance dij. Parameters αi and βi were estimated iteratively using least squares. A restriction was imposed that αi ≥ 1 and βi ≥ 0. If the recombination rate within window i (ci) is constant, then βi = 4Neci/d = ρi/d is the scaled recombination rate per unit of physical distance. For each window, we calculated the scaled recombination rate of the entire window as ρi = 0.05βi, where 0.05 corresponds to the length (in Mb) of the nonoverlapping part of the window. This quantity is summed over all windows and equated to the known map length (L in Morgan, from pedigree data; Kong et al. 2004; http://compgen.rutgers.edu/maps/index.shtml). A calibration constant, x, was estimated using the number of pairs in a window as weight, i.e., 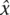Inline graphic = m[Σni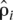Inline graphici]/[LΣni], with m the number of windows and ni the number of pairs in a window. 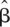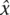For each window, the recombination rate per Mb was estimated as ĉi* = Inline graphici/Inline graphic. At least 25 pairs were required to estimate local recombination rate in a window.

Given these estimates of local recombination rates, a nonlinear least squares regression method (details below) was subsequently used to estimate Ne from recombination distance between all pairs of markers. For a given pair of markers, the recombination distance was calculated from the estimated recombination rate per unit of physical distance of the window that was the midpoint of the location of the pair and the physical distance between the pair (i.e., ĉ i(jk) = ĉi*djk). A pair was included only if the intermarker distance was <100 kb and if the number of pairs of observations that were used to estimate the local recombination rate for the window was at least 25. The number of pairs of SNPs that were used to estimate the recombination rate in the window was used as a weight in the regression analysis.

Method 2

The recombination fraction between all pairs of markers was estimated using the method described by Clarke and Cardon (2005), and the Kosambi map function was used to convert it to map distance.

Method 3

We obtained fine-scale recombination rates from two independent sets of publicly available data (Phase I HapMap [Altshuler et al. 2005] data [http://www.hapmap.org/downloads/recombination/latest/] and data generated by Perlegen Sciences [Myers et al. 2005; http://www.stats.ox.ac.uk/mathgen/Recombination.html]). We extracted marker pairs for which estimates of recombination rates were available in both data sets. This yielded 98,399 pairs that were formed from 169,545 individual markers. We used these data in four different ways to estimate Ne, using (1) r2 estimated from HapMap data (HM) and recombination rates estimated from Perlegen data (PL), (2) r2 and recombination rates estimated from HM, (3) r2 and recombination rates estimated from PL, and (4) r2 estimated from PL and recombination rates estimated from HM.

Estimation of chromosome effective population size

Given the formulae described in the theory section, and knowing r2 and c, we estimated Ne for each chromosome by fitting the nonlinear regression model

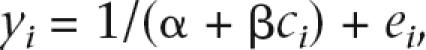graphic file with name 520equ5.jpg

with yi = (r2 − 1/n), that is, r2 adjusted for chromosome sample size, for SNP pair i at recombination distance ci (in Morgans). Parameters α and β were estimated iteratively using least squares.

Heterozygosity and LD in a population depend on Ne over the history of the population. However, LD between SNPs a large distance apart reflects more recent Ne than LD between SNPs closer together (Hayes et al. 2003). We therefore investigated the change in population size over time, as LD between loci with a recombination rate of c reflects the ancestral effective population size 1/(2c) generations ago (Hayes et al. 2003) (under the assumption of linear growth). We compared Ne estimated by recombination estimation method 1 from SNPs 5–100 kb apart. This corresponds to a time between ∼10,000 and 500 generations ago, i.e., between 200,000 and 10,000 yr ago (Hayes et al. 2003). For each chromosome, we estimated Ne from the mean r2 for average SNP recombination distances in the range of 0.01–0.5 cM. For each distance, the corresponding number of generations in the past was calculated.

Estimates of the scaled recombination rate and effective population size per chromosome obtained by method 1 were compared with the number of genes and length of the chromosome (NCBI build 35; http://www.ncbi.nlm.nih.gov/mapview/map_search.cgi?taxid=9606&build=previous) using correlation and linear regression.

The frequency distribution of the SNPs ascertained by the HapMap project is different from the frequency distribution of SNPs that have been completely ascertained (Nielsen et al. 2004). To determine if the HapMap SNP ascertainment procedure was biasing our estimates of Ne, we carried out coalescent (Hudson 1983) simulations for a neutral model and constant population size. Simulations were performed using the program “ms” (Hudson 2002; http://home.uchicago.edu/~rhudson1/source/mksamples.html). For a segment length of 25 Mb and an effective population size of 2000, the chosen input parameters equate to a mutation rate of 10−8 per nucleotide and a recombination rate of 0.01 per Mb. For each replicate, the average r2 was calculated for bins of 1 kb spacing and adjusted for chromosome sample size. A nonlinear regression model was used to relate the adjusted r2 to physical distance. Under this model, the estimate of the regression coefficient is an estimate of the scaled recombination rate ρ. One thousand replicates were run.

Results

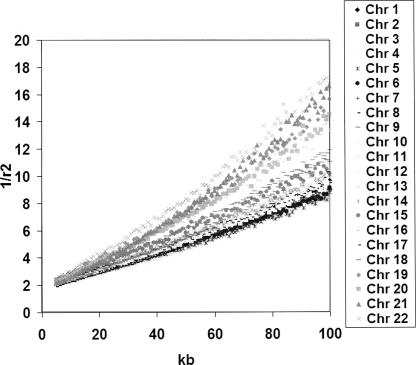
Figure 1 shows, as expected, a near linear relationship between 1/r2 and physical distance between pairs of SNPs. Linearity of the reciprocal of r2 with physical distance at small values, and a concave relationship at larger values, is clearly shown, consistent with a population that has increased over time.

Figure 1.

Figure 1.

Open in a new tab

Reciprocal of r2 plotted against physical distance for each of the 22 autosomes for the CEU population. The X-axis shows the physical distance in kilobases and the Y-axis shows 1/mean(r2). The mean value of r2 was calculated in 1 kb bins.

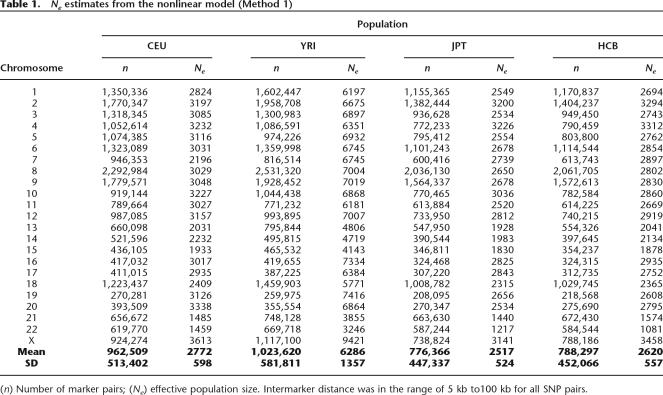
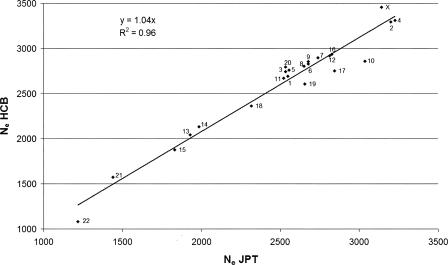
For the first method of estimating c, the average estimates of effective population size for CEU are similar to those for JPT and HCB, but lower than those for YRI (Table 1). This is expected under the out-of-Africa theory of ancestral human population expansion (Templeton 2002), because, when humans moved out of Africa, only a subset of the amount of genetic variation present in the African population at that time was represented in the migrants. An ANOVA on the estimates of Ne, fitting population and chromosome as factors, resulted in significance (P < 0.001) for both population and chromosome. The correlation between samples of Ne obtained from different chromosomes ranged from 0.87 (JPT, YRI) to 0.98 (JPT, HCB). Figure 2 shows the estimates of Ne from each of the 23 chromosomes for the JPT plotted against those estimated for the HCB. The remarkable similarity between JPT and HCB estimates most likely indicates common ancestry.

Table 1.

Ne estimates from the nonlinear model (Method 1)

graphic file with name 520tbl1.jpg

Open in a new tab

(n) Number of marker pairs; (Ne) effective population size. Intermarker distance was in the range of 5 kb to100 kb for all SNP pairs.

Figure 2.

Figure 2.

Open in a new tab

Comparison of the estimate of Ne from each of the labeled 23 chromosomes for the JPT and HCB population (Method 1). The X-axis shows the effective population size for each autosome and the X chromosome estimated from the JPT sample using a nonlinear regression of r2 on physical distance between pairs of SNPs. The Y-axis shows the estimates of Ne for each chromosome from HCB sample. The fitted linear regression line fits nearly perfectly, presumably reflecting common ancestry of the two populations.

There were significantly different from zero and positive correlations between Ne and chromosome length in Mb (with significance values ranging from P = 0.002 for HCB to P = 0.06 for YRI) and number of genes (with significance values ranging from P = 0.02 for CEU to P = 0.05 for YRI), but not between Ne and gene density (with significance values P > 0.6 for all four populations). The significant correlations were driven by the low estimate of Ne for the short chromosomes 21 and 22.

The second method, which estimates recombination rates between each pair of adjacent HapMap markers from a model-free method that detects recombination hotspots from LD (Clarke and Cardon 2005; Visscher and Hill 2006), changed the estimate of Ne between +33% and −45% with an average reduction of 27% (mean Ne = 1901) when compared with that obtained from the first method (results not shown in Tables).

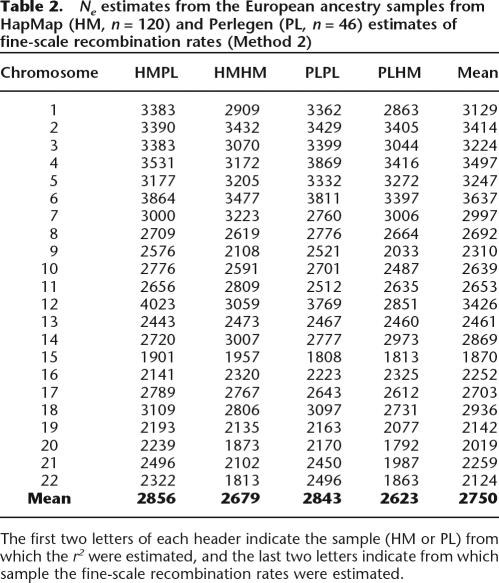
The third method used estimates of fine-scale recombination rates (rather than using physical distance as a proxy for recombination rate) from coalescent models from either Phase I HapMap (Altshuler et al. 2005) data or data generated by Perlegen Sciences (Myers et al. 2005). These estimates are shown in Table 2 and are consistent with estimates presented in Table 1.

Table 2.

Ne estimates from the European ancestry samples from HapMap (HM, n = 120) and Perlegen (PL, n = 46) estimates of fine-scale recombination rates (Method 2)

graphic file with name 520tbl2.jpg

Open in a new tab

The first two letters of each header indicate the sample (HM or PL) from which the r2 were estimated, and the last two letters indicate from which sample the fine-scale recombination rates were estimated.

Hence, using three different methods to estimate recombination rate and using two different samples of individuals from European descent gave estimates of the effective population size ranging from 1901 (Method 2) to 2843 (Method 3).

From the simulation study we found that the estimation method was not biased when SNPs were simulated as if they had been completely ascertained (data not shown). We then simulated SNPs to mimic the SNP frequency distribution from the HapMap data. For this, SNPs with minor allele frequencies between 0.05 and 0.5 were ascertained with equal probability; i.e., the frequency distribution of the SNPs was uniform. The estimates of Ne obtained from mimicking the HapMap data were biased downward by ∼18% compared with the complete ascertainment data. Hence, the HapMap ascertainment strategy may bias our estimates by approximately one-fifth, giving adjusted estimates of effective population sizes of ∼3100 (non-African populations) and ∼7500 (African population).

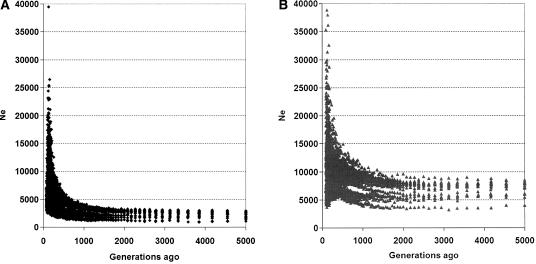
For the CEU and YRI samples we estimated effective population size as a function of time in the past. Results for the CEU data support recent dramatic population growth (Fig. 3A). This is in agreement with the likely demographic history of the ancestral population of the non-African samples; a population bottleneck, following an out-of-Africa expansion, followed by rapid growth (Watkins et al. 2001). Results for the YRI data indicate an ancestral population size of ∼7000, followed by expansion in the last ∼20,000 yr (Fig. 3B).

Figure 3.

Figure 3.

Open in a new tab

Ancestral population size estimated from 22 autosomes of the CEU (A) and YRI (B) data (Method 1). For each chromosome and for each SNP recombination distance bin (0.001 cM spacing), Ne was estimated from the mean r2, using E(r2) = 1/(α + 4Nec). The number of generations in the past was calculated as 1/(2c), and was truncated at 5000. Effective population size has increased dramatically in the last ∼1000 generations (20,000 yr), from a fairly constant ancestral size of ∼2500 (CEU) and ∼7000 (YRI).

Discussion

Overall, the estimates of Ne appear to be much lower than the usually quoted value of 10,000 (Takahata 1993). Earlier studies using mtDNA data suggested an Ne in the range of 1000–6000 (Rogers and Harpending 1992; Harpending et al. 1993; Sherry et al. 1994), for a population ∼200,000 yr ago (∼10,000 generations ago). Erlich et al. (1996) estimated a recent population size of ∼10,000 from HLA polymorphisms. Sherry et al. (1997) estimated an ancestral population size of ∼17,800 during the last one to two million yr from Alu repeats evolution. Our estimates of Ne were reasonably consistent across chromosomes and methods, and similar to estimates of Ne obtained from LD in 10 small genomic regions in a sample of 15 Italians (Frisse et al. 2001) and from three Y chromosome genes from a worldwide sample of Y chromosomes (Thomson et al. 2000). Relative to estimates of Ne from polymorphism levels, these estimates are approximately two to three times smaller. Why is this the case? We propose that the most likely explanation is that different studies implicitly or explicitly have estimated Ne at a different point in time and that the estimates can be reconciled by taking the time element into account. The human population size has not been constant in the last few 100,000 yr and, in addition to an increase in population size in recent times, there has been evidence for population bottlenecks following the out-of-Africa expansion (Reich et al. 2001; Zhang et al. 2004). Population growth and bottlenecks both have an effect on the estimates of effective population size using either marker heterozygosity or LD, but to a different degree. Service et al. (2006) reported heterozygosity and LD for chromosome 22 markers in 12 human populations, of which 11 were isolates (i.e., populations that had recently experienced increased levels of inbreeding). The average level of heterozygosity varied very little across all populations, with a range of 0.359–0.373. However, the amount of LD per unit of physical distance varied nearly twofold. These observations are consistent with heterozygosity reflecting average population size over a long period of time including before bottlenecks (inbreeding) and LD reflecting a more recent population size. Reich et al. (2001) found, using simulations, that in order to explain their European data, the population had to go through a bottleneck with a size substantially smaller than 10,000 individuals. Estimates of Ne from variation at Y chromosome and autosomal microsatellite markers in populations of African, European, and Asian descent were similar to ours (Pritchard et al. 1999; Zhivotovsky et al. 2003). Microsatellites, due to their high mutation rate, reflect more recent population history than SNPs. Using a model that incorporates geographic distances among populations, as well as genetic data, Liu et al. (2006) inferred an Ne of ∼1000 for the founding population from which modern humans derive. Other anthropological and genetic evidence has also suggested that the long-term Ne has been about three times larger in African populations than in non-African populations (Relethford and Harpending 1994; Relethford and Jorde 1999; Eller 2001), which is what we observed.

Our estimate of Ne for the X chromosome was 30%–50% larger than that for the autosomes. The X chromosome in humans has a number of unusually long haplotypes (Altshuler et al. 2005). However, estimates from coalescent methods using the same data also give an increase of ∼50% in the estimate of Ne for the X chromosome compared with autosomes, although this difference disappears when using HapMap Phase II data (G. McVean, pers. comm.). It is not clear why the average LD, when adjusted for the absence of recombination in males, is smaller for the X chromosome.

We determined by simulation how the approximate ascertainment of SNPs in HapMap Phase I could bias our estimates of Ne, and adjusted these accordingly. Recently, Pe’er et al. (2006) have reported small upward biases in the estimation of LD from HapMap I data, consistent with a downward bias in the estimate of Ne. These biases would also affect our analyses and would not have been fully corrected for by our adjustment, which was based upon the allele frequencies of the ascertained SNPs. In addition, if there is variation in recombination rate that has not been reflected in our estimates of c using the three different methods, then our estimate of Ne would be biased downward.

In populations in which effective population size has changed over time, such as human populations, it is not meaningful to discuss effective population size without reference to a point in time (Hayes et al. 2003). For example, assuming a constant Ne when it has increased over time and estimating it from data on marker heterozygosity will result in an estimate of an average Ne over long periods of time, before bottlenecks if these have occurred recently. Methods, including the coalescent-based ones, that fail to take into account that Ne has changed over time will produce biased population parameter estimates, in particular when inference depends on the observed relationship between recombination distance and linkage disequilibrium.

We have used a relatively small sample of individuals, combined with high-density genome-wide marker genotyping, to infer ancestral population size based upon the observed amounts of LD. Our study has shown that human effective population size estimated from entire human chromosomes is considerably lower than previously suggested, at least during a bottleneck up to ∼20,000 yr ago when a large expansion began.

Acknowledgments

We thank W.G. Hill for helpful discussions and help in the derivation of X-linked Ne, and N. Barton, B. Weir, J. Taylor, G. McVean, T. Johnson, and A. Morris for helpful discussions. A.T. acknowledges Cancer Research UK; P.N. was supported by the Genes to Cognition Project; and P.M.V. acknowledges the UK Biotechnology and Biological Sciences Research Council, the Wellcome Trust, and the Australian National Health and Medical Research Council for funding.

Footnotes

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.6023607

References

  1. Altshuler D., Brooks L.D., Chakravarti A., Collins F.S., Daly M.J., Donnelly P., Brooks L.D., Chakravarti A., Collins F.S., Daly M.J., Donnelly P., Chakravarti A., Collins F.S., Daly M.J., Donnelly P., Collins F.S., Daly M.J., Donnelly P., Daly M.J., Donnelly P., Donnelly P. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barrett J.C., Fry B., Maller J., Daly M.J., Fry B., Maller J., Daly M.J., Maller J., Daly M.J., Daly M.J. Haploview: Analysis and visualization of LD and haplotype maps. Bioinformatics. 2005;21:263–265. doi: 10.1093/bioinformatics/bth457. [DOI] [PubMed] [Google Scholar]
  3. Clarke G.M., Cardon L.R., Cardon L.R. Disentangling linkage disequilibrium and linkage from dense single-nucleotide polymorphism trio data. Genetics. 2005;171:2085–2095. doi: 10.1534/genetics.105.047431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Eller E. Estimating relative population sizes from simulated data sets and the question of greater African effective size. Am. J. Phys. Anthropol. 2001;116:1–12. doi: 10.1002/ajpa.1096. [DOI] [PubMed] [Google Scholar]
  5. Erlich H.A., Bergstrom T.F., Stoneking M., Gyllensten U., Bergstrom T.F., Stoneking M., Gyllensten U., Stoneking M., Gyllensten U., Gyllensten U. HLA sequence polymorphism and the origin of humans. Science. 1996;274:1552–1554. [PubMed] [Google Scholar]
  6. Frisse L., Hudson R.R., Bartoszewicz A., Wall J.D., Donfack J., Di Rienzo A., Hudson R.R., Bartoszewicz A., Wall J.D., Donfack J., Di Rienzo A., Bartoszewicz A., Wall J.D., Donfack J., Di Rienzo A., Wall J.D., Donfack J., Di Rienzo A., Donfack J., Di Rienzo A., Di Rienzo A. Gene conversion and different population histories may explain the contrast between polymorphism and linkage disequilibrium levels. Am. J. Hum. Genet. 2001;69:831–843. doi: 10.1086/323612. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Harpending H.C., Sherry S.T., Rogers A.R., Stoneking M., Sherry S.T., Rogers A.R., Stoneking M., Rogers A.R., Stoneking M., Stoneking M. The genetic structure of ancient human populations. Curr. Anthropol. 1993;34:483–496. [Google Scholar]
  8. Hayes B.J., Visscher P.M., McPartlan H.C., Goddard M.E., Visscher P.M., McPartlan H.C., Goddard M.E., McPartlan H.C., Goddard M.E., Goddard M.E. Novel multilocus measure of linkage disequilibrium to estimate past effective population size. Genome Res. 2003;13:635–643. doi: 10.1101/gr.387103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hill W.G. Linkage disequilibrium among multiple neutral alleles produced by mutation in finite population. Theor. Popul. Biol. 1975;8:117–126. doi: 10.1016/0040-5809(75)90028-3. [DOI] [PubMed] [Google Scholar]
  10. Hill W.G. Estimation of effective population size from data on linkage disequilibrium. Genet. Res. 1981;38:209–216. [Google Scholar]
  11. Hill W.G., Robertson A., Robertson A. Linkage disequilibrium in finite populations. Theor. Appl. Genet. 1968;38:226–231. doi: 10.1007/BF01245622. [DOI] [PubMed] [Google Scholar]
  12. Hudson R.R. Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 1983;23:183–201. doi: 10.1016/0040-5809(83)90013-8. [DOI] [PubMed] [Google Scholar]
  13. Hudson R.R. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
  14. The International HapMap Consortium. The International HapMap Project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
  15. Kong X., Murphy K., Raj T., He C., White P.S., Matise T.C., Murphy K., Raj T., He C., White P.S., Matise T.C., Raj T., He C., White P.S., Matise T.C., He C., White P.S., Matise T.C., White P.S., Matise T.C., Matise T.C. A combined linkage–physical map of the human genome. Am. J. Hum. Genet. 2004;75:1143–1148. doi: 10.1086/426405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Liu H., Prugnolle F., Manica A., Balloux F., Prugnolle F., Manica A., Balloux F., Manica A., Balloux F., Balloux F. A geographically explicit genetic model of worldwide human-settlement history. Am. J. Hum. Genet. 2006;79:230–237. doi: 10.1086/505436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lynch M., Walsh B., Walsh B. Genetics and analysis of quantitative traits. Sinauer Associates; Sunderland, MA: 1998. [Google Scholar]
  18. McVean G.A.T. A genealogical interpretation of linkage disequilibrium. Genetics. 2002;162:987–991. doi: 10.1093/genetics/162.2.987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Myers S., Bottolo L., Freeman C., McVean G., Donnelly P., Bottolo L., Freeman C., McVean G., Donnelly P., Freeman C., McVean G., Donnelly P., McVean G., Donnelly P., Donnelly P. A fine-scale map of recombination rates and hotspots across the human genome. Science. 2005;310:321–324. doi: 10.1126/science.1117196. [DOI] [PubMed] [Google Scholar]
  20. Nielsen R., Hubisz M.J., Clark A.G., Hubisz M.J., Clark A.G., Clark A.G. Reconstituting the frequency spectrum of ascertained single-nucleotide polymorphism data. Genetics. 2004;168:2373–2382. doi: 10.1534/genetics.104.031039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Pe’er I., Chretien Y.R., de Bakker P.I.W., Barrett J.C., Daly M.J., Altshuler D.M., Chretien Y.R., de Bakker P.I.W., Barrett J.C., Daly M.J., Altshuler D.M., de Bakker P.I.W., Barrett J.C., Daly M.J., Altshuler D.M., Barrett J.C., Daly M.J., Altshuler D.M., Daly M.J., Altshuler D.M., Altshuler D.M. Biases and reconciliation in estimates of linkage disequilibrium in the human genome. Am. J. Hum. Genet. 2006;78:588–603. doi: 10.1086/502803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pritchard J.K., Seielstad M.T., Perez-Lezaun A., Feldman M.W., Seielstad M.T., Perez-Lezaun A., Feldman M.W., Perez-Lezaun A., Feldman M.W., Feldman M.W. Population growth of human Y chromosomes: A study of Y chromosome microsatellites. Mol. Biol. Evol. 1999;16:1791–1798. doi: 10.1093/oxfordjournals.molbev.a026091. [DOI] [PubMed] [Google Scholar]
  23. Reich D.E., Lander E.S., Lander E.S. On the allelic spectrum of human disease. Trends Genet. 2001;17:502–510. doi: 10.1016/s0168-9525(01)02410-6. [DOI] [PubMed] [Google Scholar]
  24. Reich D.E., Cargill M., Bolk S., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Cargill M., Bolk S., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Bolk S., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Ireland J., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Sabeti P.C., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Richter D.J., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Lavery T., Kouyoumjian R., Farhadian S.F., Ward R., Kouyoumjian R., Farhadian S.F., Ward R., Farhadian S.F., Ward R., Ward R., et al. Linkage disequilibrium in the human genome. Nature. 2001;411:199–204. doi: 10.1038/35075590. [DOI] [PubMed] [Google Scholar]
  25. Relethford J.H., Harpending H.C., Harpending H.C. Craniometric variation, genetic theory, and modern human origins. Am. J. Phys. Anthropol. 1994;95:249–270. doi: 10.1002/ajpa.1330950302. [DOI] [PubMed] [Google Scholar]
  26. Relethford J.H., Jorde L.B., Jorde L.B. Genetic evidence for larger African population size during recent human evolution. Am. J. Phys. Anthropol. 1999;108:251–260. doi: 10.1002/(SICI)1096-8644(199903)108:3<251::AID-AJPA1>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
  27. Rogers A.R., Harpending H., Harpending H. Population growth makes waves in the distribution of pairwise genetic differences. Mol. Biol. Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]
  28. Service S., DeYoung J., Karayiorgou M., Roos J.L., Pretorious H., Bedoya G., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., DeYoung J., Karayiorgou M., Roos J.L., Pretorious H., Bedoya G., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., Karayiorgou M., Roos J.L., Pretorious H., Bedoya G., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., Roos J.L., Pretorious H., Bedoya G., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., Pretorious H., Bedoya G., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., Bedoya G., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., Ospina J., Ruiz-Linares A., Macedo A., Palha J.A., Ruiz-Linares A., Macedo A., Palha J.A., Macedo A., Palha J.A., Palha J.A., et al. Magnitude and distribution of linkage disequilibrium in population isolates and implications for genome-wide association studies. Nat. Genet. 2006;38:556–560. doi: 10.1038/ng1770. [DOI] [PubMed] [Google Scholar]
  29. Sherry S.T., Rogers A.R., Harpending H., Soodyall H., Jenkins T., Stoneking M., Rogers A.R., Harpending H., Soodyall H., Jenkins T., Stoneking M., Harpending H., Soodyall H., Jenkins T., Stoneking M., Soodyall H., Jenkins T., Stoneking M., Jenkins T., Stoneking M., Stoneking M. Mismatch distributions of mtDNA reveal recent human population expansions. Hum. Biol. 1994;66:761–775. [PubMed] [Google Scholar]
  30. Sherry S.T., Harpending H.C., Batzer M.A., Stoneking M., Harpending H.C., Batzer M.A., Stoneking M., Batzer M.A., Stoneking M., Stoneking M. Alu evolution in human populations: Using the coalescent to estimate effective population size. Genetics. 1997;147:1977–1982. doi: 10.1093/genetics/147.4.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sved J.A. Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor. Popul. Biol. 1971;2:125–141. doi: 10.1016/0040-5809(71)90011-6. [DOI] [PubMed] [Google Scholar]
  32. Takahata N. Allelic genealogy and human evolution. Mol. Biol. Evol. 1993;10:2–22. doi: 10.1093/oxfordjournals.molbev.a039995. [DOI] [PubMed] [Google Scholar]
  33. Templeton A.R. Out of Africa again and again. Nature. 2002;416:45–51. doi: 10.1038/416045a. [DOI] [PubMed] [Google Scholar]
  34. Thomson R., Pritchard J.K., Shen P.D., Oefner P.J., Feldman M.W., Pritchard J.K., Shen P.D., Oefner P.J., Feldman M.W., Shen P.D., Oefner P.J., Feldman M.W., Oefner P.J., Feldman M.W., Feldman M.W. Recent common ancestry of human Y chromosomes: Evidence from DNA sequence data. Proc. Natl. Acad. Sci. 2000;97:7360–7365. doi: 10.1073/pnas.97.13.7360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Visscher P.M., Hill W.G., Hill W.G. Estimation of recombination rate and detection of recombination hotspots from dense single-nucleotide polymorphism trio data. Genetics. 2006;173:2415–2417. doi: 10.1534/genetics.106.056531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Watkins W.S., Ricker C.E., Bamshad M.J., Carroll M.L., Nguyen S.V., Batzer M.A., Harpending H.C., Rogers A.R., Jorde L.B., Ricker C.E., Bamshad M.J., Carroll M.L., Nguyen S.V., Batzer M.A., Harpending H.C., Rogers A.R., Jorde L.B., Bamshad M.J., Carroll M.L., Nguyen S.V., Batzer M.A., Harpending H.C., Rogers A.R., Jorde L.B., Carroll M.L., Nguyen S.V., Batzer M.A., Harpending H.C., Rogers A.R., Jorde L.B., Nguyen S.V., Batzer M.A., Harpending H.C., Rogers A.R., Jorde L.B., Batzer M.A., Harpending H.C., Rogers A.R., Jorde L.B., Harpending H.C., Rogers A.R., Jorde L.B., Rogers A.R., Jorde L.B., Jorde L.B. Patterns of ancestral human diversity: An analysis of Alu-insertion and restriction-site polymorphisms. Am. J. Hum. Genet. 2001;68:738–752. doi: 10.1086/318793. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Weir B.S., Hill W.G., Hill W.G. Effect of mating structure on variation in linkage disequilibrium. Genetics. 1980;95:477–488. doi: 10.1093/genetics/95.2.477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zhang W.H., Collins A., Gibson J., Tapper W.J., Hunt S., Deloukas P., Bentley D.R., Morton N.E., Collins A., Gibson J., Tapper W.J., Hunt S., Deloukas P., Bentley D.R., Morton N.E., Gibson J., Tapper W.J., Hunt S., Deloukas P., Bentley D.R., Morton N.E., Tapper W.J., Hunt S., Deloukas P., Bentley D.R., Morton N.E., Hunt S., Deloukas P., Bentley D.R., Morton N.E., Deloukas P., Bentley D.R., Morton N.E., Bentley D.R., Morton N.E., Morton N.E. Impact of population structure, effective bottleneck time, and allele frequency on linkage disequilibrium maps. Proc. Natl. Acad. Sci. 2004;101:18075–18080. doi: 10.1073/pnas.0408251102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zhivotovsky L.A., Rosenberg N.A., Feldman M.W., Rosenberg N.A., Feldman M.W., Feldman M.W. Features of evolution and expansion of modern humans, inferred from genomewide microsatellite markers. Am. J. Hum. Genet. 2003;72:1171–1186. doi: 10.1086/375120. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES