Abstract
An important industrial problem that provides fascinating puzzles in pattern formation is the tendency for granular mixtures to de-mix or segregate. Small differences in either size or density lead to flow-induced segregation. Similar to fluids, noncohesive granular materials can display chaotic advection; when this happens chaos and segregation compete with each other, giving rise to a wealth of experimental outcomes. Segregated structures, obtained experimentally, display organization in the presence of disorder and are captured by a continuum flow model incorporating collisional diffusion and density-driven segregation. Under certain conditions, structures never settle into a steady shape. This may be the simplest experimental example of a system displaying competition between chaos and order.
The understanding of the fundamentals of granular mixing is incomplete, particularly when compared with that of fluid mixing (1). Mixing of granular materials is important in industry and natural processes; industrial examples appear in the pharmaceutical, food, chemical, ceramic, metallurgical, and construction industries (2–4); examples in nature may include the formation of sedimentary structures and debris flows (5). What makes mixing of granular materials complex is that, under flow, granular materials often segregate. The understanding of prototypical systems yields, however, considerable insight.
Recently it was shown that chaotic advection can be generated in granular flows of noncohesive particles. This concept was investigated experimentally and computationally in pseudo two-dimensional rotating containers of different shapes (6).
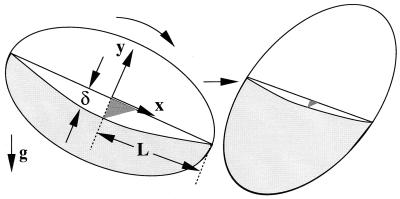
Consider the system depicted in Fig. 1. Under suitable conditions, easy to achieve in the laboratory, the flow of noncohesive granular materials moves in a continuous flow, the so-called rolling regime. The flow is confined to the top free surface in the form of a thin shear-like flat layer whereas the rest of the material moves in solid-like rotation with the mixer walls. Material is fed into the flowing layer with thickness δ (x) for x<0 and leaves the layer for x>0. The simplest case is a circle rotating at a constant speed ω. In this case L, δ, and the streamlines are time invariant. A two-dimensional flow can be derived from a streamfunction ψ, such that vx = ∂ψ/∂y, vy = −∂ψ/∂x. If the flow is steady, ψ = ψ(x,y) and the streamlines coincide with the pathlines. The structure of such a flow is Hamiltonian with one degree of freedom, and therefore it cannot be chaotic (1). However, if the container is noncircular, the velocity is time periodic, ψ = ψ(x,y,t) = ψ(x,y,t+T), and the flowing layer grows and shrinks in time. The system has one-and-a-half degrees of freedom, and chaotic advection is possible (1, 7, 8). Experimental studies using colored tracer particles in mono-disperse granular materials show that increased mixing rates occur in noncircular containers (6).
Figure 1.
Instantaneous view of continuous granular flow in a rotating container. The curve denotes the interface, δ(x,t), between the flow layer at time t and the region of solid body rotation. As the container changes orientation, the length, L(t), and the depth of the layer, δ, change in a time-periodic manner.
On the other hand there may be unmixed regions. Because the system is time-periodic, a nonlinear mapping, F(.), may be used to represent particle motion. A periodic point of order n of the mapping F, is a point such that a particle initially located at p returns to p after n periods; that is, p = Fn(p), where the n is the smallest value satisfying the equality (1). Periodic elliptic points are surrounded by Kolmogorov-Arnold-Moser (KAM) curves and form regular regions or islands where there is no chaos (7, 8). Although islands undergo a net rotation, they preserve identity and contain always the same material. They represent the primary obstacle to mixing.
Differences in particle properties make the system’s behavior considerably more interesting from a dynamical systems viewpoint. It is well known that small differences in size and/or density of the particles of the granular material lead to flow-induced de-mixing or segregation (9). In circular mixers this often leads to radial segregation (Fig. 2f) (10–12). The normal to the streamfunction, ∇ψ, and the gradient of concentration, ∇f, are colinear. Thus, a radially segregated structure in a circle is an invariant structure. In long cylinders axial banding may result (relatively pure, single-component bands along the axis of rotation) (13–15). In noncircular mixers, the dynamics are much more complex as there is no simple relationship between ∇ψ and a radially segregated structure.
Figure 2.
Experimental and theoretical results for half-full quasi two-dimensional tumbling mixers. E denotes experimental results; C denotes computational results, and P denotes computationally obtained Poincaré sections for a system of equal size and density particles. The Poincaré sections represents the evolution of strategically selected initial conditions (continuum particles) identified with different colors. The positions of the particles are marked after every half-revolution (quarter-revolution for the square). All images are taken while the mixer is rotated, though the images of the square are rotated counter-clockwise by ≈30° to maximize the use of space. The mixtures consist of binary D-systems (2-mm glass and steel spheres) and ternary S-systems (0.8-mm blue, 1.2-mm clear, and 2.0-mm red glass spheres). The volume fraction of steel/glass beads in the D-system is ¼:¾, and the volume fraction of the small/medium/large beads in the S-system is ½:¾:¾. Computational results are shown for binary mixtures of D-systems. The last two columns show the variation in the Poincaré sections and the segregation patterns when the filling level is changed about one-half for the square mixer. The results are similar for the ellipse. The pattern in the circular mixer remains radially segregated state for all filling levels examined. The Poincaré sections reveal that the flow patterns and, particularly, the locations of the elliptic and hyperbolic points, are sensitive to fill level about one-half, where several bifurcations occur. The corresponding entries in rows 2 and 3 show the long-term segregation patterns for just under and just over half-full. Because of instabilities in the flow discussed in the text, the 55% full S-systems never reach a final segregated pattern, but instead have changing patterns of streaks. In the last row images are shown for equilibrium structures in ¼-full and ¾-full mixers.
In this paper we present the results of experiments on the interaction between chaotic mixing and segregation in two kinds of systems: systems with particles of the same size and different densities (D-systems) and systems with particles of the same density and different size (S-systems). The emphasis of the experimental studies is on two-dimensional systems and the computations presented are restricted to D-systems. In the experiments the material is confined by two closely spaced walls (aspect ratio ≈1/40) and thus cannot be strictly regarded as a thin slice of the full three-dimensional case (the density, for example, is expected to be significantly affected by the walls). The implications of the results for the three-dimensional case are discussed at the end. Consider now the model used to investigate the behavior of these systems.
The Model
The starting point of the model is given in ref. 16; it applies to mixing of noncohesive identical powders. The model describes the flow in the continuous-flow regime where the flowing layer is steady, thin, and nearly flat, the rest of the particles moving in solid body rotation. (The case for slower avalanching flow is treated in ref. 17.) The point of departure is a half-full cylinder.
Kinematic considerations, and assuming the density in the bed and the layer to be nearly the same, give the volumetric flow rate of particles per unit width in the layer as in ref. 18:
 |
1 |
A boundary layer analysis of the flow (16), assuming a velocity profile of the form
 |
2 |
and a frictional-collisional equation for the stress yields the mean velocity in the x-direction, u(x), and consequently the layer thickness profile δ(x) = Q/u. Computations, supported by experiments, show u ≈ constant for −L<x<L so that δ = δ0(1 − x2/L2) and u = ωL2/(2δ0), where δ0 = δ(0). Mass conservation then gives
 |
3 |
The model has a single parameter, δ0, which is obtained from flow visualization experiments. For an alternate analysis, see ref. 19.
Adaptation to noncircular mixers requires that L be time dependent. For example, for an elliptical mixer:
 |
4 |
where a and b are the major and minor semi-axes of the ellipse, respectively, and α is the angle between the free surface and the major axis of the ellipse at t = 0. Experiments (6) show that the layer maintains geometric similarity, so that δ0(t)/L(t) is a constant while u ≈ L changes with mixer orientation; the longer the layer, the faster and deeper the flow.
Eqs. 2 and 3 allow for the computation of particle pathlines, blob deformation, and Poincaré sections by integration of dx/dt = vx and dy/dt = vy with initial conditions x = X and y = Y at t = 0. As is standard in fluid mechanics, in the computation of Poincaré sections the flow is interpreted in a continuum sense and collisional diffusion is not included. In the case of a circle (Fig. 2a) the streamlines act as barriers to convective mixing; diffusion controls and mixing are slow. Noncircular cases are more interesting. Fig. 2 b and c shows the Poincaré sections for a half-filled ellipse and square, respectively, illustrating KAM islands (marked in red) and chaotic regions where convective mixing enhances diffusional mixing. We remark that additional computations indicate that different velocity fields, for example vx∼y3/2, vy∼xy5/2, inspired by the Bagnold profile, give essentially the same mixing patterns, demonstrating that macroscopic geometrical effects (i.e., the shape of the container) control the important details of the physics.
The effect of collisional diffusion is incorporated in terms of the model developed by Savage (20). The collisional diffusion, Dcoll, is given by
 |
5 |
where dvx/dy is the velocity gradient across the layer, and d is the particle diameter. The prefactor g(η), obtained by Savage via particle dynamics simulations, is a function of the solids volume fraction, η; in our simulations we assume Dcoll to be a constant and take g = 0.025 obtained by fitting to experimental data for mixing of identical particles in a rotating cylinder. In terms of our model, Eq. 5 becomes Dcoll = 0.025d2 ωL2/δ02; we use the value at x = 0. The physical picture is as follows: a blob initially placed in the shear layer is deformed into a filament by the shear flow and blurred by collisional diffusion until particles exit the layer. Particles then execute a solid body rotation in the bed and re-enter the layer, and the process repeats.
Collisional diffusion enters as a Langevin term in the particle advection equations. Denote by S a white-noise term such that upon integration over a time interval (Δt) it gives a Gaussian random number with variance 2DcollΔt. The term S is added to the right side of Eq. 3. Diffusion along the x-direction is neglected. In our experiments the Péclet number along the layer, uL/Dcoll (a measure of the relative importance of convection to diffusion) is about 102. The Péclet number in the direction normal to the flow is factor (δ0/L)2 smaller (∼0.0025). Thus, diffusion is important only in the y-direction.
Consider D-systems. The effects of segregation are incorporated in terms of drift velocities with respect to the mean mass velocity (21). The effects of segregation, as well as those of collisional diffusivity described earlier, are significant only in the direction normal to the flow (apparent, again, when the Péclet numbers in each direction are considered). The segregation velocity for the more dense particles (labeled 1) can be written as
 |
6 |
and for the less dense particles (labeled 2) as
 |
7 |
Here, β is the so-called dimensionless segregation velocity (21), ρ̄ is the density ratio, d is the particle diameter, and f(x,y,t) is the number fraction of the more dense particles. Similar expressions can be obtained for the case of systems differing in size, at low solids volume fractions (22). For elastic particles, β is inversely proportional to the granular temperature; however, for real particles a simple expression for β is not available and we treat it as a fitting parameter. In our simulations we take β = 2. This model has been tested in circular (nonchaotic) containers (21).
To add segregation into the advection model, assume first that the mean flow is still the same as if all particles were identical, so that Eqs. 2 and 3 still apply. This is reasonable for equal-sized particles with different density, however, for mixtures of different-sized particles the flow is significantly affected by the composition of the layer, and consequently the velocity field and concentration field are coupled. There are however, two kinds of advection equations, for particles 1 and 2. The y-component of the dynamical system representing the motion of the more dense particles (labeled 1) is:
 |
8 |
whereas for the less dense particles (labeled 2), Eq. 8 becomes:
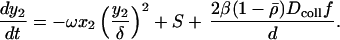 |
9 |
The two equations given above together with the corresponding equations for the x coordinates for each of the species describe the evolution of the two interpenetrating continua from a Lagrangian viewpoint. Computations using this formulation are straightforward. A large number of particles (from a continuum viewpoint) is randomly distributed in the domain and advected according to the equations of motion for each type of particle. The number fraction field, f(x,y,t), is determined by defining a grid and calculating the fraction of the more dense particles in each bin of the grid.
Experimental Details
Experiments on D- and S-systems were conducted by using a variety of noncohesive spherical beads (Quackenbush, Crystal Lake, IL) with sizes ranging from 0.8 to 2 mm and densities of 2.5 and 7.8 g/cm3 (glass and steel, respectively). The areas of the circular, square, and elliptical mixers are all the same. The ratio of the minor to major axis of the ellipse is 0.5. The square mixer has side length of 25 cm. The depth of all mixers is 6 mm. The faceplate of the mixer is Plexiglas while the rear plate is fashioned of aluminum and is grounded to minimize electrostatic effects.
All systems are initially well mixed. A computer-controlled stepper motor (Compumotor, Rohnert Park, CA) rotates the mixers at approximately 1 revolution per min so that a steady flow with a flat free surface is developed. The Froude number, F = ω2L/g, is about 0.0002 for the circle. Images were obtained with a Kodak charge-coupled device camera for quantitative image analysis.
Results
Fig. 2 shows segregation structures produced by D-systems (Fig. 2 f–j) and S-systems (Fig. 2 k–o). It is apparent that the shape of the container plays a significant role in determining the segregation structures for the different systems. The classic radially segregated structure (circular mixers) is shown in Fig. 2 f and k. In this case, the dynamics in the flowing layer cause the smaller (more dense) particles to move down in the layer. These particles have a low probability of reaching the end of the layer, leading to a segregated core. A circular core is time invariant, because it coincides with the streamlines. The segregation structures obtained in noncircular mixers do not follow this simple rule. This is quite evident in the case of a half-filled square mixer (Fig. 2 h and m). A region with a high concentration of the small (dense) particles is located away from the center of rotation and is nearly separated into two separate regions nearly spanning the corners of the square and the center of rotation. The corresponding segregation structure for the ellipse also shows that the smaller (denser) particles are pulled away from the center of rotation. The shape of the segregated region is periodic in time and depends on the instantaneous orientation of the mixer.
Experiments show that initially all D- and S-systems radially segregate (see insets in Fig. 3a). Some systems stay radially segregated whereas others evolve into more complicated patterns. The steady-state (and non-steady-state) segregation patterns are quite sensitive to fill level in both square and elliptical containers. In this work we focus primarily on the square container at one-half fill. Fig. 2 d and e illustrates that several bifurcations occur in the Poincaré section for the square mixer near the one-half level. An analysis based on symmetry considerations (23) shows that there are critical transition points at 25% and 75%. At these levels, the radially segregated pattern continues to evolve until it reaches steady segregation patterns resembling the Poincaré sections with segregated regions of small (dense beads) aggregating in and around the regular islands. We find that in ternary S-systems the intermediate size particles concentrate in the periphery of the islands.
Figure 3.
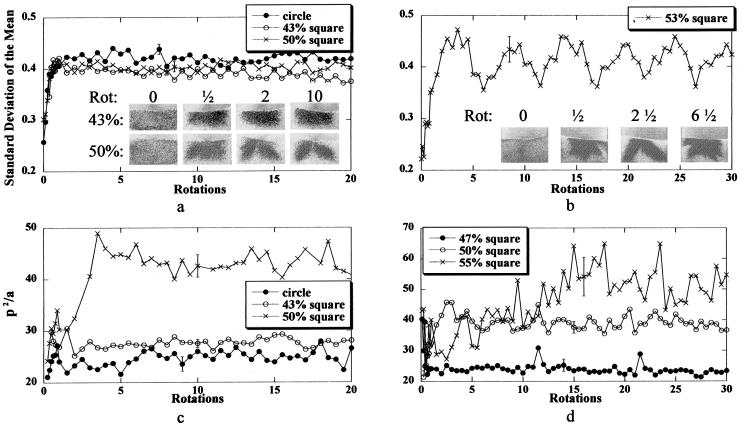
Measurements of the segregation pattern for D- and S-systems in the half-full circular mixer and at different fill levels in the square mixer as noted. Experimental figures are not square to focus on the granular patterns and maximize the use of space. The SEM (a and b) reflects the degree of segregation and does not distinguish between different equilibrium segregation patterns as shown in the inset (a). This method does reflect oscillations of the degree of segregation for unstable segregation patterns found near the half-full level (b). The nondimensional measure p2/a described in the text captures the different segregation structures (c and d). Measurements were taken for the region of the segregated structure of 75% or greater dense beads. Compare results in c with the images in the inset of a, and compare results for d with the images in Fig. 4. The error bars represent the variance of the results from their mean values once the segregated structure reached its equilibrium state (after five full rotations). For 55%, the segregated structures never reach equilibrium.
Both the D- and S-systems in square mixers show leg patterns at 25%, 50%, and 75% resembling the Poincaré sections. There are substantial differences in behavior though. S-systems develop segregated streaks, whereas D-systems do not. For S-systems the segregation patterns formed just above the one-half fill level never reach a stable pattern, but instead vary with time where materials segregate into streaks. Changing the percentage of dense beads in D-systems results in a quantitative change in size of islands formed; qualitatively the systems remain the same. Changing the percentage of small beads in S-systems, however, results in qualitatively different patterns, particularly near half full. A higher percentage of small beads results in an increased appearance of stripes (Fig. 2f).
Analysis.
The analysis is based on two types of information: (i) assessment of the degree of mixing in the different systems and (ii) determination of some aspects of pattern structure. Both measures rely on quantitative image analysis. The most common measure of mixing is the SD of the concentration fluctuations about the mean concentration—the so-called intensity of segregation (24). For the systems in this study, this measure of segregation captures the initial radial segregation but, in general, fails to capture differences in spatial structure (see Fig. 3a). It does however, capture the oscillations between a radially segregated pattern and pattern reflecting the regular islands in the Poincaré sections (Fig. 3b).
The measure of pattern structure selected is p2/a; p corresponds to the length of an iso-concentration line c(x,y) = K, with K being a suitable threshold, and a being the area enclosed by c(x,y) (in our image analysis studies we take K = 0.75, i.e., regions of segregation containing 75% or greater concentration of dense beads). For a semicircle p2/a = (2/π)(2+π)2 ≈ 17. Deviations from purely radial segregation increase the value of p2/a. We observe that the values for the square filled 43% full and 50% full and a circle remains nearly constant, between 20 and 25 (Fig. 3c). The equilibrium values for a half-filled square rise to nearly 40 and becomes erratic for the irregular stripping pattern for 55% full S-systems (Fig. 3d). In general the value of p2/a oscillates depending on the orientation of the mixer. All measurements correspond to the orientation shown in the insets of Fig. 3 a and b.
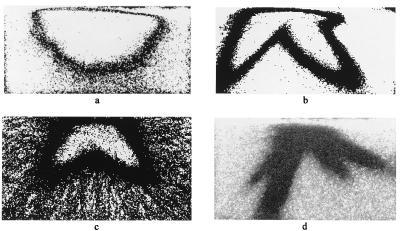
A direct way to distinguish steady and nonsteady structures is by superposition of the contours of isoconcentration regions (Fig. 4) obtained via image analysis. Denote the perimeter by p(x,y,t). Steady (or time-periodic) structures correspond to p(x,y,t) = p(x,y,t+T), where T denotes the time of return of the mixer shape to the same orientation (Fig. 4 a and b). We note that T is a function of the symmetries of the container; in square it is 90°, in ellipses 180°. Other structures do not return to their initial locations. An example is a 55% full square mixer (see Fig. 4d). The superposition of snapshots of this system show that, over time, the fingers occupy most regions in the square resulting in Fig. 4c.
Figure 4.
Examples of equilibrium (a), periodic (b), and nonequilibrium structures (c). The superposition of iso-concentration contours shows an invariant structure in a whereas in the nonequilibrium case the fingers of the segregated region cover the entire domain in just 10 rotations. (d) An instantaneous view corresponding to c.
Discussion.
In the systems described above chaotic advection interacts in nontrivial ways with segregation and serves as a prototype as a simple experimental system displaying organization in the presence of disorder (25). The experiments are remarkably simple. A few comments, however, seem in order because care is needed in the interpretation of the results.
The results displayed in Figs. 2 and 3 are representative of a much larger body of work. The analysis is based on two types of experimental information: degree of mixing and p2/a; both are subject to experimental errors. The data analysis is based on digital images taken during the run and assumes that the concentration of the lighter particles is proportional to the light intensity in the images. Deviations from linearity are caused by particle shadows and uneven light reflection. The major error, however, is caused primarily by variation in initial conditions from run to run. While the beads start out approximately well mixed, it is manifestly impossible to produce the exact same condition twice. This variability can make a big difference in the initial portions of the run. The long-term results, however, are highly reproducible.
We note also that the segregation patterns resemble the Poincaré sections with heavier (smaller) particles tagging the regular regions in the flow, which allows for a rough experimental estimate of the Poincaré section of the flow. This is significant and is described in more detail below. Observe also that while the more dense or smaller particles (depending on the mixture) appear to occupy the positions of greatest stability in the mixer (in and near regular islands), in general, they do not occupy the positions of lowest kinetic energy as is the case for radial segregation.
The Lagrangian formulation is useful for interpreting the behavior of the system. The simplest case is when there is no diffusion (S = 0). Note first that the introduction of the segregation drift velocity results in a qualitative change in the dynamical behavior of the system. In the case of a binary system (see Eqs. 8 and 9) we calculate ∇⋅v1 = ∇⋅v2 = 2β(1 − ρ̄)/d(∂f/∂y), where v1 and v2 are velocities in phase space of species 1 and 2. Thus, the space for each species contracts in the layer as the larger particles sink to lower y values (i.e., ∂f/∂y < 0). In pure regions, f = 0, 1, the segregation velocities vanish and volume is conserved. The case of circular mixers is easily visualized. The denser particles sink to lower positions in the layer while lighter particles rise, which translates into a radial motion with the denser particles moving to the central core and the less dense moving to the periphery. Such motion continues in regions that contain both species. However, in pure regions (f = 0,1) the segregation drift velocity vanishes and the motion of the particles coincides with the streamlines of the one component system. At equilibrium there is complete segregation with all of the denser particles in the central core and all of the lighter particles in the periphery, the boundary between the two being given by the streamline bounding an area fraction equal to the volume fraction of the denser beads.
In noncircular mixers there is also an initial tendency for the dense particles to move to form a central core and for the lighter particles to migrate to the periphery. However, in this case streamlines are not invariant curves, and thus the core is distorted and mixed because of advection. The key to the structure formation lies in the invariant curves of the mapping. An invariant curve composed entirely of one of the species is preserved by the mapping (which now coincides with that for a single component because the segregation velocity vanishes). Thus, the structure formed is determined by the surviving KAM curves of the Poincaré section for the single-component system. The region within the outermost KAM curve enveloped by the core formed by the dense particles is invariant as is the peripheral pure region of light particles outside the innermost KAM curve. The effect of diffusion is primarily to blur the structures. When the core size exceeds that of the invariant region, chaotic advection and diffusion act in concert to mix the particles outside the invariant region.
We observe also that the Poincaré sections are symmetric but the segregation patterns are often asymmetric, which is most obvious in the case of the ellipse (Fig. 2 g and l). Poincaré sections are computed for a system of identical particles (i.e., a base continuum description of the granular flow). When mixtures of particles of different densities are used, the trajectory of the heavier particles deviates from this “base case,” owing to their segregation velocity, and this deviation is always downward in the flowing layer, which leads to the asymmetry observed in the computations (see Fig. 2q).
The computations presented apply to D-systems. The discussion can be extended to S-systems. Instead of a segregation velocity caused by a difference in mass, different-sized particles have a differential probability of percolation within the flowing layer; smaller particles fall through the gaps between the larger particles. Constitutive models for mixtures of different-sized particles can be incorporated into advection-diffusion computations. The models available, however, apply to specific regimes, for example, when the density is low, and are not as robust as the ones for segregation caused by density (22).
S-systems introduce additional important physical effects; unlike the case of D-systems, the flow in the layer changes (noticeably) according to the particles present. For example, if the flowing layer consists entirely of small particles, it is thinner and moves faster. Conversely, larger particles form a deeper and slower flowing layer. The velocity field is coupled to the composition of the particles in the layer. A consequence of the coupling between velocity and concentration is the radial streak structure shown in Fig. 2o. This instability resembles that observed in a two-dimensional sand pile (26–28). We noticed that this happens in mixers that filled just above the one-half level. In this case, each entire stripe enters the flowing layer all at the same time, so that the instability is reinforced. This phenomenon appears to be independent of the underlying Poincaré section; it occurs in mixers of all shapes.
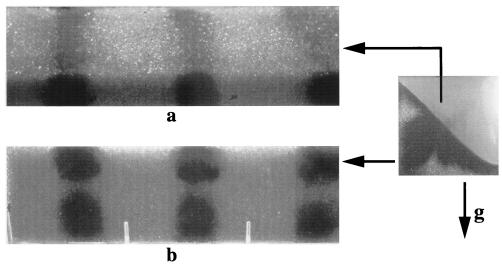
One might ask to what extent these results apply to the full three-dimensional case, long drum mixers where axial segregation occurs (Fig. 5). The insights obtained above appear to be valuable. Previously, it has been suggested that radial segregation (observed in the circular mixer) is a necessary precursor to axial segregation (29). Because in the two-dimensional square mixer we do not observe radial segregation for more than one revolution, this finding would suggest that either axial segregation should not exist in a three-dimensional square mixer, or the two-arm patterm shown in Figs. 2 and 4 is merely an artifact of the two-dimensional case. However, neither is true. We conducted experiments in 30-in long drum mixers with a 5-inch square cross-section. When the degree of filling is one-half, not only did axial segregation occur (Fig. 5a), but the axial segregated patterns show unmistakable signs of the two-arm structure (Fig. 5b). Thus it appears that radial segregation is not a necessary condition for axial segregation. The full implications of the two-dimensional patterns discovered here on mixing in long cylinders, however, await full investigation. It is also apparent that the physics underlying the simpler two-dimensional chaotic-segregating systems considered here is quite complex. The results presented may be only part of a much richer inventory of possible behaviors.
Figure 5.
Axial segregation observed in a three-dimensional square drum mixer (aspect ratio 6). The views correspond to the orientation shown to the right. The standard axial segregation pattern is clearly observed in the top flowing layer (a), while the two lobes seen in the two-dimensional square mixer are evident on side views of the mixer (b).
Acknowledgments
This work was supported by the Engineering Research Program of the Office of Basic Energy Sciences of the Department of Energy, the National Science Foundation, Fluid, Particle and Hydraulic System, and the Petroleum Research Fund, Administered by the American Chemical Society. D.V.K. acknowledges the support of the Department of Science and Technology, India through award of the Swarnajayanti Fellowship (DST/SF/8/98).
Abbreviation
- KAM
Kolmogorov-Arnold-Moser
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Ottino J M. The Kinematics of Mixing: Stretching, Chaos, and Transport. Cambridge, U.K.: Cambridge Univ. Press; 1989. [Google Scholar]
- 2.Bridgwater J. Chem Eng Sci. 1995;50:4081–4089. [Google Scholar]
- 3.Cooke M H, Stephens D J, Bridgwater J. Powder Technol. 1976;15:1–15. [Google Scholar]
- 4.Fan L T, Chen Y-M, Lai F S. Powder Technol. 1990;61:255–277. [Google Scholar]
- 5.Hashimoto H, Tsubaki T. Trans Japan Soc Civ Eng. 1985;15:282–284. [Google Scholar]
- 6.Khakhar D V, McCarthy J J, Gilchrist J F, Ottino J M. Chaos. 1999;9:195–205. doi: 10.1063/1.166390. [DOI] [PubMed] [Google Scholar]
- 7.Lichtenberg A J, Lieberman M A. Regular and Stochastic Motion. New York: Springer; 1983. [Google Scholar]
- 8.Hilborn H C. Chaos in Nonlinear Systems. New York: Oxford Univ. Press; 1994. [Google Scholar]
- 9.Rosato A, editor. Segregation in Granular Flows: International Union of Theoretical and Applied Mechanics Symposium, June 5–10, 1999. Dordrecht, The Netherlands: Kluwer; 1999. , in press. [Google Scholar]
- 10.Ristow G H. Europhys Lett. 1994;28:97–101. [Google Scholar]
- 11.Cantelaube F, Bideau D. Europhys Lett. 1995;30:133–138. [Google Scholar]
- 12.Dury C M, Ristow G H. J Phys (France) 1997;7:737–745. [Google Scholar]
- 13.Donald M B, Roseman Br Chem Eng. 1962;7:749–752. [Google Scholar]
- 14.Das Gupta S, Khakhar D V, Bhatia S K. Chem Eng Sci. 1991;46:1513–1517. [Google Scholar]
- 15.Hill K M, Kakalios J. Phys Rev E. 1995;52:4393–4400. doi: 10.1103/physreve.52.4393. [DOI] [PubMed] [Google Scholar]
- 16.Khakhar D V, McCarthy J J, Shinbrot T, Ottino J M. Phys Fluids. 1997;9:31–43. [Google Scholar]
- 17.Metcalfe G, Shinbrot T, McCarthy J J, Ottino J M. Nature (London) 1995;374:39–41. [Google Scholar]
- 18.Rajchenbach J. Phys Rev Lett. 1990;65:2221–2224. doi: 10.1103/PhysRevLett.65.2221. [DOI] [PubMed] [Google Scholar]
- 19.Elperin T, Vikhansky A. Europhys Lett. 1998;42:619–623. [Google Scholar]
- 20.Savage S B. In: Disorder and Granular Media. Bideau D, Hansen A, editors. Amsterdam: Elsevier; 1993. pp. 255–285. [Google Scholar]
- 21.Khakhar D V, McCarthy J J, Ottino J M. Phys Fluids. 1997;9:3600–3614. [Google Scholar]
- 22.Khakhar D V, McCarthy J J, Ottino J M. Chaos. 1999;9:594–610. doi: 10.1063/1.166433. [DOI] [PubMed] [Google Scholar]
- 23.Franjione J G, Ottino J M. Philos Trans R Soc London. 1992;338:301–323. [Google Scholar]
- 24.Danckwerts P V. Appl Sci Res A. 1952;3:279–296. [Google Scholar]
- 25.Goldenfeld N, Kadanoff L P. Science. 1999;284:87–89. doi: 10.1126/science.284.5411.87. [DOI] [PubMed] [Google Scholar]
- 26.Makse H A, Cizeau P, Stanley H E. Phys Rev Lett. 1997;78:3298–3301. [Google Scholar]
- 27.Koeppe J P, Enz M, Kakalios J. Phys Rev E. 1998;58:R4104–R4107. [Google Scholar]
- 28.Makse H A, Havlin S, King P R, Stanley H E. Nature (London) 1997;386:379–382. [Google Scholar]
- 29.Hill K M, Caprihan A, Kakalios J. Phys Rev Lett. 1997;78:50–53. [Google Scholar]