The Genetic Structure of Drosophila ananassae Populations From Asia, Australia and Samoa

Abstract

Information about genetic structure and historical demography of natural populations is central to understanding how natural selection changes genomes. Drosophila ananassae is a widespread species occurring in geographically isolated or partially isolated populations and provides a unique opportunity to investigate population structure and molecular variation. We assayed microsatellite repeat-length variation among 13 populations of D. ananassae to assess the level of structure among the populations and to make inferences about their ancestry and historic biogeography. High levels of genetic structure are apparent among all populations, particularly in Australasia and the South Pacific, and patterns are consistent with the hypothesis that the ancestral populations are from Southeast Asia. Analysis of population structure and use of F-statistics and Bayesian analysis suggest that the range expansion of the species into the Pacific is complex, with multiple colonization events evident in some populations represented by lineages that show no evidence of recent admixture. The demographic patterns show isolation by distance among populations and population expansion within all populations. A morphologically distinct sister species, D. pallidosa, collected in Malololelei, Samoa, appears to be more closely related to some of the D. ananassae populations than many of the D. ananassae populations are to one another. The patterns of genotypic diversity suggest that many of the individuals that we sampled may be morphologically indistinguishable nascent species.

THE impact of population subdivision on levels and patterns of DNA sequence variation across chromosomes is central to our understanding of genome evolution. Although we have learned a great deal about the effects of natural selection on genome variation from studies of model organisms such as Drosophila melanogaster and D. simulans, these organisms provide limited insight into the influence of gene flow on genome variation because natural populations appear to be essentially panmictic outside of Africa. Drosophila ananassae is also a cosmopolitan species but, in contrast to D. melanogaster and D. simulans, populations throughout its geographic range are highly structured. A sibling species (D. pallidosa; Bock and Wheeler 1972) has been recorded in the Fijian–Samoan Islands. The body coloration of D. ananassae is, furthermore, thought to be variable throughout its range (McEvey et al. 1987). It is the only cosmopolitan species of Drosophila that has been studied extensively by geneticists, has a completed genome sequence, and exists in highly structured populations throughout its geographic range (reviewed in Tobari 1993; Das et al. 2004). Like D. melanogaster and D. simulans, D. ananassae is found most frequently in association with humans and, outside Southeast Asia, rarely in natural habitats (Bock and Parsons 1978). Ancestral populations of D. ananassae are believed to be from Southeast Asia (Dobzhansky 1972; Vogl et al. 2003; Das et al. 2004). Range expansion away from Southeast Asia is suspected on the basis of both isozymes (Johnson et al. 1966; Johnson 1971) and DNA sequence polymorphism (Vogl et al. 2003; Das et al. 2004).

Genetic studies of D. ananassae have revealed intriguing evidence that natural selection has a significant impact on genome variation among populations. For examples, studies of single nucleotide polymorphism at three randomly chosen genes on the X chromosome of four D. ananassae populations from Sri Lanka, Bhubaneshwar, Mandalay, and Kathmandu have found that natural selection may be involved in generating and maintaining the genetic differentiation among populations (Stephan and Langley 1989; Stephan et al. 1998; Chen et al. 2000). At Om(1D), which is in a region of the X chromosome with normal rates of recombination, a pattern of isolation by distance and low genetic differentiation was observed. In contrast, at vermilion and furrowed, which are in regions of the X chromosome with low rates of recombination, high genetic differentiation was observed. Patterns of variation at vermilion and furrowed deviated significantly from neutral expectations and were best explained by selection of positive mutations (selective sweeps). The strong signals of selection at furrowed appear throughout a larger geographic range of the species and likely represent two independent selection events consistent with positive Darwinian selection (Baines et al. 2004). These studies suggest that, historically, gene flow has been limited by geographic distance among populations in and around India and that adaptive mutations have had a significant influence on molecular variation across broad regions of the genome.

One approach to differentiating the effects of natural selection and demographic processes, such as migration and population size fluctuations, on genetic variation is to use rapidly evolving genetic markers spread across the genome to infer the influences of genetic drift and migration by inferring the ancestry of the populations and the demographic events that have influenced genome variation as the species colonized and adapted to new geographic regions. This information can then be used as a framework for interpreting patterns of variation at individual genes whose pattern of genetic variation has been determined by natural selection. The development of powerful Bayesian-based approaches (Pritchard et al. 2000; Corander et al. 2003) to detect population structure in multilocus data sets makes D. ananassae an ideal species for determining the relative impacts of population structure and natural selection on genome variation in natural populations. Studies of DNA sequence variation in D. ananassae to date have not included populations from the South Pacific islands, which have been colonized by humans for the past 4000 years. Previous studies of isozymes, chromosomal polymorphisms, and morphology suggest that D. ananassae in the South Pacific are genetically diverse, are highly structured, and have a recent ancestry (Tobari 1993). The recent origin, the potential for current gene flow via human traffic, and the past estimates of genetic and morphological diversity suggest that South Pacific populations may provide additional insight into the impact of colonization, migration, and adaptive evolution on genome variation in very recently established populations.

Here we analyze repeat-length variation at 23 dinucleotide repeat microsatellite loci spread across the genome of D. ananassae (Schug et al. 2004) in 12 populations, including one from the species putative ancestral geographic range in Indonesia, 5 from Australia and the South Pacific, and 7 additional samples from Asia that have previously shown a pattern of isolation by distance and potential local geographic adaptation (Stephan and Langley 1989; Stephan et al. 1998; Chen et al. 2000; Vogl et al. 2003; Das et al. 2004). We additionally include a population of D. pallidosa from Malololelei, Samoa. We test the hypothesis that D. ananassae populations are structured in Asia, Australia, and the South Pacific, examine the utility of these DNA markers compared to multilocus, single nucleotide variation at introns (Vogl et al. 2003; Das et al. 2004), and make inferences about the ancestry, historic migration routes, and demographic history, particularly in Australia and the South Pacific.

MATERIALS AND METHODS

Population samples:

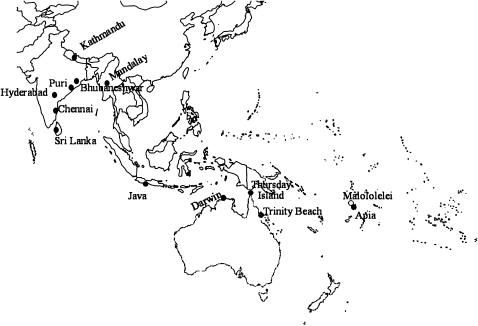
We assayed 209 individuals collected from 13 locations in Asia, Indonesia, Australia, and Samoa (Figure 1). We used the same samples from Kathmandu, Mandalay, Puri, Bhubaneshwar, Hyderabad, Chennai, Colombo, and Darwin that were described in Das et al. (2004); samples from Bogor were provided by M. Matsuda in 2002. We collected in Australia and Samoa (the island Upolu) during June 2003. Our collection locations and species identification were based on reports of previous collections from these locations by Bock and Wheeler (1972) and by Futch (1973). We collected near major metropolitan areas where D. ananassae is thought to be the dominant species except in Malololelei, Samoa, which is near a farm where D. pallidosa was previously collected (Futch 1973). D. ananassae females are indistinguishable from D. bipectinata, D. phaeopleura, D. pseudoananassae, and D. pallidosa. We thus inspected sex combs of male offspring from all wild-caught females to identify D. ananassae and D. pallidosa.

Figure 1.—

Map of sample locations.

F₁ individuals from wild-caught females from Apia, Malololelei, Thursday Island, and Trinity Beach (Cairns) were assayed. Individuals from established inbred, isofemale lines maintained in the lab as independent cultures were assayed for all other populations. Isofemale lines were established from a single wild-caught female and subsequently maintained by serial transfer every 10–12 days. Inbreeding leads to rapid fixation at most loci, and each inbred isofemale line is subsequently treated as a single haploid genotype sampled from the original population. In cases where we observed heterozygous genotypes, we randomly chose one allele. It is not possible to calculate the observed heterozygosity for isofemale lines, so we analyzed this measure only for the samples from the F₁ diploid genotypes assayed in Apia, Malololelei, Trinity Beach, and Thursday Island.

DNA extraction and microsatellite genotyping:

DNA was extracted from a single fly for each line using a PUREGENE DNA isolation kit (Gentra Systems, Minneapolis) and the presence and quantity of DNA was determined by ethidium bromide staining after electrophoresis on a 1% agarose gel. Isolation and characterization of dinucleotide repeat microsatellites is described in Schug et al. (2004). The following (AC)_n microsatellite repeat loci were assayed for polymorphism: DAN4, DAN9, DAN20, DAN21, DAN26, DAN27, DAN31, DAN32, DAN33, DAN42, DAN59, DAN65, DAN69, DAN70, DAN71, DAN73, DAN76, DAN78, DAN81, DAN82, DAN120, DAN136, and DAN154. The position of these loci in the scaffold sequences in the whole-genome assembly suggests that the loci are distributed across the three chromosomes (Schug et al. 2004). All are at least 1 Mb from one another if they within the same scaffold in the current assembly, except DAN32 and DAN154, which are ∼0.5 Mb from one another. There was no indication from patterns of linkage disequilibrium (LD) that any of the loci segregate in a pattern consistent with close physical linkage.

PCR of each locus was performed in 10-μl reactions using a tailed-primer approach, where the forward primer was constructed with a 19-nucleotide sequence complementary to the universal M13 primer on the 5′-end. In addition to the forward and reverse PCR primers, the M13 universal primer, labeled with IRD700 or IRD800, was added to the reaction. PCR conditions are described in Schug et al. (2004). Briefly, we used a touchdown approach with identical thermal cycling conditions for all primers and a 50° final anneal temperature in a 96-well format. Using this approach, PCR fragments ultimately contain an IRD700/800 label on the end with the forward primer that was detected by electrophoresis on a 6% Long Ranger sequencing gel on a LiCor Global IR2 automated DNA analyzer. Sizes of the DNA fragments were determined by reference to size standards that were distributed across the gel in lanes adjacent to the samples using Genescan version 4.05 software (Scanalytics). We included reference individuals of known genotype on all gels. In our experience, DNA fragments differing by 2 bp in length are consistently distinguishable using this technique and reproducible on multiple gels. Stutter bands are uncommon and when present clearly distinguishable from heterozygotes. Genotypes were binned into fragment sizes consistent with 2-bp (one-repeat-unit) increments. Diploid genotypes were determined from a single F₁ female from wild-caught females in the Thursday Island, Trinity Beach, Apia, and Malololelei populations.

Statistical analysis:

Summary statistics were calculated using MSA2 (Dieringer and Schlötterer 2003), except Nei's unbiased heterozygosity, which was calculated using PowerMarker version 3.2 (Liu and Muse 2004). Deviations from Hardy–Weinberg equilibrium (HWE) for each locus within populations and pairwise linkage disequilibrium (D′) between loci within each population were estimated with PowerMarker version 3.2 (Liu and Muse 2004). Statistical significance was evaluated using χ² and exact tests as implemented in PowerMarker version 3.25, and P-values were obtained using permutation and the Markov chain Monte Carlo (MCMC) approach (Guo and Thompson 1992; Raymond and Rousset 1995). We did not adjust the P-values for multiple comparisons. Correcting P-values for multiple comparisons using a method such as the Bonferroni correction is appropriate if we are interested in the statistical significance of each individual pairwise D′. However, for comparisons of the percentage of loci that display significant D′-values, it is more appropriate to set a level of statistical significance such as P = 0.05 and evaluate the proportion of pairwise comparisons with P-values below that threshold. By chance, one would expect 5% of loci to show statistically significant D′-values. Higher proportions suggest more LD than would be expected within the population sample.

We used several methods to estimate population structure among the samples, including Structure version 2 (Pritchard et al. 2000), BAPS version 4.1(Corander 2004), and traditional F_ST analysis (Weir and Cockerham 1984). Both Structure and BAPS perform a Bayesian analysis to identify hidden population structure by clustering individuals into genetically distinguishable groups on the basis of allele frequencies and linkage disequilibrium. One of our goals was to identify the contribution of ancestral and current migration among populations to the extant levels and to patterns of polymorphism. Individually based admixture models attempt to identify the ancestral source of alleles observed in different individuals where the ancestral source population is unknown (Pritchard et al. 2000; Corander et al. 2003; Corander and Marttinen 2006). Structure and BAPS differ in their approach to estimating admixture. Whereas Structure infers the highest likelihood of both the individual clusters and the admixture of genotypes using allele frequency and LD information from the data set directly, BAPS first infers the most likely individual clusters in the sample population and then performs the most likely admixture of genotypes (Corander et al. 2003). This approach is more powerful in identifying hidden structure within populations (Corander and Marttinen 2006).

For Structure, we performed 10–20 runs for each K-value ranging from 4 to 14, where K is the potential number of genetic clusters that may exist in the overall sample of individuals. This program performs a Bayesian analysis to assign individuals to a predefined number of clusters on the basis of a probabilistic analysis of the multilocus genotypes. We performed both an individual and an admixture analysis using different levels of K with a burn-in period of 50,000 generations and MCMC simulations of 100,000 iterations. We found that values higher and lower than K = 14 did not provide more biologically meaningful results than setting K = 13. For the BAPS analysis, we estimated individual clustering using K-values ranging from 4 to 20 and used these results in an admixture analysis with 100 iterations to estimate the admixture coefficients for the individuals. We performed the analysis multiple times with 5–10 iterations of each K-value to judge the consistency of the simulation results. In each simulation, we used 200 reference individuals/population and 100 iterations to estimate the admixture coefficients of the reference individuals. We estimated F-statistics following Weir and Cockerham (1984) and using MSA2 and tested for statistical significance by permuting genotypes 10,000 times, a method that does not rely on Hardy–Weinberg equilibrium (Goudet et al. 1996). R_ST, a measure of the degree of population structure among samples based on variance in repeat unit length of microsatellites (Slatkin 1995), was calculated using GENPOP version 3.2.

We generated unrooted, neighbor-joining trees using MEGA version 3.1 (Kumar et al. 2004) based on the pairwise F_ST matrices. We tested for correlations between genetic distance (F_ST and R_ST) and geographic distance using a Mantel test with 1,000,000 permutations with zt version 1.0 (Bonnet and Van de Peer 2002) and calculated a Spearman rank-order correlation coefficient using SPSS version 14.0. Straight-line geographic distances between populations were determined using geographic coordinates of each collecting site and a web-based calculator (http://www.go.ednet.ns.ca/∼larry/bsc/jslatlng.html).

To test for deviations from a neutral mutation-drift equilibrium model, we used the program Bottleneck (Cornuet and Luikart 1996), which uses a coalescent approach to test for heterozygosity excess or deficiency based on the expected heterozygosity and the number of alleles observed at each individual locus. Deviations from mutation-drift equilibrium across all loci are assessed for statistical significance using a Wilcoxon test. Using this approach, D_h/SD values that are significant at a particular locus represent heterozygosity deficiency, characteristic of a rapidly expanding population. D_h/SD values that are positive represent heterozygosity excess, characteristic of a population that has recently experienced a bottleneck. A neutral equilibrium model predicts an equal number of loci with heterozygosity excess and deficiency. It is well accepted that many microsatellite mutations occur in a stepwise manner, but a subset occur in entirely new states (Ellegren 2000). Thus, models used to infer historic demography strictly on the basis of either the infinite alleles or the stepwise mutation model are not likely to be as accurate as a two-phase model in which a percentage of mutations occur in infinite states. Estimates of homozygosity excess or deficiency based on a strictly infinite model or a strictly stepwise mutation (SMM) model represent two extremes between which estimates based on a two-phase model (TPM) will lie. We use 30% infinite mutations for the two-phase model and report the results based on a TPM and a SMM.

RESULTS

Genetic variation within populations:

Throughout, populations are presented from the most northwest to the most southeast geographic location. In general, heterozygosity and variance in repeat unit length are high in all populations (Table 1), similar to other Drosophila species for which dinucleotide repeat microsatellites have been assayed in natural populations (Hutter et al. 1998; Noor et al. 2000; Pascual et al. 2000; Ross et al. 2003; Orsini and Schlotterer 2004). We used a univariate ANOVA to test for differences among populations in levels of expected heterozygosity and variance in repeat unit. Differences among populations in mean expected heterozygosity were significant (F = 2.24, d.f. = 12, 284, P < 0.01) and variance in repeat unit were not significant (F = 1.04, d.f. = 12, 284, P = NS). Posthoc Tukey and SNK tests revealed that the significant difference in mean expected heterozygosity among populations reflected the low expected heterozygosity in Mandalay relative to all other populations. When we removed Mandalay from the data set and repeated the analysis, there were no significant differences among populations.

TABLE 1.

Genetic variation of microsatellite loci for 13 populations of D. ananassae

	Mean n	Mean He	Variance in repeat unit	Average no. of alleles	Average minimum repeat units	Mean repeat units	Average maximum repeat units	Mean D′		% D′ significant P < 0.05 subgroups
Population																	Total	1	2
Kathmandu	16.87	0.61	14.17	4.65	5.70	10.77	17.04	0.74	21.0	2.5a	0.65b
Mandalay	6.86	0.42	10.73	2.30	6.26	10.05	11.70	0.71	15.0	—	—
Bhubaneshwar	7.61	0.55	3.88	3.17	8.17	10.19	12.17	0.82	0.58	—	—
Puri	17.87	0.58	7.83	4.86	7.28	10.67	14.63	0.67	1.6	—	—
Hyderabad	13.74	0.59	5.85	4.52	7.04	10.55	13.99	0.76	6.2	—	—
Chennai	19.48	0.61	8.43	4.96	6.13	10.51	15.78	0.59	5.15	—	—
Colombo	6.0	0.47	9.97	2.56	7.56	10.71	12.71	0.91	0.65	—	—
Bogor	25.91	0.62	10.53	6.82	5.82	11.60	16.73	0.69	3.5	—	—
Darwin	8.96	0.52	8.95	3.17	8.61	10.96	14.63	0.82	0.28	—	—
Thursday Island	40.95	0.61	4.19	6.30	6.19	10.36	13.43	0.58	51.5	18.8c	3.9d
Trinity Beach	47.83	0.60	4.13	6.52	6.19	10.48	13.47	0.61	44.7	4.7c	11.2e
Apia	37.82	0.57	4.81	6.30	6.15	9.80	13.82	0.60	10.2	8.9f	—
Malololelei	20.95	0.51	4.15	4.81	7.33	11.29	13.52	0.73	4.2	—	—

“Mean n,” average number of chromosomes sampled; “Mean H_e,” expected heterozygosity; Mean D′, average LD for all pairwise comparisons of loci; “% LD significant P < 0.05,” percentage of pairwise comparisons between loci with probability of <5% on the basis of an unbiased estimate of the exact P-value of a contingency table using the permutation test of Raymond and Rousset (1995).

^aBlue subgroup, D′ = 0.78 (Figure 3).

^bLavender subgroup, D′ = 0.81 (Figure 3).

^cRed subgroup, D′ = 0.60 (Figure 3).

^dTan subgroup, D′ = 0.66 (Figure 3).

^eTan subgroup; D′ = 0.69 (Figure 3).

^fLight blue subgroup, D′ = 0.59 (Figure3).

F_IS-values and deviations from HWE in the Trinity Beach, Thursday Island, Apia, and Malololelei population samples on which we assayed diploid genotypes were high and significant in the direction of excess homozygosity at many of the loci as follows: 86% of the polymorphic loci in the Trinity Beach population (n = 23 polymorphic loci), 59% of the polymorphic loci in the Thursday Island population (n = 21), 57% of the loci in the Apia population (n = 20), and 19% of the loci in the Malololelei population (n = 20). Such a pattern may reflect hidden population structure within the sampled populations, causing a Whalund effect, the presence of null alleles due to polymorphism in the primer annealing sites flanking the microsatellite or large allele dropout (the tendency of PCR to preferentially amplify the smaller of two alleles in a heterozygote genotype). Short of resequencing PCR products of microsatellite genotypes and redesigning primers, there is no good method for distinguishing null alleles from population-level phenomena such as the Whalund effect that similarly cause homozygosity excess. Even resequencing alleles may not solve the problem because there may be additional polymorphisms in the newly identified primer sites causing null alleles, and redesigning primers would not resolve a problem with large allele dropout.

Since estimates of population genetic parameters may be significantly affected by departures from HWE due to null alleles, it is essential to estimate their potential contribution to allele frequencies if the genotypes are to be analyzed statistically using population genetic models. We thus used several approaches to explore the potential sources of deviations from HWE. Because null alleles are a common feature of microsatellites (Dakin and Avise 2004), we first regenerated the allele frequencies assuming all of the deviations were due to null alleles (Chakraborty et al. 1992) and analyzed population structure and tests for deviations from neutral equilibrium models on the corrected allele frequencies. Results that are largely inconsistent with a biological explanation would suggest that the deviations cannot be resolved by assuming that they are solely a function of null alleles. Using the method of Chakraborty et al. (1992) implemented in MicroChecker (Van Oosterhout et al. 2004), we identified potential null alleles, regenerated the allele frequencies at all loci that deviated from HWE in the Thursday Island, Trinity Beach, Apia, and Malololelei populations, and calculated the genotype frequencies from the allele frequencies. This simple method is described by Van Oosterhout et al. (2004). Using the regenerated genotype frequencies to estimate F-statistics and tests for mutation-drift equilibrium had little qualitative effect on the results. This is surprising because the method used to adjust loci that deviate from HWE, assuming that they are solely due to null alleles, changes the allele frequencies and in most cases reduces the sample sizes of genotypes (Chakraborty et al. 1992). The similarity in the results despite the correction may reflect the robustness of F-statistics and tests for mutation-drift equilibrium. Alternatively, the changes in allele frequency may parallel the original estimates in such a way that statistical analysis of the readjusted allele frequencies produces similar results. The results thus do not necessarily distinguish between the possibilities that the deviations from HWE reflect null alleles or features of the population. We thus approached the analysis by testing for population-level phenomena in the original data (not adjusted for null alleles) to test for potential population effects, such as a hidden structure within populations causing a Whalund effect. The methods involve examining levels and patterns of both allele frequencies and linkage disequilibrium in the context of potential population structure, similar to an approach used to examine patterns of LD and population structure in the maize genome (Remington et al. 2001).

We used two Bayesian statistical models to search for hidden population structure. These do not require a priori information about the membership of individuals in a population, but rather infer the number and size of populations, assuming that the clusters identified represent populations that are in HWE. In our case, collection sites that are potentially composed of individuals from populations that do not mate freely in nature (subpopulations) and that were assumed to belong to the same population may be revealed as multiple subpopulations, each of which is in HWE. We also explored patterns of multilocus, pairwise linkage disequilibrium for signal demographic patterns that may affect allele frequencies. We first present the results of the population structure analysis using traditional F-statistics, then present the analysis using the Bayesian approaches implemented in Structure and BAPS, and finally present the linkage disequilibrium analysis.

Population structure:

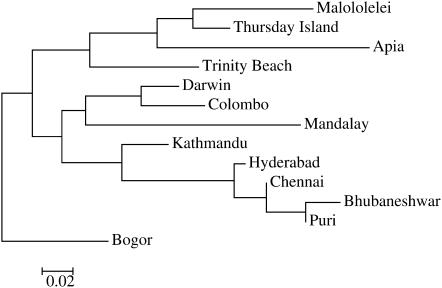
The overall level of structure among populations based on F-statistics was high and significant (F_ST = 0.220, P < 0.001). Pairwise comparisons among populations were significant in all cases (P < 0.001) and were highest among the South Pacific populations and lowest among populations in India (Table 2). Measures of structure based on R_ST were higher (Table 2). F_ST was correlated with R_ST (P < 0.01, Mantel's test). The relationship among populations reveals two distinct clades, one representing populations from Northwest Asia and the other representing populations from Thursday Island, Trinity Beach, Apia, and Malololelei (Figure 2). Bogor and Darwin are distinct from both clusters. The pattern of relationship is similar, using a proportion of shared alleles, R_ST, and Nei's standard genetic distance. A pattern of isolation by distance is apparent from correlations between F_ST and the geographic distance between populations (r = 0.40, P < 0.002). The correlation between R_ST and geographic distance was negative and not significant (r = 0.39, P = 0.01).

TABLE 2.

Genetic divergence among populations of D. ananassae

Population	1	2	3	4	5	6	7	8	9	10	11	12	13
1. Kathmandu		0.175	0.279	0.256	0.223	0.257	0.207	0.320	0.289	0.220	0.298	0.377	0.224
2. Mandalay	0.171		0.099	0.121	0.086	0.099	0.021	0.289	0.138	0.238	0.296	0.292	0.199
3. Bhubaneshwar	0.195	0.261		0	0.070	0	0.288	0.352	0.302	0.264	0.281	0.282	0.242
4. Puri	0.194	0.335	0.073		0.005	0	0.201	0.259	0.224	0.174	0.179	0.254	0.094
5. Hyderabad	0.107	0.296	0.114	0.048		0	0.112	0.183	0.173	0.187	0.172	0.292	0.095
6. Chennai	0.113	0.272	0.046	0.036	0.052		0.174	0.261	0.172	0.159	0.157	0.235	0.079
7. Colombo	0.164	0.225	0.288	0.266	0.212	0.201		0.183	0.083	0.345	0.324	0.412	0.231
8. Bogor	0.189	0.234	0.245	0.241	0.206	0.204	0.220		0.197	0.328	0.275	0.405	0.189
9. Darwin	0.173	0.260	0.310	0.271	0.212	0.203	0.116	0.210		0.211	0.227	0.297	0.206
10. Thursday Island	0.235	0.289	0.273	0.259	0.243	0.233	0.236	0.239	0.215		0.113	0.219	0.149
11. Trinity Beach	0.184	0.233	0.228	0.211	0.182	0.182	0.213	0.197	0.202	0.127		0.267	0.259
12. Apia	0.263	0.326	0.311	0.302	0.290	0.276	0.295	0.277	0.277	0.152	0.182		0.259
13. Malololelei	0.275	0.369	0.334	0.323	0.316	0.283	0.270	0.288	0.267	0.126	0.213	0.206

F_ST below diagonal; R_ST above diagonal.

Figure 2.—

Unrooted neighbor-joining tree using pairwise F_ST as a genetic distance. Bogor is placed in the basal position because it is the inferred ancestral population (Das et al. 2004) and for comparison to Figure 4.

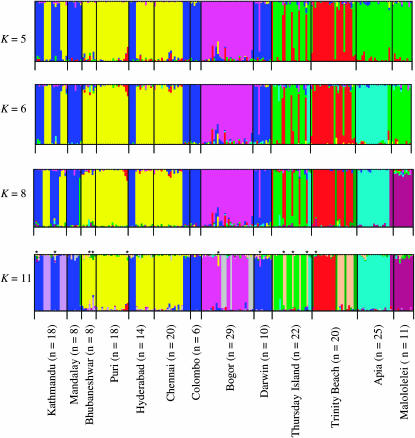
Both Structure and BAPS identify similar clusters for the individual-level analysis except that the highest posterior probabilities stabilized at K = 8 for Structure and at K = 11 for BAPS. Structure produced inconsistent and variable results for the admixture analysis whereas BAPS identified 11 independent clusters for both the individual and admixture models. Corander and Marttinen (2006) discuss the advantages of performing individual analysis prior to estimating admixture, which likely explains both the higher level of K and the stability between simulations achieved by BAPS. The BAPS results for the admixture analysis are shown in Figure 3. The individual-level analysis for Structure shows the same clusters as BAPS for K = 5 to K = 8. At K = 5, Bogor is clearly distinct from both the Asian and the Australian/South Pacific populations. In both the Asian and the Australian/South Pacific populations, two independent clusters are evident. At K = 6, Apia forms an independent cluster with two individuals from Thursday Island. At K = 8, Malololelei becomes an independent cluster with two individuals from Apia. At K = 11, independent clusters emerge in Kathmandu and Bogor. A third cluster, most common in Trinity Beach and containing individuals from Thursday Island, is also evident. Admixture is low in all samples and statistically significant in 11 of the 209 individual multilocus genotypes (Figure 3).

Figure 3.—

Inferred clusters of individual genotypes using BAPS. Shown are K-values at which clusters that had significant biological meaning were achieved. Highest posterior probabilities of likelihood values were obtained at K = 11. Each vertical bar represents one individual multilocus genotype. Individuals with multiple colors have admixed genotypes from multiple clusters. Statistically significant admixture for an individual multilocus genotype is noted with an asterisk above K = 11. Each color represents the most likely ancestry of the cluster from which the genotype or partial genotype was derived. Clusters of individuals are represented by colors and populations are separated by black vertical lines.

The most striking pattern emerging from the Bayesian approaches is the strong pattern of structure within populations from Kathmandu, Puri, Chennai, Bogor, Thursday Island, Trinity Beach, Apia, and Malololelei (Figure 3). Each population has at least two independent genotypes with no significant levels of admixture. The sample from Bogor, which lies near or within the putative ancestral geographic range (Vogl et al. 2003; Das et al. 2004), has two distinct clusters that are not observed in any other population. Inspection of the genotypes for the seven individuals in the least-represented cluster (Figure 3, gray) revealed four individuals with missing genotypes at 12 loci (a result of failure to amplify by PCR). This subgroup thus may represent a case where BAPS clustered genotypes erroneously. Missing data were uncommon in all other individuals in all of the populations. Kathmandu has a genotype (Figure 3, lavender) that shows no admixture with a second genotype (blue), which is also common in Mandalay, Hyderabad, Chennai, Colombo, and Darwin. Chennai has two distinct genotypes, both of which are found in other Asian populations and one of which is represented by Darwin. Thursday Island has one genotype (green) shared with individuals from Trinity Beach and Mandalay, a second (tan) also found in Trinity Beach, and a third genotype (blue) found in Apia. Trinity Beach has one independent genotype (red), a second genotype (tan) found on Thursday Island, and a third genotype (green) also found on Thursday Island and Mandalay. Apia has one genotype (blue) also found in Thursday Island, and a second found in Malololelei. Malololelei has one common genotype found in Apia.

Linkage disequilibrium:

Both of the Bayesian approaches estimate population structure and admixture on the basis of estimates of allele frequency and LD. Thus, it is possible that substructure identified by BAPS reflects, in part, significant levels of LD. We examined the allele frequencies between loci for evidence of significant pairwise linkage disequilibrium across populations, which is expected if any of the loci are physically close to one another and do not segregate independently. We constructed pairwise estimates of D′ and tested for significance of each pairwise estimate using both the MCMC and permutation algorithms in PowerMarker (Liu and Muse 2004). For comparisons of the percentage of loci deviating from LD in each population or subpopulation, it is not appropriate to correct for multiple tests, but rather to choose a P-value as a cutoff for significance and use the percentage of significant D′-values as a measure of overall LD. In our case, choosing a P-value of 0.05 rather than ≤0.01 would lead to a conservative estimate of genomewide LD, so we considered all D′-values with P < 0.05 as statistically significant LD.

The results showed first that there was no consistent pattern of significant D′-values between any of the individual markers among all or most of the populations, as would expected if the loci were physically linked. Although the statistical power to detect significant LD between pairs of loci varies across populations because of variation in sample sizes, the pattern is consistent with the scattered distribution of the microsatellites across the genome. Second, when we averaged D′-values for all pairwise comparisons between loci for all populations and examined the percentage of D′-values that were statistically significant, LD varied widely across loci and populations ranging from mean D′ = 0.58 in Thursday Island to mean D′ = 0.91 in Colombo (Table 1). All but four of the populations (Kathmandu, Thursday Island, Trinity Beach, and Apia) had ∼5% or fewer statistically significant pairwise comparisons (Table 1). Since ∼5% of the pairwise comparisons would be expected to be significant using P < 0.05 as a criterion for statistical significance, the results suggest that LD is not a feature of the microsatellite allele frequencies except in the population samples from Kathmandu, Thursday Island, Trinity Beach, and Apia. To determine if this reflected a hidden structure within each of the populations, we subdivided the data set into multilocus genotypes identified as clusters by BAPS (Figure 3) and calculated the percentage of statistically significant pairwise D′-values within each subgroup. We did not perform this analysis for the Mandalay sample because the sample size of individuals was too small. Because we were testing the same genotypes subdivided into different subpopulations multiple times, we applied a Bonferroni correction to the P-values for both the original and the subdivided data to arrive at the percentage of loci deviating from linkage equilibrium. This correction, however, had only minor effects on the results as most significant P-values were < 0.001. In the Kathmandu, Thursday Island, Trinity Beach, and Apia populations, subdividing the populations necessarily reduces the sample sizes and thus the statistical power to reject the null hypothesis of no LD. Nevertheless, in each case the percentage of significant pairwise D′-values was reduced substantially (Table 1), as would be expected if the clusters identified by BAPS within the three populations reflected patterns of LD. The strong reductions suggest that at least some of the LD in the full populations can be explained by the substructure within each of these populations detected by BAPS (Figure 4).

Figure 4.—

Unrooted neighbor-joining tree of 11 clusters identified by BAPS. Colors correspond to BAPS output shown in Figure 3. Bogor is placed in the basal position because it is the inferred ancestral population (Das et al. 2004) and for comparison to Figure 2.

We next reanalyzed the allele frequencies in Trinity Beach, Thursday Island, Apia, and Malololelei for departures from HWE by dividing them into the subgroups identified by BAPS. In all cases, the percentage of loci deviating from HWE was reduced. As for the LD analysis, we applied a Bonferroni correction to the P-values to arrive at the percentage of loci deviating from HWE. As for the LD analysis, the Bonferroni correction had little effect on the results. In the Trinity Beach population, the reduction was from 86% in the original sample to 31.82% of the loci in the red subgroup and 27.27% of the loci in the tan subgroup. In Thursday Island, the reduction was from 59% in the original sample to 22.73% of the loci in the green subgroup and 18.18% of the loci in the tan subgroup. In Apia, the reduction was from 57% in the original sample to 30.0% of the loci in the brown subgroup; the sample size was too small to test for HWE in the remaining purple subgroup (n = 2). As was the case for statistical analysis of the LD estimates, subdividing the data necessarily reduces the sample size below the sample size in the original data set and consequently reduces the statistical power to reject the null hypothesis of no deviation from HWE. Nevertheless, some of the reductions in the number of loci deviating from HWE are substantial, suggesting that at least a portion of the deviations observed originally may be attributed to a Whalund effect, particularly in Thursday Island and Trinity Beach.

Tests for deviations from neutral equilibrium expectations:

We examined the allele-frequency distributions for homozygosity excess or deficiency using the program Bottleneck, applying options of a stepwise mutation model and a two-phase model in which 30% of the mutations are assumed to be to an entirely new allelic state and 70% from a stepwise mutational process. The test assumes HWE, and reasonably high statistical power to detect significant deviations from equilibrium requires a sample size of ∼20 individuals/population (Cornuet and Luikart 1996). For 9 of the 13 populations, it was not possible to test for deviations from HWE because they were assayed from isofemale lines, and similarly we can be sure that there is no problem with null alleles because any polymorphisms in the primer sites preventing amplification would appear as missing data and simply reduce the sample size of that locus. Large allele dropout is not a possible complication because the loci are all homozygous. Sample sizes of individuals are smaller than is optimal for this statistical approach, and we thus cannot be sure if we fail to reject the null hypothesis (mutation-drift equilibrium) that the populations are biologically at mutation-drift equilibrium. The test is thus conservative, and a rejection of the null hypothesis would indicate strong evidence for heterozygosity excess or deficiency. The results are shown in Table 3.

TABLE 3.

Tests for deviations from the neutral equilibrium model

					TPMa		SMM
Population	No. of polymorphism loci	Mean n	Mean H	Mean no. of alleles	% loci homozygosity excess	Two-tailed Wilcoxon P-value	% loci homozygosity excess	Two-tailed Wilcoxon P-value
Kathmandu	22	16.82	0.60	4.82	77.27	0.002	81.82	<0.001
Kathmandu SG1 (blue)	19	9.56	0.57	3.83	84.21	<0.001	89.47	<0.001
Kathmandu SG2 (lavender)	18	7.05	0.49	2.89	94.44	<0.001	94.44	<0.001
Mandalay	17	7.18	0.43	2.71	94.12	<0.001	94.12	<0.001
Bhubaneshwar	19	7.53	0.58	3.63	89.47	<0.001	89.47	<0.001
Puri	22	17.87	0.55	4.87	95.45	<0.001	95.45	<0.001
Hyderabad	21	13.71	0.59	4.81	90.47	<0.001	95.24	<0.001
Chennai	22	19.45	0.60	5.14	81.81	<0.001	90.91	<0.001
Colombo	18	6.0	0.50	3.0	100	<0.001	100	<0.001
Bogor	23	25.91	0.60	6.83	86.96	<0.001	91.30	<0.001
Darwin	15	9.38	0.57	3.81	86.67	<0.001	86.67	<0.001
Thursday Island	21	41.0	0.62	6.55	80.95	<0.001	90.48	<0.001
Thursday Island SG1 (green)	21	20.5	0.56	4.91	95.24	<0.001	100	<0.001
Thursday Island SG2 (tan)	22	11.64	0.53	3.77	81.82	<0.001	86.36	<0.001
Trinity Beach	23	47.45	0.59	6.52	95.65	<0.001	100	<0.001
Trinity Beach SG1 (red)	21	23.40	0.44	3.36	52.38	0.632	61.90	0.146
Trinity Beach SG2 (tan)	21	15.18	0.55	4.55	57.14	0.99	71.43	0.01
Apia	20	36.76	0.60	6.71	85.0	<0.001	100	<0.001
Malololelei	20	18.85	0.52	4.67	90.0	0.004	95.0	<0.001

“Mean n,” average number of chromosomes sampled; “Mean H,” Nei's unbiased gene diversity.

^aTwo-phase mutation model with 30% of alleles mutating to a unique state and 70% mutating in a stepwise manner.

For all populations, deviations from a neutral equilibrium model were significant in the direction of homozygosity excess. Because the Kathmandu, Thursday Island, and Trinity Beach populations showed significant levels of Hardy–Weinberg disequilibrium (discussed above), which violates the assumptions of the tests for deviations from neutral equilibrium expectations (Cornuet and Luikart 1996), we reanalyzed the data by dividing the populations into the subgroups identified by BAPS in which HWE deviation was substantially reduced. Again, although sample sizes were reduced, significant deviations from the neutral equilibrium model remained in all but the Trinity Beach subgroup 2 (Figures 3 and 4, tan). In this subgroup, statistical significance was apparent only for the SMM. Thus, confining the analysis to genotypic data within clusters that show no evidence of HWE deviations appears to have no effect on the detection of departures from mutation-drift equilibrium. All populations and subpopulations, with the exception of a subgroup within Trinity Beach, show deviations consistent with population expansion.

DISCUSSION

Our analysis of microsatellite variation in D. ananassae populations from Asia, Australia, and the South Pacific reveals a more complex pattern of population structure than has been previously reported. The results are consistent with an Indonesian ancestry and subsequent radial migration patterns featuring a pattern of isolation by distance in the peripheral populations and population expansion, as has been suggested by DNA sequence variation of 10 introns in the Indonesian and Asian populations (Das et al. 2004). However, the results indicate that the peripheral D. ananassae populations, particularly in the South Pacific geographic range, are at least as genetically differentiated as D. pallidosa is from other D. ananassae populations. Furthermore, the Bayesian analysis implemented in BAPS identifies 11 independent lineages, some of which appear within populations and show little or no evidence of admixture, suggesting that they may not interbreed and thus have independent ancestries. The results raise questions about reproductive isolation within and between populations of D. ananassae and about the species status of D. ananassae populations and D. pallidosa and have implications for studies of natural selection in this species. We discuss both the potential biological implications and the potential statistical limitations of population structure analysis using multilocus microsatellite genotypes.

The first pattern that emerges from the results is the close genetic relationship of D. ananassae to D. pallidosa. F_ST is higher among some of the population samples of D. ananassae than between D. pallidosa (Malololelei) and populations of D. ananassae. Furthermore, both Structure and BAPS cluster D. ananassae populations independently at lower levels of K than they distinguish D. pallidosa from D. pallidosa. For example, at levels of K < 8, D. pallidosa is not distinguishable from Thursday Island, and at K = 5, D. pallidosa clusters with both Thursday Island and Apia. In total, six of the other clusters identified by the Bayesian analysis represent lineages of D. ananassae that are more distantly related to one another than D. pallidosa is to Thursday Island and Apia. Together, these results suggest that many of the D. ananassae clusters are more divergent from one another than they are from D. pallidosa.

One might suspect that the population samples that we collected represent a mix of D. ananassae and D. pallidosa or that the sample collected from Malololelei is, in reality, D. ananassae because the species are the most difficult species to distinguish in the ananassae complex on the basis of morphology (Bock and Wheeler 1972). In the field, we identified D. pallidosa by the pale body color noted in Malololelei specimens by Bock and Wheeler (1972), which contrasts sharply with the dark body color of D. ananassae in Samoa. Bock and Wheeler (1972, pp. 39–40) note that, aside from the body-color difference in Samoa, the single morphological difference is “the reduced number of rows of the sex-comb of D. pallidosa in comparison with D. ananassae.” In the specimens that they examined, D. pallidosa had between 11 and 18 teeth in three to four rows on the metatarsus, barely overlapping with the range of 18–28 teeth found in D. ananassae (McEvey et al. 1987). We are fairly certain, however, that our collections represent D. pallidosa as it was described by Bock and Wheeler (1972). We collected females of both species to return to the lab and examined F₁ offspring male sex combs to confirm their identity as D. pallidosa and D. ananassae. Furthermore, Malololelei is very close to the location in which collections of the pale-body-colored D. pallidosa were obtained by Futch (1973).

In one case, the multilocus genotypes appear to remain inconsistent with the morphological criteria for this species. Two individuals in Apia (Figure 3, purple) have genotypes that cluster with D. pallidosa from Malololelei. Morphologically, these individuals have dark abdomens and sex combs similar to those of the Apia D. ananassae. We are thus confident that by morphological standards our species identification is correct. A similar level of relatedness between D. ananassae and D. pallidosa is reported in a study of intron SNP polymorphisms (Das et al. 2004), suggesting that our observations are not a function of microsatellite polymorphisms, but are a general feature of similarity in the genomes of these sister species. We have also conducted extensive multiple-choice experiments in which we found that Malololelei females discriminated completely against Apia and mated freely with the D. pallidosa that we subsequently collected from Fiji (Killon-Atwood 2005), consistent with previous reports of prezygotic reproductive isolation between D. pallidosa and D. ananassae (Futch 1973; Doi et al. 2001).

The second pattern that emerges from the data is the distinct clusters within populations that show little evidence of admixture identified by the Bayesian analysis. Prior to performing the Bayesian analyses, we suspected potential assortative mating because of the deviations from HWE and the significant levels of linkage disequilibrium. By subsequently splitting the populations into clusters identified by BAPS, the patterns of HWE and LD were reduced to nearly nonsignificant levels, also suggesting distinct independent lineages within populations. Both Structure and BAPS identify clusters within Kathmandu, Hyderabad, Chennai, Thursday Island, Trinity Beach, and Apia. BAPS further identifies clusters within Trinity Beach and Bogor at K = 11. These results indicate that lineages exist both within and among populations that have not admixed in recent history and presently do not interbreed freely. Although the clusters identified within the Bogor population may reflect statistical anomalies due to individuals with missing genotypes, the remaining clusters appear to reflect structure within subpopulations.

There are two possible interpretations of the observed substructure within populations. If indeed the populations are substructured in nature as the statistical analysis suggests, the lack of evidence for admixture within each cluster suggests that they do not mate in the wild and may represent assortative mating populations or cryptic species that were collected in the same geographic location in our banana traps. Alternatively, the clusters may represent statistical anomalies due to the presence of null alleles. We attempted to distinguish between these hypotheses by examining patterns of LD and HWE within the clusters. In both cases, the percentage of loci showing significant LD and deviations from HWE was reduced significantly when we accounted for the substructure. This is expected if LD and deviations from HWE observed in the whole population are a function of population substructure caused by a Whalund effect. However, this approach is not a perfect solution because by examining clusters within each population, we are also reducing the sample sizes and consequently the statistical power to detect significant LD and HWE deviations. If the reductions in LD and HWE deviations are primarily due to a sample size effect, they may have no biological basis, but rather represent a statistical anomaly caused by null alleles. Thus while it would be intriguing to conclude that the clusters represent biologically real substructure within each geographic location, we cannot reject the hypothesis that the effect is strongly influenced by null alleles. The one exception to this is the substructure identified in the Kathmandu population in which null alleles were not possible and patterns of LD were reduced within each cluster. The biological reality of a substructure within populations potentially representing assortative mating populations or cryptic species must nevertheless be verified independently by further behavioral and genetic studies.

The origin of D. ananassae populations in Asia, Australia, and the South Pacific is likely very recent, particularly in Oceania and Australia, which were colonized by voyagers from Indonesia during the past 5000 years (Lum et al. 1998; Lum and Cann 2000). We note that, because of this recent origin and our results that the populations are not in mutation-drift equilibrium (Table 3), the genetic relationships based on F_ST-values may not reflect the true ancestral origins of populations, and it is thus not possible to know if the phylogenetic trees that we constructed on the basis of pairwise F_ST are true representations of the migration history of the lineages identified in the Bayesian analysis. Furthermore, as we point out above, the clusters identified by BAPS within populations must be verified experimentally. Nevertheless, the structure between geographic locations is strong and unlikely to be a function of statistical or technical anomalies. We can thus use these patterns to speculate about the biogeographic history of D. ananassae and D. pallidosa in the geographic regions from which we sampled and make some general inferences about the potential origin of the clusters identified by BAPS.

Both the Bayesian and phylogenetic analyses suggest that the population structure is featured by two major migration events arising from the putative ancestral population (Bogor; Vogl et al. 2003; Das et al. 2004), one representing the Northwest Asian populations and the other representing the Southeast Asian populations. Within the Northwest Asian region, three major migration events may be inferred from the results: one represented by individuals in Bhubaneshwar, Puri, Hyderabad, and Chennai; a second represented by individuals in Kathmandu, Mandalay, Chennai, Colombo, and Darwin; and a third represented by individuals restricted to Kathmandu whose genotype appears to be admixed with individuals in Bhubaneshwar. The second major migration is the lineage restricted to Kathmandu (Figure 3, lavender), which is most closely related to a common lineage in Bhubaneshwar, Puri, Hyderabad, and Chennai. Lineages coexist within Kathmandu, Hyderabad, and Chennai (Figure 3, blue) that show no evidence of admixture but are shared with other populations.

The Southeast Asian populations appear to have a common feature of multiple migration events from independent lineages followed by rapid population expansion. Three migration scenarios are possible in Thursday Island, Trinity Beach, and Samoa. D. ananassae may have colonized Thursday Island, Trinity Beach, and Samoa multiple times, each time represented by different lineages that diverged previously. Alternatively, populations that first colonized these geographic regions may have diverged from the ancestral population, and subsequent colonization events from the ancestral population appear as independent lineages. Finally, a combination of pre- and postcolonization divergence may have occurred with subsequent migration among the islands. Although we cannot definitively distinguish among these hypotheses, we believe that the most likely explanation is multiple colonization events from ancestral lineages that diverged elsewhere because of the likely young age of the populations and their commensal relationship with humans. For example, Thursday Island appears to have three ancestral lineages, two of which are shared with Trinity Beach and a third of which is shared with Apia. Apia has one ancestral lineage, which is shared with Thursday Island, and two individuals that most likely represent D. pallidosa from Malololelei. Trinity Beach has three ancestral lineages, two of which are shared with Thursday Island. The third lineage is unique to Trinity Beach. The colonization events of lineages across the sampled geographic range appear to be associated with a rapid expansion, which may have proceeded an initial population bottleneck, a pattern also observed in the intron DNA sequence polymorphism in the Northwest Asian populations (negative Tajima's D-values, Table 2; Das et al. 2004).

If we accept that D. pallidosa is a separate species represented by our sample from Malololelei, then what are the implications of its similarity in genetic relatedness to the D. ananassae populations for our understanding of the ancestry of these species? By all measures, D. pallidosa is as similar genetically to D. ananassae as many of the populations of D. ananassae are to one another, and in many cases the F_ST analysis shows higher levels of divergence between D. ananassae populations than to D. pallidosa. Furthermore, it clusters within the populations from Australia and the South Pacific rather than appearing as an independent unit. It thus appears that if we are willing to accept D. pallidosa as a species, then we must consider the possibility that some of the samples that we collected and that have been described previously as D. ananassae on the basis of morphology in fact are different species and that sex combs and body color are not morphologically distinguishing features.

The hypothesis that cryptic species exist in our samples can be tested using behavioral experiments to quantify levels of prezygotic, postzygotic, and gametic isolation (Coyne and Orr 1997). We know already that D. ananassae and D. pallidosa show strong prezygotic isolation, yet produce fertile hybrids (Futch 1966, 1973; Killon-Atwood 2005). Is this a feature of the lineages that we have identified within many of the D. ananassae populations? Is it also possible that D. pallidosa and other species in this geographic range, known or cryptic, may be much more widespread than has previously been recorded? A taxonomic study based on genital and sex comb morphology, chromosomal inversions, and DNA sequences of rapidly evolving loci will be required for a clear understanding of the population and species distribution of D. ananassae and D. pallidosa in Oceania and Australasia.