Dynamics of spatial summation in primary visual cortex of alert monkeys

Abstract

One of the fundamental tasks of the visual cortex is to integrate input from different parts of the retina, parsing an image into contours and surfaces, and then assembling these features into coherent representations of objects. To examine the role of the primary visual cortex in the integration of visual information, we measured the response properties of neurons under different stimulus conditions. Surprisingly, we found that even the most conventional measures of receptive field (RF) size were not fixed, but could vary depending on stimulus contrast and foreground–background relationships. On average, the length of the excitatory RF was 4-fold greater for a low-contrast stimulus than for a stimulus at high contrast. Embedding a high-contrast stimulus in a textured background tended to suppress neuronal responses and produced an enlargement in RF size similar to that observed by decreasing the contrast of an isolated stimulus. The results show that RF dimensions are regulated in a dynamic manner that depends both on local stimulus characteristics, such as contrast, and on global relationships between a stimulus and its surroundings.

Each neuron in the primary visual cortex (V1) is activated by stimuli over a limited range of visual space called its receptive field (RF). The simplest description of RFs in this area of the brain is based on the use of a single stimulus such as a bar of light or an edge (1). However, this description may not be adequate for understanding how cells respond to complex scenes. The responses of cells can be strongly modulated by stimuli placed far from the outer borders of their RFs (as delineated by a simple stimulus), indicating important nonlinearities in responses to visual scenes. Although inhibitory surrounds, particularly those involved in end inhibition, have long been included in the definition of RFs (2–9), strong extra-RF facilitation may play an equally important role (10–14). Regions of the nonclassical RF that give rise to facilitatory interactions appear to overlap with end-inhibitory regions, and the relationships among these kinds of interactions is poorly understood.

The existence of surround effects has led investigators to draw distinctions between “classical” and “nonclassical” RFs, although the original descriptions of visual RFs included modulatory as well as suprathreshold influences (15). Here we attempt to bridge the gap between classical RF properties, such as end inhibition and facilitation outside of the classical RF. We show that the boundary between the classical and nonclassical RF is not fixed; even the simplest measures of the classical RF can reveal stimulus-dependent changes in RF size.

Methods

Experiments were performed with four macaque monkeys (Macaca mulatta). The monkeys were comfortably seated in a primate chair 1.5 m from a computer monitor (1200 × 800-pixel resolution, 60-Hz refresh rate). The background luminance of the monitor was 3 cd/m². Stimulus contrast was calculated from Michelson’s equation. Experiments were performed under photopic conditions with ambient light. All procedures complied with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and were approved by the institutional animal review boards.

Experimental and surgical procedures were as previously described (12). Briefly, stimuli were presented in the near periphery while animals performed a foveal dimming task that helped to maintain tight fixations. The animals received a juice reward if they held fixation within a 0.7–1.0° diameter window, and indicated the dimming by releasing a lever at the appropriate time. Neural recordings were obtained in 600-ms epochs. The stimulus was turned on 200 ms after the start of the recording and was presented for 100 ms. Each fixation trial consisted of three to five recording epochs separated by at least 300 ms.

The stimuli used to make each curve were interleaved in random blocks. Different curves, e.g., length-tuning curves at different contrasts, were obtained in different blocks of recordings, and were not interleaved. The peak of each length-tuning curve was defined as the stimulus length that produced the largest response.

Neural activity was recorded from the operculum of the striate cortex with glass-coated platinum-iridium electrodes. Neural signals were amplified, band-pass-filtered between 300 and 3000 Hz, and fed through a time–amplitude window discriminator to isolate single units or small clusters of two to four units. All recordings were from superficial cortical layers, the neurons that form the main output from V1 to the extrastriate cortex. All single units were complex cells, and all multiunit recordings had complex cell-like properties.

The time window that was used to calculate the evoked response from each neuron was adjusted according to the composite temporal response profile of that cell over the entire set of experiments performed. The number of spikes occurring in this window was converted to spikes per second by dividing the response by the window length. Spontaneous activity for each experiment was defined as the neural activity in the 200 ms before stimulus onset, averaged across all stimulus presentations within an experiment, and converted to spikes per second. The displayed results represent the mean evoked response of the neuron over 10 or more trials for each stimulus after subtracting spontaneous activity; the error bars show one standard error of the mean above and below this value.

At each recording site, we measured the basic properties, e.g., its orientation tuning and RF center, of the single neuron or the multineuron cluster under study. The eccentricities of the RF centers ranged from 2° to 7° from the fovea, averaging about 4°. We ensured the stability of each recording session by measuring one tuning curve at several time points during the recording. The curves usually superimposed almost perfectly. If they did not, all recordings between these particular time points were discarded. Using this criterion, we selected 18 single units and 62 multiunit clusters from a larger total pool. Because we did not observe significant differences between single and multiunit recordings, we refer to both types of recordings as “cells” or “neurons” for the purposes of clarity. The results shown in Figs. 1 and 2e are from single-unit recordings; the rest of the figures are recordings from multiunit clusters.

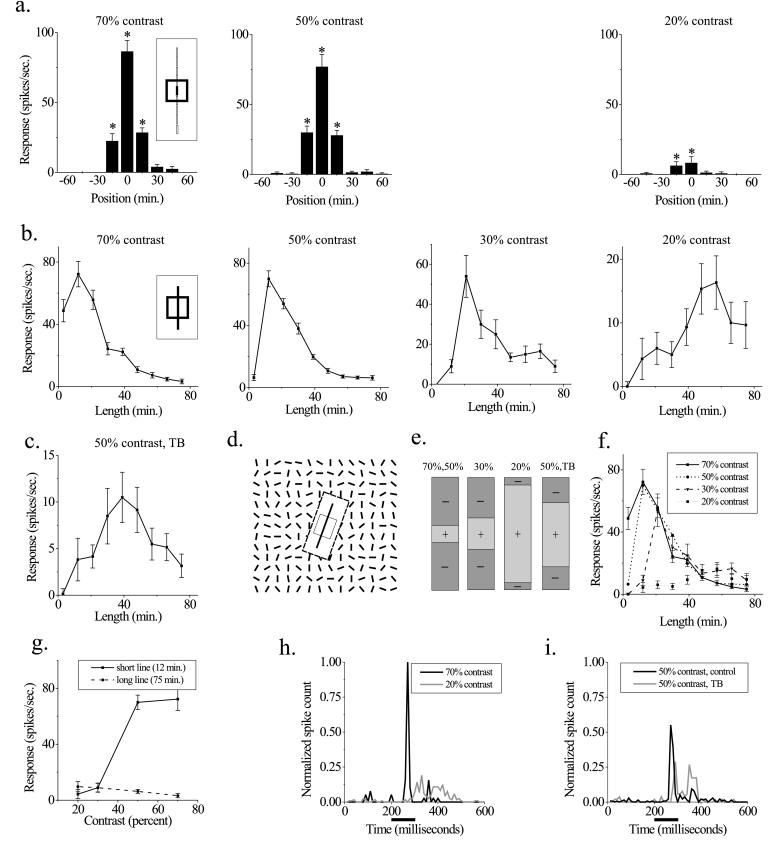
Figure 1.

The dimensions of V1 receptive fields are stimulus-dependent. (a) Minimum response field (MRF) measurements. Neuron responses to a small bar (measuring 15′ × 3′) were measured at adjacent positions along the orientation axis of the RF (Inset) at three different contrasts (Left, 70%; Center, 50%; and Right, 20%). Significant responses (P < 0.01, t test) are indicated by an asterisk. RF size is defined as the center-to-center distance between the outermost significant points, or 30′ for the two higher contrasts and 15′ for the lowest contrast. (b) Length-tuning measurements in these four panels show the neuron’s responses to optimally oriented bars of different lengths and 3′ wide, presented at the RF center at four different contrasts. The extent of the excitatory RF is defined as the stimulus length that produces the maximal response at each contrast. The neuron shows spatial summation over a region 5-fold larger at low contrasts than at high contrasts. Note that the change in RF size is in the opposite direction to that observed in a. (c) Length-tuning measurements in a textured background (TB). The stimulus is described in d. The background stimulus causes a suppression in the response to the bar stimulus and enhances spatial summation, even though the local contrast of the bar is still 50% (compare with 50% contrast condition in b). Response to background stimulus alone is 0.8 ± 1.2 spikes/sec. (d) Schematic of the textured background stimulus used in e. A 5° × 5° array of randomly oriented lines surrounds the RF (each bar measures 15′ × 3′ and RF is depicted as an open square), whereas an optimally oriented bar is presented at different lengths at the center of the RF. To keep the surround stimulus from eliciting a response on its own, the display is masked over a region larger than the RF by a black rectangle (here shown as a white rectangle bounded by dashed lines). (e) Schematic summary of the changes in size of excitatory and inhibitory RF subregions under different stimulus conditions. Plus symbols (+) represent excitatory subregions and minus symbols (−) represent inhibitory subregions. As stimulus contrast is decreased, the excitatory region becomes larger and the inhibitory flanks become smaller. Embedding a high-contrast stimulus in a textured background produces changes similar to those produced by lowering its contrast. (f) Curves from b are overplotted to show the convergence of curves at long line lengths. (g) Responses at two different line lengths are plotted as a function of stimulus contrast. For the short line, the neuron’s response increases with contrast, but for the long line, the response is contrast-independent. (h and i) The temporal profile of responses to long lines under different stimulus conditions. The neural responses to the four longest line lengths from f were summed and normalized to obviate small differences in their overall firing rates. (h) Comparison of high and low contrasts. Although the average firing rate is similar under these two conditions, the shapes of the curves are quite different. The bar below the x axis denotes the time over which the stimulus is presented. (i) Comparison of control and textured background conditions at the same contrast. A shift occurs in the position of the spikes from the early to the late part of the response. Spike rates are normalized as in h and displayed at the same scale.

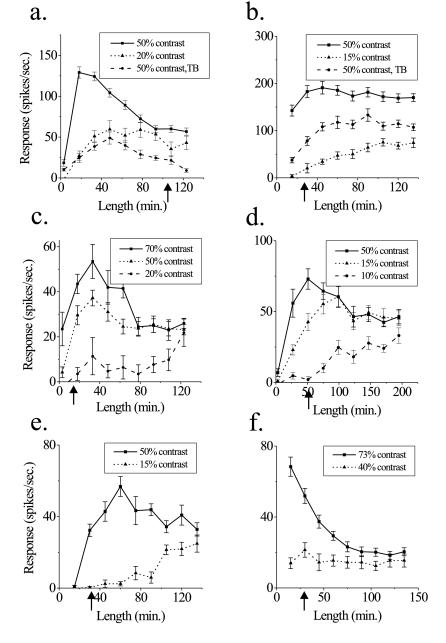
Figure 2.

Changes in RF dimensions are consistent over the population of cells. (a–f) Length-tuning relationships for bar stimuli for different cells are compared with minimum response measurements of RF size at high contrast (indicated by arrows on y axis). Almost every cell showed a similar trend toward increased spatial summation at low contrasts. Response to background stimulus alone is −1.1 ± 0.8 spikes/sec in a and 33.1 ± 4.7 spikes/sec in b.

The population tuning curves shown in Fig. 4 a and b were created by averaging length-tuning curves over a population of cells. A pair of tuning curves under different conditions was obtained from each individual cell and normalized to the peak of the 50% contrast curve without surround stimulation. This normalization served to minimize the differences in overall responses caused by the number of neurons being recorded, while preserving differences in the response between the two stimulus conditions. We used the same range of stimuli lengths to obtain each pair of tuning curves from a single recording site; however, these values could differ between cells—the smallest stimulus tested in each cell had a length of 3′, but the maximum value differed from cell to cell. To avoid using extrapolation procedures to merge the data, we combined the nine stimulus conditions of each experiment regardless of their particular scale. The means of the maximum line lengths for each analysis were similar (124′ for Fig. 4a and 140′ for Fig. 4b), allowing direct comparison of the different parts of the figure.

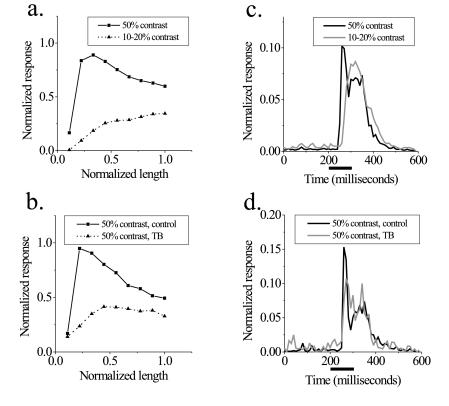
Figure 4.

Analysis of the population of length-tuning curve shapes and temporal response properties. (a) Comparison of high and low contrasts. The high-contrast curve reaches a peak at short line lengths and decreases as line length increases, whereas the low-contrast curve shows length summation over the entire range. For short lines, the difference in the response to the two contrasts is great, but the tuning curves tend to converge at longer line lengths, and this difference is greatly reduced. (b) Comparison of control and textured background conditions at 50% contrast. We subdivided the population of cells into three categories based on the magnitude of surround suppression. The one-third with the greatest surround suppression is shown. Surround suppression forces cells to behave as if they were at a lower contrast, and the extent of spatial summation increases. Similar to the comparison of low and high contrasts, the difference in response to the two conditions is greatest for short lines and smaller as line length increases. Note that this population of neurons shows more end inhibition than the general population. (c and d) Comparison of temporal responses. The temporal structure of neural responses is compared for the longest line lengths in a and b, respectively. (c) Comparison of high and low contrasts. In the high-contrast condition, a sharp peak of activity is followed by a smaller sustained response. At low contrast, the response is more uniform with a longer latency. The area under the curves is normalized to eliminate the difference in overall response rate. (d) Comparison of control and textured background conditions at the same contrast. A shift occurs in the positions of spikes from the early to the late part of the response, but latency does not change.

The population post stimulus time histograms (PSTHs) in Fig. 4 c and d were constructed by collecting the spike times from each cell into 10-ms bins, beginning 200 ms before stimulus onset. The area under individual PSTHs was normalized to unity and then averaged across cells.

Because we were unable to obtain satisfactory curve fits to the data, we used Monte Carlo simulations to test statistical significance (see supplemental data on the PNAS web site, www.pnas.org). For each real tuning curve, we created 10⁴ simulated tuning curves, and then compared the distribution of peak values across experimental conditions. The value of each data point for each simulated curve was given a value equal to the mean firing rate at that condition, plus or minus a randomly assigned error term (a), where the probability (p) of that value was related to the SEM by the following equation:

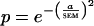The peak of each simulated curve was defined as the position with the maximum response. The number of simulated curves with a peak at each of the nine positions was divided by the number of simulations to create a probability distribution for peak position. The overlap of the probability distributions of two tuning curves (e.g., one high-contrast and one low-contrast) were then compared to test the null hypothesis that the peaks of the two curves are located at the same position. The probability that the curves have the same peak is the sum of the products of the individual probability distributions at each position.

Eye positions were monitored with a scleral search coil, digitized at a rate of 100 Hz, and saved for offline analysis in a subset of experiments. Typically, the animals were able to maintain fixation to better than 0.1°. An analysis of these data is contained in the supplemental data (www.pnas.org).

Results

We recorded the action potentials of superficial layer cells in the primary visual cortex while stimuli were presented in the near periphery. The length of the RF in each neuron was measured by two techniques. In the minimum response field (MRF) method, small bars are presented at different positions along the orientation axis (Inset, Fig. 1a), and length-tuning curves are made by presenting bars of different lengths at the RF center. The two techniques often produced quite different measures of RF size.

A representative example from a single unit recording is shown in Fig. 1. The MRF of the neuron is studied at three different contrasts. Although the RF measured in this way is slightly smaller at the lowest contrast, the difference is relatively small (Fig. 1a). However, length-tuning curves obtained at different contrasts demonstrate a dramatic shift in the balance between excitation and inhibition in the RF and a corresponding change in RF size (Fig. 1b). At high contrasts (70% and 50%), the response of the neuron shows spatial summation as the length of the bar is increased to 12′, and is strongly inhibited as the bar is lengthened further. At a contrast of 30%, the neuron shows length summation to 20′. Finally, as the contrast is decreased to 20%, the region of summation increases to 60′, a 5-fold enlargement from the excitatory region measured at high contrast.

Similar changes in spatial summation were obtained by embedding a high-contrast stimulus in a textured environment. This kind of pattern in the RF surround tended to suppress the response of the neuron (2, 16), and was accompanied by summation over longer stimulus lengths, even though the local contrast of the bar in the RF center was still high (Fig. 1 c and stimulus in d). The surround causes the neuron to behave as though the stimulus were at a lower contrast, suppressing its response and increasing its area of summation. Taken as a whole, these findings show an antagonism between a central excitatory core and surrounding inhibition in the RF, which is regulated in a dynamic, stimulus-dependent manner (Fig. 1e).

Length-tuning curves obtained at different contrasts are plotted over one another at the same scale in Fig. 1f. The lower contrast curves converge on the higher contrast curves as length is increased; they then follow the same course as the bar length is increased even more. For short lines, therefore, neuronal response increases as a function of contrast, but the response to long lines is contrast-independent over the tested range (Fig. 1g).

The temporal characteristics of the responses to long lines vary considerably, even when the integrated responses are quite similar. At high contrasts, there is a short-latency, transient response at stimulus onset with relatively little sustained activity; whereas, for the low-contrast case, there is a longer latency and a more sustained response (Fig. 1h). In the textured background, the position of action potentials shifts from the early to the late part of the response (relative to the control condition) but latency changes little (Fig. 1i).

Changes in spatial summation are apparent in almost every cell. Results from several example recordings are shown in Fig. 2 a–f. In many neurons, there was a close correspondence between length-tuning curves obtained with an isolated, low-contrast stimulus and a high-contrast stimulus surrounded by a textured background (Fig. 2a). Although most of the neurons displayed some degree of end inhibition, changes in spatial summation were also observed in non-end-inhibited cells (Fig. 2b). In this cell (Fig. 2b), a small response to the textured background stimulus presented in isolation occurred, even though it was positioned outside the MRF of the neuron. The background, which itself produced a small response, still suppressed the response of the cell to the center stimulus, and led to an increase in spatial summation. Eliminating those cells with background responses did not change the findings significantly.

We rarely observed changes in optimal stimulus length at contrasts greater than 50%, even though the response to short lines could be greater (Fig. 2c). However, the scale over which summation changes did occur varied from cell to cell. In some cells, a change in contrast as small as 5% could change spatial summation characteristics considerably (Fig. 2d). The largest extent of spatial summation defined by length-tuning curves could be many times the size of the MRF (Fig. 2e). Even in cells where the changes in spatial summation were modest, there could be a dramatic reduction in end inhibition (Fig. 2f). On a cell-to-cell basis, it was impossible to predict neuronal responses to long bars from the responses to the smaller stimuli used in MRF measurements.

Population-Based Analyses.

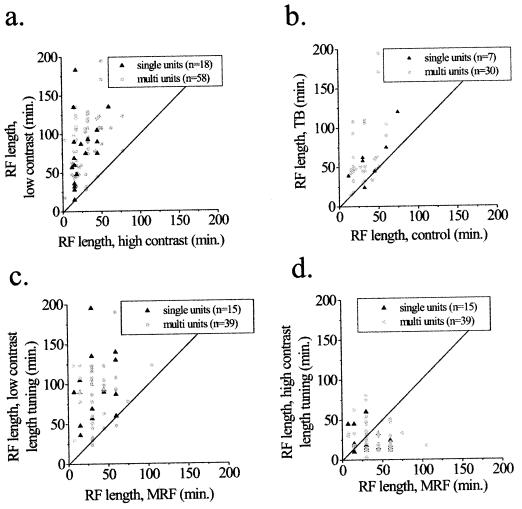
Similar trends in RF length, contrast–response relationships, and temporal response properties were observed over the entire population of cells studied. The RFs were, on average, 3.93 times longer at low contrasts compared with high contrasts (Fig. 3a, P < 1 × 10⁻²², paired t test), and 2.12 times longer in the textured background condition compared with the control condition (Fig. 3b, P < 1 × 10⁻⁵, paired t test), as derived from the peak of length-tuning curves.

Figure 3.

Population analysis of changes in RF dimensions. Each point in the graphs represents the results of one recording site from either a single unit or a multiunit cluster. The unity lines indicate the expected position of all points if there were no change in RF characteristics. (a and b) Comparison of RF length, as measured by the peak response of length-tuning curves under different stimulus conditions. (a) The length of the RF is plotted as a function of the highest and lowest contrasts tested for each cell. (b) Comparison of RF length between a high-contrast bar alone and one embedded in a textured background. The contrast of the stimulus in the RF is the same in both conditions. Note the consistency of the results in a and b. (c and d) Comparison of RF length measured by length-tuning curves at different contrasts and the MRF obtained at high contrast. (c) At low contrasts, length-tuning measures produce a larger measure of RF size than that of the MRF. (d) The relationship between these two measures of length varied more at high contrasts; but over the population of cells, a trend emerged for length-tuning curves to produce smaller measures of RF length than those of the MRF.

To establish a statistical criterion for changes in spatial summation on a cell-by-cell basis, we performed Monte Carlo simulations, incorporating the measurement errors from the experimental results (see Methods). At the 95% confidence interval (P < 0.05), 75% of the cells showed statistically significant changes as a function of contrast, and 50% of the cells showed significant changes in the textured background condition.

We also compared measurements of the MRF, obtained at high contrasts with length-tuning measures at different contrasts (Fig. 3 c and d). On average, length-tuning curves produced larger measures of RF size at low contrasts (median ratio of 2.2 × MRF, P < 1 × 10⁻⁹, paired t test), and smaller measures at high contrasts (median ratio of 0.6 × MRF, P = 0.01, paired t test), than did the MRF measure.

The results for individual cells show that many length-tuning curves obtained at different contrasts tend to converge at long line lengths. To obtain an independent measure of the changes in length summation over the recorded population, we calculated population length-tuning curves by averaging tuning curves from many cells. The individual tuning curves were normalized to allow for different spatial scales and response rates, which were sometimes caused by multiunit recordings. Fig. 4a shows the population length-tuning relationships as a function of stimulus contrast. This analysis is a summary of all 55 cells in which at least one tuning curve was obtained at a contrast of 50% and another curve was obtained at a contrast of 20% or less. The high-contrast curve reaches an early peak with the response decreasing at longer line lengths. The low-contrast curve shows spatial summation over the entire range of lengths. Although there is a large difference in firing rate between the contrast conditions for short line lengths, the difference between the high and low-contrast stimuli becomes much smaller at longer line lengths. The residual difference found in this analysis is likely to be an overestimate, because several of the low-contrast curves did not have an asymptote over the range of stimulus lengths tested.

A similar trend in response rates is observed in the suppression caused by the textured background stimulus. The analysis in Fig. 4b is based on 24 cells in which length-tuning curves were obtained at a contrast of 50%, with and without a textured surround. This population was subdivided into three sets of eight cells each, depending on the magnitude of surround suppression. The group with the strongest surround suppression was associated with the largest increase in the extent of spatial summation (Fig. 4b), whereas the group showing the least suppression is accompanied by little change in the summation region (data not shown). Similar to the comparison between high and low contrasts, the difference in firing rates between the two conditions is greatest for short lines; the curves tend to converge at longer line lengths.

Although the overall response rate of the neurons tended to converge at long line lengths for different stimuli, there were systematic time-course differences in the responses that were preserved at the population level. We averaged normalized poststimulus time histograms of the response to the longest line tested for the 55 neurons in Fig. 4a, above. The high-contrast stimulus produced a large transient response, which decayed to a lower level of sustained firing (Fig. 4c). In comparison, the low-contrast stimulus produced a longer latency response, which did not seem to be separated into transient and sustained components. A similar analysis was performed for the population of cells showing strong surround suppression in Fig. 4b. The textured surround causes a reduction in the transient component of the response without a corresponding change in latency (Fig. 4d). Taken as a group, these population analyses show that the main results for individual cells (Figs. 1 and 2) are consistent over the entire population studied.

Discussion

Our findings show that the dimensions of V1 RFs are not static. Excitatory and inhibitory inputs are spatially overlapping and operate in a push–pull manner; the balance between them can be modified. High-contrast stimuli invoke strong end inhibition; lowering the stimulus contrast or embedding the stimulus in a textured surround leads to enhanced spatial summation along the RF’s orientation axis.

Although length-tuning curves produce longer RF measurements at low contrasts, MRF measurements show the opposite trend. Previous studies comparing these two measures of RF size have generally found that they produce similar results; the exceptions to this rule occur mainly in deep cortical layers. Cat layer-5 cells show measures of RF size with length-tuning curves smaller than those in the MRF (4, 17, 18), whereas neurons in layer 6 often show the opposite relationship (4). Here we demonstrate that even single neurons display all three types of behavior. The relationship between the MRF and the optimal stimulus length changes in a stimulus-dependent manner, making it impossible to predict the response of a neuron to long bars from its responses to a number of shorter bars.

These findings link classical experiments on the inhibitory effects of RF surrounds, such as end inhibition, and more recent evidence for excitatory surround effects. In previous experiments, we showed that the response of a neuron to a stimulus in the center of its RF can be facilitated by a second, collinear stimulus presented in the RF surround (12). This interaction depends on stimulus contrast (14), which is consistent with the results of other studies (14, 19–22). However, the results presented here show that contrast can affect the size of the RF as well as the interactions between multiple stimuli placed inside and outside the RF. Interactions between the center of the RF and its surround are not limited to multiple, discontinuous stimuli but are an important feature of visual processing that can be observed with even the most simple visual stimuli, such as continuous lines.

An important aspect of these findings is that factors other than contrast, such as foreground–background relationships, can play an equally important role in determining RF properties. Embedding a high-contrast stimulus in a textured surround produces changes in spatial summation that are similar to changes from lowering the stimulus contrast. This effect would improve the detection of long, smooth contours in textured environments by enhancing the neural representation of these contours relative to their surroundings. Although the textured surround might be equated to a low-contrast stimulus, where the contrast is integrated over a larger spatial scale, the temporal profile of the responses in the two conditions is not equivalent.

The results force one to reconsider the current terminology in the field, which subdivides the RF into “classical” and “nonclassical” components. Even classical measurements of RF size, such as length-tuning curves, show that neuronal responses can be modulated by stimuli that extend over considerable visual distances, corresponding to many millimeters on the cortical surface. At an eccentricity of 4°, the magnification factor of macaque V1 is 2.5 mm per degree (23), suggesting that a length-tuning curve that shows summation over 2° of visual space receives input from 5 mm or more across the cortical surface. The extent of spatial integration suggests that the effects are mediated by cortico-cortical connectivity, such as is obtained by the long-range horizontal connections formed by pyramidal neurons within V1; these connections extend over similar distances (24–31), but feedback from higher cortical areas may also play a role. The mechanism underlying the dynamic change in the balance between excitation and inhibition is unlikely to involve changes in synaptic weight; it may be related to similar reversals of horizontal inputs, observed in intracellular recordings (32, 33).

Changes in length-summation properties cause many neurons to show the same overall response rate for long lines under different stimulus conditions. However, there are differences in the time course of the responses that may provide additional information about the stimulus. The latency of a neuron response can change as a function of stimulus contrast, which is consistent with the results of other studies (34). As opposed to lowering contrast, surround suppression does not cause a systematic change in response latency over the present population of cells, showing that temporal information can distinguish the three stimulus conditions (high contrast, low contrast, and high contrast in a textured surround), even though the integrated response for long lines is similar or identical.

Our results show that (i) changes in spatial summation result from changes in local contrast, and (ii) more global stimulus parameters can influence RF size. A role is thereby suggested for dynamic changes in RF spatial structure in contour saliency that is consonant with effects observed in psychophysical studies (35–37). The ability of V1 neurons to change their extent of spatial summation indicates that, even at the earliest stages in visual cortical processing, neurons represent active filters and alter their tuning properties in a stimulus-dependent manner.

Abbreviations

MRF

minimum response field

RF

receptive field

V1

primary visual cortex