Optimal decoding of correlated neural population responses in the primate visual cortex

Abstract

Even the simplest environmental stimuli elicit responses in large populations of neurons in early sensory cortical areas. How these distributed responses are read out by subsequent processing stages to mediate behavior remains unknown. Here we used voltage-sensitive dye imaging to measure directly population responses in the primary visual cortex (V1) of monkeys performing a demanding visual detection task. We then evaluated the ability of different decoding rules to detect the target from the measured neural responses. We found that small visual targets elicit widespread responses in V1, and that response variability at distant sites is highly correlated. These correlations render most previously proposed decoding rules inefficient relative to one that uses spatially antagonistic center-surround summation. This optimal decoder consistently outperformed the monkey in the detection task, demonstrating the sensitivity of our techniques. Overall, our results suggest an unexpected role for inhibitory mechanisms in efficient decoding of neural population responses.

A fundamental feature of mammalian cerebral cortex is its use of orderly topographic maps to represent sensory and motor information^1–3. Because cortical neurons tend to respond to a broad range of stimuli⁴ or movements⁵, and because there are generally multiple neurons tuned to the same range of parameters within one cortical column^6,7, even the simplest sensory stimulus or motor response elicits activity that is distributed over a substantial population of neurons^5,8,9. Electrophysiological studies in behaving primates suggest that perceptual and motor responses are indeed mediated by populations of neurons rather than by single neurons^10–13. These observations raise several fundamental questions: how are stimuli and movements encoded by neural population responses, what are the optimal strategies for decoding (pooling) the population responses, and how efficient are different non-optimal pooling strategies?

Several models of neural pooling in the brain have been proposed^11,14–19. These include monitoring only the most sensitive neurons (at the extreme, a single neuron)¹⁶, simple averaging over the active neural population¹¹ and weighted summation, where the contribution of each neuron in the pool is proportional to its sensitivity¹⁷ or proportional to the parameter value at the peak of its tuning function^14,15,18,19.

Importantly, evaluating these and other decoding rules has been held back because of limited experimental techniques for reliably monitoring neural population responses. Optical imaging with voltage-sensitive dyes (VSD) measures neural population responses at high spatial and temporal resolutions²⁰. Only recently, however, has this technique been applied successfully to behaving animals^21,22. In the current study, we use for the first time VSD imaging in behaving monkeys to investigate possible decoding rules for population responses in V1.

RESULTS

Experimental design

Two monkeys were trained to detect a small oriented visual target, indicating target presence by making a saccadic eye movement to the target location as soon as it was detected (Fig. 1a). While the monkeys performed this task, VSD imaging was carried out through a cranial window over V1 (Fig. 1b). Performance in the detection task is likely to depend on neural signals provided by topographic maps in V1 that can be directly identified by optical imaging^23–25. Because V1 is retinotopically organized, information regarding the presence or absence of the target is confined to several square millimeters of cortex within V1. Optical imaging allows us to localize this cortical region precisely and visualize the pattern of population activity within this entire region, in real-time, as behavior unfolds. Furthermore, in primates, V1 provides the main source of visual information to other cortical areas, and thus, optical imaging may allow us to visualize most of the information that is potentially available to subsequent processing stages in our task. However, because VSD signals are likely to be dominated by subthres-hold synaptic activity, it is possible that some of this information is not transmitted from V1.

Figure 1.

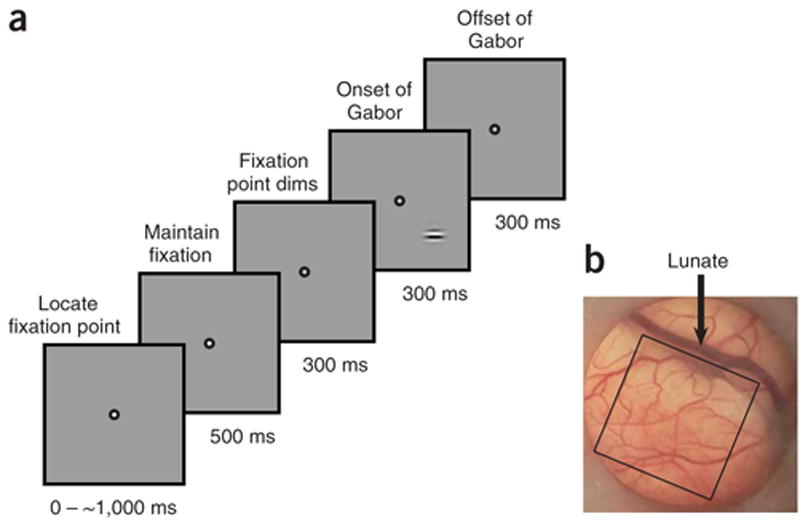
Behavioral task and recording chamber. (a) Task and stimulus (see Methods). (b) The cranial window over V1 in the left hemisphere in one monkey. The cortex is seen through a transparent artificial dura⁴⁴. A typical imaged area of 10 × 10 mm is indicated by the black square.

To evaluate the efficiency of possible decoding mechanisms and to determine the optimal Bayesian decoding strategy, we began by analyzing in detail the statistical properties of neural population responses.

Statistical properties of V1 population responses

The major goal in this study was to determine how target-related neural population responses in V1 could be pooled by subsequent processing stages in order to mediate visual detection. The efficiency of a pooling method depends on three key properties of V1 population responses: (i) the amplitude and spatial spread of the response, which determines the size of the neural population that could contribute to detection; (ii) the variability of the population response, which influences the quality of the signals provided by neurons at each imaging site (a single pixel or a binned group of pixels); and (iii) the magnitude and extent of spatial correlations in response variability, which can have a large impact on the gain that can be attained by pooling^14,26–29. Our first step was to examine these three key properties of V1 responses.

High-quality VSD responses were recorded in eight experiments (recording sessions) from V1 in two monkeys. We use the results from one VSD experiment as an illustrative example (Fig. 2). The VSD response in a small V1 region that corresponds to the target location increased rapidly shortly after stimulus onset (Fig. 2a). Response amplitude decreased and response latency increased as target contrast was reduced (Fig. 2b, thick lines). Target-evoked responses could easily be seen in individual trials (Fig. 2b, thin green lines), indicating that population responses in this small V1 region were highly reliable.

Figure 2.

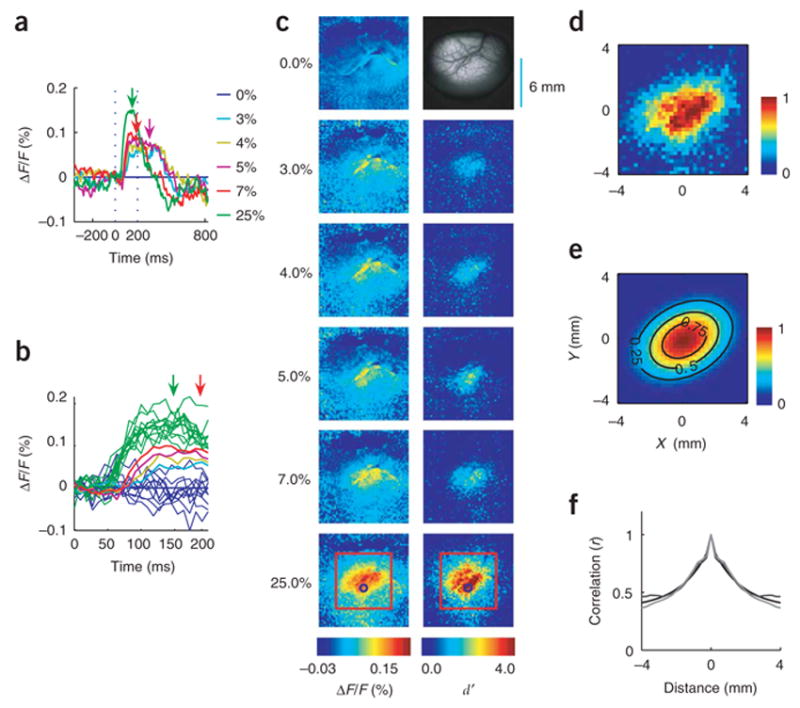
Neural population responses in V1 to a Gabor target (see Methods) measured with VSD imaging in one experiment. Gabor target parameters: σ = 0.33° , spatial frequency = 1.4 c.p.d., eccentricity = 2.7° . (a) Average time course of VSD responses. Response was measured in a small region of 0.25 × 0.25 mm, centered at the location of the small circle in c, bottom panels. Time courses are averaged across repetitions (n = 10 for each target contrast for target-present trials; n = 50 for target-absent trials). For display purposes, the average time course in target-absent trials is subtracted from each curve. Note that the animal was allowed to saccade to the target as soon as it was detected. Arrows indicate median reaction times at target contrasts in which at least three saccades were made. At high target contrasts, reaction times were short, leading to an early drop in the VSD response. (b) Single-trial time courses (thin lines) in the first 200 ms after target onset. The average time courses for each condition are shown in thick lines. (c) Spatial distribution of response amplitudes (left column) and response sensitivity (right column) for different target contrasts. Top right panel, image of cortical vasculature. To compute response amplitude, the response at each site is time averaged during a short interval after target onset and then averaged across repetitions (see Methods). Response sensitivity is measured as the signal-to-noise ratio d ′ (see text). Red squares in the bottom panels indicate the 8 × 8 mm ROI used for further data analysis. The circle indicates the site with maximal d ′ . Non uniform responses at 0% contrast (top left panel) represent residual noise in the mean response around large blood vessels. (d) Response amplitude in target-present trials averaged across all target contrasts after subtraction of the mean response in target-absent trials. (e) Two-dimensional Gaussian fit to the average response in d. (f) Average spatial correlations between pairs of sites as a function of their separation. To eliminate the effect of target contrast on spatial correlations, the average response (across repetitions) for each condition was first subtracted from the response in each trial before computing the correlations between the residual responses.

Spread of V1 population response

To quantify the amplitude of the VSD response in single trials, the average response was computed for each site in the imaged area over a short interval following the onset of the neural response and prior to the behavioral response (see Methods). The neural response to the small target increased with contrast and extended over an area of several square millimeters (Fig. 2c, left column), indicating that a large population of V1 neurons carries target-related signals that could be used by the monkey to detect the target. Consistent with previous studies demonstrating anisotropy in the map of visual space in V1, the response to the target was anisotropic, with the long axis of the response oriented parallel to the V1/V2 border along the lunate sulcus^8,30. Average response across all target contrasts (Fig. 2d) was well fitted by a two-dimensional (2D) Gaussian with a standard deviation along the major axis (σ _maj) of 1.97 mm, and along the minor axis (σ_min) of 1.34 mm (Fig. 2e). Although response amplitude depended strongly on target contrast, the spatial profile of the response was not significantly affected by contrast (Supplementary Fig. 1 online).

The extent of spatial spread varied somewhat across experiments (σ _maj = 2.20 ± 0.07 mm, σ _min = 1.54 ± 0.13 mm, n = 8; values are given as mean ± s.e.m.). Because VSD responses are thought to be dominated by subthreshold activity²⁰, the spread of spiking activity in V1 may be more limited. Control analysis demonstrated that the large spread was not due to variability in eye position (Supplementary Fig. 2 online). Thus, our results show that a large population of V1 neurons, encompassing several square millimeters of cortex, carries information regarding the presence or absence of the target in our task.

Reliability of V1 population responses

The reliability of neural population responses depends on their variability across trials. A common measure of reliability is the signal-to-noise ratio d′ , which is based on signal detection theory³¹:

$$d^{\prime }=|E_{\text{S}}-E_{\text{N}}|/\sqrt{\frac{{({\sigma }_{\text{S}})}^2+{({\sigma }_{\text{N}})}^2}{2},}$$

where E_S represents the mean amplitude of the response in target-present trials (signal trials), E_N represents the mean amplitude of the response in target-absent trials (noise trials) and σ_S and σ_N represent the corresponding standard deviations.

We find that σ_S does not increase with stimulus contrast and is not significantly different from σ_N (Supplementary Fig. 3 online). This is surprising because in single cortical neurons, the variance of the spike count during a short interval is proportional to the mean^17,32. However, as described in the next subsection, the relationship of the mean and the variance of the response can be significantly weaker in large pools of weakly correlated neurons (such as the ones contributing to each site in our VSD experiments). Response variance was nearly constant across space within our 8 × 8 mm region of interest (ROI, red square in Fig. 2c).

As with response amplitude, positive values of d′ were widespread and the values increased significantly with target contrast (Fig. 2c, right column). Note that even for contrast as low as 3%, reliable responses (d′ > 1) could still be measured.

Spatial correlations in V1 population responses

To characterize the spatial correlations in V1 population responses, we computed the average Pearson correlation (across trials) between the VSD responses at pairs of sites, as a function of their separation (Fig. 2f). The average correlations between neighboring sites in the imaged area were high, and fell off gradually with distance. The correlation structure was not significantly different between target-present trials (thin black curve) and target-absent trials (thin gray curve) (also, see Supplementary Fig. 3), suggesting that correlated variability in population responses is independent of the stimulus. These spatial correlations are well described by Gaussian noise (Supplementary Fig. 3) that is the sum of three components (Fig. 2f, thick black curve): a spatially independent noise (white noise), a correlated noise, where the correlations fall off exponentially over space, and a spatially uniform noise that varies only across trials (random DC).

The observed correlation values seem, at first, surprisingly high and widespread given the low correlations in spiking activity typically observed between pairs of cortical neurons^27,33–35. However, it is important to note that such high correlations at the level of neural populations are expected even if the underlying correlations between individual neurons are very weak. In large pools of neurons, the independent neural noise within the pool averages out, leaving the weak correlated noise unaffected; this leads to much higher correlations between the pooled responses. For example, assuming approximately 200,000 neurons per mm² of V1 cortex and a uniform pairwise correlation of 0.001 between neurons, the expected correlation between two neighboring 0.25 × 0.25 mm pixels is 0.926 (Supplementary Fig. 4 online; see also Supplementary Methods online). This simple computational analysis demonstrates that pairwise correlations that are undetectable at the level of single neurons can create dramatic correlations at the level of neural pools. Therefore, single-unit electrophysiology may be an inadequate tool for studying the correlations that are relevant at the level of neural populations.

Our results are also consistent with the long-range correlations observed between electrophysiological responses and VSD responses in the visual cortex of anesthetized cats³⁶. Control measurements using an ‘‘artificial cortex’’³⁷ verified that the imaging system does not contribute significantly to the spatial correlations reported here (Supplementary Fig. 5 online). The effect of pooling may also explain the weak relationship between mean and variance in the VSD responses: in large pools, the variance is dominated by the weak correlated noise, which may be relatively stimulus-independent.

Widespread correlations were observed in all of our experiments (mean τ = 2.07 ± 0.1 mm, n = 8; where τ is the space constant of the exponential noise component). As will be described below, such correlations impose significant constraints on the way information from pools of neurons should be combined.

To summarize, we found that V1 population responses, as measured by VSD imaging, can be described as the sum of (i) a spatially extended stimulus-evoked response that varies in amplitude (but not shape) with stimulus contrast and (ii) a stimulus-independent Gaussian noise with widespread spatial correlations.

Candidate spatial pooling rules

The results presented in the previous section demonstrate that target-related neural responses are widespread in V1. Neural responses at some, or all, of these V1 sites could contribute to the monkey’s behavior. How might these responses be combined over space to detect the target? How do different candidate pooling rules compare in terms of the detection sensitivity they support? How should V1 signals be pooled to maximize detection accuracy?

To address these questions, we explored different candidate decoding rules that combine information from multiple sites in V1 (the important issue of how to dynamically pool information over time will be addressed elsewhere). The rules that we consider here (see Table 1) are based on linear summation, in which the VSD responses from each site in V1 are summed to form a pooled response,

Table 1.

Candidate pooling rules

Maximal Average Amplitude: wi ≠ 0 only for the site with maximal average amplitude Maximal d ′ : wi ≠ 0 only for the site with maximal d ′ Maximal Amplitude: wi ≠ 0 only for the site with maximal amplitude in a given trial Mean Amplitude: wi = 1/n Weighted Average Amplitude: wi ∝ E(xi) Weighted d ′: wi ∝ d ′i Optimal: see equation (2) and Supplementary Methods

$$x_{\text{pooled}}=\sum _{i=1}^n{w}_i{x}_i$$ (1)

where w_i is the weight given to response x_i from site i. This pooled response is the ‘decision variable’ used to determine if the target is present or absent on a given trial (discussed below). The rules differ in the weights that they assign to each site. Pooling rules can be divided into two classes. In the first, detection is based on signals provided only by a single V1 site. In rule 1 the selected site is the one with the Maximal Average Amplitude; in rule 2 the selected site is the one with the Maximal d′ ; in rule 3 the selected site is the one with the Maximal Amplitude (in this case, the site may vary from trial to trial).

In the second class of rules, detection is based on the weighted average of VSD responses from all sites within a given pooling area (i.e., an area containing the whole active population). In rule 4 equal weights are given to all sites (Mean Amplitude). In rule 5 the weights are proportional to the average amplitude (Weighted Average Amplitude). In rule 6 the weights are proportional to d′ (Weighted d′ ). Finally, under certain assumptions it is possible to derive an Optimal pooling rule (rule 7) for combining information from multiple sites^26,38. The derivation of this Optimal pooling rule is described in the next section.

Optimal spatial pooling

The first six pooling rules in Table 1 do not take into account possible spatial correlations in population responses. Our results, however, indicate that at the level of large populations of neurons, spatial correlations are strong and widespread (Fig. 2f). What is the optimal way to pool correlated neural responses?

The optimal rule for combining information from multiple sites can be derived if the response amplitude in each site is a Gaussian-distributed random variable that is independent across trials (but not necessarily independent across space and time within a trial), and if the covariance of the responses is independent of the stimulus. Under these assumptions, which apply to the measured responses (Supplementary Fig. 3), a linear summation rule (equation (1)) is optimal, and no nonlinear rule can significantly exceed its sensitivity³⁸.

The optimal set of weights, w = {w₁, …, w_n}, is given by

$$\mathbf{w}={\mathrm{\Sigma }}^{-1}\mathbf{s}$$ (2)

where ∑⁻¹ is the inverse of the response covariance matrix ∑ , and s is the mean difference in response between the signal and noise trials (see Supplementary Methods). The expected sensitivity of the decoder that uses the optimal weights is given by the Mahalanobis distance between the mean of the noise and signal distributions³⁸:

$$d_{\text{pooled}}^{\prime }={[{\mathbf{s}}^T{\mathrm{\Sigma }}^{-1}\mathbf{s}]}^{1/2}$$ (3)

where s^T is the transpose of s.

To demonstrate the principles of optimal pooling in correlated noise and provide intuitions about how correlated noisy responses should be combined, we first consider the simple case of combining responses from two sites. We then proceed to the general case of pooling across n sites, where n can be arbitrarily large.

Optimal pooling from two sites

Consider responses from a pair of sites with sensitivity {d′₁, d′₂} and correlation r. Using equations (2) and (3) we derived the optimal weights and the combined sensitivity at the two sites (see equations (4) and (5) in Supplementary Methods). We then computed the values of d′_pooled as a function of r, for different values of d′₂, with d′₁ set arbitrarily to 1.0 (Fig. 3a). As can be seen, there are two basic regimes and corresponding strategies for efficient pooling of information, depending upon the values of d′₂ and r. When d′₂ is equal to d′₁ (blue curve), the best pooled performance occurs when the two sites are uncorrelated (d′ _pooled = √2). On the other hand, when d′₂ is much lower than d′ 1 (e.g., d′₂ = 0, yellow curve), the best pooled performance occurs when the responses at the two sites are highly correlated (e.g., d′_pooled > 2 for r = 0.9). In this case, d′_pooled can be much higher than when the two d′ values are high and uncorrelated. This demonstrates that under some conditions, correlations can significantly improve neural sensitivity^26,28,35. The reason for this improvement is simple. If the variability in an uninformative site is highly correlated with the variability in an informative site, then pooled sensitivity can be improved by estimating the common noise and removing it from the informative site. This is accomplished by giving a negative weight to the uninformative d′₂ site.

Figure 3.

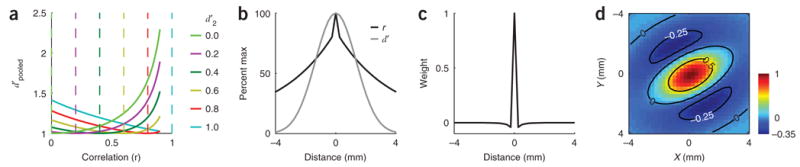
Optimal two-site and multiple-site pooling. (a) Each colored curve represents pooled sensitivity over two sites with different relative sensitivities as a function of the correlation between the sites (computed using equation (5), Supplementary Methods). Dashed vertical lines indicate the point of transition from positive pooling (on the left) to negative pooling (on the right). (b) Normalized falloff in sensitivity along the minor axis of the average response in Figure 2e (gray) and falloff in correlations along the same axis (black). (c) One-dimensional cut through the optimal whitening filter that, when convolved with the imaging responses, generates responses that are statistically independent across space. (d) Optimal set of weights obtained by convolving the whitening filter twice (see Methods) with the average response amplitude (Figure 2e). Note that the optimal filter contains a positive region at the center and a large negative region in the surround.

The key property that determines which form of pooling is more efficient is the relative rates of falloff in d′ and r over space. Specifically, if the ratio of the d′ values at two sites falls below the correlation between the two sites, then the activity from the sites should be combined using a negative weight. To examine the interactions between d′ and r, we fitted descriptive functions for d′ and r from the VSD imaging data in the example experiment (Fig. 3b). Because d′ falls off more rapidly than r (note that r = 1 at a distance of 0), the highest sensitivity (improvement of 7% relative to d′_max) is obtained by combining the site with maximal d′ with a second site approximately 3.2 mm away, using a negative w₂ (see Supplementary Fig. 6 online).

Optimal pooling from multiple sites

The basic results for optimal pooling over two sites apply in the more general case where responses are pooled from multiple sites. We obtained the optimal weights for the example experiment (Fig. 3d) by using a decorrelating filter (whitening filter) (Fig. 3c; see Supplementary Methods). This set of weights contains positive and negative values, just as when optimally pooling VSD signals from two sites. The exact shape of the optimal weighting function depends on the spatial pattern of the neural responses and on the correlated variability. In all eight experiments examined here, the optimal weights contained a central positive region and a larger negative surround. To the best of our knowledge, such antagonistic center-surround pooling models have not been previously considered for decoding neural population responses in the cortex.

Using equation (3) we can compute the expected d′_pooled when responses are pooled from all sites in an 8 × 8 mm ROI (e.g., Fig. 2c) using the optimal weights (e.g., Fig. 3d). While the maximal improvement when pooling only two sites was ~7% relative to d′_max, the improvement when using the optimal weights and pooling over all sites in a ROI of 8 × 8 mm was much larger (an average increase of 61 ± 17%, n = 8).

Neural and behavioral detection sensitivity

To evaluate the relative efficiency of different candidate pooling rules, we next developed a method for measuring detection sensitivity from the VSD signals that also allows direct comparison with the behavioral sensitivity of the monkey.

Consider first the sensitivity of the monkey. The proportion of trials in which the monkey reported that the target was present increased monotonically as a function of target contrast (Fig. 4b, black triangles). At 25% contrast, the monkey detected the target on every trial. As the contrast was lowered, the probability of detection dropped monotonically. The monkey’s performance was first fitted with a standard psychometric function³⁹ (see Methods), and then the overall accuracy (overall percent correct) and the contrast threshold (contrast at which accuracy is 75%) were computed.

Figure 4.

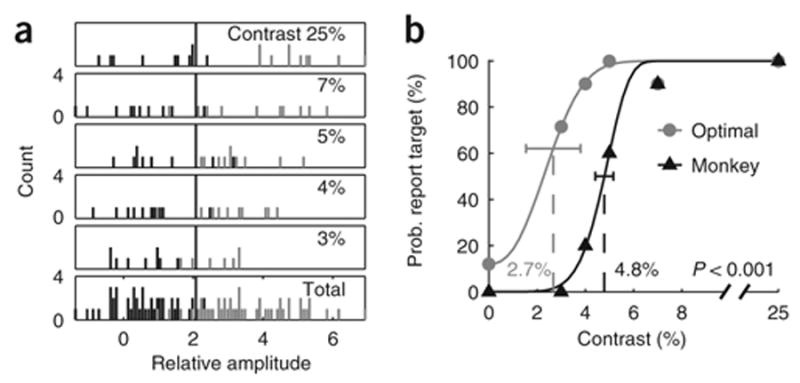
Methods for measuring neural and behavioral detection sensitivity. (a) Distributions of the VSD responses in the example experiment, pooled over an area of ~8 × 8 mm of cortex using the optimal set of weights (Fig. 3d). Pooled responses in target-present trials (gray) and target-absent trials (black) are separated according to target contrast. The bottom panel shows combined distributions across all target-present and all target-absent trials. The vertical line represents an optimally placed criterion for separating target-present trials from target-absent trials (see text). (b) Proportion of trials in which the observer reported that the target was present as a function of target contrast. Zero contrast represents target-absent trials (the probability at this point is the false alarm rate). Black triangles, monkey’s performance. Gray circles, performance of an observer that uses the Optimal rule to pool V1 responses. Solid curves are the best fitting Weibull functions³⁹. The dashed vertical lines and the corresponding numbers are the thresholds (see Methods). The model’s detection threshold was significantly lower than the monkey’s detection threshold (bootstrap test, P < 0.001). Horizontal error bars indicate 95% confidence interval. The model’s threshold was still significantly lower than the monkey’s threshold even with suboptimal criterion that reduced the false alarm rate of the model to a level comparable to that of the monkey.

Detection sensitivity of the optimal pooling rule

Next, consider the sensitivity of V1 population responses in the example experiment. For each trial, the neural responses were pooled across space using the optimal set of weights (Fig. 3d). Pooled responses in target-present trials (Fig. 4a, gray bars) and target-absent trials (Fig. 4a, black bars) are plotted separately for each target contrast. There was no overlap between the two distributions at high target contrasts. The overlap increased significantly as target contrast was reduced.

To determine the approximate detection sensitivity implied by these distributions, we computed how well an observer could detect the target from these pooled responses. The observer uses a criterion to decide whether the target is present or absent on a given trial. This criterion (Fig 4a, vertical line) is the one that minimizes the error rate for the combined distributions (Fig. 4a bottom panel). Once this criterion is found, we can compute for each target contrast the probability that the observer would report that the target was present; this is simply the proportion of trials in which the pooled response at that target contrast exceeds the criterion. To ensure that we did not overestimate the detection sensitivity, the analysis was performed separately for each trial using a jackknife procedure⁴⁰ (see Supplementary Methods).

Next, we compared the performance of the Optimal rule (Fig. 4b, gray circles) with the performance of the monkey (Fig. 4b, black triangles). The solid curves show the monkey’s psychometric function (black) and the neuro-metric function obtained with the Optimal rule (gray). The threshold of the neurometric function is significantly lower than the threshold of the psychometric function. In other words, under conditions in which the monkey fails to detect the target, neural population responses in V1 continue to provide reliable information regarding the target. This result was consistent across all eight experiments (Fig. 5c). This finding is important for two reasons. First, it demonstrates that VSD imaging in behaving monkeys is highly sensitive. Second, it shows that V1 population responses are not used optimally by the brain in this task.

Figure 5.

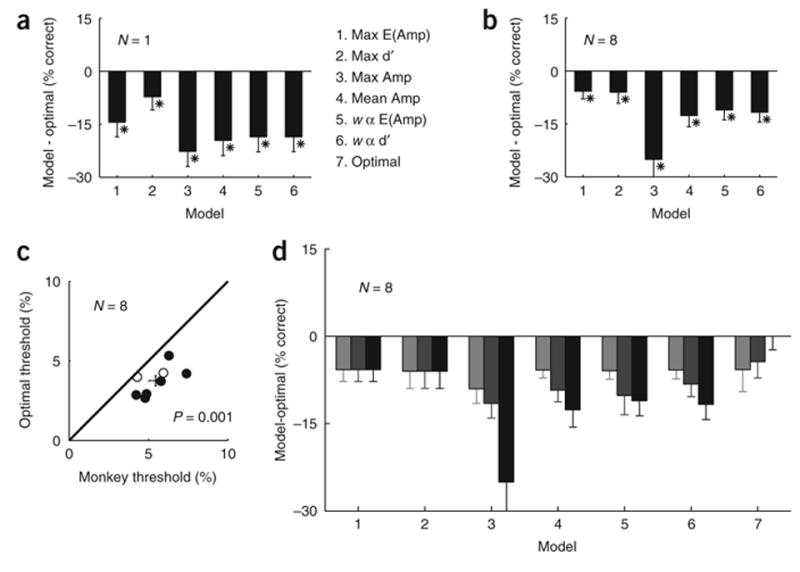
Comparing detection sensitivity of candidate pooling rules. (a) Difference in overall percent correct between the first six pooling rules from Table 1 and the Optimal rule, in the example experiment. Asterisks indicate rules with performance significantly different from the Optimal (bootstrap test, P < 0.05; error bars = 95% confidence interval). (b) Average difference across all eight experiments in overall percent correct between the six pooling rules and the Optimal rule. Same conventions as in a. Asterisks indicate rules with performance significantly different from the Optimal rule across experiments (paired t-test, n = 8). (c) Scatter plot of threshold for the Optimal pooling rule vs. the monkeys. Filled symbols indicate experiments in which the Optimal model’s detection threshold was significantly lower than the monkey’s threshold (bootstrap test, P < 0.05). Error bars indicate one s.e.m. centered on the mean. (d) Average difference in overall percent correct between the Optimal rule using an 8 × 8 mm pooling area and the seven pooling rules at three pooling areas (2 × 2 mm, light gray; 4 × 4 mm, dark gray; 8 × 8 mm, black). Error bars in b and d show one s.e.m.

Our next step was to compare the detection sensitivity of the different pooling rules in Table 1.

Detection sensitivity of all pooling rules

Detection sensitivity for all the pooling rules was obtained using the same procedure described above. We computed the difference in overall percent correct between the first six pooling rules in Table 1 and the Optimal rule, for the example experiment (Fig. 5). As expected, all pooling rules performed significantly worse than the Optimal rule. Importantly, rules based on averaging, such as Mean Amplitude or Weighted Average Amplitude, performed significantly worse than the Maximal d′ rule, which uses a single, highly informative, 0.25 × 0.25 mm site. The Maximal Amplitude rule also performed poorly. The same pattern of results holds across all eight experiments (Fig. 5b). Finally, we note that the threshold of the Optimal rule was consistently lower than the threshold of the monkey (Fig. 5c).

To examine the effect of the pooling area on the performance of the models, we computed the average accuracy of the seven models across all experiments, for three pooling areas (Fig. 5d). Because the pooling area was always centered on the peak of the average response, the performance of the Maximal d′ and the Maximal Average Amplitude rules remained constant as pooling area changed. As the pooling area was increased, the performance of most pooling rules decreased. Thus, including more neurons in the pool caused a significant decrement in the overall accuracy of most pooling models. The Optimal rule was the exception; it was the only rule where performance improved as the pooling area increased.

The non-optimal rules perform poorly when pooling over a large area due to the spatial correlations (Fig. 2f). Because the pool contains both highly sensitive and weakly sensitive neurons, averaging these together reduces the signal without reducing the correlated noise.

Importantly, rules that rely on a single-site, such as Maximal d′, performed poorly when considering sites that are significantly smaller than 0.25 × 0.25 mm (Fig. 6). With smaller sites, independent noise dominates the response, leading to decreased performance.

Figure 6.

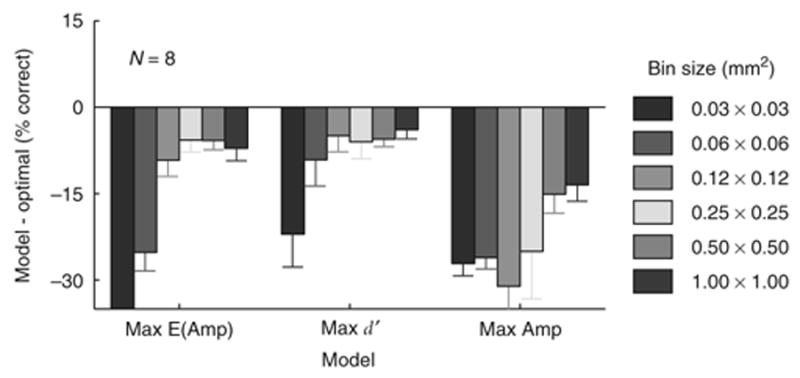
Effect of spatial binning on accuracy of the three pooling rules that rely on the response in a single site. Each bar indicates the difference in percent correct between the three pooling models at different bin size and the Optimal rule at the original bin size. Pooling rules that combine signals from a large area were relatively insensitive to the site size. For example, the Mean Amplitude rule gives exactly the same results irrespective of the site size. Error bars = one s.e.m.

Finally, we determined how the parameters of the temporal intervals used in our analysis affect the accuracy of the seven pooling rules (Fig. 7). The results of this analysis demonstrate that the relative performance of the different pooling rules is insensitive to the exact values of these temporal parameters.

Figure 7.

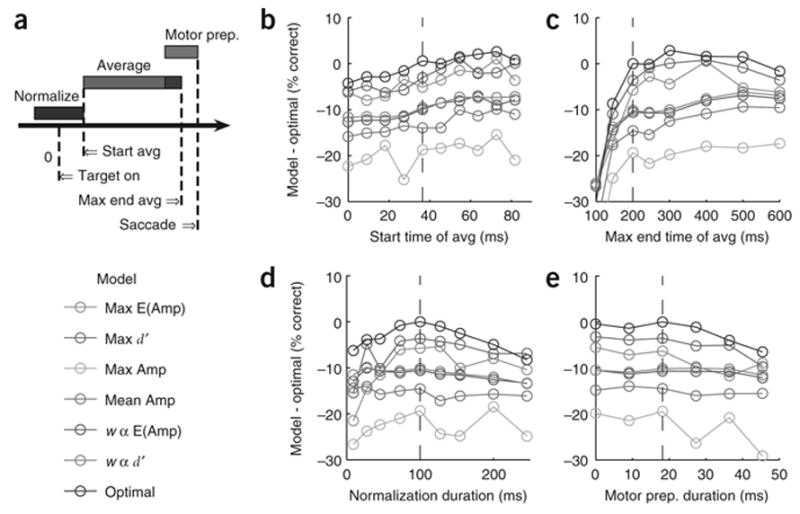
Effects of timing parameters on the accuracy of the seven pooling rules. (a) A diagram illustrating the four timing parameters used in our analysis. VSD signals at each site in each trial were first normalized by the average signal during a short normalization interval (blue bar) and then averaged during a short temporal interval (light red bar). The averaging interval started at a fixed time after stimulus onset (Start) and ended either at a fixed time before saccade initiation (the beginning of a Motor prep., green bar), or, if saccade did not occur or was sufficiently late, at the maximal time of averaging (Max end avg.). In the example in the diagram, the averaging period ends before the maximal averaging time because the maximal averaging interval and the motor preparation interval overlap (dark red region). (b–e) The average difference in percent correct between the Optimal rule using the default timing parameters and each of the seven models using different combinations of timing parameters, averaged over the eight experiments. (b) Effect of start time. (c) Effect of maximal averaging time. (d) Effect of normalization period duration. (e) Effect of motor preparation duration. Dashed blue vertical lines indicate default values.

DISCUSSION

In summary, our primary goal here was to characterize the statistical properties of population responses in V1, as measured by VSD imaging, and to determine the neuro-computational implications of those statistical properties for efficient decoding of population responses. We found that V1 population responses can be exquisitely sensitive to the presence of the visual target, and provide reliable information even at contrasts that are below psychophysical detection threshold. Target-related signals are distributed over several mm² in V1, even for small targets, and thus responses from a large population of neurons are available to subsequent decision and preoculomotor circuits. We observed strong and widespread spatial correlations in V1 responses, which set limits on the improvement that can be attained by pooling across the neural population. We found that the effect of these spatial correlations on subsequent processing stages could be minimized by using a simple pattern of excitatory and inhibitory connections.

The optimal antagonistic center-surround decoding rule that we report here for VSD signals in V1 is similar to decorrelation mechanisms that have been discussed extensively in the literature in the context of encoding⁴¹. These mechanisms, however, are conceptually quite different. While the decorrelation operation in the context of encoding is done for the purpose of redundancy reduction, the decorrelation at the decoding stage has to do with noise rejection. To the best of our knowledge, decorrelation for noise rejection has not been considered as an important decoding strategy at the level of neural populations.

It is important to note that, in general, it is difficult to draw strong conclusions about which decoding strategy is actually used by the subject from comparisons of neural and behavioral sensitivities. A decoding model could outperform the subject and still be used by the brain if inefficiencies downstream of the recorded area lead to a drop in behavioral performance. Similarly, a decoding model that performs worse than the subject could, in principle, still be used in the brain since recorded signals inevitably contain only a subset of the available neural information and may be contaminated by non-neural sources of noise. Therefore, our analysis is not aimed at determining which pooling rule is most consistent with the monkeys’ behavior.

Our finding that optimal pooling of VSD signals consistently outperforms the monkey demonstrates that VSD imaging is a sensitive measure of neural population responses and that inefficiencies at, or downstream to, V1 limit behavioral performance in our detection task. This finding would be less compelling if the monkeys were not performing as well as possible, perhaps because easy high-contrast trials were mixed with difficult low-contrast trials. This possibility is unlikely for three reasons. First, monkeys are heavily trained on this task and their performance is stable. Second, the monkeys’ performance at low contrast was not significantly improved when tested in control experiments in which only low-contrast targets were present. Finally, human performance on the same task, under identical conditions, did not differ significantly from monkey performance.

Recent results from our laboratory (C.R. Palmer, S.Y. Cheng and E.S., Soc. Neurosci. Abstr. 31, 509.11, 2005) suggest that some single units in V1 can be as sensitive as the monkey in the detection task. However, it is not clear whether subsequent processing stages can isolate the signals from those specific neurons and use them for performing the task. A more global pooling rule with excitatory and inhibitory connections could be more robust, efficient and easier to implement with neural circuits.

Communication between brain areas is primarily mediated by spike activity, whereas VSD responses emphasize subthreshold activity. It follows that some of the information in the VSD responses may not be transmitted from V1 to subsequent processing stages. Nonetheless, we note that the subthreshold responses are produced by spike activity in presynaptic neurons that are predominantly located within V1 (ref. ⁴²), and thus, the VSD signals are still likely to be tightly linked to spike activity in V1.

The widespread correlations and the relatively stimulus-independent response covariance observed here seem surprising at first, but in fact, are an expected consequence of pooling weakly correlated single neuron responses (whether subthreshold or suprathreshold). Furthermore, at each stage of processing, weak correlations may be an inevitable consequence of the cortical architecture with its massive convergence and widespread lateral and feedback connections. Given these considerations, it seems likely that decorrelation mechanisms (such as the one we propose) are widespread throughout the central nervous system.

The finding that antagonistic center-surround pooling is optimal in the face of significant spatial correlations may provide an additional and unexpected explanation for the pervasive center-surround receptive field organization, and the lateral inhibitory interaction between nearby populations of neurons in the cortex. More generally, our analysis shows that under conditions where the correlation between populations of neurons is high, computing the difference in the response between two highly correlated populations of neurons with different tuning properties should dramatically improve sensitivity. This could help explain why populations of neurons with opposite tuning properties are commonly found at adjacent locations in the cortex. For example, in macaque MT, neurons with opposite direction preferences are frequently located in adjacent columns⁴³. This architecture could allow subsequent mechanisms to remove correlated noise by pooling over a few nearby columns.

Although there are many ways in which the brain could deal with wide-spread spatial correlations, one general and efficient method would be to decode the population responses in two steps. First, apply a local whitening filter to the neural responses, and then apply a rule such as Weighted d′ (which is optimal for signals with uncorrelated variability) to the whitened signals. In this scheme, the whitening operation in the first step could be beneficial for multiple tasks.

In conclusion, we report that (i) most previously proposed models for decoding population responses are highly inefficient because of the strong and long-range spatial correlations, and (ii) a simple, biologically plausible decorrelation operation that uses excitatory and inhibitory mechanisms leads to optimal decoding in pattern detection tasks. These correlations have a potential detrimental impact on neural information processing in any perceptual or motor task. Thus, antagonistic pooling over populations of neurons with different tuning properties could be a general and robust strategy that is employed by the brain for efficient decoding of correlated neural population responses.

METHODS

Behavioral task and visual stimulus

Monkeys were trained to detect a small oriented Gabor target (sine wave grating multiplied by a Gaussian window) in a uniform gray background (Fig. 1a). Gabor targets have the advantage of being localized both in space and in the Fourier domain. Such targets are well optimized for activation of V1 neurons. Gabor target parameters were: σ = 0.25–0.33° , spatial frequency = 1.4–1.7 c.p.d., eccentricity = 2.7–4.0° ; orientation was typically horizontal. During each recording session, the monkey performed several hundred detection trials. Each trial began when the monkey fixated a small spot of light (0.1° × 0.1° ) on a video display. Following an initial fixation, the fixation point dimmed. In 50% of the trials, no target was presented and the monkey was required to maintain gaze within a small window (<2° full width) around the dimmed fixation point for a total of 1,500 ms, in order to receive a liquid reward. In the remaining trials, a target appeared 300 ms after the fixation point dimmed and remained on for 300 ms. The monkey was required to shift gaze to the location of the target within 600 ms from target onset and maintain gaze at that location for an additional 300 ms in order to receive the reward. Monkey reaction times (time of saccade initiation) were short for the highest contrast (median reaction time across all experiments ≈150 ms) and significantly longer for the lower contrasts (median reaction time > 300 ms), suggesting that a longer integration time is required for detection of low contrast targets. Within a block of trials, the target contrast was varied pseudorandomly between four to six levels, spanning the monkey’s detection threshold.

Behavioral results were fitted by a Weibull function³⁹:

$$P(C)=1-(1-\text{FA})\cdot {\text{e}}^{-{(\text{C}/\alpha )}^{\beta }}$$

where FA is the false alarm rate, C is the target contrast, and α and β are the offset and slope terms, respectively. The threshold was computed as the contrast at which accuracy is 75% (note that the threshold takes into account the false alarm rate).

Visual stimuli were presented on a high-end 21’’ color display. The display subtended 20.5° × 15.4° at a viewing distance of 108 cm, had a pixel resolution of 1024 × 768, 30-bit color depth and a refresh rate of 100 Hz. Visual stimuli were generated using a high-end graphics card on a dedicated PC, using custom-designed software. All stimuli were presented at a fixed mean luminance of 30 cd/m² on a gamma-corrected monitor. Behavioral measurements and data acquisition were controlled by a PC running a software package for neurophysiological recordings from alert animals (Reflective Computing). Eye movements were measured using an infrared eye-tracking device (Dr. Bouis Inc.).

Optical imaging with VSD

The experimental techniques for optical imaging with VSD in behaving monkeys have been described elsewhere^21,22,44. All procedures have been approved by the University of Texas Institutional Animal Care and Use Committee and conform to NIH standards. Briefly, we used oxonol voltage-sensitive dyes⁴⁵ to stain the cortical surface and an Imager 3001 system (Optical Imaging) to image brain activity. VSD responses measure the sum of changes in membrane voltage across all the elements within the superficial layers of the cortex²⁰.

Imaging data were collected using resolution of 512 × 512 at 110 Hz. For most further analysis, the VSD responses were further binned to a resolution of 64 × 64 pixels (sites), where each site corresponds to 0.25 × 0.25 mm. Bin size had a significant effect on the pooling models that rely on a single site (Fig. 6), but no significant effect on other pooling models (data not shown).

Our recording chambers were located on the dorsal portion of V1, with the anterior portion of the chamber reaching close to the lunate sulcus and the border between V1 and V2. We used intrinsic imaging and electrophysiology to determine the retinotopical organization in each recorded region and the layout of orientation columns. The cortex in our cranial windows represents stimuli that are ~2.5–5° away from the fovea in the lower quadrant of the contralateral hemifield.

Analysis of imaging data

We completed 15 VSD experiments in two hemispheres of two macaque monkeys. From these experiments, we selected for further analysis eight experiments in which the maximal d′ at 25% contrast stimulus exceeded 3.0. Experiments with lower sensitivity were usually attributable to poor staining or excessive noise.

Our analysis was divided into three steps: (i) we removed trials with aberrant VSD responses (generally less than 5% of the trials); (ii) we normalized the responses in each site by the average fluorescence in a 100 ms interval prior to stimulus onset; and (iii) we extracted from the VSD responses at each site the average response amplitude over a given temporal interval. The normalization in (ii) serves to minimize the effects of uneven illumination and staining, and to eliminate the effect of slow drift across trials in the VSD response. VSD responses were averaged during an interval that started 36 ms after stimulus onset and ended either 200 ms after stimulus onset or 20 ms before saccade onset in trials where reaction time was shorter than 220 ms (Fig. 7a). Our results are relatively insensitive to the exact values of these temporal parameters (Fig. 7b–e).

To remove trials with aberrant VSD responses, we evaluated the average response amplitudes at the site with the maximal d′. For each condition, the average across all repetitions was subtracted from the response in each trial and the standard deviation of the distribution of residuals was computed. Trials with residual response greater than two standard deviation values were excluded from further analysis. This simple procedure eliminates trials where the animal made excessive movements.