Noisy information processing through transcriptional regulation

Abstract

Cells must respond to environmental changes to remain viable, yet the information they receive is often noisy. Through a biochemical implementation of Bayes's rule, we show that genetic networks can act as inference modules, inferring from intracellular conditions the likely state of the extracellular environment and regulating gene expression appropriately. By considering a two-state environment, either poor or rich in nutrients, we show that promoter occupancy is proportional to the (posterior) probability of the high nutrient state given current intracellular information. We demonstrate that single-gene networks inferring and responding to a high environmental state infer best when negatively controlled, and those inferring and responding to a low environmental state infer best when positively controlled. Our interpretation is supported by experimental data from the lac operon and should provide a basis for both understanding more complex cellular decision-making and designing synthetic inference circuits.

For cells to interact with their environment, the DNA and regulatory machinery, which are intracellular, require information from the cell surface. This information is conveyed through gene and protein networks and is transferred via biochemical reactions that are potentially significantly stochastic (1–4). Stochastic fluctuations will undermine both signal detection and transduction. Cells are therefore confronted with the task of predicting the state of the extracellular environment from noisy and potentially unreliable intracellular signals. For example, a bacterium must decide from intracellular levels of a nutrient whether or not the nutrient is sufficiently abundant extracellularly to express the appropriate catabolic enzymes. Similarly, a smooth muscle cell must decide from concentrations of second messengers whether or not extracellular hormone levels are high enough to warrant contracting.

Here, we consider if, and how, it is possible for biochemical networks to correctly infer properties of the extracellular environment based on noisy, intracellular signals. Suppose that the cell should respond under high concentrations of an extracellular molecule. Suppose further that the concentration of an intracellular signaling molecule is related to the concentration of the extracellular molecule through a signal transduction mechanism. A simple inference network could establish a concentration threshold for the intracellular molecule. Only if the molecule is above threshold is the extracellular concentration judged to be high enough for a cellular response. This network performs poorly, however, in fluctuating extracellular and intracellular environments. First, fluctuations lead to input molecules crossing threshold even when the state of the environment is unchanged. Second, a threshold scheme cannot specify the degree of certainty in the inference, which may be important for the ultimate response. For example, a bacterium may express a catabolic operon once the degree of certainty in high extracellular levels of a particular nutrient reaches 40%, but it may only shut down other catabolic operons once the degree of certainty is larger, say 80%.

The method of Bayesian inference both accounts for fluctuations and gives a degree of uncertainty in predictions (5). We postulate that the cellular regulatory machinery may have evolved to perform Bayesian inference on some intracellular inputs. Typically, a cellular decision has two levels: first, predicting the state of the environment; second, choosing the appropriate response. At this second level, the expected costs must be compared with expected benefits (6). Although Bayesian theory can handle both problems, we focus here on the first: classification of the local environment.

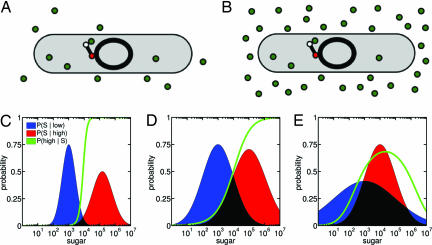
As an example, consider a bacterium with a nutrient scavenging operon that encodes enzymes to import and catabolize a sugar (Fig. 1 A and B). Suppose the environment can be in one of two states: a high or a low sugar state, for example, the high- and low-lactose environments of the small intestine (7). The intracellular concentration of the sugar depends on the extracellular state, although in a stochastic fashion. To optimize growth, the bacterium must predict the extracellular state from intracellular sugar because expressing the operon involves a significant metabolic cost (6, 8). Let S be the intracellular sugar level at a particular time. We denote the probability (i.e., the fraction of time) that there are S intracellular sugar molecules given that the environment is in the low sugar state as P(S|low). Similarly, we denote the probability that there is S intracellular sugar molecules given that the environment is in the high sugar state by P(S|high). If fluctuations are negligible, these two distributions will be sharply peaked functions of S, and they will be broader as fluctuations become significant.

Fig. 1.

A two-state classifier problem and its Bayesian solution, the posterior probability. A cell must infer from intracellular concentrations of a nutrient or signaling molecule (green circles) whether the molecule is in high or low concentrations in the extracellular environment. (A and B) Fluctuations in the environment and molecule detection and transport can lead to similar intracellular concentrations of the molecule for different extracellular conditions. The cellular decision-making machinery, shown as a simple genetic network, must decide from intracellular information the probable state of the extracellular environment. (C) Two distributions for intracellular numbers of a sugar molecule: the low sugar state is in blue, the high sugar state is in red. For an intracellular sugar level S, the green curve is the posterior (predicted) probability that the extracellular state is the high sugar state, P(high|S). (D) For two intracellular distributions that overlap substantially, the posterior probability for the high sugar state transitions gradually from low to high values. (E) The posterior probability, P(high|S), need not be monotonic. The low sugar state is more probable at both low and high intracellular sugar, and P(high|S) goes through a maximum.

The bacterium must determine the probability that its extracellular environment is in a high sugar state based on levels of intracellular sugar. This probability is denoted P(high|S). A Bayesian approach assumes that some information about the long-term probable states of the environment is known. This information could be simply that the environment is expected to be in one of two states, either a low or a high sugar state, and that each state is a priori equally likely. In one particular environment (for example, the soil), though, a low sugar state may occur more often on the long term. The a priori probability for this state will then be higher. Such a priori, or prior, probabilities are denoted P(high) and P(low). Once sugar enters the cell, the a priori probabilities are updated based on the levels of sugar detected. The more intracellular sugar, the larger the predicted probability of the environment being in the high sugar state (and the smaller the corresponding probability of the low sugar state). This a posteriori probability of the high state is P(high|S). It is referred to as the posterior (predicted) probability of the high state given intracellular sugar S.

Bayes's rule states explicitly how the prior probabilities are correctly updated to their posterior values for the levels of sugar detected (9) (see Materials and Methods):

Intuitively, the more likely a particular intracellular S is in the high extracellular state compared with the low extracellular state [the greater P(S|high) is compared with P(S|low)], the higher the posterior probability of a high state environment. For simplicity, we will assume that the environment is a priori equally likely to be in either state: P(high) = P(low) = 1/2. The prior probabilities then play no mathematical role in Eq. 1. Often the posterior distribution, P(high|S), is a sigmoidal curve. Fig. 1C shows two distributions for numbers of sugar molecules: a distribution for a low extracellular sugar state (in blue) and a distribution for a high extracellular sugar state (in red). The corresponding posterior probability curve is shown in green in Fig. 1C. If the intracellular sugar level, S, is low, there is a high predicted probability that the extracellular state is low, with the converse holding for high intracellular sugar levels. In an intermediate range of S, lying in the overlap between the two state distributions, P(high|S) switches from low probability to high probability. When fluctuations are more significant and the overlap between the two distributions is greater, the transition is more gradual (Fig. 1D). The posterior probability need not always be sigmoidal: Fig. 1E shows a long-tailed distribution for the low sugar state that results in a nonmonotonic posterior curve.

We will argue that a single gene can make probabilistic inferences about extracellular states through a biochemical implementation of Bayes's rule. By tuning the kinetic rates of the system, the promoter efficacy, the fraction of time the promoter is capable of initiating transcription, can match the posterior probability of high extracellular sugar. Consider a negatively controlled operon. We view the repressors controlling the gene as detectors that monitor intracellular sugar levels. Repressors thermally flip back and forth between two allosteric forms (10): one DNA binding and the other non-DNA binding. As each repressor diffuses in the cytosol, it samples intracellular sugar. At low sugar levels, the DNA binding form of the repressor is stable, and the operon is not expressed. At high sugar levels, the non-DNA binding form is stable, leading to expression. Repressor binding sites on the promoter “read” the allosteric form of cytosolic repressors and control transcription. Promoter efficacy is therefore a readout of the number of non-DNA binding repressors, which, in turn, are a readout of sugar levels.

Cis-Regulatory Regions as Inference Modules

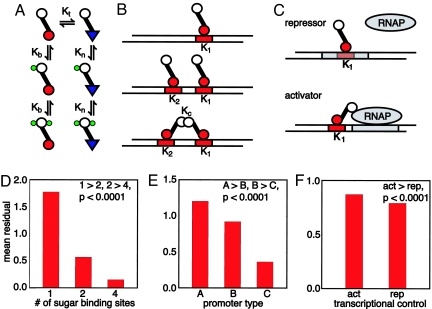
We tested the ability of different regulatory mechanisms to classify a two-state environment. We considered 18 different networks (Fig. 2 A–C): regulation can be positive or negative, transcription factor can allosterically bind either one, two, or four sugar molecules, and promoters can be one of three different types. Network input is the number of sugar molecules, which range from zero to ≈2,000 times the number of transcription factors. Network output is promoter efficacy (i.e., promoter bound by an activator for positive control and free of repressor for negative control). Rather than specialize to particular sugar distributions for the high and the low states, we generated 50 different pairs of lognormal distributions for S. Each pair corresponded to a different inference problem and had a different, but always sigmoidal, posterior probability. We fit the kinetic rates of each network to minimize the squared error between promoter efficacy and P(high|S) as a function of S for each of the 50 posteriors (see Materials and Methods). A network that fits this collection of posterior curves well has a network architecture able to solve a variety of (two state) inference problems; it is an inference module.

Fig. 2.

A comparison of different regulatory mechanisms for solving the two-state discrimination problem; highly cooperative, negatively controlled genetic networks perform the most accurate inference. (A) The Monod–Changeux–Wyman model of an allosteric transcription factor. Association constants are denoted by Ks. The protein flips between DNA binding (red circles) and non-DNA binding forms (blue triangles). If K_b ≫ K_n, sugar stabilizes the DNA binding state. Conversely, if K_n ≫ K_b, the non-DNA binding state is stabilized. Two sugar binding sites are shown, but we also test models with one and four binding sites. (B) We consider three different promoters: type A, one active operator site (Top); type B, two active operator sites, but with no cooperative binding between transcription factors (Middle); and type C, one active and one inactive operator with cooperative transcription factor binding (Bottom). (C) Transcription can by regulated either negatively, via repressors that obstruct RNA polymerase (RNAP) binding, or positively, via activators that help stabilize RNAP binding. The RNAP binding site (sigma site) is shown in gray, operators in red. (D) Mean residuals (a high residual implies a poor fit) from fits to 50 different posterior probabilities for the models grouped by the numbers of sugars bound by transcription factor. Models with four transcription binding sites perform the best inference (P value for one model type consistently performing better than the other is given; see SI Appendix). (E) Mean residuals for models grouped by promoter type. Cooperative promoters perform best (type C). (F) Mean residuals for models grouped by their mode of transcriptional control. Repressors perform better than activators (for >70% of the fits, corresponding to a P value substantially <10⁻⁴).

Networks with higher cooperativity, either through the ability of transcription factor to allosterically bind sugar or cooperative binding of transcription factors to DNA, perform best (Fig. 2 D and E). A genetic inference system with low cooperativity is unable to generate a promoter efficacy curve that switches sharply with S (10). These models thus perform poorly on those inference problems with distinct sugar distributions and therefore strongly sigmoidal posterior probabilities (compare the posterior probabilities for Fig. 1 C and D).

Less intuitively, negatively controlled inference systems perform significantly better than positively controlled systems (Fig. 2F). Positively controlled systems are less able to exploit cooperativity. Activators should bind DNA as sugar levels rise. Consequently, K_b ≫ K_n in Fig. 2A. For low sugar, the posterior probability is close to zero (Fig. 1 C and D), and no activators at all should bind DNA. Therefore K_b must be small, and the more activators present, the smaller K_b must be. As K_b ≫ K_n, both K_b and K_n are small: there is weak sugar binding, and cooperative binding occurs only at high sugar levels. Contrarily, in a negatively controlled system, K_n ≫ K_b, so that sugar lifts repressor off DNA. For low sugar, just one repressor must bind DNA to maintain a low promoter efficacy. More repressors allow K_b to be smaller, giving greater, not less, flexibility in K_n. Altering K_t, the equilibrium between the DNA and non-DNA binding forms in the absence of sugar and can partly offset the inherent frustration in the activator system, but not completely (Fig. 2F). Therefore, negatively controlled promoters are best able to tune promoter efficacy to track P(high|S).

Although negatively controlled systems can better match their promoter efficacy to P(high|S) than positively controlled systems, the opposite holds for matching P(low|S). This posterior probability satisfies P(low|S) = 1 − P(high|S) and so has the opposite behavior to P(high|S). The argument given above is reversed. Thus, for systems that respond to a low state of the environment, positive control gives the best inference.

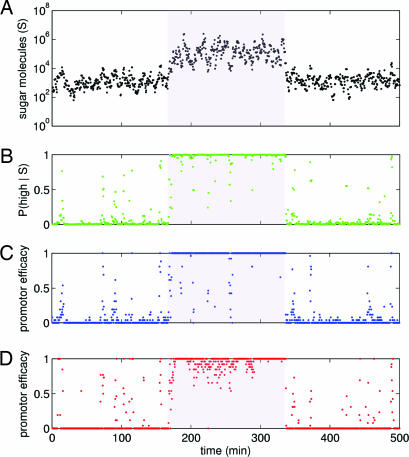
Fig. 2 demonstrates that model genetic networks can perform inference, with equilibrium promoter efficacy tracking posterior probability; Fig. 3 shows that inference can occur in real time in noisy environments. For the two sugar distributions in Fig. 1C, we chose the activator and repressor networks that best fit the posterior probability of the high sugar state. We performed a stochastic simulation of each of these networks by using the best-fit parameters, and let the environment change from a low to a high and back to a low sugar state. In each state, we sampled from the appropriate sugar distribution, mimicking intracellular fluctuations, and producing a time series of intracellular sugar (Fig. 3A). For each sugar level, there is a different posterior probability of the high extracellular sugar state (Fig. 1C). This instantaneous posterior probability is shown in Fig. 3B. Most often, P(high|S) is very low (near zero) or very high (near one). It should be compared with the response of each network, measured by their promoter efficacies (Fig. 3 C and D). The promoter efficacy of the repressor network (Fig. 3C) and the activator network (Fig. 3D) closely follow the instantaneous posterior probability, although the activator network underestimates the probability of the high sugar state. A quantitative measure of the goodness of fit of each promoter efficacy to P(high|S) shows that repressor performs more than twice as well as activator [see supporting information (SI) Appendix].

Fig. 3.

Two-state inference by simulated genetic networks. (A) A time series of intracellular sugar molecules as the extracellular environment moves from a low to a high (shaded region) and back to a low sugar state. Histograms of the intracellular sugar distributions are shown in Fig. 1C. Sugar was sampled every 25 s. In the low state, mean sugar numbers are ≈10³; in the high state, mean sugar numbers are ≈10⁵. (B) The instantaneous posterior probability of the high sugar state, P(high|S), for the particular sugar level existing at the current time point. Posterior probability points come from the green curve in Fig. 1C. (C) The average promoter efficacy for the best repressor network of Fig. 2, four sugar binding sites on the repressor and promoter type C. The actual promoter efficacy is either zero (promoter bound by repressor) or one (promoter not bound). An average over the 25-s period chosen to sample the sugar is shown. (D) The average promoter efficacy for the best activator network of Fig. 2, again four sugar binding sites on the activator and promoter type C. Simulation details are in SI Appendix.

Inference in the lac Operon

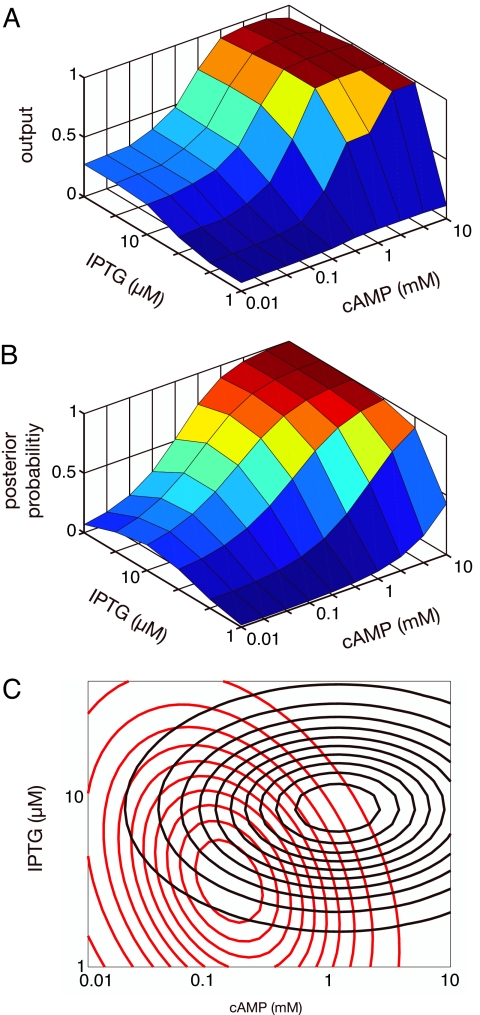
Viewing networks as inference modules gives additional interpretations of in vivo behavior. For example, Setty et al. (11) measured the transcription rate of the lac operon in Escherichia coli as a function of two inputs: isopropyl β-d-thiogalactoside (IPTG), an analogue of lactose, and cAMP. Traditionally, transcription of the lac operon is described as being “on” in the presence of sufficient cAMP and sufficient lactose, i.e., its cis-regulatory region performs a logical “AND” on the two inputs (12). Setty et al. found more complex behavior: with enough IPTG, there is significant transcription at low cAMP, and transcription increases smoothly, rather than in a switch-like fashion, as cAMP increases (Fig. 4A). The shape of this surface can be explained if the lac operon has evolved to solve a two-state inference problem. The high state corresponds to a state where the lac operon should be expressed, an extracellular environment rich in lactose and poor in glucose, resulting in both high intracellular lactose and cAMP [cAMP concentrations are inversely proportional to glucose levels (13)]. The low state, where the lac operon should not be repressed, corresponds to an extracellular environment poor in lactose and rich in glucose. We interpret S in Eq. 1 as the set of two variables: intracellular IPTG and cAMP concentrations (see Materials and Methods). Assuming bivariate lognormal distributions for IPTG and cAMP in each state, we fit the parameters of the distributions so that the posterior probability, P(high|S), matches the data of Fig. 4A (Fig. 4B). Two lognormal distributions that generate this posterior are shown in Fig. 4C. [Note that the axes represent measured extracellular levels, which are assumed to be proportional to intracellular levels (11).] The lac transcription rate is explained well by a two-state model in which mean intracellular levels of IPTG are approximately three times higher in the high state than in the low state and cAMP levels are 10 times higher.

Fig. 4.

Inference by the lac operon in E. coli. (A) Observed transcriptional output (transcription rate) as a function of extracellular concentrations of IPTG and cAMP (both log-scaled), normalized to range from zero to one (data from ref. 11). (B) Posterior probability, fit to the data in A, that the environment is in a high state given the concentrations of IPTG and cAMP. (C) A possible two-state model for E. coli's view of its extracellular environment. The low state is in red (peak at approximately 3 μM IPTG and 0.2 mM cAMP), and the high state is in black (peak at 8 μM IPTG and 1.2 mM cAMP). Both states are described by bivariate lognormal distributions.

Discussion

We have argued that a single gene through allosteric control and its cis-regulatory region can statistically infer the state of the extracellular environment from intracellular inputs. Cis-regulatory regions are often considered to perform logical operations on their input, allowing gene expression only under a particular combination of inputs (14, 15). Such a view has been especially successful in understanding development (16), where gene expression occurs in an ordered manner. Cell behavior need not, however, follow a predetermined pattern, and in these cases a cell that infers the state of its environment may have an evolutionary advantage. A genetic network, or more generally a biochemical network, that performs inference allows the cell to optimally interpret fluctuating inputs. Expression of the lac operon is a possible example, but inference is also likely to occur in signal transduction networks. Although we have emphasized the sigmoidal character of the posterior probability, networks that perform Bayesian inference need not have a sigmoidal output. Fig. 1E shows two sugar distributions that produce a biphasic posterior probability. Such behavior has been reported, for example, in the E. coli gal operon (17), and is hard to justify within a logic gate description.

We predict that a positively controlled genetic inference module is more likely to infer the probability of the environment being in a low state and that a negatively controlled system is more likely to infer the probability of the environment being in a high state. For example, the cAMP receptor protein in E. coli is an activator and promotes high promoter efficacy of the lac operon when glucose levels are low; LacI is a repressor and promotes high promoter efficacy when lactose levels are high (12). This bias is expected to be stronger for networks with less cooperativity.

Although we have focused on a single estimate of the probability of the extracellular state, cells might be expected to perform long-term integration of noisy signals. Such integration could occur by changing the prior probabilities of the high and low states. For example, an E. coli previously exposed to lactose has a higher concentration of lactose permease in its cell membrane than one not exposed (18). This greater permease concentration may reflect an increase in the prior probability of the high extracellular lactose state, i.e., P(high) > P(low). Eq. 1 then predicts a sigmoidal response that favors the high state: the posterior probability curve is shifted toward lower sugar levels. This change mimics the change expected in promoter efficacy of the lac operon: higher permease concentrations lead to gene expression (higher promoter efficacy) at lower extracellular lactose levels because lactose more efficiently enters the cell.

In our framework, the output of different networks are distinct functions of their input because each network is solving a different inference problem. For example, if the intracellular distributions of the two extracellular states strongly overlap, a repressor may have a high allosteric constant (K_t in Fig. 2A) to give a more sigmoidal promoter efficacy curve, reflecting the steep posterior probability. The promoter efficacy curve is most sensitive, however, to the inducer binding affinity (K_n for repressors and K_b for activators). Its sensitivity is more than three times higher than the next most sensitive parameter (K_t) (see SI Appendix). If the extracellular environment substantially changes, leading to a new inference problem, the most efficient way to evolve to the new posterior probability is to modify the sugar binding affinity. This modification has the benefit of preserving the connectivities of preexisting genetic networks.

Cellular inference need not follow the simple two-state classifier model proposed here. Multistate classifiers and real-time averaging methods are more appropriate for some problems. Nevertheless, given the prevalence of sigmoidally responding biochemical networks (19), the two-state classifier, whose solution is often a sigmoidal posterior probability, may be an essential component of many inference and decision-making networks in cells. Interpreting biochemical networks as inference modules may be an important step for both unraveling cellular behavior and designing selective, synthetic gene circuits.

Materials and Methods

Modeling Genetic Networks.

We use the Monod–Wyman–Changeux model (10) to describe allosteric transcription factors. We assume that both the total amount of sugar and the total amount of transcription factors are conserved. Given these values, we numerically solve for the amount of free sugar and the total amount of transcription factor in the DNA binding state, irrespective of the number of sugars each individual transcription factor has bound (see SI Appendix).

To calculate promoter efficacies, we follow a statistical mechanics approach (20) to describe the equilibrium occupancies of the different states of the promoters of Fig. 2B (see SI Appendix).

Comparison of the Models as Bayesian Classifiers.

To test the ability of the models to implement a Bayesian classifier, we fit each model to the posterior probabilities for 50 different two-state classification problems. For each problem, we generated two sugar distributions corresponding to a low and a high sugar state. From these distributions, we calculated the posterior probability of being in the high state for each concentration of sugar S:

We can rewrite the expression for the probability of a sugar concentration as:

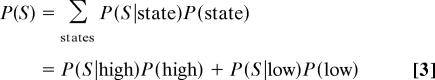to derive Eq. 1. For simplicity, we assume equal priors; allowing unequal prior probabilities for the two states does not change our results.

We considered two-state classification problems generated by Poisson, normal, and lognormal distributions of sugar. The results of Fig. 2 D–F are for lognormal distributions, but are qualitatively the same independent of the distribution type chosen. The probability P(S|state) in Eq. 1 is therefore:

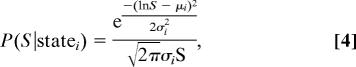where i = 1 for the low state and i = 2 for the high state. Each state has a different μ_i and σ_i, which define the mean and standard deviation in log space of the distribution. We chose 50 posterior probability curves that best gave a range of different inference problems (see SI Appendix).

We used a least-square fit to score how well a model matches the posterior probability of the high state. To fit we use an interior-reflective Newton method (lsqnonlin in Matlab, Mathworks, Natwick, MA). Each posterior probability curve generated has 100 points (evenly spaced in log space), and we fit all 18 models to each curve 500 times with different initial conditions, for a total of 450,000 fits. The P values for the residual comparisons were computed by using a Wilcoxon two-sided signed rank test (signrank in Matlab). For each fit, we calculated the difference in the residual for a particular pair of models. The null hypothesis was that these differences came from a distribution with median zero.

Stochastic Simulation.

We simulated both a repressor and an activator model. We chose a posterior probability from the 50 used in the fitting (the posterior of Fig. 1C) and the repressor and activator model that fit it best (parameters are given in SI Appendix). The selected repressor and activator models both have four sugar binding sites and promoter type C in Fig. 2B. To generate a relatively smooth time series of sugar levels, we used a Markov chain Monte Carlo method (5) to produce fluctuating, dependent samples of sugar from the appropriate distribution in Fig. 1C. For each sugar sample, the cytosolic sugar levels were changed to the new sampled value. A stochastic simulation of the genetic network was then run for a fixed time interval of 25 s by using the Gillespie algorithm (21) (results for different time intervals are given in SI Appendix). A new sugar sample was then taken and the simulation of the genetic network run again. The average value of the promoter efficacy during each simulation run is shown in Fig. 3 C and D.

Fitting a Posterior Probability to the Transcription Rate of the lac Operon.

We fit the data of Fig. 4A to Eq. 1 where each state is characterized by two variables: s₁ corresponding to the logarithm of the IPTG concentration and s₂ corresponding to the logarithm of the cAMP concentration. P(S|high) is then a bivariate normal distribution:

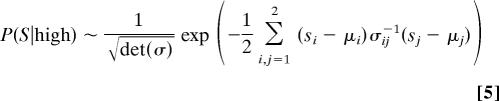with μ₁ the mean of s₁, μ₂ the mean of s₂, and σ the covariance matrix of s₁ and s₂, all for the high state. A similar set of parameters is needed to describe the low state. The problem of fitting Eq. 1 to a given posterior probability surface is degenerate: different sets of parameters can result in the same posterior surface (see SI Appendix). However, we can identify a unique posterior probability surface that best fits the lac operon data (Fig. 4B) along with the family of two-state discrimination problems that generate the posterior surface. Fig. 4C shows one example of this family.

Abbreviation

IPTG

isopropyl β-d-thiogalactoside.