An exceptionally fast actomyosin reaction powers insect flight muscle

Abstract

Insects, as a group, have been remarkably successful in adapting to a great range of physical and biological environments, in large part because of their ability to fly. The evolution of flight in small insects was accompanied by striking adaptations of the thoracic musculature that enabled very high wing beat frequencies. At the cellular and protein filament level, a stretch activation mechanism evolved that allowed high-oscillatory work to be achieved at very high frequencies as contraction and nerve stimulus became asynchronous. At the molecular level, critical adaptations occurred within the motor protein myosin II, because its elementary interactions with actin set the speed of sarcomere contraction. Here, we show that the key myosin enzymatic adaptations required for powering the very fast flight muscles in the fruit fly Drosophila melanogaster include the highest measured detachment rate of myosin from actin (forward rate constant, 3,698 s⁻¹), an exceptionally weak affinity of MgATP for myosin (association constant, 0.2 mM⁻¹), and a unique rate-limiting step in the cross-bridge cycle at the point of inorganic phosphate release. The latter adaptations are constraints imposed by the overriding requirement for exceptionally fast release of the hydrolytic product MgADP. Otherwise, as in Drosophila embryonic muscle and other slow muscle types, a step associated with MgADP release limits muscle contraction speed by delaying the detachment of myosin from actin.

In Drosophila melanogaster two sets of antagonistic, asynchronous flight muscles oscillate at ≈200 beats per second, powering the wings indirectly by deforming the thoracic cuticle into which the muscles and wings insert. Although the myofibrillar basis of oscillatory work and power production is known (1–5), the molecular adaptations that allow the indirect flight muscles (IFM) to operate at very high frequencies are less well understood. In muscles of slow-to-moderate speed, muscle velocity is thought to be limited by prolonging the time myosin spends strongly bound to actin before detachment (6, 7). The prolongation is essential for coupling enzyme chemical kinetics, which normally occur rapidly, to the slower movements of the sarcomere during normal muscle function. In most vertebrate striated muscle types, the comparatively slow release of MgADP (one of the products of MgATP hydrolysis) is thought to be the rate-limiting step (8–13). However, recent studies suggest MgADP release may not be rate limiting for faster muscle types (14–16). If so, we reasoned that a shift in rate-limiting step to another part of the cross-bridge cycle should be most readily apparent in working indirect insect flight muscle, the fastest known muscle type.

We had directly shown that myosin isoforms determine Drosophila IFM speed by using genetic engineering methods to substitute a relatively slow embryonic myosin (EMB) for the native fast myosin (IFI) in the IFM (Fig. 1A Inset) (17, 18). This substitution transformed the normally superfast IFM into a comparatively slow muscle because an 8-fold reduction in frequency of maximal oscillatory work was observed. Laser-trap studies showed that both isoforms have similar unitary step size (19, 20), leading to the conclusion that differences in duration of at least one state of the cross-bridge cycle accounts for the observed differences in IFI and EMB kinetics. To identify which steps are modified to enable D. melanogaster IFM to achieve their remarkable speeds, we compared mechanical performance indices of skinned IFI and EMB transgenic IFM fibers upon manipulation of MgATP or Pi concentration ([MgATP] or [Pi]) (18).

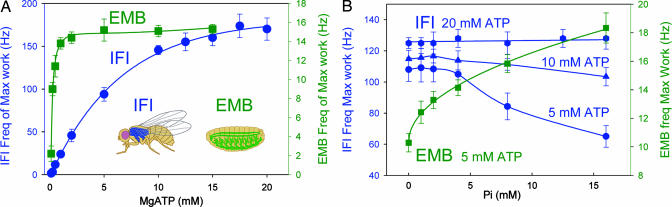
Fig. 1.

IFI fiber kinetics showed an unusual response to [MgATP] and [PI], whereas IFM expressing the slow EMB myosin isoform showed the typical response. (A) Effect of MgATP on frequency of maximum work (fw_max) during small-amplitude sinusoidal-length perturbations. pCa 5.0, 300 units/ml creatine kinase, 20 mM creatine phosphate, 0 mM MgADP, and 0 mM Pi. Number of fibers (n) = 6 for EMB and 8 for IFI. All values are mean ± SEM. The high [MgATP] (≈15 mM) required for maximal fw_max is not because of inadequate regeneration or diffusion of MgATP into our skinned-fiber system, because elevating the concentrations of key components of the MgATP-regenerating system above the levels used for this experiment had no effect on fw_max when MgATP levels are >5 mM (see Fig. 5, which is published as supporting information on the PNAS web site). (Inset) Illustrations showing native locations of the two myosins transgenically expressed in the indirect flight muscle. Very fast IFI is found in the asynchronous IFM fibers (blue). A slow EMB is found in some of the embryonic and larval body wall muscles (green). (B) Effect of Pi on frequency of maximum work (f_Wmax) at 0 mM MgADP, 30 mM CP, and 900 units/ml CK; n = 8, 10, 3, and 6 for IFI at 5 mM, 10 mM, and 20 mM MgATP and EMB fibers at 5 mM MgATP, respectively. Increasing or decreasing MgATP concentration had no effect on EMB's response to Pi (data not shown). These unusual responses to MgATP and Pi were also observed with tension (see Fig. 6, which is published as supporting information on the PNAS web site). Under subsaturating conditions (5–10 mM), IFI myosin's unusually weak affinity for MgATP explains the decrease in fw_max observed with increasing Pi, because the lower affinity allows for competitive binding between Pi and MgATP for myosin. In slower fiber types, competition is observed only at very high Pi-to-MgATP ratios (31).

Results and Discussion

Although the slower EMB-expressing fibers exhibited conventional responses to changes in [MgATP] or [Pi], the response of the superfast IFI fibers to the chemical perturbations produced two highly unusual and unexpected responses (Fig. 1): (i) an unusually high [MgATP] was required for IFI fibers to work at their maximum speed (Fig. 1A) and (ii) a qualitatively different response to phosphate (Fig. 1B). For both IFI and EMB, elevating [MgATP] increased the frequency of optimum work production (fw_max) to a saturating level (Fig. 1A), a result qualitatively similar to that observed in other muscle types (11, 12, 21). However, ≈15 mM MgATP was required to reach maximal fw_max in IFI compared with ≈2 mM for EMB-expressing fibers, which suggests that the affinity of MgATP for myosin is much lower in IFI than in EMB.

The remarkable qualitative difference observed in response to phosphate (Fig. 1B) suggests that IFI has a distinctly different rate-limiting step than EMB in the working muscle. In IFI fibers at saturating levels of MgATP (15–20 mM), fw_max was insensitive to changes in [Pi]; at 10 mM MgATP, fw_max showed a slight tendency to decrease with increasing [Pi]; at 5 mM MgATP, fw_max decreased significantly with increasing [Pi]. These trends are opposite to the Pi-dependent rise in fw_max observed in EMB fibers and all other striated muscle fiber types studied by using this technique (10–12, 21). The lack of IFI fw_max sensitivity to [Pi] at saturating [MgATP] strongly suggests a departure from the typical myosin cross-bridge scheme, where, with MgADP rate limiting for oscillatory work production, fw_max is not independent of [Pi] in working muscle (9–12, 21–23).

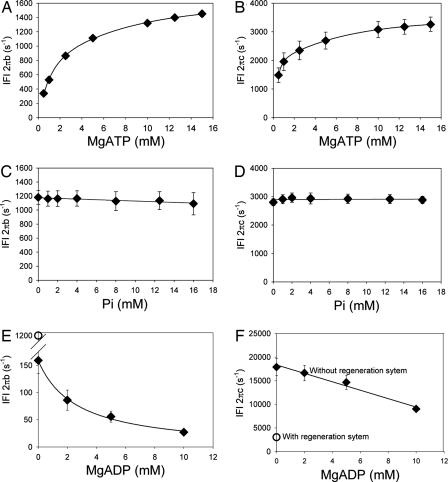
To identify the correct rate-limiting step for IFI, we examined the qualitative effects of [MgATP], [MgADP], and [Pi] on the characteristic frequencies of the work-producing (B) and work-absorbing (C) processes of IFI fibers undergoing small-amplitude sinusoidal oscillations (see Materials and Methods and Fig. 4, which is published as supporting information on the PNAS web site). Fig. 2 depicts the substrate dependencies of the apparent rate constants 2πb and 2πc of processes B and C (derived by fitting a 3-term expression to the complex modulus of the calcium-activated fiber, see Materials and Methods). The data (schematically depicted in Fig. 3A) were compared with predictions from eight alternative biochemical schemes (Fig. 3 B and C) deduced by using analytical techniques developed by Kawai and colleagues (9). Steady-state solutions were obtained by solving the differential equations that describe each reaction scheme (Supporting Methods, which is published as supporting information on the PNAS web site). At saturating levels of MgATP (10–20 mM), the IFI data uniquely fit a scheme in which Pi release is the rate-limiting step (Fig. 3 A and C), in accord with a recent biochemical study that suggests MgADP release is extremely fast from Drosophila IFI myosin (15). The slow EMB-fiber data, on the other hand, fit a configuration in which the rate-limiting step is an isomerization of myosin before MgADP release (Fig. 3 A and C), consistent with reaction schemes proposed for other slow striated muscles (11, 12, 21).

Fig. 2.

The response of IFI fiber sinusoidal rate constants 2πb and 2πc to [MgATP] (A and B), [Pi] (C and D), and [MgADP] (E and F). (A and B) 0 mM Pi, 0 mM MgADP, 45 mM CP, and 1,200 units/ml CK; n = 10. (C and D) 10 mM MgATP, 0 mM MgADP, 45 mM CP, and 1,200 units/ml CK; n = 10. (E and F) 5 mM MgATP, 0 mM Pi, 0 mM CP, and 0 mM CK; n = 5. To vary [MgADP], the MgATP-regeneration system (CP and CK) was, by necessity, omitted in the solutions of E and F, resulting in large changes in 2πb and 2πc (compare with open symbols showing values with the regeneration system present). Because the changes are not related to the direct effect of [MgADP], the [MgADP] data are included for qualitative comparisons only.

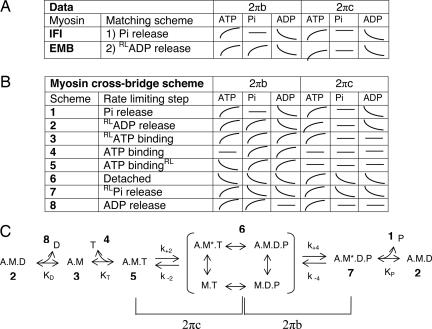
Fig. 3.

Determination of the rate-limiting step for IFI and EMB myosin isoforms. (A) Observed direction of shifts of IFI and EMB apparent rate constants with increasing concentrations of MgATP, MgADP, or Pi. The 2πb and 2πc are apparent rate constants of work-producing and work-absorbing cross-bridge processes, respectively. Curves indicate direction of change, if any, with increasing concentrations, in the manner shown. (B) Predicted shifts of apparent rate constants from calculations based on eight schemes with different rate-limiting steps (corresponding to numbers in the cross-bridge scheme in C). The details of the calculations are given in supporting information. The rate-limiting step (RL) in schemes 2, 3, 5, and 7 is an additional structural isomerization within the corresponding cross-bridge state labeled in C (before or after ligand binding or release). (C) Generic cross-bridge scheme for work production (modified from refs. 11, 12, and 21), where M is myosin, A is actin, T is MgATP, D is MgADP, and P is phosphate. An asterisk identifies a second conformational state. For conceptual purposes, the primary steps that determine 2πb and 2πc are highlighted. The complete relationships of 2πb and 2πc to the elementary rate constants k₊₂, k₋₂, k₊₄, and k₋₄, affinity constants for MgADP (K_D), MgATP (K_T), and phosphate (K_P), and population of cross-bridge states are fully described in supporting information.

With the appropriate scheme in hand, we calculated the unique cross-bridge rate constants for IFI fibers from analytical expressions for 2πb + 2πc and 2πb × 2πc as functions of [MgATP], returned from least-squares fits to the data (Materials and Methods and Fig. 7, which is published as supporting information on the PNAS web site). Table 1 compares the kinetic constants obtained for IFI fibers with corresponding values reported for three rabbit fast skeletal-muscle fiber types (12). The IFI results extend trends seen in the vertebrate fast muscle, where increased muscle speed correlates with a decrease in the MgATP-affinity constant and an increase in forward rate constants k₊₂ and k₊₄, both of which are higher than any reported to date. Elementary rate constant k₊₂ characterizes the forward reaction of the work-absorbing A.M.T isomerization associated with cross-bridge detachment, whereas k₊₄ characterizes the forward reaction of the work-producing A.M.D.P isomerization associated with cross-bridge attachment (Fig. 3C). Increased muscle speed in vertebrate fast muscle is also correlated with increases in k₋₂ and k₋₄ (reverse rate constants), but the upward trend is reversed for superfast IFI, where the values of k₋₂ and k₋₄ are considerably less than those for the fastest fiber type in rabbit (IIB). Notably, the value of k₋₄ is essentially zero compared with the forward rate constant k₊₄ (ratio, 1:161). Thus, IFM evolved a mechanism of nearly irreversible binding of myosin to actin at a step in the cycle closely associated with the power stroke. The nearly irreversible binding evolved for at least two reasons: (i) to promote the forward reactions, which need to occur very quickly and (ii) to promote the storage of elastic energy during the wing beat by having a population of myosin heads strongly bound to actin filaments when the muscle nears the end of its lengthening cycle (4). The stored potential energy is converted back to mechanical energy during subsequent shortening, thereby increasing efficiency.

Table 1.

Comparison of kinetic constants for IFM fibers and rabbit fast skeletal-muscle fibers

		Rabbit skeletal*			Drosophila
Constant	Units	Type IIA	Type IID	Type IIB	IFM
KATP	mM−1	14.7 ± 1.6	4.9 ± 1	0.8 ± 0.1	0.19 ± 0.02
k+2	s−1	205 ± 18	352 ± 23	526 ± 76	3698 ± 219
k−2	s−1	30	121 ± 30	328 ± 32	8 ± 37
k+4	s−1	12 ± 1	58 ± 4	143 ± 10	1778 ± 190
k−4	s−1	16 ± 2	63 ± 9	81 ± 6	11 ± 31
KATPk2	μM−1s−1	3.01 ± 0.06	1.72 ± 0.37	0.44 ± 0.09	0.70 ± 0.06
Muscle speed	Relative	Fast	Very fast		Superfast

Values for K_ATP and the elementary rate constants associated with work-producing cross-bridge attachment (k₊₄ and k₋₄) and work-absorbing cross-bridge detachment (k₊₂, k₋₂). Mean ± SEM, n = 7 for Drosophila. Values were obtained by the sinusoidal analysis method using Scheme 2 for three fast rabbit fiber types and Scheme 1 for the Drosophila data (Fig. 3). Details of the calculations are given in supporting information.

*Rabbit skeletal data are from Galler et al. (12). Temperature, 20°C, rabbit; 15°C, Drosophila.

The association constant for MgATP (K_ATP) is 5-fold lower in IFI (0.19 mM⁻¹) than the fastest rabbit muscle type, IIB (0.8 mM⁻¹), keeping with the downward trend with muscle speed observed in fast muscle types (Table 1). Intuitively, one might expect that very fast muscles have high MgATP affinities for myosin to speed up myosin detachment from actin, but Table 1 shows the opposite is true; that is, increased muscle speeds are associated with reduced MgATP affinity. We and others posit that this inverse relationship reflects the critical requirement that MgADP's adenosine moiety must be released very rapidly from the nucleotide-binding pocket in very fast muscles to achieve high velocity (16).

Although it was not possible to calculate a reliable value for K_ADP from the data of Fig. 2 E and F, we conclude that MgADP release must be very fast (and therefore K_ADP very low) to achieve a forward detachment rate constant k₂ of 3,698 s⁻¹ for IFI at 15°C (Table 1). Further evidence for a very fast MgADP release rate from IFI comes from solution studies of IFI myosin, where an off rate of 4,090 s⁻¹ was calculated based on a measured MgADP-affinity constant of 2.5 mM⁻¹ (at 22°C) (15). MgADP release is likely to be even faster in fibers because of the effects of mechanical stress and/or strain on the myosin head (see Supporting Methods for calculated estimate).

We conjecture that evolutionary pressure selected for myosin with low MgADP affinity in very fast muscle types, which required a concomitant decrease in MgATP affinity. Drosophila may compensate for the low MgATP affinity by elevating intracellular [MgATP] in the IFM to promote MgATP binding. Alternatively, Drosophila IFM may operate at subsaturating levels of [MgATP]. If this is the case, MgATP binding would be rate limiting rather than Pi release. For instance, if [MgATP] were as low as 6.4 mM, an estimate based on measurements reported for blowfly IFM (24), the frequency of maximum oscillatory work production would be 60% less than that observed at 15 mM [MgATP] (Fig. 1). Given the pronounced dependency of frequency of oscillatory work on [MgATP], metabolic control of [MgATP] could be a unique mechanism by which Drosophila modulates optimal frequency of work and muscle power production.

In conclusion, we have shown that in the fastest known muscle type, insect asynchronous IFM, constraints on strong binding steps of the cross-bridge cycle are unleashed by moving the rate-limiting step of the cycle to be closely associated with phosphate release. The constraints on strong binding are also relaxed by equipping the muscle with a high density of mitochondria that not only supplies the large quantities of MgATP fuel required for energetically costly flight (2, 25) but likely also to maintain an unusually high [MgATP]. The high concentration compensates for the necessity of a very weak affinity of myosin for MgADP and MgATP, otherwise their respective release and binding rates would decrease flight muscle speed to the point where work could no longer be generated at the high speeds required to power small insect flight.

Materials and Methods

Creation of the EMB transgenic line and expression in the Mhc¹⁰ background is described in Wells et al. (26). The creation of IFI (referred to as pWMhc2) and expression in Mhc¹⁰ (a myosin null) is described in Swank et al. (27). This control line was used rather than wild-type Drosophila to allow direct comparison (in the same genetic background) with EMB-expressing lines. Transgenes were inserted into the Drosophila germ line by P element-mediated transformation. The resulting transgenic lines expressed myosin at wild-type levels, and myosin was produced only from the transgene (26, 27).

IFM from 2- to 3-day-old female flies were used for the IFI study. For the EMB study, female flies 3 min to 2 h after eclosion were used because studies had shown that EMB flight muscle becomes progressively disrupted >2 h after eclosion (18, 28, 29). Studies had shown that IFI flight muscle mechanical performance indices (f_max and other kinetic parameters) at 3 min after eclosion are identical to 2- to 3-day indices (17, 18), thus allowing direct comparison of IFI and EMB results without age-related influences on kinetic measures.

Six dorsal longitudinal IFM fibers were dissected from half thoraces, split lengthwise, and chemically demembranated (for 1 h at 4°C) with 50% wt/vol glycerol and 0.5% Triton X-100 in relaxing solution (pCa 8). Aluminum T-clips were attached to each segment, yielding a preparation ≈0.6 mm long and ≈0.1 mm wide. The segment was transferred to a 30-μl drop of glycerol- and detergent-free relaxing solution and mounted between a piezoelectric motor and strain gauge on a mechanical rig (25). The temperature was set at 15°C. The fiber was stretched until just taut and then lengthened by 1% muscle length increments until it reached 5% of just-taut length. The fiber was activated to pCa 5.0 by three partial solution exchanges of the initial relaxing solution with activating solution (pCa 4.0). Sinusoidal length perturbation analysis was performed (see Supporting Methods) after a sequence of 2% stretches, until oscillatory work was maximized. Isometric force was measured. Pi, MgATP, MgADP, creatine phosphate (CP), or creatine kinase (CK) concentrations were varied as described, and sinusoidal analysis and isometric force measurements were repeated. Initial maximum work conditions were repeated at least once later in the experiment to assure reversibility. We discarded fibers in which the amplitude of maximum oscillatory work decreased by >15%.

Standard relaxing solution contained 10 mM MgATP, 1 mM free Mg²⁺, 20 mM CP, 900 units/ml CK, 1 mM DTT, 5 mM EGTA, and 20 mM BES, pH 7.0, ionic strength 250 mM, adjusted with sodium methane sulfonate. CK and CP were omitted from the solutions for the MgADP experiments.

For each solution condition, the complex modulus of each fiber was fitted to a three-term equation (25, 30) by following the method of Kawai and Brandt (22): Y(f) = A (2π if/α)^k − B if/(b + if) + C if/(c + if), where f is the applied frequency of oscillation (0.5–1,000 Hz), i is the square root of 1, α is defined as 1 Hz, and k is a unitless exponent. The first term (A) reflects the viscoelastic properties of passive structures within the fiber, whereas the second and third terms (B and C) reflect cross-bridge-dependent processes (changes in dynamic stiffness moduli because of the strain-sensitivity of cross-bridge states) that are exponential in the time domain. Processes B and C appear as hemispheres in the Nyquist plot of Fig. 4, with characteristic frequencies b and c. In the time domain, these frequencies correspond to rate constants 2πb and 2πc (22). Varying [Pi], [MgADP], or [MgATP] alters the steady-state distribution of cross-bridges states, a shift observed as changes in 2πb and 2πc (Fig. 3 and Supporting Methods). All reagents were from Sigma (St. Louis, MO).

Abbreviations

IFM

indirect flight muscle

IFI

indirect flight muscle myosin

EMB

embryonic myosin

IFI

native fast myosin

[MgATP]

concentration of MgATP

[Pi]

concentration of Pi.