Subunit Dependence of Na Channel Slow Inactivation and Open Channel Block in Cerebellar Neurons

Abstract

Purkinje and cerebellar nuclear neurons both have Na currents with resurgent kinetics. Previous observations, however, suggest that their Na channels differ in their susceptibility to entering long-lived inactivated states. To compare fast inactivation, slow inactivation, and open-channel block, we recorded voltage-clamped, tetrodotoxin-sensitive Na currents in Purkinje and nuclear neurons acutely isolated from mouse cerebellum. In nuclear neurons, recovery from all inactivated states was slower, and open-channel unblock was less voltage-dependent than in Purkinje cells. To test whether specific subunits contributed to this differential stability of inactivation, experiments were repeated in Na_V1.6-null (med) mice. In med Purkinje cells, recovery times were prolonged and the voltage dependence of open-channel block was reduced relative to control cells, suggesting that availability of Na_V1.6 is quickly restored at negative potentials. In med nuclear cells, however, currents were unchanged, suggesting that Na_V1.6 contributes little to wild-type nuclear cells. Extracellular Na⁺ prevented slow inactivation more effectively in Purkinje than in nuclear neurons, consistent with a resilience of Na_V1.6 to slow inactivation. The tendency of nuclear Na channels to inactivate produced a low availability during trains of spike-like depolarization. Hyperpolarizations that approximated synaptic inhibition effectively recovered channels, suggesting that increases in Na channel availability promote rebound firing after inhibition.

INTRODUCTION

Many neurons in the cerebellum fire action potentials at rates of tens to >100 spikes/s, both in vivo (1,2) and in vitro (3,4). In Purkinje cells, this rapid firing depends on specialized voltage-gated channels. These include tetrodotoxin (TTX)-sensitive Na channels with “resurgent” kinetics, which are subject to a voltage-dependent open-channel block and unblock by an endogenous blocking protein, and high-voltage-activated K channels, which deactivate rapidly and restore a high input resistance upon repolarization (5–9). Like Purkinje cells, cerebellar nuclear cells have resurgent Na kinetics as well as high-threshold, rapidly deactivating K currents (10,11), but they fire more slowly than Purkinje neurons, even with synaptic input blocked (4,10,12–15). These observations suggest that, despite a gross similarity of ion channel properties, the detailed properties of Na currents, as well as the resulting interaction with other conductances, may not be identical in the two cell types.

Diverse kinetics of Na channels may result from differences in inactivated states, i.e., the blocked state, the classical fast-inactivated state, and/or the slow-inactivated state, mediated, respectively, by the endogenous blocking protein, the linker between domains III and IV (16,17), and rearrangements of the channel pore (18–21). Among the factors contributing to such differences may be the identity of Na channel subunits expressed in each cell. Although Purkinje and nuclear cells have both been reported to express Na_V1.1, Na_V1.2, and Na_V1.6 α-subunits (22–25), previous studies indicate that the two cell types respond differently when external Na is reduced below physiological levels. Specifically, in nuclear neurons, but not Purkinje cells, resurgent Na current decreases greatly and steady-state inactivation curves for transient Na current shift negative by >10 mV (11). Because the external Na concentration affects all types of inactivated states (11,20,26), these results raise the possibility that, despite a similar pattern of mRNA expression, Purkinje and nuclear cells may express Na channels that are molecularly distinct.

Comparisons of Na currents in normal and Na_V1.6-null (med) mice indicate that Na_V1.6 channels contribute strongly to Purkinje Na currents. In these cells, Na_V1.6 channels enter fast-inactivated states relatively slowly and are more susceptible to open-channel block and unblock than other α-subunits (27–29). Although slow inactivation has not previously been examined in neurons from Na_V1.6-null mice, expression studies demonstrate that Na_V1.6 channels depress to a lesser extent with repeated depolarization than do Na_V1.1 and 1.2 channels (30,31), raising the possibility that Na_V1.6-subunits may be generally less prone than other subunits to slow inactivation. The subunit dependence of cerebellar nuclear Na currents has not yet been examined.

To quantify differences in Na channel kinetics and to test their dependence on subunit expression, we measured the properties of fast, slow, and block-induced inactivation in Purkinje neurons and cerebellar nuclear neurons in wild-type and med mice. The results indicate that open-channel block is influenced strongly by the molecular composition of the Na channel α-subunits, whereas fast and slow inactivation depend not only on subunit identity but also on other cell-specific factors. All inactivated states were more stable in cerebellar nuclear neurons, suggesting that a low availability of Na channels may be a limiting factor in setting firing rates in these neurons.

METHODS

Cell preparation

All animal procedures were conducted in accordance with institutional guidelines. Cerebellar Purkinje cells and nuclear cells were acutely dissociated, as in previous works (10,27), from either C57BL6 mice (Charles River, Wilmington, MA) or med mutant mice (Scn8a^med, Jackson Labs, Bar Harbor, ME). Genotypes of med mice were confirmed by Northern blot (27). To dissociate Purkinje cells, mice aged P13–P22 were deeply anesthetized with halothane and decapitated. The superficial layers of the cerebellum were removed and minced in ice-cold dissociation solution containing (in mM): 82 Na₂SO₄, 30 K₂SO₄, 5 MgCl₂, 10 HEPES, 10 glucose, and 0.001% phenol red (pH 7.4 with NaOH). The tissue was incubated in dissociation solution with 3 mg/mL protease XXIII (pH 7.4) for 7 min at 31°C with oxygen blowing over the surface of the fluid, then washed and microdissected in 1 mg/mL bovine serum albumin and trypsin inhibitor (pH 7.4) and finally transferred to Tyrode's solution (in mM: 150 NaCl, 4 KCl, 2 CaCl₂, 2 MgCl₂, 10 HEPES, and 10 glucose, pH 7.4 with 5 mM NaOH). Individual neurons were released by trituration with polished Pasteur pipettes. Cells settled in the recording dish for 1 h, and recordings were made 1–6 h after trituration.

For cerebellar nuclei, the cerebellum was removed from mice aged P13–P16 and placed in cooled, oxygenated Tyrode's solution. Parasagittal slices were cut on a McIlwain tissue chopper (Mickle Laboratory Engineering, Gomshall, Surrey, UK), and transferred to dissociation solution, composed of 10 mM HEPES, 0.5 mM EDTA, 1 mM cysteine, 40 units/mL papain (Worthington), and 0.5 unit/mL chondroitinase ABC in 2 mL MEM (Invitrogen, Grand Island, NY), pH 7.2 with NaOH. After incubation for 20 min at 31°C with oxygen blowing across the surface of the fluid, the tissue was transferred to a wash solution with 1 mg/mL each of bovine serum albumin and trypsin inhibitor in MEM with (mM) 10 HEPES, 1 EDTA, and 2 cysteine, and the cerebellar nuclei were dissected from the slices. The nuclei were then triturated in Tyrode's solution as described above.

Electrophysiological recording

Borosilicate pipettes (A-M Systems, Carlsborg, WA; 1.8–3.0 MΩ) were wrapped with parafilm to reduce capacitance and filled with an intracellular solution containing (mM): 108 CsCH₃SO₃, 9 NaCl, 1.8 MgCl₂, 9 HEPES, 1.8 EGTA, 45 sucrose, 4.5 tetraethylammonium (TEA)-Cl, 14 Tris-CreatinePO₄, 4 MgATP, 0.3 TrisGTP (pH 7.4 with CsOH). For one experiment (see Fig. 4), internal Na was reduced to 1.8 mM (osmolarity maintained with sucrose), to shift E_Na sufficiently positive so that inward current could be measured at +60 mV. Voltage-clamp recordings were made with an Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA) and series resistance was compensated by >85%. Data were digitized and recorded with Digidata 1322A and pClamp 9.0 (Molecular Devices) and analyzed with IgorPro 4.09A (Wavemetrics, Lake Oswego, OR). Cells were positioned in front of a series of gravity-driven flow pipes containing Tyrode's, 10 mM TEA-Cl, 0.3 mM CdCl₂ ± 900 nM TTX or (in mM) 150 NaCl, 10 TEA-Cl, 0.3 CdCl₂, 2 BaCl₂, 10 glucose ± 900 nM TTX. To isolate Na currents, traces recorded in TTX were subtracted from control traces. For some recordings, 30 nM TTX was added to control solutions to reduce Na current amplitudes and to improve the quality of the voltage clamp. No differences were evident in the properties of well-clamped currents with or without 30 nM TTX, and the data were pooled. In some experiments, 100 mM external NaCl was replaced with isotonic TEA-Cl or CsCl, as noted. Drugs were from Sigma-Aldrich (St. Louis, MO) except for TTX, which was from Alomone (Jerusalem, Israel).

FIGURE 4.

Interaction between open-channel block and slow inactivation in Purkinje cells. (A, left) Voltage protocols and representative traces for detecting the extent of block during long (50- to 500-ms) conditioning steps to different potentials, as labeled. (A, right) Normalized peak resurgent current versus conditioning pulse duration. Data are fitted with a single exponential, with parameters given in Results. For the +60-mV step, N = 6; for the +30-mV step, N = 7, and for the 0-mV step, N = 8. (B, upper) Voltage protocol and representative traces to test the effect of conditioning voltage on slow inactivation. (B, lower) Reference and test steps at higher gain, illustrating the onset of the difference in availability at longer conditioning durations. Test currents evoked after all four conditioning voltages are shown; arrows indicate largest and smallest amounts of recovery and are labeled with the corresponding conditioning voltages. (C) Plot of the percent availability increase after steps to −30, +30, and +60 mV relative to that after steps to 0 mV, as a function of conditioning duration. All recovery intervals were 100 ms. For intervals <100 ms, N = 8; for intervals >100 ms, N = 10. Dotted line indicates no change relative to 0 mV.

Data are reported as mean ± standard error. Statistical significance was assessed with Student's unpaired, two-tailed t-tests or two-way repeated-measures analyses of variance (ANOVAs, SPSS, Chicago, IL). For comparisons of slow inactivation in wild-type and med neurons, fewer intervals were assayed than in the initial description in wild-type cells. The data in both cases were fit with sums of exponentials, but the reduced number of data points made the fit parameters less well constrained in the comparisons of genotypes. Therefore, statistical differences in the raw data were evaluated directly with ANOVAs. In cases in which a statistical difference was evident, fit parameters were subsequently compared with Student's unpaired, two-tailed t-tests. Despite interstimulus intervals of >10 s, accumulation of Na channels into exceedingly long-lived inactivation states occurred in some of the longest protocols, leading to small variations in the amount of recovery (<10%) estimated by different protocols. Therefore, statistical comparisons were performed only on data obtained with identical protocols in the different cell types or genotypes and ANOVAs were used to assess differences in properties.

RESULTS

Differences in inactivation in Purkinje and nuclear cells

To compare Na channel availability in acutely isolated Purkinje and cerebellar nuclear cells, we examined recovery of TTX-sensitive Na currents from various inactivated states. These recordings were made in near-physiological concentrations of Na (155 mM) to avoid the stabilization of inactivated states induced by nonphysiological reductions in extracellular Na (11,20). First, to measure recovery from block and/or fast inactivation, we applied a 2-ms conditioning step to 0 mV and then assayed availability with a test step to 0 mV after variable recovery intervals at −90 mV (Fig. 1 A, upper). Next, to measure recovery from long-lived “slow” inactivated states, we repeated the experiments with a 500-ms conditioning step and longer recovery intervals (Fig. 1 A, middle). Availability was calculated as the ratio of the test to the conditioning current amplitude and was plotted versus recovery interval.

FIGURE 1.

Properties of inactivation in Purkinje and cerebellar nuclear cells. (A) Voltage protocols and representative traces for recovery from 2-ms (upper) and 500-ms (middle) conditioning steps. Recovery interval, 1–5000 ms. Overlay of representative traces from 500-ms conditioning and test steps at a higher gain (lower). (B) Fraction of available channels versus recovery interval. After 2-ms conditioning steps, recovery was biexponential. Purkinje cells (PKJ), N = 11; cerebellar nuclear cells (CBN), N = 10. After 500-ms conditioning steps, channels recovered in three exponential phases: fast, intermediate, and slow. PKJ, N = 8; CBN, N = 9. Parameters of the fits are given in Table 1. (C, upper) Voltage protocols and representative traces for entry into inactivated states. Conditioning pulse, 0.5–2500 ms. Current amplitudes were tested after a 100-ms interval to allow recovery from fast inactivation. (C, lower). Overlay of representative traces from conditioning and test steps at a higher gain. The current evoked by the briefest (1-ms) conditioning step deactivates upon repolarization, so the current terminates earlier than in the other traces. (D) Fraction of available channels versus conditioning pulse interval. Data are fitted with double exponentials (PKJ, N = 7; CBN, N = 7). Parameters of the fits are given in Table 1.

After inactivation by the 2-ms conditioning step, recovery was biexponential in both cell types, but occurred more rapidly in Purkinje cells (Fig. 1 B). As shown in Table 1, Purkinje and nuclear Na channels had similar brief time constants (p = 0.5) but the longer time constant was larger in nuclear cells (p < 0.001) and accounted for a greater percentage of the total recovery (p < 0.001). A slower recovery by nuclear cells was also evident after the 500-ms step. In both cell types, recovery after this step followed a triple exponential, in which the briefest time constant, as well as the intermediate time constant, was longer in nuclear cells (p < 0.05; p < 0.01). With either short or long conditioning pulses, greater recovery by Purkinje cells was most evident during the 3-ms to 300-ms recovery period. Since firing rates in both cell types usually range from a few tens to a few hundred spikes per second, these data suggest that Purkinje neurons may maintain a higher availability of Na channels during normal interspike intervals. Moreover, the pronounced slow components of recovery in nuclear cells, which was evident with either conditioning step, suggests that long-lived inactivated states are more stable in cerebellar nuclear than in Purkinje Na channels.

TABLE 1.

Inactivation parameters of fit

			% not inactivated	% fast	τ fast (ms)	% intermediate	τ intermediate (ms)	% slow	τ slow (ms)	n
Recovery from 2-ms step	Fig. 1	PKJ	26 ± 2	67 ± 2	2.6 ± 0.2			7 ± 1	61 ± 13	11
		CBN	23 ± 2	56 ± 3	2.8 ± 0.4			21 ± 3	165 ± 24	10
	Fig. 3	PKJ WT	26 ± 2	67 ± 2	3.4 ± 1.1			7 ± 1	79 ± 12	21
		PKJ med	17 ± 1	78 ± 1	2.7 ± 0.1			5 ± 0.3	115 ± 17	7
		CBN WT	26 ± 2	56 ± 2	2.3 ± 0.2			18 ± 2	208 ± 27	21
		CBN med	30 ± 3	57 ± 2	1.7 ± 0.1			13 ± 1	191 ± 36	8
Recovery from 500-ms step	Fig. 1	PKJ	2 ± 1	20 ± 5	4.3 ± 0.7	38 ± 8	123.0 ± 28.9	40 ± 10	948 ± 210	8
		CBN	4 ± 1	12 ± 1	10.4 ± 2.3	57 ± 7	231.0 ± 21	27 ± 7	3857 ± 2074	9
	Fig. 3	PKJ WT	3 ± 1	19 ± 3	4.8 ± 0.9	41 ± 6	132.8 ± 20	37 ± 6	1260 ± 397	13
		PKJ med	1 ± 1	15 ± 2	6.1 ± 0.9	49 ± 9	188.5 ± 37	35 ± 9	1739 ± 1009	7
		CBN WT	4 ± 1	14 ± 1	7.9 ± 1.4	60 ± 3	208.5 ± 22	22 ± 3	2124 ± 643	17
		CBN med	3 ± 1	11 ± 2	4.4 ± 0.4	49 ± 9	113.3 ± 28	37 ± 8	1942 ± 1328	5
Entry into slow inactivation	Fig. 1	PKJ	26 ± 5	51 ± 2	80.3 ± 3.4			23 ± 3	1284 ± 481	7
		CBN	35 ± 4	36 ± 6	70.5 ± 19			29 ± 6	759 ± 146	7
	Fig. 3	PKJ WT	28 ± 2	49 ± 2	85.4 ± 4.7			23 ± 1	1705 ± 212	12
		PKJ med	29 ± 1	52 ± 2	80.2 ± 7.8			19 ± 2	1143 ± 181	8
		CBN WT	33 ± 2	36 ± 3	73.1 ± 13.5			31 ± 2	1555 ± 255	16
		CBN med	31 ± 4	43 ± 3	79.7 ± 4.8			26 ± 3	1840 ± 102	5

To compare the rate of entry into slow-inactivated states in the two cell types, we applied variable-duration steps to 0 mV to allow block, fast inactivation, and/or slow inactivation to develop. These steps were followed by a 100-ms recovery interval at −90 mV. This interval, which allowed >90% recovery from 2-ms pulses in both Purkinje and nuclear cells, was chosen as the optimal interval to exclude fast-inactivated and blocked states and restrict the analysis to long-lived inactivated states. After the recovery interval, availability was assessed with a 2-ms step to 0 mV (Fig. 1 C) and fitted with double exponentials (Fig. 1 D and Table 1). The pattern of entry into slow inactivation was different in the two cell types, in that ∼10% of Na channels remained unavailable for >100 ms after even the briefest conditioning steps in nuclear but not Purkinje cells. As a result, entry into slow inactivated states in Purkinje cells lagged behind that in nuclear cells (Fig. 1 D), although the onset of this difference was too rapid to be resolved by the exponential fits. Therefore, to evaluate differences between the data sets that did not rely solely on curve fitting, the raw data were compared with an ANOVA. This analysis revealed a significant interaction of the recovery profile and cell type (F(33,363) = 3.3, p < 0.05), further supporting the idea that nuclear Na channels enter slow-inactivated states more readily than do Purkinje Na channels.

This moderate degree of slow inactivation by Purkinje cells appears consistent with their ability to fire rapidly for prolonged periods. This trait is also facilitated by voltage-dependent open-channel block, which produces resurgent current while quickly restoring channel availability at negative potentials (5). Cerebellar nuclear neurons also have resurgent kinetics, but the more stable slow inactivation in these cells raises the question of whether accumulation in inactivated states offsets any gain in availability through relief of block. To address this question, we characterized open-channel block in nuclear cells and assessed its interaction with slow-inactivated states. We began by comparing the properties of resurgent current in both cell types. Cells were held at −90 mV, stepped to +30 mV to promote channel block, and repolarized to potentials between −20 and −60 mV to elicit resurgent Na current (Fig. 2 A, upper traces). Consistent with previous results (11), resurgent Na current was significantly larger in Purkinje than in cerebellar nuclear cells, even when normalized to the transient current in each neuron (Fig. 2 B, solid and hatched black bars). In addition to the difference in relative amplitude, the kinetics of resurgent Na current, measured at −30 mV, were significantly slower in nuclear cells, with a nuclear versus Purkinje time to peak of 6.2 ± 0.4 ms (N = 51) vs. 4.9 ± 0.1 ms (N = 78, p < 0.0001) and decay time constant (τ_decay) of 30.1 ± 1.2 ms vs. 20.7 ± 0.3 (p < 0.001). In addition to indicating that unblock occurs more slowly in nuclear Na channels, these data support the idea that resurgent current may have diverse kinetics in different neurons (32–34).

FIGURE 2.

Resurgent Na current in wild-type and med neurons. (A) Voltage protocol to elicit resurgent current and representative traces from Purkinje and cerebellar nuclear cells. Currents are normalized to the peak of the transient Na current elicited by a step to 0 mV. (B, left and center bar groups) Average transient (0 mV) and resurgent current (−30 mV) amplitudes from PKJ wild-type (WT) (N = 78), PKJ med (N = 19), CBN WT (N = 48), and CBN med (N = 8) neurons (left axis). Note that transient current is divided by 10, for an axis range of 0–15 nA, whereas the resurgent-current amplitude range is 0–1.5 nA. (B, right bar group) Resurgent current normalized to the transient current at 0 mV (right axis).

Effects of subunit identity on inactivation

Because resurgent Na current in Purkinje cells is known to depend on expression of Na_V1.6 (27,29), we considered the possibility that the differences in the kinetics of the resurgent component of Na current might result from differences in subunit expression. We therefore examined transient and resurgent Na currents in Purkinje and nuclear cells isolated from med mice (Fig. 2 A, lower traces). Similar to previous reports (27), transient and resurgent currents in med Purkinje cells were reduced by ∼50% and 75%, respectively, compared to cells from wild-type animals (Fig. 2 B, solid bars), and the resurgent/transient ratio dropped from 7.7 ± 0.4% to 2.5 ± 0.3% (p < 0.0001). Moreover, in med Purkinje cells, the kinetics of resurgent current were prolonged relative to wild-type, with a rise time and decay constant of 6.8 ± 0.7 ms and 32.0 ± 2.0 ms (N = 18, p < 0.0001; p < 0.0001). Interestingly, these values are much closer to those in wild-type cerebellar nuclear neurons, raising the possibility that the resurgent current in nuclear neurons may be dominated by non-Na_V1.6-subunits. Consistent with this idea, neither the transient nor the resurgent current amplitudes were significantly reduced in nuclear neurons from med mice (p = 0.4; p = 0.2; Fig. 2 B, hatched bars). In addition, the rise and decay of resurgent current in med nuclear neurons were not significantly different from their wild-type counterparts (6.5 ± 1.0 ms and 32.6 ± 4.0 ms, N = 7, p = 0.7; p = 0.5). Together, these data suggest that Na_V1.6 is not highly expressed in wild-type cerebellar nuclear somata, and/or that these subunits do not have distinct properties from the other expressed α-subunits.

To test the extent to which the differences in slow inactivation between the two cell types could be attributed to a preponderance of Na_V1.6 expression in Purkinje but not nuclear cells, we compared the kinetics of slow inactivation in both classes of med neurons. In med Purkinje cells, recovery from both brief and long conditioning steps slightly lagged behind that in wild-type cells (Fig. 3, A and B, and Table 1), with ANOVAs indicating a significant interaction between genotype and availability both for brief (F(8,168) = 10.6, p < 0.001) and long (F(11,198) = 2.5, p < 0.01) conditioning steps. After brief conditioning steps, this lag in recovery was limited to the first ∼10 ms, and resulted primarily from a larger proportion of inactivated channels after the briefest interval (p < 0.01, Table 1). After a long conditioning step, however, the lag was more prominent, and persisted for ∼1 s, supporting the idea that slow inactivation is less stable in Na_V1.6 than in other α-subunits. Entry into slow-inactivated states, however, was unchanged in med Purkinje neurons relative to wild-type (F(10,180) = 1.6, p = 0.1).

FIGURE 3.

Recovery from and entry into inactivated states in wild-type and med neurons. (A and C) Wild-type and med mean fraction of available channels versus recovery interval for (A) Purkinje neurons (2 ms: WT, N = 21; med, N = 7; 500 ms: WT, N = 13; med, N = 7) and (C) cerebellar nuclear neurons (2 ms: WT, N = 20; med, N = 8; 500 ms: WT, N = 17, med, N = 5). Channels recovered from a 2-ms step according to a double exponential and from a 500-ms step according to a triple exponential. Parameters of the fits are given in Table 1. Gray circles in C are the data from med Purkinje neurons, for comparison. For some data points, error bars are smaller than the symbols. (B and D) Wild-type and med average fraction of available channels versus conditioning pulse interval for (B) Purkinje neurons (WT, N = 12; med, N = 8) and (D) cerebellar nuclear neurons (WT, N = 15; med, N = 5). Channels entered slow-inactivated states in two phases (Table 1). Gray circles in D are the data from med Purkinje neurons, for comparison. For some data points, error bars are smaller than the symbols.

In contrast, in med nuclear neurons, recovery from brief steps, recovery from long steps, and the onset of slow inactivation were all indistinguishable from those in wild-type nuclear cells (interaction of genotype and availability: F(8,160) = 4.76, p = 0.9; F(11,220) = 0.55, p = 0.9; F(10,180) = 0.18, p = 0.9; Fig. 3, C and D, and Table 1). These data are again consistent with a low contribution of Na_V1.6 to the total nuclear Na current or kinetics similar to those of other α-subunits. Loss of Na_V1.6 from Purkinje cells, however, did not make inactivation identical to that in nuclear cells (Fig. 3, C and D, Recovery from 2-ms step: F(8,104) = 27.9, p < 0.001; Recovery from 500-ms step: F(11,110) = 2.0, p < 0.05; Entry into slow inactivation: F(11,110) = 6.0, p < 0.001) . These data suggest, therefore, either that the subunit composition of Na channels remaining in med cells actually differs between Purkinje and nuclear cells, and/or that other cell-specific factors make slow-inactivated states more stable in wild-type nuclear cells than in Purkinje cells.

Relation between block and slow inactivation

Mutation studies as well as cysteine-scanning mutagenesis experiments on expressed Na channels have suggested that slow inactivation may result from rearrangement of either the external or the internal channel pore (35–39). Based on the idea that the endogenous open channel blocker senses the membrane field and is therefore likely to bind within the internal pore, we tested whether the greater propensity for Na channel block in normal Purkinje cells influences the stability of slow-inactivated states. First, to verify that the blocking particle could remain bound to the channel for periods on the timescale of slow inactivation, we applied conditioning steps of variable duration (50–500 ms) to three different depolarized potentials (0, +30, and +60 mV), followed by repolarization to −30 mV to assay for resurgent Na current. A measurable resurgent component persisted even with the longest conditioning steps, confirming that channels can remain blocked for as long as 500 ms (Fig. 4 A, left). Nevertheless, the amplitude of resurgent current was largest with brief conditioning steps and decreased as the duration of the step was prolonged (Fig. 4 A, right). Additionally, the peak resurgent current dropped more slowly with more depolarized conditioning steps (Purkinje: +60 mV, τ = 315 ± 58 ms, N = 6; +30 mV, τ = 174 ± 24 ms, N = 7; 0 mV, τ = 41 ± 3 ms, N = 8; τ at +30 and +60 relative to 0 mV: p < 0.001).

These observations support previous models, which predict that open channels first enter the blocked state at all potentials, but then equilibrate into the fast inactivated state, and that this equilibration proceeds more rapidly at less depolarized potentials because of the voltage dependence of unblock (7). As suggested by Fig. 1, however, some slow inactivation also occurs on timescales as short as a few tens of milliseconds. We therefore took advantage of the voltage dependence of unblock to assay whether the occupancy of the channel by the blocker might oppose slow inactivation. If so, conditioning steps to the most positive potentials, at which block is most stable, might produce less slow inactivation than conditioning steps to less depolarized potentials. In contrast, if slow inactivation and block are independent, increasingly positive conditioning steps might cause slow inactivation to saturate or to increase further (35,40). To distinguish between these possibilities, we measured the amount of slow inactivation induced by conditioning steps of variable duration (10–500 ms) at four different voltages (−30, 0, +30, and +60 mV) (Fig. 4 B). For conditioning steps ≤50 ms, the amount of slow inactivation after a 100-ms recovery interval was similar across conditioning potentials, indicating that binding of the blocker did not appreciably interfere with the onset of relatively rapid-onset slow-inactivated states.

For longer steps (60–500 ms), however, different conditioning voltages produced different amounts of recovery, as was evident from normalizing the availability after conditioning at each potential to that after the 0-mV conditioning step (Fig. 4, B, lower, and C). Consistent with a lesser degree of slow inactivation at more negative voltages, conditioning at −30 mV led to less slow inactivation than conditioning at 0 mV (Fig. 4 C, open circles). After steps to positive potentials, however, availability was also greater than for 0-mV conditioning steps; in the most extreme case, ∼15% more channels were available after 500-ms steps to +60 mV versus 0 mV. Although this result may reflect a nonmonotonic dependence of slow inactivation on voltage, a more likely possibility seems to be that the binding of the blocker in the internal pore impedes entry into the slow-inactivated states favored by longer depolarizations. In this way, the extent of slow inactivation in Purkinje cells may be partly regulated by the voltage dependence of open-channel block.

Voltage-dependence of block in Purkinje and cerebellar nuclear cells

In nuclear neurons, however, measurements of resurgent current after increasingly long conditioning steps illustrated that the open-channel block differed from that in Purkinje cells. Specifically, although the peak amplitude of resurgent current after steps to +30 mV dropped with τ = 192 ± 17 ms (N = 5), a time course similar to that in Purkinje cells, steps to 0 mV accelerated this decay to a lesser extent than in Purkinje cells (to 77 ± 6 ms, N = 6; Fig. 5 A). This apparently weaker voltage dependence of unblock is consistent with the slower rise (and decay) times of resurgent current in nuclear cells. To compare the voltage sensitivity of block more systematically, we applied 50-ms steps to voltages between −20 and +50 mV and then repolarized to −30 mV to elicit resurgent current (Fig. 5 B). Linear fits to the data confirmed that the voltage dependence of block was steeper in Purkinje cells, with normalized resurgent current amplitudes falling off by 8.7 ± 0.5% per 10-mV hyperpolarization of the conditioning step (N = 8), as compared to 5.9 ± 1.1% per 10-mV hyperpolarization (N = 6) in nuclear cells (p < 0.05, Fig. 5 C). The absolute disparity in the amount of block is predicted to increase with further hyperpolarization, such that the rapid restoration of Na channel availability by unblock that occurs in Purkinje cells may not occur as readily in nuclear neurons. Instead, in nuclear neurons, block itself may limit availability at normal interspike potentials.

FIGURE 5.

Voltage dependence of open-channel block. (A) Normalized peak resurgent current versus conditioning pulse duration for cerebellar nuclear neurons. Data from Purkinje cells are reproduced for comparison. Data are fitted with single exponentials, with parameters given in Results. For the +30-mV step, N = 5; for the 0-mV step, N = 6. (B) Voltage protocol and representative traces to measure the voltage dependence of block. (C) Resurgent current normalized to the resurgent current evoked after a step to +50 mV and fitted with a straight line for WT Purkinje cells (N = 8), WT nuclear cells (N = 6), and med Purkinje cells (N = 9).

To test whether the presence of the Na_V1.6 α-subunit might contribute to the steeper voltage sensitivity of block in Purkinje Na channels, we repeated the experiment in med Purkinje cells. Indeed, the amplitude of resurgent current in med Purkinje cells decreased by only 5.1 ± 0.9% per 10-mV hyperpolarization of the conditioning step (p < 0.01 vs. wild-type Purkinje), supporting the idea that the open-channel blocker penetrates more deeply in the pore or otherwise detects the membrane field more strongly when it binds to Na_V1.6 than to other α-subunits.

Effect of permeant and impermeant ions on properties of inactivation

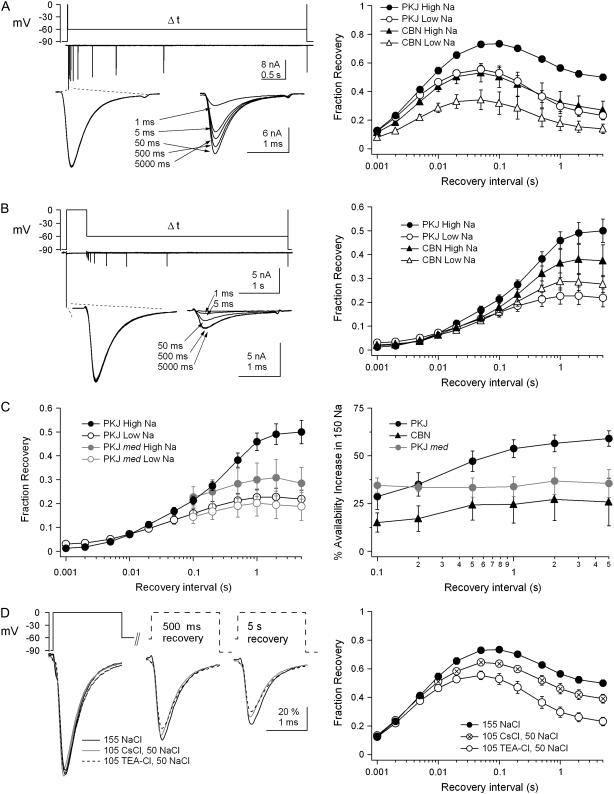
Previous work has shown that slow inactivation can be reduced by external alkali metal cations (19,20). These cations are thought to bind in the mouth of the channel where they oppose the structural rearrangements that may contribute to collapse of the external pore and consequent slow inactivation. Therefore, to explore whether the slow-inactivated states induced by our protocols could be attributed in part to external pore collapse, as well as to test whether Purkinje and nuclear Na channel inactivation showed a differential sensitivity to external cations, we assayed recovery in both high-Na (155 mM) and low-Na (50 mM, with 105 mM TEA⁺). We applied 2- and 500-ms conditioning steps to 0 mV and allowed channels to recover for variable intervals at −60 mV before assaying recovery with a step to 0 mV. This moderately hyperpolarized recovery voltage of −60 mV was selected because the effect of extracellular Na concentration on steady-state inactivation is greatest near −60 mV (11).

In both cell types, in high as well as low Na, recovery from the brief step was nonmonotonic, increasing with intervals up to 100 ms and decreasing with longer intervals, presumably as the initial recovery from blocked and/or fast inactivated states was followed by equilibration into slow- and/or fast-inactivated states (Fig. 6 A). The reduction of extracellular Na ions reduced the amount of recovery by ∼10–25% in both cell types at all intervals >2 ms, although the amount of recovery was consistently greater in Purkinje cells (F(9,108) = 2.08, p < 0.05). Interestingly, however, although the percent reduction of current by low Na after the 2-ms step was smaller in Purkinje than in nuclear cells at brief recovery intervals (at 5 ms, Purkinje, 14 ± 7%, versus nuclear, 31 ± 5%), it was actually greater at long intervals (at 5 s, Purkinje, 53 ± 4%, versus nuclear, 32 ± 17%, Fig. 6 A). Consistent with this observation, when recovery at −60 mV was assayed after 500-ms conditioning steps, the amount of recovery was greater in Purkinje cells in high Na but tended to fall below that of nuclear Na channels in low Na (Fig. 6 B). As a result, the percent increase in availability in high Na was significantly greater for Purkinje cells (Fig. 6 C, right, F(9,90) = 5.66, p < 0.001). Together, these data indicate that external Na ions indeed play a substantial role in limiting slow inactivation, and that this effect is particularly pronounced in Purkinje Na channels.

FIGURE 6.

Effect of permeant and impermeant ions on inactivation. (A and B, upper left) Voltage protocols and representative traces for recovery at −60 mV from 2-ms (A) and 500-ms (B) steps to 0 mV. (A and B, lower left) Responses to conditioning and test steps at higher gain. (A and B, right) Fraction of available channels versus recovery interval for Purkinje and cerebellar nuclear neurons in high and low Na for 2-ms conditioning steps for PKJ high Na (N = 11), PKJ low Na (N = 6), CBN high Na (N = 10), and CBN low Na (N = 8), and for 500-ms conditioning steps for PKJ high Na (N = 8), PKJ low Na (N = 7), CBN high Na (N = 6), and CBN low Na (N = 5). (C, left) Data as in B, right, but for med PKJ cells. High Na (N = 6), low Na (N = 6). Data from wild-type PKJ cells are superimposed for comparison. (C, right) Increase in availability in high Na relative to low Na for wild-type PKJ, med PKJ, and wild-type CBN cells. (D, left) Voltage protocol and representative traces for currents in 100 mM NaCl, CsCl, or TEA-Cl from Purkinje cells. (D, right) Fraction of available channels versus recovery interval for 155 NaCl, (N = 11), 105 CsCl and 50 NaCl (N = 5), and 105 TEA-Cl and 50 NaCl (N = 6).

To test the contribution of Na_V1.6 to the heightened sensitivity of Purkinje channels to the external Na concentration, we repeated the experiment in med Purkinje cells. Relative to wild-type, the amount of recovery after 500-ms conditioning steps was reduced in high Na but comparable in low Na (Fig. 6 C, left; high Na. F(5,60) = 16.8, p < 0.0001; low Na, F(5,55) = 0.16, p = 0.98). To compare directly the sensitivity of the different cell types to external Na, we plotted the percent increase in availability induced by high relative to low Na (Fig. 6 C, right). In wild-type Purkinje cells, the effect of high Na increased with longer intervals, reaching a 59 ± 4% enhancement at 5 s. In contrast, in nuclear cells, the sensitivity to Na changed only slightly across intervals, reaching only ∼25% increase by high Na at the longest interval. In med Purkinje cells, the effect of high Na remained just under 40% at all recovery intervals, significantly less than in wild-type Purkinje cells (F(5,55) = 9.8, p < 0.0001), but indistinguishable from nuclear cells (F = (5,45) = 0.26, p = 0.93). These results are consistent with the idea that external Na is particularly effective in limiting slow inactivation of Na_V1.6 channels.

As mentioned, Na ions might reduce slow inactivation simply by occupying the external pore and opposing pore collapse. Additionally, their permeation might be important in preventing or destabilizing inactivation (20,26). To test the extent to which permeation rather than pore occupancy limited slow inactivation of wild-type Purkinje Na channels, we repeated the measurements of recovery from brief conditioning steps in low Na with 105 mM Cs⁺ rather than TEA⁺ as the substituted cation. Cs⁺ was selected because it is impermeant through Na channels, but, as an alkali metal cation, is expected to bind in the mouth of the channel (20). Consistent with this idea, at long intervals, recovery from brief steps was greater in low Na with Cs ions than in low Na with TEA ions (Fig. 6 D). Nevertheless, recovery in high Na was greater still (Fig. 6 D), supporting the idea that permeating ions are relatively more effective at preventing slow inactivation. Thus, in normal physiological saline, occupancy of the channel by Na ions contributes substantially to maintaining availability of Purkinje Na channels.

Inactivation by physiological stimuli

In contrast, the propensity of nuclear Na channels to enter long-lived inactivated states at potentials near −60 mV, even with brief depolarizations and physiological Na concentrations, suggests that slow inactivation is likely to affect excitability of nuclear neurons in the intact cerebellum. To test the availability of nuclear Na channels during patterns of stimuli that mimic physiological activity, we applied trains of 2-ms steps to 0 mV from −60 mV with an interstep interval of 50 ms, to approximate the voltage trajectory of a nuclear cell firing spontaneous action potentials at 20 spikes/s (4). After 10 such stimuli, availability began to reach a steady state near 40% (Fig. 7, A and B). Because nuclear cells are heavily innervated by GABAergic Purkinje cells, such activity patterns may be interrupted in vivo by Purkinje-mediated synaptic inhibition, during which time the cells are hyperpolarized to voltages near the chloride equilibrium potential, generally between −65 and −75 mV. After such periods of hyperpolarization, cells often respond with a rebound burst of action potentials (4,12). Therefore, to test how recovery from inactivation might increase the availability of Na channels and possibly contribute to rebound burst firing, we followed the 10-step train with a 250-ms step hyperpolarization to voltages between −60 and −80 mV, and then assayed channel availability with a 100-Hz train of three brief 0-mV steps (Fig. 7, A and B). Hyperpolarization to −60 mV allowed channels to recover by just more than 50%, whereas the step to −80 mV increased availability to 90% (Fig. 7 C). The increased availability was apparent primarily during the first step after the hyperpolarization, dropping back to ∼ 40% availability on the subsequent steps. These results suggest that inhibition on the order of a few hundred milliseconds may promote recovery from inactivation of nuclear Na channels, thereby contributing to initiating, but not maintaining, bursts of rebound action potentials.

FIGURE 7.

Na-channel inactivation in cerebellar nuclear cells induced by quasiphysiological voltage steps. (A) Voltage protocol and representative traces for a cerebellar nuclear cell, mimicking depolarizations occurring during spontaneous firing at 20 Hz, a 250-ms period of inhibition, and a rebound burst of three action potentials at 100 Hz. (B) Peak transient Na currents normalized to the amplitude of the first current, plotted time locked to the traces in A (N = 5). For the rebound burst, symbols designate the voltage of the preceding hyperpolarization. (C, left) Voltage protocol and representative traces for rebound burst (B, boxed area) at high gain. (C, right) Rebound currents from B plotted versus recovery voltage (N = 5). The data set for each rebound current was fit with a straight line (rebound current 1, 2%/mV; rebound current 2, 0.5%/mV; rebound current 3, 0.3%/mV).

DISCUSSION

These results indicate that even neurons with nominally the same profile of expressed Na-channel α-subunits can differ significantly in their properties of inactivation. Specifically, fast, slow, and block-mediated inactivated states were more stable in cerebellar nuclear neurons than in Purkinje neurons. Given that firing rates are dictated in part by the availability of Na channels, such differences are likely to be meaningful in the context of the patterns of signaling characteristic of these neurons.

The basis for the differences in inactivation in the two cell types may lie in part in the molecular composition of the Na channel complexes expressed, i.e., the α-subunits themselves, the associated proteins, or the state of posttranslational modification of any of the participating proteins. Regarding the α-subunits, it is generally agreed that Purkinje somata express Na_V1.1 and Na_V1.6 (22,23,25,41,42). Although some studies find evidence of Na_V1.2 transcripts (23,24), single-cell polymerase chain reaction and antibody labeling indicate that Na_V1.2 expression is low or absent (22,25,41). It is therefore most likely that the Purkinje Na current that we have measured in wild-type cells is carried primarily by Na_V1.1 and Na_V1.6 α-subunits.

Like in Purkinje cells, although Na_V1.2 is not always found in cerebellar nuclear neurons (22,24,25), Na_V1.1 and Na_V1.6 appear to be abundant (22,25,42,43). The subcellular distribution of Na_V1.6 has not been examined in nuclear cells, however, leaving open the question of the extent to which Na_V1.6 contributes to somatic currents. In the present recordings, the lack of significant changes in current amplitude or kinetics in med mice might result if Na_V1.6 expressed in nuclear cells has properties identical to Na_V1.1, and its loss triggers an up-regulation of Na_V1.1-subunits. Changes in expression of various channels have indeed been documented in med mice (44,45); nevertheless, the nearly exact compensatory match in kinetics and amplitude of Na currents in wild-type and med nuclear cells seems unlikely. A more plausible scenario may be that cerebellar nuclear somata have a low level of Na_V1.6 expression, so that their somatic currents are dominated by Na_V1.1 channels and therefore remain relatively unaffected by loss of Na_V1.6. This interpretation is also consistent with the idea that the high contribution of Na_V1.6 to Na currents in Purkinje somata provides the basis for the more rapid recovery from all forms of inactivated states that distinguish Purkinje from nuclear cells.

Regarding associated proteins, the Na channel complex also includes β-subunits. β-subunit expression appears similar in Purkinje and nuclear cells, with both cell types expressing β1, β2, and β4 (42,46). Both β1- and β2-subunits can not only affect trafficking, but may also modify kinetics, either directly or by recruitment of other proteins to the complex (47–51). In Purkinje cells, however, neither the β1- nor the β2-subunit changes Na currents significantly (52). In contrast, the β4-subunit has been implicated indirectly in the production of resurgent Na current, as a peptide with the sequence of the β4 cytoplasmic tail induces resurgent current in Na channels that lack resurgent kinetics (52). It is yet unknown, however, whether the full-length β4 protein naturally, or necessarily, behaves as the endogenous open-channel blocker. The distinct resurgent kinetics in different cells may in fact be indicative of diversity at the level of the blocking particle. Our data indicate that open-channel block of wild-type Purkinje Na channels is steeply voltage-dependent, whereas block is relatively weakly sensitive to voltage in nuclear cells and med Purkinje cells. Thus, an alternative possibility is that the blocking particle is the same molecular entity, possibly β4, in all cells with resurgent kinetics, but that it binds more stably to Na_V1.1 than to Na_V1.6 channels. Further support for a differential affinity of α-subunits for the blocker comes from neurons of the subthalamic nuclei, in which resurgent currents resemble those in the cerebellar nuclei, and total Na current kinetics are relatively unchanged in med mice (32). From a physiological standpoint, in cells whose Na channels bind the blocker more stably, the resulting persistence of the blocked state at moderately negative potentials may in fact make resurgent kinetics participate to a lesser extent in spontaneous or driven firing. Instead, a role for resurgent kinetics of non-Na_V1.6 channels, such as those in the cerebellar and subthalamic nuclei, might only be revealed during hyperpolarizations to more negative voltages, at which the blocking particle is more readily expelled from the pore.

Comparison of med currents in the two cell types indicates that the differences in slow inactivation that we observed between Purkinje and nuclear Na channels cannot be explained solely on the basis of Na_V1.6 expression. A possible basis for the remaining disparity is the modulation state of the channels, as phosphorylation of Na channels has been implicated in promoting slow inactivation (21,53). Thus, the greater stability of slow inactivated states in both med and wild-type nuclear neurons may in part result from a greater degree of constitutive phosphorylation of nuclear Na channels. In this context, it is also interesting that Na_V1.6 channels have fewer phosphorylation sites than do Na_V1.1 channels (54,55), and may therefore slow-inactivate less readily.

Even in expression systems, however, in which phosphorylation is not expected to be a variable, Na_V1.6 channels with the fast-inactivation gate made nonfunctional by mutation tend to facilitate with repeated stimulation rather than to slow-inactivate like Na_V1.2 (30); this disparity in the tendency to inactivate is maintained in channels expressed in dorsal root ganglion neurons, with fast-inactivation gates unaltered (31). These results suggest that a relative resistance to slow inactivation may be intrinsic to the Na_V1.6 channel. Our data indicate that slow inactivation of Purkinje Na channels is particularly sensitive to external cations, and that this sensitivity is reduced in med mice. Interpreted in the context of the studies of heterologously expressed Na_V1.6, these data raise the possibility that the binding site for external cations in Na_V1.6 channels is relatively deep in the mouth of the channel or otherwise strategically placed to be particularly effective in preventing pore collapse. In addition, slow inactivation induced by long conditioning steps was reduced at voltages at which open-channel block was most prominent. This result suggests that the structural rearrangements responsible for the long-lived inactivated states induced in this study may include the external pore, as in K channels and cardiac Na channels (19,20,56–59), as well as the internal pore, as in skeletal Na channels (39).

Taken together, the data begin to address the issue of how the characteristics of Na current inactivation relate to the signaling abilities of the neurons. Although our recordings are for the most part limited to somatic membrane, and possibly some part of the initial segment, slice recordings indicate that firing rates and patterns are largely dictated by the availability of these perisomatic Na currents, at least in Purkinje neurons (60). Our recordings were also made at room temperature, so the measured rates of recovery from inactivation are likely to be slower than at physiological temperatures. Nevertheless, the tendency for cerebellar nuclear Na channels to inactivate relatively more (and Purkinje Na channels relatively less) is likely to translate into the intact cerebellum. Purkinje cells, for example, can fire more than 100 spikes/s for sustained periods, and previous work has provided evidence that rapid open-channel block and unblock of Na_V1.6 α-subunits may be an adaptation that maintains the high availability of Na channels required for signaling at such rates (7,29,44). This work further suggests that the relatively rapid exit from long-lived inactivated states may constitute an additional specialization that keeps availability high during prolonged firing by Purkinje cells. In contrast, the propensity for nuclear Na channels to slow-inactivate suggests that even at basal firing rates, cells are likely to operate with a relatively low availability (10). Consequently, small hyperpolarizations, such as those arising from inhibition by afferent Purkinje cells, may permit recovery of Na channels to an extent that significantly changes neuronal output. Specifically, upon relief of inhibition, a newly recovered pool of available Na channels is likely to contribute to a rapid depolarization, promoting the rebound firing that is characteristic of these neurons (12,15,61,62). Importantly, fast depolarizations are more likely to recruit low-threshold “rebound” Ca currents, which are thought to participate in plasticity of intrinsic as well as synaptic currents (63–65); in fact, slow depolarizations from hyperpolarized potentials inactivate these rebound currents and block potentiation of excitatory synaptic currents (65). In this way, inactivation and recovery of cerebellar nuclear Na channels may contribute to the plasticity of cerebellar signaling.