Spontaneous Creation of Macroscopic Flow and Metachronal Waves in an Array of Cilia

Abstract

Cells carrying cilia on their surface show many striking features: alignment of cilia in an array, two-phase asymmetric beating for each cilium, and existence of metachronal coordination with a constant phase difference between two adjacent cilia. We give simple theoretical arguments based on hydrodynamic coupling and an internal mechanism of the cilium derived from the behavior of a collection of molecular motors to account qualitatively for these cooperative features. Hydrodynamic interactions can lead to the alignment of an array of cilia. We study the effect of a transverse external flow and obtain a two-phase asymmetrical beating, faster along the flow and slower against the flow, proceeding around an average curved position. We show that an aligned array of cilia is able to spontaneously break the left-right symmetry and to create a global average flow. Metachronal coordination arises as a consequence of the internal mechanism of the cilia and their hydrodynamic couplings, with a wavelength comparable to that found in experiments. It allows the cilia to start beating at a lower adenosine-triphosphate threshold and at a higher frequency than for a single cilium. It also leads to a rather stationary flow, which might be its major advantage.

INTRODUCTION

Many cells and bacteria have cilia or flagella on their surfaces. Examples are sperm cells that have one flagellum used for propulsion, the green alga Chlamydomonas that uses two flagella, and the much studied protozoan Paramecium, which is covered by ∼4000 cilia that produce a very efficient motion with a velocity of order 1 mm/s in water, corresponding to 10× the Paramecium size per second. Humans have ciliated cells in several organs: in the brain (ependymal cells that create cerebrospinal fluid flow (1)), the retina (photoreceptor connective cilia), the respiratory tract (epithelial cells), the ear (hair bundles), the Fallopian tube, or the kidney (2).

Cilia have two major roles: i), detection (sensory cilia or flagella), for example, in the retina, the ear, and the kidney; and ii), propulsion or creation of fluid flow (motile cilia or flagella) as for Paramecium or in the respiratory tract where the fluid flow is used to move away the mucus.

The common structure of most cilia and flagella is an axoneme wrapped by the plasma membrane. The (9 + 2) axoneme is made of nine microtubule doublets arranged on a circle around a central pair of microtubules (3). The cilium or flagellum is attached to the cell membrane by a basal body made of nine microtubule triplets that has a structure very similar to that of a centriole. The basal body is attached to the cell membrane by anchoring fibers (4). Typically the radius of an axoneme is 0.1 μm. The main structural difference between cilia and flagella is their length (10 μm for cilia, up to 100× longer for flagella (5)). Dynein molecular motors are attached to the nine microtubule doublets. Upon consumption of adenosine-triphosphate (ATP), dynein motion generates forces that induce a sliding between adjacent microtubules. Because the whole structure is attached at its base, this sliding motion induces the bending of the cilium or flagellum and its beating (3,6).

We here focus on ciliated cells creating fluid flow. These are cells with cilia on their surface, beating in one preferred direction in a coordinated way. One central feature of cilia beating is the existence of two phases with a broken symmetry. Each beating can be decomposed into an effective stroke that propels the fluid and a recovery stroke where the cilium is coming back against the flow. In the example of Paramecium in water, the effective stroke lasts typically 9 ms whereas the recovery stroke lasts 26 ms. The typical beating frequency in water is 30 Hz (7). The beating of Paramecium cilia is three-dimensional but for some species like Opalina or Chlamydomonas, it remains essentially planar (8). In this work, we discuss the role of an external velocity field in this left-right symmetry breaking between the effective stroke and the recovery stroke for planar beating.

One of the most striking features of an assembly of beating cilia is that they all beat in the same direction: the surrounding fluid can only be propelled efficiently if all the beatings have the same orientation. In mature ciliated cells, the beating direction is defined by the anchoring of the basal foot on the basal body. Only newly formed or developing cilia are randomly oriented (9). When they start beating, they tend to spontaneously align to finally beat in the same direction. One of the questions addressed in this article is the nature of the parameters that control this orientation.

Another important feature of ciliated cells is the existence of waves propagating all along the surface. These are called metachronal waves and might be due to the coordination of adjacent cilia, for example, via hydrodynamic interactions. Experimentally metachronal waves are observed to propagate in all possible directions: in the direction of the effective stroke (symplectic metachronal waves), in the opposite direction (antiplectic), or even in a perpendicular (laeoplectic or dexioplectic) or oblique direction. The origin of these waves and the mechanisms controlling their formation are not well understood. We show in this article that metachronism can arise naturally from the hydrodynamic couplings between cilia. Using a two-state model for the dynein motion as an internal mechanism of the cilia, metachronism appears to be a local minimum in the oscillation threshold of the motors (10,11). It decreases the amount of ATP necessary for beating, but it also increases the beating frequency and induces a rather stationary flow that accounts for the regular swim of ciliated organisms like Paramecium. This last effect could be the major interest of metachronal coordination.

The local [Ca²⁺] concentration has a strong influence on the beating pattern of cilia or flagella. For example detergent-treated Paramecium are able to swim forward at low [Ca²⁺] concentration (<10⁻⁶M) and backward at high [Ca²⁺] concentration (>10⁻⁶M) because of ciliary reversal: the directions of effective and recovery strokes are switched (12,13). In any case, the wild-type Paramecium can have a very efficient backward motion monitored by calcium tanks in its body. We only discuss here qualitative aspects of the role of calcium.

In this article, we address the question of the spontaneous alignment of an array of beating cilia and the possibility of a spontaneous symmetry breaking in the beating that leads to the appearance of a macroscopic fluid flow. The internal mechanism of the cilia is described by the model of references (10,11) that is based on a two-state model to describe the cooperative effects between dynein motors and only considers the relative sliding of two microtubules in the axoneme. The coordination between the cilia is due to hydrodynamic interactions that are discussed in details in a coarse-grained description where the effect of the cilia on the flow is replaced by an effective force.

The outline of the article is as follows. In the next section, we give a simple model for the alignment of beating cilia. In the “Axonemal beating” section, we discuss the beating of one cilium following the model of Jülicher and Camalet (10,11). Finally, in “Left-right beating symmetry breaking and metachronal coordination”, we discuss the spontaneous breaking of the left-right symmetry of the beating due to the flow created by the cilia themselves and the existence of metachronal waves. The interest of our approach is to study the role of hydrodynamic effects on some characteristic features of ciliated cells; proteins, Ca²⁺ waves, or more generally chemical signals may not be the only answers to all these questions.

SPONTANEOUS ALIGNMENT OF AN ARRAY OF CILIA

Experimental results

In an assembly of cilia covering the surface of a mature cell, cilia are beating in a preferred direction, and only newly formed or developing cilia are randomly oriented (9). We first discuss the experiments showing how this preferred orientation is chosen.

As mentioned before, the ciliary axoneme grows from a basal body analogous to a centriole. Two basal body appendages, the basal foot and the striated rootlet, located in the plane of the effective stroke, confer an asymmetrical organization to the basal body. The basal foot is laterally associated with two consecutive triplets and points in the direction of the effective stroke (14,15). The striated rootlet, associated with the proximal end of the basal body, sinks into the cytoplasm in the opposite direction (14). These two appendages define therefore an orientation of a cilium before beating motion.

During ciliogenesis, newly formed basal bodies migrate toward the cell membrane where they anchor with no apparent order. Anchoring induces axoneme assembling, and cilia grow in random orientations. While cilia are growing, they do not beat immediately. A reorientation by rotation of the basal bodies in a common direction occurs at the final stage of ciliogenesis, when mature cilia beat (16). The preferred direction of the assembly is then well defined. In primary ciliary dyskinesia (PCD) also known as immotile cilia syndrome, axonemes are incomplete, and the ciliary activity is abnormal or absent: the fluid is poorly or not propelled. At the cell level, the basal bodies are randomly oriented (17).

These experimental facts suggest that the beating and orientation of cilia are closely related. Our working hypothesis is that the alignment of an assembly of beating cilia is mostly due to hydrodynamic coupling between cilia. The global flow created by the other cilia tends to orient a given cilium and above a certain beating amplitude, all cilia orient on average in the same direction. We now give a simple modeling of this cooperative alignment.

Alignment transition

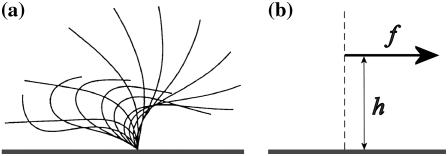
We assume in the following that the beating is planar. It is the case for Opalina, for example, but not exactly for Paramecium where the recovery stroke is not in the plane of the effective stroke. Near the top of the ciliary layer, observations show that the velocity is time independent and uniform (18). Consequently, we average the beating over one time period and replace each cilium of length L (and its effective and recovery stroke) by a single force (stokeslet) 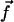, parallel to the surface, created in the fluid of viscosity η at height h < L above the membrane, as sketched in Fig. 1.

FIGURE 1.

(a) Beating pattern of a cilium. The fluid is efficiently propelled during the effective stroke. During the recovery stroke, the cilium comes back close to the surface, minimizing the viscous effects. (b) Effective force in the fluid 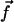applied at a height h above the cell membrane, to mimic the cilium beating.

We choose the x axis in the direction of the effective stroke and the z axis perpendicular to the cell surface that we approximate by a plane. The stokeslet along the x axis (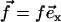) is located at point 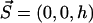. The velocity created at point 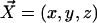by this stokeslet with a no-slip boundary condition on the plane z = 0 is given by:

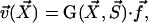where the response tensor G is given in Blake (19) and reads:

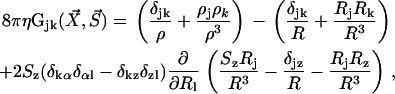(1)

where 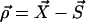, 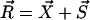and α = x, y.

To simplify the hydrodynamic problem, we assume in all the following that the cilia are far away from each other. In this asymptotic limit, it is consistent to describe the effect of the cilium in the fluid by a stokeslet. We introduce the two-dimensional vector along the cell surface 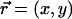and consider the limit 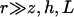. We are interested in the velocity in the vicinity of the ciliary layer, typically 0 < z < 1.5L. At lowest order in z/r, the velocity reads:

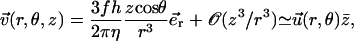(2)

where we have defined a dimensionless height 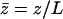. In the following, we use mostly the velocity 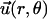. At this order, the flow field is a radial flow centered on the cilium-stokeslet. Note that because of the no-slip boundary condition on the surface, the force appears in the velocity field (Eq. 2) in the combination fh homogeneous to a momentum.

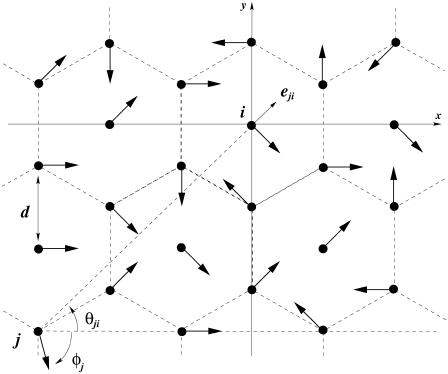
We consider now a regular array of cilia; this is a reasonable assumption for Paramecium, which shows a beautiful and very regular array of cilia on its surface (20). We assume that this array is in an infinite plane. Cilium i is defined by its position in the xy plane (the cell surface) by a vector 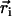and by the angle of its plane of beating with the x axis, φ_i as displayed on Fig. 2. The total velocity at the cilium i at height z, 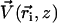is the sum of all the velocities 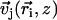created by the other cilia j ≠ i:

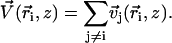FIGURE 2.

Hexagonal lattice of cilia with a distance d between two neighboring cilia. Cilium j exerts on the fluid a force f in the direction φ_j; 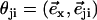, where 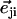is the unit vector from cilium j to cilium i.

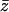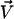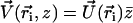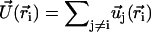We single out the dependence of writing with and

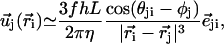(3)

where 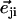is a unit vector from cilium j to cilium i and 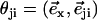, as shown on Fig. 2. We now use a mean field approximation, replacing the velocity 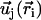by its average over the directions 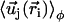given by:

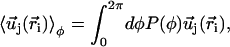(4)

where P(φ) is the probability for a cilium to make an angle φ with the x axis. The velocity at cilium i is 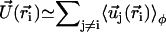. The mean field approximation assumes that the fluctuations around a given angle determining the direction of the flow are small. We choose the x axis in the direction of the flow without any loss of generality, so that the probability P(φ) is peaked around φ = 0.

To determine the probability P(φ), we write a stationary Fokker-Planck equation ∂_φJ = 0. The probability current J = P∂_tφ − D_r∂_φP is the sum of two terms: a convection term and a diffusion term where D_r is a rotational diffusion coefficient. The beating plane can fluctuate due to thermal fluctuations. Because of the flow, if the beating plane of one cilium is at an angle φ with the flow direction, the cilium is subject to a torque 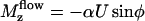along the z axis that tends to align it in the direction of the flow, where 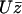is the velocity of the global flow and α a viscosity coefficient involving the geometry of the cilium. A rotating cilium is also subject to a viscous torque M^viscous opposing the rotation 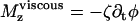where ζ is the rotational friction constant. The total torque on the cilium vanishes (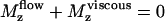) and the probability distribution satisfies the Fokker-Planck equation:

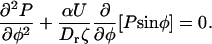We define the effective temperature as D_rζ = k_BT. We introduce the dimensionless velocity 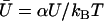and we impose the normalization condition 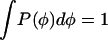. We obtain:

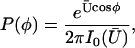(5)

where 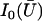is the modified Bessel function defined in Gradshteyn and Ryzhik (21). The velocity 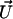can then be self-consistently determined by calculating 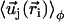, and summing over all the lattice sites. We obtain:

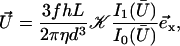(6)

where 𝒦 is a constant depending on the nature of the lattice, d is the lattice constant (the distance between cilia), and 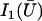is a modified Bessel function (21). For a hexagonal lattice, the explicit calculation yields:

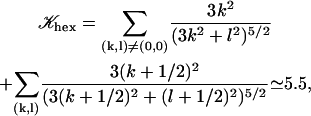(7)

(for a square lattice 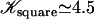). The self-consistent Eq. 6 for the flow velocity can be discussed by expanding the integrals I₀ and I₁ in the vicinity of 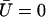: there are two solutions 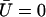, and a solution at a finite velocity that exists only within a certain range of parameters:

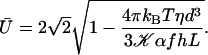(8)

This solution exists only if:

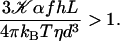(9)

Within the mean field approximation Eq. 9 defines a dynamical phase transition between a nonmoving fluid with randomly oriented cilia and a moving fluid with a global flow 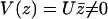given by Eq. 8 where all cilia are spontaneously aligned in the same orientation. This dynamical phase transition is second order (with a continuous velocity at the transition) and it is associated to a spontaneous breaking of the initial O(2) symmetry.

The influence of some of the parameters can be directly analyzed on Eq. 9. A decrease of the distance d between two cilia favors the alignment, increasing the hydrodynamic coupling. A decrease of the temperature T also favors alignment as the random thermal motion opposes it. An increase of the effective hydrodynamic force of one cilium f is associated to an increase in the interactions between cilia and leads to a better alignment. The same effect occurs for α and the cilium length L. Finally, increasing h helps to create a global flow, since the velocity on the membrane vanishes and the higher the force is exerted, the more efficient.

An analysis only involving the geometrical and kinetic parameters of the cilium requires the estimation of the parameters f, α, and h. Even if the exact motion of the cilium is necessary for a quantitative study, it is worth going further qualitatively in the analysis. The height h is of the order of the cilium size h ∼ L. The calculation of α is given in Appendix I for a general beating (Eq. 48). It turns out that α is linked to the difference of the areas covered during the effective and recovery strokes. Here we approximate 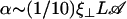, where ξ_⊥ is the perpendicular friction constant per unit length of the cilium (10,22) and 𝒜 the amplitude of the tip movement.

To give a simple estimation of the effective hydrodynamic force, we consider that the friction coefficient takes the perpendicular value ξ_⊥ during the effective stroke, and the parallel value ξ_‖ during the recovery stroke. Introducing the beating frequency ω, we estimate 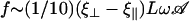(see Eq. 48). A more precise calculation of these two quantities as a function of the beating patterns is given in Appendix I. The numerical factor is such that 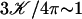. Consequently, we obtain:

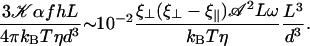The difference between the two local drag coefficients ξ_⊥ and ξ_‖ is the key to an efficient beating. Increasing the amplitude 𝒜 or the frequency ω of the beating favors the alignment of cilia, as could be expected. Increasing the viscosity of the medium could also promote the transition at first sight because it seems to increase the coupling between cilia (since ξ_⊥, ξ_⊥ ∝ η). Nevertheless, this last argument requires more attention because the beating pattern (force exerted by the cilium, amplitude) and its frequency depend on the medium viscosity. Indeed, in Machemer (23) measures a decrease of the frequency when η increases, as we get in “Axonemal beating”. Moreover, we can also expect a decrease of 𝒜 with η. Thus, increasing viscosity may lower the coupling between cilia (as suggested in Gheber et al. (24)) and disadvantage their alignment.

Equation 9 is satisfied even for rather large d. Indeed, taking 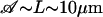, ξ_⊥ ∼ 10η_water (25), ω ∼ 10²rad s⁻¹, k_BT ∼ 10⁻²¹J we get:

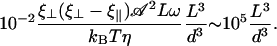Thus, Eq. 9 remains true even for d ∼ 10L: hydrodynamic effects should be sufficient to induce alignment in several cases since for many ciliated cells, d < L. In the following, we take a closer look at the internal beating mechanism of one cilium and then at the beating of an array of cilia to obtain a more precise and quantitative description.

AXONEMAL BEATING

In this section we discuss the beating mechanism of a single cilium. We follow closely the work of Camalet and Jülicher (11), which mimics the cilium by two microtubule filaments sliding along one another under the action of the dynein motors and uses a two-state model to describe the collective motion of the dyneins. We use as boundary conditions for the motion those introduced recently (I. Riedel-Kruse, A. Hilfinger, J. Howard, and F. Jülicher, unpublished data; (26,27)) that seem to have good experimental support (28). In the next section, we use the same model to discuss the coordination between cilia.

Equation of motion

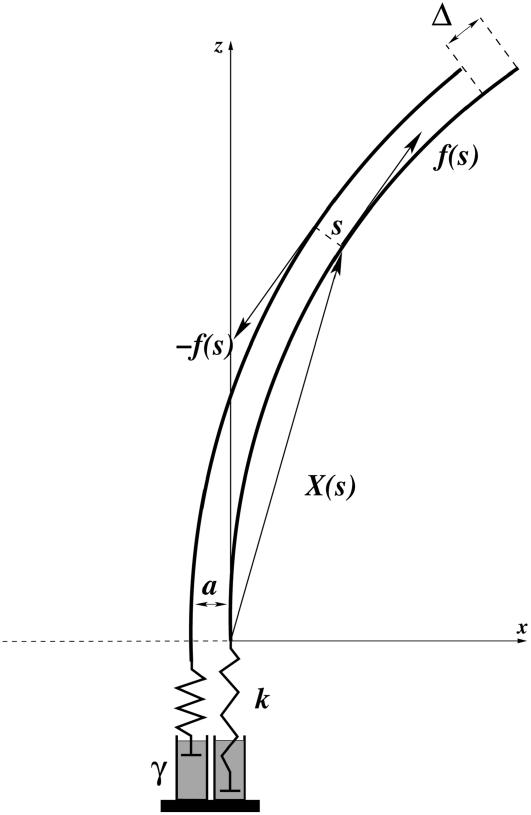
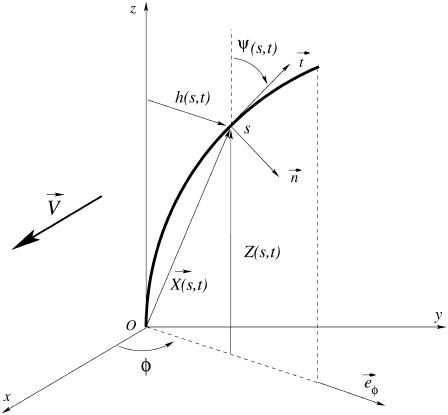
Each microtubule doublet within the axoneme can be described effectively as an elastic rod. Deformations of this rod lead to local sliding displacements of neighboring microtubules. Here, we only consider planar deformations in the (xz) plane. In this case the geometrical coupling between bending and sliding can be captured by considering two parallel elastic filaments (corresponding to two microtubule doublets) with a constant separation a along the whole length of the rod (see Fig. 3). At one end, which corresponds to the basal end of an axoneme, the two filaments are elastically attached and are allowed to slide with respect to each other, but not to tilt (26,29). The basal connection is characterized by an elasticity k and a frictional drag γ. The configurations of the axoneme are described by the shape of the filament pair given by the position of one filament 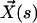at arclength s. The shape of the other filament is then given by 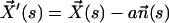, where 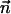is the filament normal. In the following, we describe the filament conformation by the angle ψ between the local tangent vector and the z axis or by the deformation h in the transverse direction defined in Fig. 12.

FIGURE 3.

Two filaments (full curves) 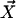and 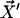at constant separation a are connected to the membrane at the bottom end where s = 0. Internal forces f(s) are exerted in opposite directions, tangential to the filaments. The displacement Δ at the tip s = L is indicated.

The energetics of the filament pair is due to the bending elasticity. In addition to filament bending, we also take into account internal stresses due to the active elements (dyneins). We characterize them by the force per unit length f(s) acting at position s in opposite directions on the two filaments. This force density corresponds to a shear stress within the cilium that tends to slide the two filaments with respect to each other. The local curvature is C = ∂_sψ (see Fig. 12). The sliding displacement, Δ(s, t) is related to the sliding displacement at the base Δ₀(t) by Δ(s, t) − Δ₀(t) = aψ(s, t), because we impose the boundary condition ψ(0, t) = 0.

A configuration of a filament pair of length L is associated to the free energy functional:

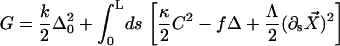Here, κ denotes the total bending rigidity of the filaments. The inextensibility of the filaments is taken into account by the Lagrange multiplier Λ(s), which enforces the constraint 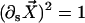. The first term of this expression is the elastic energy due to the basal sliding occurring with a connection of elasticity k. The tangent component of the integrated forces acting on the filament between s and L is denoted by τ(s). Assuming that there is no external force applied at the end s = L of the cilium:

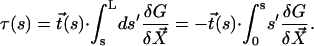We assume for simplicity that the hydrodynamic effects of the surrounding fluid can be described by two local friction coefficients ξ_⊥ and ξ_‖ for normal and tangential motion. The total friction force per unit length exerted by the cilium on the fluid is then 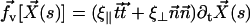. The force balance at arclength s can then be written as:

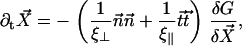(10)

which leads to:

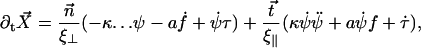(11)

where the derivatives with respect to arclength have been denoted by a dot.

The beating of the filaments is very sensitive to the boundary conditions imposed at its ends. As the force density 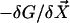is equilibrated by the density of friction force exerted by the fluid on the system (see Eq. 10), the boundary contributions coming from the free energy variation δG are equilibrated by external forces and torques 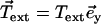applied at the ends. At the free end of the cilium, both the external force and the external torque vanish and:

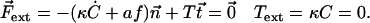(12)

At the base, s = 0, the boundary conditions are:

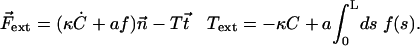(13)

The external torque and force are chosen in such a way that the base is fixed (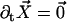) and that the cilium remains perpendicular to the surface ( 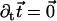or ψ(0) = 0). The final boundary condition is associated to the basal sliding

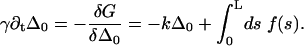(14)

The determination of the cilium motion requires a model for the shear force created by the dyneins that we calculate using a two-state model.

Two-state model for the cilium

Following Camalet and Jülicher (11), we now introduce the two-state model of coupled molecular motors (30,31) to describe the internal mechanism of the cilium. This model allows the calculation of the shear force f due to the dyneins.

Each motor has two different chemical states, a strongly bound state, 1, and a weakly bound state, 2. The interactions between a motor and a filament in both states are characterized by potential energy landscapes W₁(x) and W₂(x), where x denotes the position of a motor along the filament. The potentials have the filament symmetry: they are periodic with period l, W_i(x) = W_i(x + l) and are, in general, spatially asymmetric, W_i(x) ≠ W_i(−x).

In the presence of ATP, the motors undergo transitions between states with transition rates ω₁ and ω₂. Introducing the relative position ξ of a motor with respect to the potential period, (x = ξ + nl with 0 ≤ ξ < l and n an integer), we define the probability P_i(ξ, t) for a motor to be in state i at position ξ at time t. The relevant Fokker-Planck equations are:

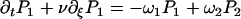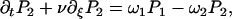where ν = ∂_tΔ = a∂_tψ(s) is the sliding velocity between the two filaments.

The simplest choice of the two potentials W_i, is a saw-tooth potential (with barrier height 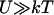) representing a strongly bound state for W₁, and a flat potential W₂ representing a weakly bound state. Here, for simplicity, we use the symmetric potentials:

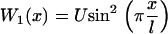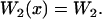Although this choice is somehow arbitrary, we checked that the final results only depend qualitatively on the actual shape of the potentials and of the rates defined below.

When a number of motors act together to propel a filament, the direction of motion is a collective property: the filament might move in either direction (31). The absence of asymmetry in the potentials implies that an individual motor is not able to move directionally. It is not the case for an assembly of motors: even with a symmetric potential, provided that detachment can only take place at a localized position near the bottom of a potential well, oscillations can occur.

We define the distance from equilibrium Ω:

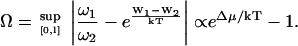Ω is related to the chemical potential difference between ATP and its hydrolysis products, Δμ = μ_ATP − μ_ADP − μ_P. At equilibrium, Δμ = 0 and Ω = 0. We assume for simplicity that the binding rates ω₂ and the detachment rate ω₁ are given by:

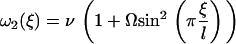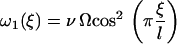Note that, with this choice the sum ω₁ + ω₂ = ν(1 + Ω) does not depend on ξ, and that if Ω = 0, ω₁ = 0 and no directional movement is possible. Here ν is a constant transition rate. If we assume that the motors are uniformly distributed along the filaments with a density ρ, the probabilities P₁ and P₂ satisfy the relationship P₁ + P₂ = ρ. The Fokker-Planck equations reduce then to a single equation for P = P₁:

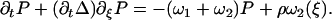(15)

This model leads to an expression for the shear force per unit of length f(s, t) created by the dyneins and driving the cilium beating. Using the results of Prost et al. (30), and the fact that W₂ is a constant:

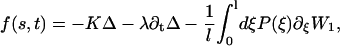(16)

where K is an elastic stiffness per unit length mimicking the influence of the nexins that are proteins acting as springs in the axonemal structure, and λ is an internal friction coefficient per unit length modeling the friction encountered by the motors. Equations 11 and 15 allow in principle a complete calculation of the beating motion.

In the following, we assume that the beating occurs with a “small” amplitude, which means that both 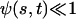and 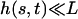. A quick look at the beating pattern of a cilium of Paramecium shows that the beating occurs with a large amplitude. Nevertheless, this approximation allows us to extract interesting information on the parameters controlling the beating. Moreover, the work of Hilfinger shows that larger amplitude beating patterns are very similar to small amplitude patterns (26). We must however keep in mind that our approach is valid only if the system stays close to an oscillation bifurcation, which is consistent with the fact that we consider only small movements.

We use the deformation h, rather than ψ or Δ to describe cilium motion and work at second order in |h| so that 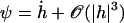. In the absence of any external flow, the equation of motion 11 projected on 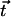imposes that 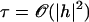(10,11). The projection of the equation of motion on 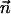then yields:

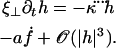(17)

The nonlinear terms are not important here but they will turn out important in the following section. Indeed, experiments show that the beating is clearly asymmetrical (ES and RS), and we must expand at least to the next order if we want to capture this phenomenon. With this variable and at this order, the boundary conditions read:

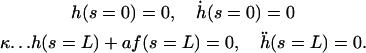(18)

The explicit solution of the equation of motion 17 is obtained by Fourier expansion in time 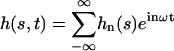. The explicit derivation of the equation satisfied by the Fourier components is given in Appendix II. At linear order the effect of the motors is characterized by a susceptibility:

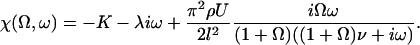(19)

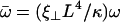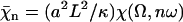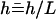Using dimensionless variables, , , , and , the equation of motion for the Fourier component n reads:

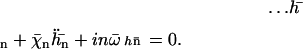(20)

Note that 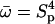where S_p is the “sperm number” introduced in Lowe (32). The boundary conditions at the base are:

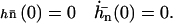(21)

At the free end of the cilium, :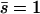

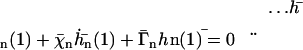(22)

with 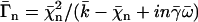where we have introduced the dimensionless parameters 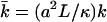and .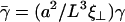

Beating pattern

In the absence of any external flow the beating is symmetric and the Fourier components n = 0 and n = 2 of h vanish for symmetry reasons. Close to the oscillation bifurcation threshold, cilium beating is dominated by the first Fourier component n = 1. The solution of the linear equation of motion 20 is written as the sum of four exponentials:

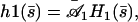(23)

with

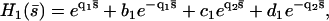where the two inverse decay lengths are given by:

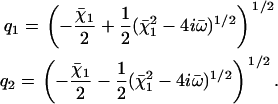(24)

The boundary conditions are explicitly discussed in Appendix II. The condition for existence of nonvanishing solutions is given by Eq. 57 of Appendix II. This is a complex equation that gives therefore two conditions that determine both the critical value of the distance from equilibrium where the oscillations start Ω_c, and the reduced oscillation frequency 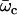. The critical value Ω_c is a Hopf bifurcation threshold: there are no oscillations if Ω ≤ Ω_c and cilium beating is only possible if Ω ≥ Ω_c. At the bifurcation threshold, the amplitude of the oscillations vanishes. It is not possible to calculate the amplitude of the oscillations above the bifurcation threshold with the linear theory presented here. This requires a complete determination of the third order terms in the equation of motion that goes far beyond the scope of this work. This very complex problem is addressed in the work of Hilfinger and Jülicher (26).

Determination of the Hopf bifurcation threshold and the beating frequency at this threshold does not seem to be possible analytically. We therefore rely on a numerical solution, choosing reasonable values of the various parameters. We study a cilium of length L = 12 μm, which is the length of a Paramecium cilium. It moves in a fluid of viscosity η ∼ 4η_water = 410⁻³ Pa s, which is higher than the water viscosity to take into account the proteins above the cell body. We estimate κ = 410⁻²²Nm² corresponding to 20 microtubules and to what is measured in Ishijima and Hiramoto (33). The other parameters are l = 10 nm, a = 20 nm, U = 10 kT, 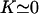, ρ = 510⁸m⁻¹, and λ = 1 Pa s very similar to those of Camalet (10). To match the typical frequency observed in Paramecium, and to obtain a realistic pattern of the beating, we take ξ_⊥ = 35η = 1410⁻² Pa s and we choose k = 6.5 Nm⁻¹, γ = 7.3η_water, and ν = 600 s⁻¹. The value of ξ_⊥ is rather high, but it must include the hydrodynamic interactions of the cilium with the cell surface (34), which are not taken into account if we use the classical friction per unit length of a cylinder (35).

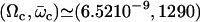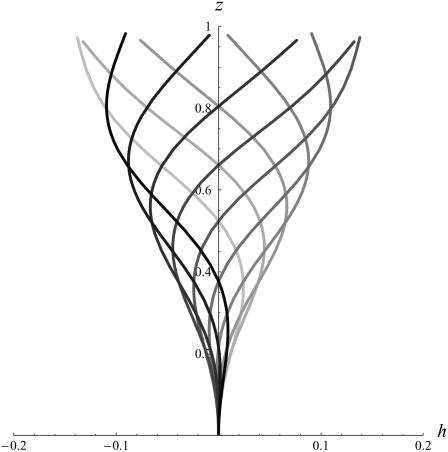
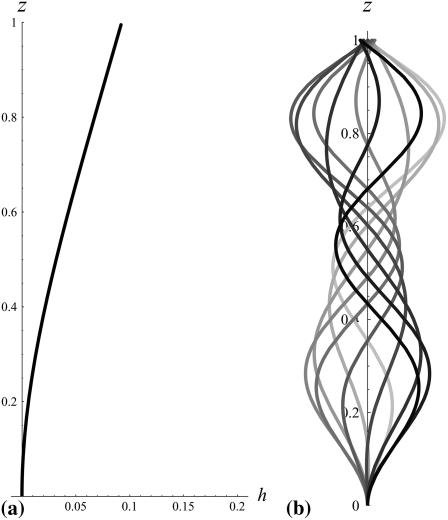
The numerical resolution of Eq. 57 then yields . This corresponds to a critical beating frequency 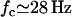, which is the typical value for Paramecium (7). The calculated beating pattern of the cilium is shown on Fig. 4. It corresponds to a superposition of waves propagating from the base of the cilium to the free tip as observed experimentally.

FIGURE 4.

Approximate cilium deformation 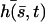at different times steps (corresponding to different gray levels) during a beating period with 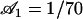. The beating is symmetrical with respect to the vertical axis. Deformations are propagating from base to tip.

A detailed study shows that the equation giving the bifurcation threshold and the beating frequency has several solutions 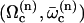with 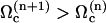. A first guess would be that the axoneme starts beating at the lowest threshold 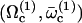. However, it is known experimentally that during the beating the deformation waves propagate from the base to the tip and not from the tip to the base (36). The first two oscillating modes correspond to waves propagating in the opposite direction. To be consistent with the observations we do not consider them here. A better choice of the transition rates ω₁ and ω₂ would perhaps allow to justify this choice. The direction of propagation of the wave is extremely sensitive to the boundary conditions. We have allowed here basal sliding as suggested by some experiments and we have imposed that the cilium is clamped at its base with an angle ψ = 0. This also seems consistent with some experiments analyzed in Hilfinger (26). The other extreme limit of a completely free cilium (a vanishing external torque at the base) leads to a wave propagating form the base to the tip for the first mode. We have tried to use an intermediate boundary condition where the torque at the base is an elastic torque and varying the related stiffness, however, we were not able to obtain a beating pattern looking like the experimental one. We therefore proceed, considering only the third beating mode .

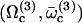On the other hand, it is not surprising that the lowest beating threshold corresponds to a tip to base propagation because the tip is free to move whereas the base is not. The same phenomenon has been observed in Dreyfus et al. (25): the authors construct an artificial flagellum with magnetic particles. One end is attached to a red blood cell and the other end is free to move. The beating is driven by an applied transverse oscillating magnetic field. As a result, a bending wave propagates from the free end, which is more mobile. The easiest way to move a filament being to start with its free end, our result may not be an artifact of the model. The cell must then impose an ATP concentration such that 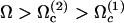so that the third mode is selected.

The beating frequency f_c varies with the viscosity of the medium. Experimentally, when methyl-cellulose is added in water, the viscosity increases significantly. We predict here a decrease of f_c with increasing external viscosity as observed in the experiments of Machemer (23) and in numerical simulations (37) (see Table 1). We observe an approximate linear decrease of the beating frequency when plotted against log(η/η_w) as in the simulations performed in Gueron and Levit-Gurevich (37) (we find similar values for the frequency).

TABLE 1.

Viscosity and beating frequency

External viscosity	Critical frequency fc	Simulations
ηw	28 Hz	29 Hz
2ηw	19 Hz	17 Hz
3ηw	14 Hz	12 Hz

Decrease of the beating frequency with increasing external viscosity as observed in experiments (23). Comparison with the simulations done in Gueron and Levit-Gurevich (37) for one single cilium.

The effect of [Ca²⁺] on the beating can also be studied qualitatively. As mentioned in the introduction, [Ca²⁺] has a strong influence on the beating pattern. Calcium concentration variations are at the basis of the shock responses of many organisms, changing the ciliary-type beating into a flagellar-type beating in Chlamydomonas, or switching the directions of effective stroke and recovery stroke in Paramecium, or in reversing the direction of the “wave” propagation on the flagellum and thus reversing the direction of the movement in Chritidia (38).

This last example can be explained qualitatively within our approach. In Chritidia, both directions are possible for the deformation wave propagation. Calcium may affect the chosen mode of beating, allowing the system to choose 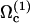and its tip-to-base pattern instead of .

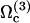Calcium is also likely to change the attachment/detachment rate (and thus change the parameter ν) or the boundary conditions at the base of the cilium (and thus change k). In Chlamydomonas, calcium has a contractile effect on the striated fibers connecting the basal bodies of the two flagella (39). These changes induce a change in the beating pattern, and may result in a switch from base-to-tip to tip-to-base wavelike propagation.

LEFT-RIGHT BEATING SYMMETRY BREAKING AND METACHRONAL COORDINATION

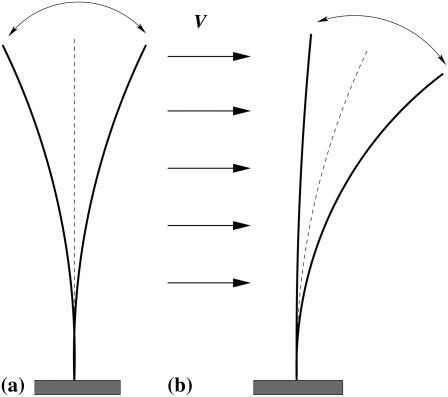
In the presence of a transverse external flow, the beating can no longer be symmetrical as sketched on Fig. 5. The cilium tends to beat faster and quite straight in the direction of the flow, whereas it comes back slower and more curved against the flow. This looks like a two-phase beating with an effective and a recovery stroke.

FIGURE 5.

Effect of an external flow 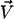on the beating of a single cilium. (a) Symmetrical beating. (b) Broken symmetry due to the external flow.

If the beating is asymmetrical, the cilium exerts a force in the fluid that can itself produce a flow. In a certain range of parameters, one can therefore expect that a continuous flow is spontaneously generated by hydrodynamic interactions between cilia: an assembly of cilia, beating symmetrically, is able to break spontaneously this left-right symmetry of the beating to create a global flow. This idea of a spontaneous breaking of the left-right symmetry has already been suggested (40) with a more abstract system (called rowers) having two internal energy states.

In this section, we first study the effect of an external velocity imposed by the experimentalist on the beating symmetry of a single cilium. We then consider an array of aligned cilia and determine the conditions under which this assembly of cilia breaks its left-right symmetry and generates a global flow. Metachronal coordination between cilia naturally emerges from hydrodynamic coupling as a local minimum of the oscillation threshold Ω_c.

External breaking of the beating symmetry: cilium submitted to an external flow

We impose an external flow 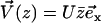along the x axis for simplicity, and satisfying the no-slip boundary condition on the cell membrane as in “Spontaneous alignment of an array of cilia: a simple model”, with the same notations (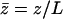). It is found experimentally that the velocity above the cilia sublayer is time independent (18), justifying our choice. This flow is in this first part externally fixed and we consider the limit of vanishingly small flows. The force per unit length exerted by the cilium on the fluid 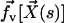depends on the external velocity .

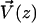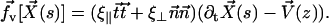(25)

The equation of motion 11 reads then:

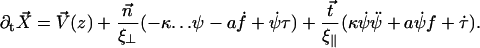(26)

The boundary conditions are the same as in the absence of the neighboring cilia and are given by Eqs. 12–14. Following the same procedure as for a cilium in the absence of flow, we find the equation of motion for the deformation of the cilium h:

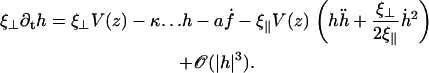(27)

The introduction of the external flow breaks the h → −h symmetry (or left-right symmetry) introducing in Eq. 17 terms of zeroth and second order in h in the equation of motion. The boundary conditions do not depend on the external flow. Because the height z where we consider the flow depends on the arclength s, we write (expanding Eq. 47):

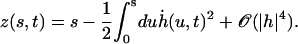(28)

Note that we cannot simply write 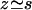and get rid of the second term because it is of order |h|². As above, we expand the deformation of the cilium h in Fourier components in time. Using the same notations as before, the equation of motion of the Fourier components can be written as:

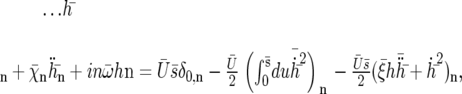(29)

for n = 0, 1, 2 and where we have introduced the new dimensionless parameters:

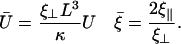In the limit of small external velocities, we have neglected terms of order , and we keep this approximation throughout our calculations.

The equation for the first mode is identical to Eq. 55, with the same boundary conditions. At this order in Ū, the fundamental mode is not affected by the external flow. Consequently, the oscillation threshold and the beating frequency are the same as in the absence of flow and the Fourier component 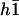is given by Eq. 23.

The zeroth Fourier component 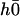gives the average deformation of the cilium. It is a solution of:

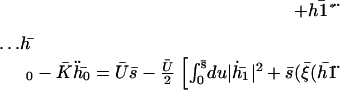(30)

with the same boundary condition as before. Nevertheless, 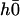does not vanish at first order in velocity because of the broken symmetry due to the external flow that is reflected in the right-hand side of Eq. 30. We write the solution as the sum of two contributions: 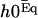, corresponds to the curvature of the cilium under the flow V(z) at equilibrium, i.e., in the absence of any beating (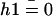), and 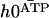, corresponds to the corrections to this equilibrium deformation due to the beating when there is enough ATP in the medium: 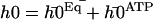. If as above, we ignore the elasticity of the nexins ():

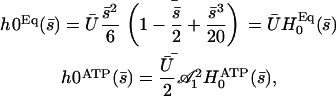(31)

where 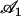is the amplitude of the first Fourier mode of the oscillation defined in Eq. 23 and 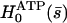is a function calculated numerically only depending on 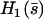(see Eq. 23). In the limit U = 0, 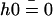as expected. The average deformation of the cilium is plotted on Fig. 6 a, which shows the bent shape under the action of the external flow.

FIGURE 6.

(a) Average position of a cilium that is curved in the direction of the flow, 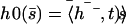. (b) Second Fourier component of the deformation 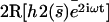at different times during a beating period. The scale is dilated: 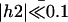with the parameters 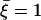, , 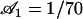and .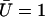

The second Fourier component gives the asymmetry of the beating. It is obtained from the equation of motion:

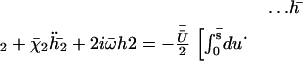(32)

We write the solution of Eq. 32 as:

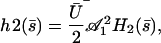where 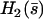is calculated numerically from 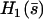as well. Here also, in the limit U = 0, 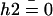. The plot at different times on Fig. 6 b, leads to a complicated pattern.

The total deformation of the cilium 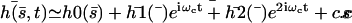. is plotted at different times equally spaced on Fig. 7. To stress the fact that the beating is easier and faster in the direction of the flow, and more difficult and slower against the flow, we have chosen rather large values of the parameters, 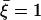, , 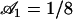and 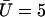, and we plot 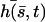for 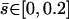on Fig. 7.

FIGURE 7.

Beating pattern at the base of the cilium (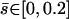) with the parameters 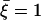, , 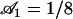and 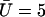: the cilium beats faster in the direction of the flow and slower in the opposite direction around a curved average position.

The external flow thus breaks the left-right symmetry in two ways. First the average position of the cilium is not the vertical axis but a cilium curved in the direction of the flow. Second, the beating itself is no longer left-right symmetric: the cilium goes faster in the direction of the flow and comes back slower against the flow. The beating pattern looks like a two-phases beating with an effective stroke and a recovery stroke. This effect increases with 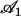and Ū and is consequently even more significant in real ciliary beatings. The external flow may therefore be an important factor in the asymmetry of the beating.

Another important result is that, because the beating propagates a base-to-tip deformation, the curved cilium exerts a finite average force in the fluid in the direction of the flow. Thus, if an external flow breaks the left-right beating symmetry, the cilia create a force in its direction and can amplify this flow. This is the basis of the left-right spontaneous symmetry breaking that we discuss in the next section.

The external flow is not always the only source of symmetry breaking. If it were so, Paramecium would always go in the same direction once it started moving. This is not the case because this organism is able to go backward when it bumps into an obstacle, thanks to the release of calcium that reverses the beating. Nevertheless, some ciliary assembly never reverse their beating and create a flow in a unique direction. This is the case for the respiratory, ependymal and Fallopian cilia for instance. In those examples, the flow is transverse and always in the same direction. Our approach may be relevant for this category of cilia for which an external flow might take a significant part in the breaking of the beating symmetry.

Spontaneous breaking of the beating symmetry: array of aligned cilia

We now consider a regular array of cilia on a cell body, beating all in the same direction. Starting from a symmetrical beating, we show that the left-right symmetry is spontaneously broken within a certain range of the parameters controlling the beating due to the hydrodynamic couplings between cilia.

Equations of motion

For a cilium located in the xy plane at position 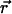, we call 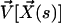the velocity created by the other cilia at the point 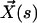of arclength s. The equation of motion of the cilium is similar to that obtained previously with an external flow field and we write up to the third order in h as:

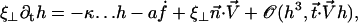(33)

where the projection of the local external velocity on the cilium normal is:

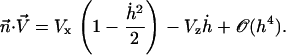(34)

The boundary conditions for the motion are the same as in the previous section. The velocity 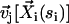created at arclength s_i of the cilium i by a cilium j is given by:

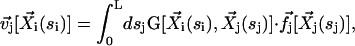where G is the second order hydrodynamic tensor given by Eq. 1 and 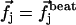is the force per unit of length created by the beating of the cilium j. The total velocity at the arclength s_i of the cilium i is thus given by:

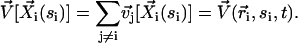As in “Spontaneous alignment of an array of cilia: a simple model”, we consider the limit 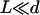and we only keep terms of the second order in s/r, r being the distance between two cilia in the array so that:

This means that only the velocity along the x axis created by the component f_x of 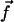plays a role and that we can ignore the other component V_z of the velocity appearing in Eq. 34. Using the notations of Fig. 2, and noting that 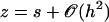, we obtain:

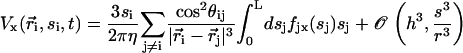(35)

As in the previous sections, we expand the velocity, the force, and the cilium deformation in Fourier modes in time. For simplicity, we only consider here the first two Fourier components and do not look at h₂ that characterizes the asymmetry of the beating. The Fourier components of the velocity are related to those of the force by:

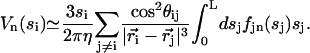The Fourier components of the force f₀ = 〈 f_x 〉 and f₁ are calculated using the expression of f^beat and its average over one time period given by Eq. 48 in the small movements approximation:

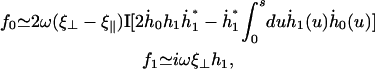(36)

where 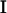is the imaginary part of a complex number. We assume that all cilia are identical, and that they all beat with the same pattern. The only difference in the beating patterns of cilia j and i is a possible phase difference that we call ϕ_ij. Defining:

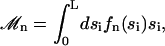(37)

and dropping the index i, we write the Fourier components of the velocity as:

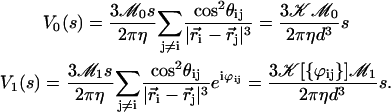(38)

The geometrical constant 𝒦 is given by Eq. 7 for a hexagonal lattice of cilia spaced by d. The constant 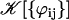depends on the relative phases between the cilia. If the phases ϕ_ij are randomly distributed, then 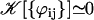and V₁ = 0: there is no oscillating component of the velocity.

On the contrary, because we know that metachronism occurs in an array of beating cilia, we choose a constant phase difference ϕ between two consecutive cilia in the direction of the plane of beating: ϕ_i,j+1 − ϕ_i,j = ϕ. This is the case for symplectic and antiplectic metachronal coordination. We only consider those cases (and not laeoplectic or dexioplectic metachronism) here. Experimentally, for Opalina (symplectic) and Pleurobrachia (antiplectic) that both have planar beatings, no metachronal wave in the transverse direction of the beating can be seen (34), which justifies our choice. We stress that we do not impose the phase difference ϕ. The system is free to adjust its phase. We then write 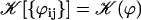with:

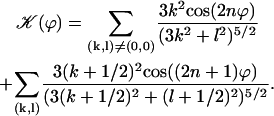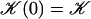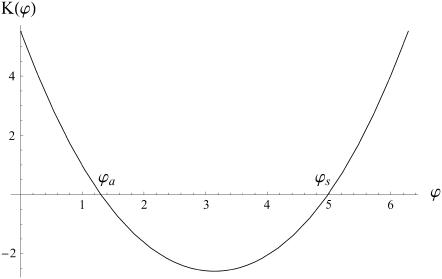
Note that . The function 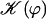is plotted on Fig. 8 for a lattice of 500² cilia. For two particular values of ϕ that we denote by ϕ_s and ϕ_a this function vanishes, 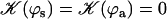, as in the case where the relative phases of the cilia are randomly distributed. This corresponds to a constant flow with no oscillating component. We now define the two dimensionless velocities Ū and 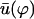by:

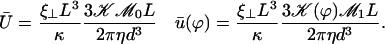(39)

FIGURE 8.

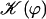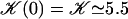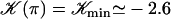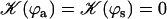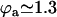over one period (φ ∈ [0, 2π]). Remarkable values: ; ; with and .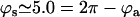

The equations of motions of the Fourier components 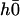and 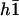can then be written as:

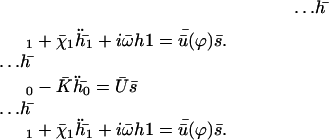(40)

In writing Eq. 40, we only kept the term 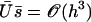that breaks the left-right symmetry and that lead to h₀ ≠ 0, ignoring any other term that would not create a macroscopic motion.

Beating pattern and metachronal waves

We first study the equation of motion of the first Fourier mode in Eq. 40, which corresponds to the oscillatory motion of the cilium. The right-hand side of this equation does not vanish due to the existence of an oscillatory external flow due to the other cilia. Note, however, that we have not treated in details the hydrodynamic interactions for one cilium since we have only taken them into account through the two local friction coefficients ξ_⊥ and ξ_‖. We are here more interested in the qualitative aspects of the coordination between cilia than in the accurate calculation of the flows created by each cilium.

The general solution of Eq. 40 can be written as 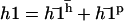with:

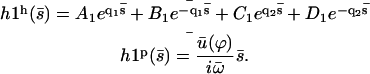(41)

It is convenient to rewrite the external velocity as 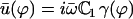with:

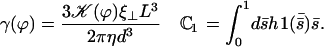The constant 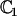can be determined self-consistently as it varies linearly with 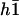. We obtain:

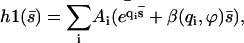with

The effect of the hydrodynamic interactions between cilia is embodied here in the coefficient γ(ϕ). The variation of this coefficient with the phase difference ϕ is similar to that of 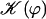. The limit where γ(ϕ) = 0 leads back to the previous situation were one cilium is beating alone; it may however correspond to the finite phase shifts between cilia ϕ = ϕ_s or ϕ_a.

The four boundary conditions on 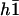can as before be written in a matrix form and the oscillation threshold and the critical beating frequency can be determined as the zeros of a determinant insuring the consistency of this matrix equation. This leaves an unknown amplitude of the beating motion that could only be calculated by expanding the equation of motion to higher order. The beating pattern can then still be written as:

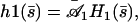with now

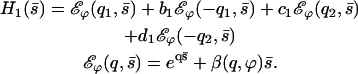(42)

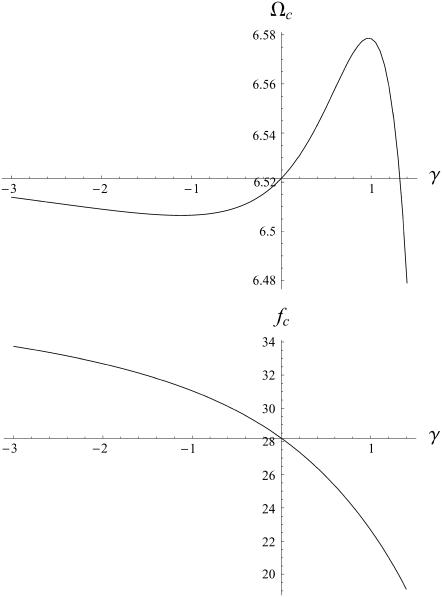
The values of both the oscillation threshold Ω_c and the frequency 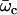depend on the phase shift ϕ, through γ(ϕ). We first discuss the variation of this bifurcation point with the constant γ(ϕ), which is a more convenient variable. On Fig. 9, we plot Ω_c and the critical frequency f_c against γ. There is a local minimum of Ω_c for 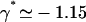and a local maximum for 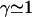. The beating frequency, f_c, is a decreasing function of γ.

FIGURE 9.

Oscillation threshold Ω_c and critical frequency f_c (Hz) as functions of γ for γ ∈ [ −3, 1.4]. Ω_c has a local minimum that corresponds to the existence of metachronal waves (symplectic or antiplectic). The horizontal axes indicate Ω_c and f_c for γ = 0.

We here need a selection criterion that determines the value of the phase shift between cilia. The simplest conjecture for the selection criterion is that the system chooses the local minimum of Ω_c corresponding to 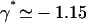. This corresponds to a metachronal wave propagating in the assembly of cilia, as widely confirmed by experimental observations ((23,36) for instance).

With this selection criterion, the oscillation threshold is now 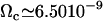and the critical frequency is 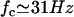. The hydrodynamic couplings between cilia slightly decrease the oscillation threshold Ω_c and increase the critical frequency f_c. Thus, the coordination between cilia favors cilium beating by creating a metachronal wave corresponding to γ < 0.

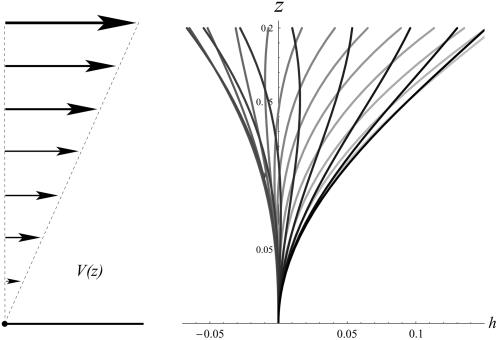
The beating pattern is slightly changed as shown on Fig. 10 where we have plotted 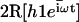at different time steps with the same amplitude and for γ = γ*. The phase difference ϕ* between two consecutive cilia corresponding to 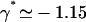depends on the values of the parameters. If we take d/L = 2, then 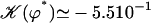, which yields 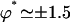. This value corresponds to a wavelength λ = 4.2d ∼ 4d for the metachronal waves or approximately five cilia, which is the correct order of magnitude (the wavelength is seven cilia in Machemer (23)).

FIGURE 10.

Beating pattern of a cilium in an array in the presence of a metachronal wave. The pattern is different from that of an isolated cilium mostly around the base. The first Fourier component 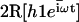at various time steps during a period is plotted with 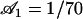and γ = γ*.

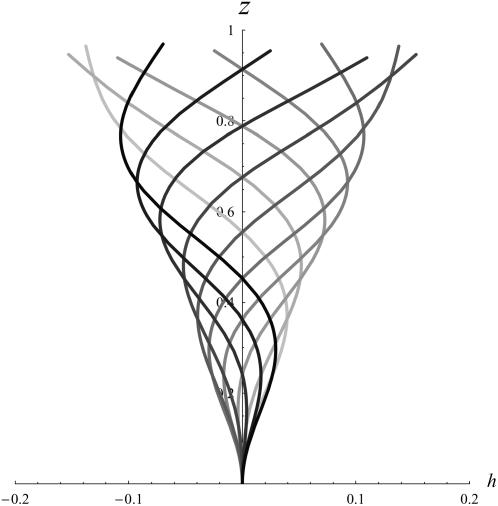
We plot 40 cilia on a line for γ = γ* and submitted to a lateral flow (from left to right) at four different times covering one period. Indeed, as explained just below, an array of cilia can create spontaneously a nonzero average flow in one direction that breaks the beating symmetry and defines the direction of the effective stroke. Two opposite values of ϕ lead to γ*: ϕ* < 0 corresponds to symplectic metachronal waves (Fig. 11 a), and ϕ* > 0 to antiplectic (Fig. 11 b). In our model those two types of metachronal coordination are equivalent. An arrow is following one pattern during one period, it thus moves over one wavelength.

FIGURE 11.

Line of 40 cilia in the presence of a metachronal wave and a lateral flow (dilated scale). The flow breaks the beating symmetry and defines the direction of the effective stroke (toward the right here). The arrows follow one pattern through its displacement on one period. (a) Symplectic metachronism (ϕ* < 0). (b) Antiplectic metachronism (ϕ* > 0).

Note that we have chosen d/L = 2 so that our calculations remain consistent and to remain close to what is observed experimentally (d < L); d/L = 2 might seem far from our assumption 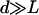, but in Eq. 2 (and Eq. 35) the relevant ratio is not L/d but L³/d³, which justifies our choice. Moreover, experimentally it is possible to obtain partially deciliated Paramecium that verifies d > L ((41), for example), and it would be interesting to test our predictions on such systems.

Global flow and left-right symmetry breaking

We now discuss the left-right symmetry breaking and the appearance of a global flow. We solve Eq. 40 for the zeroth Fourier component of the deformation with the same boundary conditions as before in the limit 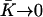. We obtain:

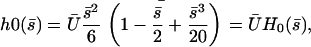(43)

which defines 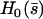. The cilium oscillates around a curved average position 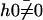if 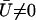, if there exists a global flow. We show below that this is possible within a certain range of parameters. The determination of the average velocity U requires the calculation of the integral 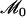defined in Eq. 37; we get:

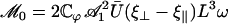with

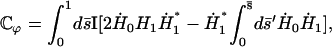(44)

which can be numerically calculated knowing H₀ and H₁ (given by Eqs. 43 and 42). 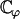depends on ϕ through H₁. Using the value of ϕ = ϕ* corresponding to metachronal waves, we obtain:

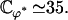A self-consistent equation is then obtained for the average velocity Ū:

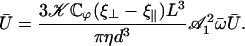(45)

If 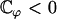this equation has the only solution U = 0 and no global flow can exist: the left-right symmetry is not broken. If 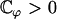this equation can have two extra nonzero solutions U ≠ 0 corresponding to a global flow along the x axis given by:

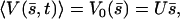and the left-right symmetry is then broken. Note that it is indeed 𝒦 given by Eq. 7 that appears in Eq. 45 and not . The condition for appearance of a global flow is:

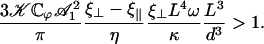(46)

To evaluate this criterion we take for our parameters the value previously used in this section (d = 2L, 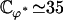) and “Axonemal beating”. We get a lower bound for the factor :

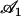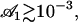which is satisfied, even with our assumption of small beating amplitude (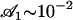 leads to 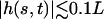). Spontaneous breaking of the beating symmetry can occur thanks to hydrodynamic coupling. As for the oscillation amplitude, our calculation only gives the threshold of appearance of the global flow. A determination of the actual value of the velocity would require an expansion of the equations of motion to higher orders.

DISCUSSION AND CONCLUDING REMARKS

We have studied in this paper how hydrodynamic interactions between cilia contribute to the coordination of the beating motion in ciliated cells. Three major effects have been studied: the spontaneous alignment of an array of cilia, the breaking of the beating symmetry and the appearance of a macroscopic flow, and the existence of metachronal waves. We have shown for all these problems that there exists a dynamic transition where symmetry is broken and where a coordination between the beating of neighboring cilia appears. Hydrodynamic interactions can lead to the alignment of an assembly of cilia within some range of the physical parameters (distance between cilia, beating amplitude, beating frequency…). In “Left-right beating symmetry breaking”, we show that a transverse external flow can break the symmetry of a symmetrical beating to induce an asymmetrical beating, faster along the flow and slower and more curved against the flow. In the last section, we have shown that an array of cilia can create a macroscopic flow and spontaneously breaks the left-right beating symmetry, but also within a certain range of parameters (distance, frequency, bending rigidity, phase difference between neighbors…). Finally, metachronal coordination appears as a self-organized phenomenon and helps the beating, lowering the beating threshold and increasing its frequency. Last but not least, it accounts for rather stationary flow observed experimentally (18).

Our work is based on several simplifying approximations that we believe make the analysis tractable analytically but that should preserve the essential physical effects. Our aim is to point out the relevant parameters controlling biophysical phenomena in ciliated cells. For this purpose, we use an analytical approach rather than numerical simulations. We only studied hydrodynamic interactions between distant cilia that can be treated by introducing simple distributions of forces in the fluid to describe the motion of one cilium. This is rarely true experimentally but the hydrodynamic interactions between closer cilia are even stronger and strongly favor the transitions that we study. We also only consider planar beating, which is observed for many organisms (Opalina (8), Ctenophore (42), gill cilia of mollusc (14), Chlamydomonas (43), sea urchin sperm (44), human respiratory cilia (45)…). A recent work of Vilfan and Jülicher (46) studies three-dimensional cilia beating and the coupling between two cilia using a simplified hydrodynamic description. We have replaced the complex architecture of the axoneme by two microtubules sliding against one another under the action of dynein motors that are described by a two-state model for molecular motors as done earlier (11). This is a rather sketchy description but it allows a calculation of the internal forces that drive the cilium motion and it gives some physical insight. Future work will have to take into account the ninefold symmetry of the axoneme and the influence of its central doublet as done in Gueron et al. (47). Finally, we have only considered small amplitude beating. This is sufficient to determine the oscillation threshold but it does not allow a quantitative comparison between the calculated beating and the experimental ones that often occur far from any threshold. All our results are qualitatively consistent with the experimental observations and for example the beating frequency is close to both the experimental ones and to the ones obtained in numerical simulations (48).

The essential result of our work is the emergence of metachronism and of a macroscopic flow in an array of cilia as self-organized phenomena under some conditions on the physical parameters. The criterion for appearance of the global component of the flow given by Eq. 46 requires only very small amplitudes (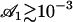), which means that hydrodynamic effects should be strong enough to break the beating symmetry and create a macroscopic flow. An essential ingredient for the macroscopic flow to appear is that the constant 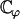defined in Eq. 44 be positive so that the average force created by one cilium favors the flow and does not oppose it (which occurs if ϕ = 0). Another striking example of self-organization due to hydrodynamic coupling can be found in the experiments performed (49) where spermatozoa assemble into a hexagonal array of dynamic vortices. As suggested in this work, future studies on coordination between cilia will have to introduce a stochastic noise on the phase ϕ and address the transition between noncoordinated and coordinated beating of cilia.

As long as we allow a constant phase shift between neighboring cilia we observe metachronal coordination as a consequence of hydrodynamic interactions and of the internal beating mechanism of the cilium. A selection criterion is then needed for these waves. We have conjectured that the existing metachronism is the one that corresponds to the local minimum of the oscillation threshold. A more complete calculation that goes far beyond the scope of this work would have to consider the nucleation of the metachronal wave and to determine the fastest growing wave. One of the interesting predictions of our calculation is that the existence of metachronal coordination leads to a flow that is far more stationary than if all the cilia were beating in synchrony. The oscillating component of the flow is proportional to the constant 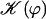(see Eq. 39) that has a much smaller value when metachronism exists (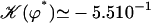) than if all cilia are beating in synchrony (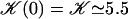). Metachronal coordination thus contributes to the creation of a very steady movement of swimming organisms that could for example make easier the detection of the organism environment. This effect, which does not depend on the kind of metachronism (symplectic, antiplectic,…), might be the major advantage of metachronal coordination, the energetic gain being rather small.

The problem of multicilia configuration and energetic gain has also been addressed (50) using numerical simulations. Our analytical approach is consistent with their results: in an assembly of cilia the beating pattern of one cilium is affected by the presence of its neighbors, the beating frequency is increased, and multicilia configuration can reduce the energy required for beating. As in our model, metachronal coordination is due to hydrodynamic interactions and to the dependence of the internal engine on the external flow. These two conditions seem to be necessary for metachronism. Nevertheless, their approach shows that an assembly of cilia induces both metachronal coordination and a decrease of the beating energy, but does not allow one to conclude whether this energetic gain is a direct consequence of coordination. Our study shows that without any coordination between cilia, the beating threshold for each cilium is not changed, whereas for metachronal coordination, it can be decreased or increased depending on the phase difference ϕ. In other respects, they obtain a wavelength in their simulations (λ ∼ 100 cilia) much larger than the experimental value (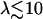 cilia (23,36)). We obtain a closer value (λ ∼ 5 cilia). This might be due to our internal engine, which is driven by the collective behavior of molecular motors, whereas theirs is based on a geometric switch hypothesis (37,51) that might not be relevant. For this reason, and more generally because the internal mechanism is one of the keys to metachronism, a precise description is needed.

Our most important conclusion is the idea that metachronism and the existence of macroscopic flow around ciliated organisms can exist as self-organized phenomena driven by hydrodynamic couplings. We must stress, however, that other mechanisms could be at the origin of these cooperative effects.

APPENDIX I: AVERAGE FORCE CREATED BY A CILIUM

The aim of this appendix is to calculate the force and momentum created by a general periodic beating of a single cilium averaged over one time period. We make two assumptions: the beating is planar and there is a stationary external flow. In the “Left-right beating symmetry breaking” section, the average flow is created by the neighboring cilia.

We call φ the angle between the plane of beating and the direction of the external flow 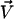that we take along the x axis. The cilium of length L is located at the origin and it is fixed at its basis. We denote by h(s, t) the distance between a point at arclength s on the cilium and the z axis at time t and by Z(s, t) the distance between a point at the arclength s on the cilium and the (xy) plane. The angle between the tangent vector 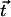to the cilium and the z axis is denoted by ψ(s, t) (see Fig. 12). The coordinates of the tangent vector are 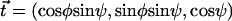. The angle ψ is related to the cilium deformation h by sin ψ = ∂_sh.

FIGURE 12.

Sketch of a beating cilium in a plane at an angle φ with the direction of the external flow V.

The point on the cilium at the arclength s is located at position 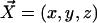, with:

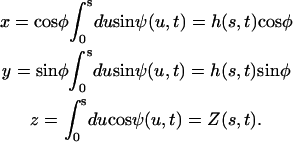(47)

The velocity of this point is calculated by derivation with respect to time, 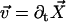. The force per unit length exerted by the cilium on the fluid expressed in the Frenet basis is:

where ξ_‖ and ξ_⊥ are the two local friction coefficients for tangential and normal motion, respectively. We decompose this force as a sum of two forces, 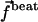depending on the local velocity and 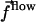depending on the external flow velocity and calculate the average force over a beating period .

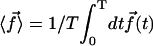The average beating force 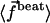can be explicitly calculated. Defining δ(u, s) = 2ψ(s) − ψ(u), we get:

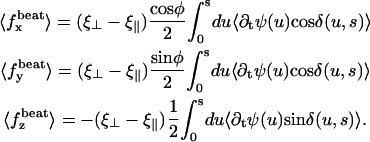This force is proportional to (ξ_⊥ − ξ_‖) as mentioned in the section “Spontaneous alignment of an array of cilia: a simple model”. The difference between the two local friction coefficients ξ_⊥ and ξ_‖ is at the basis of the flow generation by an assembly of beating cilia. Indeed, this is because the shape of the beating in the effective stroke is different from that in the recovery stroke that a force can be exerted in the fluid on average.

The average force due to the external flow is:

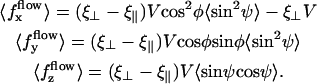It is important to note that 〈 (s) 〉 < 0: this force opposes the flow. The last term of is a static term, whereas the first positive term depends on the beating pattern and reduces the effects of this static term. In an assembly of cilia, the external velocity is due to the beating of the other cilia.

In the section “Spontaneous alignment of an array of cilia: a simple model”, we introduce a viscous coefficient α that characterizes the tendency for a cilium, beating in a plane at an angle φ with the flow, to align with the other cilia. A torque along the z axis due to the flow 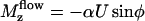is exerted on this cilium. We now express α as a function of the cilium beating pattern. We call 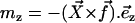the torque along z exerted by the fluid on the cilium per unit length (the minus sign is due to the fact that 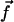is the force exerted by the cilium on the fluid). The local torque per unit length exerted by the fluid on the cilium is:

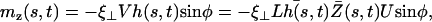where we have used the dimensionless coordinate 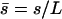and 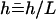. The total momentum along z averaged over time, is obtained by integration:

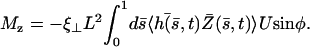This defines the friction coefficient α:

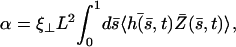(48)

which can be calculated if the motion of the cilium is known.

APPENDIX II: FOURIER MODE EXPANSION AND THRESHOLD OF OSCILLATION

In this appendix, we derive the equations satisfied by the Fourier components of the deformation h of a single beating cilium and we determine the threshold of spontaneous oscillations of the cilium.

Fourier mode expansion

Axoneme beating is periodic and can be studied by expansion in Fourier modes in time of all the physical parameters:

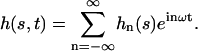The definition is similar for the other parameters. Starting from Eqs. 16 and 14, we obtain the Fourier components:

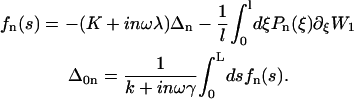(49)

To determine the nonlinear relationship between f and Δ, we follow the lines of Jülicher and Prost (52) and write:

The coefficients can be calculated by first rewriting Eq. 15 as:

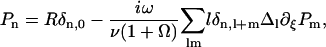(50)

where

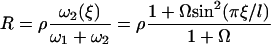is the static probability (ω = 0), corresponding to a medium with not enough ATP to generate the beating. Inserting the ansatz:

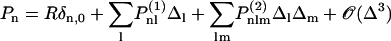into Eq. 50, we obtain a recursion relation for the :

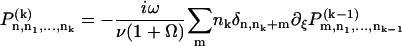that now allows us to calculate . Our choice of a symmetric potential W₁ imposes that a change must change . This symmetry imposes thus f^(2k) = 0. The only nonvanishing coefficient at linear order is 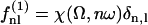with:

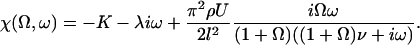(51)

The force and the sliding displacement are thus related by:

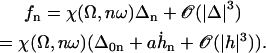(52)

Equation 52 models the response of the molecular motors to the bending of the axoneme. From Eq. 49 we obtain:

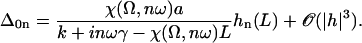(53)

We solve the equation of motion of the cilium (Eq. 17) for each order of the Fourier expansion.

Equation of motion of the Fourier modes

We look for an approximate solution of the form:

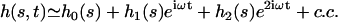At linear order, there is no coupling between the modes and using Eq. 17, the equation of motion of the n^th Fourier component reads:

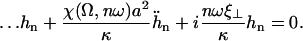(54)

It is convenient to introduce the dimensionless variables:

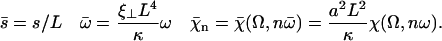In dimensionless form, Eq. 51 can be written:

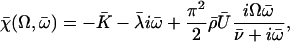with:

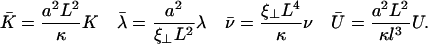We have anticipated here the fact that 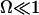. Defining, 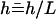, and denoting by a dot the derivation with respect to , we obtain the equation of motion Eq. 20 and the boundary conditions given by Eqs. 21 and 22.

Threshold of spontaneous oscillations

In the absence of external flow only the first Fourier component of h does not vanish and satisfies the equation of motion:

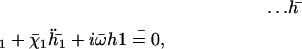(55)

where the relevant dimensionless parameters are:

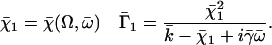The boundary conditions are given by Eqs. 21 and 22 for n = 1. The solution to this linear equation is a superposition of exponentials given by Eq. 23. The four boundary conditions on 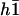can be written in a matrix form:

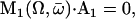(56)

where A₁ is the vector made by the amplitudes of the exponentials in Eq. 23 and the matrix M₁ is given by:

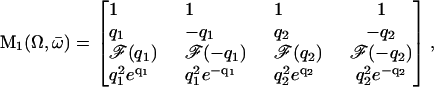with

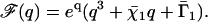The system 56 has nontrivial solutions only if:

(57)

Because Eq. 57 is a complex equation, it determines both the oscillation threshold Ω_c and the dimensionless beating frequency .