Structure and tie strengths in mobile communication networks

Abstract

Electronic databases, from phone to e-mails logs, currently provide detailed records of human communication patterns, offering novel avenues to map and explore the structure of social and communication networks. Here we examine the communication patterns of millions of mobile phone users, allowing us to simultaneously study the local and the global structure of a society-wide communication network. We observe a coupling between interaction strengths and the network's local structure, with the counterintuitive consequence that social networks are robust to the removal of the strong ties but fall apart after a phase transition if the weak ties are removed. We show that this coupling significantly slows the diffusion process, resulting in dynamic trapping of information in communities and find that, when it comes to information diffusion, weak and strong ties are both simultaneously ineffective.

Uncovering the structure and function of communication networks has always been constrained by the practical difficulty of mapping out interactions among a large number of individuals. Indeed, most of our current understanding of communication and social networks is based on questionnaire data, reaching typically a few dozen individuals and relying on the individual's opinion to reveal the nature and the strength of the ties. The fact that currently an increasing fraction of human interactions are recorded, from e-mail (1–3) to phone records (4), offers unprecedented opportunities to uncover and explore the large scale characteristics of communication and social networks (5). Here we take a first step in this direction by exploiting the widespread use of mobile phones to construct a map of a society-wide communication network, capturing the mobile interaction patterns of millions of individuals. The data set allows us to explore the relationship between the topology of the network and the tie strengths between individuals, information that was inaccessible at the societal level before. We demonstrate a local coupling between tie strengths and network topology, and show that this coupling has important consequences for the network's global stability if ties are removed, as well as for the spread of news and ideas within the network.

A significant portion of a country's communication network was reconstructed from 18 weeks of all mobile phone call records among ≈20% of the country's entire population, 90% of whose inhabitants had a mobile phone subscription [see supporting information (SI) Appendix]. Whereas a single call between two individuals during 18 weeks may not carry much information, reciprocal calls of long duration between two users serves as a signature of some work-, family-, leisure-, or service-based relationship. Therefore, to translate the phone log data into a network representation that captures the characteristics of the underlying communication network, we connected two users with an undirected link if there had been at least one reciprocated pair of phone calls between them (i.e., A called B, and B called A) and defined the strength, w_AB = w_BA, of a tie as the aggregated duration of calls between users A and B. This procedure eliminates a large number of one-way calls, most of which correspond to single events, suggesting that they typically reach individuals that the caller does not know personally. The resulting mobile call graph (MCG) (4) contains N = 4.6 × 10⁶ nodes and L = 7.0 × 10⁶ links, the vast majority (84.1%) of these nodes belonging to a single connected cluster [giant component (GC)]. Given the very large number of users and communication events in the database, we find that the statistical characteristics of the network and the GC are largely saturated, observing little difference between a two- or a three-month-long sample. Note that the MCG captures only a subset of all interactions between individuals, a detailed mapping of which would require face-to-face, e-mail, and land line communications as well. Yet, although mobile phone data capture just a slice of communication among people, research on media multiplexity suggests that the use of one medium for communication between two people implies communication by other means as well (6). Furthermore, in the absence of directory listings, the mobile phone data are skewed toward trusted interactions (that is, people tend to share their mobile numbers only with individuals they trust). Therefore, the MCG can be used as a proxy of the communication network between the users. It is of sufficient detail to allow us to address the large-scale features of the underlying human communication network and the major trends characterizing it.

Results

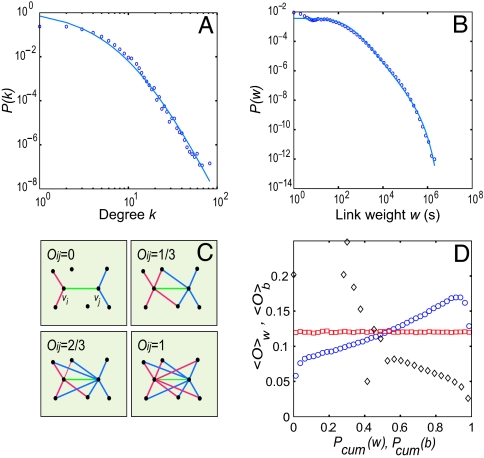
The MCG has a skewed degree distribution with a fat tail (Fig. 1A), indicating that although most users communicate with only a few individuals, a small minority talks with dozens (4, 7). If the tail is approximated by a power law, which appears to fit the data better than an exponential distribution, the obtained exponent γ_k = 8.4 is significantly higher than the value observed for landlines (γ = 2.1 for the in-degree distribution; see refs. 8 and 32). For such a rapidly decaying degree distribution, the hubs are few, and therefore many properties of traditional scale-free networks (33), from anomalous diffusion (9) to error tolerance (10), are absent. This decay is probably rooted in the fact that institutional phone numbers, corresponding to the vast majority of large hubs in the case of land lines, are absent, and in contrast with e-mail, in which a single e-mail can be sent to many recipients, resulting in well-connected hubs (1), a mobile phone conversation typically represents a one-to-one communication. The tie strength distribution is broad (Fig. 1B), however, decaying with an exponent γ_w = 1.9, so that although the majority of ties correspond to a few minutes of airtime, a small fraction of users spend hours chatting with each other. This finding is rather unexpected, given that fat-tailed tie strength distributions have been observed mainly in networks characterized by global transport processes, such as the number of passengers carried by the airline transportation network (11), the reaction fluxes in metabolic networks (12), or packet transfer on the Internet (13), in which case the individual fluxes are determined by the global network topology. An important feature of such global flow processes is local conservation: All passengers arriving to an airport need to be transported away, each molecule created by a reaction needs to be consumed by some other reaction, or each packet arriving to a router needs to be sent to other routers. Although the main purpose of the phone is information transfer between two individuals, such local conservation that constrains or drives the tie strengths are largely absent, making any relationship between the topology of the MCG and local tie strengths less than obvious.

Fig. 1.

Characterizing the large-scale structure and the tie strengths of the mobile call graph. (A and B) Vertex degree (A) and tie strength distribution (B). Each distribution was fitted with P(x) = a(x + x₀)^−x exp(−x/x_c), shown as a blue curve, where x corresponds to either k or w. The parameter values for the fits are k₀ = 10.9, γ_k = 8.4, k_c = ∞ (A, degree), and w₀ = 280, γ_w = 1.9, w_c = 3.45 × 10⁵ (B, weight). (C) Illustration of the overlap between two nodes, v_i and v_j, its value being shown for four local network configurations. (D) In the real network, the overlap 〈O〉_w (blue circles) increases as a function of cumulative tie strength P_cum(w), representing the fraction of links with tie strength smaller than w. The dyadic hypothesis is tested by randomly permuting the weights, which removes the coupling between 〈O〉_w and w (red squares). The overlap 〈O〉_b decreases as a function of cumulative link betweenness centrality b (black diamonds).

Complex networks often organize themselves according to a global efficiency principle, meaning that the tie strengths are optimized to maximize the overall flow in the network (13, 14). In this case the weight of a link should correlate with its betweenness centrality, which is proportional to the number of shortest paths between all pairs of nodes passing through it (refs. 13, 15, and 16, and S. Valverde and R. V. Sole, unpublished work). Another possibility is that the strength of a particular tie depends only on the nature of the relationship between two individuals and is thus independent of the network surrounding the tie (dyadic hypothesis). Finally, the much studied strength of weak ties hypothesis (17–19) states that the strength of a tie between A and B increases with the overlap of their friendship circles, resulting in the importance of weak ties in connecting communities. The hypothesis leads to high betweenness centrality for weak links, which can be seen as the mirror image of the global efficiency principle.

In Fig. 2A, we show the network in the vicinity of a randomly selected individual, where the link color corresponds to the strength of each tie. It appears from this figure that the network consists of small local clusters, typically grouped around a high-degree individual. Consistent with the strength of weak ties hypothesis, the majority of the strong ties are found within the clusters, indicating that users spend most of their on-air time talking to members of their immediate circle of friends. In contrast, most links connecting different communities are visibly weaker than the links within the communities. As a point of comparison, when we randomly permute the link strengths among the connected user pairs (Fig. 2B), in what would be consistent with the dyadic hypothesis, we observe dramatically more weak ties within the communities and more strong ties connecting distinct communities. Finally, even more divergent with the observed data (Fig. 2A), we illustrate what the world would be like if, as predicted by the global efficiency principle and betweenness centrality, intercommunity ties (“bridges”) were strong and intracommunity ties (“local roads”) weak (Fig. 2C). To quantify the differences observed in Fig. 2, we measured the relative topological overlap of the neighborhood of two users v_i and v_j, representing the proportion of their common friends (20) O_ij = n_ij/((k_i − 1) + (k_j − 1) − n_ij), where n_ij is the number of common neighbors of v_i and v_j, and k_i (k_j) denotes the degree of node v_i (v_j). If v_i and v_j have no common acquaintances, then we have O_ij = 0, the link between i and j representing potential bridges between two different communities. If i and j are part of the same circle of friends, then O_ij = 1 (Fig. 1C). The dyadic hypothesis implies the absence of a relationship between the local network topology and weights, and, indeed, we find that permuting randomly the tie strengths between the links results in O_ij that is independent of w_ij (Fig. 1D). We find, however, that according to the global efficiency principle 〈O〉_b decreases with the betweenness centrality b_ij, indicating that on average the links with the highest betweenness centrality b_ij have the smallest overlap. In contrast, for the real communication network, 〈O〉w increases as a function of the percentage of links with weights smaller than w, demonstrating that the stronger the tie between two users, the more their friends overlap, a correlation that is valid for ≈95% of the links (Fig. 2D). This result is broadly consistent with the strength of weak ties hypothesis, offering its first societal-level confirmation. It suggests that tie strength is, in part, driven by the network structure in the tie's immediate vicinity. This suggestion is in contrast with a purely dyadic view, according to which the tie strength is determined only by the characteristics of the individuals it connects, or the global view, which asserts that tie strength is driven by the whole network topology.

Fig. 2.

The structure of the MCG around a randomly chosen individual. Each link represents mutual calls between the two users, and all nodes are shown that are at distance less than six from the selected user, marked by a circle in the center. (A) The real tie strengths, observed in the call logs, defined as the aggregate call duration in minutes (see color bar). (B) The dyadic hypothesis suggests that the tie strength depends only on the relationship between the two individuals. To illustrate the tie strength distribution in this case, we randomly permuted tie strengths for the sample in A. (C) The weight of the links assigned on the basis of their betweenness centrality b_ij values for the sample in A as suggested by the global efficiency principle. In this case, the links connecting communities have high b_ij values (red), whereas the links within the communities have low b_ij values (green)..

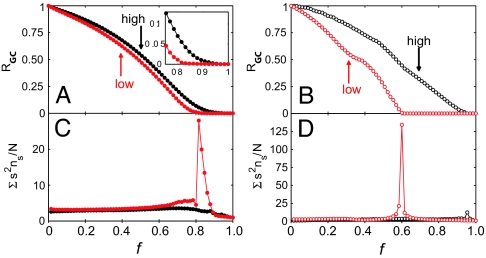
To understand the systemic or global implications of this local relationship between tie strength and network structure, we explore the network's ability to withstand the removal of either strong or weak ties. To evaluate the impact of removing ties, we measure the relative size of the giant component R_gc(f), providing the fraction of nodes that can all reach each other through connected paths as a function of the fraction of removed links, f. We find that removing in rank order the weakest (or smallest overlap) (Fig. 3 A and B) to strongest (greatest overlap) ties leads to the network's sudden disintegration at f^w = 0.8 (f^O = 0.6). In contrast, removing first the strongest (or highest overlap) (Fig. 3 A and B) ties will shrink the network but will not precipitously break it apart. The precise point at which the network disintegrates can be determined by monitoring S̃ = Σ_s<smaxn_ss²/N, where n_s is the number of clusters containing s nodes. According to percolation theory, if the network collapses because of a phase transition at f_c, then S̃ diverges as f approaches f_c (21, 22). Indeed, we find that S̃ develops a peak if we start with the weakest (or smallest overlap) links (Fig. 3 C and D). Finite size scaling, a well established technique for identifying the phase transition, indicates that the values of the critical points are f_c^O(∞) = 0.62 ± 0.05 and and f_c^w(∞) = 0.80 ± 0.04 for the removal of the weak ties, but there is no phase transition when the strong ties are removed first.

Fig. 3.

The stability of the mobile communication network to link removal. The control parameter f denotes the fraction of removed links. (A and C) These graphs correspond to the case in which the links are removed on the basis of their strengths (w_ij removal). (B and D) These graphs correspond to the case in which the links were removed on the basis of their overlap (O_ij removal). The black curves correspond to removing first the high-strength (or high O_ij) links, moving toward the weaker ones, whereas the red curves represent the opposite, starting with the low-strength (or low O_ij) ties and moving toward the stronger ones. (A and B) The relative size of the largest component R_GC(f) = N_GC(f)/N_GC(f = 0) indicates that the removal of the low w_ij or O_ij links leads to a breakdown of the network, whereas the removal of the high w_ij or O_ij links leads only to the network's gradual shrinkage. (A Inset) Shown is the blowup of the high w_ij region, indicating that when the low w_ij ties are removed first, the red curve goes to zero at a finite f value. (C and D) According to percolation theory, S̃ = Σ _s<smaxn_ss²/N diverges for N → ∞ as we approach the critical threshold f_c, where the network falls apart. If we start link removal from links with low w_ij (C) or O_ij (D) values, we observe a clear signature of divergence. In contrast, if we start with high w_ij (C) or Oij (D) links, there the divergence is absent. Finite size scaling shows that the small local maximum seen in D at f ≈ 0.95 does not correspond to a real phase transition (see SI Appendix).

Taken together, these results document a fundamental difference between the global role of the strong and weak ties in social networks: The removal of the weak ties leads to a sudden, phase transition-driven collapse of the whole network. In contrast, the removal of the strong ties results only in the network's gradual shrinking but not its collapse. This finding is somewhat unexpected, because in most technological and biological networks the strong ties are believed to play a more important structural role than the weak ties, and in such systems the removal of the strong ties leads to the network's collapse (10, 23–25). This counterintuitive finding underlies the distinct role weak and strong ties play in a social network: Given that the strong ties are predominantly within the communities, their removal will only locally disintegrate a community but not affect the network's overall integrity. In contrast, the removal of the weak links will delete the bridges that connect different communities, leading to a phase transition driven network collapse.

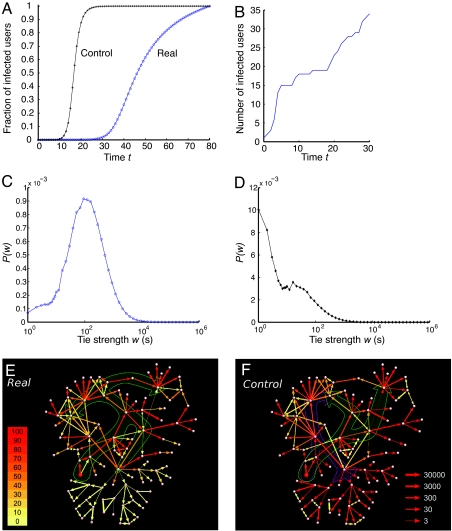
The purpose of the mobile phone is information transfer between two individuals. Yet, given that the individuals are embedded in a social network, mobile phones allow news and rumors to diffuse beyond the dyad, occasionally reaching a large number of individuals, a much studied diffusion problem in both sociology (26) and network science (7). Yet, most of our current knowledge about information diffusion is based on analyses of unweighted networks, in which all tie strengths are considered equal (26). To see whether the observed local relationship between the network topology and tie strength affects global information diffusion, at time 0 we infected a randomly selected individual with some novel information. We assumed that at each time step, each infected individual, v_i, can pass the information to his/her contact, v_j, with effective probability P_ij = xw_ij, where the parameter x controls the overall spreading rate. (Note that the qualitative nature of results is independent of the choice of x; see SI Appendix for details.) Therefore, the more time two individuals spend on the phone, the higher the chance that they will pass on the monitored information. The spreading mechanism is similar to the susceptible-infected model of epidemiology in which recovery is not possible, i.e., an infected individual will continue transmitting information indefinitely (27). As a control, we considered spreading on the same network, but replaced all tie strengths with their average value, resulting in a constant transmission probability for all links.

As Fig. 4A shows (the real diffusion simulation), we find that information transfer is significantly faster on the network for which all weights are equal, the difference being rooted in a dynamic trapping of information in communities. Such trapping is clearly visible if we monitor the number of infected individuals in the early stages of the diffusion process (Fig. 4B). Indeed, we observe rapid diffusion within a single community, corresponding to fast increases in the number of infected users, followed by plateaus, corresponding to time intervals during which no new nodes are infected before the news escapes the community. When we replace all link weights with an average value w̄ (the control diffusion simulation) the bridges between communities are strengthened, and the spreading becomes a predominantly global process, rapidly reaching all nodes through a hierarchy of hubs (23).

Fig. 4.

The dynamics of spreading on the weighted mobile call graph, assuming that the probability for a node v_i to pass on the information to its neighbor v_j in one time step is given by P_ij = xw_ij, with x = 2.59 × 10⁻⁴. (A) The fraction of infected nodes as a function of time t. The blue curve (circles) corresponds to spreading on the network with the real tie strengths, whereas the black curve (asterisks) represents the control simulation, in which all tie strengths are considered equal. (B) Number of infected nodes as a function of time for a single realization of the spreading process. Each steep part of the curve corresponds to invading a small community. The flatter part indicates that the spreading becomes trapped within the community. (C and D) Distribution of strengths of the links responsible for the first infection for a node in the real network (C) and control simulation (D). (E and F) Spreading in a small neighborhood in the simulation using the real weights (E) or the control case, in which all weights are taken to be equal (F). The infection in all cases was released from the node marked in red, and the empirically observed tie strength is shown as the thickness of the arrows (right-hand scale). The simulation was repeated 1,000 times; the size of the arrowheads is proportional to the number of times that information was passed in the given direction, and the color indicates the total number of transmissions on that link (the numbers in the color scale refer to percentages of 1,000). The contours are guides to the eye, illustrating the difference in the information direction flow in the two simulations.

The dramatic difference between the real and the control spreading process raises an important question: Where do individuals get their information? We find that the distribution of the tie strengths through which each individual was first infected (Fig. 4C) has a prominent peak at w ≈ 10² seconds, indicating that, in the vast majority of cases, an individual learns about the news through ties of intermediate strength. The distribution changes dramatically in the control case, however, when all tie strengths are taken to be equal during the spreading process. In this case, the majority of infections take place along the ties that are otherwise weak (Fig. 4D). Therefore, in contrast with the celebrated role of weak ties in information access (17, 19), we find that both weak and strong ties have a relatively insignificant role as conduits for information (“the weakness of weak and strong ties”), the former because the small amount of on-air time offers little chance of information transfer and the latter because they are mostly confined within communities, with little access to new information.

To illustrate the difference between the real and the control simulation, we show the spread of information in a small neighborhood (Fig. 4 E and F). First, the overall direction of information flow is systematically different in the two cases, as indicated by the large shaded arrows. In the control runs, the information mainly follows the shortest paths. When the weights are taken into account, however, information flows along a strong tie backbone, and large regions of the network, connected to the rest of the network by weak ties, are only rarely infected. For example, the lower half of the network is rarely infected in the real simulation but is always infected in the control run. Therefore, the diffusion mechanism in the network is drastically altered when we neglect the tie strengths responsible for the differences between the curves seen in Fig. 4 A and B.

Discussion

Although the study of communication and social networks has a long history, examining the relationship between tie strengths and topology in society-spanning networks has generally been impossible. In this paper, taking advantage of society-wide data collection capabilities offered by mobile phone logs, we show that tie strengths correlate with the local network structure around the tie, and both the dyadic hypothesis and the global efficiency principle are unable to account for the empirical observations.

It has been long known that many networks show resilience to random node removal, but are fragile to the removal of the hubs (10, 28–30). In terms of the links, one would also expect that the strong ties play a more important role in maintaining the network's integrity than the weak ones. Our analyses document the opposite effect in communication networks: The removal of the weak ties results in a phase transition-like network collapse, although the removal of strong ties has little impact on the network's overall integrity. Furthermore, we find that the observed coupling between the network structure and tie strengths significantly slows information flow, trapping it in communities, explaining why successful searches in social networks are conducted primarily through intermediate- to weak-strength ties while avoiding the hubs (3). Therefore, to enhance the spreading of information, one needs to intentionally force it through the weak links or, alternatively, adopt an active information search procedure.

Taken together, weak ties appear to be crucial for maintaining the network's structural integrity, but strong ties play an important role in maintaining local communities. Both weak and strong ties are ineffective, however, when it comes to information transfer, given that most news in the real simulations reaches an individual for the first time through ties of intermediate strength.

The observed coupling between tie strengths and local topology has significant implications for our ability to model processes taking place in social networks. Indeed, many current network models either assign the same strength to all ties or assume that tie strengths are determined by the network's global characteristics, such as betweenness centrality. In addition, some of the most widely used algorithms used to identify communities and groups in complex networks use either betweenness centrality (16) or are based on topological measures (31). Our finding that link weights and betweenness centrality are negatively correlated in mobile communication networks, together with the insights provided by the visually apparent community structure (Fig. 2), offer new opportunities to design clustering algorithms that are tailored to communication networks, and force us to reevaluate many results that were obtained on unweighted graphs. Putting the structural and functional pieces together, we conjecture that communication networks are better suited to local information processing than global information transfer, a result that has the makings of a paradox. Indeed, the underlying reason for characterizing communication networks with global network concepts, such as path length and betweenness centrality, is rooted in the expectation of communication networks to transmit information globally.

Abbreviation

MCG

mobile call graph.