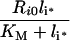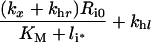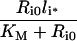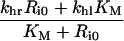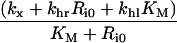Endosomal receptor kinetics determine the stability of intracellular growth factor signalling complexes

Abstract

There is an emerging paradigm that growth factor signalling continues in the endosome and that cell response to a growth factor is defined by the integration of cell surface and endosomal events. As activated receptors in the endosome are exposed to a different set of binding partners, they probably elicit differential signals compared with when they are at the cell surface. As such, complete appreciation of growth factor signalling requires understanding of growth factor–receptor binding and trafficking kinetics both at the cell surface and in endosomes. Growth factor binding to surface receptors is well characterized, and endosomal binding is assumed to follow surface kinetics if one accounts for changes in pH. Yet, specific binding kinetics within the endosome has not been examined in detail. To parse the factors governing the binding state of endosomal receptors we analysed a whole-cell mathematical model of epidermal growth factor receptor trafficking and binding. We discovered that the stability of growth factor–receptor complexes within endosomes is governed by three primary independent factors: the endosomal dissociation constant, total endosomal volume and the number of endosomal receptors. These factors were combined into a single dimensionless parameter that determines the endosomal binding state of the growth factor–receptor complex and can distinguish different growth factors from each other and different cell states. Our findings indicate that growth factor binding within endosomal compartments cannot be appreciated solely on the basis of the pH-dependence of the dissociation constant and that the concentration of receptors in the endosomal compartment must also be considered.

INTRODUCTION

Endocytosis enables cells to internalize a diverse set of compounds from serum proteins, to growth factors and viruses [1]. Ligand–receptor complexes formed at the cell surface are transported into common endosomes [2], from which they are sorted to a variety of destinations. The form and nature of the internalized complexes determine their kinetics and fate. Several ligands including, low-density lipoprotein, asialoglycoproteins, α₂-macroglobulin and lysosomal enzymes dissociate from their receptors within the endosomes prior to delivery of ligand to lysosomes [1]. These compounds fall close to a polar extreme, wherein pronounced dissociation leads to recycling of receptors to the cell surface, where they can re-internalize as part of a new round of endocytosis. Compounds like transferrin represent the other extreme as they do not dissociate from their receptors within endosomes and are recycled together with their receptors [1,3]. Growth factors classically fall in a broad middle-range with a variable balance of recycling and degradation [1]. EGF (epidermal growth factor) is the conventional model for a growth factor that remains predominantly bound to its receptor, EGFR (EGF receptor), during the major intracellular trafficking steps preceding lysosomal degradation [4,5]. TGFα (transforming growth factor α) on the other hand also binds and activates EGFR, but readily dissociates from its receptor in the sorting endosomes [6–8].

Interest in the stability of intracellular growth factor complexes initially focused on surface receptor down-regulation [6,7]. More recently, it has been established that many internalized growth factor–receptor complexes remain phosphorylated and continue to signal in the endosome [8–14]. Association of the growth factor to the internalized receptor is a requisite for endosomal signalling. Stability of the internalized complex is thus a crucial factor determining the magnitude and duration of endosomal signalling, and has been invoked to explain the differential signalling elicited by various ligands of EGFR [8,10,15,16]. Moreover, compartmentalization of signalling molecules suggests a differential role for surface and endosomal signalling [8–10,17–20], and implies that surface and endosomal receptors are inter-related complimentary targets for growth factor delivery. Classic correlation of biological response with steady-state surface receptor activation [21] is therefore simplistic. Optimization of growth factor presentation kinetics more likely requires the maintenance of an intricate balance between activation of surface and intracellular receptors. Mathematical modelling can be a useful tool for investigating these processes across the broad range of intrinsic and environmental conditions. Since the seminal paper of Wiley and Cunningham [22], kinetic models have augmented and supported the experimental analysis of growth factor trafficking experiments and have contributed to the conceptual understanding of these processes [20–26].

We examined the factors that govern the stability of endosomal growth factor complexes with a model of EGFR trafficking. All the relevant trafficking parameters including surface and endosomal binding constants have been experimentally estimated using the B82 cell line [23,26]. Surprisingly, simulations of the model using published parameter estimates (Tables 1 and 2) implied that internalized TGFα is predominantly bound (85%) and not dramatically different from the binding state of EGF (93%). These results are insensitive to the magnitude of the endocytosis rate constant, but are sensitive to alterations in the endosomal volume. To define explicit criteria for the stability of internalized ligand complexes, we examined the case with a minimal endocytosis rate constant. Though such an analysis approximates the expected kinetics of receptors that do not appreciably downregulate [26–28], our modelling validates findings in down-regulating receptors, including EGFR. Constitutively trafficked non-down-regulating receptors follow simple surface binding and internalization kinetics, and are therefore ideal systems for focusing on downstream endosomal interactions. Application of a combination of model reduction techniques [29–31] enabled us to fully characterize the dynamics of endosomal growth factor as a function of ligand load, receptor expression and apparent dissociation constant. We demonstrate that the stability of endosomal complexes is determined by three primary and seemingly independent factors: the endosomal dissociation constant, the total endosomal volume and the number of endosomal receptors. We show further that these factors can perhaps be best appreciated as an integrated force, and when distilled into a single dimensionless parameter uniquely define each growth factor in its application space. More specifically, complex stability is guaranteed whenever the concentration of endosomal receptors greatly exceeds the binding dissociation constant, consistent with standard notions on the thermodynamics of chemical reactions. Our findings imply that stability of intracellular signalling complexes is not an inherent property of the ligand and the receptor, which can be divorced from the intracellular milieu. Rather, it is a systems property, which must be studied in the appropriate context. Receptor complexes would tend to be more stable in cells that overexpress receptors, thereby altering the signalling bias between cell-surface bound and internalized receptors. This may, in part, explain the correlation between receptor overexpression and aberrant intracellular signalling, as indicated by the high incidence of overexpression in tumour derived cells.

Table 1. Constitutive trafficking parameters for EGFR.

Constitutive trafficking parameters for EGFR transfected into B82 fibroblasts [23,26,35] and four ligands: EGF, TGFα and the EGF analogs E40A and Y13G [35].

(a) Surface parameters
Parameter	Meaning	Baseline value
ke*	Endocytosis rate constant	0.165 min−1
kt†	Constitutive internalization rate constant	0.030 min−1
n	Cell density	108 cells/l
Rs0†	Surface receptor number	118576/cell
(b) Endosomal parameters
Parameter	Meaning	Baseline value
khr†	Receptor degradation rate constant	0.0022 min−1
khl†	Ligand degradation rate constant	0.010 min−1
kx†	Receptor recycling	0.058 min−1
ksyn†	Receptor synthesis rate	130 receptors/cell min−1
Ve†	Total endosomal volume	10−14litres/cell
Ri0†	Endosomal receptor number	59091/cell

*Average estimates for B82 fibroblasts [23].

†Published estimates for B82 fibroblasts [26].

Table 2. Binding rate constants for EGFR.

Binding rate constants for EGFR transfected into B82 fibroblasts [23,26,35] and four ligands: EGF, TGFα and the EGF analogs E40A and Y13G [35].

	Surface receptors*		Endosomal receptors†
Ligand	Binding off rate constant kr (min−1)	Equilibrium dissociation constant Kd≡kr/kf (nM)	Binding off rate constant kr′ (min−1)	Equilibrium dissociation constant Kd′≡kr′/kf′ (nM)
EGF	0.16	2.5	0.66	78
TGFα	0.27	6.3	2.30	404
E40A	0.41	61	1.75	417
Y13G	1.24	133	1.41	164

* Estimated from EGF binding to B82 fibroblasts at pH 7.4 [35].

† Estimated from EGF binding to B82 fibroblasts at pH 6.0 [35].

THE MODEL

The accepted rate limiting steps in constitutive EGF trafficking [23,26] can be modelled using the following kinetic equations (Figure 1)

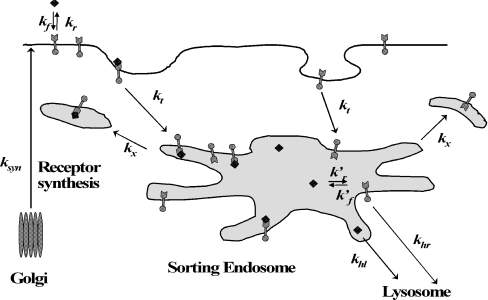
Figure 1. Rate limiting constitutive trafficking steps considered by Starbuck and Lauffenburger [26].

New receptors are continually synthesized in the Golgi and brought to the cell surface at a rate k_syn. Surface receptors (round-headed arrows) are internalized constitutively with rate constant k_t. Internalized receptors can either recycle to the surface with rate constant k_x or be sorted to degradation and exocytosis with rate constant k_hr. Extracellular ligand (◆) binds reversibly to free surface receptor with on rate k_f and off rate k_r and does not alter the trafficking of unoccupied receptors. Ligand–receptor complexes (round-headed arrows attached to ◆) are endocytosed with rate constant k_e. Internalized complexes can either recycle to the surface with rate constant k_x or be sorted to degradation and exocytosis with rate constant k_hl. This model only considers the rate limiting steps of receptor–ligand trafficking and neglects fast processes such as dimerization of surface receptors, activation of occupied receptors and binding to surface proteins, etc. [23].

Surface species:

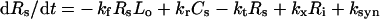(1)

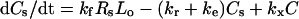(2)

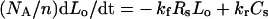(3)

Intracellular species:

(4)

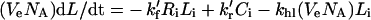(5)

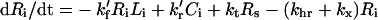(6)

Similar models have been used to model the trafficking of asiaglycoprotein [32], transferrin [3], IL-2 (interleukin 2) [33] and granulocyte colony stimulating factor [34].

ANALYSIS OF LIGAND INTERNALIZATON KINETICS

Ligand internalization is typically studied in vitro by exposing homeostatic cells to a bolus of extracellular ligand at 37 °C. As such the following initial conditions hold:

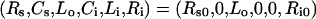(7)

where R_s0 and R_i0 are the surface and internal homoeostatic receptor numbers [23]:

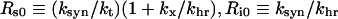(8)

We simulated eqns (1–7) for 10 nM boluses of four different EGFR agonists (Tables 1 and 2) and plotted the corresponding numbers of internalized complexes, C_i, and total internalized ligand molecules:

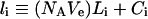(9)

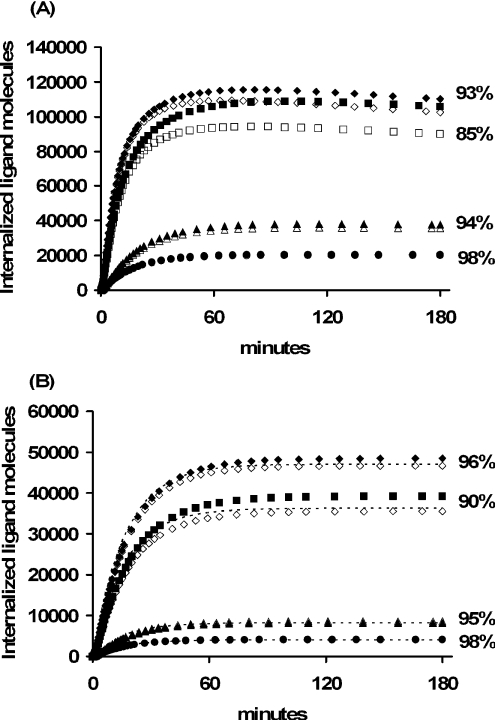
Remarkably, all four agonists remain predominantly bound to the EGFR after internalization, (Figure 2A). Such binding is expected for EGF, but surprising for TGFα, E40A and Y13G, which are thought to be predominantly free in the sorting endosomes [35]. Indeed, the EGF analogues E40A and Y13G were specifically designed to have unusually high dissociation constants at pH 6.0. Increasing the basal endocytosis rate constant 2-fold (k_e=0.33 min⁻¹) provided for similar endosomal binding patterns: EGF (91%), TGFα (82%), E40A (93%) and Y13G (98%). Decreasing the endocytosis rate constant 5.5-fold to its minimal constitutive value k_e=k_t=0.03 min⁻¹ reduced the number of internalized ligand molecules, but did not significantly alter the endosomal binding fractions (Figure 2B). Taken together, these examples suggest that the stability of endosomal complexes is not strongly influenced by the endocytosis rate constant. We therefore focused on a subclass of constitutively internalized receptors [26–28] for which the mathematical analysis is greatly simplified, but explicitly tested the relevance of our results for wild-type EGFR (which are shown in Figure 5 and will be discussed in more detail below).

Figure 2. Internalized growth factor following a 10 nM bolus of EGF (diamonds), TGFα (squares), E40A (triangles) and Y13G (circles) for wild-type (A) and internalization impaired (B) EGFR.

Total number of intracellular growth factor (closed symbols) is contrasted with the number of bound intracellular growth factor molecules (open symbols) and Eqn 11 (dashed lines) for each of the EGFR ligands. Simulations used the parameter values listed in Tables 1 and 2. The percentage of bound ligand is listed next to the corresponding internalization curves.

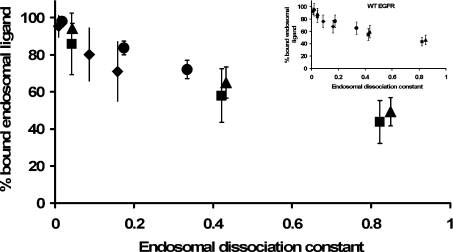
Figure 5. Endosomal binding versus endosomal dissociation constant.

Simulations of the internalization protocol were used to evaluate the fraction of bound endosomal ligand at the end of 180 min incubation with extracellular EGF (◆), TGFα (■), E40A (▲), or Y13G (●). Results are averaged for pre-incubation concentrations of 0.1 nM, 1 nM, 10 nM and 100 nM, and plotted against a normalized dissociation constant K′_d/R_i0)N_AV_e for V_e=1×10⁻¹⁴ litres, 1×10⁻¹³ litres and 2×10⁻¹³ litres. The inset panel shows the corresponding simulation results for downregulating receptors (k_e). Standard deviations reflect sensitivity to the magnitude of the pre-incubation concentration.

Eqns (1–6) imply the following conservation laws for constitutively internalized surface complexes:

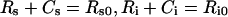(10)

This is the mathematical statement that shows that constitutively trafficked receptors do not downregulate. When a negligible fraction of endosomal ligand is free, steady-state is achieved when the clearance rate of bound ligand,(k_x+k_hr)C_i, approximately balances the rate of ligand internalization, k_tC_s. Assuming that extracellular binding is sufficiently fast to justify a steady-state approximation C_s≈R_s0L₀/(K_d+L₀)(K_d≡k_r/k_f) we can approximate the kinetics of intracellular complex as dC_i/d_t≈k_tR_s0L₀/(K_d+L₀–(k_x+k_hr)C_i with the solution:

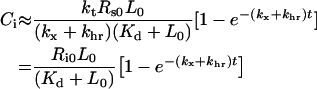(11)

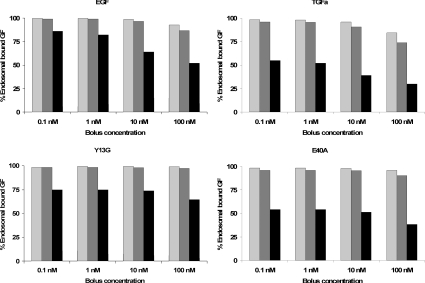
Numerical simulations using baseline parameter estimates (Tables 1 and 2) illustrate that eqn (11) is a good approximation for all four ligands of EGFR (Figure 2B). We repeated the simulations depicted in Figure 2(B) for bolus concentrations in the range 0.1–100 nM and in each case also varied the endosomal volume between its reported minimal and maximal values, 4×10⁻¹⁵ and 2×10⁻¹³ litres [36] (Figure 3). More than 50% of the endosomal ligand is bound for all but three of the simulated cases. Moreover, more than 73% of the endosomal ligand is bound in simulations that assume minimal and basal endosomal volumes. Increasing the endosomal volume to its maximum resulted in a significant decrease in the percentage of bound ligand. For example, the percentage of bound TGFα and EGF decreased by 45.2±4.5% and 24.4±11.0% respectively as the endosomal volume was increased from its basal value to its maximum (S.D. reflects sensitivity to the initial bolus concentration). Simulations with the basal endocytosis rate constant yielded essentially the same binding fractions, with deviations of the order of 1% from the results depicted in Figure 3. Interestingly, E40A (45.0±4.8%) behaved like TGFα, whereas Y13G (26.0±4.4%) behaved like EGF. These similarities will be explained by our analysis of eqns (1–6).

Figure 3. Percent bound endosomal ligand at the end of a 180 min incubation for a range of ligands, incubation concentrations and endosomal volumes of 4×10⁻¹⁵ litres/cell (light grey bars), 1×10⁻¹⁴ litres/cell (grey bars) and 2×10⁻¹³ litres/cell (black bars).

Simulation results are for internalization impaired receptors using the parameter estimates listed in Tables 1 and 2.

Taken together, the examples depicted in Figures 2 and 3 illustrate that the stability of endosomal complexes is not a simple function of their pI, and also depends nonlinearly on the magnitude of the endosomal volume and pre-incubation conditions. To gain a better understanding of these issues, we analysed eqns (1–6) for an accepted steady-state sorting protocol [7,36].

ANALYSIS OF STEADY-STATE SORTING

Steady-state sorting protocol

In the hypothetical experiments under consideration, following a 3h pre-incubation in warm binding medium (37 °C), cells are washed in a cold mild-acid solution to remove the surface-bound ligand [6]. Subsequently, cell plates are transferred to a pre-warmed water bath (37 °C) and incubated for various times before extracellular, surface and intracellular ligand concentrations are measured. The initial conditions corresponding to this protocol:

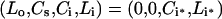(12)

uniquely define the initial number of free surface and intracellular receptors via eqn (10).

Model reduction

Typical in vitro cell densities justify a significant reduction of the model equations (see Supplementary Results at http://www.BiochemJ.org/bj/402/bj4020537add.htm). The total number of intracellular ligand molecules (eqn 9) is the sole dependent variable in the reduced model and its kinetics are governed by the first order differential equation:

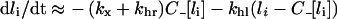(13)

with the initial condition:

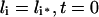(14)

Here:

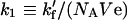(15a)

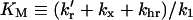(15b)

and

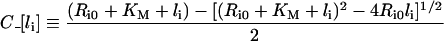(16)

is the quasi-steady state number of endosomal receptor–ligand complexes. The concentrations of surface bound ligand and degraded ligand in the medium are both dependent variables in the reduced model and are given, respectively, by:

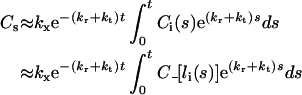(17)

and

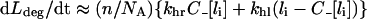(18)

Stability of intracellular complex

The steady-state fraction of bound endosomal ligand C_[l_i*]/l_i* (eqn 16) is a direct measure of the stability of the endosomal complexes. Previous analysis shows that C_[l_i*]/l_i* decreases with total intracellular ligand as in any saturated binding state [30]. We now demonstrate that this fraction increases as R_i0 rises relative to K_M and tends to unity as R_i0/K_M→∞ (see Supplementary Results). This implies that the necessary and sufficient condition for intracellular complex stability is:

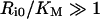(19)

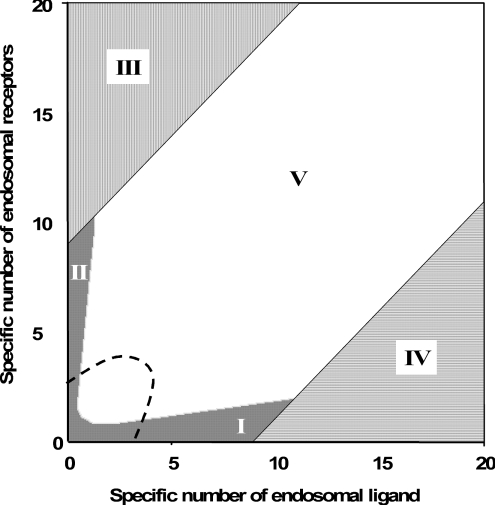
It is noteworthy that R_i0/K_M is inversely proportional to the endosomal volume, as this implies that endosomal complex stability decreases with increasing endosomal volume. Although the general expression for the fraction of bound endosomal ligand (eqn 16) is unintuitive, it reduces to intuitive forms in four partially overlapping but distinct zones of the plane of initial conditions (l_i*, R_i0) (Figure 4). These zones are defined by the inequalities [29,30]:

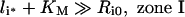(20)

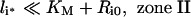(21)

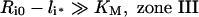(22)

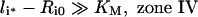(23)

and correspond to states of low-affinity binding (C_i*/l_*≪1, zone I), linear binding (C_i*/l_i*≈R_i0/K_M, zone II), high-affinity binding (C_i*/l_i*≈1, zone III) and binding under ligand excess (C_i*/l_i*≈R_i0/l_i*, zone IV) respectively. Numerical evaluation of C_[l_i*][30] illustrates that the stable endosomal-complex regime is fully spanned by the validity domain of inequality (eqn 22), and that the fraction of free endosomal ligand increases for total endosomal ligand levels that increasingly violate the inequality shown by eqn (23).

Figure 4. Classification of endosomal binding regimes as a function of the specific concentrations l_i*/K_M and R_i0/K_M.

Vertical lines, inequality 22 is valid, C_≈l_i*; solid grey area, inequalities 20 or 21 are valid, C_≈R_i0l_i*/(K_M+R_i0+l_i*); horizontal lines, inequality 23 is valid, C_≈R_i0; and, white area, the square root regime. Points lying beneath the diagonal imply that the total number of endosomal ligand molecules is larger than the total number of endosomal receptors, which is only possible with an unstable endosomal complex. Dashes enclose the region where the notion of a quasi-steady-state concentration of bound ligand may break down in the case of low endosomal desorption rate constant (see Supplementary Figure S1 at http://www.BiochemJ.org/bj/402/bj4020537add.htm). Importantly, the dashed region does not intersect the zone of stable binding (III).

Apparent trafficking parameters

French and Lauffenburger [36] defined an apparent rate constant of intracellular ligand degradation, k_h, as the slope of the initial linear rise of the concentration of degraded ligand molecules in the medium, divided by the total concentration of intracellular ligand molecules, (n/N_A)l_i*, eqn (18) implies:

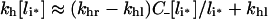(24)

The decrease in C_[l_i*]/l_i* with l_i* [30] implies that k_h[l_i*] increases (decreases) with total intracellular ligand (l_i*) when k_hl>k_hr (k_hl<k_hr) and that the maximal variation of k_h[l_i*] is bounded by the absolute difference between the degradation rate constants of free and bound ligand:

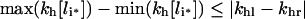(25)

Moreover, the constraint C_i≤R_i0 implies the high intracellular ligand load limit:

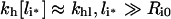(26)

Noting that endosomal ligand is depleted either by recycling or degradation, we can define an apparent intracellular clearance rate constant as:

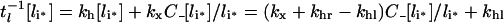(27)

This notation reflects that t_l is the apparent time scale for endosomal ligand depletion. At high endosomal ligand loads clearance is dominated by degradation of free ligand.

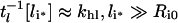(28)

French et al. [37] also defined an apparent recycling fraction, f_x, as the steady-state ratio of the recycling rate to the total clearance rate of endosomal ligand, −dl_i/dt. Using our results we find:

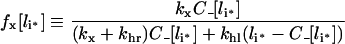(29)

The relationships:

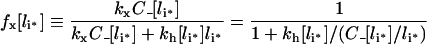and

imply that f_x[l_i*], always decreases with total intracellular ligand.

Ligand time-course curves

The following approximate ligand time-course curves can be derived (see Supplementary Results) when either of inequalities 20–22 is valid:

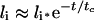(30)

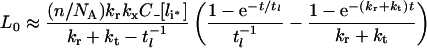(31)

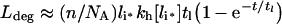(32)

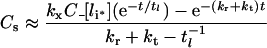(33)

The parameters t_l, C_[l_i*] and k_h[l_i*] are defined in Table 3. Double-exponential approximations have been used in the past to fit steady-state sorting data and can be derived directly from a base model that presumes the stability of internalized complexes [31]. That eqns (30–33) have the same functional form under conditions ranging from perfectly stable to fully dissociated endosomal complex suggests that their validity extends to states that violate inequalities 20–22 (Figure 4, zone V). To test this idea we shall also substitute the general forms of C_[l_i*], k_h[l_i*] and t_l[l_i*] (eqns 16, 24 and 27) to evaluate eqns (30–33).

Table 3. Definition of lumped variables used in the evaluation of the uniformly valid approximations, Eqns (30–33).

Zone	C_[li*]	kh[li*]	tl−1
I		khl
II
III	li*	khr	kx+khr
IV,V	Eqn 16	Eqn 24	Eqn 27

NUMERICAL EXAMPLES

Since the total number of endosomal ligand molecules after 3 h incubation (l_i*) is an implicit function of the initial number of endosomal receptors (R_i0) there is no guarantee that inequalities (20–23) span all the physically relevant scenarios of endosomal complex stability. We used numerical examples to determine which zones of the (l_i*, R_i0) plane are physically accessible and to test the approximations that lead to eqns (30–33).

Endosomal complex stability

To capture a range of potential steady-state sorting behaviours, we re-examined the relationship between the homoeostatic internalized receptor number and endosomal ligand for the cases depicted in Figure 3. Remarkably, the reduced model (eqn 16) approximated the fraction of bound endosomal ligand for all 48 permutations depicted in Figure 3 to within a 1% error. Of these, over a quarter (13/48) are not classified in zones I–IV, over half (26/48) are classified as high-affinity binding states (zone III, Figure 4), seven as linear binding sates (zone II, Figure 4) and two as states of ligand excess (zone IV, Figure 4). None of the cases are classified as states of low-affinity binding (zone I, Figure 4), suggesting that the number of intracellular receptors is not limiting for EGFR. Importantly, inequality 19 is satisfied by all four ligands at the basal endosomal volume, in agreement with their stability at low and basal endosomal volumes (Figure 3). At the highest reported endosomal volume, 2×10⁻¹³ litres/cell, we find that R_i0/K_M is 5.8 for EGF, 1.2 for TGFα, 1.2 for E40A and 2.9 for Y13G, consistent with their fractional binding at this volume (Figure 3).

These examples corroborate the validity of the suggested criterion for the stability of endosomal complexes (inequality 19). Since K_M>(k′_r/k′_f)N_AV_e, we can recast that criterion in terms of the endosomal dissociation constant, K′_d≡k′_r/k′_f. Namely, stability of the endosomal complex dictates that the concentration of endosomal receptors, R_i0/(N_AV_e), be much higher than the endosomal dissociation constant:

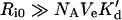(34)

Numerical simulations support this conclusion not only for mutant EGFR, but also for-wild type EGFR (Figure 5).

Steady-state trafficking parameters

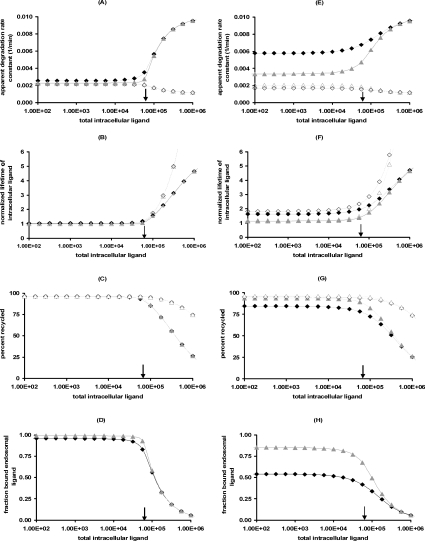
The validity of the reduced model for the cases considered in Figure 3 supports our definitions of steady state trafficking parameters (eqns 24, 27 and 29). At high endosomal ligand loadings k_h[l_i*] (Figures 6A and 6E), t_l[l_i*] (Figures 6B and 6F) and f_x[l_i*] (Figures 6C and 6G) depend strongly on the ratio k_hl/k_hr, whereas the fraction of bound endosomal ligand only varies with K_M and is therefore independent of k_hl (Figures 6D and 6H). The fraction of free endosomal ligand increases with endosomal ligand load and correspondingly k_h[l_i*] tends to the free ligand degradation rate constant. At endosomal ligand loads in excess of endosomal receptors the percentage of recycled ligand (Figures 6C and 6G) decreases, whereas the lifetime of endosomal ligand (Figures 6B and 6F) increases to its asymptotic value k_hl⁻¹.

Figure 6. Apparent trafficking constants as a function of the endosomal volume.

Left-hand panels, V_e=1×10⁻¹⁴ litres/cell; right-hand panels, V_e=2×10⁻¹³ litres/cell. (A and E) k_h[l_i*], (B and F) (k_x+k_hr)t_l[l_i*], (C and G) 100f_x[l_i*] and (D and H) C_[l_i*]/l_i*. Eqns (24, 27 and 29) are evaluated for EGF (triangles) and TGFα (diamonds) with k_hl=0.001min⁻¹ (closed symbols) or k_hl=0.0011min⁻¹ (open symbols). k_hl−k_hr is positive for the closed symbols and negative for the open symbols, but K_M is unaltered by variations in k_hl. Solid arrows denote the location of the threshold value l_i=R_i0.

It is noteworthy that the apparent trafficking parameter curves are all steeper for the lower endosomal volume (Figures 6A–D), and correspondingly lower K_M value. The shape of these curves reflects that l_i≈R_i0 is the crossover point between high- affinity binding (C_i*/l_i*≈1; inequality 22) and binding under ligand excess (C_i*/l_i*≈R_i0/l_i*; inequality 23) and the width of the crossover is approximately 2 K_M. In contrast, simulations that employ the maximal endosomal volume (Figures 6E–H) are representative of linear binding [C_i*/l_i*≈R_i0/(R_i0+K_M); inequality 21] at low intracellular ligand loads and the transition to excess ligand states (inequality 23) is smoother and occurs at higher ligand loads. Thus, at the basal endosomal volume the low ligand load limit of the apparent trafficking parameters is representative of the bound ligand, k_h[l_i*]≈k_hr, t_l[l_i*]≈k_x+k_hr and f_x[l_i*]≈1/(1+k_hr), whereas at maximal endosomal value the apparent trafficking parameters are also strongly influenced by the free ligand. These examples challenge the naïve perception that near-constant values of the steady state trafficking parameters k_h[l_i*], k_x[l_i*] and f_x[l_i*] are hallmarks of stable endosomal complexes.

Time-course curves

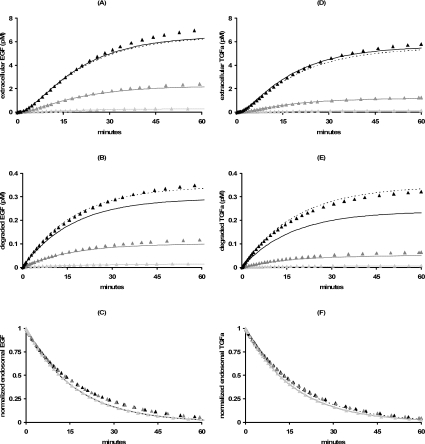
As experiments typically follow the time course of intact and degraded extracellular ligand and total intracellular ligand, we tested how well these quantities are estimated by their corresponding approximations (eqns 30–32) for a range of EGF and TGFα incubations. At basal endosomal volume, incubations with 0.1–10 nM EGF guarantee that K_M/(R_i0+l_i*)<0.09. Accordingly, the approximate forms corresponding to high-affinity binding (zone III, Table 3) closely approximate the initial time courses of the extracellular ligand and total intracellular ligand, and then begin to deviate after about 15 min, but match the overall trend in all cases (Figure 7, left-hand panels). Using the non-linear least squares regression error (1−R²) to estimate the a posteriori error, we find less than 9.2% error for the total endosomal EGF, less than 11.2% for the intact extracellular EGF and less than 24.7% for degraded EGF. The exceptionally high fractional a posteriori error for the degraded ligand is due to the differential degradation of ligand versus receptor (e.g., k_kl=4.5 k_hr). For example, when C_i=0.90 l_i, neglecting the term k_hl(l_i−C_[li]) in the equation for EGF degradation (eqn 18) leads to a 34% error in our approximate solution of this equation (eqn 32). Consequently, the error in degraded EGF decreases to less than 14% when the full-reduced model is used to evaluate eqns (30–32), whereas the errors in intact and total endosomal EGF are essentially unchanged. At basal endosomal volume, incubations with 0.1–10 nM TGFα (Figure 7, right-hand panels) display very similar trafficking kinetics to EGF (Figure 7, left-hand panels), in accord with the classification of these cases as states of high-affinity binding [K_M/(R_i0+l_i*)<0.13]. A posteriori we find less than 8.8% error for the total endosomal TGFα, less than 6.2% for the intact extracellular TGFα and less than 46.7% for degraded TGFα. The error in degraded TGFα decreases to less than 8.5% when using the full-reduced model to evaluate eqns (30–32), whereas the errors in intact and total endosomal TGFα are essentially unchanged.

Figure 7. Trafficking kinetics at basal endosomal volume.

Eqns (30–32) specialized for the square root regime (dashed lines; zone V) or the high affinity binding limit (solid lines; zone III; Table 3) are contrasted with the corresponding simulations of the full model for a range of (180 min) pre-incubation concentrations of labelled EGF (left-hand panels) or TGFα (right-hand panels): 0.1 nM (light grey triangles), 1.0 nM (grey triangles) and 10 nM (black triangles). Parameter values are as listed in Tables 1 and 2. (A and D) Intact extracellular ligand, (B and E) degraded extracellular ligand and (C and F) total endosomal ligand.

Increasing the basal endosomal volume 20-fold to its maximum results in significantly more degraded EGF (1.6–2.1-fold) and TGFα (3.2–3.7-fold), but only slightly more intact extracellular (Figures 8A and 8D) and endosomal (Figures 8C and 8F) EGF and TGFα. These trends are captured by the reduced model, which observably deviates from the numerical time-course curves only after approx. 15 min. Interestingly, whereas approximately the same percentage (4%) of preloaded EGF (Figure 7B) and TGFα (Figure 7E) were degraded at basal endosomal volume, at maximal endosomal volume a significantly smaller percentage of preloaded EGF (6.7–9.1%, Figure 8B) is degraded than preloaded TGFα (14.6–18.2%, Figure 8E). This heightened sensitivity of total ligand degradation to the magnitude of the endosomal volume stems from the differential degradation of free and bound endosomal ligand (e.g., k_hl⋙k_hr). For example, in zone III, where the majority of preloaded ligand is in complex, the fractional change in total recycled ligand and total degraded ligand upon dissociation of x endosomal complexes is −x/l_i and (k_hl/k_hr)x/l_i respectively.

Figure 8. Trafficking kinetics at maximal endosomal volume.

Dashed lines, eqns (30–32) specialized for the square root regime (zone V; Table 3) are contrasted with the corresponding simulations of the full model for a range of (180 min) pre-incubation concentrations of labelled EGF (left-hand panels) or TGFα (right-hand panels): 0.1 nM (light grey triangles), 1.0 nM (grey triangles) and 10 nM (black triangles). Parameter values are as in Tables 1 and 2, except for the endosomal volume, which is set at 2×10⁻¹³ litres/cell. (A and D) Intact extracellular ligand, (B and E) degraded extracellular ligand and (C and F) total endosomal ligand.

DISCUSSION

EGF and TGFα both bind EGFR, but, whereas EGF remains predominantly bound to EGFR inside the sorting endosome, a significant fraction of endosomal TGFα is thought to be dissociated [4,5,8]. Yet, our numerical simulations using published parameter estimates (Tables 1 and 2) surprisingly predict that internalized TGFα is predominantly bound to EGFR, and to an extent similar to EGF (Figure 2). This discrepancy can be understood in the major part when one considers endosomal volume as a critical parameter in growth factor–receptor association. TGFα and EGF follow similar binding kinetics. Both are bound to the receptor when simulations consider low endosomal volumes and are dissociated as the volume values are increased (Figure 3). Full appreciation of the relevance of predicted binding scenarios, however, requires introduction of a means of prioritizing the volume estimation. The wide range of published volume estimates can then be appreciated if these values are scaled to other cellular kinetic parameters. A central result of the present analysis is that the fraction of bound endosomal ligand is governed by a single dimensionless parameter (inequality 19) that depends on three primary factors: the total endosomal volume, the apparent endosomal dissociation constant and the number of endosomal receptors.

Though standard protocols have shed great light on receptor kinetics, they are not sensitive to the binding state of the internalized ligand. A mathematical manifestation of such insensitivity to the binding state of internalized ligand is that ligand kinetics are approximated by the same formulae (eqns 30–33) for states that encompass the limits of perfectly stable (C_i≈l_i) and irreversibly dissociating (C_i≪l_i) endosomal complex. In this sense, our analysis illustrates that the study of growth factor trafficking may be hampered by issues of kinetic distinguishability [38]. Nevertheless, the stability of the internalized complex can be resolved by determining the pools of free and bound endosomal ligand. The fraction of bound ligand can be determined indirectly from plots of the apparent trafficking parameters versus intracellular ligand load (Figure 6). In particular, the difference between the apparent clearance rate constant t_l⁻¹[l_i*] (eqn 27) and the apparent degradation rate k_h[l_i*] (eqn 24) is proportional to the fraction of bound ligand, C_[l_i*]/l_i* and is thus a direct measure of complex stability. As C_[l_i*]/l_i* is near-constant only when the total number of endosomal ligand molecules is smaller than the apparent endosomal dissociation constant, K_M (Figures 6D and 6H), the latter can be estimated as the intracellular ligand loading for which t_l⁻¹[l_i*]′−k_h[l_i*] drops to half its value.

Endosomal volume

The impact of endosomal volume can be profound. Dissociation of the receptor–ligand complex is predicted to be enhanced with increasing endosomal volume (Figure 3 and inequality 34). The dependence of binding on volume has been noted in a computational study of a more detailed model of endosomal sorting [36], but has never been prioritized before. Our results illustrate the importance of directly estimating the endosomal volume for a given cell type and of reporting a sensitivity analysis on this parameter. Schoeberl et al. [25] set the endosomal volume at 0.00003% of the intracellular volume (4.2×10⁻¹⁸ litres), whereas others [39] set it to 100% of the total intracellular volume (1.0×10⁻¹² litres). Yet volume estimates predetermine the fate of the endosomal ligand, almost irrespective of the binding constants (Figure 3). Simulations that employ the smaller value invariably result in a very stable endosomal complex, whereas simulations that employ larger volumes invariably create especially unstable complexes.

Endosomal dissociation constant

In our model, endosomal volume and the number of intracellular receptors at homoeostasis are intrinsic cell parameters and do not vary with ligand type. Thus, for a given cell line, the endosomal ligand–receptor dissociation constant determines the differential stability of intracellular signalling complexes of various ligands of the same receptor. For example, the range of reported equilibrium dissociation constants (Table 2) dictates that the stability of E40A should be similar to that of TGFα, whereas the stability of Y13G should be similar to EGF over a wide range of pre-incubation conditions and endosomal volumes (Figure 3).

The finding that the criteria for endosomal stability of constitutively trafficking receptors (inequalities 19 and 34) do not depend on the receptor internalization rate constant, strongly suggests that these criteria remain valid for down-regulating receptors. Numerical simulations support this conclusion (Figure 5) and reflect that down-regulation increases the total number of endosomal receptors beyond their initial number, R_i0, such that, if inequality 19 is valid at time zero, it remains so when R_i,tot≡R_i+C_i is substituted for R_i0. Moreover, numerical simulations of internalization experiments corresponding to wild-type down-regulating receptors, illustrate that the fraction of bound intracellular ligand is well approximated by the relationship

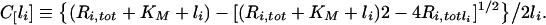The significance of our analysis is not limited to EGFR. For example, inequality 34 provides a rational basis for the empiric finding that the recycling fraction of IL-2 increases with endosomal dissociation constant [33], once allowance is made for the fact that in this system free ligand is recycled rather than being bound, as is the case in EGFR trafficking.

Receptor expression

Stability of endosomal signalling complexes is not only a property of the specific ligand–receptor pair, but also depends upon the intracellular milieu. The stability of the endosomal receptor complex is then a ‘systems property’ of the cell that is amenable to evolutionary optimization and dynamic control. Cells can modulate the level of endosomal signalling by varying their endosomal volume, and by regulating one receptor over another (inequality 34). At homoeostasis, the number of endosomal receptors is determined by the balance of receptor synthesis and degradation (eqn 8). Thus, it becomes possible to stabilize an otherwise unstable receptor complex by increasing the rate constant of receptor synthesis (inequality 34). For example, at the maximal endosomal volume, the fraction of bound endosomal TGFα at the end of a 180 min incubation with 10 nM TGFα increases from 39% at k_syn=130 receptors/cell·min⁻¹ to 83% at k_syn=1300 receptors/cell·min⁻¹ (R_s0=1185760 and R_i0=590910). The corresponding numbers for wild-type EGFR are 39% and 77%. In a sense then, the convenience of conducting experiments with cell lines that overexpress receptors, might create a biased state where endosomal complexes are artificially stable. The finding that complex stability increases with the number of endosomal receptors also cautions against the practice of neglecting the internalization flux of unoccupied receptors in computational studies of receptor sorting [36]. Numerical simulations illustrate that such neglect significantly misrepresents the dynamics of endosomal sorting as well as its steady-state (see Supplementary Results at http://BiochemJ.org/bj/402/bj4020537add.htm).

At the maximal endosomal volume R_i0>K_M for all four EGFR agonists (Tables 1 and 2), implying that all four agonists are relatively stable after internalization. It is instructive to compare these findings with other cytokines and cells that express several hundred intracellular receptors two orders of magnitude less than EGFR in B82 fibroblasts. As an example, R_i0>7K_M for IL-2 and its analogue 2D1 even at the maximal endosomal volume [33], implying that both cytokines remain predominantly bound to their endosomal receptors. Thus, the experimental estimates of the equilibrium dissociation constant of 2D1 and IL-2 at pH 6.0 cannot explain why the steady-state recycling fraction of 2D1 is 1.7-fold less than that of IL-2 in these cells [33]. This example raises the question of whether extracellular binding constants measured at pH 6.0 are representative of endosomal binding?

Surface signalling versus endosomal signalling

It is now appreciated that growth factor receptors can remain phosphorylated in the sorting endosome and can continue to signal from this environment. Endosomal signalling is biologically significant, and is capable of independently suppressing apoptosis [40] and inducing proliferation [41]. Compartmentalization of signalling molecules suggests a differential role for surface and endosomal signalling [17–19]. Thus, the absolute numbers of surface and intracellular signalling complexes, as well as their ratios are important factors that determine cellular responses and distinguish between extracellular cues. The total number of signalling complexes is limited by the total number of receptors and the magnitude and kinetics of the extracellular ligand perturbation. Our analysis sheds new light on the factors governing the ratio of surface and intracellular signalling complexes. For stable intracellular complexes the ratio of internalized to surface complexes is independent of ligand, and is determined by the balance of endocytosis, degradation and recycling C_i/C_s≈k_e/(k_hr+k_x) (eqn 4 and [42]). Intracellular dissociation alters this simple relationship and allows greater control over the signalling bias. The number of stable internalized complexes should increase with the ratio V_e⁻¹R_i0/(N_AK′_d) (inequality 34). Similarly, the number of surface complexes should increase with the ratio nR_s0/[N_AK_d (app)] where K_d (app)=(k_t/k_e)(k_r+k_e)/k_f [22] for down-regulating receptors and K_d (app)=(k_r+k_t)/k_f for constitutively trafficking receptors (eqn 11). Thus, different biases between surface and internalized receptor complex are expected. Cell density, endosomal volume, surface and intracellular receptor levels at homoeostasis, and the ratio of the dissociation constant of the surface complex to the endosomal complexes (Table 2) will all influence this bias. As the kinetics of growth factor presentation to surface receptors can have an impact on the stability of internalized complexes, delivery modalities might be designed to minimize or maximize endosomal signalling to meet specific pharmacologic goals. It may well be that this is the manner by which endogenous cytokines mediate growth factor signalling bias. Up-regulation of EGFR by TGFα [43], VEGF (vascular endothelial growth factor) [44] and PDGF (platelet-derived growth factor) [45] (but not EGF), or up-regulation of the PDGF receptors by FGF2 (fibroblast growth factor 2) [46] may fall into this category. Our results suggest that cytokine-induced upregulation not only amplifies surface signalling, but also pushes the signalling bias towards intracellular signals as both the number of intracellular receptors and the proportion of bound receptors increases.

Limitations

The generic model studied in the present paper is based on three simplifying assumptions: (a) that the recycling rate constant of endosomal receptors is independent of occupancy; (b) that sorting to the lysosome is nonspecific; and (c) that fluid phase uptake is negligible. Assumption (a) is valid for a class of EGFR including the kinase-active internalization impaired receptor c'973 [26], but is invalid for a range of wild-type and internalization impaired EGFRs [47]. However, as our analysis illustrates, intracellular dissociation alters the apparent recycling rate constant of occupied receptors, whereas the recycling rate constant of unoccupied receptors is set by homoeostasis (eqn 8). Assumption (b) is valid for ligands that are predominantly in fluid phase inside endosomes (presumably TGFα). Experiments suggest that lysosomal sorting can saturate at higher intracellular loads of EGF [37,47]. Although specific lysosomal sorting is beyond the scope of our model, we expect the criterion for complex stability (inequality 34) to remain valid under more general circumstances. This may be the case as this inequality reflects a thermodynamic balance of receptor concentration and the equilibrium dissociation constant. Thus, at sufficiently low endosomal volumes, EGF and TGFα are predicted to be predominantly bound to EGFR, and we would expect both to saturate the lysosomal sorting machinery. At the extreme of high endosomal volume we would anticipate both EGF and TGFα to be predominantly in fluid phase.

Internalization of molecules by fluid-phase endocytosis is proportional to their concentration in the extracellular fluid, and can be accounted for in our model by adding the ligand depletion term k_fpN_AL₀ in eqn (3), where k_fp has the dimensions of volume·cell⁻¹·min⁻¹ [23]. The contribution of fluid- phase internalization relative to receptor mediated internalization scales as the dimensionless ratio k_fpN_AL₀/(k_eC_s). Estimating the rate of receptor internalization as k_eC_s≈k_eR_s0L₀/(K_d+L₀) we conclude that fluid-phase uptake is significant when k_fpN_A(K_d+L₀)/k_eR_s0)>0.1. The reported value for NR6 fibroblasts of k_fp≤3.4×10⁻¹⁶ litres·cell⁻¹·min⁻¹ [48] suggests that in these cells fluid uptake only becomes significant for extremely high extracellular ligand concentrations (L₀>60K_d=150 nM). Thus, assumption (c) seems to be justified for the examples considered here. At high extracellular ligand concentrations that render fluid-phase uptake significant, the steady state number of intracellular ligand molecules can significantly exceed the number of intracellular receptors. In such cases the fraction of bound endosomal ligand no longer reflects the stability of the internalized ligand–receptor complexes. Although the detailed analysis of the effects of fluid-phase ligand uptake are beyond the scope of this work, first principles considerations (e.g., Le Chatelier's principle) imply that fluid-phase internalization would tend to stabilize the endosomal ligand–receptor complex, thereby enhancing intracellular signalling. Moreover, when fluid-phase internalization dominates, the majority of ligand molecules enter the cell unbound, rather than receptor bound as assumed in our model, and endosomal complex stability is rendered independent of endosomal volume.

Conclusions

Mathematical modelling of biological systems is indispensable, particularly when experimental studies define areas of importance, but cannot characterize them fully. Numerical simulations of model equations can generate a wide spectrum of possible scenarios in silico, but are inefficient at prioritizing critical determinants. Augmentation of numerical simulation by careful time-scale analysis can provide direct information on parameter sensitivity over a wide range of values. This numerical–analytical approach has provided a novel insight into the predominant factors that govern the average lifetime of intracellular signalling growth factor complexes. Such insights call for a reconsideration of the conventional view that growth factor–receptor complex stability is solely governed by endosomal pH.