Force-Induced DNA Slippage

Abstract

DNA containing repetitive sequences displays richer dynamics than heterogeneous sequences. In the genome the number of repeat units of repetitive sequences, known as microsatellites, may vary during replication by DNA slippage and their expansion gives rise to serious disorders. We studied the mechanical properties of repetitive DNA using dynamic force spectroscopy and found striking differences compared with ordinary heterogeneous sequences. Repetitive sequences dissociate at lower forces and elongate above a certain threshold force. This yield force was found to be rate dependent. Following the rapid stretching of the DNA duplex, the applied force relaxes by stepwise elongation of this duplex. Conversely, contraction of the DNA duplex can be observed at low forces. The stepwise elongation and shortening is initiated by single slippage events, and single-molecule experiments might help to explain the molecular mechanisms of microsatellites formation. In addition to the biological importance, the remarkable properties of repetitive DNA can be useful for different nanomechanical applications.

INTRODUCTION

Not only is DNA the key molecule for life, it has also become an extremely versatile tool kit for man made nanoscale structures and devices (1). Despite the fact that structure and dynamics of DNA were studied extensively, many of the discovered intramolecular processes, which exhibit complex dynamics and a distinct biological function, still lack satisfactory explanation. Microsatellites formation and bulge loop propagation in repetitive sequences are prominent examples (2). Two complementary DNA strands with heterogeneous sequences can only bind in a well-defined, unique conformation. Thermodynamic fluctuations lead to excitations in the double-stranded DNA, which results in a fast opening and closing of short stretches of basepairs (3,4). These fluctuations are localized and do not propagate through the DNA duplex.

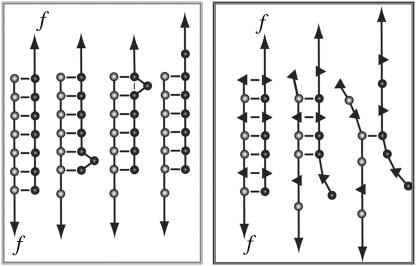
In contrast, double-stranded DNA, containing short repetitive sequences, so-called microsatellites, displays a more complex dynamic behavior (5–9) with potential applications in nanotechnology. Two complementary strands can hybridize in various different conformations in which sufficiently long stretches are aligned to build up thermodynamically stable structures. Rapid transitions between these different conformations may occur. This so-called bulge loop formation and propagation (see Fig. 1) is called DNA slippage. It is considered to play a central role in the evolution of microsatellites, which can be found throughout the genome (10).

FIGURE 1.

Comparison of the behavior of repetitive (left) and heterogeneous (right) DNA sequences under an externally applied force. Repetitive DNA sequences can form bulge loops. These bulge loops can propagate to the other end of the DNA duplex and therefore cause a lengthening of the molecule. In contrast, this dissociation path is not available for heterogeneous DNA sequences. Heterogeneous DNA sequences simply dissociate in an all or none mode.

The repeat units of these microsatellites usually consist of one to six bases, e.g., (A)_N, (GT)_N, or (GTT)_N. The corresponding length of the microsatellites, i.e., the number of consecutive identical repeat units, N, changes rapidly in evolution, presumably due to DNA slippage events during replication. Because of this length variability, the microsatellites frequently are used as genetic markers, e.g., for forensic purposes, or to determine the genetic similarity between different populations. On the other hand, certain human neurodegenerative diseases, such as fragile X or Chorea Huntington, are related to expansions of trinucleotide repeats of microsatellites beyond certain thresholds (11).

Investigations of DNA slippage in vitro (2,12) showed that DNA bulge loop formation at the end of the duplex occurs on a timescale of microseconds. As a result, the two strands can be shifted relative to each other by propagation of a bulge loop toward the other end of the duplex (compare Fig. 1). In recent years, single molecule techniques have been used to study the mechanical properties of single DNA molecules. For example, the elasticity (13–16) and unzipping of λ-phage DNA (17,18), the interactions between proteins and double-stranded DNA (19,20) and the dissociation forces of short DNA duplexes (21–23) have been measured using different experimental setups. Recently, a theoretical work suggested studying DNA slippage with an atomic force microscope (AFM) (24): The two complementary strands of a DNA duplex with a repetitive sequence are predicted to move relative to each other if the externally applied force exceeds a critical force, the slipping threshold f_c. This slipping threshold can be estimated by balancing the work performed by the external force with the binding free energy, which is lost if both strands are shifted relative to each other by one repeat unit. When shifting the two strands, the contour length of the single-stranded parts of the duplex elongates by twice the length of one repeat, whereas the double-stranded part shortens by one repeat unit. This simple argument leads to the slipping threshold f_c:

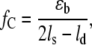(1)

where ɛ_b is the binding free energy of one repeat unit, l_S is the effective length of one unit when unbound and stretched by the force f, and l_d the length of the hybridized repeat unit. For a trinucleotide (GTT) the basepairing energy is ɛ_b ≈ 7–8 k_BT, the length of three basepairs in the duplex is l_d ≈ 1 nm, and the effective length of three single-stranded bases is l_S ≈ 1.5 nm. Inserting these values in Eq. 1 a slipping threshold f_c of roughly 15 pN can be predicted. For a dinucleotide (GT) f_C is roughly 13 pN, with l_s ≈ 1 nm, l_d ≈ 0,7 nm, and ɛ_b ≈ 4–5.5 k_BT. However, this estimate has to be taken with care, since the deformation of the duplex and finite size effects will affect the true value of f_c. The rate of this motion of the two DNA strands relative to each other is determined by the diffusion of bulge loops from one end of the strand to the other (see Fig. 1). The slipping process can be characterized with the following parameters: the slipping rate, which describes the speed of the movement of the bulge loops along the DNA duplex; the slipping length, which describes the length increase or decrease that is determined by the number of bases in one repeat unit; and the slipping threshold, which describes the critical force for the appearance of slipping.

Here we report on an investigation on the response of short DNA duplexes to an externally applied shear force and compare these repetitive sequences with heterogeneous sequences with respect to their slipping rate, slipping length, and slipping threshold with the intent to test the concept of bulge loop mediated elongation. The dependence of the dynamics on the number of repeat units and the number of bases in one repeat unit is investigated.

MATERIALS AND METHODS

Oligonucleotides modified with a thiol group at the 5′-terminus (for details see Table 1; IBA GmbH, Göttingen, Germany; Metabion GmbH, Martinsried, Germany) were immobilized on amino-functionalized surfaces using a heterobifunctional poly(ethylene glycol) (PEG) spacer. One oligonucleotide was immobilized on the cantilever and the complementary sequence was coupled to the surface. Note that such a chemical functionalization leaves the molecule the freedom to rotate because of the single covalent bonds in the PEG chain. The cantilevers (Bio-lever, Olympus, Tokyo, Japan) were cleaned and functionalized as described previously (25). Instead of epoxy-functionalized cantilevers, amino-modified surfaces on the cantilevers were prepared using 3-aminopropyl-dimethylethoxysilane (ABCR GmbH, Karlsruhe, Germany). Commercially available amino-functionalized slides (Slide A, Nexterion, Mainz, Germany) were used.

TABLE 1.

DNA sequences

DNA duplex	Sequence (cantilever)	Sequence (slide)
(X)ID	5′SH-TTTTTTTTTTTTTTTTTTTTCGTTGGTGCGGATATCTCGGTAGTGGGATACGACGATACOGAAGACAGCTCATGTTATATTATG-3′	5′SH-TTTTTTTTTTTATCCCACTACCGAGATATCCGCACCAACG-3′
(GT)ID	5′SH-TTTTTTTTTTGTGTGTGTGTGTGTGTGTGT-3′	5′SH-TTTTTTTTTTACACACACACACACACACACA-3′
(GT)ID	5′SH-TTTTTTTTTTGTGTGTGTGTGTGTGTGTGTGTGTGTGTGT-3′	5′SH-TTTTTTTTTTACACACACACACACACACACACACACACAC-3′
(GGT)ID	5′SH-TTTTTTTTTTGGTGGTGGTGGTGGTGGTGGTGGTGGTGGT-3′	5′SH-TTTTTTTTTTACCACCACCACCACCACCACCACCACCACC-3′

From this step on, the surfaces of cantilever and slide were treated in parallel as described in Blank et al. (26). They were incubated in borate buffer pH 8.5 for 1 h. This step was necessary to deprotonate the amino groups for coupling to the N-hydroxysuccinimide groups (NHS) of the heterobifunctional NHS-PEG-maleimide (MW 5000 g/mol; Nektar, Huntsville, AL). The PEG was dissolved in a concentration of 50 mM in borate buffer at pH 8.5 and incubated on the surfaces for 1 h. In parallel, the oligonucleotides were reduced using TCEP beads (Perbio Science, Bonn, Germany) to generate free thiols. After washing with ultrapure water, a solution of the oligonucleotides (1.75 μM) was incubated on the surfaces for 1 h. Finally, the surfaces were rinsed with phosphate buffered saline (PBS) to remove noncovalently bound oligonucleotides and stored in PBS until use.

All force measurements were performed with a MFP-3D atomic force microscope (AFM) (Asylum Research, Santa Barbara, CA) at room temperature in PBS. Force-clamp, distance jump experiments and analysis of the data were carried out in Igor 5.3 with self-written procedures. Cantilever spring constants were determined by thermal calibration (6–8 pN/nm).

RESULTS

For the AFM experiments, the complementary DNA strands were covalently anchored via poly(ethylene glycol) (PEG) spacers. One strand was bound to the surface of a glass slide (26) and the complementary strand was coupled to the cantilever tip, respectively.

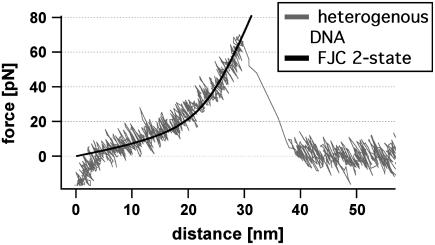
In all experiments the slide was approached with the tip of the cantilever, allowing the two single strands to hybridize and form a duplex. To avoid double rupture events the binding probability was adjusted to <30% by the applied force and duration time on the surface. Subsequently, the cantilever was retracted and the DNA duplex was loaded with a gradually increasing force until it finally ruptured and the cantilever relaxed back into its equilibrium position. The force applied to the DNA duplex via the PEG spacers was recorded as a function of the distance between the cantilever tip and the surface (Fig. 2). This curve was fitted with a two-state freely jointed chain (FJC) model, which describes the enthalpic and entropic behavior of polymers under an applied force (27).

FIGURE 2.

Example of a force-extension curve of a heterogeneous DNA duplex. While retracting the cantilever from the surface the polymer spacer and the DNA duplex are set under stress. The elastic behavior of the polymer-DNA duplex can be described with the FJC fit (black dashed line). At a force of 62 pN the double-stranded DNA dissociates and the cantilever drops back into its relaxed state.

Because most biologically relevant interactions are comparable in strength to thermal energies, force-induced processes such as the separation of receptor-ligand systems or in our case DNA duplexes are fluctuation-assisted processes (28). Therefore the distribution of the unbinding forces is broadened significantly (29). At a given force rate and at a fixed bond energy, a shift of the histograms directly reflects the difference in the effective width of the binding potentials (30,31) and indicates different unbinding pathways in the energy landscape.

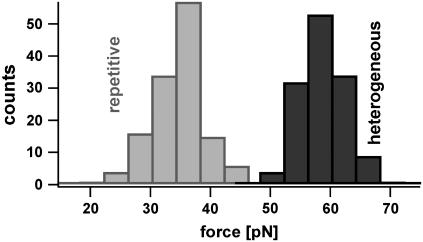
To investigate, whether DNA duplexes with repetitive sequences have different unbinding pathways and therefore show different unbinding forces than heterogeneous sequences, both systems were analyzed. Fig. 3 shows the resulting distributions of the rupture forces of a heterogeneous (X)₃₀ and a repetitive DNA sequence (GT)₁₅ recorded at approximately the same pulling speed. Although both sequences have similar thermodynamic properties, which mainly correlate with the GC content of the sequence, their rupture force distributions differ drastically. The histogram for the repetitive DNA sequence (blue) is shifted toward lower dissociation forces. The DNA complex typically dissociates at forces below 40 pN. We conclude that an additional dissociation path is available for the repetitive sequence. Note that the repetitive sequence might also bind fractionally and therefore might lead to lower dissociation forces. But without the assumption of an additional unbinding path this effect would lead to a broadening of the force distribution containing also higher forces similar to those of the heterogeneous sequence. The specificity of the measured interactions was proven, by replacing one single DNA strand with a noncomplementary sequence. This leads to <0.5% interactions.

FIGURE 3.

Histograms of the unbinding forces of DNA duplexes with a heterogeneous (X)₃₀ and a repetitive (GT)₁₅ sequence measured at similar pulling speeds. The duplex with the repetitive sequence dissociates at markedly lower forces, although its binding energy equals the binding energy of the heterogeneous sequence. The force distribution of the repetitive DNA is detruncated at a force of 40 pN. This gives evidence for an additional unbinding path, which is favored if an external force is applied.

Having established that repetitive DNA has characteristics, which are absent in heterogeneous sequences, two repetitive sequences with a different number of bases per repeat unit were compared with a heterogeneous sequence. The study of the unbinding mechanism of (GTT)₁₀ and (GT)₁₅ should reveal more detailed insights in the unbinding mechanism.

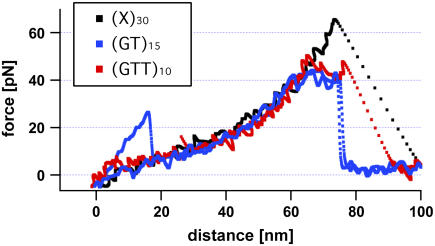
The theoretically predicted unbinding path represents a stepwise elongation of the repetitive DNA duplex by moving both strands against each other (see Fig. 1) as soon as the externally applied force exceeds a certain threshold (slipping threshold f_c). Such an elongation can indeed be observed in the recorded force-extension curves. Fig. 4 shows several typical force-extension curves obtained for two different repetitive and one heterogeneous DNA sequence. The force-extension curves for repetitive DNA deviate from the FJC behavior at forces above 40 pN, whereas the curves for heterogeneous DNA follow the FJC fit up to much higher forces. Apparently, repetitive DNA gets elongated at a slipping threshold between 35 and 40 pN. In the following we will use the expression “slipping threshold” for the value of the applied force beyond which the DNA duplex starts to slip or creep.

FIGURE 4.

Typical force-extension curves of a heterogeneous (X)₃₀, a repetitive (GT)₁₅, and a (GTT)₁₀ sequence. In contrast to the force-extension curve of the heterogeneous DNA sequence, which follows the two-state FJC behavior, the repetitive DNA duplexes elongate at a force (slipping threshold) of ∼35–40 pN until they finally dissociate (rupture force).

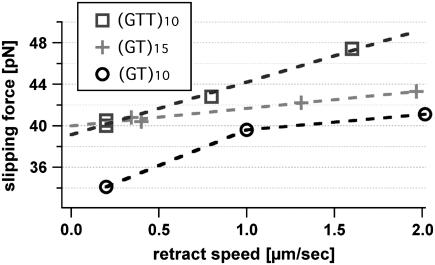
Whereas the results described above show further proof that repetitive sequences slip under load, the following experiment was carried out to examine the dependence of the slipping process on the length of the elementary repeat unit and the number of repeats. These experiments were carried out with the following sequences: (GTT)₁₀, (GT)₁₀, and (GT)₁₅. These DNA duplexes were probed at different pulling speeds because the slipping threshold is expected to be speed dependent. Because the slipping thresholds only differ by a few piconewtons, each data set was recorded with one cantilever to avoid calibration errors. In Fig. 5 the maxima of the slipping force distributions are plotted against the pulling speed of the cantilever. As can be seen in this figure, the slipping threshold shows a weaker dependence on the pulling speed for dinucleotide than for trinucleotide repeat units. Furthermore, the slipping thresholds are lower for the shorter repetitive sequence (GT)₁₀ than for the sequence containing 15 repeat units. In a linear response, the velocity of a particle in a viscous environment is given by the product, containing the mobility of the particle and the applied force. Close to the slipping threshold f_c, the relationship between the measured force and the velocity of DNA slippage can be treated similarly. Here an effective friction for relative strand motion arises from the need to nucleate bulge loops to shift both strands.

FIGURE 5.

Pulling speed dependence of the slipping threshold for different repetitive DNA sequences. To avoid spring calibration errors every data set for one sequence is performed in a single experiment with the same cantilever. The maxima of the slipping threshold histograms, containing 80–150 force curves, are plotted against the pulling speed of the cantilever. The slipping threshold depends on the pulling speed and shows a linear time dependency as a first approximation.

Close to slipping threshold f_c the slipping velocity v(f) increases linearly with the measured force due to v(f) = dv/df × (f − f_c). The variable u₀ = dv/df represents the effective slipping mobility, which depends on the bulge loop nucleation rate, microscopic slipping rate, and the number of repeat units. In our experiments, we correlated the slipping velocity v(f) with the retract speed of the cantilever and measured the resulting slipping threshold.

From a linear fit, we achieve a slipping mobility u₀ of 580 nm/s·pN for a dinucleotide and 250 nm/s pN for a trinucleotide sequence. This is in agreement with the theoretical predictions and with bulk experiments that observed faster expansions for shorter repeat units. To form a bulge loop in a dinucleotide sequence, fewer basepairs have to open up than in a trinucleotide sequence and hence the rate to create these defects is smaller for longer repeat units. However, the additional length increase per step for longer repeat units does not compensate the lower rate.

So far the experimental results confirm that repetitive DNA strands can slide against each other and that the slipping threshold can be determined for different retract speeds. The values obtained for the slipping mobility are in good agreement with theoretical predictions. However, the time resolution in an usual force-extension measurement is not sufficient enough to discriminate individual steps, which would give direct evidence of the stepwise microscopic sliding mechanism.

Initial force clamp (32) measurements (data not shown) performed with the AFM only showed a lengthening of the different DNA duplexes at forces of 35–40 pN, but failed to resolve the expected individual steps. Therefore, a new measurement protocol was implemented, whose time resolution is limited only by the relaxation of the cantilever. These measurements were carried out as follows: i), The cantilever was lowered, to allow the DNA to hybridize and form a duplex. ii), The cantilever was gradually retracted from the surface allowing a certain force, well below the slipping threshold, to build up. iii), Then, in one step, the cantilever was retracted an additional 3–7 nm away from the surface. As a result of this distance jump, the force acting on the DNA duplex rises almost instantaneously to a new higher value. Initially, the contour length, which gives the total length under force, does not change. If, in response, the DNA duplex elongates due to slipping, an increase of the contour length is observed. In addition, the applied force drops, which can be detected by the cantilever.

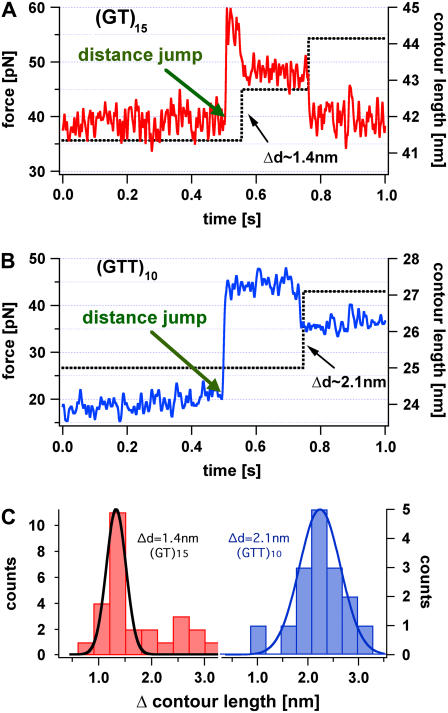
Fig. 6 A shows two typical curves, force versus time and distance versus time, for a 15-times repetitive dinucleotide DNA duplex (GT)₁₅ recorded with the measurement protocol described above. First, the force acting on the DNA molecule is fluctuating around 38 pN, a value close to the previously observed slipping threshold. As indicated with the blue arrow in the force versus time graph a 4-nm distance jump was performed. As a result of the distance jump the force (red) increases to nearly 57 pN, but the contour length stays constant. Within a fraction of a second the measured force decreases to a value below 40 pN in discrete steps. The final force is again close to the observed slipping threshold. This rapid and discrete decrease of the force can only be explained with a stepwise lengthening of the DNA molecule, which compensates the performed distance jump. These observations show that a single relaxation process increases the contour length of the dinucleotide DNA system by ∼1.4 ± 0.3 nm. This value was obtained by a Gaussian fit of the contour length increase histogram (see Fig. 6 C) of several experiments, with a confidence interval of 90% certainty. This effect can be well explained by a relative sliding of one repeat unit (dl = 2l_s − l_d = 4 × 0.5 nm − 2 × 0.34 nm = 1.4 nm). Unfortunately, only a limited number of steps can be observed, because the probability of holding these DNA duplexes under such a high force for a long time is very low and decreases further with every step.

FIGURE 6.

Force versus time (red) and contour length versus time curve (black) of a repetitive (GT)₁₅ and (GTT)₁₀ DNA duplex, initially held at a force below the slipping threshold. After 0.5 s a distance jump of the cantilever was performed resulting in a force step above the slipping threshold, but leaving the contour length of the molecule constant. In panel A the contour length of the (GT)₁₅ DNA complex relaxes in two discrete elongation steps and the force acting on the duplex drops below the slipping threshold. In panel B the contour length (black curve) of the (GTT)₁₀ DNA complex elongates in one discrete step and the force drops below the slipping threshold. Panel C shows the distribution of the contour length change for the di- and trinucleotide sequence. The additional peak at (∼2.8 nm) in the dinucleotide sequence may occur from double slipping events.

Fig. 6 B shows the equivalent experiment for a trinucleotide (GTT)₁₀ sequence. As expected, the contour length increase of ∼2.1 ± 0.3 nm, determined analogous to the (GT) sequence, is higher than for the dinucleotide sequence. Analogous experiments performed with the heterogeneous sequence did not show any discrete steps (data not shown).

To exclude the possibility, that the observed steps are artifacts of multiple binding the following arguments are pointed out. First of all the overall elasticity of the measured PEG polymer spacer would be much stiffer. Secondly, the presumption of three bound molecules in parallel mimicking the three steps of the single molecule shown in Fig. 5 would require the respective PEG polymer spacers to differ in length by <2 nm. This would mean that the total force acting on the cantilever would be distributed on three duplexes and as a consequence the lifetime for the duplexes would be much longer than our experimental findings. Dissociation of one duplex increases the split force applied to the remaining duplexes and reduces their lifetime drastically. For this reason multiple binding as potential artifact can be excluded with a very high certainty.

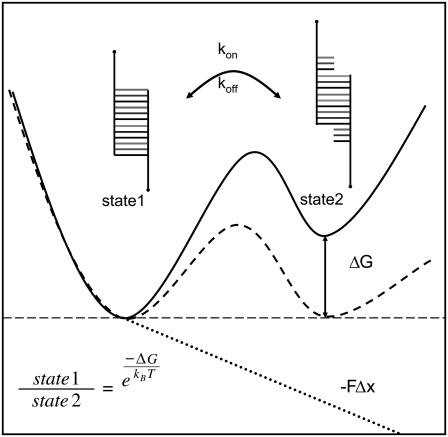
Having shown that all characteristic parameters describing the slipping process can be determined experimentally, we wanted to obtain more detailed information about the behavior near the slipping threshold. The system for the native and elongated conformation of the repetitive DNA duplex can be described with a two-state potential illustrated in Fig. 7. Application of an external force allows the tuning of the potential, so that the Gibbs free energy of these two states is the same as shown with the dashed line in Fig. 7. If this force equals the slipping threshold f_c the system can fluctuate in equilibrium. This was achieved in the measurement shown in Fig. 8. Using the above-mentioned measurement protocol a distance jump is performed and the force on the DNA duplex first increases over the slipping threshold limit f_c. As a result the DNA duplex elongates and the force drops to the slipping threshold. At this force the system starts to perform multiple back and forth slipping events. An additional distance jump forces the DNA duplex in its elongated conformation until it finally ruptures completely.

FIGURE 7.

Gibbs free energy of a two-state system under an external force. The model describes the completely bound and the first lengthened state of a repetitive DNA duplex. The potential is tilted due to an externally applied force. This results in a leveling of the energy of the two states, allowing the DNA duplex to fluctuate between the two states in equilibrium.

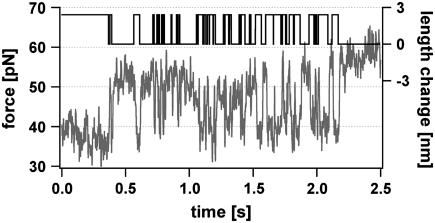
FIGURE 8.

Example for the slipping of the DNA duplex between the elongated and the short state. A repetitive (GTT)₁₀ DNA duplex is held at a constant force analogous to Fig. 6. A distance jump drives the force above the slipping threshold. This results in a lengthening of the DNA duplex and the force drops down to the slipping threshold. Consequently, the duplex lengthens and shortens due to forward and backward slipping. The measured time trace (red) of the fluctuation process was analyzed with a telegraph noise algorithm to extract the dynamics of the length changes (black). The mean lifetimes were found to be 0.031 s for the fully hybridized state and 0.022 s for the lengthened state.

These fluctuations of the DNA duplex between the two states can be analyzed with random telegraph noise analysis similar to ion channel recordings (Fig. 8, black curve). The hidden Markovian process can be characterized with the transition rates from one state to the other (33). The data trace shown in Fig. 8 exhibits mean lifetimes of 0.031 s for the elongated and 0.022 s for the shortened state. Note that these lifetimes are very dependent on the applied force. The energy difference between these two states varies between the binding energy of the DNA duplex and the bending energy of the cantilever. The energy was found to be ∼7 k_BT, which is close to well-established values of about ∼8 k_BT for a trinucleotide GTT repeat unit. Other experiments underline this value. Due to the sensitivity of the system regarding the applied force and the low detection probability a closer examination will require substantial instrumental improvements. The observed multiple forward and backward jumps in Fig. 8 could be detected with short polymer spacers with lengths between 15 and 20 nm only. A possible reason for this finding could be that the fluctuations of the cantilever allow the duplex to form a bulge loop at lower forces, which eventually diffuses to the other end. For longer spacers these fluctuations are averaged by the elasticity of the polymer (34). The alternative scenario, that the observed shortening is a simple transient bulge loop formation at the stretched end, can be ruled out because the lifetime of these bulge loops, even if they travel some steps into the molecule, is orders of magnitude too small to explain the observed frequencies.

DISCUSSION

The data presented here show that repetitive DNA duplexes elongate under an applied shear force and dissociate at significantly lower forces of ∼38 pN than for heterogeneous DNA sequences. Because of the possibility of fractional binding for repetitive sequences, lower dissociation forces are possible in regular force distance curves (see Fig. 2). This is due to an additional unbinding path that allows the repetitive DNA duplex to increase its contour length without having to overcome a large free energy barrier. It should be pointed out that this unbinding path energetically is not favored over other paths but gets populated by force.

The theoretically predicted length increase occurs in discrete slipping steps. We could show that the resulting length increase of the whole DNA duplex is consistent with the length increase obtained by shifting both strands of di- and trinucleotide sequences by one repeat unit. Slippage is faster for shorter repeat units and smaller repeat numbers. This is consistent with the theory of bulge loop diffusion because the expected slipping velocity decreases with the energy needed to produce a bulge loop. In addition, the diffusion of a bulge loop through the molecule is faster for shorter duplexes. The mechanism of relative strand motion caused by the creation, diffusion, and absorption of bulge loop defects is similar to defect propagation in crystal lattices.

The slipping threshold determined in the measurements was found to be larger than the theoretically predicted slipping threshold f_c. This may be due to the small number of repeat units used in the experiments and to the simplistic model used for the theory. For instance, deformations and conformational changes in the backbone of the DNA duplex resulting from an externally applied force are not included in the model.

The slipping velocity is expected to scale inversely with the number of repeat units. This prediction could not be unambiguously confirmed because only rather short sequences were available. Further experiments are necessary to quantify the dependence of the slipping dynamics on the repeat number and flanking sequences. More detailed experiments will shed some light on the kinetics of the processes involved in expansion of microsatellites during replication. Because of its bidirectional property DNA slippage, itself, is not the cause for the asymmetric increase effect of repeat units in the human genome.

Besides the biological importance of repetitive sequences, the remarkable properties of repetitive DNA might also be useful for different nanomechanical applications (35–37). Because the rupture force distribution for repetitive sequences is truncated sharply at forces close to 40 pN, repetitive DNA could serve as a programmable force sensor, with a threshold force that can be fine tuned by sequence composition. Adjustable viscoelastic building blocks in DNA self-assembly structures can be realized with repetitive sequences.

Furthermore, the relaxation of a large force to a slipping threshold force f_c with a time constant that can be chosen by length and sequence composition could be used as a length independent force normal. Conversely, if extended, repetitive double-stranded DNA contracts until the slipping threshold force f_c is built up if the initial force is below f_c. Therefore, complementary repetitive single-stranded DNA could be applied for self-tightening connections in nanostructures. After initial hybridization, two single strands tend to maximize their overlap, i.e., the number of basepairs, until a tension of the order of the slipping threshold f_c is built up. These adjustable force-induced tensions at confident locations establish completely new features in nanoscale structures.