DISPLAR: an accurate method for predicting DNA-binding sites on protein surfaces

Abstract

Structural and physical properties of DNA provide important constraints on the binding sites formed on surfaces of DNA-targeting proteins. Characteristics of such binding sites may form the basis for predicting DNA-binding sites from the structures of proteins alone. Such an approach has been successfully developed for predicting protein–protein interface. Here this approach is adapted for predicting DNA-binding sites. We used a representative set of 264 protein–DNA complexes from the Protein Data Bank to analyze characteristics and to train and test a neural network predictor of DNA-binding sites. The input to the predictor consisted of PSI-blast sequence profiles and solvent accessibilities of each surface residue and 14 of its closest neighboring residues. Predicted DNA-contacting residues cover 60% of actual DNA-contacting residues and have an accuracy of 76%. This method significantly outperforms previous attempts of DNA-binding site predictions. Its application to the prion protein yielded a DNA-binding site that is consistent with recent NMR chemical shift perturbation data, suggesting that it can complement experimental techniques in characterizing protein–DNA interfaces.

INTRODUCTION

Protein–DNA interactions play central roles in a wide range of biological processes such as gene regulation and DNA replication and repair. A fundamental question is how recognition is achieved, both on the DNA side and on the protein side. On the DNA side, recognition by a protein involves features that distinguish a short stretch of nucleotides, to which the protein specifically binds, from other nucleotide sequences on the DNA. On the protein site, recognition by a DNA involves features that distinguish a patch of residues, to which the DNA binds, from other areas on the protein surface. This article presents a method for predicting the DNA-binding site on a protein surface. The method is called DISPLAR, or DNA-Interaction Site Prediction from a List of Adjacent Residues.

DISPLAR is built on our method, PPISP, developed previously for protein–protein interaction site prediction (1,2). The approach is based on a number of distinguishing features that residues in protein–protein or protein–DNA interfaces have over non-interface residues on the protein surface. In the case of protein–DNA interfaces, such distinguishing features have been reported before. These include enrichment of positively charged Arg and Lys residues (3–8) and sequence conservation (9). The former can be easily rationalized by the negatively charged phosphate group on each nucleotide; the latter can be rationalized by structural and functional requirements on the interface. In DISPLAR, like in PPISP, these two features are captured by position-specific sequence profiles as obtained by running PSI-blast (10). In addition, the solvent accessibility of interface residues is also distinct from that of non-interface residues and is used as an input for DISPLAR as well as for PPISP. These input parameters are used to train a neural network for prediction.

The approach of PPISP seems to be ideally suited for adaptation to DNA-binding site prediction. The binding partners, i.e. different DNA, have common structural and physical properties. All DNA share the basic double-helix architecture; structural variability due to local bending and twisting is much less compared to variability in the case of proteins from different folds. Variability among nucleotides also seems to be much less than among amino acids. There are only four different nucleotides compared to 20 amino acids. More importantly, the variable part of each nucleotide, i.e. the base, is involved in base pairing and less exposed than the constant part, i.e. the phosphate. The latter, as noted earlier, carries a negative charge. In contrast, in the case of amino acid, the variable part, i.e. the side chain, is usually more exposed than the constant part, i.e. the backbone, in folded proteins. In short, the partners in protein–DNA recognition are much more uniform than those in protein–protein recognition. Since a neural network is trained to learn common features of interface residues and has been found to work well for protein–protein interface prediction, it may be expected that the same approach would work well for predicting DNA-binding site.

Several attempts at predicting DNA-binding have been made previously. Stawiski et al. (4) used percentages of Arg and Lys residues and other physical properties to classify whether a protein is nucleic-acid binding. Jones et al. (5) used electrostatic potential surface of DNA-binding proteins to predict the binding surface patch. Of a set of 56 proteins, 38 (i.e. 68%) had top-ranked patches with more than 70% residues that are actually DNA-contacting. Keil et al. (11) used electrostatic potential and other physical properties to classify protein surface patches as protein, DNA, ligand or non-binding. Ferrer-Costa et al. (12) used electrostatic potential to classify whether proteins with the helix-turn-helix motif are DNA-binding. Tsuchiya et al. (13) also used electrostatic potential to classify whether a protein is DNA-binding. Recently Kummerfeld and Teichmann (14) used homology to predict transcription factors.

Two methods that have the most resemblance to DISPLAR are by Ahmad et al. (6) and by Kuznetsov et al. (15). Like our method, the predictions by these two groups are at the residue level (i.e. whether a residue is DNA-contacting), instead of the patch or protein level. Like our method, Ahmad et al. also used PSI-blast sequence profiles and solvent accessibility as input to train neural networks, while Kuznetsov et al. used similar input to train a support vector machine predictor. However, there are important differences between these two methods and DISPLAR, resulting in the latter's much higher accuracy. Ahmad et al. reported coverage of 40% of actual DNA-contacting residues by their predictions, and from their reported data, a very low accuracy for positive prediction, at 13%, is obtained. The method of Kuznetsov et al. applied to our set of 264 proteins has a coverage of 60% of actual DNA-contacting residues and an accuracy of 56% for positive prediction. In comparison, DISPLAR test results show a coverage of 60% and an accuracy of 76%.

The high level of prediction accuracy suggests that DISPLAR can complement experimental techniques in characterizing protein–DNA interfaces. As an illustration, we applied the method to the prion protein, which has recently been shown to interact with DNA (16). The predicted DNA-binding site agrees well with NMR chemical shift perturbation data.

MATERIALS AND METHODS

Generation of the data set

All 1091 entries containing both protein chains and DNA chains were downloaded from the Protein Data Bank (May 2006 release) (http://www.rcsb.org/). To obtain a representative data set, sequence alignment between protein chains from different PDB entries was made by the PSI-blast program (10) with a default (10⁻³) e-value. When a match was identified, the ratio of the number of aligned identical residues to the total length of the query entry was calculated as the sequence identity. Redundant entries were removed manually at an identity threshold of 50%, with the entry having the highest resolution typically retained as representative. In addition, entries with all protein chains shorter than 40 residues were not included; such chains could not yield a position-specific scoring matrix by PSI-blast. At the end a representative set of 264 PDB entries was obtained (listed in Supplementary Table S1). Not included in this set were two nonhomologous entries (1i6h and 1w36) of protein complexes, each with more than a total of 2000 residues; these two entries were later used in an additional test of DISPLAR. Throughout this study, only protein chains constituting a single copy of a complete biologically significant multimer in each PDB entry were used. Such chain information was found from ‘REMARK 350 BIOMOLECULE’ of PDB files (or similar remarks in older PDB files). All protein chains with less than 40 residues were discarded, again because they could not yield a position-specific scoring matrix by PSI-blast.

Among the 264 PDB entries, 139 have a single protein chain and the remaining 125 have at least two chains. In all there are 428 protein chains. The total number of residues is 80 983. For each PDB entry, protein residues that contact DNA chains were found. A contact was defined as a pair of heavy atoms across the protein–DNA interface with a distance less than 5 Å. There are a total of 11 305 DNA-contacting, or, interface, residues.

Within the data set of 264 protein entries, 140 were found to not have any homologs. Of the remaining 124 entries, those having homologs with sequence identities in the brackets of <10, 10–20, 20–30, 30–40 and 40–50% numbered 6, 17, 38, 29 and 34, respectively.

We focused on protein surface residues. For this purpose, exposed surface areas of residues in each protein multimer were calculated using the DSSP program (17), and surface residues were taken to be the ones with exposed surface areas at more than 10% of maximum values (1). The ratio of exposed surface area and the maximal value will be referred to as the solvent accessibility for each residue. With the threshold of 10% solvent accessibility, 56 093 were classified as surface residues; among these, 10 062 were interface residues. The percentage of interface residues among surface residues is 18%. The 10 062 interface residues will be collectively referred to as the interface group; the remaining 46 031 non-interface surface residues will be referred to as the non-interface group.

Statistics of interface and non-interface surface residues

Residues in the interface and non-interface groups were separately collected according to amino acid types. From these the percentages of the 20 types of amino acids in the interface and non-interface groups were calculated. For each type of amino acid in either the interface or non-interface group, the average solvent accessibility was calculated.

As already alluded to, sequence profiles were obtained as the position-specific scoring matrix produced by PSI-blast (10). The search was limited to three rounds with the default e-value threshold (10⁻³). The database consisted of 3 625 149 non-redundant protein sequences (May 2006 release of NCBI nr at ftp://ftp.ncbi.nlm.nih.gov/blast/db/). The substitution matrix was BLOSUM62 (18). The position-specific scoring matrix for each query sequence has Q × A elements, where Q is the length of the query sequence and A is the size (i.e. 20) of the amino acid alphabet. If position q (=1 to Q) of the query sequence is occupied by amino acid type a (=1 to A), then sequence conservation at this position was measured by the (q, a) element of the scoring matrix. The higher this element, the less frequent the query amino acid's substitution in the multiple sequence alignment and hence the more conserved the amino acid for the particular position. For type a amino acid, the conservation score was taken as the average of the (q, a) elements over query positions which were occupied by type a amino acid and were either in the interface or non-interface group.

Neural network architecture

DISPLAR was largely adapted from the latest implementation of PPISP (2). Unless otherwise indicated, model parameters were inherited from that implementation. The predictor had two types of input: solvent accessibility and sequence profile. Prediction for each residue was based on the input variables of the residue itself plus 14 of its closest spatial neighbors. The solvent-accessibility input for each residue was averaged over the residue and six of its closest spatial neighbors. The sequence-profile input for each residue (say at position q) consisted of the 20 elements in the qth row of PSI-blast position-specific scoring matrix.

Two feed-forward, back-propagation neural networks were used consecutively as before. The first network had 15 × 21 input nodes, in which the first quantity was the window size, i.e. one for the residue under consideration plus 14 for its spatial neighbors, and the second quantity was the number of input variables for each residue in the window (one for solvent accessibility plus 20 for sequence profile). The first network was completed with a hidden layer of 150 nodes, and an output layer of two nodes (one for predicting interface and one for predicting non-interface). The input layer of the second network had 15 × 3 nodes, in which the first quantity was window size and the second quantity consisted of the two output values of the first network plus the solvent accessibility. The second network had 30 hidden nodes and again two output nodes. Training of the neural networks amounted to modifying the weight matrix, which was assigned random values initially.

Training, cross-training and test sets

In most previous prediction studies, the same proteins were used for selecting the optimal protocol and also for reporting the prediction performance (1,2,15,19,20). The dual use of the test proteins likely leads to inflated performance scores. To avoid this pitfall, for the purpose of reporting prediction performance, we randomly divided the data set of 264 protein entries into 10 groups. In turn, 8 groups were pooled for training; one of the two remaining groups was used for cross-training; and the last group was used for testing. Training resulted in a list of weight matrices (up to 20 rounds). Cross-training entailed selecting an optimal collection of weight matrices from different rounds for building consensus predictions (described below). Testing involved obtaining predictions for the group not used either in training or cross-training. With the three-tier division of the data set into 10 groups, each group was part of a training set 45 times, and used for cross-training 9 times and for testing also 9 times. For each residue, the majority outcome of the 9 test results was taken as the final prediction.

The three-tier division of the data set avoids the use of the same proteins for both optimizing prediction protocol and reporting performance scores. A priori it was not clear this division was the best use of the data set for making new predictions. Therefore we also investigated using the data set in the more traditional way (1,2), with 239 of the 264 entries constituting a single training set and the remaining 25 entries reserved for cross-training. For unequivocal identification, these training and cross-training sets are referred to as ‘two-tier.’ To lessen any possible cross-contamination between training and cross-training, in selecting the two-tier cross-training set, we set an upper bound of 30% sequence identity. That is, we ensured that all entries in the two-tier cross-training set either are nonhomologous or have no more than 30% sequence identities among themselves or with any entry in the training set. The two-tier cross-training set has a total of 5004 surface residues, of which 870 are DNA-contacting (Table 1).

Table 1.

Prediction results for the two-tier cross-training set

PDBa	Unbound PDB (RMSD Å)b	Surface residues	Ndc	Npr		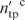Coverage (%)	Accuracy (%)
1brnL	1a2pC (0.4)	81	18	24	11 (3)	44	46
1cl8A,B	1qc9A (1.6)	320	53	47	39 (8)	58	83
1cqtA,I		132	48	33	30 (9)	44	91
1d5yA,B		405	33	64	43 (23)	61	67
1dh3A,C		104	27	42	42 (15)	100	100
1f5eP	2alcA (5.8)	54	21	32	29 (10)	90	91
1gd2E,F		119	32	44	43 (12)	97	98
1gm5A		525	32	41	40 (14)	81	98
1gxpA,B	1qqiA (1.7–1.8)	152	44	50	41 (8)	75	82
1imhC,D		393	32	44	26 (13)	41	59
1l1mA,B	1lqc (1.8–2.2)	110	57	79	73 (19)	95	92
1leiA,B	1iknA,C (16.3)	413	39	48	34 (16)	46	71
1m3qA	1ko9A (0.9)	199	25	15	14 (2)	48	93
1mowA		176	71	49	47 (12)	49	96
1ornA	2abk (2.4)	149	27	27	26 (5)	78	96
1r7mA		150	53	79	69 (22)	89	87
1rfiB	1qzqA (0.3)	241	14	33	14 (6)	57	42
1s40A		133	33	15	12 (2)	30	80
1sfuA,B		115	17	18	17 (7)	59	94
1u1qA	1l3kA (2.0)	137	48	31	30 (9)	44	97
1xyiA	1xx8A (2.4)	56	20	13	13 (1)	60	100
1zrfA,B	1g6nA,B (2.0)	292	43	44	41 (8)	77	93
1ztwA	1mml (1.6)	181	8	6	4 (1)	38	67
1zziA	1zzkA (1.3)	67	19	15	12 (5)	37	80
2aq4A		300	56	62	54 (18)	64	87
All		5004	870	955	804 (248)	63.9	84.2

^aFor each entry, the PDB code is followed by the chains that make up the DNA-binding protein multimer.

^bC_α RMSD were obtained by using the Dali server (http://www.ebi.ac.uk/DaliLite/). In three cases the bound structures (1cl8, 1gxp and 1l1m) are homodimers, but the unbound structures (1qc9, 1qqi and 1lqc) have only one chain. The RMSD of the unbound monomer against both subunits of the bound homodimer are listed. In reporting predictions using the unbound structures for these three proteins, both true and false positives were multiplied by two in order to make a fair comparison with predictions using bound structures. The sequence identity between 1orn and 2abk is only 45%; in all other cases the aligned sequences of bound proteins and their unbound counterparts have perfect or almost perfect identity.

^cThe number in parentheses lists − n_tp, i.e. the number of predictions that are considered true positives because they are among the four nearest neighbors of actual DNA-contacting residues.

Trimming of non-interface residues

There is an imbalance of interface and non-interface residues (the former accounts for just 18% of all surface residues in our data set of 264 proteins), randomly trimming some of the non-interface residues in the training process may improve accuracy (2,15). Training was carried out without and with one-third trimming of non-interface residues. Both sets of results were used to build consensus predictions (described next).

Consensus prediction from different neural-network weight matrices

Either with or without non-interface trimming, different rounds of neural network training result in different coverage and accuracy. Typically, the number of DNA-contacting predictions would initially increase with the increase in the round of training, leading to increasing coverage but decreasing accuracy; excessive training then leads to decrease in coverage. Our last implementation of PPISP (2) suggested that taking the consensus of positive predictions from different weight matrices may enhance accuracy at a given coverage. This approach was taken here.

The consensus approach consisted of two steps: (1) clustering of all positive predictions using different weight matrices, and (2) selecting a cluster or clusters as the final predictions. In the first step, each positively-predicted residue was assigned a consensus score, defined as the number of times positive predictions were made by the different weight matrices. These residues were then sorted according to consensus score. Starting with the batch having the highest consensus score, residues were clustered if they were among the 19 nearest neighbors of each other. Then the next batch of residues with the second highest consensus score was used to grow the clusters and add new clusters. The process was continued until all the positive predictions were clustered. When a cluster was composed of predictions from different batches, the highest consensus score among all predictions within the cluster was assigned to the cluster. For later reference the maximum consensus score among all clusters is denoted as σ_max. The number of predictions in a cluster is referred to as the cluster size.

In the second step, clusters were selected according to consensus score and cluster size. First of all, clusters were eliminated if their consensus scores were less than σ_max − 5. The largest size (s_max) of the remaining clusters was then found. All clusters with the maximum consensus score were automatically retained. Clusters with consensus scores between σ_max − 5 and σ_max − 1 were then eliminated if their sizes were less than either 4 or s_max − 4.

Assessment of predictions

The performance of DISPLAR was assessed by coverage and accuracy. If N_pr residues are predicted to be DNA-contacting, of which n_tp are true positives (i.e. among N_dc actual DNA-contacting residues) and the remaining n_fp are false positives, then coverage is n_tp/N_dc. For defining accuracy, we loosened the criterion of ‘true positive’ by counting as positive four nearest neighbors of the N_dc actual DNA-contacting residues. If the number of true positives using this loose criterion is , then accuray is .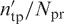

Optimal collection of weight matrices

We attempted to exhaustively search for the optimal collection of weight matrices. This was done in two stages. The first stage involved only training without non-interface trimming. All possible combinations of weight matrices from the first round to the round in which coverage reached maximum (as reported on the cross-training set) were applied to the crossing-training set. Among those with coverage above a threshold, the combination of weight matrices with the highest accuracy was selected. There were three possible coverage thresholds. The highest was 58%; when prediction did not reach this coverage, the threshold was successively lowered to 50 and 40%.

In the second stage, the selected list of weight matrices from the first stage was added to all possible combinations of weight matrices of training with one-third non-interface trimming, again from the beginning round to the round in which coverage reached maximum. Applied to the cross-training set, the combination of weight matrices with the highest coverage among those with accuracies within 1 or 3 percentage points of the highest accuracy was selected as the final collection of weight matrices.

The same two-stage optimization procedure was used for both the three-tier and two-tier divisions of the data set. The only difference was in the final collection of weight matrices, with the three-percentage-point accuracy window for the former and the one-percentage-point accuracy window for the latter. The optimal collection for the two-tier cross-training set was composed of weight matrices from rounds 3 and 13 of training without non-interface trimming and rounds 5 and 6 of training with one-third non-interface trimming.

RESULTS AND DISCUSSION

Characteristics of DNA-contacting residues

As noted in the Introduction, a number of properties distinguishing DNA-contacting residues from non-contacting residues on proteins have been reported in previous studies. As such distinctions form the basis of DISPLAR, the database for constructing the prediction method was analyzed to find the level of contrast between interface and non-interface residues.

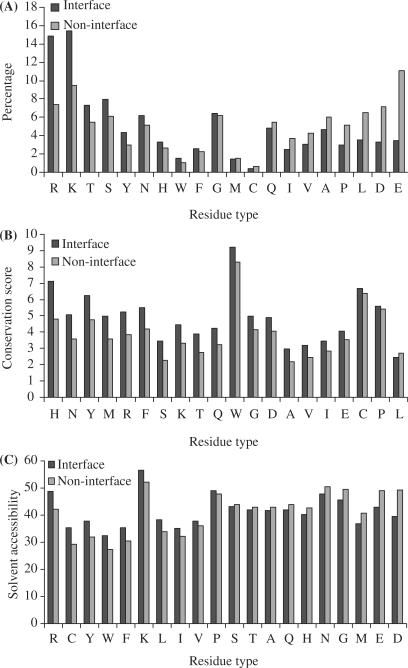
Figure 1A displays the distributions of the 20 types of amino acids in the interface and non-interface groups. It is clear that, in the interface group, positively charged Arg and Lys residues are enriched whereas negatively charged Asp and Glu are depleted. Together Arg and Lys account for 30.3% of the interface group, relative to 16.9% in the non-interface group. Asp and Glu account for only 6.8% of the interface group, relative to 18.2% in the non-interface group. Residues with polar side chains (Thr, Ser, Tyr and Asn) are also relatively enriched in the interface group, perhaps reflecting their hydrogen-bonding ability. In contrast, residues with nonpolar side chains (Leu, Ala, Val and Ile) are diluted in the interface group. The conservation scores, calculated from the PSI-blast position specific scoring matrix, for the 20 types of amino acids are shown in Figure 1B. Except for Leu, all amino acids in the interface group show a higher conservation score than in the non-interface group.

Figure 1.

Comparison between DNA-contacting surface residues and non-contacting surface residues. A Percentages of the 20 types of amino acids in the interface and non-interface groups. The abscissa is in descending order of the difference between the two groups. B Conservation scores in the interface and non-interface groups for the 20 types of amino acids, in descending order of the difference. C Solvent accessibilities in the interface and non-interface groups for the 20 types of amino acids, in descending order of the difference. Results were obtained from analysis of 56 093 surface residues in the data set of 264 representative DNA-binding proteins.

The contrast in solvent accessibility between the interface and non-interface groups also shows an interesting pattern (Figure 1C). The strongest conclusion that can be made is that Arg and Lys are more exposed in the interface group than in the non-interface group, whereas for Asp and Glu the opposite is true. The positively charged residues in the interface group presumably are poised for interacting with the DNA, while their counterparts in the non-interface have to contend with neighboring atoms on the same proteins. Interactions with the neighboring atoms likely lower the solvent accessibility in the non-interface group. The negatively charged residues in the interface group perhaps tend to minimize their contact with the DNA, thereby reducing their solvent accessibility.

Compared to similar statistical analysis for protein–protein interfaces (1,2), the contrasts between the interface and non-interface groups shown here appear to be significantly stronger and better correlated among the three different measures. The hope is then that the neural network approach will work even better for DNA-binding site prediction.

Overall assessment of predictions

With the three-tier division of the data set, the accuracies of the 10 test sets averaged 76.4%, with a standard deviation of 4.7%; the corresponding coverages averaged 60.1%, with a standard deviation of 5.3%. The variations of accuracy and coverage were partly related to their anticorrelation: higher accuracy corresponded to lower coverage.

The test-set results were regrouped according to homology levels of the protein entries. The 140 entries without homologs had an accuracy of 73.7% and coverage of 51.3%. In comparison, protein entries with homologs had higher accuracy, averaging 79.7%, and higher coverage, averaging 71.6%, among identity brackets of 10–20, 20–30, 30–40 and 40–50%. Variations of accuracy and coverage among identity levels fell within the standard deviations. The insensitivity to identity level suggests that the better predictions were not due to homology between test protein and training set per se. Instead it points to benefits from alignments with other DNA-binding proteins in the generation of PSI-blast sequence profiles. Nevertheless it is quite encouraging that DISPLAR yielded prediction accuracy over 70% at a coverage of over 50% for DNA-binding proteins without other homologs in the PDB.

We can now list a number of important differences between DISPLAR and the method of Ahmad et al. (6) [these authors have recently adapted their method for predicting DNA-binding sites from protein sequence only (21); such predictions were also done in two other studies (19,20)]. We eliminated buried residues from the data set. They included only two sequential neighbors whereas we included 14 spatial neighbors. We added a second neural network. Our method benefited from a much more exhaustive training set and a much more exhaustive sequence database for generating sequence profiles. Another technical reason for the poor performance of their method is that they used a 3.5-Å cutoff for defining DNA-contacting whereas we used 5 Å. The shorter cutoff distance leads to an excessively small fraction (∼6.5%) of interface residues among the data set. Such a small interface fraction makes it trivial to predict non-interface residues and leads to a tendency for over-predicting interface residues to ensure a reasonable coverage (Ahmad et al.'s positive interface predictions were three times the actual interface residues). The over-prediction was masked in their study because they chose to include negative predictions in accuracy assessment. In our opinion, only positive interface predictions are meaningful for accuracy assessment, since the goal is to identify DNA-binding sites. This point is especially important because of the imbalance between interface and non-interface residues.

An obvious difference between DISPLAR and the method of Kuznetsov et al. (15) is the use of neural networks versus support vector machine (SVM). In implementing the predecessor of DISPLAR, i.e. PPISP, we compared neural network and SVM predictions and did not find the latter to be better (2), even though in another study we found the two methods to be competitive in predicting solvent accessibility (22). The more substantive difference between DISPLAR and the method of Kuznetsov et al. lies in the use of structural information. As noted, the list of 14 spatial neighbors is coded in DISPLAR. In contrast, Kuznetsov et al. used six sequential neighbors and included information of spatial neighbors in the form of occurrence frequencies for the 20 types of amino acids within a 12-Å sphere around each residue. This use of spatial information appears to have limited value, improving accuracy by just a few percentage points (15). Kuznetsov et al. has provided their method in a web server (http://lcg.rit.albany.edu/dp-bind/). Applying their method on our data set of 264 protein entries, the coverage and accuracy (calculated in the same way as for our predictions) are found to be 60 and 56%, respectively. At the same coverage of 60%, the gap of 20 percentage points from our average prediction accuracy is over five times the latter's standard deviation, thus clearly demonstrating better performance of our method.

Predictions for the two-tier cross-training set

To help resolve whether the three-tier division or the two-tier division was a better use of the data set, test results and cross-training results from the three-tier training were gathered for the two-tier cross-training set of 25 protein entries. The accuracy and coverage of the test results were 64.7 and 79.6%, respectively. The cross-training results showed only slight increases in accuracy and coverage, at 64.8 and 80.2%, respectively. In comparison, the cross-training resulting from the two-tier training had accuracy and coverage of 63.9 and 84.2%, respectively (Table 1). While the difference in accuracy of 4% is within the standard deviation (4.7%) found from the three-tier test sets, other comparisons also consistently showed modestly better performance for the two-tier training. These included interface predictions for the prion protein and two large DNA-binding proteins and classification of proteins into DNA binding and non-binding. We therefore concluded that the two-tier training was superior and from here on, results from the two-tier training are reported.

We also used the two-tier cross-training set to investigate contributing factors to the performance of DISPLAR. One such factor is consensus prediction, based on the weight matrices from rounds 3 and 13 of training without non-interface trimming and rounds 5 and 6 of training with one-third non-interface trimming. Without non-interface trimming, the highest coverage was obtained in round 14; that coverage was 58.5% and the corresponding accuracy was 79.7%. With one-third non-interface trimming, the highest coverage was expectedly raised, to 64.0%, in round 12, but the corresponding accuracy was lowered, to 75.9%. The consensus prediction had statistically higher coverage than the best single training without non-interface trimming and statistically higher accuracy than the best single training with non-interface trimming.

For a multimeric protein, in generating the position-specific scoring matrix there are two alternatives. One is to use the individual chains of the protein as separate query sequences and then concatenate the resulting scoring matrices. The other is to concatenate the sequences first and then generate a single scoring matrix. We found the scoring matrix of the first alternative to be more robust. The contrast in sequence conservation between the interface and non-interface groups is stronger, and the predictions of interface residues are more accurate. Apparently using the separate chains as queries allows PSI-blast to focus the search on the chains, generating higher quality alignments. This method is what was used in generating the results reported in Table 1. A similar method was used for predicting protein–protein interfaces of a multimeric protein complex (2).

We also found the second neural network to be very useful. The idea of a second network was inherited from neural network predictions of protein secondary structures (23). The second network plays the role of reconciling conflicting predictions for (sequentially or spatially) neighboring residues. We found that in DISPLAR the second neural network indeed plays this role. The predictions from the first network tend to be scattered throughout the protein surface. After the second network, the predictions are more clustered, and the accuracy is much higher.

Detailed comparison of predicted and actual interface residues on four proteins

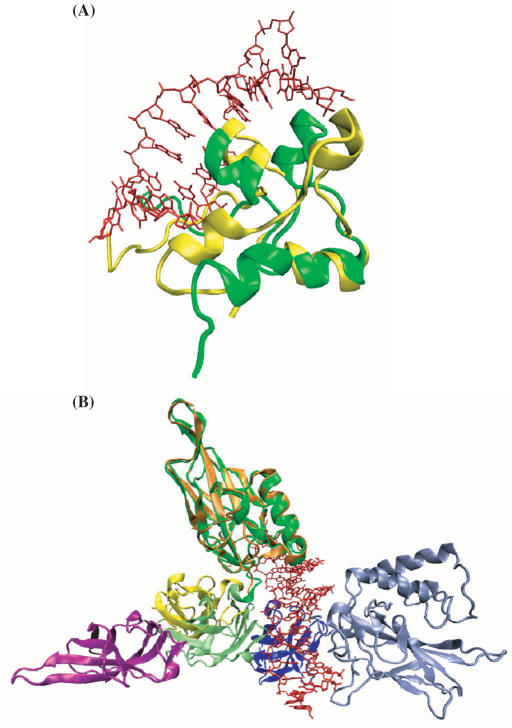
The accuracies and coverages of the 25 protein entries in the two-tier cross-training set are listed in Table 1. The coverages for individual entries range from 30% (for 1s40A) to 100% (for 1dh3A,C), while the accuracy is above 50% for all but two entries (1briL and 1rfiB). To illustrate the range of prediction quality, we now present detailed comparison between predicted and actual DNA-contacting residues for four proteins. They include a worst-case scenario (PDB 1brn), for which both the coverage and accuracy were low; a representative (PDB 1gd2) of the successful cases with both high coverage and high accuracy; and two (PDB 1s40 and 1u1q) of the more typical situations with medium coverage and high accuracy.

Figure 2A displays PDB 1brn, the complex between barnase and a tetradeoxynucleotide, d(CGAC) (24). Eight of the 18 DNA-contacting residues are among the 24 predicted interface residues. These are S38, I55-E59, F82 and R83, shown in blue in Figure 2A. Three other predicted residues (G61, T70 and G81) are spatial neighbors of the actual interface residues and are shown in cyan. The remaining 13 predictions (T16-H18, G65-R69, T79, S80, S92, Q97 and F106) were deemed incorrect and are shown in green. Barnase represents the worst-case scenario for the performance of DISPLAR, yet even here the predictions correctly line the DNA-binding site.

Figure 2.

Predicted DNA-contacting residues shown on the protein–DNA complexes. Predictions are shown in three different colors: actual DNA-contacting residues are in blue, their nearest neighbors are in cyan and incorrect predictions are in green. The rest of the protein surface is in yellow; the bound DNA is shown as red lines. (A) 1brn. (B) 1gd2. (C) 1s40. (D) 1u1q. In the last panel, there are two protein chains related by a 2-fold rotation, one on the left and one on the right. Within the left chain, the C and N-terminal RNA recognition motifs are at the top and bottom, respectively. The pictures here and those in Figures 4 and 6 are generated with PyMOL (http://www.pymol.org).

Pap1 is a basic region leucine zipper transcription factor that binds the consensus DNA sequence TTACGTAA. In the structure of the complex (PDB 1gd2; Figure 2B), 32 protein residues contact the DNA (25). DISPLAR performed very well in predicting the DNA-binding site. The 44 predicted residues include all but one of the 32 actual DNA-contacting residues (shown in blue in Figure 2B). Of the remaining 13 predictions, 12 are nearest neighbors of DNA-contacting residues (shown in cyan).

In the complex between the DNA-binding domain of yeast telomere-binding protein Cdc13 and a cognate telomeric single-stranded DNA (PDB 1s40; Figure 2C), 33 surface residues are found to contact the DNA (26). DISPLAR predicted only 15 DNA-contacting residues. Of these 10 (Y27, S38, D40, K41, A43, F44, S46, K81, I83 and N136) are actually in the protein–DNA interface, providing an outline of the ridge to which the DNA binds (Figure 2C). Of the remaining five predictions, two (R8 and F39) are close neighbors of DNA-contacting residues.

The UP1 region (residues 1–195) of heterogeneous ribonucleoprotein A1 contains two RNA recognition motifs, which have high affinity for both single-stranded RNA and the telomeric sequence d(TTAGGG)_n. In the complex between UP1 and d(TTAGGG)₂ (Figure 2D), two copies of the single-stranded DNA ligand bind to two copies of the protein molecule (27). The PDB file (1u1q) contains one copy each of the protein and the DNA. The second copy is related to the first by a 2-fold rotation. Each protein molecule binds to both copies of DNA, with the N-terminal RNA recognition motif interacting with the 5′ end of one DNA chain and the C-terminal RNA recognition motif interacting with the 3′ end of the other DNA chain. Together there are 48 surface residues contacting the DNA chains. DISPLAR predicted 31 DNA-contacting residues, 21 of which are actual DNA-contacting residues, covering both the N-terminal and C-terminal RNA recognition motifs (Figure 2D).

Prediction with unbound protein structures

Fourteen of the 25 proteins in the two-tier cross-training set have unbound structures deposited in the PDB (see Table 1). These provided an opportunity to apply DISPLAR in a real situation. At the outset it should be noted that DISPLAR and its predecessor PPISP by design only include input parameters that are not particularly sensitive to binding-induced conformational changes, and the preservation of prediction coverage and accuracy using unbound structures has been demonstrated for PPISP (1,2). Indeed, the solvent accessibility, the property that is most likely to be affected by conformational changes upon binding DNA, calculated using the 14 unbound structures show the same distinction between interface and non-interface residues as seen in Figure 1C. The coverage and accuracy of DISPLAR using bound structures of the 14 proteins were 64.2 and 82.1%, respectively, which are comparable to those found for the full cross-training set of 25 proteins. Using the unbound structures, the coverage and accuracy became 57.9 and 77.4%, respectively. Both performance parameters show statistically significant, but modest deterioration with the unbound structures.

For 12 of the 14 proteins, the root-mean square deviations (RMSD) of C_α atoms between bound and unbound structures are below 2.5 Å. The two exceptions are 1f5e/2alc and 1lei/1ikn, representing two different types of gross conformational changes. The former is a case of global distortion, with the overall RMSD of 5.8 Å distributed throughout the protein structure (Figure 3A). DISPLAR made very similar predictions using both structures. Using the bound structure 1f5e, 19 predictions are among actual DNA-contacting residues, 10 are their nearest neighbors, and three predictions are incorrect. With the unbound structure 2alc, these numbers changed to 19, 8 and 5, respectively.

Figure 3.

Two types of gross conformational changes upon DNA binding. (A) Global distortion from the unbound (PDB 2alc; in yellow) to the bound (PDB 1f5e; in green) structures. (B) Domain rearrangement from the unbound (PDB 1ikn) to the bound (PDB 1lei) structures. The N- and C-terminal domains of chain A in 1ikn are shown in orange and yellow; the C-terminal domain of chain C in 1ikn are shown in magenta. The N- and C-terminal domains of chain A in 1lei are shown in dark and light green; the N- and C-terminal domains of chain B in 1lei are shown in dark and light blue. The light green and dark blue domains in 1lei are rotated by ∼180° from the corresponding yellow and magenta domains in 1ikn when the dark green domain of 1lei and the orange domain of 1ikn are superimposed. The counterpart of the light blue domain of 1lei is missing in 1ikn. Bound DNA are shown as red lines in both panels. The pictures are generated with VMD (http://www.ks.uiuc.edu/Research/vmd/).

The second type of gross conformational changes is rearrangement between protein domains. The DNA-bound structure 1lei has two different chains (A and B), both consisting of two domains. Only three of the domains are present in the unbound structure 1ikn (missing the N-terminal domain of chain B; the C-terminal domain of chain B is labeled as chain C in 1ikn). The N-terminal domain of chain A (residues 19–188) in 1lei superimposes to its counterpart in 1ikn with a RMSD of 1.1 Å; the C-terminal domain of chain A (residues 191–291) and the C-terminal domain of chain B (residues 245–350) together in 1lei superimpose to their counterparts in 1ikn with a RMSD of 0.8 Å. However, these two portions experience a relative rotation of about 180° upon binding DNA (Figure 3B), with an overall RMSD of 16.3 Å for the three domains together. In the bound structure, all four domains contact DNA, with the N- and C-terminal domains of chain A contributing 21 and 4 residues and the N- and C-terminal domains of chain B contributing 9 and 5 residues, respectively, to the DNA-binding site. Correspondingly DISPLAR predicted 14, 9, 22 and 3 DNA-contacting residues for these four domains using the bound structure. With the N-terminal domain of chain B missing in the unbound structure, DISPLAR predicted 19 and 1 residue, respectively, for the N- and C-terminal domains of chain A, and nothing for the C-terminal domain of chain B. The results using the unbound structure are probably as good as can be expected based on those using the bound structure, demonstrating that DISPLAR also performs well when binding-induced domain rearrangements occur.

Specific versus non-specific DNA binding

In addition to specific DNA sequences, many proteins also bind to non-specific DNA. In the dataset of 264 proteins, there are structures for a few non-specific complexes. Three of the proteins, the λ Cro repressor, the lac repressor headpiece dimer and the DNA-adenine methyltransferase, have structures for both specific and non-specific complexes (28–32). The binding sites for specific and non-specific DNA largely overlap, with the same set of residues switching from electrostatic interactions with the DNA backbone in a non-specific complex to specific interactions with base pairs in a cognate DNA sequence. There are also many additional residues that interact with DNA in the specific complexes. The numbers of DNA-contacting surface residues are 18, 57 and 33 in the three specific complexes, compared to 12, 49 and 17 in the non-specific complexes. The numbers of interface residues that are in common in specific and non-specific complexes are 7, 38 and 5, respectively.

The lac repressor headpiece dimer is in the two-tier cross-training set. Using the unbound structure (PDB 1lqc), DISPLAR predicted mostly residues that contact DNA in both the specific and non-specific complexes. With the specific complex (PDB 1l1m) as target, the coverage was 77% and accuracy was 100%. Another protein in the two-tier cross-training set is Sac7d (PDB 1xyi and 1xx8 for the bound and unbound structures, respectively), which is a small chromatin protein that binds to DNA without any particular sequence preference (33,34). DISPLAR predictions using both the bound and the unbound structures had a coverage of >40% and an accuracy >90%. These values fall within the range of DISPLAR performance shown in Table 1.

Application to prion protein

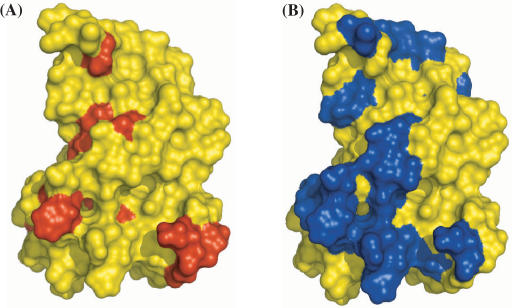
Lima et al. (16) recently showed that the prion protein binds DNA and used NMR chemical shift perturbation to characterize the binding interface. In the structured region (residues 125–228) of the protein, 15 residues are implicated for DNA binding as indicated by large changes in ¹H or ¹⁵N chemical shifts upon DNA binding. We applied DISPLAR to this protein (PDB 1b10) and obtained 23 predicted DNA-contacting residues. As shown in Figure 4, the two groups of residues largely overlap. This application demonstrates that DISPLAR is sufficiently accurate to complement experimental techniques in characterizing protein–DNA interfaces.

Figure 4.

Comparison of prion protein (PDB 1b10) residues (A) implicated by NMR chemical shift perturbation and (B) predicted by DISPLAR for DNA binding. Putative DNA-contacting residues are shown in red or blue.

Classification of DNA binding and non-binding proteins

An inherent assumption in using DISPLAR is that a protein is known to bind DNA. What would DISPLAR predict if it is applied to a non-binding protein? Can DISPLAR prediction results be used to predict whether a protein is a binder or non-binder? To answer these questions, we applied DISPLAR to the full set of 264 DNA-binding proteins and to a set of 250 non-binders collected by Stawiski et al. (4). For this purpose we used consensus predictions based on weight matrices from rounds 3 and 13 of training without non-interface trimming. This consensus approach resulted in less number of positive predictions than the one including weight matrices also from rounds 5 and 6 of training with non-interface trimming; we thought less positive predictions would be helpful for obtaining more balanced success rates for classifying both binders and non-binders.

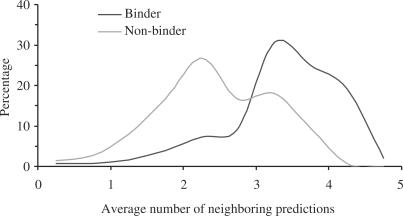
An immediate difference in DISPLAR results between the binders and non-binders is that only three of the 264 proteins in the former group had no positive predictions, but 100 of the 250 proteins in the latter group had no positive predictions. Of the proteins with positive predictions, the predicted residues also show very different characteristics. First, the binder group has a total of 80 983 residues, of which 56 093 are on the surface, and 11 050 (or 20%) were predicted as DNA-contacting. In contrast, the non-binder group has a total of 41 091 residues, of which 25 820 are on the surface, and only 2307 (or 9%) were predicted as DNA-contacting. Second, the distributions of the positive predictions among the 20 types of amino acids were different. The distribution of the binder group reflected that of the DNA-binding interface, whereas the distribution of the non-binder group appeared similar to the non-interface of DNA-binding proteins (see Figure 1A). The positive predictions of the binder group had an R² = 0.71 correlation with the interface surface residues in distribution (compared to R² = 0.43 for the non-binder group), while the positive predictions of the non-binder group had an R² = 0.60 correlation with the non-interface surface residues in distribution (compared to R² = 0.44 for the binder group). Third, more of the positive predictions were close neighbors of each other in the binder group than in the non-binder group. The difference could be quantified by calculating the average number of other predictions that were among the list of five closest neighbors for each protein. The average number of neighboring predictions thus defined ranged from 0 to 5. Figure 5 shows the distributions of the 261 binders and 150 non-binders within this range. Relative to the non-binder group, the average number for the binder group was significantly shifted to the high end of the range.

Figure 5.

The distributions of average numbers of neighboring predictions for protein binding and non-binding proteins.

These large differences between the two groups motivated us to develop a classifier using DISPLAR prediction results. First of all, a protein without any positive predictions was automatically classified as a non-binder. If positive predictions were obtained, then the results were processed and fed to a neural network for further classification. This neural network had 23 inputs for each protein, 20 of which were the percentages of the 20 types of amino acids among the positive predictions. The remaining three inputs were: the average number of neighboring predictions, the percentage of positive predictions among all surface residues and the percentage of surface residues among all residues. One hundred and forty-nine binders were randomly picked to mix with 149 of the non-binders to train the neural network. The non-binder that was left out was then tested. In all, only 42 of the non-binders were misclassified, giving a success rate of 83% for classifying non-binders. A final training was carried out with 149 binders and all the 150 non-binders. Tested on the remaining 112 binders, 15 were found to be misclassified. On account of the three binders that were misclassified due to the lack of positive DISPLAR predictions, the overall success rate for classifying binders was 86%. These success rates are competitive against classification methods that directly use structural data (4–6). That this level of success was achieved using prediction results provides another demonstration of the accuracy of DISPLAR.

Application to RNA-binding proteins

Many proteins bind to both RNA and DNA. It is thus interesting to see whether DISPLAR could also predict RNA-binding sites. We collected a representative set of 106 RNA-binding proteins with sequence identity less than 50%. DISPLAR had modest success on these proteins, with a coverage of 31.3% of the 3695 actual RNA-contacting residues and a prediction accuracy of 54.1%. Using the two-tier approach of DISPLAR, we randomly picked 86 of the RNA-binding proteins to train a neural network. When tested on the remaining 20 proteins (with less than 30% identity among themselves and with the training set), the coverage and accuracy improved to 57.1 and 63.3%, respectively. The accuracy is significantly less than the counterpart for DNA-binding proteins. The difference may be partly due to the smaller training set and partly due to higher diversity among RNA-binding proteins than among DNA-binding proteins.

Application to large protein–nucleic acid complexes

Most nucleic-acid-targeting proteins form multi-subunit complexes in their biological processes. Two of such large complexes, the RNA polymerase II elongation complex and the RecBCD–DNA complex, have their structures determined (PDB 1i6h and 1w36) (35,36). These two complexes, without any homologs in the data set of 264 protein entries, were not included in the development of DISPLAR partly because of the concern that the scarcity of large complexes would not allow for accurate predictions on them and partly because of the thought that alternative approaches, such as one focusing on one subunit or one domain therein at a time, might be more suited.

Once DISPLAR was found to be quite accurate on the test sets, we became curious about its applicability to the two large protein–DNA complexes. The two complexes (1i6h and 1w36) have 10 and 3 protein subunits, respectively; we took each subunit as a separate test protein. The prediction of DNA-contacting residues appears very encouraging. Figure 6A displays the predicted DNA-contact residues of the RNA polymerase II elongation complex on the 1i6h structure. Out of a total of 2495 surface residues on the whole complex, 177 residues were predicted to contact DNA. The percentage of positive prediction, 7%, is substantially lower than the portion of DNA-contacting residues (18%) among surface residues in the database for constructing DISPLAR. Apparently DISPLAR was able to correctly avoid making positive predictions throughout the complex. Indeed, 146 of the 177 predictions are located on the three chains, A, B and E, that are known to contact DNA (a simple procedure was able to automatically filter out all the small numbers of isolated predictions located on chains C, H, I and J; hence these are not shown in Figure 6A). These predictions line the binding site for the DNA–RNA hybrid substrate, and also define the binding site for downstream DNA. The former 102 residues, shown in blue, cyan or green, cover 52% of the DNA-contacting residues at the substrate binding site of 1i6h with an accuracy of 66%; the latter 44 residues are shown in magenta (downstream DNA is not resolved in 1i6h).

Figure 6.

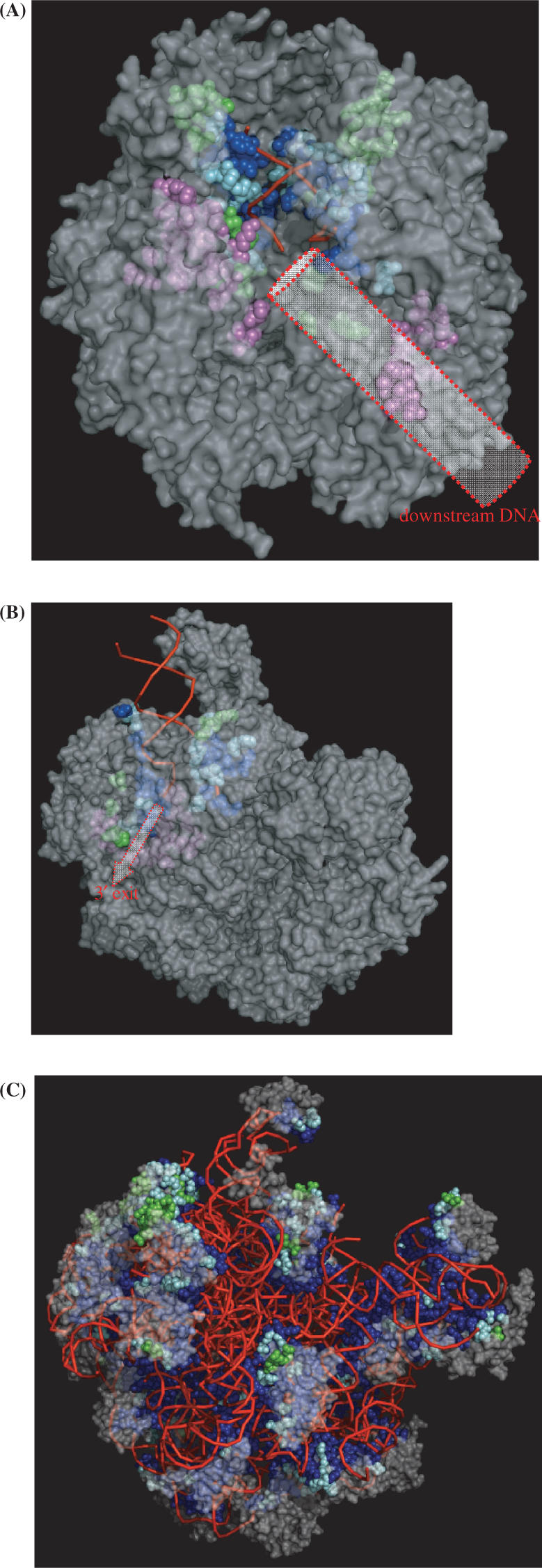
Predicted nucleic acid-contacting residues shown on the protein–nucleic acid complexes. Predicted residues are shown as spheres, with blue indicating actual DNA-contacting residues, cyan their nearest neighbors, and green incorrect predictions. The rest of the protein surface is in semi-transparent gray; the backbone trace of bound DNA is displayed by red lines. (A) RNA polymerase II elongation complex (PDB 1i6h). A cylinder is drawn to indicate downstream DNA; predicted residues in its binding site are shown in magenta. (B) RecBCD–DNA complex (PDB 1w36). An arrow is drawn to indicate the 3′ exit; predicted residues along the exit are shown in magenta. (C) Ribosome (PDB 1vqp). In (A) and (B) residues shown in magenta were not used in reporting prediction accuracy since at these sites DNA structures were not resolved.

Predictions for the RecBCD–DNA complex are shown in Figure 6B. Out of 1836 surface residues of the three protein chains, 50 and 20 residues, respectively, on chains B and C were predicted to contact DNA. Forty-six of these residues, shown in blue, cyan or green, cover 45% of the binding site for the duplex DNA and the first few bases of the split strands, with an accuracy of 85%. The remaining 24 predicted residues, shown in magenta, line one of two alternative exits for the 3′-terminated strand (36).

We also applied DISPLAR to the largest complex in the PDB, ribosome, which turned out to be a very easy target. Using training with RNA-binding proteins, we predicted 1560 of the of 2938 surface residues on the large ribosomal subunit of Haloarcula marismortui (37) to be RNA-contacting (Figure 6C). These cover 75% of the actual RNA-contacting residues (as found in PDB 1vqp) and have an accuracy of 95%.

Further studies

We have shown that protein residues making up a binding site for DNA have strong characteristics, such as enrichment of Arg and Lys and depletion of Asp and Glu, and based on these characteristics we have developed a method, DISPLAR, for predicting residues that form the DNA-binding site. Mutations of DNA-contacting residues, such as those on the tumor repressor protein P53 (38), may be directly involved in human diseases. DISPLAR can thus be used to predict such disease mutations. Perhaps most importantly, the predictions of DISPLAR can be used to guide the docking of a protein and its cognate DNA to build a structure for the complex (39). Such an approach has already been shown to be successful for protein–protein complexes (40) and seems promising for protein–DNA complexes.

The performance of DISPLAR can be further improved in several respects. Dividing the data set into subgroups with similar properties for separate training has been found to be useful in PPISP (2). Such a strategy may be adapted for protein–DNA complexes; the division could be based on clustering the interfaces through spatial relations of protein residues and DNA bases (41,42). Additional spatial features, such as the electrostatic potential surface (5,11–13) and the protein surface curvature (11), may also increase accuracy. Besides neural networks, the input data can be used to train other predictors such as support vector machine (15), and the results of different predictors can be pooled to give an ensemble prediction (22). These improvements will be explored in the future.

The prediction of DNA-binding sites on protein surfaces by DISPLAR complements work on prediction of protein-binding sites on DNA. A number of methods have been developed to predict DNA sequences recognized by transcription factors (TF), including position-specific weight matrix (43) and threading of DNA sequences through a TF–DNA complex either by a statistical potential (44,45) or by an atomistic energy function (7,46,47). Work on both the protein side and the DNA side will contribute to our understanding of their interactions.

The DISPLAR web server can be found at http://pipe.scs.fsu.edu/displar.html.

SUPPLEMENTARY DATA

Supplementary Data is available at NAR Online.