A Genomewide Single-Nucleotide–Polymorphism Panel for Mexican American Admixture Mapping

Abstract

For admixture mapping studies in Mexican Americans (MAM), we define a genomewide single-nucleotide–polymorphism (SNP) panel that can distinguish between chromosomal segments of Amerindian (AMI) or European (EUR) ancestry. These studies used genotypes for >400,000 SNPs, defined in EUR and both Pima and Mayan AMI, to define a set of ancestry-informative markers (AIMs). The use of two AMI populations was necessary to remove a subset of SNPs that distinguished genotypes of only one AMI subgroup from EUR genotypes. The AIMs set contained 8,144 SNPs separated by a minimum of 50 kb with only three intermarker intervals >1 Mb and had EUR/AMI F_ST values >0.30 (mean F_ST=0.48) and Mayan/Pima F_ST values <0.05 (mean F_ST<0.01). Analysis of a subset of these SNP AIMs suggested that this panel may also distinguish ancestry between EUR and other disparate AMI groups, including Quechuan from South America. We show, using realistic simulation parameters that are based on our analyses of MAM genotyping results, that this panel of SNP AIMs provides good power for detecting disease-associated chromosomal segments for genes with modest ethnicity risk ratios. A reduced set of 5,287 SNP AIMs captured almost the same admixture mapping information, but smaller SNP sets showed substantial drop-off in admixture mapping information and power. The results will enable studies of type 2 diabetes, rheumatoid arthritis, and other diseases among which epidemiological studies suggest differences in the distribution of ancestry-associated susceptibility.

Admixture mapping is a promising method for identifying chromosomal regions containing ancestry-linked traits when the distribution of the susceptibility genes is different among the founding populations.^1–4 Recent admixture mapping studies of African Americans (AFA) provide strong evidence of susceptibility regions for multiple sclerosis and prostate cancer associated with ancestry.^5,6 These investigations have underscored the potential value of applying this approach to diverse admixed populations and multiple common diseases. In particular, there is substantial interest in applying this method toward studies of type 2 diabetes mellitus (MIM #125853) and its complications^7,8 and autoimmune diseases, including rheumatoid arthritis (MIM #180300), in Amerindian (AMI) admixed populations. Epidemiological studies indicate that AMI populations have unusually high prevalences of these diseases compared with European populations (EUR).^9–11 The very large populations of Mexican Americans (MAM) and Mestizo Mexicans with large variance in AMI and EUR¹² contributions suggests that admixture mapping methods may be particularly useful for genetic analysis of these common complex diseases with high morbidity. The current study emerged from the need to develop these markers for the Family Investigation of Nephropathy and Diabetes (FIND), as described elsewhere.⁸

In contrast with studies of African and EUR admixed populations, the application of admixture mapping in MAM populations has been limited by the relatively small number of markers that have been identified that distinguish between AMI and EUR populations. Although several hundred markers identified elsewhere have allowed analysis of the population-genetics structures of AMI admixed populations,^12–17 admixture mapping requires several thousand ancestry-informative markers (AIMs) for genomewide definition of chromosomal segments. The number of AIMs necessary for admixture mapping is, in part, a function of the number of generations since admixture in the study population. Ascertainment of these admixture characteristics for MAM and other AMI admixed populations has likewise been hampered by the relative paucity of AIMs. Large numbers of AIMs are necessary to estimate this parameter from ancestry definition of chromosomal segments—that is, identification of ancestry recombination events that have occurred along each chromosome. The current study addresses the need for AIMs that are useful for admixture mapping in MAM and examines the parameters necessary for studying this population.

A potential problem in defining AIMs and applying admixture mapping is the inability to study the actual parental populations that contributed to the current admixed populations. Although previous studies have suggested that the differences in allele frequencies within different continental populations^{13,15,18–20} is relatively small compared with differences between continental populations, this issue remains a concern. In the current study, we have used Pima Indians, a northern Uto-Aztecan AMI group, as our initial representative of the AMI contribution to MAM. Importantly, we have also examined a second disparate AMI group, Mayan (a group that does not speak a Uto-Aztecan language), in our assessment of marker and population characteristics. Another problem is admixture within the presumptive parental population, a factor that deserves special consideration in indigenous AMI populations in the Americas, where many AMI groups may have a history of substantial EUR gene flow. This issue was addressed both by our careful selection of participants and by screening those subjects with small numbers of EUR/AMI/AFR AIMs, to identify and exclude clear population outliers from these studies (see the “Methods” section).

Recently, we reported a set of AIMs that provide extensive genomewide coverage for admixture mapping in AFA and that took advantage of HapMap genotyping results, including genotyping data from ∼3.5 million SNPs.¹⁹ This strategy could not be used in the present study, because large-scale analysis of SNP variations in AMI populations had not yet been performed. In the present work, we used two different strategies to screen and partially validate a set of AIMs for MAM admixture mapping: (1) a screen of the Illumina 100K gene-rich and 317K HapMap SNP–enriched SNP arrays and (2) a set of ∼20,000 SNPs selected for informativeness between East Asian and EUR populations. The latter strategy was suggested by our previous studies¹³ in which a 10-fold enrichment in the frequency of EUR/AMI SNP AIMs was achieved by selecting SNPs with East Asian/EUR F_ST>0.30, compared with random SNPs. Together, these strategies identified large numbers of SNP AIMs and provide a strong basis for admixture mapping studies in MAM.

Methods

Population Samples

DNA samples or genotyping results from 230 European Americans (EURNY), 274 EURs (EURNIHLN), 60 CEPH EURs (CEU), 72 Pima AMIs, 29 Mayan AMIs, 48 Quechuan AMIs, 24 Nahua AMIs, 24 MAM, and 90 East Asians (Japanese from Tokyo [JPT] and Han Chinese from Beijing [CHB]) were included in various aspects of this study. These populations were based on self-identified ethnic affiliation. The EURNY were from New York City; Pima individuals were from Arizona (samples provided by R.L.H. and W.C.K.); Mayan and Quechuan individuals were from Guatemala and Peru, respectively (samples provided by G.S. and J.B.); the Nahua were from central Mexico (samples donated by Dr. David Smith of the University of California–Davis [UC-Davis]), and the MAM were from California. (The admixture characteristics of this Mayan group is very different from the Mayan subjects in the Human Diversity Panel who have been reported to have European admixture.¹⁶) The CEU, JPT, and CHB were the HapMap panel genotypes,²¹ and the EURNIHLN genotypes were available from the National Institutes of Health (NIH) Laboratory of Neurogenetics at the Queue at Coriell Web site. All DNA and blood samples were obtained in accordance with protocols and informed-consent procedures approved by institutional review boards and were labeled with an anonymous code number or, in the case of the MAM, in accordance with approved procedures. The studied subjects were all healthy, and they were not first-degree relatives of each other, according to self-report. For the AMI groups, the DNA samples were chosen after initial screening of samples, to exclude individuals with large EUR admixture. This was performed using AIMs and criteria (to remove outliers) as described elsewhere.¹³ Of AMI samples, <10% were excluded on this basis. MAM were randomly chosen from a previous set of subjects,¹² with the exclusion of 2 individuals (of 94) with evidence of African contribution >10%.

Statistical Methods

F_ST was determined using Genetix software, which applies the Weir and Cockerham algorithm.²² Hardy-Weinberg equilibrium was examined using an exact test implemented in the FINETTI software, which can be accessed interactively (Institut fur Humangenetik). Population admixture proportions were determined using the Bayesian clustering algorithms developed by Pritchard and implemented in the program STRUCTURE (v. 2.1).^23,24 Individual admixture proportions and the number of generations since admixture were determined using STRUCTURE 2.1 and ADMIXMAP.

For STRUCTURE, each analysis was performed without any prior population assignment and was performed at least three times, with similar results, with use of >5,000 replicates and 2,000 burn-in cycles under the admixture model. We used the “infer α” option with a separate α estimated for each population (where α is the Dirichlet parameter for degree of admixture). Runs were performed under the λ=1 option, where λ parameterizes the allele-frequency prior and is based on the Dirichlet distribution of allele frequencies. The log likelihood of each analysis at varying numbers of population groups (k) is also estimated in the STRUCTURE analysis and, as expected, favored two population groups in the MAM. For analyses using different values of k (k=2, 3, 4, 5, or 6), at least 95% of the ancestry in the MAM population was derived from two clusters that corresponded to the AMI and EUR clusters. For ADMIXMAP analysis of the MAM genotypes, 23,000 iterations and 2,000 burn-in cycles were used under the random-mating model. The runs were performed under prior allele-frequency estimation with use of the results of the parental allele–frequency determinations. The number of generations was allowed to vary and thus was determined for each gamete by the Markov chain–Monte Carlo (MCMC) algorithm.

Admixture mapping of simulated data sets was performed using ADMIXMAP.¹ This program evaluates evidence of ancestry linkage by application of a score test to either case-only or case-control analyses. For case-only analysis, the null hypothesis is that the risk ratio between populations at each locus equals one. For case-control analysis, the null hypothesis is that there is no effect on locus ancestry, compared with individual admixture. For both analyses, the ancestral transitions are derived from application of the MCMC algorithm.

The simulations were performed by modification of a program developed elsewhere.⁴ Most runs were performed using 2,000 iterations and 400 burn-in cycles. Similar results were obtained using longer runs (23,000 iterations and 2,000 burn-in cycles), and monitoring of ergodic averages showed the sampler had run long enough for the posterior means to have been estimated accurately. A normalized score of 4.0 was found to approximate a conservative genomewide α level (∼0.01), on the basis of large numbers of simulations run under different conditions (i.e., with different ethnicity risk ratios [ERRs] and genomic intervals).

Genotyping and SNP Sets

Three different genotyping platforms and four different sets of SNPs were used in this study: (1) Illumina array platform and 100K gene set (Illumina), (2) Illumina array platform and 317K SNP set (HumanHap 300 BeadChip), (3) Perlegen Sciences photolithographic array and 20K SNPs selected for EUR/East Asian allele-frequency differences, and (4) TaqMan assays and 40 SNP AIMs. For the Illumina arrays, Perlegen Sciences arrays, and TaqMan assays, the genotyping was performed and genotypes assigned as described elsewhere.^12,25–27 For the third set of SNPs, the SNPs were chosen from the HapMap Project²¹ on the basis of both EUR/East Asian F_ST values and genomic position. This strategy was based on our previous studies showing enrichment for AMI/EUR AIMs by use of this methodology.¹³

Genotypes from 60 unrelated subjects (parents) from CEU and 90 unrelated East Asian subjects (JPT and CHB HapMap data sets) were available for ∼4 million SNPs in the combined phase 1 and phase 2 HapMap results. Initial examination of these sets identified >300,000 SNPs with an F_ST>0.25. High F_ST values favor selection of markers that are closer to fixation in one parental population. With use of the F_ST measurement, ∼30,000 SNPs were selected from this set of 300,000 SNPs by choosing a maximum of 4 SNPs in 500-kb windows, with a minimum distance of 50 kb between SNPs. Additional SNPs were added in regions with lower informativeness, SNPs were thinned in regions of high informativeness, and SNPs that failed assay-design algorithms for the Perlegen Sciences lithographic array platform were replaced with other informative SNPs, to complete the set of 20,000 SNPs.

For all genotyping, SNPs were excluded if the results did not meet either (1) 85% complete genotyping results in each population group or (2) Hardy-Weinberg equilibrium criterion in any of the parental populations (P<.005). These exclusion criteria reduced the total number of SNPs by <2%.

Selection of EUR/AMI SNP AIMs for MAM Admixture Mapping Panels

As described in the “Results” section, the SNP AIMs were chosen on the basis of three criteria: (1) EUR/combined AMI F_ST values >0.35, (2) EUR/Pima and EUR/Mayan F_ST values both >0.3, and (3) Pima/Mayan F_ST values <0.05. For one MAM admixture mapping panel, we optimized the choice of SNP AIMs from the 317K Illumina array that were separated by a minimum of 50 kb. This selection was performed by first choosing the SNP with the greatest F_ST value in each successive 100-kb bin and by then removing the SNP AIM with the lower F_ST when two SNPs were present within a 50-kb interval. The same procedure was performed with a combination of the three sets of SNP AIMs. These SNP AIMs are provided in our Rich Text Format (RTF) files RTF1, RTF2, RTF3, RTF4, and RTF5.

Genetic Map

For the present study, the analyses were performed using the deCODE²⁸ genetic maps. The position of each SNP was determined by interpolation with use of markers that were on the genetic map and for which an unambiguous physical map position was available in National Center for Biotechnology Information build 35. Any markers that were not in the same relative order in both the genetic and physical maps were omitted as anchors for the interpolation of the genetic positions of the SNPs.

SNP AIM Subsets

Smaller subsets of SNP AIMs examined in this study were derived from the total SNP AIM set (n=8,144) described above. A set of 4,072 SNPs was chosen simply by selecting every other SNP AIM in order of chromosomal position. A set of 5,287 SNPs enriched for information content were obtained by (1) allowing a maximum of three SNPs in each 1-cM segment of the deCODE map and (2) allowing only two SNPs in 1-cM segments of the deCODE map if there were SNPs in both flanking 1-cM segments, the sum of the F_ST values was >1.0, and the segment was not within 10 cM of a chromosome end (RTF5). In each case, our method removed the SNP with the smallest F_ST value. Finally, a set of 3,000 SNP AIMs was obtained by choosing the best SNP AIM in each 1-cM bin.

The set of 39 SNP AIMs used for the comparisons of multiple AMI groups by TaqMan assays included rs3768641, rs762656, rs7504, rs1426654, rs262838, rs9847748, rs730570, rs4478653, rs1880550, rs2380316, rs300152, rs6587216, rs7995033, rs9295009, rs883399, rs2065160, rs2384319, rs1638567, rs1266874, rs2165139, rs901304, rs17638989, rs814597, rs6086473, rs1475930, rs1648180, rs293553, rs1951936, rs2065982, rs1540979, rs734329, rs9937955, rs1931059, rs6601288, rs953786, rs2439522, rs1417999, rs1572396, and rs1418032.

Power Analysis

Power was assessed in MAM by simulations and ADMIXMAP analyses, by use of marker-allele frequencies and map positions (deCODE) for our current SNP sets. For each level of admixture information, the disease allele was placed in the middle of one of three different chromosomal regions that corresponded to the level of admixture information being examined (for 80%, chromosome 3 [138 cM], chromosome 5 [102 cM], and chromosome 14 [44 cM]; for 70%, chromosome 3 [80 cM], chromosome 4 [135 cM], and chromosome 13 [72 cM]; for 60%, chromosome 3 [152 cM], chromosome 6 [36 cM], and chromosome 14 [94 cM]). Simulations (>150 for each ERR) were performed using a 15-generation continuous-gene-flow (CGF) model and 50:50 EUR:AMI admixture.

Results

Screening of EUR/AMI SNP AIMs

To develop a genomewide panel of EUR/AMI SNP AIMs, the genotypes of EUR subjects and Pima AMI subjects were initially examined for three sets of SNPs: (1) gene-rich 100K Illumina array, (2) 317K Illumina array, and (3) a set of 20,000 SNPs enriched for large allele-frequency differences between EUR and East Asian populations. Genotypes were ascertained or available for the following subject sets: set 1, 192 EUR and 24 Pima; set 2, 222 EUR and 23 Pima; and set 3, 74 EUR and 72 Pima. A total of >400,000 unique SNPs that were not excluded by our quality assessment were analyzed for allele-frequency differences. For the combined sets, analysis of the EUR/Pima allele frequencies showed a total of 46,450 SNPs with F_ST>0.30 and 11,999 SNPs with F_ST>0.5.

To validate the identification of SNPs informative for EUR versus AMI ancestry, we performed a second screen, using DNAs from subjects of Mayan AMI ancestry (set 1, 16 subjects; set 2, 24 subjects; set 3, 29 subjects). Mayan subjects were chosen for this confirmation since they are part of another AMI group, distinct from Pima AMI, who are members of the larger Ito-Aztecan AMI grouping and whose ancestors are thought to have provided a large contribution to admixed populations in southern Mexico. The majority of SNPs with large EUR/Pima differences (F_ST>0.3) also had large EUR/Mayan allele-frequency differences (table 1). Interestingly, there were a substantial number of SNPs that showed large differences between the Mayan and Pima AMIs. For example, of the SNPs with EUR/Pima F_ST>0.5, 3.5% (425 of 12,001) showed a EUR/Mayan F_ST<0.1, and 7.8% (939 of 12,001) showed a EUR/Mayan F_ST<0.2. This was not due simply to relatively small numbers of AMI subjects, because, when two different independent sets of 24 Pima AMI were genotyped with the same SNPs, very few SNPs showed this phenomenon. Of 2,334 SNPs with EUR/Pima F_ST>0.5 in the first set of 24 Pima individuals, only 2 (0.1%) showed a EUR/Pima F_ST<0.1 and only 6 (0.3%) showed a EUR/Pima F_ST<0.2 in a second independent set of 24 Pima AMI. In addition, there was a substantially lower frequency of SNPs with disparate results in the two AMI groups in the SNPs selected for EUR/East Asian differences. For the latter group, 0.6% of SNPs with EUR/Pima F_ST values >0.5 showed EUR/Mayan F_ST<0.01.

Table 1. .

Summary of SNP-Screening Results for SNPs with EUR/Pima F_ST Values >0.3^[Note]

	No. of SNPs with EUR/Mayan FST Values
EUR/Pima FST	.0–.1	.1–.2	.2–.3	.3–.4	.4–.5	.5–.6	.6–.7	.7–.8	.8–.9	.9–1.0
.3–.4	2,981	3,716	6,158	6,040	2,083	699	215	41	0	0
.4–.5	909	1,419	2,175	3,411	3,023	1,082	388	102	9	0
.5–.6	316	403	665	1,179	1,771	1,524	636	165	23	1
.6–.7	97	104	177	329	566	1,008	810	251	60	8
.7–.8	12	7	28	68	129	274	452	356	108	11
.8–.9	0	0	2	8	10	23	73	129	148	36
.9–1.0	0	0	0	0	0	0	0	2	7	25

Note.— F_ST values were calculated using the Weir and Cockerham method.²²

We next examined whether either Pima or Mayan individuals alone could adequately represent the AMI contribution to MAM. Using 24 MAM typed in the 317K Illumina array, we compared results, using sets of >100 unlinked AIMs with the following different characteristics: (1) EUR/Pima and EUR/Mayan F_ST>0.35, (2) EUR/Pima F_ST>0.35 and EUR/Mayan F_ST<0.15, and (3) EUR/Mayan F_ST>0.35 and EUR/Pima F_ST<0.15. When STRUCTURE was used, the three sets of AIMs showed different results. When SNPs without differences between the two AMI groups were used, the EUR:AMI admixture ratio was 0.531:0.469, whereas a smaller AMI contribution was estimated using the sets showing inter-AMI differences: EUR:AMI=0.703:0.293 for group 2, and EUR:AMI=0.648:0.352 for group 3. From these studies, we hypothesize that SNP AIMs showing differences between these two AMI groups are likely to underestimate the AMI ancestry within the admixed MAM population. On the basis of these studies, we limited our further analyses to those AIMs with combined EUR/AMI F_ST>0.35, EUR/Pima F_ST>0.3, EUR/Mayan F_ST>0.3, and relatively small allele-frequency differences between Pima and Mayan AMI (F_ST<0.05), because inclusion of SNPs with large inter-AMI differences may lead to misleading ancestry information for some chromosomal segments in admixture mapping studies. A summary of the results for each of the individual SNPs (25,596 SNP AIMs) meeting these criteria is provided in RTF1.

Additional studies were performed to ascertain whether most SNPs selected using both Pima and Mayan screens would be useful in many EUR/AMI admixed populations. A subset of 39 AIMs with these characteristics were examined by genotyping an additional set of EUR, another Ito-Aztecan AMI group (Nahua), and a third disparate AMI group (Quechuan) from South America (Peru). Those AIMs with EUR/AMI F_ST >0.35 and Pima/Mayan F_ST<0.05 showed large EUR/Nahua, large EUR/Quechuan, and small intra-AMI F_ST values (table 2). For each SNP, the individual intra-AMI F_ST value was <10% of the EUR/AMI F_ST, which suggests that our screen with two disparate AMI groups is an effective strategy for ascertaining SNPs that may be useful for many AMI admixed populations.

Table 2. .

Comparison of F_ST Values for EUR/AMI AIMs^[Note]

	FST for
Population	EUR	Pima	Mayan	Nahua
Pima	.645
Mayan	.632	.015
Nahua	.585	.027	.019
Quechuan	.543	.039	.028	.027

Note.— Results are mean F_ST values for 39 SNP AIMs (see the “Methods” section) meeting initial criteria of EUR/Pima F_ST>0.3, EUR/Mayan F_ST>0.25, and Pima/Mayan F_ST<0.05. The assays were performed using a minimum of 48 EUR, Pima, and Quechuan subjects and a minimum of 24 Nahua subjects.

Estimation of Admixture Characteristics of MAM

The number of generations since admixture is a parameter necessary for power simulations in admixture mapping. We used a set of 24 MAM subjects genotyped using the 317K Illumina panel to provide an estimate of the number of generations since admixture. For these estimates, only the AIMs with EUR/AMI F_ST>0.30 and Pima/Mayan F_ST<0.05 were used (RTF2). In addition, we selected each SNP AIM to have a minimum 50-kb intermarker distance, to minimize the effects of LD in parental populations that may affect the probability of ancestry assignment (RTF3). Although this set of AIMs does not provide the level of genomewide coverage of the entire AIMs set (including two additional SNP screens), the density of markers was sufficient to enable extraction of the majority of ancestry information (presented below). Analyses with use of both STRUCTURE and ADMIXMAP were performed for each chromosome (table 3). The average number of generations varied for each chromosome, probably because of the small sample size, since the admixture mapping information was similar for each chromosome. The STRUCTURE and ADMIXMAP algorithms showed a mean (±SD) of 15.7±3.15 and 13.3±4.1 generations, respectively. The number of generations for each chromosome estimated using these two algorithms were highly correlated (r²=0.60; P=.0004, by paired t test). The difference between the STRUCTURE and ADMIXMAP estimations is probably due to the difference between these algorithms; STRUCTURE estimates the admixture generation for each individual, whereas ADMIXMAP estimates the number of generations for each gamete separately. On the basis of these results, we chose 15 generations as a reasonable estimation of the number of generations since admixture. If this is an overestimate, then the admixture mapping coverage would be greater; conversely, if this is an underestimate, then the coverage would be lower than that shown in our simulation studies.

Table 3. .

Estimation of the Number of Generations since Admixture for MAM^[Note]

	Mean No. (± SD)of Generations		SNPs Used
Chromosome	STRUCTURE	ADMIXMAP	No.	Size (cM)
1	13.2±1.1	12.3±5.3	530	274
2	17.2±1.4	16.8±7.3	597	263
3	14.6±1.2	15.2±6.0	487	221
4	15.9±1.6	14.3±6.5	401	205
5	16.8±1.7	12.8±5.1	417	206
6	18.8±1.8	17.6±9.1	436	189
7	13.9±1.4	14.7±7.5	345	188
8	18.3±1.8	18.7±9.6	370	167
9	13.5±1.4	14.5±7.5	290	160
10	18.0±1.9	16.1±7.2	337	180
11	24.0±2.5	25.2±11.7	325	153
12	13.8±1.4	11.7±6.1	310	172
13	14.3±1.8	11.5±4.3	244	129
14	13.0±1.7	8.4±3.9	238	125
15	16.0±2.1	14.0±7.4	226	134
16	11.7±1.5	9.8±5.3	193	136
17	18.9±3.5	9.5±4.0	170	136
18	16.0±2.6	11.2±6.0	189	122
19	9.8±1.8	5.4±2.9	136	110
20	12.1±1.8	8.1±3.9	168	112
21	16.4±3.2	11.5±6.3	97	77
22	19.1±2.9	13.0±5.6	106	71

Note.— Estimations were performed using the 6,897 Illumina 317K SNP AIMs (see RTF3) for 24 MAM subjects.

Assessment of Genomewide Information Content of EUR/AMI AIMs

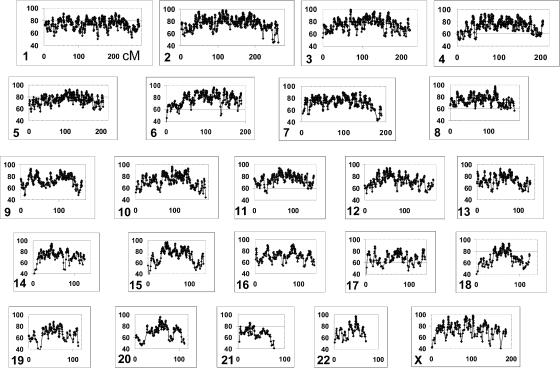
The ability of the EUR/AMI AIMs to extract admixture mapping information was assessed using ADMIXMAP.¹ ADMIXMAP determines the ability to assign ancestry along the chromosome in the admixed population with use of the ratio of the observed information about the ancestry risk ratio compared with the complete information that would be extracted if locus ancestry and parental-admixture proportions were observed directly. The extracted information in the admixed population is determined on the basis of the ancestry information content of the markers, the genetic map, and the empiric assessment of the admixture model (number of generations since admixture for each gamete). For estimation of the admixture mapping information, we used the mean extracted information between adjacent SNPs as the information content of each interval. The analyses are based on simulating the MAM subjects with use of 15 generations and a continuous-gene-flow model (see the “Methods” section). This estimated admixture mapping information was calculated for the entire set of 8,144 SNP AIMs (RTF4) that met our criteria (EUR/AMI F_ST>0.30 and Pima/Mayan F_ST<0.05) and for smaller subsets of AIMs, including those with only the 317K Illumina array SNPs (fig. 1 and table 4). The complete panel of 8,144 SNP AIMs extract >50% of the admixture information for >99% of the genome and >60% of the admixture information for >85% of the genome. With use of 5,287 SNPs selected for informativeness (RTF5), the coverage was only marginally decreased for these levels of extracted admixture information. A set of 6,897 SNP AIMs derived exclusively from the 317K Illumina SNPs also provided good levels of admixture mapping information but was marginally worse than the selected 5,287 SNP AIMs set (table 4). Smaller sets of SNP AIMs, with choice of either every other SNP from the total set or of the best SNP AIM in 1-cM bins (selected 3K set), showed larger decreases in admixture mapping information.

Figure 1. .

Admixture mapping distribution for each chromosome. The admixture mapping information (ordinate) is shown for each position on the deCODE sex-average map. The information was determined using the ADMIXMAP analysis of genotyping results with use of 8,144 SNP AIMs.

Table 4. .

Genomewide Admixture Mapping Information for SNP AIM Panels^[Note]

	Genomic Coverage by SNP AIM Panel(%)
Admixture Mapping Information (%)	Complete	Half	Selected 5K	Selected 3K	317K Illumina
80	19	3	6	0	12
70	58	18	44	10	45
60	88	53	84	57	79
50	99	84	99	93	96

Note.— Results are based on simulations with use of the actual EUR and AMI allele frequencies and deCODE genetics map positions. The simulations were performed using EUR:AMI 50:50 admixture proportions, 15 generations, and a CGF model. The Complete SNP AIM panel contains the largest set of AIMs (8,144 SNPs) with minimum intermarker distance of 50 kb that meet our AIMs criteria (see the “Screening of EUR/AMI SNP AIMs” section and RTF4). The Half set contains every other marker from the complete SNP AIM panel. The Selected 5K panel contains 5,287 SNPs that were selected as described in the “Methods” section, to optimize mapping information in a reduced SNP AIMs panel. Similarly, the Selected 3K panel was also chosen to optimize admixture mapping information in a smaller set of SNP AIMs. The 317K Illumina panel contains the largest set (6,897 SNPs) derived exclusively from the Illumina array with a minimum intermarker distance of 50 kb.

Analysis of Power with Use of Simulated Data Sets

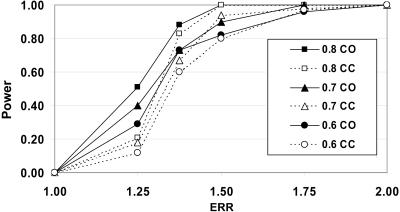
To examine the relative efficacy of admixture mapping with use of different densities of AIMs, we examined simulation models using different ERRs, where ERR is the ratio of the risk attributed to one parental population compared with the other parental population in the admixed population.⁴ For each ERR, the power was examined for different regions corresponding to the level of extracted admixture mapping information (see the “Methods” section). For each model, both case-only and case-control analyses were performed using the same case sample size (fig. 2). The power for the case-control analyses was modestly less than that for the case-only analyses. This result contrasts with previous results of similar admixture mapping–power analyses in AFA, where the power is substantially higher in case-only compared with case-control analyses. Also, in contrast to AFA admixture mapping,¹⁹ good power is still observed with 0.6 admixture mapping information at an ERR=1.5. These results, together with our analysis of admixture mapping information, suggest that the current SNP AIMs provide good power for admixture mapping.

Figure 2. .

Power for admixture mapping as a function of admixture mapping information. The power was determined from simulations with 800 cases and 800 controls and SNP sets with admixture information corresponding to the legend for the SNP set used (see the “Methods” section). The power curves were determined using the ADMIXMAP program and deCODE genetics map for either case only (CO) or case control (CC). The appropriate α level for these analyses was a normalized score of 4.0, based on extensive simulations. The result for each measurement point is based on a minimum of 50 separate simulations for each of three different genomic positions and analyses. The simulations were performed with the assumption of 15 generations, a continuous-gene-flow model, and 50:50 EUR:AMI admixture. The power simulations were performed under an additive model. Previous studies have shown similar power for additive, multiplicative, and even recessive models when the theoretic limits (ancestry for each segment known) are examined.²⁹

We also assessed the CIs that can be achieved with admixture mapping in MAM. The CI to which a susceptibility locus could be assigned was examined using a 2-SCORE fall-off in probability in the ADMIXMAP analysis. This was examined as a function of both ERR and admixture mapping information (table 5). The results show that the critical regions in MAM are substantially smaller than those observed using data from similar analyses of AFA subjects under admixture mapping parameters appropriate for this admixed population.¹⁹ This is true, even when the greater admixture mapping information that can be extracted in AFA is considered—for example, by comparison of 0.6 admixture mapping information in MAM (CI=6.0±3.3 cM for ERR=1.75, case only) and 0.8 admixture mapping information extraction in AFA (CI=15.1±4.6 for ERR=1.75, case only).

Table 5. .

Evaluation of CIs for Admixture Mapping with SNP AIMs^[Note]

	CI by Information Level(cM)
ERR, Population, and Analysis	80%	60%
1.75:
MAM:
Case-control	2.8±.9	3.8±1.8
Case only	2.4±.7	2.8±1.7
AFA:
Case-control	17.3±7.7	24.8±9.2
Case only	15.1±4.6	23.5±6.9
1.5:
MAM:
Case-control	5.1±1.5	7.0±2.8
Case only	4.8±1.6	6.0±3.3
AFA:
Case-control	18.8±7.3	22.9±4.6
Case only	19.3±7.1	28.4±10.3

Note.— The CIs were determined by the length in cM (±1 SD) for a 2-SCORE drop off in ADMIXMAP significance from the peak SCORE. For both MAM and AFA, the analyses were based on three different genomic intervals for each level of admixture mapping information (80% or 60%) and included >100 simulations. The MAM analyses were performed using the complete AIM SNP set in the current study (8,144 SNPs), and the AFA analyses were performed using the complete AFA SNP AIM set (4,222 SNPs), as described elsewhere.¹⁹

Discussion

The current study provides a set of 8,144 SNP AIMs that are useful for admixture mapping in EUR/AMI admixed populations. Our studies suggest that these genomewide SNP AIMs can differentiate EUR and AMI ancestry in many admixed population with predominant contributions from these two parental groups. The SNPs were selected on the basis of a standard measurement of interpopulation difference (F_ST) through use of SNPs with only small intrapopulation differences. For AMI, as presented in our “Results” section, only SNPs with F_ST<0.05 between Mayan and Pima AMI were used. For EUR, the differences between different EUR populations are very small (mean intrapopulation F_ST values <0.01 and >99% of SNPs with F_ST values <0.05), even when disparate EUR groups—for example, Italian versus Swedish—are examined³⁰ (M.F.S., unpublished data). Further studies will be necessary to confirm that these SNPs adequately inform all AMI admixture in MAM and to extend the application of these SNP AIMs to other AMI admixed populations, such as South American populations. Although our preliminary studies of another disparate AMI group (Quechuan from Peru) suggest that many of these AIMs will be applicable to such investigations, it should be emphasized that large differences in allele frequencies observed in several AMI populations^16,17 will require empirical testing of these AIMs in multiple AMI groups to determine more general applicability of this AIM set.

Recently, a study suggested that it may be preferable to perform admixture mapping using SNP panels for whole-genome association.³¹ This strategy has the benefit of providing additional information for linkage disequilibrium to disease traits that is not dependent on continental ancestry linkage. Although this may be a practical approach, depending on the cost of whole-genome panels (e.g., 317K or 500K SNP arrays) compared with that of selective panels of 5,000–10,000 SNPs, our results introduce a major caveat—that is, that special considerations are necessary to adjust for potential variation in parental-population allele frequencies in the AMI population. Thus, we suggest that such a strategy requires genotyping at least two disparate AMI groups and the use of only SNP AIMs that meet criteria similar to those used here—that is, EUR/AMI F_ST>0.30 and inter-AMI F_ST<0.05. SNPs with lower ratios of intercontinental information compared with intra-AMI differences may inhibit accurate ancestral definition of chromosomal segments. For the Illumina 317K set, the current study provides such a list of SNPs that can be used for admixture mapping (RTF2 and RTF3). However, the admixture mapping coverage is less than that obtained using the panel of SNP AIMs derived from multiple sources (table 4).

In screening for EUR/AMI AIMs, we observed a higher percentage of SNPs with large allele-frequency differences, using the 100K gene-rich panel (2.78% with F_ST>0.5), compared with the percentage when we used the Illumina 317K panel (2.34% F_ST>0.5) (P<.001). In addition, when we examined the 317K SNP results, the EUR/AMI F_ST values observed for SNPs within genes (F_ST=0.116) were significantly greater than those for SNPs within noncoding regions (F_ST=0.101) (P=2.8×10^-141, by t test). This result, similar to those of other studies, suggests that positive selection may be an important feature in shaping the genomes of different continental populations.^27,32–34 Further analysis did not show a difference between synonymous and nonsynonymous base-pair differences within genes (3.7% F_ST>0.5 for both groups). However, this lack of difference may reflect the relatively large regions that are part of selective sweeps. These data are generally consistent with previous studies that also did not show large differences between synonymous and nonsynonymous base changes, in contrast to genic versus nongenic SNPs.²⁷

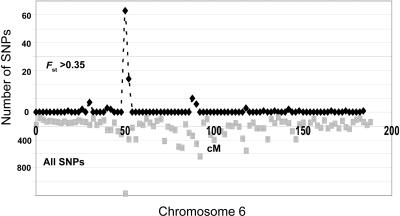
It is noteworthy that the proportion of SNPs with large frequency differences between Pima and Mayan AMIs are also greater in the 100K gene array than in the 317K SNP array. For SNPs with EUR/Pima F_ST>0.3, we observed a larger frequency of Pima/Mayan F_ST>0.3 in the 100K (2.6%) than in the 317K array (2.1%). Finally, we also observed a clustering of many of the SNPs with large frequency differences between Mayan and Pima AMIs. Notably, when 2-cM intervals were examined, the greatest number of SNPs with large Mayan/Pima differences was observed on chromosome 6, within the human leukocyte antigen (HLA) region (fig. 3). Whereas some of the clustering of these SNPs is due to the uneven frequency distribution of SNPs along the chromosome, the frequency of SNPs with high Pima/Mayan F_ST (97 of 1,547 within the HLA region) compared with the frequency of SNPs in the rest of chromosome 6 (42 of 19,171) was markedly different (P<.0001, by two-tailed χ² test). These preliminary observations suggest the potential value of further studies that address the possibility that positive selection is important in shaping differences between subcontinental populations and the possibility that such studies may suggest variations of biologic importance, as has been previously advanced for continental populations.^21,34

Figure 3. .

Clustering of SNPs showing large F_ST between Pima and Mayan AMIs on chromosome 6. The ordinate shows the number of markers with Pima/EUR F_ST>0.35 in each 2 cM (above abscissa) and the frequency of all SNPs (below abscissa). The abscissa shows the chromosome position in cM. The results are from analysis of genotypes with use of the 317K Illumina array. The same peak is also observed in the 100K gene-enriched array after removal of all SNPs overlapping with the 317K Illumina array. The peak could not be explained by the density of SNPs on the genetic map, which averaged 122 SNPs/cM on chromosome 6 and was 196 SNPs/cM in the HLA region.

The current study enables admixture mapping studies to be extended to MAM. This is likely to be particularly important in studies of diseases, such as type 2 diabetes and rheumatoid arthritis, that have a higher prevalence in AMI than in EUR populations.^9,10,35–37 This marker set will be used for mapping by admixture linkage disequilibrium (MALD) in the MAM MALD sample of the Family Investigation of Nephropathy and Diabetes, as described elsewhere.⁸ Admixed populations and admixture mapping can be particularly useful in studying complex diseases, since there is the potential to map and identify genes that are not sufficiently polymorphic in either parental population. In addition, admixture mapping is less sensitive to independent mutations of the same susceptibility gene than are association methods, since identification of chromosomal regions depends on ancestry association and is not deterred by multiple haplotypes in the parental population.

It is worth noting that, in comparison with AFA, the admixture ratios in MAM both in the United States and Mexico are much closer to an equal contribution of the two parental populations^12,13,38 and that the number of generations since admixture is substantially greater. This larger number of average generations since admixture leads to a requirement for a much larger set of AIMs for extracting admixture mapping information. Our simulations suggest that over double the number of AIMs are necessary to extract comparable levels of information, compared with our similar studies in AFA.¹⁹ However, for power, the near-equal admixture of parental populations compensates for the lower information content of AIMs, consistent with previous simulation studies.^2,29 Thus, the current study suggests that admixture mapping in MAM is potentially more powerful than in AFA. Similarly, although the current AIMs panel provides good admixture mapping information when the parental admixture proportions deviates from 50:50 (e.g., for the 70:30 EUR:AMI simulation, the AIMs panel shows 0.75 genomewide coverage compared with 0.88 for the 50:50 admixture proportion when 60% admixture mapping information is considered), the admixture mapping power will decrease in populations when there is a much larger contribution from only one parental population. This effect on power is greatest when the ERR is modest, the admixture ratios are more extreme, and the susceptibility gene derives from the parental population with the larger contribution.^2,29 In addition, it is notable that the increased number of generations decreases the length of the chromosomal region in which susceptibility genes of comparable ERRs can be located (table 5). Additional studies will be necessary to explore the power and ability of these methods to be applied to admixture populations with large contributions from three continental populations, such as for the Puerto Rican population.¹² In summary, the current study should provide an initial set of AIMs for extending admixture mapping studies to large populations with EUR and AMI admixture.