Patterns of Human Diversity, within and among Continents, Inferred from Biallelic DNA Polymorphisms

Abstract

Previous studies have reported that about 85% of human diversity at Short Tandem Repeat (STR) and Restriction Fragment Length Polymorphism (RFLP) autosomal loci is due to differences between individuals of the same population, whereas differences among continental groups account for only 10% of the overall genetic variance. These findings conflict with popular notions of distinct and relatively homogeneous human races, and may also call into question the apparent usefulness of ethnic classification in, for example, medical diagnostics. Here, we present new data on 21 Alu insertions in 32 populations. We analyze these data along with three other large, globally dispersed data sets consisting of apparently neutral biallelic nuclear markers, as well as with a β-globin data set possibly subject to selection. We confirm the previous results for the autosomal data, and find a higher diversity among continents for Y-chromosome loci. We also extend the analyses to address two questions: (1) whether differences between continental groups, although small, are nevertheless large enough to confidently assign individuals to their continent on the basis of their genotypes; (2) whether the observed genotypes naturally cluster into continental or population groups when the sample source location is ignored. Using a range of statistical methods, we show that classification errors are at best around 30% for autosomal biallelic polymorphisms and 27% for the Y chromosome. Two data sets suggest the existence of three and four major groups of genotypes worldwide, respectively, and the two groupings are inconsistent. These results suggest that, at random biallelic loci, there is little evidence, if any, of a clear subdivision of humans into biologically defined groups.

In various areas of applied genetics, it is customary to regard the human species as divided in distinct and objectively recognizable groups. Forensic scientists compare DNA profiles from the place of a crime with databases from the general population, usually grouped into broad racial categories (for instance, African–American, European–American, Asian, and Hispanic), to estimate the probability that an unrelated individual would have the identical DNA profile. The markers chosen for DNA profiling are considered to be essentially uniform across populations of the same category. Although the existence of problems with group definition has been acknowledged (e.g., Weir 2001), the fact that some individuals may not be easy to allocate to any such group is usually regarded as unimportant (National Research Council 1992; Lander and Budowle 1994; Morton 1994; Roeder 1994; Gill and Evett 1995). In clinical practice, a correlation of racial affiliation, as assessed from skin color, facial characteristics, hair texture, and so forth, with disease pathology and drug response is widely believed to exist. A PubMed search with the keywords “human races” (January 10, 2002) yielded 34,143 papers, including Benar et al. (2001), Estrada and Billett (2001), Hartz et al. (2001), Hoffman et al. (2001), and Shaw and Krause (2001).

In contrast, population studies have suggested that genetic variation is essentially continuous through space among humans, and have failed to identify a set of genetically distinct and internally homogeneous groups. Regardless of whether estimated at the protein (Lewontin 1972; Latter 1980), craniometric (Relethford 1994), or DNA (Barbujani et al. 1997, Jorde et al. 2000) level, individual differences between members of the same population have been reported to account for about 85% of the overall genetic diversity, and differences between populations within the same continent account for a further 5% to 10%. Only about 10% of variation can be assigned to differences between continental groups.

The existence of such different views in related areas of science has probably more than one cause, but a clearer picture of human genetic diversity is necessary to at least reduce the levels of disagreement. One open problem has to do with the exact amount of genetic diversity that can be attributed to the various levels of population subdivision. The figures mentioned earlier were estimated from populations that were well separated in space, and therefore they may exaggerate the between-group component of genetic variance. On the other hand, most of the markers studied are thought to be approximately neutral, which may have the opposite effect if between-group variation reflects adaptation to spatially variable factors such as climate. A second question is whether the apparently continuous distribution of genetic variation implies in practice that meaningful groups cannot be identified, as has been argued by Templeton (1999). In fact, genetic variances among groups, although small, are significantly greater than zero at several loci. That may mean that, by jointly considering many loci, distinct groups may emerge, even though those groups cannot be discriminated at the single-locus level.

We shall start by borrowing a definition from evolutionary and conservation genetics. In those fields, races or subspecies are defined as recognizable lineages within a species that have diverged genetically because mating barriers have separated them for a sufficiently long time (Templeton 1999; see also Pennock and Dimmick 1997). We shall ask if there is genetic evidence that the human species is subdivided in groups of that kind. To address that question, we consider fast-evolving DNA markers as less than optimal. Indeed, STR and mitochondrial polymorphisms, such as most of those considered by Barbujani et al. (1997) and Jorde et al. (2000), have high mutation rates, and hence their patterns of variation are likely to reflect relatively recent divergence. Evidence of long-term subdivision among populations, if any, is more likely to be found by analyzing slow-mutating DNA sites, typically biallelic polymorphisms, which presumably evolved only once (“unique-event polymorphisms”; see Markovtsova et al. 2000) in human history.

For that purpose, we typed 21 Alu insertion polymorphisms in population samples from five continents, and we analyzed published biallelic DNA polymorphism data at several other nuclear loci, both autosomal and Y linked. On the five data sets thus assembled, we estimated the components of variance that can be attributed to differences between individuals, between populations of the same continent, and between continental groups, and we compared our estimates with previously published values. In addition, we investigated with what degree of accuracy individuals can be attributed to their continent on the basis of their genotypes, and which are the most likely clusters of individuals that can be inferred from multilocus genotypes, regardless of their geographical provenance.

RESULTS AND DISCUSSION

Alu Insertion Frequencies

Table 1 reports the frequencies of the alternative alleles (presence or absence of the insertion, the latter representing the likely ancestral state; Watkins et al. 2001) at the 21 loci typed in this study. The standardized genetic variance, F_st, summarizes for each locus the global differentiation among populations of all continents. Values of F_st close to 15% are often observed in worldwide analyses of humans (Cavalli-Sforza et al. 1994). Hence, most Alu loci of this study display what can be considered “normal” levels of interpopulation diversity.

Table 1.

Alu Insertion Frequencies at 21 Alu Loci and Overall Standardized Genetic Variance Among Populations, F_st

Population	SB22777	SB18874	SB23467	HS2.25	HS2.43	HS3.23	HS4.14	HS4.32	HS4.59	HS4.65	HS4.69	HS4.75	COL3A1	TPA25	ACE	APO	FXIIIB	PV92	D1	B65	A25
Abazinian	0.05	0.18	0.33	0	0	0.65	0.04	0.21	0.14	0.03	0.04	1	0.25	0.29	0	NA	NA	0.04	0.10	0.78	0.03
African American	0.46	0.07	0.51	0.16	0.03	0.88	0.6	0.46	0.55	0.19	0.2	0.76	0.20	0.43	0.44	0.59	0.07	0.20	0.47	0.36	0.07
Alaskan Native	0.03	0.14	0.79	0.17	0.01	0.79	0.03	0.21	0.54	0.06	0	1	0.03	0.26	0.45	0.98	NA	0.29	0.34	0.49	0.05
Armenian	0.23	0.08	0.76	0.21	0.1	0.74	0.61	0.63	0.73	0.06	0	0.93	0.23	0.43	0.48	0.87	0.34	0.01	0.15	0.45	0.06
Azerbaijani	0.24	0.29	0.84	0.42	0.04	0.69	0.74	0.64	0.63	0	0	0.99	0.06	0.51	0.22	0.94	0.10	0.38	0.33	0.70	0
Bantu speakers	0.46	0	0.38	0.05	0	0.95	0.51	0.04	0.59	0.18	0.14	0.75	0.18	0.30	0.33	0.73	0	0.28	0.21	0.46	0.08
Bretons	0.24	0.28	0.9	0.19	0.1	0.89	0.34	0.61	0.76	0.01	0.21	1	0.03	0.32	0.28	0.90	0.16	0.27	0.47	0.51	0.17
Cajun	0.13	0.18	0.9	0.29	0.09	0.72	0.74	0.64	0.76	0.03	0.4	1	0	0.43	0.46	0.96	0.06	0.21	0.28	0.43	0.13
Cherkessian	0.20	0.18	0.43	0.29	0.02	0.74	0.72	0.61	0.63	0.02	0	0.79	0.47	0.39	0.39	0.93	0.44	0.17	0.17	0.65	0.05
Darginian	0.20	0.39	0.5	0.32	0	0.88	0.5	0.77	0.58	0.03	0	0.68	0.06	0.36	0.17	0.86	0.14	0.17	0.35	0.32	0.03
European American	0.31	0.32	0.95	0.34	0.10	0.77	0.83	0.60	0.54	0.02	0.28	0.99	0	0.54	0.5	0.93	0.06	0.23	0.21	0.58	0.14
French	0.32	0.31	0.92	0.37	0.09	0.89	0.78	0.55	0.78	0.01	0.31	1	0.01	0.60	0.41	0.95	0.29	0.16	0.39	0.49	0.09
Georgian	0.23	0.38	0.83	0.07	0.04	0.79	0.68	0.81	0.60	0.04	0	0.99	0.03	0.49	0.35	0.93	0.61	0.25	0.42	0.73	0.09
German	0.35	0.28	0.93	0.21	0.07	0.85	0.82	0.55	0.77	0.02	0.36	0.97	0.03	0.51	0.46	0.87	0.05	0.1	0.31	0.35	0.14
Greek Cypriot	0.25	0.39	0.90	0.17	0	0.72	0.64	0.69	0.72	0.04	0.25	0.97	0.02	0.51	0.33	0.95	0.18	0.15	0.15	0.53	0
Greenland Native	0.07	0.21	0.79	0.28	0.01	0.97	0.91	0.46	0.39	0.03	0	1	0.07	0.46	0.59	0.99	NA	0.71	0.48	0.31	0.18
Hispanic American	0.17	0.27	0.82	0.26	0.06	0.64	0.85	0.25	0.68	0.03	0.25	0.94	0.04	0.56	0.53	0.97	0.5	0.51	0.35	0.02	0.15
Hungarian	0.28	0.24	0.94	0.34	0	0.84	0.57	0.67	0.67	0.03	0.38	0.99	0.12	0.50	0.38	0.97	0	0.12	0.46	0.45	0.04
Ingushian	0.13	0.10	0.64	0.14	0.02	0.81	0.54	0.40	0.42	0	0.03	0.59	0.55	0.22	0.34	0.94	0	0.13	0	0.21	0.07
Kabardinian	0.14	0.17	0.50	0.21	0.05	0.74	0.57	0.60	0.64	0.02	0.02	1	0.14	0.29	0.27	0.93	0.14	0.15	0.13	0.43	0.11
Kung	0.38	0.05	0.06	0.08	0	0.95	0.09	0.24	0.64	0.07	0.10	0.36	0.04	0.14	0.13	0.99	0.07	0.17	0	0.48	0.23
Maya	0.11	0.06	0.48	0.23	0	0.61	0.74	0.27	0.67	0.02	0.36	0.98	0	0.64	0.67	0.96	0.88	0.7	0.35	0.29	0
Moluccas	0	0.04	0.55	0.10	0	0.59	0.52	0.28	0.62	0.18	0.09	0.86	0	0.55	0.56	0.75	0.78	0.69	0.2	0.25	0
Mvskoke	0.02	0.17	0.68	0.26	0.05	0.89	0.64	0.3	0.69	0.02	0	1	0.06	0.53	0.57	1	0.56	0.53	0.46	0.55	0.14
Nguni	0.29	0.02	0.31	0.02	0	0.91	0.45	0	0.77	0	0.04	0.73	0	0.20	0.36	0.60	0.09	0.18	0	0.34	0.27
Nusa Tenggarans	0	0.06	0.67	0.16	0	0.71	0.59	0.33	0.57	0.13	0.08	0.95	0	0.39	0.61	0.78	0.81	0.51	0.17	0.40	0.05
PNG Coastal	0.01	0.07	0.65	0.18	0.01	0.34	0.43	0.31	0.34	0.10	0.38	0.99	0	0.17	0.66	0.66	0.18	0.29	0.08	0.20	0.02
PNG Highland	0	0.03	0.63	0.16	0	0.23	0.26	0.34	0.45	0.03	0.39	1	0	0.14	0.75	0.66	0.01	0.18	0.01	0.13	0
Swiss	0.25	0.32	0.91	0.16	0.02	0.83	0.84	0.25	0.77	0.03	0.32	0.94	0.02	0.50	0.39	0.94	0.16	0.16	0.34	0.57	0.15
Syrians	0.10	0.35	0.82	0.05	0.07	0.55	0.70	0.52	0.74	0.06	0.32	0.96	0.04	0.51	0.40	0.93	0.28	0.18	0.29	0.31	0
Turk Cypriot	0.22	0.06	0.89	0.19	0.02	0.75	0.74	0.79	0.76	0.04	0.30	0.94	0	0.40	0.36	0.96	0.01	0.15	0.31	0.39	0.08
Yanomamo	0	0	0.19	NA	0	0.63	0.55	0.24	0.33	0	0	1	0	0.69	0.75	1	1	0.96	0.33	0.33	0
Fst	0.146	0.151	0.158	0.068	0.153	0.130	0.169	0.181	0.061	0.137	0.260	0.091	0.115	0.080	0.115	0.175	0.406	0.214	0.140	0.106	0.109

(NA) Not available. 

Genetic Differences among Continental Groups

For both Alu-insertion data sets (Alu8 and Alu21, comprising information, respectively, on 8 and 21 loci), an analysis of molecular variance, AMOVA (Excoffier et al. 1992) was run once for each locus, and once for the multilocus genotypes. The Y-chromosome (Y98, Y99 data sets) and β-globin (BGL data set) data were each subjected to independent runs of AMOVA using all the available sequence information. For most Alu loci, for the compound Alu genotypes, and for the BGL data set, around 80% of the overall genetic diversity is allocated to differences among members of the same sample (Table 2). About 10% is attributed to differences among populations within the same continent (less for the BGL data set, where most continents, however, were represented by only one population), and the rest, a little over 10%, to differences among continents. The exceptions are one Alu locus (FXIIIB) and the Y chromosome, which show a lower component of variance within populations (between 42 and 46%) and a higher component between continental groups (close to 40%). Even for these loci, the greatest fraction of genetic variance occurs within populations.

Table 2.

Components of Genetic Variance (%) at Three Levels of Population Subdivision

Locus	Between continents	Between populations within continents	Within populations
TPA	5.97	4.84	89.19
ACE	12.05	7.12	80.83
APO	7.26	13.77	78.97
FXIIB	38.17	14.97	46.86
PV92	18.51	16.22	65.27
D1	4.80	8.89	86.32
B65	1.53	8.24	90.23
A25	2.27	9.26	88.47
SB22777	13.27	6.70	80.03
SB18874	8.39	8.39	83.22
SB323467	15.54	19.32	65.14
HS2.25	6.29	7.29	86.42
HS2.43	1.31	5.44	93.25
HS3.23	19.05	4.27	76.68
HS4.14	6.22	17.18	76.60
HS4.32	11.90	12.47	75.63
HS4.59	3.90	5.71	90.39
HS4.65	4.10	5.71	90.19
HS4.69	8.81	22.80	68.39
HS4.75	20.76	16.91	62.33
COL3A1	−4.68	39.36	65.32
Alu8 overall	12.70	9.96	77.34
Alu21 overall	8.90	8.22	82.87
β-globin	17.80	2.80	79.39
Y98	38.99	14.71	46.30
Y99	40.11	17.39	42.50

The Alu8 data set is used for the first eight loci; the Alu21 data set is used for the remainder. 

In two previous Y-chromosome studies based, respectively, on a combination of SNP and STR markers, Hammer et al. (2001) and Jorde et al. (2000) estimated lower variances among continents and higher variances within populations. In Jorde et al.'s (2000) STR study, in particular, variances between continents were practically zero. The simplest explanation is that different mutational mechanisms generate diversity at biallelic sites and at STR loci. Because of the higher mutation rate of the latter (average 2.8 × 10^–3 per locus per generation; Kayser and Sajantila 2001) and of probable constraints to allele size (Deka et al. 1999), it seems that most populations tend to approach a common allelic distribution for those markers. Conversely, biallelic polymorphisms mutate more slowly (about 5 × 10^–7 per site per generation; Jobling et al. 1997), and therefore their distribution reflects more the effects of demographic history than those of mutation.

The genetic variances among continents inferred in this study from the Y-chromosome data sets are greater than those observed for autosomal markers. The same is true, to a lesser extent, of mtDNA, where the fraction of variance between continents, 12.5%, is still higher than for the nuclear genes of the same study (Seielstad et al. 1998). These results were expected under a model of neutral evolution, driven by genetic drift and gene flow. If selection is negligible, the genetic variance among populations (F_st) tends to reach an equilibrium value, which, in Wright's (1969) classical model, is inversely proportional to N, the population size, times m, the gene flow rate. We do not know whether our populations are at equilibrium, but N of mitochondrial and Y-chromosome loci is one-fourth that of autosomal loci, so that the impact of drift is greater on the former. Therefore, it seems that the genetic drift that has been going on since the (apparently recent and incomplete) separation of continental human groups has so far been able to generate appreciable differences only at uniparentally transmitted loci.

Inferring the Geographic Origin of a Genotype

To test the extent to which continents are associated with specific sets of alleles, we initially disregarded the geographic information. We took one genotype at a time, and attributed it to its most likely continent according to eight methods of discriminant analysis, three of them parametric and five nonparametric (listed in the caption to Table 3). Then we calculated the rate of misassignment for each method, that is, the percentage of individuals who were wrongly allocated (Table 3). Among nuclear loci, the worst results are obtained for the BGL data set: more than half of the genotypes are misclassified. The Alu data sets give better results, as would be anticipated for multilocus data. The NNET and LOG methods each give error rates of 38% and 32% for Alu8 and Alu21, whereas with the RM method, 37% and 30% of the genotypes, respectively, were misclassified.

Table 3.

Percentage of Misclassification in Discriminant Analysis by Data Set and Method Used

Data set	Parametric			NNET	Nonparametric			RM
LDA	LOG	QDAa	KER	1NN	3NN
Alu21	40	32	NA	38	37	32	36	30
Alu8	49	35	51	35	49	42	38	37
β-globin	58	63	65	52	58	52	53	50
Y98	79	71	70	27	61	27	27	40
Y99	83	81	73	27	43	27	27	37

^aThe QDA method could not be used for the Alu21 data set because of the insufficient number of individuals with the complete, 21-locus genotype in some samples.(LDA) Linear discriminant analysis; (LOG) logistic discriminant analysis; (QDA) quadratic discriminant analysis; (NNET) neural networks; (KER) nonparametric discriminant analysis with Gaussian kernel; (1NN and 3NN) nonparametric discriminant analysis with, respectively, 1 and 3 nearest neighbors; (RM) Rannala and Mountain (1997) method. 

For the Y-chromosome data sets, the parametric methods again perform poorly, with misclassification rates at least 70%. However, NNET, 1NN, and 3NN each give an error rate of 27%, better than the 40% obtained using the RM method and also better than the error rates obtained using the same methods for the multilocus data sets. Although only a single locus, the Y chromosome is relatively powerful for discrimination because its between-group variance is higher, as revealed by AMOVA (this study; Hammer et al. 2001) and by previous independent studies (Underhill et al. 2000).

Table 4 is an example of the so-called confusion matrix for the classification of individuals from the Alu8 data set using the method that gave the lowest rate of misclassification, NNET. The entry in row i and column j gives the number of individuals drawn from continent i that are classified into continent j (so that the diagonal entries correspond to correct classifications). Table 5 gives the same information for the Y99 data set, again using the method giving the most accurate results for that data set, 1NN. At the bottom of Table 5, Asia was further subdivided in two subregions, which caused an increase in the misclassification rate. Overall, the results indicate poor discrimination, with even the best method and data set leading to nearly 30% misclassification. Even our relatively large data sets do not suffice to allow accurate assignment of individuals into their continent.

Table 4.

Confusion Matrix from the NNET Discriminant Analysis of the Alu8 Data Set

Sample in	Assigned to
Africa	Europe	Asia	Americas	Australia	Total
Africa	28%	52%	13%	0%	7%	138
Europe	4%	72%	22%	0.4%	1.6%	457
Asia	2%	18%	73%	4%	3%	580
Americas	0%	6%	75%	19%	0%	89
Australia	13%	15%	21%	0%	51%	67
Total	81	517	627	42	64	1331

Each cell contains the fraction of individuals whose origin is in the row continent, who were allocated to the continent indicated by the column label; correct allocations are therefore on the main diagonal. Totals are numbers of individuals. 

Table 5.

Confusion Matrices from Two 1NN Discriminant Analyses of the Y99 Data Set

Sampled in	Assigned to
Africa	Europe	Asia	Americas	Australia	Total
Africa	90%	5%	4%	0%	0%	348
Europe	42%	5%	53%	0%	0%	175
Asia	3%	1%	95%	0%	0%	1168
Americas	5%	1%	41%	53%	0%	374
Australia	0%	0%	100%	0%	0%	133
Total	440	47	1506	205	0	2198

Sampled in	Assigned to
Africa	Europe	NC Asia	SE Asia	Australia	Americas	Total
Africa	90%	5%	3%	2%	0%	0%	348
Europe	42%	5%	51%	2%	0%	0%	175
NC Asia	2%	1%	75%	22%	0%	0%	801
SE Asia	6%	1%	20%	73%	0%	0%	367
Americas	5%	1%	41%	0%	0%	53%	374
Australia	0%	0%	31%	69%	0%	0%	133
Total	440	47	960	546	0	205	2198

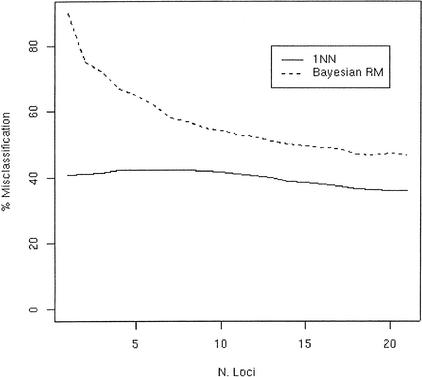
To test how the number of loci considered affects these results, we repeatedly (500 times) analyzed subsets of the Alu21 data set, consisting of increasing numbers of loci chosen at random from the 21 available. The rate of misclassification decreased rapidly at the very beginning, but then leveled off (Fig. 1), suggesting that the error rate will not become zero, even further increasing the number of loci. This supports the view that error rate reflects, in part, factors other than the limited number of loci considered, including genetic exchanges leading to extensive allele sharing among populations. In principle, these results might be explained by the presence of a few hybrid populations at the boundaries between continents, but that proves not to be the case. If one looks at the geographic origin of the misclassified individuals (Table 6 is an example), it is evident that many other populations contain genotypes or haplotypes that discriminant analysis classifies along with those of another continent. For the Y99 data set, there seems to be a tendency to misclassify individuals from populations at nearby latitudes. Seventy-four European haplotypes are wrongly allocated to Africa, and they are mostly Greeks and Italians. Conversely, among the 90 Europeans that are allocated to North-Central Asia, most are British, Russians, and Germans. In the Americas, most of the 152 individuals allocated to North-Central Asia come from Northern and Central America (Tanana, Cheyenne, Pima, Havasupay, and Pueblos), whereas the misclassification rate decreases as one moves southward. The results are less clear for the Alu data sets (data not given), where we could not recognize a clear pattern of misclassification. This could be due to factors such as the lower number of populations available, their spatial distribution, or the already discussed effect of population sizes. However, a crucial factor to consider is the absence of recombination for Y-chromosome markers, so that migrant Y chromosomes may convey evidence of their source population for many generations.

Figure 1.

Relationships between the misclassification rate of the discriminant analysis (Y axis) and the number of loci used for the discrimination (X axis), using two different methods and the Alu21 data set. The graphs represent averages over 500 independent replicates. (Broken line) 1NN, (solid line) RM with Bayesian approach. The loci were added sequentially by Montecarlo randomization, so that their order is not expected to affect the misclassification rate.

Table 6.

Origin of Misclassified Individuals, Y99 Data Set

Assigned to	Sampled ina	Detailed origin of the misclassified individualsa
Africa	42% Europe	19% British, 38% Germans, 49% Italians, 76% Greek, 17% Russians
NC Asia	51% Europe	78% British, 56% Germans, 41% Italians, 21% Greek, 73% Russians
NC Asia	20% SE Asia	7% Japanese, 9% Taiwanese, 12% S. Chinese, 25% Korean, 36% Indonesians, 3% S. Asian, 52% Indians
NC Asia	31% Australia	58% Australians, 11% PNG, 33% Melanesians
NC Asia	41% Americas	25% A. Eskimos, 45% I. Eskimos, 50% Tanana, 45% Navajos, 77% Cheyenne, 50% Havasupay, 58% Pima, 50% Pueblos, 20% Zapotecs, 18% Ngobe, 20% Wounan, 10% Mixtecs, 50% Wayus, 33% Chileans
SE Asia	22% NC Asia	37% Komi, 55% F. Nentsi, 73% T. Nentsi, 6% Buryats, 2% S. Eskimos, 41% M. Evenks, 4% Oroquens, 5% Yakuts, 8% Koriats, 34% Mongolians, 10% Altais, 93% Tibetans, 23% Kazaks, 7% Selkups
SE Asia	69% Australia	42% Australians, 89% PNG, 67% Melanesians

^aFigures are percentages of individuals misclassified over the continent's or the population's totals, respectively. 

Indeed, the greater differences among continents observed for Y-chromosome markers (all of them mapping on the nonrecombining portion of the chromosome) did not lead to a much better allocation of genotypes of unknown origin. Haplotypes are transmitted as a single unit, and can in principle be followed through time and place. On the other hand, though, each of those haplotypes can be regarded as one variant of a multiallelic locus, and the power of discriminant analysis increases with the number of independent loci considered (compare the Alu and Y-chromosome data sets in Table 3).

The low accuracy of discriminant analysis does not depend on a poor definition of the continental groups considered. In fact, the more groups are considered, the higher the misclassification rate. Compare, for example, the top and the bottom of Table 5; one-fifth of North-Central Asians were classified as South-Eastern Asians and vice versa, when these two groups were separately considered. At a subcontinental level, inferring the geographic origin of a person from her/his genotype becomes more complicated, and therefore it seems unlikely that classification errors would be reduced by choosing among a higher number of potential origins.

Most misclassified individuals were assigned to Europe and Asia in Table 4 (Alu8 data set), and to Africa and Asia in Table 5 (Y99 data set). Many individuals from Australia and the Americas were attributed to Asia, where the first settlers came from, and 13% (Table 4) of Australians, intriguingly, to Africa. These observations suggest that the distribution of misclassified individuals reflects, at least in part, past population movements. We are currently developing a formal model to infer past migrations from the results of discriminant analysis.

Inferring Population Structure from Genotypes

So far we have been trying to assign individuals to groups defined a priori on the basis of geography. An alternative is to identify groups a posteriori on the basis of genotypes, namely, to cluster genotypes until a certain number of genetically homogeneous groups is defined. The program STRUCTURE (Pritchard et al. 2000) infers the most likely number of such groups, and assigns individuals to each of them, on the basis of probabilities estimated from a set of independently transmitted loci. Because Y-chromosome markers are genetically linked, this approach was suitable to analyze only the Alu data sets.

The most likely number of groups, k, was estimated as three and four, respectively, for Alu8 and Alu21 (Table 7). All alternatives could be rejected with a high level of confidence. Individuals were then associated with posterior probabilities to belong to each of the previously identified groups, and were assigned to the most likely group (Table 8; had we chosen to attribute an individual to a group only when one of those posterior probabilities is higher than 50%, 287 genotypes of the Alu8 data set and 162 of the Alu22 database would have been unclassified). The results inferred from the two data sets differ markedly. Not only is the number of groups different, but also the geographical ranges of the groups do not overlap. For the Alu8 data set, the analysis suggests the existence of a largely Eurasian group, plus two groups whose distribution is essentially worldwide. Conversely, for the Alu21 data set, all African and most Oceanian genotypes fall into the first group, whereas the other three groups roughly correspond to Asia and the Americas (2), and Eurasia (3 and 4). Using a set of X-chromosome data and the same method, Wilson et al. (2001) identified yet another set of groups (four, roughly corresponding to Europe, New Guinea, Africa, and Asia).

Table 7.

Estimates of the Number of Groups, K, in the Alu Data Sets

K	Alu8		Alu21
in pr(x|k)	p(k|x)	in pr(x|k)	p(k|x)
1	−12560	∼0	−9700	∼0
2	−12072	∼0	−9700	−0
3	−11974	−1	−9585	0.05
4	−12048	−0	−9582	0.95
5	−12050	∼0	−9668	∼0

Under the assumption of Hardy-Weinberg equilibrium, In Pr(X|K) is the likelihood of the data, given K, and P(K|X) is the posterior probability of K, given the data. 

Table 8.

Assignment of Individuals to the Groups Identified by STRUCTURE

	Alu8			Alu21
group 1	group 2	group 3	group 1	group 2	group 3	group 4
Americas	9	85	6	0	84	8	8
Oceania	13	50	35	78	9	4	9
Europe	51	19	30	6	22	36	36
Asia	31	38	31	13	46	18	23
Africa	12	50	38	100	0	0	0

Percent values on the total of individuals from that continent. Overall sample size is 1331 for Alu8 and 476 for Alu21. 

Conclusions

Previous studies have shown that differences among continental groups represent a rather small fraction of the global STR and RFLP diversity of our species (Barbujani et al. 1997; Jorde et al. 2000; Brown and Armelagos 2001). In this study we found that a between-continent variance accounting for 5% to 20% of the total is the rule also for numerous nuclear biallelic polymorphisms, on the basis of independent loci typed in a large number of samples. We identified an exception, Y-chromosome polymorphisms, and we tried to better understand the evolutionary meaning of both the rule and the exception. For that purpose, we asked what is the probability of allocating an individual to the correct continent, on the basis of her or his genotype. Different statistical methods gave somewhat different results, but three conclusions appear justified: (1) most individuals are allocated correctly, but (2) the rate of misclassification is never < 27%, and (3) the rate of misclassification is roughly the same, whether allocation is based on autosomal or Y-chromosome polymorphisms, although for the latter the variance among continents is four times as large. New Y-chromosome data sets containing many new polymorphisms are being assembled (Underhill et al. 2000; Hammer et al. 2001), and their analysis may somewhat modify details of this picture.

Continent-specific and population-specific polymorphisms do exist in humans, and individuals carrying certain, generally pathologic, alleles, can be assigned to a specific geographic area with a high degree of confidence. Popular examples are the alleles for Tay-Sachs disease among Ashkenazi Jews, and for thalassemia in the Mediterranean area. However (with one exception, the Duffy-null alleles in Africa), very few members of those populations carry those rare alleles, and the mutations that generated them are recent (Oddoux et al. 1999; Hamblin and Di Rienzo 2000; Weatherall 2001). Alleles common in a continent, and absent or nearly so elsewhere, which would support the existence of a substantial ancestral differentiation among human groups, have been identified in this or previous studies only in the Y chromosome. Even the X-chromosome haplotypes that initially appeared to be restricted, respectively, to African and to non-African populations (Harris and Hey 1999), turned out to be shared across continents when sample sizes were increased (Yu and Li 2000).

In summary, discriminant analysis confirms the existence of some degree of geographical structuring in humans, contra Templeton (1999). If one considers a set of biallelic loci from an individual's genome, and asks which continent that genotype comes from, the answer will be correct most of the time. However, even when jointly considered, all of the markers we could use, including those of the Y chromosome, did not prove able to assign more than 70% of the individuals to their continent of origin. That is not what one would expect, if the human species were subdivided, and deep genetic discontinuities existed among continental groups. We have also shown, albeit in a relatively small sample, that the genetic variances among continents at a locus undergoing selection, β-globin, are not greater than those estimated at neutral loci.

The genetic uniformity of the human species contrasts with what is observed for other large mammals (reviewed in Templeton 1999), whose populations tend to be more diverse, even when restricted to a much narrower geographic range. Groups occupying distinct territories, and each characterized by peculiar combinations of genes that are absent or at least rare elsewhere, can be found among gorilla (Ruvolo et al. 1994), chimpanzee and bonobo (Gagneaux et al. 1999), gray wolf and elephant (Templeton 1999), and gazelle (Arctander et al. 1996), but not, so far, in humans. Two, not necessarily alternative, explanations seem reasonable, namely: (1) a comparatively recent common ancestry of all modern humans, so that there has been little time for groups to diverge, and (2) gene flow rates high enough to homogenize groups.

Our attempt to identify major human groups by clustering genotypes yielded contradictory results. Different numbers of groups, and different distributions of genotypes within such groups, were observed. Moreover, these results do not overlap with those of another study (Wilson et al. 2001) based on the same method and different data. These observations mean that there is no reason to expect that the same groups will be identified on the basis of different sets of genes. As a consequence, both for evolutionary studies and practical applications (such as predicting liability to certain diseases or response to certain drugs), what seems to matter is the individual genotype, much more than the ethnic or geographic affiliation.

This study shows that, by assuming homogeneity of individuals within their continent, one disregards between 8% (as estimated in the Alu21 data set) and17% (Y99 data set) of the total biallelic human diversity (Table 2). The practical consequences of that depend on the composition of the population studied, and may be trivial in forensic applications, especially if STR markers are used, if the populations are homogeneous. However, the error may not be negligible in metropolitan areas, or where very different communities coexist. In those cases, up to 30% of individuals (Table 3) may carry genotypes that appear so different from the bulk of the others that discriminant analysis would assign them to another continent. As for clinical practice, it seems a clear distinction should be made between population-specific polymorphisms (which exist, albeit rare, and may be a useful diagnostic tool), and continent- or (the term could then be appropriate) race-specific genetic polymorphisms. To the best of our knowledge, no example of the latter has been described in humans. Going back to the evolutionary definition of race that we cited in the Introduction, this study found no evidence suggesting the existence in humans of recognizable lineages that have diverged because they have long been separated by reproductive barriers. The present study of biallelic, presumably ancient, polymorphisms does not suggest that there is a basis for an objective and unequivocal definition of distinct biological groups within the human species.

METHODS

DNA Samples and Alu Genotyping

Twenty-one Alu insertion polymorphisms were typed in 1330 individuals from 32 populations (listed in Table 7 along with the sample sizes). The cell lines used to isolate control DNA samples were as follows: human (Homo sapiens), HeLa (ATCC CCL2); chimpanzee (Pan troglodytes), Wes (ATCC CRL1609); gorilla (Gorilla gorilla), Ggo-1 (primary gorilla fibroblasts) provided by Dr. Stephen J. O'Brien, National Cancer Institute, Frederick, MD, USA. Cell lines were maintained as directed by the source and DNA isolations were performed using Wizard genomic DNA purification (Promega). Diverse human DNA samples were isolated from peripheral blood lymphocytes (Ausubel et al. 1996), most of which had been collected for previous studies (Stoneking et al. 1997; Nasidze and Stoneking 2001). African–American, Bantu speakers, Hispanic–American, Hungarian, Syrian, and Yanomamo DNA samples were available in Batzer's laboratory.

PCR amplification of each Alu insertion polymorphism was performed in 25-μL reactions using 50–100 ng of target DNA, 40 pM of each oligonucleotide primer, 200 μM dNTPs in 50 mM KCl, 1.5 mM MgCl2, 10 mM Tris-HCl (pH 8.4) and Taq DNA polymerase (1.25 units), as recommended by the supplier (Life Technologies). Each sample was subjected to the following amplification cycle: an initial denaturation of 2:30 min at 94^oC, 1 min of denaturation at 94°C, 1 min at the annealing temperature, 1 min of extension at 72°C, repeated for 32 cycles, followed by a final extension at 72°C for 10 min. Twenty microliters of each sample was fractionated on a 2% agarose gel with 0.25 μg/mL ethidium bromide. PCR products were directly visualized using UV fluorescence. The sequences of the oligonucleotide primers, annealing temperatures, PCR product sizes, and chromosomal locations for the loci have been reported previously (Arcot et al. 1996, 1997, 1998; Stoneking et al. 1997).

Data Sets

Five data sets were considered in this study (Table 9). The Alu21 data set represents the newly typed, unlinked autosomal Alu insertion polymorphisms in the 32 populations of Table 10.

Table 9.

Sample Sizes (Individuals) by Continental Group for Each Data Set

Group	Data set
Y98	Y99	Alu8	Alu21	BGL
Africa	380	348	170	130	103
Asia	787	1168	883	266	67
Europe	217	175	657	650	46
Americas	44	389	198	164	48
Australia	116	118	162	120	85
Total	1544	2198	2070	1330	349

Table 10.

Sample Sizes for the Alu21 Data Set in 32 Populations

Population	SB22777	SB18874	SB23467	HS2.25	HS2.43	HS3.23	HS4.14	HS4.32	HS4.59	HS4.65	HS4.69	HS4.75	COL3AI	TPA25	ACE	APO	FXIIIB	PV 92	D1	B65	A25	Total
Abazinian	11	20	23	12	21	13	13	14	11	16	26	10	20	19	12	0	0	23	10	23	18	315
African American	68	69	67	69	69	68	69	69	66	69	64	60	69	68	68	69	68	69	68	69	67	1422
Alaskan Native	38	47	46	39	47	40	18	45	41	47	36	44	36	46	46	40	0	41	38	43	42	820
Armenian	41	42	43	36	35	43	42	42	43	43	43	42	41	43	43	35	35	38	43	43	43	859
Azerbaijani	36	38	37	24	38	37	34	36	35	38	36	36	33	38	37	35	20	34	36	38	35	731
Bantu speakers	40	45	47	48	48	47	40	36	40	44	32	48	48	47	48	44	47	48	48	48	48	941
Bretons	72	72	64	62	72	71	56	71	72	72	57	71	72	67	66	68	62	71	59	67	72	1416
Cajun	68	66	63	67	69	68	64	66	58	69	52	55	57	68	67	68	44	68	51	57	69	1314
Cherkessian	37	42	44	40	44	40	43	36	32	44	44	38	44	44	41	37	33	42	36	43	44	848
Darginian	15	19	16	17	19	16	18	15	13	19	18	17	16	18	18	11	14	18	13	14	18	342
European American	70	71	71	68	71	71	64	71	68	71	65	65	69	70	71	63	62	71	70	71	71	1444
French	66	72	72	71	71	71	65	67	69	72	67	72	72	70	71	68	68	69	66	68	70	1457
Georgian	68	58	68	65	68	68	68	64	62	68	68	67	60	68	65	68	68	68	67	66	68	1390
German	69	66	69	67	69	68	69	65	68	70	69	52	69	70	69	64	61	65	63	69	70	1401
Greek Cypriot	42	46	46	47	49	43	46	40	47	50	48	49	50	50	49	47	44	47	49	48	47	994
Greenland Native	49	50	50	49	50	50	50	48	50	49	50	49	49	50	48	50	0	50	50	50	50	991
Hispanic American	72	71	71	72	72	70	66	62	65	72	71	72	70	72	72	71	59	68	65	64	71	1448
Hungarian	69	68	69	68	70	62	65	69	61	62	69	70	65	66	69	65	59	65	67	67	70	1395
Ingushian	12	29	29	32	29	24	28	26	25	29	31	22	31	29	25	17	8	31	22	31	30	540
Kabardinian	25	18	28	19	31	29	30	26	25	26	30	24	21	31	30	22	18	31	30	30	27	551
lKung	26	42	32	38	42	40	40	39	38	38	40	37	38	42	39	37	35	38	38	40	33	792
Maya	28	26	28	28	28	28	25	28	27	28	28	28	27	28	26	28	24	27	26	26	28	570
Moluccas	48	42	44	49	50	43	47	46	46	50	37	37	22	50	51	50	46	50	37	38	47	930
Mvskoke	25	32	30	31	31	31	32	30	31	32	32	32	25	32	29	31	24	32	25	30	32	629
Nguni	21	33	35	33	35	17	30	22	24	22	26	37	16	44	43	39	43	42	41	41	42	686
Nusa Tenggarans	89	52	63	81	95	82	91	77	84	93	60	87	62	92	97	97	90	96	81	86	92	1747
PNG Coastal	49	48	41	48	49	45	40	49	48	47	49	49	46	49	43	45	47	48	42	48	49	979
PNG Highland	46	54	60	60	60	58	60	60	46	59	48	59	47	59	55	57	46	56	43	38	57	1128
Swiss	61	71	70	65	69	68	63	60	68	71	67	65	69	69	70	51	65	66	71	71	71	1401
Syrians	68	57	69	68	70	69	69	63	69	64	67	57	68	70	70	68	69	68	69	70	66	1408
Turkish Cypriot	52	51	59	53	58	55	59	56	59	59	59	58	57	59	59	56	41	59	55	58	59	1146
Yanomamo	27	26	26	0	27	27	21	27	23	26	27	26	23	27	16	26	6	26	21	27	24	479
TOTAL	1508	1543	1580	1526	1656	1562	1525	1525	1514	1619	1516	1535	1492	1655	1613	1527	1306	1625	1500	1582	1630

African Americans, Caucasian Americans, Hispanic Americans, and Cajun were disregarded in all statistical analyses. 

Four additional data sets were assembled and analyzed. The Alu8 data set includes Alu insertion genotypes at 8 autosomal loci (TPA25, PV92, APO, ACE, FXIIIB, D1, A25, B65), with 1500 individuals from 32 worldwide populations (Stoneking et al. 1997), representing 1331 distinct multilocus genotypes. Further populations were incorporated into the Alu8 database, bringing the total number of populations to 46. Although all loci of the Alu8 data set are also found in the Alu21 data set, the populations are not the same (for example Eastern Asian populations are absent from Alu21), and therefore we chose to analyze the two databases separately. The Y98 and Y99 data sets are drawn from two surveys (Hammer et al. 1998; Karafet et al. 1999) of 12 biallelic Y-chromosome polymorphisms, defining respectively 12 and 14 distinct haplotypes in 1544 males from 35 populations (Y98), and 2198 males from 60 populations (Y99). The final data set comes from a study of a 3-kb region encompassing the β-globin gene in nine populations (Harding et al. 1997) (BGL data set). The gene tree constructed from 326 sequences includes 29 haplotypes, 13 of them apparently resulting from recombination or gene conversion. The latter haplotypes are all rare, and to avoid choosing arbitrary weights for nucleotide substitution, recombination, and gene conversion events, we chose to consider only the remaining 16 haplotypes, assuming they have been generated by nucleotide substitution alone.

The geographical distribution of the samples for each data set is shown in Figure 2. The Y99 and Y98 data sets have the widest global coverage. Alu8 has samples almost everywhere apart from North Asia, whereas Alu21 and BGL are smaller data sets; in particular, for most continents, BGL has only one sample.

Figure 2.

Geographical distribution of the five data sets.

Statistical Analysis: AMOVA

The genetic differences within and among population samples were quantified, and their significance was assessed, using AMOVA, a nonparametric method for the analysis of variance suitable for molecular data (Excoffier et al. 1992). Genetic variances were estimated from allele-frequency differences between populations, and from measures of molecular difference between alleles. The overall genetic variance was then subdivided into three hierarchical components: between individuals within populations, between populations of the same group, and between groups. Because morphological studies of the last two centuries led to lists of human races containing from 3 to 200 items (Armelagos 1994; Barbujani 2001), and in the absence of other solid criteria for group definition, we decided to use groups corresponding to continents. The significance of the variance components was tested by a randomization approach. Each individual, or population, was reassigned to a random location, according to three resampling schemes. The molecular variances were recalculated, and the procedure was repeated 1000 times to obtain empirical null distributions of all relevant variances.

Statistical Analysis: Discriminant Analysis

In discriminant analysis, also known as supervised classification (Ripley 1996), variables measured on individuals whose grouping is known (the training data set) are combined to construct a new variable that can be used to classify individuals (or, in our case, genotypes) of unknown group (query genotypes). For the analyses described following, we have used the classification functions implemented for the statistical package Splus that are freely available on the StatLib server (S Archive: http://lib.stat.cmu.edu/) (Venables and Ripley 1997). The genotypes were coded as strings of binary digits, so that distances estimated between pairs of individuals reflected the minimum (and most likely) number of mutational events separating them. This coding allows one to use both parametric and nonparametric forms of discriminant analysis.

We initially considered three standard parametric methods, namely, linear (LDA), logistic (LOG), and quadratic (QDA) discriminant analysis. All of these assume that the variables are at least approximately normal, which does not hold for our data. They performed poorly and are not discussed further here, although some results are included following for comparison. We then resorted to four standard nonparametric methods, which do not assume a probabilistic model for the observations, namely, a neural network (NNET), Gaussian kernel density estimation (KER), and k-nearest neighbor with k = 1 (1NN) and k = 3 (3NN) (Venables and Ripley 1997).

Neural networks are collections of mathematical models, and related computer programs, which identify patterns in a data set by emulating some properties of biological nervous systems and by drawing on the analogies of adaptive biological learning (Jennions and Brooks 2001). NNETs are composed of a large number of interconnected processing elements that are analogous to neurons, and are tied together with weighted connections that are analogous to synapses. By a process of trial and error, nonlinear functions are estimated from randomly sampled subsets of the original data set. These functions are then used by NNETs to classify the remaining genotypes. The goodness of the classification obtained is evaluated, and iterations are run until a desired level of accuracy is obtained.

The KER method starts by estimating the density of the genotype frequencies in each group, and then assigns a new observation (genotype) to the group for which its estimated density is maximal. Lastly, with the simplest method, the nearest neighbor, each genotype is assigned to the group whose first k nearest genotypes (one for what we refer to as 1NN, or three for 3NN) are closest.

The previously described classification methods are not specifically designed for genetic data. We also implemented a method (RM) that, for the autosomal data sets, exploits the assumptions of Hardy-Weinberg and linkage equilibria (independence within and between loci) to improve the estimation of genotype relative frequencies in each group (Rannala and Mountain 1997). The RM method uses Bayesian posterior expectations given a symmetric Dirichlet prior distribution to overcome the potential problem of zero frequency in the training data for an allele observed in the query genotype. In the case of nonrecombining haploid data, the equilibrium assumptions are not appropriate, and the natural analog of the RM method reduces to a trivial comparison of (posterior) haplotype frequencies.

For the Alu8 and Alu21 data sets, we included only those individuals with complete information (over all 8 or 21 loci), reducing the sample sizes to 1331 and 477 individuals, respectively. For these data sets, the variables involved in the discriminant analysis are the individual genotypes at each locus. For the other data sets (BGL, Y98 and Y99), the entire haplotype is treated as a single variable. One by one, each individual's known source population is temporarily ignored, and each of the classification methods is implemented to classify that individual into her or his most likely source population, with all the other individuals being used as the training set. At the end of this cross-validation procedure, the proportion of correct continental allocations was recorded.

Statistical Analysis: Inference of Population Structure

We estimated the most likely number of genetically homogeneous groups in the data sets, and assigned each individual to her or his most likely group by means of an approach implemented in the program STRUCTURE (Pritchard et al. 2000). Multilocus genotypes are considered, and no particular mutational model is assumed. Each individual's genotype is considered to result from a mixture of contributions originating in k population groups, and q(i) is the fraction of the genes of that individual that come from the ith group defined. Under the assumption that each of the populations is in Hardy-Weinberg equilibrium, k is estimated by a Monte Carlo-Markov Chain algorithm. Then, for each individual, regardless of her or his geographical provenance, the vector q(1), q(2)…q(k) is estimated, and ultimately each individual can be assigned to one of the inferred groups, that is, the one with the highest probability.