Abstract
The development of statistical methodologies for quantitative trait locus (QTL) mapping in polyploids is complicated by complex polysomic inheritance. In this article, we propose a statistical method for mapping QTL in tetraploids undergoing bivalent formation at meiosis by using single-dose restriction fragments. Our method is based on a unified framework, one that uses chromosome bivalent pairing configuration and gametic recombination to discern different mechanisms of gamete formation. Our bivalent polyploid model can not only provide a simultaneous estimation of the linkage and chromosome pairing configuration—a cytological parameter of evolutionary and systematic interest—but also enhances the precision of estimating QTL effects and position by correctly characterizing gene segregation during polyploid meiosis. By using our method and a linkage map constructed in a previous study, we successfully identify several QTL affecting winter hardiness in bivalent tetraploid alfalfa. Moreover, our results reveal significant preferential chromosome pairing at meiosis in an F1 hybrid population, which indicates the importance of reassessing the traditional view of random chromosome segregation in alfalfa.
Statistical strategies and techniques for genomic mapping are well developed for diploid species (Lander and Botstein 1989; Wu 1999) but are lagging in the more complex polyploids. Polyploids include many important agricultural crops such as alfalfa, potato, and sugarcane (Zeven 1979; Averett 1980; Hilu 1993) and are recognized to play a pivotal role in the evolution of flowering plants (Ramsey and Schemske 1998; Ronfort et al. 1998; Otto and Whitton 2000; Soltis and Soltis 2000). The genomic mapping of polyploids, in which the genome number is higher than two, is complicated for many factors, such as: (1) uncertainty about the genotype-phenotype correspondence owing to unknown ploidy level, unknown number of gene copies (known as the dosage; Burner 1997), and unknown allelic configuration (Luo et al. 2001); (2) complex pairing behaviors undergoing gamete formation during meiosis (Bever and Felber 1992); (3) heterozygous genome structures resulting from predominantly outcrossing mating systems (Soltis and Soltis 2000); and (4) increased allelic and nonallelic combinations because of the increased number of chromosomes in the homologous set (Kempthorne 1957). The first three factors make it difficult to predict the pattern of gene segregation in a progeny family from its parental genotypes (Grivet et al. 1996; Ming et al. 1998; 2001), whereas the fourth factor leads to an exponential increase of unknown parameters, thus reducing the efficacy of the underlying model. All of them must influence the estimation of genetic parameters, including the recombination fraction and gene effects of quantitative trait loci (QTLs) on phenotypes, which thus deserve an in-depth exploration and should be incorporated into the framework of polyploid genome mapping.
We will first formulate statistical models for QTL mapping in polyploids by specifically considering different gamete formation mechanisms (factor 2). Models for incorporating the other factors will be proposed subsequently. Unlike the other factors, gamete formation mechanisms are polyploid dependent. Polyploids are traditionally classified either as allopolyploids derived from distinct genomes or as autopolyploids from genetically similar genomes (Bever and Felber 1992). But from a viewpoint of meiotic configurations, the nature of polyploids can be better described by bivalent polyploids and multivalent polyploids (R. Wu et al. 2001; S. Wu et al. 2001). In bivalent polyploids, only two chromosomes pair during meiosis at a time so that each bivalent pair contributes one chromosome to the chromosomal set in each gamete. In contrast, in multivalent polyploids, multiple chromosomes pair simultaneously, during which a gamete is formed owing to a free combination of all chromosomes in the set. Different chromosome pairing mechanisms make these two groups of polyploids different from one another in gene segregation (R. Wu et al. 2001).
In this article, we propose a new statistical method for mapping QTL in bivalent polyploids. Currently, there are only three papers that address QTL mapping methodologies for bivalent polyploids (Doerge and Craig 2000; Xie and Xu 2000; Hackett et al. 2001). As noted by Hackett (2001), the statistical model of Xie and Xu (2000) was not based on a proper biological model of polyploid meiosis. The other two papers also have limits in theory and applications. Doerge and Craig (2000) assumed preferential pairings; that is, pairings occur strictly between the same chromosomes in the set. In the paper by Hackett et al. (2001), random chromosome pairings are assumed; that is, all chromosomes have an equal opportunity to pair with one another. These two assumptions help to simplify the model derivations but may not reflect biological reality. In real life, there are a number of intermediate types between these two assumptions (Allendorf and Danzmann 1997; Fjellstrom et al. 2001), in which the probability of pairings may be higher between more similar chromosomes than between less similar chromosomes. Such a difference of pairing probability is described by the preferential pairing factor (Sygenba 1994, 1995).
In our statistical model for QTL mapping in bivalent polyploids, the preferential pairing factor specifying bivalent pairing behaviors is incorporated. To facilitate our analysis, we focus on the performance and robustness of the bivalent polyploid model built on single-dose restriction fragments (simplex). Simplex markers, as used for QTL mapping, have two major advantages: (1) they are economically cheap and readily characterized, and (2) they are abundant in many polyploids. For example, simplex markers represent 70% of the detectable polymorphic loci resulting from the segregation of alleles of different dosages (Da Silva 1993). The statistical aspects of linkage analysis in polyploids based on simplex markers have been discussed by Wu et al. (1992), Hackett et al. (1998), Ripol et al. (1999), and Skinner et al. (2000). Here, we explore the influences of gamete formation mechanisms on polyploid linkage mapping by using the simplex markers. Our new mapping model incorporating preferential chromosome pairings will be validated by a case study in autotetraploid alfalfa.
Alfalfa, as one of the most important perennial forage crops in the world, offers an excellent model system for testing our theoretical model for QTL mapping in bivalent polyploids. First, chromosomes in alfalfa predominantly pair as bivalents, but display polysomic inheritance owing to its autopolyploid nature (Bingham and McCoy 1988). Earlier studies all assume that chromosome segregation in alfalfa is random (Yu and Pauls 1993). This assumption is likely violated when a genome analysis is based on an F1 hybrid progeny derived from two different species or populations. Second, alfalfa has diploid relatives; thus, results between polyploid alfalfa and its diploid relatives can be compared. Third, a few genetic linkage maps of molecular markers have been constructed in alfalfa (Yu and Pauls 1993; Brouwer and Osborn 1999; Diwan et al. 2000), providing a foundation for the genetic analysis of complex traits and marker-assisted selection.
RESULTS
We derive theoretical models for mapping QTLs in bivalent tetraploids using single-dose restriction fragments (simplex) by incorporating the preferential pairing factor defined to describe bivalent chromosome behavior (Sybenga 1994, 1995, 1996). These models are then applied to map QTLs affecting winter hardiness traits in alfalfa. The statistical methods for estimating the linkage, preferential pairing factor and QTL effects are presented in the Methods section.
The statistical model proposed in this article is used to map QTLs affecting winter hardiness based on simplex markers in a published data set of tetraploid alfalfa (Brouwer and Osborn 1999). Alfalfa is regarded as an autotetraploid, in which bivalent pairings are a predominate process during meiosis (Bingham and McCoy 1988). Earlier linkage analyses assumed random chromosome segregations, although this may deviate from biological reality (Yu and Pauls 1993; Brouwer and Osborn 1999). This assumption will be relaxed in our analysis by providing a direct estimate of the preferential pairing factor denoted as p. According to Sybenga (1994), p is defined as two-thirds of the difference between the pairing frequencies of more similar chromosomes and of less similar chromosomes, plus a constant one-third. Thus, when p = 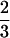 , less similar chromosomes do not pair; that is, chromosomal pairings happen strictly between the homologs. When p = 0, all the four chromosomes are homologous, and they will pair randomly. The value of p theoretically ranges from 0 to
, less similar chromosomes do not pair; that is, chromosomal pairings happen strictly between the homologs. When p = 0, all the four chromosomes are homologous, and they will pair randomly. The value of p theoretically ranges from 0 to 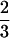 .
.
Two contrasting tetraploid plants, winter-hardy Blazer XL (B17) and winter-sensitive Peruvian 13 (P13), were crossed to generate an F1 hybrid population, which was then backcrossed to each parent (Brouwer and Osborn 1999). Each backcross obtains 101 progenies used for mapping. Two hardiness traits, freezing injury measured by electrical conductivity and winter injury, were measured in two successive years (Brouwer et al. 2000). Because the two original parents are not pure inbred lines, the two-way backcrosses virtually present a full-sib family in which many different marker types may be segregating (Wu et al. 2002). Brouwer and Osborn (1999) used 82 testcross (pseudo-test backcross) markers derived from single-dose restriction fragment length polymorphisms to construct two genetic linkage maps for each backcross population. In total, four homologous coupling-phase cosegregation groups, of which two were derived from the backcross to B17 (A and B) and the other two from the backcross to P13 (C and D), were detected for seven of the eight linkage groups. In a previous regression analysis, Brouwer et al. (2000) found that there was a higher probability of detecting significant QTLs for winter hardiness on cosegregation groups A and B than on C and D. Thus, groups A and B are used as an example to test and validate our statistical method for mapping QTLs affecting complex traits in alfalfa. The QTLs mapped are statistically tested on the basis of a critical threshold value at the significance level 5% calculated from 200 permutation tests (Churchill and Doerge 1994).
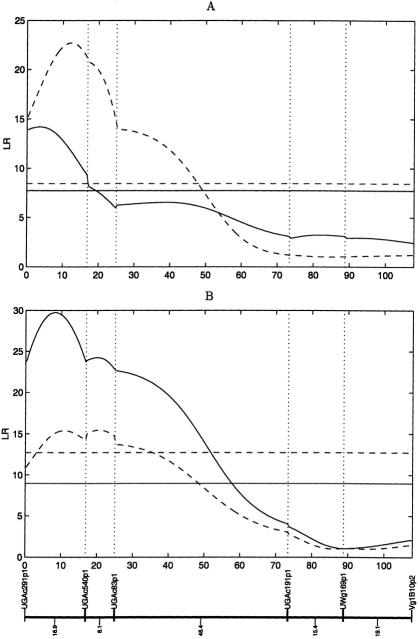
By using our newly developed method, we successfully detect five and four significant QTLs responsible for freezing injury and winter injury, respectively, in the backcross to B17. The detection of these QTLs was based on a largest likelihood value at a particular preferential pairing factor under a most likely marker-QTL linkage phase. Tables 1 and 2 give the estimates of the QTL chromosomal locations and allelic effects on the two injury traits. We present an example of the detection of the QTL for each trait, in which the peaks of the profiles of the log-likelihood ratio test statistics correspond to a likely position of the QTL detected (Fig. 1).
Table 1.
The Locations and Effects of QTL Affecting Freezing Injuries Measured by Electrical Conductivity in Two Successive Years (1995 and 1996) for Bivalent Tetraploida Alfalfa
| Linkage groupa | Marker interval | Year | LRb | Threshold | Additive effect | R2c | MarkerQTL Phase | p̂d |
|---|---|---|---|---|---|---|---|---|
| 4A | ugac118pl–vgle9p1 | 1995 | 4.63 | 9.60 | 0.5 | |||
| 1996 | 14.91 | 9.66 | 33.56 | 12.5 | A2 | 0.4 | ||
| 5A | vg2a2p1–vg2e5p1 | 1995 | 2.08 | 9.85 | 0.6 | |||
| 1996 | 15.91 | 10.03 | 17.93 | 8.6 | A2 | 0.6 | ||
| 5B | vg2a11p1–vg1h10p1 | 1995 | 13.11 | 7.84 | 15.69 | 8.7 | A2 | 0.6 |
| 1996 | 3.85 | 8.47 | 0.6 | |||||
| 6A | ugac281p1–vg2c2p1 | 1995 | 5.53 | 8.78 | 0.6 | |||
| 1996 | 14.12 | 8.81 | 17.53 | 9.2 | A2 | 0.6 | ||
| 8A | ugac235p1–ugac291p1 | 1995 | 14.20 | 8.40 | 19.48 | 8.5 | A2 | 0.6 |
| 1996 | 22.72 | 8.46 | 21.56 | 13.7 | A2 | 0.6 |
Significant QTL, as evidenced by larger log-likelihood ratios (LRs) than the thresholds calculated from 200 permutation tests, are indicated in boldface.
Linkage groups refer to Brouwer and Osborn (1999).
The LR between the full model (there is a QTL) and the reduced model (there is no QTL).
The proportion of the total phenotypic variance explained by the QTL detected.
The preferential pairing factor (p) is estimated by a grid approach within its space. The estimates of p are also given for nonsignificant QTL.
Table 2.
The Locations and Effects of QTL Affecting Winter Injuries in Two Successive Years (1996 and 1997) for Bivalent Tetraploid Alfalfa
| Linkage groupa | Marker interval | Year | LRb | Threshold | Additive effect | R2c | MarkerQTL Phase | p̂d |
|---|---|---|---|---|---|---|---|---|
| 1B | vg2b9p1–vg2g1p1 | 1996 | 6.31 | 12.74 | 0.4 | |||
| 1997 | 15.25 | 12.62 | 4.50 | 8.4 | A3 | 0.1 | ||
| 5A | hg2b12p1–vg2a2p1 | 1996 | 10.01 | 10.25 | 0.6 | |||
| 1997 | 16.68 | 16.58 | −1.37 | 8.9 | A1/A2 | 0.2 | ||
| 8A | ugac235p1–ugac291p1 | 1996 | 29.74 | 8.96 | 1.10 | 10.4 | A2 | 0.6 |
| 1997 | 15.45 | 12.72 | 0.77 | 10.2 | A2 | 0.6 | ||
| 8B | ugac109p1–vg1b10p1 | 1996 | 20.20 | 21.15 | 0.6 | |||
| 1997 | 34.33 | 26.64 | 1.63 | 12.8 | A2 | 0.6 |
Significant QTL, as evidenced by larger log-likelihood ratios (LRs) than the thresholds calculated from 200 permutation tests, are indicated in boldface.
Linkage groups refer to Brouwer and Osborn (1999).
The LR between the full model (there is a QTL) and the reduced model (there is no QTL).
The proportion of the total phenotypic variance explained by the QTL detected.
The preferential pairing factor (p) is estimated by a grid approach within its space. The estimates of p are also given for nonsignificant QTL.
Figure 1.
The profiles of the likelihood ratio test statistics across linkage group 8A in bivalent tetraploid alfalfa. Two horizonal lines indicate the thresholds at the significance level 5% calculated from 200 permutation tests (Churchill and Doerge 1994). QTL for freezing injuries (A) measured in 1995 (blue) and 1996 (pink); QTL for winter injuries (B) measured in 1996 (blue) and 1996 (pink).
Of the five QTLs detected for freezing injury, four mapped to F1-specific linkage groups 4A, 5A, 6A and 8A, whereas only one mapped to B17-specific linkage group 5B. For linkage group A, the positive allelic effect of a QTL indicates that parent P13 contributes an increasing allele for injury trait values. Our estimates of positive allelic effects (Table 1) indicate that parents B17 and P13 contribute cold-tolerant and cold-sensitive alleles to their F1 hybrids, respectively, conforming to the biological attributes of these two parents. But the positive allelic effect of a QTL on 5B implies that parent B17 may also contribute cold-sensitive alleles.
According to our estimate, the marker-QTL linkage phase with the largest probability is one for which the presence of the simplex markers (P13 alleles) is in repulsion phase with the QTL allele, leading to smaller trait values and therefore larger hardiness. We found strong evidence for the change of QTL activity over different ages. More significant QTLs were detected in the second year than in first year (Table 1). A same marker interval on linkage group 8A carries a QTL responsible for freezing injury in both years, with an increased LR value for the second year than for first year.
Similar patterns of QTL expression were also observed for winter injury in alfalfa (Table 2). But most of the QTLs detected are different between freezing and winter injuries. Two chromosomal segments on 5A and 8A detected to affect both freezing and winter injuries may contribute to their moderate correlation (Brouwer et al. 2000).
One of the major advantages of our method is that it can estimate the preferential pairing factor during polyploid meiosis. The estimated preferential pairing factor, p̂ = 0.6 (0 ≤ p ≤ 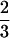 ), consistently obtained from most marker intervals regardless of the significance of their association with a QTL (Tables 1, 2), indicates that chromosome pairings of tetraploid alfalfa are actually not random.
), consistently obtained from most marker intervals regardless of the significance of their association with a QTL (Tables 1, 2), indicates that chromosome pairings of tetraploid alfalfa are actually not random.
A Simulation Study
We performed a simulation study to test the performance and robustness of our bivalent polyploid model incorporating the preferential pairing factor. Our interest was to investigate the effects of two major assumptions, completely preferential pairing, as assumed in Doerge and Craig (2000), and random segregation, as assumed in Hackett et al. (2001), on the precision of parameter estimation. We simulated two interval markers and one QTL, determining a normally distributed trait for a pseudo-test backcross population of 200 offspring. The two markers and the QTL are assumed in coupling phase. The two markers are separated 20 cM from each other, between which the QTL is located at 5 cM from the left marker. The Kosambi map function is used to convert the map distance in the corresponding recombination fraction. The QTL is hypothesized to have the additive effect of 0.5 and to explain 20% of the total phenotypic variance. Based on these conditions, a data set of markers and phenotypes are simulated under the assumption of p = 0.33 using the genotype frequencies given in Table 3.
Table 3.
Joint Probabilities of Three-Locus Genotypes for a Putative QTL Bracketed by Two Simplex Markers Under Different QTL-Marker Linkage Phases as Given in Expressions 2 Through 4 in a Pseudo-Test Backcross Design.
The conditional probabilities of the QTL genotypes upon the marker interval are calculated according to Bayes' theorem.
There are two marker genotypes 1000 and 0000 for each marker in the pseudo-test backcross design 1000 × 0000. The recombination fractions between the left marker of the interval and the QTL, and the QTL and the right marker of the interval are denoted by r1 and r2, respectively. The preferential pairing factor is denoted by p.
Three methods are used to analyze the simulated data set, the first being Doerge and Craig's method of assuming completely preferential pairings, the second being Hackett et al.'s method of assuming random segregation, and the third being our method as proposed in this article. Our method takes into account all possible cases of chromosome bivalent pairings by estimating the preferential pairing factor p. The results from our analyses are summarized as follows: (1) Doerge and Criag's method gave the most biased estimates for all QTL and model parameters, although it is computationally fast; (2) Hackett et al.'s method also had significant biases for QTL position and effect estimates (biased by 10% to 20%); and (3) as expected, our method displayed reasonable estimation accuracy and precision for all parameters. An additional important advantage of our method is that it provides a direct estimate of the preferential pairing factor that is of typical interest to evolutionary and systematic biologists.
DISCUSSION
We have for the first time devised a statistical method for mapping QTLs in recalcitrant polyploids by considering the chromosome pairing mechanism of polyploid meiosis. The pairing mechanisms in polyploids include two types, bivalent and multivalent configurations. In this article, bivalent chromosome pairings are considered. Our bivalent polyploid model based on maximum-likelihood methods can provide not only the estimates of the map position of QTL, its effect, and inheritance mode but also the estimate of the preferential pairing factor (p), a cytological parameter of evolutionary and systematic importance. In addition, our model incorporating bivalent pairing mechanisms can enhance the estimation precision of QTL parameters in polyploids. As demonstrated by a simulation study, greater-bias parameter estimates will be obtained if the preferential pairing factor is not considered, as assumed by Doerge and Craig (2000) and Hackett et al. (2001).
In earlier analyses of alfalfa by Brouwer and Osborn (1999) and Brouwer et al. (2000), random chromosome pairing was assumed. But our current result reveals significant preferential pairings at meiosis in the same material (p̂ = 0.60). Our result can be regarded as being closer to biological reality for three reasons. First, the assumption of random chromosome pairings is obtained from more traditional cytological approaches that may not be accurate enough to make exclusive conclusions (Sybenga 1994). Molecular markers specifying a small chromosomal segment are indicated to have more power of detecting chromosome pairing behaviors at meiosis. Second, our model takes into account the general meiotic property of a polyploid, which can cover random chromosome pairings. As long as a polyploid undergoes random bivalent pairings, they can be diagnosed by our model.
Third and most important, our model has been validated by a real-world example. North American alfalfa cultivars have been bred from nine sources, most of which are categorized as Medicago sativa spp. sativa; however, one is considered a distinct subspecies, M. sativa spp. falcata (Barnes et al. 1988). Although these germ plasm sources have been intermated and selected to derive alfalfa cultivars, the nine original sources have been maintained separately. A previous analysis showed that seven of the nine germ plasm sources were genetically very similar, one M. sativa spp. sativa source (Peruvian) was somewhat distinct, and the M. sativa spp. falcata source was very distinct (Kidwell et al. 1994). Two tetraploid plants, Blazer XL 17 and Peruvian 13, derived from these different sources (Peruvian and Falcata) likely display preferential chromosome segregation behavior because they are genetically distinct from each other.
Because no statistically powerful and biologically relevant approach is available in the current literature, QTL mapping in polyploids was performed by using a regression-based analysis of variance (Brouwer et al. 2000; Ming et al. 2001). Based on the alfalfa mapping material used by Brouwer et al. (2000), we detected several significant QTLs affecting winter hardiness. But only one of the QTLs detected from our newly developed model is consistent with the result from the analysis of variance approach. This is not surprising given that this concordant QTL, located on linkage group A, exhibits a large additive effect. Theoretically, a large QTL can be relatively easily monitored, even by a less powerful approach. Although we should be cautious with the inconsistency of most of the QTLs detected by our method and by analysis of variance, the inherited limits of analysis of variance may give us good reasons to favor our findings. Basically, the marker-associated analysis of variance cannot clearly distinguish between large-sized but distantly localized QTLs and small-sized but closely localized QTLs. Also, it is not easy to incorporate meiotic mechanisms into analysis of variance, another reason that the results from analysis of variance may not well reflect biological reality.
We have devised a powerful statistical method for QTL mapping in tetraploids by using single-dose restriction fragments, but it is crucial to modify this method to other different situations. In this article, we assumed the meiotic mechanism of bivalent pairings. Many species also undergo multivalent formation, from which a particular genetic phenomenon called double reduction results (Darlington 1929; Butruille and Boiteux 2000). Our method can be modified to consider the mechanism of multivalent formation. In addition, the model should be extended to consider double- (duplex) or multiple-dose restriction fragments that are often used in several polyploid studies (Ming et al. 1998, 2001). For dominant duplex markers, at which there are two genotypes segregating 5:1 in a tetraploid pseudo-test backcross, we will need to derive new conditional probabilities of the QTL genotypes to fit segregation patterns of the duplex marker interval. For codominant duplex markers that segregate a 1:4:1 ratio, we will need one more parameter to model the dominant effect of a QTL. We assumed that the markers and the QTL have the same dosage level. But it is possible that simplex markers are linked with a duplex QTL or that a simplex QTL is bracketed by two duplex markers (Skinner et al. 2000). Our analysis is based on the simplest pseudo-test backcross design (Grattapagalia and Sederoff 1994) and should be extended to consider a full-sib polyploid family, in which there may be many more complicated cross types, as shown in Wu et al. (2002). A general model for simultaneously using all different marker types to map QTLs should be developed. Our model integrates the linkage and linkage phase estimation into a unified framework, displaying an advantage that it overcomes the problem owing to poor estimation for the linkage between different markers and QTL in a repulsion phase (see Hackett et al. 1998). Yet, this integration requires more powerful computational algorithms. We are now implementing new algorithms, such as genetic algorithms (Gaspin and Schier 1998), in our linkage analysis model of polyploids. After all of these extensions are developed, we will have more power to tackle complicated problems of QTL mapping resulting from the polysomic inheritance of polyploids.
METHODS
The Mixture Model
A fundamental model for QTL mapping is the statistical mixture model (McLachlan and Peel 2000). In this mixture model, each observation yi is assumed to have arisen from one of n (n possibly unknown but finite) components, each component being modelled by a density from the parametric family f:
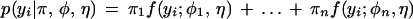 |
1 |
where π = (π1,…,πn) are the mixture proportions that are constrained to be nonnegative and sum to unity; φ = (φ1,…,φn) are the component specific parameters, with φj being specific to component j; and η is a common parameter which is common to all components.
For the mixture model used in genetic mapping (Lander and Botstein 1989), each component represents a class of QTL genotypes, and thus, the mixture model provides a framework by which observations may be clustered together into different classes of QTL genotypes. The mixture proportions represent the relative frequency of occurrence of each QTL genotype in the population. Within a particular marker genotype, the relative frequency of each QTL genotype is its conditional probability on the marker genotype.
For a pseudo-test backcross tetraploid population, there are two groups of genotypes at a single gene. Thus, the mixture model of polyploids contains two components of QTL genotypes that are predicted by four marker genotypes at a marker interval. The proportions of mixtures πk present the probabilities of QTL genotypes conditional on marker genotypes, which have been derived in Table 1. As seen from the table, the conditional probabilities contain the information of QTL position. Each mixture is assumed to follow a normal distribution fk(yi), with the expected mean specified by the genotypic value of the corresponding QTL genotype and the common residual variance σ2. The genotypic values of the two QTL genotypes are expressed as μ1 = μ + ½a for Qqqq and μ1 = μ − ½a for qqqq. In quantitative genetics, μ is the overall mean, and a is the additive effect of allele Q, which is the effect of substituting q by Q.
Conditional Probabilities
For species like polyploids, in which it is difficult to generate classical pure inbred lines, we generally use a pseudo-test backcross design, derived from two outcrossing parents, for linkage mapping (Grattapaglia and Sederoff 1994). We are interested in those markers that are heterozygous in one parent but homozygous in the second. For a simplex marker, a 1:1 segregation ratio is expected in an F1 tetraploid hybrid family if one parent is heterozygous (1000), whereas the other is null (0000). Consider two simplex markers for a heterozygous bivalent tetraploid with four chromosomes—labeled by 1, 2, 3, and 4—in a set. If these four chromosomes are completely identical, the allelic configurations of the two simplex markers can be described by a coupling phase or repulsion phase (Hackett et al. 1998). But if these four chromosomes are different, as considered in this article, with chromosome pairs 1 and 2, and 3 and 4 (homologous) being more similar than chromosomes pairs 1 and 3, 2 and 4, 1 and 4, and 2 and 3 (homoeologous), then the repulsion phase of the two simplex markers have two types: (1) homologous repulsion and (2) homoeologous repulsion.
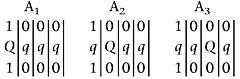
Now, consider a putative QTL for a quantitative trait that is bracketed by the two simplex markers. Two alternative alleles of this QTL, denoted by Q and q, form a genotype Qqqq in the heterozygous parent and qqqq in the homozygous parent. When the two markers are in a coupling phase, we have three different phases between the QTL and markers:
 |
2 |
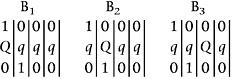
where the lines denote chromosomes 1, 2, 3, and 4 in order. In Equation 2A1, the QTL and markers are in a coupling phase, whereas in Equations 2A2 and 2A3, the QTL is in a homologous and homoeologous repulsion phase with the markers, respectively. Similar QTL-marker phase types can be detected as
 |
3 |
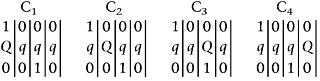
for the marker homologous repulsion phase, and as
 |
4 |
for the marker homoeologous repulsion phase.
Wu et al. (2002) have given a 6 × 6 gametic probability matrix of two fully informative markers generated by a tetraploid undergoing bivalent pairings. The gametic probabilities are a function of not only the recombination fraction r (as is the case in a diploid population, or has been assumed in previous polyploid mapping studies) but also the preferential pairing factor p. The gamete probability matrix of fully informative markers can be collapsed into a 2 × 2 matrix if both of the markers are simplex. Such a collapsed matrix, however, will have different structures, when different marker linkage phases (Equations 2–4) are considered. When a QTL is tested on the interval of the two fully informative markers, we will have a 36 × 6 matrix for the conditional probabilities of six QTL gamete genotypes on 36 marker gamete genotypes formed by a bivalent tetraploid. Similarly, this full conditional probability can be collapsed into a 4 × 2 matrix when two simplex markers are used to predict a biallelic QTL (Table 3). The structures of the collapsed matrix differ depending on different marker-QTL linkage phases (Equations 2–4; Table 3).
Generally, the linkage phase between two flanking markers is known before they are used to estimate QTL effects and position. Thus, our question for QTL mapping will be reduced to detect a most likely QTL-marker linkage phase from Equation 2 when the two markers are in a coupling phase, from Equation 3 when the two markers are in a homologous repulsion phase, or from Equation 4 when the two markers are in a homoeologous repulsion phase. S. Wu et al. (2001) used Bayes' theorem to characterize the most likely linkage phase based on a separate likelihood analysis of all possible phases. The estimation of the recombination fraction is then based on the most likely linkage phase detected. Using this approach, however, we cannot simultaneously use the information of all linkage phases. Here, all possible linkage phases will be incorporated within an integrated framework of the mixture QTL mapping model.
Assume that the probabilities of the three phases in Equation 2 are denoted by ϕ1 (A1), ϕ2 (A2), and ϕ3 (A3) (ϕ1 + ϕ2 + ϕ3 = 1). Thus, a simple mixture model (Equation 1), as used for regular QTL mapping (Lander and Botestein 1989), is changed into a two-stage hierarchical mixture model that combines the phase probabilities and conditional probabilities of QTL genotypes
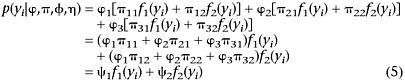 |
5 |
where πjk is the conditional probability of the kth QTL genotype under linkage phase j (Table 3), k = 1 for QTL genotype Qqqq and k = 2 for QTL genotype qqqq; j = 1,2,3. From Equation 5, the proportions (ψk = ϕ1π1k + ϕ2π2k + ϕ3π3k) of two QTL genotypes are the combinations of the conditional probabilities weighted by the phase probabilities ϕ1 − ϕ3.
Computational Algorithm
We formulate the EM algorithm (Dempster et al. 1977; Meng and Rubin 1993) to estimate the preferential pairing factor, QTL effects, and position in a full-sib family derived from two outcrossing tetraploids. The likelihood of the phenotypes (y) for N offspring in the full-sib family is expressed as
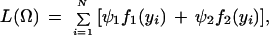 |
6 |
where Ω = (μ, a, r1 or r2, σ2, p, ϕ1, ϕ2) is the vector of unknown parameters containing the overall mean, QTL effects, QTL position, residual variance, the preferential pairing factor and the phase probabilities. The log-likelihood is given by
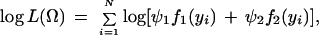 |
7 |
with derivatives for each unknown Ωm:
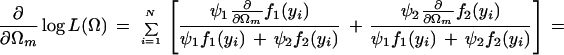 |
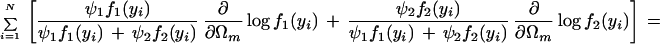 |
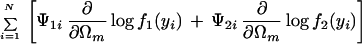 |
where we define
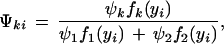 |
8 |
which could be thought of as a posterior probability that progeny i have QTL genotype k. We then implement the EM algorithm with the expanded parameter set {Ω, Ψ}, where Ψ = {Ψk, k = 1, 2}. Conditional on Ψ, we solve for the zeros of (∂/∂Ωm) log L(Ω) to get our estimates of Ω (the M step). The estimates are then used to update Ψ (the E step), and the process is repeated until convergence. The values at convergence are the MLEs.
Unlike the treatment of characterizing a most likely linkage phase by Wu et al. (2002), we implement additional parameters, phase probabilities, within our estimation model. Because it is difficult to derive the maximum likelihood estimators from the mixture model (5) of the phase probabilities ϕ's, preferential pairing factor p and recombination fraction r1 or r2, a grid approach is used to obtain their MLEs by taking all of their possible values. For ϕ's, we increase them by every 0.1 from the range 0–1 under the constraint ϕ1 + ϕ2 + ϕ3 = 1. The values of ϕ's that lead to a maximum likelihood are regarded as their MLEs. Similarly, the MLE of p is estimated by increasing it by every 0.05 in the range from 0 to 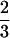 . By moving the assumed position of the QTL every 0.05 cM within a marker interval, the MLE of QTL position is estimated. The program that implements the proposed method can be obtained from http: //www.ifasstat.ufl.edu/genetics/alfalfa.html.
. By moving the assumed position of the QTL every 0.05 cM within a marker interval, the MLE of QTL position is estimated. The program that implements the proposed method can be obtained from http: //www.ifasstat.ufl.edu/genetics/alfalfa.html.
Acknowledgments
We thank Professors Sarah Otto and J. Sybenga for clarifying some ambiguities about the biological process of polyploid meiosis. This work is partially supported by an Outstanding Young Investigator Award (30128017) of the National Natural Science Foundation of China and the University of Florida Research Opportunity Fund (02050259) to R.W. The publication of this manuscript is approved as a Journal Series No. R-08796 by the Florida Agricultural Experiment Station.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL rwu@stat.ufl.edu; FAX (352) 392-8555.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.320202.
REFERENCES
- Allendorf FW, Danzmann RG. Secondary tetrasomic segregation of MDH-B and preferential pairing of homeologs in rainbow trout. Genetics. 1997;145:1083–1092. doi: 10.1093/genetics/145.4.1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Averett JE. Polyploidy in plant taxa: Summary. In: Lewis WH, editor. Polyploidy: Biological relevance. New York, NY: Plenum Press; 1980. pp. 269–273. [Google Scholar]
- Barnes DK, Goplen BP, Baylor JE. Highlights in the USA and Canada. In: Hanson AA, et al., editors. Alfalfa and Alfalfa improvement. Madison, WI: ASA, CSSA and SSSA; 1988. pp. 1–24. [Google Scholar]
- Bever JD, Felber F. The theoretical population genetics of autopolyploidy. Oxford Surv Evol Biol. 1992;8:185–217. [Google Scholar]
- Bingham ET, McCoy TJ. Cytology and cytogenetics of alfalfa. In: Hanson AA, et al., editors. Alfalfa and Alfalfa improvement. Madison, WI: ASA, CSSA and SSSA; 1988. pp. 737–776. [Google Scholar]
- Brouwer DJ, Osborn TC. A molecular marker linkage map of tetraploid alfalfa (Medicago sativa L.) Theor Appl Genet. 1999;99:1194–1200. [Google Scholar]
- Brouwer DJ, Duke SH, Osborn TC. Mapping genetic factors associated with winter hardiness, fall growth, and freezing injury in autotetraploid alfalfa. Crop Sci. 2000;40:1387–1396. [Google Scholar]
- Burner DM. Chromosome transmission and meiotic behavior in various sugarcane crosses. J Am Soc Sugarcane Technologists. 1997;17:38–50. [Google Scholar]
- Butruille DV, Boiteux LS. Selection-mutation balance in polysomic tetraploids: Impact of double reduction and gametophytic selection on the frequency and subchromosomal localization of deleterious mutations. Proc Natl Acad Sci. 2000;97:6608–6613. doi: 10.1073/pnas.100101097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–971. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darlington CD. Chromosome behaviour and structural hybridity in the Tradescantiae. J Genet. 1929;21:207–286. [Google Scholar]
- da Silva J. “A methodology for genome mapping of autopolyploids and its application to sugarcane Saccharum spp.),” Ph.D. dissertation. Ithaca, NY: Cornell University; 1993. [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via EM algorithm. J R Stat Soc Ser B. 1977;39:1–38. [Google Scholar]
- Diwan N, Bouton JH, Kochert G, Cregan PB. Mapping of simple sequence repeat (SSR) DNA markers in diploid and tetraploid alfalfa. Theor Appl Genet. 2000;101:165–172. [Google Scholar]
- Doerge RW, Craig BA. Model selection for quantitative trait locus analysis in polyploids. Proc Natl Acad Sci. 2000;97:7951–7956. doi: 10.1073/pnas.97.14.7951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fjellstrom RG, Beuselinck PR, Steiner JJ. RFLP marker analysis supports tetrasomic inheritance in Lotus corniculatus L. Theor Appl Genet. 2001;102:718–725. [Google Scholar]
- Gaspin C, Schier T. Genetic algorithms for genetic mapping. Lect Notes Comput Sci. 1998;1363:145–155. [Google Scholar]
- Grattapaglia D, Sederoff R. Genetic linkage maps of Eucalyptus grandis and Eucalyptus urophylla using a pseudo-testcross: Mapping strategy and RAPD markers. Genetics. 1994;137:1121–1137. doi: 10.1093/genetics/137.4.1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grivet L, D'Hont A, Roques D, Feldmann P, Lanaud C, Glaszmann JC. RFLP mapping in cultivated sugarcane (Saccharum spp): Genome organization in a highly polyploid and aneuploid interspecific hybrid. Genetics. 1996;142:987–1000. doi: 10.1093/genetics/142.3.987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett CA. A comment on Xie and Xu: Mapping quantitative trait loci in tetraploid species. Genet Res. 2001;78:187–189. doi: 10.1017/s0016672301005262. [DOI] [PubMed] [Google Scholar]
- Hackett CA, Bradshaw JE, Meyer RC, McNicol JW, Milbourne D, Waugh R. Linkage analysis in tetraploid species: A simulation study. Genet Res. 1998;71:143–154. [Google Scholar]
- Hackett CA, Bradshaw JE, McNicol JW. Interval mapping of quantitative trait loci in autotetraploid species. Genetics. 2001;159:1819–1832. doi: 10.1093/genetics/159.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilu KW. Polyploidy and the evolution of domesticated plants. Am J Bot. 1993;80:1491–1499. [Google Scholar]
- Kempthorne O. An introduction to genetic statistics. New York, NY: John Wiley & Sons; 1957. [Google Scholar]
- Kidwell KK, Austin D, Osborn TC. RFLP evaluation of nine Medicago accessions representing original germ plasm sources for North American alfalfa. Crop Sci. 1994;34:230–236. [Google Scholar]
- Lander ES, Botstein D. Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 1989;121:185–199. doi: 10.1093/genetics/121.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo ZW, Hackett CA, Bradshaw JE, McNicol JW, Milbourne D. Construction of a genetic linkage map in tetraploid species using molecular markers. Genetics. 2001;157:1369–1385. doi: 10.1093/genetics/157.3.1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan GJ, Peel D. Finite mixture models. New York, NY: Wiley; 2000. [Google Scholar]
- Meng XL, Rubin DB. Maximum likelihood estimation via the ECM algorithm: A general framework. Biometrika. 1993;80:267–278. [Google Scholar]
- Ming R, Liu SC, Lin YR, da Silva J, Wilson W, Braga D, van Deynze A, Wenslaff TF, Wu KK, Moore PH, et al. Detailed alignment of Saccharum and Sorghum chromosomes: Comparative organization of closely related diploid and polyploid genomes. Genetics. 1998;150:1663–1682. doi: 10.1093/genetics/150.4.1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ming R, Liu SC, Moore PH, Irvine JE, Paterson AH. QTL analysis in a complex autopolyploid: Genetic control of sugar content in sugarcane. Genome Res. 2001;11:2075–2084. doi: 10.1101/gr.198801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto SP, Whitton J. Polyploid incidence and evolution. Annu Rev Genet. 2000;34:401–437. doi: 10.1146/annurev.genet.34.1.401. [DOI] [PubMed] [Google Scholar]
- Ramsey J, Schemske DW. Pathways, mechanisms, and rates of polyploid formation in flowering plants. Annu Rev Ecol Syst. 1998;29:467–501. [Google Scholar]
- Ripol MI, Churchill GA, da Silva JAG, Sorrells M. Statistical aspects of genetic mapping in autopolyploids. Gene. 1999;235:31–41. doi: 10.1016/s0378-1119(99)00218-8. [DOI] [PubMed] [Google Scholar]
- Ronfort J, Jenczewski E, Bataillon T, Rousset F. Analysis of population structure in autotetraploid species. Genetics. 1998;150:921–930. doi: 10.1093/genetics/150.2.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner DZ, Loughin T, Obert DE. Segregation and conditional probability association of molecular markers with traits in autotetraploid alfalfa. Mol Breeding. 2000;6:295–306. [Google Scholar]
- Soltis PS, Soltis DE. The role of genetic and genomic attributes in the success of polyploids. Proc Natl Acad Sci. 2000;97:7051–7057. doi: 10.1073/pnas.97.13.7051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sybenga A. Preferential pairing estimates from multivalent frequencies in tetraploids. Genome. 1994;37:1045–1055. doi: 10.1139/g94-149. [DOI] [PubMed] [Google Scholar]
- ————— Meiotic pairing in autohexaploid Lathyrus: A mathematical model. Heredity. 1995;75:343–350. [Google Scholar]
- ————— Chromosome pairing affinity and quadrivalent formation in polyploids: Do segmental allopolyploids exist? Genome. 1996;39:1176–1184. doi: 10.1139/g96-148. [DOI] [PubMed] [Google Scholar]
- Wu KK, Burnquist W, Sorrells ME, Tew TL, Moore PH, Tanksley SD. The detection and estimation of linkage in polyploids using single-dose restriction fragments. Theor Appl Genet. 1992;83:294–300. doi: 10.1007/BF00224274. [DOI] [PubMed] [Google Scholar]
- Wu RL. Mapping quantitative trait loci by genotyping haploid tissues. Genetics. 1999;152:1741–1752. doi: 10.1093/genetics/152.4.1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu RL, Gallo-Meagher M, Littell RC, Zeng ZB. A general polyploid model for analyzing gene segregation in outcrossing tetraploid species. Genetics. 2001;159:869–882. doi: 10.1093/genetics/159.2.869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu RL, Ma CX, Casella G. A bivalent polyploid model of linkage analysis in outcrossing tetraploids. Theor Pop Biol. 2002;62:129–151. doi: 10.1006/tpbi.2002.1608. [DOI] [PubMed] [Google Scholar]
- Wu SS, Wu RL, Ma CX, Zeng ZB, Yang MCK, Casella G. A multivalent pairing model of linkage analysis in autotetraploids. Genetics. 2001;159:1339–1350. doi: 10.1093/genetics/159.3.1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie CG, Xu SH. Mapping quantitative trait loci in tetraploid populations. Genet Res. 2000;76:105–115. doi: 10.1017/s0016672399004395. [DOI] [PubMed] [Google Scholar]
- Yu KF, Pauls KP. Segregation of random amplified polymorphic DNA markers and strategies for molecular mapping in tetraploid alfalfa. Genome. 1993;36:844–851. doi: 10.1139/g93-112. [DOI] [PubMed] [Google Scholar]
- Zeven AC. Polyploidy and domestication: The origin and survival of polyploids in cytotype mixtures. In: Lewis WH, editor. Polyploidy: Biological relevance. New York, NY: Plenum Press; 1979. pp. 385–408. [DOI] [PubMed] [Google Scholar]