Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2007 Apr 30;104(19):7869–7874. doi: 10.1073/pnas.0701204104

Normal mode refinement of anisotropic thermal parameters for a supramolecular complex at 3.42-Å crystallographic resolution

Billy K Poon †, Xiaorui Chen ‡, Mingyang Lu §, Nand K Vyas §, Florante A Quiocho §, Qinghua Wang §, Jianpeng Ma †,‡,§,
PMCID: PMC1876539  PMID: 17470791

Abstract

Here we report a normal-mode-based protocol for modeling anisotropic thermal motions of proteins in x-ray crystallographic refinement. The foundation for this protocol is a recently developed elastic normal mode analysis that produces much more accurate eigenvectors without the tip effect. The effectiveness of the procedure is demonstrated on the refinement of a 3.42-Å structure of formiminotransferase cyclodeaminase, a 0.5-MDa homooctameric enzyme. Using an order of magnitude fewer adjustable thermal parameters than the conventional isotropic refinement, this protocol resulted in a decrease of the values of Rcryst and Rfree and improvements of the density map. Several poorly resolved regions in the original isotropically refined structure became clearer so that missing side chains were fitted easily and mistraced backbone was corrected. Moreover, the distribution of anisotropic thermal ellipsoids revealed functionally important structure flexibility. This normal-mode-based refinement is an effective way of describing anisotropic thermal motions in x-ray structures and is particularly attractive for the refinement of very large and flexible supramolecular complexes at moderate resolutions.

Keywords: anisotropic temperature factor, conformational flexibility, elastic normal mode analysis, tip effect, x-ray crystallographic refinement

Standard x-ray crystallographic refinement assumes that atomic motions are isotropic, harmonic, and independent of each other. These assumptions are reasonable for many small globular proteins, but they become inadequate for large complexes that carry highly flexible structural components (1, 2). These mobile components often undergo orientation-specific (anisotropic) movements, such as hinge-bending motion between two rigid bodies, that are highly collective and interdependent (3). To properly represent those motions in refinement, ideally, anisotropic thermal parameters should be used. However, large complexes containing highly flexible components often yield crystals that only diffract to moderate resolutions. Thus, limited by the relatively small number of observed diffraction intensities, a full-scale anisotropic refinement that requires three positional and six thermal parameters for each atom is impractical for many systems. Consequently, the structures usually are refined by using one isotropic thermal parameter for each atom instead. These isotropically refined models carry large errors because of the inability to accurately model large-scale anisotropic motions. The convergence of refinement also is slow.

Because normal modes are collective variables, a small set of low-frequency modes can effectively approximate the overall anisotropic motions of structures (for reviews, see refs. 4 and 5). The concept of using low-frequency normal modes as x-ray crystallographic refinement parameters to model thermal factors dates back to the early 1990s (6–11). In subsequent years, several attempts have been made to use normal modes in combination with x-ray data for molecular replacement (12, 13), positional refinement (14), and protein dynamics (15–17). Despite the obvious advantage, normal-mode-based refinement in x-ray crystallography has never been popularized for a number of reasons. One is that the traditional normal mode analysis is based on a molecular mechanics force field. It requires an initial energy minimization that shifts the atomic coordinates, especially those of residues on the protein surface (18, 19). Such positional shifts are detrimental to x-ray refinement because they very often move the atomic coordinates out of the densities. In principle, the problem with this initial minimization could be bypassed with the elastic normal mode analysis (eNMA) that treats the starting structure as the minimized structure (20). However, in the conventional eNMA, such as the anisotropic network model (21), the so-called tip effect in eigenvectors always contaminates the low-frequency modes, making them difficult to use as a continuous basis set, as required in normal-mode-based refinement. This tip effect is particularly severe in large protein complexes. Another reason is that for normal-mode refinement to be effective, the system has to be intrinsically flexible, such as hinged domain motions that are substantially larger than the overall rigid-body motions (22). Those structures usually are the large complexes and have not been very abundant until recent years. Another issue related to the effectiveness of normal-mode-based refinement is the resolution of diffraction data. As shown in our study, the method is much more effective to diffraction data at moderate resolution, e.g., ≈3–4 Å. The systems previously attempted were neither in that resolution range nor large complex structures.

To improve the quality of low-frequency modes, we recently have developed an eNMA that can produce modes with much more accurate eigenvectors without the tip effect (23). This eNMA made it possible for the effective normal-mode-based refinement of large protein complexes with regions of inherent high flexibility. In this article, we present a refinement protocol using a very small set of low-frequency normal modes as refinement parameters to model anisotropic motions. The significantly reduced number of adjustable thermal parameters, even fewer than the conventional isotropic refinement methods, results in a significant increase in the observation/parameter ratio, thus minimizing the risk of overfitting.

The refinement protocol was tested on an isotropically refined 3.42-Å structure of mammalian formiminotransferase cyclodeaminase (FTCD) (24), a 0.5-MDa homooctameric enzyme (25), which plays important roles in coupling histidine catabolism with folate metabolism (26) and integrating the Golgi complex with the vimentin intermediate filament cytoskeleton (27–29). It also is linked to two human diseases, autoimmune hepatitis (30) and glutamate formiminotransferase deficiency (31). The FTCD structure determined by x-ray crystallography and cryo-EM revealed a square doughnut structure of two layers (24).

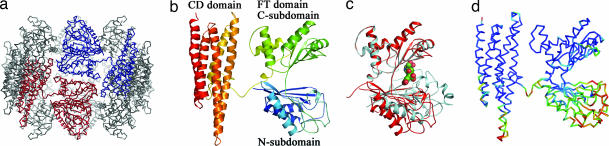
The overall structure of an FTCD octamer is shown in Fig. 1a, with each subunit composed of distinct FT and CD domains (Fig. 1b). The FT domain is divided further into N- and C-subdomains. Some of the domains and subdomains are very flexible, especially the N-subdomain in the FT domain, which from an isolated structure is known to undergo a hinged rigid-body rotation of ≈30° upon binding by folic acid (32) (shown in Fig. 1c). The intrinsic flexibility is illustrated by the rainbow-colored isotropic B factors in one of the subunits of the ligand-free structure (Fig. 1d) (24).

Fig. 1.

Fig. 1.

Open in a new tab

Structure of FTCD. (a) The square doughnut structure of an FTCD octamer. Two subunits are shown in red and blue, respectively. (b) The subunit structure of ligand-free FTCD. Backbone trace color ramped from the N terminus to the C terminus. (c) Superposition of the FT domain of human ligand-free FTCD (red) with the structure of the same domain in isolation (cyan) with the product analog, folinic acid (CPK mode), bound in the groove. (d) Rainbow-colored isotropic B factor in the original model. The hotter the color, the larger the B factors. The high flexibility of the N-subdomain, the linker region, and the lower half of the CD domain is evident.

In the original structure, although 95% of residues were fitted in the density maps, the large size of the enzyme and relatively low resolution of diffraction data made the structure refinement of FTCD slow and difficult. By applying our refinement protocol, the resulting electron density maps allowed improvements of the atomic coordinates, especially in several previously poorly resolved regions. The final model has lower values for Rcryst and Rfree than the isotropically refined model did. Moreover, the distribution of anisotropic thermal ellipsoids revealed functionally important structure flexibility. Thus, the normal-mode-based refinement is an effective way to improve the description of anisotropic thermal motions with drastically fewer adjustable parameters than the conventional isotropic refinement. We expect the method to be particularly useful in refining very large and flexible supramolecular complexes with limited diffraction data.

Results

Although FTCD is an octamer, it was crystallized with only four subunits in the asymmetric unit (24). To obtain the normal modes that represent the intrinsic flexibility of the biological unit of FTCD, we first constructed the octameric FTCD by applying the symmetry operators to the four subunits in the asymmetric unit (23). Then, the new eNMA was used to calculate the normal modes. In the normal-mode-based refinement, the first 50 nonzero modes were combined to replace the isotropic thermal B factors with anisotropic B factors to represent the internal motions. The translation, libration, and screw (TLS) method (33) was used to represent the external motions by treating all of the protein atoms in the asymmetric unit as a rigid body. Iterations of normal-mode-based anisotropic B factor refinement, TLS, positional refinement using REFMAC5 (34) in the CCP4 Suite (35), and manual adjustments using O (36) were carried out until convergence.

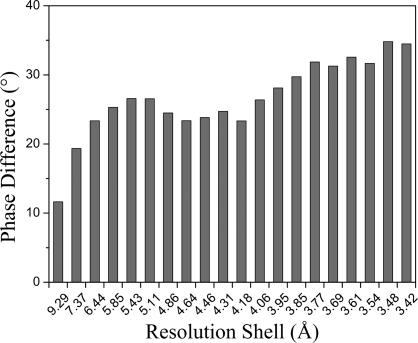
The starting point of our refinement was an unpublished all-atom model of FTCD. Its Cα positions were deposited into the Protein Data Bank (PDB ID code 1TT9). The values for Rcryst and Rfree of the original structure refined in CNS (37) were 24.6% and 28.8%, respectively (24). They became 23.5% and 28.7%, respectively, after the original model was reminimized by REFMAC5. At the beginning of the refinement, the contributions for all modes were artificially scaled to a large value. The first cycle of anisotropic B factor refinement with our normal-mode-based method and positional refinement with REFMAC5 caused a decrease in Rfree to 26.6%. The rapid improvement of Rfree mainly was from the introduction of anisotropic B factors. At the conclusion of the normal-mode-based refinement, the values for Rcryst and Rfree converged to 24.0% and 24.9%, respectively. In the refinement, the same 5% of the data set used in the original CNS refinement was used for the Rfree calculation. The improvement in the normal-mode refinement also was reflected in the ≈26° average phase angle shift. Interestingly, the improvement is larger in the high-resolution range (Fig. 2). The final model had an rmsd of 0.012 Å for bond length and 1.552° for bond angle, which are comparable to values for the original structure. The residues in the final model were distributed in the Ramachandran plot as 78.1%, 17.7%, 3.1%, and 1.1% for most favored, additionally allowed, generously allowed, and disallowed regions, respectively, as calculated by PROCHECK (38), similar to the original model.

Fig. 2.

Fig. 2.

Open in a new tab

Phase shifts of the normal-mode-refined model with respect to the original model. The results are shown as a function of resolution shells. Larger phase shifts are observed for higher resolution shells. Data were calculated by the SFTOOLS program in CCP4 suite.

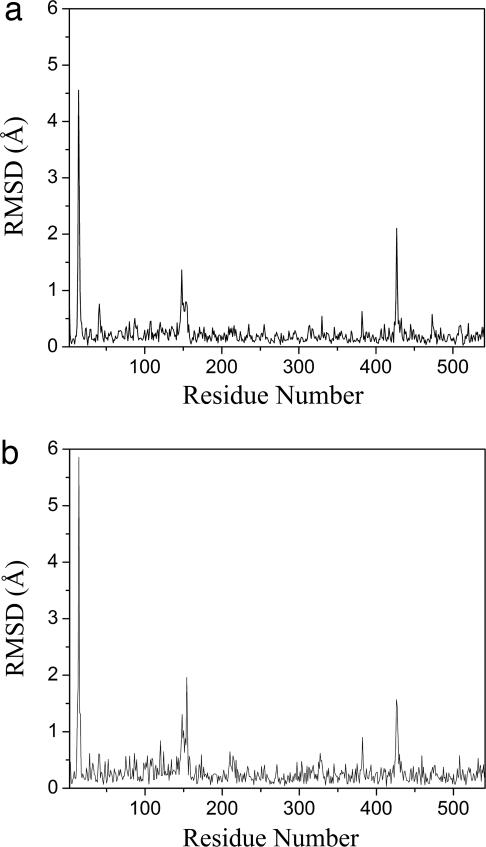
A more important outcome of the normal-mode refinement was the improvement in the electron density maps, which in turn allowed improvement of the structural model. Between the original and the new models (Fig. 3), each subunit had a total of 23 residues with rmsd >0.5 Å in main chains (Fig. 3a) and 47 residues in side chains (Fig. 3b). The overall rmsd of the entire subunit was 0.43 Å for backbone and 0.57 Å for all atoms. The improvements were especially significant in three regions, appearing as spikes in the graphs of rmsd between the two models for both main chains (Fig. 3a) and side chains (Fig. 3b). The same structural changes were observed in all four subunits (data not shown) because of a noncrystallographic symmetry constraint. All these regions were located in highly mobile regions.

Fig. 3.

Fig. 3.

Open in a new tab

Structural shifts of the normal-mode-refined model with respect to the original model. The rmsd (angstroms) along the chain of a single subunit is shown for both main chains (a) and side chains (b). Three large spikes are evident in both graphs. The results for other subunits are very similar because of a noncrystallographic symmetry constraint.

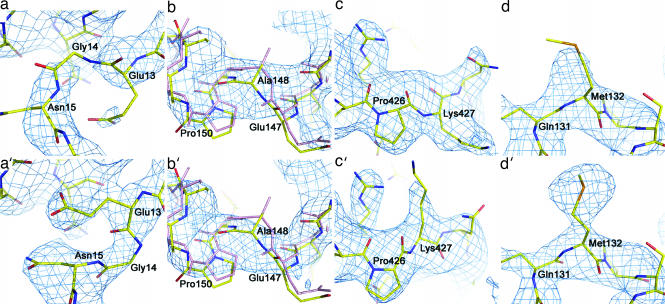
The first spike in rmsd was in the region of residues 13–15 (Fig. 3). The electron density in this region of the original structure was weak and fragmented in the original map (Fig. 4a), making the fitting highly uncertain. This region in the normal-mode-refined omit 2Fo − Fc map was improved to an extent that it allowed straightforward retracing of the backbone and refitting of the Glu-13 side chain (Fig. 4a′). The main-chain atoms in the original structure were misplaced in the density that belonged to the side chains in the refitting.

Fig. 4.

Fig. 4.

Open in a new tab

Examples of large structural adjustments in normal-mode refinement. (Upper) The original models. (Lower) Normal-mode model. (a and a′) Region Glu-13–Asn-15 superimposed with omit 2Fo − Fc map contoured at 1.5σ. (b and b′) Region Glu-147–Pro-150 superimposed with omit 2Fo − Fc map contoured at 1.0σ. In both b and b′, the original model (pink) and the new model (yellow) are superimposed to highlight the structural shifts. (c and c′) Region Pro-426–Lys-427 superimposed with omit 2Fo − Fc map contoured at 1.0σ. (d and d′) Residue Se-Met-132 superimposed with omit 2Fo − Fc map contoured at 1.5σ.

The second spike in rmsd was in the region of residues 147–150 (Fig. 3). Although the electron density of the original structure in this region was good enough for tracing (Fig. 4a), the normal-mode refinement caused a large shift in electron density (Fig. 4b′). Consequently, the backbone was retraced, and side chains were rebuilt for this region.

The third spike was in the region of residues 426–427 (Fig. 3) because of a retracing of the backbone and refitting of the side chain of Lys-427 (Fig. 4 c and c′). Although the original map had reasonable densities for the backbone and side chain of Lys-427, the electron density map in the normal-mode refinement had a large shift in this region, which suggests a flipping of the side chain of Lys-427 to an opposite position (Fig. 4c′).

Besides the structural adjustments, for each subunit of 540 residues in total, there were ≈55 residues whose missing or incomplete densities in the original map had become visible in the normal-mode-refined omit 2Fo − Fc map (with respect to the 1.0σ contour level). Most of them were clustered in very mobile regions. One such example was residue Met-132. The density for the side chain of Se-Met-132 was incomplete at the 1.5σ level in the original map (Fig. 4d), whereas the new omit map showed clear and strong density for it, allowing the placement of its side-chain atoms with ease (Fig. 4d′).

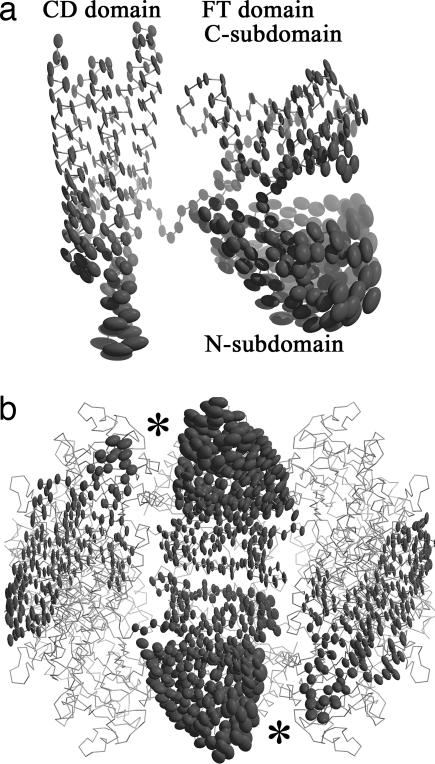
One of the most important outcomes of the refined FTCD structure is the excellent correlation of the anisotropically refined thermal ellipsoids with function. This finding is illustrated clearly in Fig. 5. The regions in the structure of the subunit that are extensively engaged in octamer assembly are significantly less mobile, which is apparent for the C-subdomain of the FT domain and the “upper” portion of the CD domain (Fig. 5a), two of the regions that make the most intersubunit contacts (Fig. 1a; see also ref. 24). In contrast, the regions most associated with catalytic function show very significant collective motion, which is best exemplified by the FT N-subdomain that exhibits the greatest collective motion in the FTCD structure (Fig. 5 a and b). In Fig. 5b, the rough locations of the two reaction centers are indicated by the two asterisks. It is consistent with prior findings that the closure of the active site cleft after binding of an inhibitor in the FT domain is achieved by the movement of the N-subdomain toward the C-subdomain (32) (see also Fig. 1c). The ends of the local two-fold related long CD–CD pair of bundle of helices, which harbors the deaminase active site (24), exhibit the second greatest motion (Fig. 5a). The coupling of the two motions could play a role in the two sequential enzyme activities of FTCD, including channeling of the product of the FT-catalyzed reaction in the FT active site to the CD site (24). The distribution of the thermal ellipsoids suggests that such a shuttling, in addition to the swinging of the anchored polyglutamate tail of the substrate, could be facilitated by the ensemble of conformational flexibility.

Fig. 5.

Fig. 5.

Open in a new tab

Anisotropic deformations of FTCD revealed by the normal-mode refinement. (a) Thermal ellipsoids for a single subunit of FTCD in the same view as Fig. 1b. It is evident that the N-subdomain of the FT domain and the lower half of the CD domain are highly flexible. (b) Side view of the square doughnut of octameric FTCD. For clarity, only the ellipsoids of two FT domains and two CD domains in a neighboring subunit are shown. The two catalytic reaction centers are indicated by the asterisks.

We would like to underscore that, although the FTCD structure refined in this study is the ligand-free form, the distribution of anisotropically refined thermal ellipsoids clearly reveals functionally important motions in the absence of ligands. This observation indicates that the functionally important conformational changes upon ligand binding are facilitated by the inherent structural flexibility encoded in the structure itself and that x-ray crystallographic data of a single “static” structure do contain functionally relevant motional information.

Discussion

This refinement protocol is expected to be very effective on low- or moderate-resolution x-ray diffraction data (e.g., close to 3.0 Å or lower) of very large and flexible complexes. For these systems, using a smaller set of collective variables as thermal parameters becomes more advantageous as a result of a much better observation/parameter ratio. In this study, only 50 low-frequency normal modes (a total of 1,275 anisotropic thermal parameters) were used in the refinement of FTCD structure that contains 16,520 nonhydrogen heavy atoms in the asymmetric unit. Thus, there was more than an order of magnitude of reduction in the number of thermal parameters than the conventional isotropic refinement. Given the total number of unique reflections of 34,749, the structural refinement of FTCD is fundamentally underdetermined. The use of 10 times fewer thermal parameters evidently is advantageous.

The small and local conformational disordering of small globular proteins, such as a single loop disordering or a side chain trapped in two distinct local minima, generally are not suitable for normal-mode-based refinement. For usefulness and limitation of normal-mode analysis, please see the recent comprehensive review in ref. 5. In our experience, this refinement protocol is best suited for large, multidomain complexes with distinct flexible domains at relatively limited resolutions because, among the three assumptions of protein motions in x-ray crystallography (isotropic, harmonic, and independent), normal-mode-based x-ray refinement already takes care of the anisotropy and interdependence, but the assumption of harmonicity remains valid. It is well known that the overall deformations of large, multidomain complexes are more harmonic than those of smaller proteins (5).

In x-ray crystallographic refinement, a related and more commonly used tool for modeling large-scale rigid-body movement is the TLS method (33). The normal-mode-based method does not conflict with the TLS method. Rather, they are complementary. In fact, in this study, the TLS method was used to model the overall rigid-body motion of the entire molecule, the so-called “external” motion (6, 7). The difference between the two methods is that the normal-mode-based method treats the “internal” motion of the molecule collectively, whereas TLS treats different rigid-body groups independently. Thus, in normal-mode refinement, the deformation of the entire protein complex along the low-frequency modes keeps the system in an energetically most favorable fashion, whereas TLS cannot maintain the contiguous rigid bodies if the protein chain is partitioned into many TLS groups. Moreover, the TLS group boundaries are not always consistent with hinge points or domain boundaries for multidomain proteins, whereas normal mode analysis is best known for illustrating the hinge points and collective domain movements [an excellent example is found in a study of the allosteric mechanism of GroEL using normal modes (3)]. Thus, in TLS refinement, if the protein chain is partitioned into many TLS groups, the insertion of breaking points into the middle of large structural units may obscure the nature and extent of the collective motions of large groups (39).

In summary, the field of structural biology has entered into a new era in which a dramatically increasing number of supramolecular complexes are being investigated. These complexes always are organized hierarchically, containing multiple subunits or domains, and almost all of them are highly flexible. Consequently, for many of those complexes, only moderate-resolution x-ray diffraction data usually can be obtained. When refined with conventional isotropic methods, the final structural models frequently contain unresolved or poorly modeled regions because of high flexibility. The inability to accurately model the flexible structural components in turn affects the overall quality of the structural models. Thus, the normal-mode-based refinement protocol described here is very timely in providing a state-of-the-art computational tool for more accurate representation of structural flexibility/disordering in x-ray crystallographic refinement. The results on FTCD have demonstrated an unprecedented ability to improve structural refinement of large, mobile biomolecular complexes at moderate resolutions.

Methods

eNMA Without Tip Effect.

The concept of normal-mode analysis (18, 19, 40) is to express the dynamics of a protein as a linear combination of a set of harmonic modes, known as normal modes, each of which describes the motion of the protein structure in a completely collective fashion. In a recent study (23), a type of eNMA was developed to avoid the so-called tip effect. The method was designed to calculate the normal modes with Cα traces or a subset of Cα traces. For a system with N Cα atoms (i = 1, 2, …, N), the degrees of freedom in internal coordinates are N − 2 bond angles {θi} and N − 3 pseudodihedral angles{ϕi}. The chosen potential function has an extra term in addition to that in conventional eNMA (21, 41):

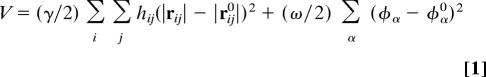graphic file with name zpq01907-6236-m01.jpg
graphic file with name zpq01907-6236-m02.jpg

where ∣rij∣ and ∣rij0∣ are the instantaneous and equilibrium values (or initial values from the coordinates) of pairwise distance between the ith and the jth Cα atoms, respectively. The value of the Heaviside step function, hij, specifies the effect of the cutoff distance, rc. The absolute value of the force constant, γ, is irrelevant to the calculation and often set to 1.0, and Hαα0 are the diagonal elements of Hessian matrix from the conventional eNMA potential in internal coordinate space. Note that the summation in the second term goes over all of the elements in the set of {φα} (all of θ and ϕ). A scaling factor, ς, is chosen so that only the smallest diagonal term is changed dramatically. This term can be adjusted for the amount of stiffness one wishes to introduce into the angular terms. In practice, its value can change from 3 to 30; the larger its value, the stiffer the angular terms. In this study, because FTCD is an extraordinarily flexible system, this term was set to 30 to effectively suppress the tip effect.

With normal modes, one can express the instantaneous displacement of atom j from its equilibrium position in terms of the normal mode variables σ as

graphic file with name zpq01907-6236-m03.jpg

The matrix E is the eigenvector matrix where each column vector represents a pattern of collective motion of atoms in a normal mode. The dimension of matrix E is 3N by M, M ∈ (1, 3N), where M is the number of low-frequency modes.

Crystallographic Refinement of Thermal B Factors.

X-ray diffraction data from a protein crystal provide information about the dynamics of a nonhydrogen atom j in the form of its thermal factor Bj, which is related to the mean-square fluctuation of that atom, 〈Δrj2〉, by Bj = (8π2/3)〈Δrj2〉. The B factors usually are optimized by minimizing the weighted sum of the residual

graphic file with name zpq01907-6236-m04.jpg

by using a least-squares method. Here, h = (h, k, l)T are reciprocal-lattice points of the crystal, w(h) is a weight function for each reflection, and ∣Fobs∣ and ∣Fcal∣ are the amplitudes of the observed and calculated structure factors, respectively. ∣Fcal∣ has

graphic file with name zpq01907-6236-m05.jpg

where q = 2πΘTh denotes a reciprocal lattice vector at a lattice point h, Θ = (a*, b*, c*)T is a 3 × 3 matrix that converts Cartesian coordinates to fractional coordinates with a*, b*, and c* being the reciprocal unit-cell vectors of the crystal. Here, fj is the atomic structure factor usually given by four Gaussian functions and 〈rj〉 is the average position (〈…〉 denotes time average). The dynamic part of the structure factor 〈exp(iqTΔrj)〉 is referred to as the Debye–Waller factor,

graphic file with name zpq01907-6236-m06.jpg

and in conventional isotropic refinement, it usually is approximated by the isotropic B factor in the form of

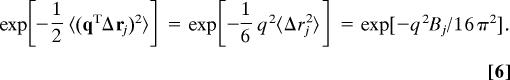graphic file with name zpq01907-6236-m07.jpg

The assumptions in the above equation are that the atomic motions are harmonic, isotropic, and independent.

Normal-Mode-Based Crystallographic Refinement.

In normal-mode-based crystallographic refinement (6, 7), the Debye–Waller factor is expanded in terms of the effective normal modes. The directions of atomic motions are defined by the theoretical eigenvectors of normal modes, and the amplitudes of the displacements of the modes (implicitly contained in the variances and covariances) are optimized against experimental structure factors, rather than by using the theoretical thermal-averaged displacements (40).

If we express the instantaneous atomic displacement of atom j, Δrj, in terms of normal modes (Eq. 2), the Debye–Waller factor in Eq. 5 becomes

graphic file with name zpq01907-6236-m08.jpg

with Ej being a 3 × M matrix representing the portion of matrix E for atom j, Πmn Inline graphic 〈σmσn〉 being the variances Πmm and covariances Πmn (m ≠ n). To assure the positive semidefiniteness of matrix Π, it is expressed by a lower triangular matrix Ω (= {Ωmn}, m, n = 1, 2, …, M; Ωmn = 0, if m < n) as:

graphic file with name zpq01907-6236-m09.jpg

Here, {Ωmn} are the independent parameters to be optimized against experimentally determined amplitudes in the refinement. For M low-frequency modes used in refinement, one has M(M + 1)/2 parameters, which usually is much smaller than the number of heavy atoms in proteins.

In our protocol, the low-frequency modes first are calculated based on the Cα trace (regardless of whether there were any missing Cα atoms along the chain). The remaining atoms of every residue are assumed to move along the same direction as its Cα atom. This Cα-based mode calculation allows applications on extremely large systems.

TLS Refinement, Overall Anisotropic B Factor, and Bulk Solvent Modeling.

With the internal motion accounted for by the normal modes, the TLS method (33) was used to describe the external motion of the molecules. REFMAC5 can calculate the TLS parameters for a system, and TLSANL (42) can take those parameters and convert them into individual anisotropic B factors for each atom. For FTCD, the rigid body was defined to be the four subunits in the asymmetric unit. A coordinate file with ANISOU records containing the TLS contributions was output after running REFMAC5 and TLSANL.

Finally, there was some anisotropy that resulted from the crystal and not from the position of the atoms. Normally, most of this anisotropy is corrected during the data processing stage, but some anisotropic effects remain in the data. We accounted for this additional anisotropy by having an overall anisotropic B factor that was common to all of the atoms.

If we assume that the possible sources of anisotropy are independent of one another, we can construct the anisotropic B factor, U, as

graphic file with name zpq01907-6236-m10.jpg

where Unm is a 3 × 3 matrix calculated from Eq. 7 (Unm = Ej〈σσT〉EjT), Utls is from REFMAC5 and TLSANL, stls is a scaling factor, and Uoverall is the overall anisotropic B factor. The scaling factor was introduced because the TLS refinement was done externally and independent of the minimization of the other parameters in Unm and Uoverall. In total, we have 20 parameters for TLS, 1 parameter for TLS scaling, and 6 parameters for the overall B factor.

To aid the minimization process, a bulk solvent correction similar to that implemented in CNS was used (37). The partial structure factors for the bulk solvent were scaled according to

graphic file with name zpq01907-6236-m11.jpg

where Fprotein is the calculated structure factor for the protein atoms, Fsolvent is the partial structure factor calculated from the solvent mask, ksolvent is like an average solvent density, and Bsolvent is a B factor for the solvent that smoothes the transition from the bulk solvent region to the atomic region. Optimal values for ksolvent and Bsolvent are found by minimizing the residual from Eq. 3.

Positional Refinement and Manual Model Adjustment.

After the normal-mode-based anisotropic B factor refinement, REFMAC5 (34) was used to refine the Cartesian coordinates. From the newly refined B factors and positional parameters in the model, a new omit 2Fo − Fc map was calculated and averaged with the fourfold noncrystallographic symmetry. The map and model were visually inspected in O (36), and manual adjustments were made as necessary. Three iterations of normal-mode-based anisotropic refinement, REFMAC5 refinement, and manual adjustment were needed before the structure convergence.

Our code was implemented in C/C++ using the CLIPPER libraries for crystallographic-related functions (43) and the Computational Crystallography Toolbox (CCTBX) for the Limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) minimizer (44). Furthermore, minimization of the parameters for the anisotropic B factors is accomplished by Brent's principal axis method (45).

Acknowledgments

This work was supported by National Institutes of Health Grants R01-GM067801 and R01-GM068826; the Rice Terascale Cluster funded by the National Science Foundation under Grant EIA-0216467; and a partnership among Rice University, Intel, and HP. B.K.P. is supported by a predoctoral fellowship from the Houston Area Molecular Biophysics Predoctoral Training Program (HAMBP), M.L. is partially supported by a predoctoral fellowship from the W. M. Keck Foundation of the Gulf Coast Consortia through the Keck Center for Computational and Structural Biology, and J.M. and F.A.Q. are supported by a Welch grant.

Abbreviations

eNMA

elastic normal mode analysis

FTCD

formiminotransferase cyclodeaminase

TLS

translation, libration, and screw.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

Data deposition: The atomic coordinates have been deposited in the Protein Data Bank, www.pdb.org (PDB ID code 2PFD).

References

  • 1.Vitkup D, Ringe D, Karplus M, Petsko GA. Proteins. 2002;46:345–354. doi: 10.1002/prot.10035. [DOI] [PubMed] [Google Scholar]
  • 2.Gerstein M, Lesk AM, Chothia C. Biochemistry. 1994;33:6739–6749. doi: 10.1021/bi00188a001. [DOI] [PubMed] [Google Scholar]
  • 3.Ma J, Karplus M. Proc Natl Acad Sci USA. 1998;95:8502–8507. doi: 10.1073/pnas.95.15.8502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Ma J. Curr Protein Pept Sci. 2004;5:119–123. doi: 10.2174/1389203043486892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Ma J. Structure (London) 2005;13:373–380. doi: 10.1016/j.str.2005.02.002. [DOI] [PubMed] [Google Scholar]
  • 6.Diamond R. Acta Crystallogr A. 1990;46:425–435. doi: 10.1107/s0108767390002082. [DOI] [PubMed] [Google Scholar]
  • 7.Kidera A, Go N. Proc Natl Acad Sci USA. 1990;87:3718–3722. doi: 10.1073/pnas.87.10.3718. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Kidera A, Go N. J Mol Biol. 1992;225:457–475. doi: 10.1016/0022-2836(92)90932-a. [DOI] [PubMed] [Google Scholar]
  • 9.Kidera A, Inaka K, Matsushima M, Go N. J Mol Biol. 1992;225:477–486. doi: 10.1016/0022-2836(92)90933-b. [DOI] [PubMed] [Google Scholar]
  • 10.Kidera A, Inaka K, Matsushima M, Go N. Biopolymers. 1992;32:315–319. doi: 10.1002/bip.360320404. [DOI] [PubMed] [Google Scholar]
  • 11.Kidera A, Matsushima M, Go N. Biophys Chem. 1994;50:25–31. doi: 10.1016/0301-4622(94)85017-8. [DOI] [PubMed] [Google Scholar]
  • 12.Suhre K, Sanejouand YH. Acta Crystallogr D Biol Crystallogr. 2004;60:796–799. doi: 10.1107/S0907444904001982. [DOI] [PubMed] [Google Scholar]
  • 13.Lindahl E, Azuara C, Koehl P, Delarue M. Nucleic Acids Res. 2006;34:W52–W56. doi: 10.1093/nar/gkl082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Delarue M, Dumas P. Proc Natl Acad Sci USA. 2004;101:6957–6962. doi: 10.1073/pnas.0400301101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Kundu S, Melton JS, Sorensen DC, Phillips GN., Jr Biophys J. 2002;83:723–732. doi: 10.1016/S0006-3495(02)75203-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Kondrashov DA, Cui Q, Phillips GN., Jr Biophys J. 2006;91:2760–2767. doi: 10.1529/biophysj.106.085894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Kondrashov DA, Van Wynsberghe AW, Bannen RM, Cui Q, Phillips GN., Jr Structure (London) 2007;15:169–177. doi: 10.1016/j.str.2006.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Levitt M, Sander C, Stern PS. J Mol Biol. 1985;181:423–447. doi: 10.1016/0022-2836(85)90230-x. [DOI] [PubMed] [Google Scholar]
  • 19.Brooks BR, Janezic D, Karplus M. J Compt Chem. 1995;16:1522–1542. [Google Scholar]
  • 20.Joti Y, Nakasako M, Kidera A, Go N. Acta Crystallogr D Biol Crystallogr. 2002;58:1421–1432. doi: 10.1107/S0907444902011277. [DOI] [PubMed] [Google Scholar]
  • 21.Atilgan AR, Durell SR, Jernigan RL, Demirel MC, Keskin O, Bahar I. Biophys J. 2001;80:505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Kuriyan J, Weis WI. Proc Natl Acad Sci USA. 1991;88:2773–2777. doi: 10.1073/pnas.88.7.2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Lu M, Poon B, Ma J. J Chem Theor Comp. 2006;2:464–471. doi: 10.1021/ct050307u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Mao Y, Vyas NK, Vyas MN, Chen DH, Ludtke SJ, Chiu W, Quiocho FA. EMBO J. 2004;23:2963–2971. doi: 10.1038/sj.emboj.7600327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Murley LL, MacKenzie RE. Biochemistry. 1995;34:10358–10364. doi: 10.1021/bi00033a006. [DOI] [PubMed] [Google Scholar]
  • 26.Shane B, Stokstad ELR. In: Folates and Pterins. Blakley RL, Benkovic SJ, editors. New York: Wiley; 1984. pp. 433–455. [Google Scholar]
  • 27.Bashour AM, Bloom GS. J Biol Chem. 1998;273:19612–19617. doi: 10.1074/jbc.273.31.19612. [DOI] [PubMed] [Google Scholar]
  • 28.Gao YS, Alvarez C, Nelson DS, Sztul E. J Biol Chem. 1998;273:33825–33834. doi: 10.1074/jbc.273.50.33825. [DOI] [PubMed] [Google Scholar]
  • 29.Gao YS, Vrielink A, MacKenzie R, Sztul E. Eur J Cell Biol. 2002;81:391–401. doi: 10.1078/0171-9335-00260. [DOI] [PubMed] [Google Scholar]
  • 30.Lapierre P, Hajoui O, Homberg JC, Alvarez F. Gastroenterology. 1999;116:643–649. doi: 10.1016/s0016-5085(99)70186-1. [DOI] [PubMed] [Google Scholar]
  • 31.Rosenblattt D. In: The Metabolic and Molecular Bases of Inherited Diseases. Scriver C, Beaudet A, Sly W, Valle D, editors. New York: McGraw-Hill; 1995. pp. 3111–3128. [Google Scholar]
  • 32.Kohls D, Sulea T, Purisima EO, MacKenzie RE, Vrielink A. Structure (London) 2000;8:35–46. doi: 10.1016/s0969-2126(00)00078-2. [DOI] [PubMed] [Google Scholar]
  • 33.Schomaker V, Trueblood KN. Acta Crystallogr B. 1968;24:63–76. [Google Scholar]
  • 34.Murshudov GN, Vagin AA, Dodson EJ. Acta Crystallogr D. 1997;55:240–255. doi: 10.1107/S0907444996012255. [DOI] [PubMed] [Google Scholar]
  • 35.Collaborative Computational Project Number 4. Acta Crystallogr D Biol Crystallogr. 1994;50:760–763. [Google Scholar]
  • 36.Jones TA, Zou JY, Cowan SW, Kjeldgaard M. Acta Crystallogr A. 1991;47:110–119. doi: 10.1107/s0108767390010224. [DOI] [PubMed] [Google Scholar]
  • 37.Brünger AT, Adams PD, Clore GM, DeLano WL, Gros P, Grosse-Kunstleve RW, Jiang JS, Kuszewski J, Nilges M, Pannu NS, et al. Acta Crystallogr D. 1998;54:905–921. doi: 10.1107/s0907444998003254. [DOI] [PubMed] [Google Scholar]
  • 38.Laskowski RA, Macarthur MW, Moss DS, Thornton JM. J Appl Crystallogr. 1993;26:283–291. [Google Scholar]
  • 39.Painter J, Merritt EA. Acta Crystallogr D Biol Crystallogr. 2006;62:439–450. doi: 10.1107/S0907444906005270. [DOI] [PubMed] [Google Scholar]
  • 40.Brooks CL, III, Karplus M, Pettitt BM. Adv Chem Phys. 1988;71:1–249. [Google Scholar]
  • 41.Tirion MM. Phys Rev Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
  • 42.Howlin B, Butler SA, Moss DS, Harris GW, Driessen HPC. J Appl Crystallogr. 1993;26:622–624. [Google Scholar]
  • 43.Cowtan K. IUCr Computing Commission Newsletter. 2003;2:4–9. [Google Scholar]
  • 44.Grosse-Kunstleve RW, Sauter NK, Moriarty NW, Adams PD. J Appl Crystallogr. 2002;35:126–136. [Google Scholar]
  • 45.Brent RP. Algorithms for Minimization Without Derivatives. Mineola, NY: Dover Publications; 2002. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES