Abstract
Spreading depression (SD) is a pathological wave of transient neuronal inactivation. We recently reported that the characteristic sustained complete depolarization is restricted to specific cell domains where the input resistance (Rin) first becomes negligible before achieving partial recovery, whereas in adjacent, more polarized membranes it drops by much less. The experimental study of the participating membrane channels is hindered by their mixed contribution and heterogeneous distribution. Therefore, we derived a biophysical model to analyze the conductances that replicate the subcellular profile of Rin during SD. Systematic variation of conductance densities far beyond the ranges reported failed to fit the experimental values. Besides standard potassium, sodium, and Glu-mediated conductances, the initial opening and gradual closing of an as yet undetermined large conductance is required to account for the evolution of Rin. Potassium conductances follow in the relative contribution and their closing during the late phase is also predicted. Large intracellular potential gradients from zero to rest are readily sustained between shunted and adjacent SD-spared membranes, which remain electroregenerative. The gradients are achieved by a combination of high-conductance subcellular domains and transmembrane ion redistribution in extended but discrete dendritic domains. We conclude that the heterogeneous subcellular behavior is due to local membrane properties, some of which may be specifically activated under extreme SD conditions.
INTRODUCTION
Waves of spreading depression (SD) (1) are responsible for the extension of neuron death in the ischemic penumbra (2). Because of the avalanche-like characteristics and the similarity to anoxic depolarization (3), the participation of individual neurons in SD has been largely underrated, and the membrane mechanisms involved are poorly understood (for review, see (4–6)).
In the CA1 hippocampal monolayer in vivo, where analogous subcellular elements are stratified, the SD-associated extracellular negative direct-current (DC) potential exhibits a nonuniform stereotyped evolution that correlates with the subcellular anatomy of pyramidal cells (7,8). This observation indicates that distinct cellular elements may behave differently during the expansion of the SD wave. Regional differences in light scattering (9) point in the same direction. Early recordings of neuron somata showed that SD produces near complete depolarization, a severe shunt of membrane input resistance (Rin), and the loss of electrical responsiveness (10–12). The almost total loss of membrane resistance led some authors to hypothesize that it was associated with membrane rupture, but studies using probe ions suggested that it was rather due to the opening of specific membrane channels of limited pore size (13). In a pioneering study, a large voltage-independent current was identified during SD using whole-cell recordings of CA1 pyramidal somata (14). Moreover, we recently showed with intradendritic recordings that the SD-related loss of membrane resistance is not homogeneous across the neuron, in keeping with the extracellular distribution of the negative DC potential (15). In fact, sustained longitudinal gradients of intracellular depolarization were found that covered different somatodendritic regions during the different phases of the extracellular SD. As such, maximally depolarized subregions presented a negligible Rin, whereas more polarized dendritic zones maintained a larger Rin and remained electrogenically active.
In this context, it is particularly relevant to identify the nature and subcellular distribution of the participating membrane conductances. The sustained depolarizing conditions of the extracellular space during SD imply that a complex mixture of activated voltage- and ligand-gated conductances will extend variably in overlapping subcellular domains. Experimental studies have not provided conclusive evidence of the membrane conductances that participate in SD, since it is only partly affected by or totally resistant to the blockage of known ligands and/or voltage-gated channels (16–18). In part, this may be due to the heterogeneous subcellular distribution of most membrane channels (19).
Biophysical simulations are an effective way to approach problems such as these. Some models have already focused on SD initiation, propagation, and ion redistribution, and these were based on the electrodiffusion of ions coupled to excitable membranes (20–24). However, such models focused on the reproduction of macroscopic features rather than neuronal membrane events, and they did not contemplate the participation of unknown conductances that might be critical to define the temporal details of SD. Since we now have the subcellular distribution of Rin and Vm at hand, we can estimate the location of the membrane shunt, its magnitude and evolution, and the membrane channels that participate at different anatomical subregions of individual neurons. We have used a detailed biophysical model that incorporates the known density and distribution of all major membrane channels in CA1 pyramidal cells (25–27) to analyze the spatial maps of Rin under depolarizing SD conditions. Experimental variability was taken into account by testing wide ranges of relevant channels. It is important to note that we also made allowance for the activation of unknown channels by calculating the complementary density of the membrane conductance required to achieve the experimental fall in Rin at specific subcellular regions for a given Vm. We took advantage of the long duration of the different phases of SD (8) in which individual conductances can be safely assumed to be at or near steady state. This enables a strong simplification, as it is the fitting of representative snapshots of a few subcellular Rin profiles corresponding to known subcellular distributions of membrane voltages for each phase of SD. It also circumvents the need for a priori knowledge of unknown membrane conductances and of a variety of extraneuronal details required to accurately estimate the evolution of transmembrane ion gradients and membrane potentials at each subcellular region.
Our calculations predict that besides the standard assortment of voltage- and ligand-gated membrane channels, an additional, as yet undetermined, conductance is required to account for the strong drop in Rin during SD. Such a conductance closes gradually during the time span of SD. Potassium conductances follow in the relative contribution and may also close by the end of the wave. We also confirm that large intracellular potential gradients, from zero to rest, can be sustained by a combination of shunted membranes and ion redistribution along extended but discrete cell subregions, whereas SD-spared dendrites remain electroregenerative.
METHODS
Model construction
The computational model was established with a view to analyzing the conductances that replicate the subcellular profile of Rin and Vm during SD. The dual restriction imposed by the local fixation of Rin and Vm limits the possible choice of membrane channels in the model. The omission of any relevant channel will necessarily change the estimated contribution of all the others. Thus, we carefully studied the contribution of both transient and noninactivating currents, placing special emphasis on their realistic density and subcellular distribution. Transient currents are often neglected when modeling long-lasting phenomena. However, their steady-state contribution to the local and global Rin may be notable, especially when Vm is not uniform throughout the cell, as is the case during SD (15). Because of the slow variation of the relevant variables, we were able to use a steady-state approach in which the macroscopic and extracellular variables related to SD can be neglected or set as constant. However, given the critical importance of mutual interactions between adjacent cell subdomains, all efforts were made to introduce a realistic cell morphology and subcellular electrogenesis into the model. Thus, we optimized a well tested and realistic compartmental model of a CA1 pyramidal cell that was specially designed to reproduce the electrophysiological repertoire of apical dendrites (25–27). The compartmental membrane potentials and transmembrane currents were calculated using the GENESIS simulator (28), and an exponential Euler (explicit) method was used with the integration time step (dt) of 0.1 μs.
Pyramidal cell morphology
To produce an accurate analysis of the subcellular conductances it is important to establish the detailed and realistic pyramidal cell morphology, and its electrotonic structure. The dendritic branching pattern of pyramidal cells varies considerably among the population and the use of a particular morphology could bias the dendrite-to-soma coupling. Hence, we have used an average branching pattern, total dendritic length, dendritic tapering, and distribution of spine density obtained from detailed morphometric studies (29,30). In this study, we chose an average pyramidal morphology with no major apical dendritic bifurcation that represents about half of the CA1 pyramidal cells. Each neuron was simulated using 287 compartments, which were distributed between the soma, the apical and basal dendritic trees, and an axon consisting of myelinated portions, nodes of Ranvier, an axon initial segment, and the axon hillock. The length of the compartments was always >0.01 and <0.2 λ. A detailed description of the cell morphology can be found in Supplementary Material (Fig. S1 and Table S1). The total effective area of the neuron was 66,800 μm2 (including spine area). The model used here was chosen because in simpler models, the electrical behavior exhibits unacceptable channel densities that deviate excessively from reported values (25).
Passive electrical properties and electrode shunt
Standard electrotonic parameters for CA1 pyramidal cells have been applied here (31). The membrane capacitance (Cm) was established at 1 μF/cm2 for the soma and dendrites, and at 0.04 μF/cm2 for myelinated axonal compartments. The internal resistivity (Ri) was 100 Ω·cm for the soma and dendrites and 50 Ω·cm for the axon. The membrane resistivity (Rm) was 50,000 Ω·cm2 for the soma, 1000 Ω·cm2 for unmyelinated axonal compartments, 500,000 Ω·cm2 for myelinated axonal compartments, and it was variable in dendrites (31) according to the following equation:
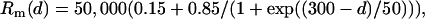 |
where d is the distance to the soma in μm.
The local input resistance (Rin) was measured as the voltage drop obtained during hyperpolarizing current pulses. When calculated in the whole-cell recording mode, this procedure yielded 63 MΩ at the soma and a time constant of 18 ms. Since the electrogenic events specific to dendrite spines are not relevant for this study, we chose to collapse them into the parent dendrites. This is a customary procedure that simplifies the compartmentalization of the morphology of the cell, and it can be considered as electrically equivalent (32). As a result, the values of Rm and Cm of the parental compartments were compensated accordingly. For apical dendrites of CA1 pyramidal cells, the surface ratio between spines and parent dendrites is 1:1 (29). Thus, we used a correction factor of 2 for spiny compartments, i.e., the Rm was halved and the Cm doubled. In other studies, 4πrl has been used to define the area of spiny compartments instead of the formal 2πrl (32).
The simulations described here aim to reproduce the experimental measurements of Rin obtained with sharp electrodes (15,33). The deficient membrane seal around such electrodes introduces a bias in the estimation of Rin. We simulated this electrode leak in the impaled compartment by including an additional shunt to obtain final Rins measured at the soma and apical shaft that fitted well to experimental data of 32 MΩ or 23–25 MΩ, respectively (15,33). Since the electrode shunt also affects measurements in adjacent regions, only the electrode-shunted compartment can be considered to reproduce the experimental conditions. Hence, each somatodendritic map of Rin was constructed using multiple simulations in which only one compartment was shunted at a time. Here, we assumed that the electrode shunt remained constant during SD. Indeed, although some tissue movement does occur during the passage of SD waves, we found no indication that the electrode shunt might vary (15,33).
Ionic channels and conductance densities
Given the sustained conditions of depolarization during SD, the most relevant channels are those that remain open at steady depolarizing potentials. We considered 14 different types of ion channels to simulate the active properties of the cell membrane. These included: three transient sodium conductances in the axon, soma, and dendrites; one persistent somatodendritic sodium current; two calcium currents (high- and low-threshold); one hyperpolarization-activated “h” current; and seven potassium currents. The channel variables were described using a Hodgkin-Huxley type formalism as set out in Tables 1 and 2, and as specified below (see kinetic plots in Supplementary Material, Fig. S2). In addition, an N-methyl-D-aspartate (NMDA)-type conductance plus another unspecific complementary conductance were employed. In preliminary calculations we determined that voltage-dependent sodium and NMDA-type channels require a systematic analysis due to their sustained contribution to steady depolarization. The initial density of potassium channels was taken from the literature (see below) and has been systematically studied in a previous model that accurately reproduces dendritic electrophysiology (25–27,34). Additional testing was performed here to fit their possible contribution to SD (see Results).
TABLE 1.
Ionic conductance kinetic parameters
| Conductance type | Steady-state activation/inactivation | Time constant |
|---|---|---|
| gNa(S,D): activation | 1/(1 + exp((−0.025 − Vm)/0.005)) | 20e−6 + 220e−6/(exp((Vm + 0.055)/0.013) + exp((Vm + 0.055)/−0.080)) |
| gNa(S,D,A): fast inactivation | 1/(1 + exp((−0.050 − Vm)/−0.004)) | 0.0006 + 0.008exp((Vm + 0.045)/0.013)/(1 + exp((Vm + 0.045)/0.0055)) |
| gNa(S): slow inactivation | (1 + 0.8exp((Vm + 0.058)/0.002))/ (1 + exp((Vm + 0.058)/0.002)) | 0.01 + 3exp((Vm + 0.060)/0.011)/(1 + exp((Vm + 0.060)/0.0022)) |
| gNa(D): slow inactivation | (1 + 0.5exp((Vm + 0.058)/0.002))/ (1 + exp((Vm + 0.058)/0.002)) | 0.01 + 3exp((Vm + 0.060)/0.011)/(1 + exp((Vm + 0.060)/0.0022)) |
| gNa(A): activation | 1/(1 + exp((−0.032 − Vm)/0.0042)) | 20e−6 + 220e−6/(exp((Vm + 0.062)/0.013) + exp((Vm + 0.062)/−0.080)) |
| gNaP: activation | 1/(1 + exp((−0.040 − Vm)/0.005)) | 6e−3 |
| gKA(P): activation | 1/(1 + exp((−0.012 − Vm)/0.0085)) | 80e−6 |
| gKA(D): activation | 1/(1 + exp((−0.024 − Vm)/0.007)) | 80e−6 |
| gKA(D,P): inactivation | 1/(1 + exp((−0.056 − Vm)/−0.007)) | 0.26(Vm + 0.050); if τ < 0.002, τ = 0.002 |
| gKDR: activation | 1/(1 + exp((0.005 − Vm)/0.011)) | 0.0012 |
| gKDR(A): activation | 1/(1 + exp((−0.002 − Vm)/0.012)) | 0.0016/(exp((Vm + 0.065)/0.080) + exp((Vm + 0.065)/−0.014)) |
| gKM: activation | 1/(1 + exp((−0.040 − Vm)/0.0075)) | 0.0009 + 0.020exp((Vm + 0.038)/0.025)/(1 + exp((Vm + 0.038)/0.007)) |
| gCaT: activation | 1/(1 + exp((−0.056 − Vm)/0.0062)) | 0.204e−3 + (0.333e−3/(exp((Vm + 0.0158)/0.0182) + exp((−Vm − 0.131)/ 0.0167))) |
| gCaT: inactivation | 1/(1 + exp((Vm + 0.080)/0.004)) | if Vm < 0.081, 0.333e−3exp((Vm + 0.466)/0.0666) |
| else 9.32e−3 + 0.333e−3exp((−0.021 − Vm)/0.0105) | ||
| gh: inactivation | 1/(1 + exp((−0.09 − Vm)/−0.004)) | 0.0006 + 0.04exp((Vm + 0.065)/0.035)/(1 + exp((Vm + 0.065)/0.0035)) |
| Conductance type | Forward rate function (α) | Backward rate function (β) |
| gCaH: activation | −160000(Vm + 0.026)/(exp((Vm + 0.026)/ −0.0045) − 1) | 40000(Vm + 0.012)/(exp((Vm + 0.012)/0.010) − 1) |
| gCaH: inactivation | 2000/exp((Vm + 0.094)/0.010) | 8000/(exp((Vm − 0.068)/−0.027) + 1) |
| gKC: activation | −7700(Vm + Vshift + 0.103)/(exp((Vm + Vshift + 0.103)/−0.012) − 1) | 1700/exp((Vm + Vshift + 0.237)/0.030), τ = 0.0011 |
| Vshift = 40Log([Ca,1]in) − 0.105 | ||
| gKC: inactivation | 1000/exp((Vm + 0.079)/0.010) | 4000/(exp((Vm − 0.082)/−0.027) + 1) |
| gKAHP: activation | 4.8e9/exp((10Log([Ca,2]in − 35)/−2) | 12e9/exp((10Log([Ca,2]in + 100)/5), τ = 0.048 |
Specification of kinetics using the rate functions α and β is equivalent to the use of the steady-state values and time constants. Units: volts, seconds, and millimolar.
TABLE 2.
Standard set of ionic currents and departing conductance densities (mS/cm2)
| Conductance type | Current | Axon | Soma | Apical dendrites | Basal dendrites |
|---|---|---|---|---|---|
| gNa(S,D) |
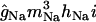 (Vm − ENa) (Vm − ENa) |
0 | 50 | 50 | 50 |
| gNa(A) |
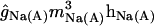 (Vm − ENa) (Vm − ENa) |
100 | 0 | 0 | 0 |
| gKA(P) |
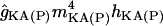 (Vm − EK) (Vm − EK) |
0 | 2 | if dx < 100, LRF(2, 21, 75) | if dx < 100, LRF(2, 40, 120) |
| if dx > 100, 0 | if dx > 100, 0 | ||||
| gKA(D) |
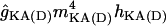 (Vm − EK) (Vm − EK) |
0 | 0 | if dx > 100, LRF(2, 21, 75) | if dx > 100, LRF(2, 40, 120) |
| if dx < 100, 0 | if dx < 100, 0 | ||||
| gKDR | ĝKDRmKDR(Vm − EK) | 0 | 4 | 4 | 5 |
| gKDR(A) |
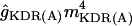 (Vm − EK) (Vm − EK) |
30 | 0 | 0 | 0 |
| gKM |
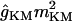 (Vm − EK) (Vm − EK) |
0 | 0.5 | 0.5 | 0.5 |
| gCaT |
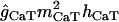 (Vm − ECa) (Vm − ECa) |
0 | 0 | if dx > 100, LRF(0, 0.1143, 1) | 0 |
| if dx < 100, 0 | |||||
| gCaH |
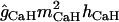 (Vm − ECa) (Vm − ECa) |
0 | 30 | if dx < 100, 3 | 3 |
| if dx > 100, 0 | |||||
| gh | ĝhmh(Vm − Eh) | 0 | 10 | SF(0.1, 0.8, 250, 50) | 0.1 |
| gKC |
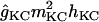 (Vm − EK) (Vm − EK) |
0 | 72 | if dx < 200, LRF(72, −32, 0) | if dx < 80, LRF(72, −70, 0) |
| if dx > 200, 0 | if dx > 80, 0 | ||||
| gKAHP | ĝKAHPmKAHP(Vm − EK) | 0 | 0.6 | LRF(0.6, −0.5, 0.1) | LRF(0.6, −0.8, 0.1) |
ĝi denotes the total conductance in the respective compartment, and Ei the reversal potential of each ionic species. LRF, linear ramp function (ini, slo, min/max): f(dx) = ini + slo (dx/100). Min and max are minimum or maximum limits for conductance densities. Whether the value is min or max depends on the sign of the slope (slo). SF(ini, end, d½, steep) is a sigmoidal function: f(dx) = ini + ((end − ini)/(1 + exp((d½ − dx)/steep))). dx, distance from the soma in micrometers. Secondary apical dendrites follow the same rules as the apical shaft.
Sodium conductances
The three transient sodium conductances incorporated into the model show similar kinetics: gNa(S), gNa(D), gNa(A) (“S” for somatic, “D” for dendritic, and “A” for axonal). An additional gate variable (35) was included in the somatic and dendritic channels to account for the slow inactivation of INa observed in CA1 neurons (36). The activation time constant was decreased to fit the faster rising slope of the action potentials (APs) in vivo. The activation curve of axonal channels was shifted −7 mV (37), and the conductance densities are shown in Table 2. In the soma and dendrites, the conductance density was uniform (38) and sufficiently high to reproduce the precise waveforms of somatodendritic APs in vivo (50 mS/cm2) (25,26). This value is two- to threefold that reported in vitro (38,39), but it is commonly applied in models, as discussed in detail by Varona et al. (25). The gNa density in the axon initial segment was twofold that in the soma (37). The persistent Na+ conductance, gNaP, was incorporated in all somatodendritic compartments, and the kinetics were adapted from French et al. (40), with a V1/2 set at −40 mV. The maximum density was initially set to 0.1 mS/cm2, and it varied within the range of 0.1- to 20-fold. This range spans different measurements that estimated gNaP as ∼1% of the transient gNa.
Calcium conductances
The kinetics of a low-threshold inactivating Ca2+ conductance gCaT (T-type) were taken from Traub et al. (32). This conductance is distributed in the apical dendritic tree and it increases in a linear manner from the proximal dendrites to the distal tuft (39) (maximum density of 1 mS/cm2; see Table 2) The reversal potential for calcium conductances (ECa) varied according to the intracellular Ca2+ concentration [Ca]i (see Calcium dynamics, below, for details). The kinetics of a generic high-threshold inactivating Ca2+ conductance gCaH was taken from Otmakhova et al. (41) and it was restricted to the perisomatic domain (maximum density 3 mS/cm2).
The hyperpolarization-activated “h” conductance (gh)
The gh is differentially distributed along the dendritic arbor of CA1 neurons (42), its density increasing from the soma (0.1 mS/cm2) to the distal tuft (0.8 mS/cm2). The empirical data was fitted in an increasing sigmoidal somatofugal manner (see Table 2), resulting in a sevenfold increase at 350 μm. The kinetics of this conductance was modified from that proposed by Magee (42) for a temperature of 35°C, accelerating the time constants with a Q10 of 4.5. The activation of this current produced a depolarizing sag in the negative voltage drop during hyperpolarizing current pulses and introduced a variable bias in the measured Rin at different somatodendritic locations. The resting values of Rin given above were obtained after fitting this current.
Potassium conductances
The potassium conductances represented are delayed rectifiers (gKDR, one axonal and one somatodendritic); a small persistent muscarinic type (gKM); a transient A-type (one proximal, gKA(P), and one distal, gKA(D)); a short-duration Ca2+- and V-dependent (gKC); and a long-duration Ca2+-dependent (gKAHP). With respect to the delayed rectifiers, the axonal gKDR(A) conductance is similar to that described in Traub et al. (43), modified by shifting the rate functions −5 mV to adjust for the repolarization of axonal spikes. The gKM mediates the initial accommodation during repetitive firing. The gKA(P) and gKA(D) prevent the initiation of APs in the dendrites, as well as limiting back propagation and reducing excitatory synaptic events. The gKC is responsible for most of the repolarization in the AP and the fast after-hyperpolarization, whereas the gKAHP is responsible for the slow after-hyperpolarization. The values of somatodendritic gKDR, gKM, gKC, and gKAHP kinetics were taken from Otmakhova et al. (41). The kinetics and densities for gKA(P) and gKA(D) were taken from Hoffman et al. (34). The density and distribution of the conductances in lateral dendrites follow the same pattern as in the apical shaft, i.e., the values depended on the absolute distance from the soma (see Table 2).
NMDA receptor mediated current
The rapid desensitization of the α-amino-3-hydroxy-5-methylisoxazole-4-proprionic acid (AMPA) currents precludes a sensitive contribution to SD (44). Nevertheless, there is evidence for the participation of Glu currents, mostly of the NMDA receptor subtype (gNMDA), in the depolarization associated with SD. However, the temporal and spatial limits of the contribution of gNMDA remain uncertain. Some authors reported that SD was totally blocked by NMDA antagonists in vitro, whereas we found shortened SD waves that specifically affected the late phase of the negative DC shift in vivo (7,8). In this work, we adopted a maximum availability for gNMDA, which can thus be activated at any phase of SD. With regard to the density and spatial distribution, we assumed homogeneous distribution and density of NMDA receptors all over, except in the soma, according to electrophysiological assays (41,45). We adopted the physiological criterion that gNMDA activates wherever Vm depolarizes enough to release the Mg2+ block. We recently found a reasonable correlation between the extracellular map of negative DC-voltage signals (and increased [K+]o) and the subcellular regions that were selectively depolarized (8,15). Thus, the subcellular regions in which [K+]o is elevated will also be subjected to gNMDA activation. These activated regions were configured as wide somatodendritic bands covering different extensions of the cell at different phases of SD (see below). For the simulations carried out here, we initially used a density of 0.1 mS/cm2 evenly distributed throughout the pyramidal cell, except in the soma, which was devoid of NMDA receptors (e.g., (22,41,45)). However, densities up to 1000-fold higher have been tested to explore their influence on the drop in Rin during SD.
The gNMDA current was built as a mixed Na+/K+ V-dependent conductance to account for the Mg2+ blockage. The permeability ratio was initially set as 1:1. The equilibrium potential varied in the control and the different SD phases, according to the intra/extracellular ion gradient ratio (0 mV at rest). The NMDA current was calculated as follows:
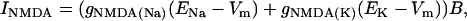 |
where gNMDA(Na) and gNMDA(K) are the Na+ and K+ conductances through the NMDA channel, ENa and EK are the ion equilibrium potentials, and B is a correction factor to account for the Mg2+ block, estimated as in Zador et al. (46):
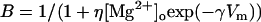 |
with [Mg2+]o set to 2 mM, η = 0.33/mM, and γ = 0.06/mV.
Unspecific Na+/K+ conductance
In the course of the simulations, it turned out that the maximum drop in Rin obtained in experiments could not be attained in the model using the maximum densities of the aforementioned channels. Therefore, it was necessary to assume the presence of additional conductances. We implemented a fake or complementary conductance termed gSD, whose density was varied to reach the experimental Rin value when combined with all other conductances at any specific Vm. We used a V-independent, noninactivating, nonspecific Na+/K+ conductance according to experimental data that suggested the presence of large V-independent currents during SD and anoxia (14,47). The Na+ and K+ component currents were calculated independently, as for the gNMDA, but without the magnesium block. The density and spatial distribution were varied systematically so as to fit the experimental spatial distribution of the drop in Rin along the neuron longitudinal axis in a trial-and-error tuning process. Homogeneous, steplike, and gradientlike spatial distributions spanning different extensions of the cell axis were tested. We focused on the somatoapical section, since no experimental data was available for the drop in Rin at the basal dendritic tree. However, we presumed that the Rin would fall to the same extent as apical membranes (<5% of control). We made no assumptions as to the nature of the gSD current; thus, it was user-activated. Whatever the activation mechanism might be, the quantitative contribution would be similar at steady state.
Equilibrium potentials and calcium dynamics
The equilibrium potential for each ionic subspecies was calculated directly from their concentrations in the intra- and extracellular compartments (3,6). During the SD phases, the compartments contained within defined somatodendritic bands were set with a different transmembrane ion distribution to conform to the experimental observations regarding the variable extracellular ion content and membrane potential (see Table 3) (8,15). The reversal potentials at rest were ENa = 53 mV and EK = −97 mV, yielding a Vm of −67 mV.
TABLE 3.
Ionic concentrations (mM)
| Phase | [K+]o | [K+]i | [Na+]i | [Na+]o |
|---|---|---|---|---|
| Rest | 3.5 | 133 | 20 | 140 |
| SDmain | 40 | 125 | 35 | 90 |
| SDlate | 30 [6] | 125 | 35 | 90 [120] |
Ion concentrations for intra- and extracellular compartments during the different phases of SD. At rest, all compartments are the same. During SDmain, the values given are for active SD compartments only; all others are as in Rest. During SDlate, the compartments that are no longer active still keep an intermediate ion concentration (in brackets).
The ECa was considered to be variable and dependent on the calcium concentrations. The intracellular calcium concentration ([Ca]in) was simulated as two different pools of Ca2+ with different time constants, both following first-order kinetics (48):
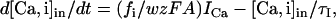 |
where τi is the removal time constant in the ith calcium pool, fi the fraction of ICa influx affecting the ith pool, w is the thickness of the diffusion shell (1 μm in compartments with a diameter >2 μm, or the radius in thinner dendrites), A is the compartment area, z is the valence of the calcium ion, and F is the Faraday constant. In pool 1, τ1 is 0.9 ms and f1 is 0.7. This pool modulates the gKC conductance and defines the reversal potential for calcium (ECa). Pool 2 has a τ2 of 1 s and f2 of 0.024, and it modulates the gKAHP conductance. The extracellular concentration ([Ca]o) remains constant at 1.2 mM and the initial intracellular (resting) concentration is 50 nM. The reversal potential for calcium was
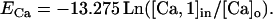 |
Simulation of stimuli
To test the effects of the electrical membrane shunt in discrete cell domains on the electrogenesis of nonshunted subregions during SD, we simulated the synaptic activation of pyramidal cells as for evoked potentials (synchronous activation of closely spaced inputs). Excitatory-inhibitory sequences were timed as in real experiments (Fig. 1). An extensive analysis of the modeled synaptic activation and dendritic integration in physiological conditions can be found in López-Aguado et al. (26) and Ibarz et al. (27).
FIGURE 1.
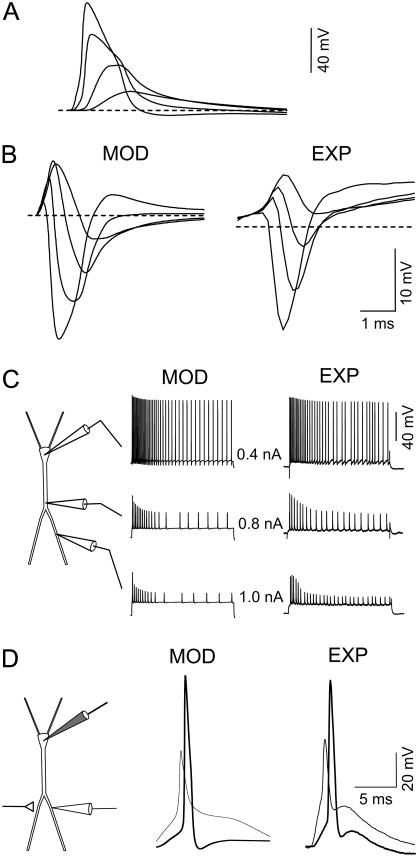
Somatodendritic electrical behavior of the model neuron (MOD) and experiments (EXP). (A) Antidromically elicited action potentials decrease in amplitude and widen during back-propagation into apical dendrites. (B) Reproduction of the spatiotemporal profile of the antidromic population spike in a multineuronal model of the CA1 region (left) in comparison to an experimental profile in the intact animal (right). Decreasing potentials correspond to recordings in the soma layer and successive apical locations in steps of 100 μm. (C) Responses to current pulse injections in the soma and two intradendritic apical loci. Note the fast and slow habituation and the activity-dependent decrease of dendritic APs. The greater the distance from the dendritic current injection, the stronger is the intensity required to obtain a similar firing pattern. (D) Response to activation of glutamatergic synapses over the apical dendritic tree recorded in the soma (thick tracings) and the apical shaft (thin tracings). Experimental recordings are from two different cells.
The synaptic currents were defined as
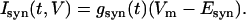 |
Excitatory synaptic input mediated by the AMPA-type Glu receptors was simulated as a dual exponential function conductance:
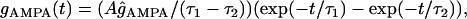 |
with a reversal potential of 0 mV, τ1 = 10.8 ms, and τ2 = 2.7 ms. A is a normalization constant chosen so that gAMPA reached a maximum value of ĝAMPA. The synaptic excitation peaked at 5 ms and had a reversal potential at 0 mV. To simulate Schaffer-commissural activation, AMPA currents were distributed from 150 to 250 μm below the soma, and gsyn = 100 nS (27). The NMDA-type synaptic currents were not used during low-frequency synaptic excitation (49).
Inhibitory synaptic conductance of the gamma aminobutyric acid (GABA)-A type followed an alpha function:
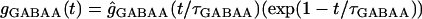 |
with a τGABAA of 7 ms and a reversal potential of −75 mV. This conductance was distributed with a maximum value at the soma that decreased to 0 pS at a distance of 120 μm, and that was delayed for 1.5 ms after excitatory activation. GABA-B inhibition is also included but it had no effect within the time of analysis used here, because its activation is delayed by 15 ms. During SD, GABA conductances were turned off to reproduce its use-dependent fading and the lack of action on SD (50,51).
Optimization of channel density and distribution
The initial values and ranges of the channel densities and their spatial distributions are shown in Table 2. To begin with, we used a model whose channel density and distribution had been optimized in earlier parametric studies to reproduce the normal physiology of CA1 pyramidal cells, with a special emphasis on dendritic electrogenesis (25–27). This model neuron accurately reproduces the synaptic and current-evoked responses in the soma and apical dendrites (Fig. 1; for detailed analysis of somatodendritic behavior see Ibarz et al. (27)). The densities and the distribution of fast Na+ and K+ channels were optimized by reproducing the single-cell antidromic AP waveforms at different somatodendritic loci, as well as the aggregate antidromic population spike in a large-scale simulation. The population spike is an extracellular field, and hence, it is the sum total of action currents at any membrane patch. Thus, its reproduction requires the fine selection of geometrical and electrotonic parameters, as well as the simultaneous fitting of all currents along the entire somatodendritic axis (for detailed analysis of population spike reproduction, see Varona (25) and López-Aguado (26)). The single-cell values considered for the antidromic AP were a soma peak amplitude of 95–103 mV, a half-width of 0.7–0.75 ms, and a rise time of 0.2 ms. In the apical shaft, the amplitude decayed up to ∼50 mV and the half-width increased by up to 2 ms at ∼200 μm from the soma. These optimized channel distributions yielded AP thresholds of 7–9 mV and ∼30 mV depolarization from rest at the soma and apical dendritic loci, respectively. These figures are well within reported experimental values (33). Slower channels were optimized through their participation in current-evoked responses and dendrite integration, including the modulation of somatodendritic forward and backward spikes (25,33,34,36,37,52).
The density of the noninactivating depolarizing conductances gNaP and gNMDA were initially set to the values obtained from the literature (45). However, given the degree of uncertainty (53,54) and their possible relevance in depolarization during SD (23), we also studied them using a range of from 0.1- to 20-fold greater than their basal setting (0.1 mS/cm2 each). The two conductances were distributed homogeneously throughout the entire cell and they were allowed to activate according to their V-dependent kinetics. The density and subcellular distribution of gSD was varied, and it was calculated so as to complement the total conductance required to obtain the experimental Rin when the optimization of all the other channels was insufficient (see above).
The steady-state approach
As mentioned, the subcellular domains affected by SD vary over time (8,15). However, the rate of change of Rin and Vm is very slow, and it can be considered to remain nearly constant for many seconds, i.e., several orders of magnitude slower than the kinetic constant of the slowest membrane channels. Thus, in practice, we can consider these domains to be at steady state, and hence, the only relevant factor to estimate their degree of activation is the Vm. This important detail enabled us to restrict the calculations to represent instants of the SD span, instead of reproducing the complete evolution of all the variables. We were thereby able to use predetermined (experimental) subcellular profiles of Vm and thus avoid the extraordinary complexity of incorporating into the model elements for the continuous estimation of transmembrane Na+ and K+ gradients, such as electrodiffusion, extracellular volume fraction, ion transport, and pumping.
Although the ion concentrations are not relevant to define the steady-state activation of a given channel (or at least their relevance is unknown), we still used 30 different levels of transmembrane Na/K ratios to calculate the local Vm (see Supplementary Material, Fig. S3). The range varies from resting to a near total intra-/extracellular equilibrium, but only a few combinations are acceptable for SD (see Table 3) (3,6,8). This restriction is supported experimentally and it limits the possible combinations of channels capable of taking the Vm to SD values. The permeability ratio was defined by the joint conductance of all membrane channels at steady state.
For technical reasons, the experimental Vm was only measured at the soma and apical dendrites. These only reached a near-zero potential when the extracellular negative potential of SD seized that particular subcellular domain (15). By analogy, the same value of Vm was assumed for the basal tree during SD.
To attain the steady state, each simulation was run until the Vm stabilized in all compartments, usually within a few hundred milliseconds. We routinely employed a stabilization time of 300 ms, after which we injected a current pulse in a selected compartment (−0.8 nA, 200 ms). The last time point was used for the construction of the spatial map of the compartmental conductances. These were represented by a choice of 16 contiguous compartments spanning the entire main basal-to-apical longitudinal axis. Of these, only the soma and seven selected apical compartments were routinely represented in the figures.
Experimental methods
To better define the subcellular anatomical coverage of SD phases and the relationships between the Vo, Vm, and Rin, we used data from earlier in vivo and in vitro experiments. We employed conventional methodology for intra- and extracellular recordings in vivo and in vitro (15,33,55). This experimental data is shown in Fig. 2, whereas all the other figures correspond to model analysis.
FIGURE 2.
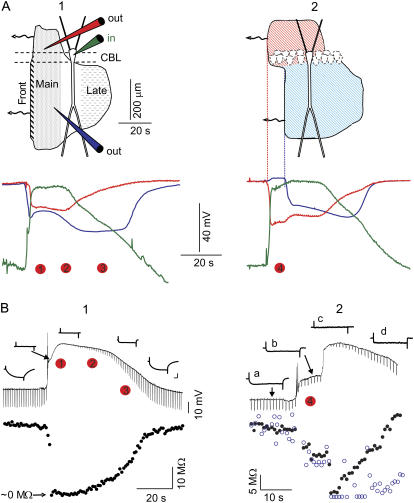
Macroscopic and cellular features of SD waves. (A) Spatiotemporal evolution of the extracellular DC potential, recorded in the soma (red) and apical (blue) regions of the CA1 field, along with the intracellular transmembrane potential (Vm) at the soma of a single pyramidal cell (green) during a typical SD (1) and in the particular case where SD was restricted to the basal dendrites (2). The shaded contour in the upper scheme is a reconstructed snapshot of the spatial progression of SD scaled to a pyramidal cell showing the elements of the neuron affected during the two principal phases. The SD advances toward the left, and the red dots mark the instances chosen for analysis with the model. (B) (Upper) Intracellular recording of a soma (1) and an apical dendrite (2) corresponding to SD waves, as in A. The local input resistance (Rin) was measured at regular intervals by measuring the voltage drop to current pulses. (Lower) Evolution of Rin (solid circles), and estimates of the variation in time constant (τ) (open circles). Inset calibrations are 10 mV and 10 ms.
RESULTS
Phases of SD waves and local variations of input resistance: experimental data
SD waves in the hippocampal CA1 region displayed a stereotyped spatiotemporal evolution. Initially, the waves almost completely covered the basal and apical dendritic trees (characterized here as the main phase), although they then became restricted to a narrow band in the proximal apical tree (characterized as the late phase or apical-only phase). As measured in vivo (8), the evolution of the extracellular negative potential associated with SD is depicted in the upper scheme of Fig. 2 (A 1). In the model, we have analyzed the subcellular conductances at representative moments of the main (apical plus basal) and late (apical-only) phases, as well as the special case where SD only covered the basal dendritic tree (Fig. 2, A 2, time period between the red and blue vertical lines). The abrupt initial depolarization at the wavefront in the apical tree (Fig. 2, A 1, Front) was not studied here, since at this point the channel kinetics shift rapidly and do not approximate to the steady-state conditions. The Vm reached near-zero potential only while the local extracellular negative potential exerted an influence on the corresponding cell domain. In part, it repolarized while SD was still present in other subcellular regions, giving rise to quasisteady intracellular longitudinal gradients of depolarization. This is illustrated in Fig. 2 A by the simultaneous extracellular evolution of the SD recorded in the soma (red) and apical (blue) layers, with the Vm recorded in the soma of a pyramidal cell (green).
The main experimental features of the local changes in Rin during SD were as follows (see (15) for details). Initially, Rin dropped in the soma until it was no longer detected (<5% of control). Subsequently, it recovered slowly during the main phase (up to ∼10–15%), and then more rapidly during the late phase (up to ∼40%), when SD had already been alleviated in the basal dendrites (Fig. 2, B 1). In basal-only SD, the Rin measured within the spared apical dendrites was only reduced and remained stable (Fig. 2, B 2, b). Later on, when SD reached the site of recording in the apical tree (Fig. 2, B 2, c), the apical Rin also dropped to a negligible value before commencing its recovery. Thus, the Rin dropped locally to negligible values at the earliest instant in which any dendritic tree was affected, and it gradually recovered thereafter. The subcellular maps of Rin during each representative phase of SD were obtained from multiple intracellular experiments and by recording from the soma and apical dendrites (15). We chose a few representative instances as milestones to be reproduced with the model (Fig. 2, numbered red dots). Dots 1 and 2 correspond to two points during the main phase, dot 3 to the late phase, and dot 4 to the basal-only SD.
The limits of Rin drop and depolarization for a standard set of membrane channels
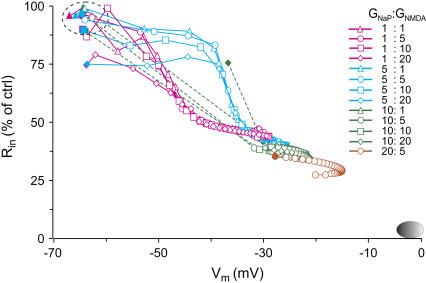
Using our model, we first analyzed the maximum drop in Rin and the Vm depolarization attainable under SD conditions. At rest, Vm is a function of the transmembrane ion gradients and the relative permeability of the ionic subspecies, two variables that are strongly modified during SD. Because of the V-dependency of most channels, the Rin will vary at different degrees of depolarization. For example, the maximum drop in Rin was calculated in the apical trunk as a function of Vm using a standard set of membrane channels and also multiple combinations of gNaP and gNMDA at increasing densities (we tested from 0.1- to 20-fold each) (Fig. 3). As described in Methods, the Vm was varied gradually by shifting the transmembrane gradients for Na+ and K+ throughout the entire cell (Supplementary Material, Fig. S3). As expected from the steady-state joint activation of some V-dependent channels, the more depolarized the Vm the lower the Rin. However, the maximum drop in Rin for the standard channel assortment (1:1) was 46.3% of control. Moreover, the Vm only reached −31.3 mV, well below the experimental values obtained during the main phase of SD (Fig. 3, oval at bottom right). Even at the highest densities of depolarizing conductances (20:20), the Rin never fell below 25% of the control values, and depolarization reached −14 mV at the most. Notably, some of the plots began from a depolarized and shunted value under resting ion gradients (Fig. 3, solid symbols out of the green-dashed oval), indicating an excessive density of gNaP and gNMDA. Indeed, such channel densities were beyond the plausible physiological range compatible with resting conditions in actual neurons.
FIGURE 3.
Estimation of Rin as a function of Vm at steady state. The data was obtained from a representative apical compartment using different combinations of gNaP and gNMDA densities (given in multiples of the control density) and the standard assortment of membrane channels. The oval at the bottom right corner marks the experimental range. Solid symbols (first value on each plot) correspond to values obtained for resting ion gradients. The Rin did not drop to <5% of the control value, nor did the Vm reach the near-zero experimental values. The sequential values in each plot correspond to increasingly depolarizing combinations of intra- and extracellular ion concentrations.
The abrupt jump of Rin across the range of Vm observed for most channel combinations was related to the density of gNaP (note the similar traces within each color set). Increasing densities of gNMDA had only a decreasing effect on Rin at potentials near rest. An apparent paradox was observed wherein an abrupt drop in Rin occurred at more positive Vm the higher the density of gNaP (Fig. 3, blue versus pink traces). The explanation for this phenomenon resides in the increase in the overall Na/K membrane permeability ratio as gNaP increased, pushing the Vm toward the ENa. The gNMDA also appeared to participate to a minor extent, since the ENMDA is more negative than ENa.
Notably, the maximum Vm lingered between −30 to −20, never approaching zero. As mentioned, the value of Vm is determined by the transmembrane distribution of ions, but the actual steady-state value depends on both the total membrane conductance and the relative ion permeability. The maximum value of Vm attainable during SD, assuming equal permeability for Na+ and K+, would be between −10 and −5 mV. In additional simulations, we calculated that stronger depolarization can be achieved either by departing from smaller internal K+ than that used here (133.5 mM) or when the Na/K permeability ratio was >1 (see below).
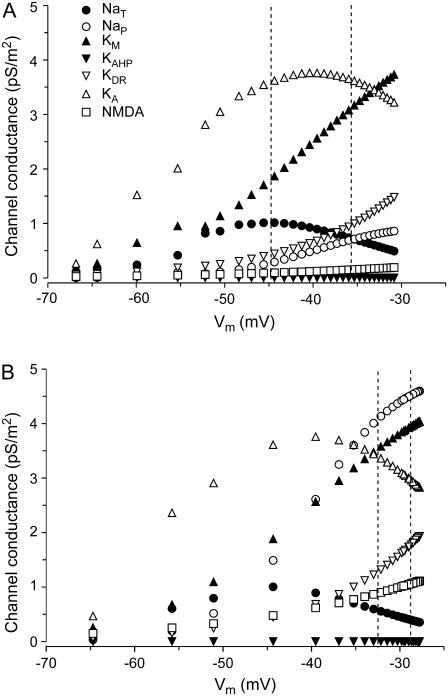
The contribution of the different membrane conductances in the total drop of Rin was analyzed as a function of the Vm. Estimations were obtained in a representative apical compartment at 200 μm from the soma (Fig. 4). Using the standard assortment of channels, the bulk of membrane conductance for the Vm range up to −30 mV was due to KM and KA potassium channels (Fig. 4 A). Only a small fraction of the total conductance (10%) was due to depolarizing channels, with gNaT and gNaP by far exceeding the gNMDA. The contribution of gNaT was due to the “window” current, whereas the values indicated between the vertical lines corresponded to the ion gradients, as in SD. When the maximum values for these conductances were each increased fivefold (Fig. 4 B), only the gNaP contributed a density of conductance similar to the potassium conductances. The latter conductances still dominated, with KM outreaching KA, and the KDR increasing notably. However, the relative contributions would have changed notably had the Vm reached the experimental SD value near zero (see the plots of kinetic behavior in Supplementary Material).
FIGURE 4.
Steady-state conductance densities for some of the membrane channels as a function of the Vm in a representative apical compartment 200 μm from the soma. Estimates (A) using the standard gNaP and gNMDA densities, and (B) when each was increased fivefold. Even for the strongest depolarizing Vm, most channels still preserve a considerable level of conductance.
From these estimations, it can be seen that with the most favorable assortment and densities of channels, the Rin always fell short of the experimental values, at least for the main SD phase. To meet the main experimental criterion of a drop in Rin below 5% of control, we assumed that an additional conductance must be present that we termed gSD, and which we implemented as a mixed Na+/K+ conductance of permeability ratio 1:1 (see Methods).
Additional conductances are required to obtain an optimal fit for the Rin profile during SD
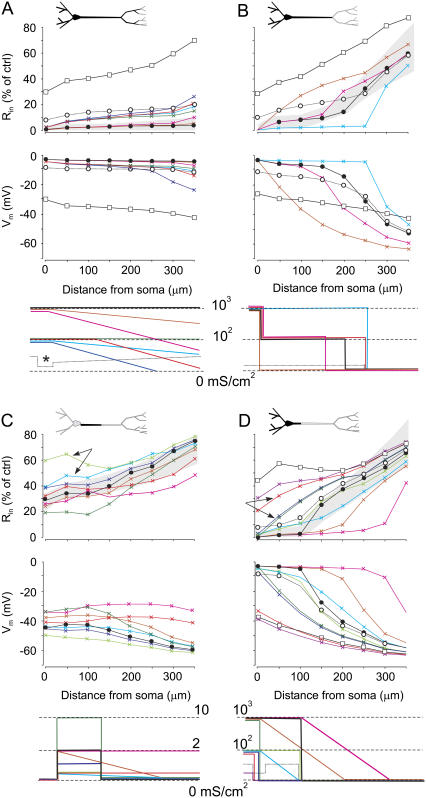
The somatoapical optimization of the membrane conductance was assessed for four representative instants of the SD waves (Fig. 2, red dots), corresponding to different spatial extensions of the SD affecting the pyramidal cell (Fig. 5). The colored plots correspond to different distributions of the complementary conductance gSD. As shown above, this was required when the standard battery of channels (open squares) was insufficient to drive Rin and Vm close to experimental values (see Methods). The gray bands in Fig. 5 correspond to the range of experimental values of the Rin obtained for each phase, used here as confident limits along the length of the apical tree. The estimations falling outside of these limits were considered to differ too greatly from experimental values.
FIGURE 5.
Somatoapical optimization of membrane conductances in four representative instances of SD wave, which correspond to the different spatial extensions of the SD-affected cell domains. The blackened portions of the neuron in the upper schemes denote the regions affected by SD in each phase. Plots correspond to estimates using only the standard assortment of membrane channels (open squares), and simulations using different distributions of the complementary conductance gSD (colored plots), varied as indicated in the lowest plots. The gray bands in the Rin graphs outline the range of experimental (optimum) values for each phase. Optimal values for Vm are near-zero potential for SD-active regions, and they follow a gradientlike decay from there on. Optimal adjustments are plotted by solid circles. (A and B) Two different instances at the beginning and end, respectively, of the main SD phase (see Fig. 2). (C) A representative instance during the late apical-only phase. Note the strong reduction of gSD required to obtain the optimum spatial Rin profile. However, the Vm was far from the near-zero experimental value expected for the active SD zone. (D) The particular case when SD selectively affects the basal dendrites. In this case, the optimum gSD conductance was similar to that for the main phase.
In Fig. 5, columns A and B correspond to two different instants at the beginning and end of the main phase, when SD affected both the basal and apical dendrites. The Rin was undetectable at the earliest point chosen, whereas it had began to recover by the second. The somatoapical optimal adjustment of Rin and Vm (solid circles) in the former required the activity of a strong complementary gSD (range 102–103 mS/cm2) throughout the entire SD affected region (Fig. 5 A). For the sake of simplification, we shall consider the complementary gSD as an additional true conductance. The overall decrease of Rin to 10–15% required a gSD of 50 mS/cm2 (open circles). This example also illustrates the marked contribution of the large dendrites at the soma. In fact, a very low somatic density of gSD (10 mS/cm2 in this example (Fig. 5 A, asterisk)), or none at all, may still be responsible for the large somatic depolarization and the drop in Rin as long as the adjacent dendritic membrane activates sufficient membrane conductance. Late in the main phase (Fig. 5 B), the distal portion of the apical dendrites did not require the activity of gSD. Thus, the gradual increase of Rin toward the apical tuft can be fitted by a strong membrane shunt localized toward the proximal apical region, whereas distal dendrites underwent total closure of the gSD. A strong presence of gSD was still required in the basal dendrites and soma.
The optimization for the late phase, when the basal dendrites were no longer affected and SD was restricted to the proximal apical tree, is also presented (Fig. 5 C). During this phase, a small presence of gSD was still required (≤2 mS/cm2) in the proximal apical dendrites, but not in the basal dendrites. The fine spatial distribution is difficult to predict, since small local changes have profound effects on the extended membrane domains. For instance, the notable differences between a narrow small steplike gSD (0.5 mS/cm2) and a wider gradientlike gSD (light green versus light blue traces) on the Rin of the proximal dendrites (arrows) and on the Vm can be appreciated throughout the apical tree. However, additional mechanisms must have been activated during this phase, as depolarization was unable to even closely approximate to the experimental Vm that reached near-zero along most of the proximal apical tree (15). The optimal spatial fitting of the Rin (solid circles) yielded a Vm that peaked at −40 mV, a considerable discrepancy that was investigated further (see below).
Finally, we analyzed the somatoapical membrane conductances for a special case of basal SD (Fig. 5 D). In this case, a very high gSD (∼102–103 mS/cm2) was required in the soma and basal dendrites, which rapidly decreased within the proximal apical shaft. Again, a gSD of only 50 mS/cm2 would be required to attain a drop in Rin of ∼10–15%. Most of the apical tree was well fitted with the standard channel assortment. As expected from the smooth geometrical transition between the two domains, the soma and the main apical dendrite, is highly relevant for estimations in the latter when no added gSD is considered. This can be appreciated when comparing two distributions with (dark blue) or without (light red) somatic gSD (Fig. 5 D, arrows).
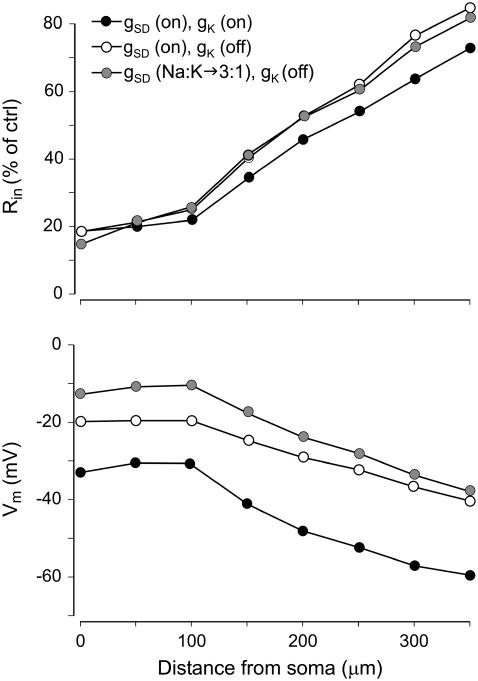
We further explored the poor depolarization obtained for the optimal Rin profile during the late SD phase (Fig. 5 C). Several possibilities were considered to increase the relative permeability of Na+ ions and to more closely reflect the ENa. Increasing the gNa and/or gNMDA conductances was unsuccessful in this respect, as they either caused a parallel decrease in the Rin outside the experimental range, or else the resting Vm could not be sustained (see also Fig. 3). Since the general trend of the complementary gSD was to decrease during the time span of SD, we considered the possibility that potassium channels behave similarly, a treatment that would also increase the Na/K permeability ratio. Indeed, the complete closure of K+ channels promoted a depolarizing shift of 15–20 mV along the entire apical tree that was paralleled by a small decrease in the drop in Rin (Fig. 6, open versus solid circles). Finally, we checked the effects of increasing the Na/K permeability ratio for gSD channels. An additional 10 mV in the depolarizing shift was obtained for a 3:1 ratio (from the initial 1:1) (Fig. 6, shaded circles).
FIGURE 6.
Further optimization for the late phase of SD. By eliminating the potassium channels (open circles), thereby increasing the Na+/K+ conductance ratio, we aimed for additional depolarization without an increase in conductance. A 15- to 20-mV depolarizing jump was achieved (open versus solid circles), and still further depolarization can be obtained by increasing the Na+/K+ permeability ratio through the gSD channels (shaded circles).
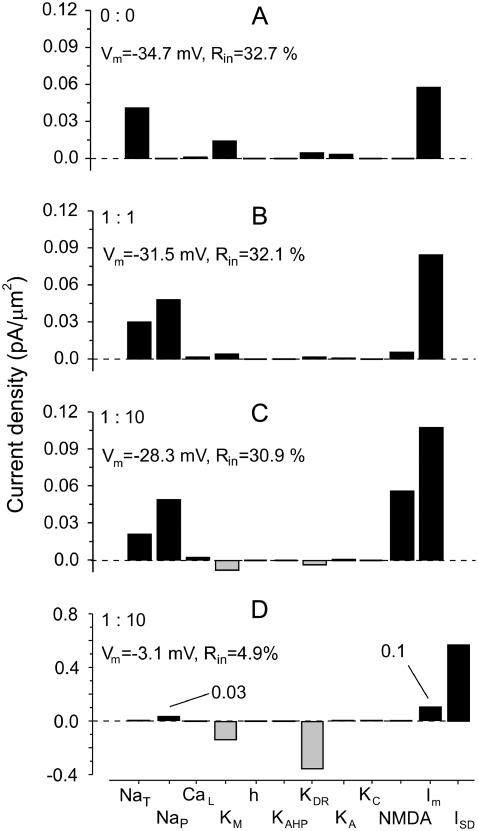
The flow of current
The simulations presented herein enabled the current flow through individual channel types during SD to be examined simultaneously. Each channel type displayed a different current flow depending on the SD phase and cell domain. The results obtained for a representative proximal apical compartment at 100 μm from the soma are shown in Fig. 7 for the instant shown in Fig. 5 B. The current densities in the absence of gNaP and gNMDA (A) and for two different proportions of gNaP and gNMDA (B and C) are illustrated. These are strongly modified when the complementary gSD conductance was included to get an optimal fit (Fig. 7 D). In all cases, there was a net inward transmembrane current (Im), and despite the influence of a very large gSD (∼102 mS/cm2), the Im in this compartment remained similar (0.1 in the presence versus 0.11 pA/μm2 in the absence). This apparent paradox can be explained by the strong spatial cancellation of current in the middle zones of extended and strongly shunted regions of the cell (not shown). In the absence of gSD conductance, the inward current flux mostly passed through transient and persistent Na and NMDA channels. The strong depolarization to a near-zero potential in the presence of gSD inactivated gNaT and decreased gNaP (from 0.05 to 0.03 pA/μm2) as it approached the equilibrium potential. The bulk of the current was carried inward through the gSD conductance and outward through KDR and KM channel types. Indeed, the outward flux of potassium ions in the presence of gSD or high gNMDA was a notable feature (Fig. 7, C and D), although this shifted inward in the two other situations (A and B). This effect was caused by the EK (∼−30 mV) becoming more positive than Vm in the latter cases.
FIGURE 7.
Current density through the different channels during SD. The example shown illustrates the current flow in a representative proximal apical compartment situated 100 μm from the soma at the instant shown in Fig. 5 B (main phase). The effects in (A) the absence of gNaP and gNMDA and (B and C) their presence in two different proportions are shown, with and without (D) complementary gSD conductance.
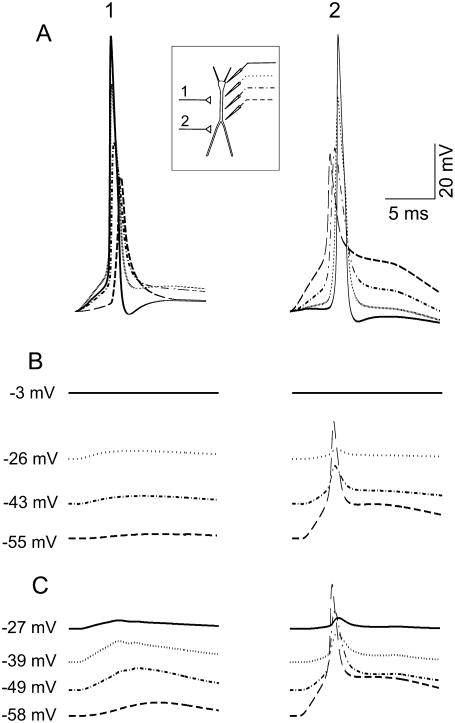
Standing internal depolarization gradients are compatible with distal electrogenesis
It was commonly believed that neuron electrogenesis was completely curtailed during the passage of SD due to excessive depolarization and membrane breakdown. As shown above, strong internal depolarization gradients can be sustained in a quasistable manner between SD-affected and SD-spared subregions of the same cell. Thus, we assessed here whether cell domains distant to the SD-shunted regions could still maintain normal electrical responses. Orthodromic activation was simulated by activation of non-NMDA glutamatergic synapses (25 nS total maximum conductance) throughout the apical dendritic compartments in one of two spatial bands: a proximal (50–150 μm from the soma) and a distal band (250–350 μm from the soma). The evoked responses recorded in the soma and several apical compartments in controls (Fig. 8 A), during basal plus soma SD (Fig. 8 B), or in basal SD alone (Fig. 8 C) were examined. Excitatory postsynaptic potentials (EPSPs) initiated backward or forward spikes during proximal (1) or distal (2) activation, respectively (25,27). As expected, the stationary gradient of depolarization was stronger when SD seized the soma (B). In this case, a reduced EPSP was observed that diminished as the compartment recorded became more depolarized. When the soma was spared by SD, a dendritic spike was initiated that propagated to a limited extent within the apical shaft. These results matched experimental observations well (15).
FIGURE 8.
Internal depolarization gradients during SD are compatible with distal electrogenesis. Orthodromic activation was simulated by activation of non-NMDA glutamatergic synapses (25 nS) in either of two spatial bands, one proximal (1) and the other (2) distal. The computed evoked responses recorded in the soma and several apical compartments (inset) are shown in the control situation (A), during SD affecting the basal dendrites and the soma (B), and during SD in the basal dendrites alone (C). Backward and forward spikes were generated during proximal and distal activation, respectively. When SD seized the soma (B), a sharper stationary gradient of depolarization developed, and only a reduced EPSP with no spike was observed. When the soma was spared, a dendritic spike was initiated distally and propagated to a limited extension within the apical shaft. These results match experimental findings demonstrating that the cell domains distant to SD-shunted regions maintain electrical excitability.
DISCUSSION
The computations presented here explore the state of channel conductances in different cell domains of CA1 pyramidal cells during SD. We found that besides the known potassium, sodium, and Glu-mediated conductances, the correct fitting of the experimental Rin and Vm in individual neurons requires an additional very large conductance (gSD). It is predicted that such gSD would initially open maximally and it would then close gradually during the span of the SD. In parallel, the gradual closure of potassium channels would also be predicted by our model. The computations also demonstrate that large gradients of intracellular potentials can be sustained in SD conditions, such that cell domains at a distance may still undergo electrogenic activity.
Macroscopic versus cellular mechanisms in previous SD models
SD dramatically alters a large number of variables at different levels of brain organization, all of which affect the membrane properties of neurons. Previous models focused on reproducing the macroscopic signs of SD, such as the changes in extracellular ions and the propagating and temporal features (20–24,56). The coupling of electrodiffusion to ion flow through excitable membranes is in the basis of the classic reaction-diffusion notion of SD. Although this approach may be suitable for the mechanism of ignition and spread, it does not apply to the depolarized phase, when most variables change slowly and are near steady state. In general, previous models simplify anatomical settings and give little attention to the subcellular physiology of SD. Also, they share a deterministic temporal evolution governed by the strict relationships that link the kinetics of the different systems involved in ion movements. Although this is a desirable goal, because of the lack of precise experimental data, many details are dealt with only superficially in existing models and a number of variables are omitted or established arbitrarily, depending on the specific mechanism to be analyzed. For example, in Shapiro's model (24) that reproduced the strong ion redistribution, the propagation of SD required direct ion flow between neurons coupled by gap junctions (44), whereas these elements were not even considered in other similar models that reproduced similar features (20,23). The support for this or another element as being central to reproduce well-known features of SD may arise from slight differences in certain parameters that modify the overall excitability of highly unrealistic model neurons. In addition, if a significant proportion of the total membrane conductance is carried through unidentified channels specifically activated during SD, as predicted here, their omission in a continuous time-dependent model will cause notable deviations in the magnitude, distribution, and temporal variation of ion flow. Our steady-state approach is relieved from most of these constraints and makes no assumptions as to the temporal succession. By compiling all time-dependent supraneuronal variables into instantaneous cell maps of Rin and Vm, our model is well suited to explore the subcellular contribution of the different membrane channels. Thus, at given instances it is highly reliable to levels unequaled by continuous time-evolving models.
Methodological considerations
Additional expansion of the model could be obtained by estimating the contribution of chloride channels and more subtypes of Ca2+ channels. Although GABA is released during SD (57), the role of inhibitory conductances is probably marginal (51). Chloride appears to be important in other aspects of SD, such as the velocity of propagation and the tissue susceptibility to initiate the reaction (13,56). However, it does not seem to contribute significantly to SD amplitude (58) and hence, it is unlikely that chloride conductances exert a significant influence in the drop in Rin. Similarly, although Ca2+ channels are known to participate in some aspects of SD (16,59), their role remains ambiguous, and their blockade does not affect SD amplitude in vivo (44). A decreasing effect of Ca2+ channel blockers on hypoxic SD-like macroscopic signals has been reported (17), but these results may not apply to normoxic SD. We found here that the estimated contribution of T and L channel subtypes to the total membrane conductance during SD is negligible. Further improvement of our model could be achieved by adjusting channel kinetics to acid conditions (60), in which Na+ and Ca2+ but not V-dependent K+ channels appear to reduce their conductance (61).
In other models, the operation of ion pumping has been taken into account to reproduce the temporal evolution of ion redistribution (e.g., (22,23)). Although this may be an important element at the front and tail of SD, when ion redistribution is strong, its putative action during the phase of depolarization causes only slow changes of ion concentrations that are well captured by our fixed sets of transmembrane ion concentrations for specific instants. Besides, whatever their efficiency, ion transporters do not modify significantly the value of Rin, and hence, they would not interfere with the activation state of V- and ligand-gated channels at steady state.
In this study, for the sake of computational efficiency we did not include a calculation of extracellular potentials. In a preliminary report (62), we found that the large extracellular negative potential strongly influences the magnitude and spatial distribution of current flow along pyramidal cell membranes (see also (56)). To compensate for this important omission, we used the experimental Vm values obtained by subtracting Vi from Vo in simultaneous intra/extracellular recording experiments (15). Thus, realistic near-zero depolarization in SD-active subcellular patches was achieved. Had we used Vi instead, the activation state of V-dependent channels would be completely different, since in the best of cases Vi only depolarized to −30 mV. At this Vm, several fast V-dependent channels still contribute a notable conductance (22,23), whereas they would be largely inactivated using the Vo-corrected to near-zero potential during SD (cf. Fig. 3). Although the magnitudes of the driving forces and current flow are not critical in this study, an incorrect definition of Vm would have caused major deviations in the local and macroscopic membrane conductance. In turn, this would have led to errors in calculating the contribution of each channel type to the drop in Rin.
A strong nonlinear relationship has been demonstrated between the density of membrane conductances and the local Rin. A deviation in the experimental estimation of Rin during SD may lead to notable changes in the estimation of the optimum density of membrane conductance. Most studies have reported a dramatic loss of somatic Rin during SD that was described as immeasurable (10,11). In hypoxic SD, values between 10% (17) and a less than detectable 5% (63) have been reported. As far as we know, our recent study (15) is the only one specifically devoted to measuring the evolution of Rin along the somatodendritic axis of pyramidal cells. The partial recovery of Rin during SD and its independent evolution in different subcellular locations indicate the importance of precisely defining the SD phase in which Rin was measured, as well as other experimental conditions. Although we abide by our experimental measurements, the optimum conductances for other estimations can also be obtained from this study, as we explored a wide range of parameters for the complementary gSD.
Known and unknown membrane conductances during SD phases
Assuming that there are no complementary (unknown) conductances, we showed that potassium channels of the KA and KM type, and to a lesser extent KDR, dominated the conductance at steady depolarization, as expected from their noninactivating kinetics. This is in agreement with experiments showing a decrease but not blockade of the extracellular voltage signal associated to SD by pharmacological blockade of some K+ channels (64). Their joint contribution to the decrease of Rin was however far from the experimental values. To anticipate possible insufficiencies in the implementation of relevant channels in the model, we checked different density ranges for those most likely to be involved in steady depolarization, such as the gNaP and gNMDA (up to 20-fold each: see refs. 22,23). Still, the activation of these two conductances even when patently in excess was largely insufficient to account for the experimental Rin and Vm. These results may appear surprising as the blockage of gNMDA has generally been reported to repress SD (65). However, the precise role of NMDA receptors on SD remains unclear, since most available experimental data cannot differentiate between the blockade of SD initiation, its propagation or the sustained depolarization. In fact, additional biophysical data points to a limited contribution of gNMDA (see below). Thus, the increase of intracellular Ca2+ or extracellular K+ featured in SD (3,6) are both expected to block the activation of NMDA receptors (53,54,66,67).
One may ask whether activation of known channel types are enough to account for the loss of Rin during SD. Some pharmacological studies using cocktails of channel blockers appear to reach such conclusion (17,18). However, much of these data actually comes from the study of SD-like hypoxic depolarization, whose pharmacology differs from normoxic SD (3,16,47). Effects such as a delayed occurrence or the failure to initiate an hypoxic SD, a diminished speed of propagation, and changes in hypoxic SD duration have been interpreted this way. Even in normoxic SD, such changes may well be accounted by drug interference with conditioning procedures, ignition or propagation of SD, whose membrane mechanisms are not well understood (23,68). The presence of different phases in SD are increasingly recognized (6) and the neuron mechanisms responsible for each may differ.
New membrane channels or subtypes of known channels are being discovered whose participation in SD cannot be explicitly modeled although it can be predicted. Their compiled contribution is captured here by the complementary conductance gSD, required to account for the absolute value of the drop in Rin. This gSD was modeled as an unspecific V-independent conductance, following the V-clamp results by Czéh et al. (14). Indeed, the calculations indicated that additional channels open in accordance with the hypothesis that a specific conductance is activated during SD. Phillips and Nicholson (13) proposed a large SD-specific membrane channel based on calculations of the pore size using probe ions (∼7 Å). Since the pore size of the NMDA complex is smaller (<5 Å) (69), one possibility is that neuronal gap junctions participate in SD as we suggested earlier (44,70,71). Gap junction hemichannels have a variable pore aperture (6–15 Å) (72) that would permit the passage of common ions. However, their involvement awaits direct confirmation. Other putative candidates are transient receptor potential channels (73) and tandem pore domain K+ channels (74), but since their distribution and kinetics are largely unknown, it is difficult to analyze their possible contribution in the model presented here. Low-Ca2+-activated cation channels are also possible candidates (75,76), as they are gated by external Ca reduction and appear to be voltage-independent, two conditions found during SD.
Although the initial fast depolarization may be dominated by fast V-dependent channels (22,23), the inactivating/desensitizing kinetics of many channels and receptors implies a reduced contribution to the transmembrane current flow and the drop of Rin during the sustained main phases. According to our estimations, the ensuing steady depolarization can thus be maintained by subsequent opening of one or several of the mentioned channel candidates well after the major ion changes that occur at the wavefront. For instance, the large drop in extracellular Ca2+, or its intracellular increase could serve as an intracellular signal triggering the opening and modulation of certain channels via second messengers. A hint to the gating mechanisms for these putative channels is in the gradual narrowing of the SD-activated dendritic zone that is here represented by the two instants corresponding to the main and late phases, respectively. This evolution is reminiscent of some wavelike intracellular process shutting down SD-activated channels. We showed, in a previous study, that in the intact animal the late phase may even lose the well-known refractoriness of SD and remain activated up to 1 h, broken only by failed attempts to recover (8). Certainly, whichever membrane channels are responsible for this peculiar behavior, their kinetics and the gating mechanisms are unlike standard V- or ligand-gated channels known so far.
The large current density required to achieve the experimental drop in Rin during the main phase of SD may appear surprising (≥102 mS/cm2). However, such a density is similar to the average maximum density typically employed in models and measured experimentally for transient Na+ channels in the soma and axon initial segment (37). For comparative purposes, this density could be achieved by the simultaneous opening of as few as 20 NMDA-type channels or 10 connexin hemichannels within a 100-μm-long section of the apical shaft. This result is also compatible with evidence showing an abnormally large increase of the holding current in V-clamp experiments (14). Interestingly, although the gSD constitutes the bulk of the active conductance during the main SD phase, it gradually decreased during the span of SD. A similar sag in the holding current during SD was also reported by Czéh et al. (14). The temporal reconstruction of events indicates an explosive spikelike initial opening of the channels represented by the gSD, followed by a slow gradual closing.
In this line, the diminished participation of gSD in the late phase led to the expected decrease of the maximum attainable depolarization, which remained far below the near-zero experimental value. Since the maximum conductance is imposed by the partially recovered Rin, further depolarization cannot be achieved by increasing channel density. In fact, it could only be achieved by increasing the relative weight of Na+ over K+ currents to drive the Vm closer to the ENa. We found a possible solution in the closing of potassium V-dependent conductances (cf. Fig. 7), a behavior analogous to the predicted activity of gSD. We suggest that this behavior may be common to several channel types during the SD span. In fact, the well-known overshoot of the Rin in the wake of SD (14,15) may reflect the visible tail of a generalized closure of membrane channels already initiated at the beginning of SD, after the explosive activation of gSD. Excessive accumulation of Ca2+, depletion of energy metabolites, and dephosphorylation are all among the possible mechanisms that may profoundly affect the kinetics of membrane channels.
Functional implications
It has been shown that the near-zero depolarization in extended portions of the dendritic tree is compatible with near resting conditions and normal electrogenesis being maintained in other parts of the same neuron. Thus, our computations presented here offer biophysical support to our recent intradendritic and field recordings during SD (15). The massive shunt of SD active membranes decreases the space constant, providing effective electrical isolation from adjacent neuron subregions. This important feature rebuts the widely held idea that membrane breakdown is the basis for neuron inactivation and silencing during SD. In contrast, our analysis supports a channel-based theory of SD. The electrical events associated with neural membranes can be fully explained by the simultaneous activity of membrane channels according to their specific subcellular location and kinetics, as in any other electrical signal related to normal functioning. The main qualitative differences are the quasi-steady-state conditions imposed by the new transmembrane ion gradients, and the activation of an undetermined membrane channel of very large conductance or density.
The estimations herein may also explain the persistent failure of previous experimental work to determine the channel conductance responsible for macroscopic SD signals. It becomes clear that a varying number of conductances are simultaneously activated in different cell subregions according to their respective kinetics and local Vm. Thus, the use of channel blockers or cocktails may be insufficient to produce a sizable reduction of the SD-associated signal, especially in the main phase, where as yet undetermined conductances play a dominant role. In this respect, one should be cautious when extrapolating pharmacological data obtained from hypoxic SD, or the effects of drugs on SD aspects other than the Rin drop. A failure of SD to initiate, or the blockade of its propagation, does not identify the mediators of current flow once initiated. Also, the partial success of a specific channel blocker by, for instance, decreasing SD duration, does not necessarily indicate a major contribution of the blocked channel to the Rin drop. One possibility is that metabotropic effects initiated by the activation of a low-density channel may lead to the opening (or modulation) of a stronger conductance.
In the literature of clinical research, SD is viewed rather simplistically as a self-maintained potassium wave to which neurons contribute rather passively by extruding more potassium due to depolarization. Certainly, although such a vicious cycle might be fueled by the opening of V-dependent channels, the kinetics of these channels is generally fast, and their density small, to account for the sustained and profound drop of Rin. The important detail that SD is a moving wave should not deviate attention from the fact that once maximal depolarization and ion redistribution are achieved at the wavefront, the ensuing events are ruled by membrane channels. An earlier report (14), supported by our estimations herein, indicate that V-independent conductances play a major part. Even if cytotoxic Ca2+ load in the cells starts at the wavefront, it is now clear that the extended duration of SD or SD-like depolarization is responsible for the subsequent neuron damage in experimental trials (12,70). Clinical trials attempting to block the main Ca2+ gates (V-dependent Ca2+ channels and NDMA receptors) in ischemia have failed to reproduce the degree of neuroprotection claimed in experimental studies. Therefore, the mixed contribution of a number of channel types would suggest that multiple membranes should be targeted simultaneously in clinical trials. Most importantly, the dominant role of unidentified conductances, predicted in this study, should serve as a prompt for molecular studies aiming to characterize the gating modes of recently discovered membrane channels not normally participating in fast electrical transmission. Also, screening studies aiming to discover new membrane channels are required. The molecular identification of such conductances may be crucial in fighting pathologies involving SD, such as ischemic neurodegeneration and migraine headaches.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank Prof. George G. Somjen, from Duke University, for the critical reading of the manuscript, and Mark Sefton (BiomedRed SL, Madrid, Spain) for editorial assistance. We also thank Dr. Belén Larrosa at the Cajal Institute for helpful comments and Dr. Jonas Dyhrfjeld-Johnsen at University of California, Irvine, for the script code of some channels.
This work was supported by grants BFI 2002/1767 and BFU 2005/8917 from the Spanish Ministries of Science and Technology, and Science and Education, respectively, from the Comunidad Autónoma de Madrid 8.5/030/2003. S.C. is supported by the Human Frontiers Science Program Organization and grant MUR2006/490 from the Consejo Superior de Investigaciones Científicas.
References
- 1.Leão, A. A. P. 1944. Spreading depression of activity in the cerebral cortex. J. Neurophysiol. 7:359–390. [DOI] [PubMed] [Google Scholar]
- 2.Fabricius, M., S. Fuhr, R. Bhatia, M. Boutelle, P. Hashemi, A. J. Strong, and M. Lauritzen. 2006. Cortical spreading depression and peri-infarct depolarization in acutely injured human cerebral cortex. Brain. 129:778–790. [DOI] [PubMed] [Google Scholar]
- 3.Hansen, A. J. 1985. Effects of anoxia on ion distribution in the brain. Physiol. Rev. 65:101–148. [DOI] [PubMed] [Google Scholar]
- 4.Marshall, W. H. 1959. Spreading cortical depression of Leão. Physiol. Rev. 39:239–279. [DOI] [PubMed] [Google Scholar]
- 5.Bureš, J., O. Burešová, and J. Krivánek. 1974. The Mechanism and Application of Leão's Spreading Depression of Electroencephalographic Activity. Academia, Prague.
- 6.Somjen, G. G. 2001. Mechanisms of spreading depression and hypoxic spreading depression-like depolarization. Physiol. Rev. 81:1065–1096. [DOI] [PubMed] [Google Scholar]
- 7.Herreras, O., and G. G. Somjen. 1993. Propagation of spreading depression among dendrites and somata of the same cell population. Brain Res. 610:276–282. [DOI] [PubMed] [Google Scholar]
- 8.Herreras, O., and G. G. Somjen. 1993. Analysis of potentials shifts associated with recurrent spreading depression and prolonged unstable SD induced by microdialysis of elevated K+ in hippocampus of anesthetized rats. Brain Res. 610:283–294. [DOI] [PubMed] [Google Scholar]
- 9.Basarski, T. A., S. N. Duffy, R. D. Andrew, and B. A. MacVicar. 1998. Imaging spreading depression and associated intracellular calcium waves in brain slices. J. Neurosci. 18:7189–7199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sugaya, E., M. Takato, and Y. Noda. 1975. Neuronal and glial activity during spreading depression in cerebral cortex of cat. J. Neurophysiol. 38:822–841. [DOI] [PubMed] [Google Scholar]
- 11.Snow, R. W., C. P. Taylor, and E. Dudek. 1983. Electrophysiological and optical changes of rat hippocampus during spreading depression. J. Neurophysiol. 50:561–572. [DOI] [PubMed] [Google Scholar]
- 12.Herreras, O., and G. G. Somjen. 1993. Effects of prolonged elevation of potassium on hippocampus of anesthetized rats. Brain Res. 617:194–204. [DOI] [PubMed] [Google Scholar]
- 13.Phillips, J. M., and C. Nicholson. 1979. Anion permeability in spreading depression investigated with ion-sensitive microelectrodes. Brain Res. 173:567–571. [DOI] [PubMed] [Google Scholar]
- 14.Czéh, G., P. G. Aitken, and G. G. Somjen. 1993. Membrane currents in CA1 pyramidal cells during spreading depression (SD) and SD-like hypoxic depolarization. Brain Res. 632:195–208. [DOI] [PubMed] [Google Scholar]
- 15.Canals, S., I. Makarova, L. López-Aguado, C. Largo, J. M. Ibarz, and O. Herreras. 2005. Longitudinal depolarization gradients along the somatodendritic axis of CA1 pyramidal cells: a novel feature of spreading depression. J. Neurophysiol. 94:943–951. [DOI] [PubMed] [Google Scholar]
- 16.Jing, J., P. A. Aitken, and G. G. Somjen. 1993. Role of calcium channels in spreading depression in rat hippocampal slices. Brain Res. 604:251–259. [DOI] [PubMed] [Google Scholar]
- 17.Müller, M., and G. G. Somjen. 1998. Inhibition of major cationic inward currents prevents spreading depression-like depolarization in rat hippocampal tissue slices. Brain Res. 812:1–13. [DOI] [PubMed] [Google Scholar]
- 18.Müller, M., and G. G. Somjen. 2000. Na+ dependence and the role of glutamate receptors and Na+ channels in ion fluxes during hypoxia of rat hippocampal slices. J. Neurophysiol. 84:1869–1880. [DOI] [PubMed] [Google Scholar]
- 19.Migliore, M., and G. M. Shepherd. 2002. Emerging rules for the distributions of active dendritic conductances. Nat. Rev. Neurosci. 3:362–370. [DOI] [PubMed] [Google Scholar]
- 20.Tuckwell, H. C., and R. M. Miura. 1978. A mathematical model for spreading depression. Biophys. J. 23:257–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tuckwell, H. C., and C. L. Hermansen. 1981. Ion and transmitter movements during spreading cortical depression. Intern. J. Neurosci. 12:109–135. [DOI] [PubMed] [Google Scholar]
- 22.Kager, H., W. J. Wadman, and G. G. Somjen. 2000. Simulated seizures and spreading depression in a neuron model incorporating interstitial space and ion concentrations. J. Neurophysiol. 84:495–512. [DOI] [PubMed] [Google Scholar]
- 23.Kager, H., W. J. Wadman, and G. G. Somjen. 2002. Conditions for the triggering of spreading depression studied with computer simulations. J. Neurophysiol. 88:2700–2712. [DOI] [PubMed] [Google Scholar]
- 24.Shapiro, B. E. 2001. Osmotic forces and gap junctions in spreading depression: a computational model. J. Comput. Neurosci. 10:99–120. [DOI] [PubMed] [Google Scholar]
- 25.Varona, P., J. M. Ibarz, L. López-Aguado, and O. Herreras. 2000. Macroscopic and subcellular factors shaping CA1 population spikes. J. Neurophysiol. 83:2192–2208. [DOI] [PubMed] [Google Scholar]
- 26.López-Aguado, L., J. M. Ibarz, P. Varona, and O. Herreras. 2002. Structural inhomogeneities differentially modulate action currents and population spikes initiated in the axon or dendrites. J. Neurophysiol. 88:2809–2820. [DOI] [PubMed] [Google Scholar]
- 27.Ibarz, J. M., I. Makarova, and O. Herreras. 2006. Relation of apical dendritic spikes to output decision in CA1 pyramidal cells during synchronous activation: a computational study. Eur. J. Neurosci. 23:1219–1233. [DOI] [PubMed] [Google Scholar]
- 28.Bower, J. M., and D. Beeman. 1998. The Book of Genesis. Exploring Realistic Neural Models with the GEneral NEural SImulation System, 2nd ed. Springer Verlag, New York.
- 29.Bannister, N. J., and A. U. Larkman. 1995. Dendritic morphology of CA1 pyramidal neurones from the rat hippocampus: I. Branching patterns. J. Comp. Neurol. 360:150–160. [DOI] [PubMed] [Google Scholar]
- 30.Trommald, M., V. Jensen, and P. Andersen. 1995. Analysis of dendritic spines in rat CA1 pyramidal cells intracellularly filled with a fluorescent dye. J. Comp. Neurol. 353:260–274. [DOI] [PubMed] [Google Scholar]
- 31.Stuart, G., and N. Spruston. 1998. Determinants of voltage attenuation in neocortical pyramidal neuron dentrites. J. Neurosci. 18:3501–3510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Traub, R. D., E. H. Buhl, T. Gloveli, and M. A. Whittington. 2003. Fast rhythmic bursting can be induced in layer 2/3 cortical neurons by enhancing persistent Na+ conductance or by blocking BK channels. J. Neurophysiol. 89:909–921. [DOI] [PubMed] [Google Scholar]
- 33.Canals, S., L. López-Aguado, and O. Herreras. 2005. Synaptically-recruited apical currents are required to initiate axonal and apical spikes in hippocampal pyramidal cells: modulation by inhibition. J. Neurophysiol. 93:909–918. [DOI] [PubMed] [Google Scholar]
- 34.Hoffman, D. A., J. C. Magee, C. M. Colbert, and D. Johnston. 1997. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 387:869–875. [DOI] [PubMed] [Google Scholar]
- 35.Migliore, M. 1996. Modeling the attenuation and failure of action potentials in the dendrites of hippocampal neurons. Biophys. J. 71:2394–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Colbert, C. M., J. C. Magee, D. A. Hoffman, and D. Johnston. 1997. Slow recovery from inactivation of Na+ channels underlies the activity-dependent attenuation of dentritic action potentials in hippocampal CA1 pyramidal neurons. J. Neurosci. 17:6512–6521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Colbert, C. M., and E. Pan. 2002. Ion channel properties underlying axonal action potential initiation in pyramidal neurons. Nat. Neurosci. 5:533–538. [DOI] [PubMed] [Google Scholar]
- 38.Stuart, G. J., and B. Sakmann. 1994. Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature. 367:69–72. [DOI] [PubMed] [Google Scholar]
- 39.Magee, J. C., and D. Johnston. 1995. Characterization of single voltage-gated Na+ and Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. J. Physiol. 487:67–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.French, C. R., P. Sah, K. J. Buckett, and P. W. Gage. 1990. A voltage-dependent persistent sodium current in mammalian hippocampal neurons. J. Gen. Physiol. 95:1139–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Otmakhova, N. A., N. Otmakhov, and J. E. Lisman. 2002. Pathway-specific properties of AMPA and NMDA-mediated transmission in CA1 hippocampal pyramidal cells. J. Neurosci. 22:199–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Magee, J. C. 1998. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J. Neurosci. 18:7613–7624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Traub, R. D., J. G. R. Jefferys, R. Miles, M. A. Whittington, and K. Tóth. 1994. A branching dendritic model of a rodent CA3 pyramidal neurone. J. Physiol. 481:79–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Herreras, O., C. Largo, J. M. Ibarz, G. G. Somjen, and R. Martín del Río. 1994. Role of neuronal synchronizing mechanisms in the propagation of spreading depression in the in vivo hippocampus. J. Neurosci. 14:7087–7098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Andrasfalvy, B. K., and J. C. Magee. 2001. Distance-dependent increase in AMPA receptor number in the dendrites of adult hippocampal CA1 pyramidal neurons. J. Neurosci. 21:9151–9159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zador, A., C. Koch, and T. H. Brown. 1990. Biophysical model of a Hebbian receptor channel kinetic behavior. Proc. Natl. Acad. Sci. USA. 10:6718–6722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tanaka, E., S. Yamamoto, Y. Kudo, S. Mihara, and H. Higashi. 1997. Mechanisms underlying the rapid depolarization produced by deprivation of oxygen and glucose in rat hippocampal CA1 neurons in vitro. J. Neurophysiol. 78:891–902. [DOI] [PubMed] [Google Scholar]
- 48.Warman, E. N., D. M. Durand, and G. L. F. Yuen. 1994. Reconstruction of hippocampal CA1 pyramidal cell electrophysiology by computer simulation. J. Neurophysiol. 71:2033–2045. [DOI] [PubMed] [Google Scholar]
- 49.Herreras, O., N. Menéndez, A. S. Herranz, J. M. Solís, and R. Martín del Río. 1989. Synaptic transmission at the Schaffer-CA1 synapse is blocked by 6,7-dinitro-quinoxaline-2,3-dione. An in vivo brain dialysis study in the rat. Neurosci. Lett. 99:119–124. [DOI] [PubMed] [Google Scholar]
- 50.Huguenard, J. R., and B. E. Alger. 1986. Whole-cell voltage-clamp study of the fading of GABA-activated currents in acutely dissociated hippocampal neurons. J. Neurophysiol. 56:1–18. [DOI] [PubMed] [Google Scholar]
- 51.Haglund, M. M., and P. A. Swartzkroin. 1990. Role of Na-K pump potassium regulation and IPSPs and seizures in immature rabbit hippocampal slices. J. Neurophysiol. 63:225–239. [DOI] [PubMed] [Google Scholar]
- 52.Herreras, O. 1990. Propagating dendritic action potential mediates synaptic transmission in CA1 pyramidal cells in situ. J. Neurophysiol. 64:1429–1441. [DOI] [PubMed] [Google Scholar]
- 53.Kiedrowski, L. 1999. Elevated extracellular K+ concentrations inhibit N-methyl-D-aspartate-induced Ca2+ influx and excitotoxicity. Mol. Pharmacol. 56:737–743. [PubMed] [Google Scholar]
- 54.Legendre, P., C. Rosenmund, and G. L. Westbrook. 1993. Inactivation of NMDA channels in cultured hippocampal neurons by intracellular calcium. J. Neurosci. 13:674–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Largo, C., J. M. Ibarz, and O. Herreras. 1997. Effects of the gliotoxin fluorocitrate on spreading depression and glial membrane potential in rat brain in situ. J. Neurophysiol. 78:295–307. [DOI] [PubMed] [Google Scholar]
- 56.Teixeira, H. Z., A. C. G. Almeida, A. F. C. Infantosi, M. A. Vasconcelos, and M. A. Duarte. 2004. Simulation of the effect of Na+ and Cl− on the velocity of a spreading depression wave using a simplified electrochemical model of synaptic terminals. J. Neural Eng. 1:117–126. [DOI] [PubMed] [Google Scholar]
- 57.Rodrigues, P. S., A. P. Guimaraes, F. A. de Azeredo, and H. Martins-Ferreira. 1988. Involvement of GABA and ACh in retinal spreading depression: effects of “low calcium-high magnesium” solutions. Exp. Brain Res. 73:659–664. [DOI] [PubMed] [Google Scholar]
- 58.Müller, M. 2000. Effects of chloride transport inhibition and chloride substitution on neuron function and on hypoxic spreading-depression-like depolarization in rat hippocampal slices. Neuroscience. 97:33–45. [DOI] [PubMed] [Google Scholar]
- 59.Richter, F., A. Ebersberger, and H. G. Schaible. 2002. Blockade of voltage-gated calcium channels in rats inhibits cortical spreading depression. Brain Res. 334:123–126. [DOI] [PubMed] [Google Scholar]
- 60.Kraig, R. P., C. R. Ferreira-Filho, and C. Nicholson. 1983. Alkaline and acid transients in cerebellar microenvironment. J. Neurophysiol. 49:831–850. [DOI] [PubMed] [Google Scholar]
- 61.Tombaugh, G. C., and G. G. Somjen. 1996. Effects of extracellular pH on voltage-gated Na+, K+, and Ca2+ currents in isolated CA1 rat neurons. J. Physiol. 493:719–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Makarova, I., J. M. Ibarz, L. López-Aguado, and O. Herreras. 2003. Selective inactivation of neuronal dendritic domains: computational approach to steady potential gradients. Lect. Notes Comput. Sci. 2626:40–45. [Google Scholar]
- 63.Yamamoto, Y., E. Tanaka, Y. Shoji, Y. Kudo, H. Inokuchi, and H. Higashi. 1997. Factors that reverse the persistent depolarization produced by deprivation of oxygen and glucose in rat hippocampal CA1 neurons in vitro. J. Neurophysiol. 78:903–911. [DOI] [PubMed] [Google Scholar]
- 64.Aitken, P. G., J. Jing, J. Young, and G. G. Somjen. 1991. Ion channel involvement in hypoxia-induced spreading depression in hippocampal slices. Brain Res. 541:7–11. [DOI] [PubMed] [Google Scholar]
- 65.Hernández-Cáceres, J., R. Macías-González, G. Brozek, and J. Bureš. 1987. Systemic ketamine blocks cortical spreading depression but does not delay the onset of terminal anoxic depolarization in rats. Brain Res. 437:360–364. [DOI] [PubMed] [Google Scholar]
- 66.Ozawa, S., M. Iino, and K. Tsuzuki. 1990. Suppression by extracellular K+ of N-methyl-D-aspartate responses in cultured rat hippocampal neurons. J. Neurophysiol. 64:1361–1367. [DOI] [PubMed] [Google Scholar]
- 67.Petzold, G. C., O. Windmuller, S. Major, K. Bucheim, D. Megow, S. Gabriel, T. N. Lehmann, C. Drenckhahn, O. Peters, H. Meierkord, U. Heinemann, U. Dirnagl, and J. P. Dreier. 2005. Increased extracellular K+ concentration reduces the efficacy of N-methyl-D-aspartate receptor antagonists to block spreading depression-like depolarizations and spreading ischemia. Stroke. 36:2070–2077. [DOI] [PubMed] [Google Scholar]
- 68.Larrosa, B., J. Pastor, L. López-Aguado, and O. Herreras. 2006. A role for glutamate and glia in the fast network oscillations preceding spreading depression. Neuroscience. 141:1057–1068. [DOI] [PubMed] [Google Scholar]
- 69.Villarroel, A., N. Burnashev, and B. Sakmann. 1995. Dimensions of the narrow portion of a recombinant NMDA receptor channel. Biophys. J. 68:866–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Largo, C., P. Cuevas, G. G. Somjen, R. Martín del Río, and O. Herreras. 1996. The effect of depressing glial function on rat brain in situ on ion homeostasis, synaptic transmission and neuronal survival. J. Neurosci. 16:1219–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Largo, C., G. Tombaugh, P. G. Aitken, O. Herreras, and G. G. Somjen. 1997. Heptanol but not fluoroacetate prevents the propagation of spreading depression in rat hippocampal slices. J. Neurophysiol. 77:9–16. [DOI] [PubMed] [Google Scholar]
- 72.Müller, D. J., G. M. Hand, A. Engel, and G. E. Sosinsky. 2002. Conformational changes in surface structures of isolated connexin 26 gap junctions. EMBO J. 21:3598–3607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lipski, J., T. I. Park, D. Li, S. C. Lee, A. J. Trevarton, K. K. Chung, P. S. Freestone, and J. Z. Bai. 2006. Involvement of TRP-like channels in the acute ischemic response of hippocampal CA1 neurons in brain slices. Brain Res. 1077:187–199. [DOI] [PubMed] [Google Scholar]
- 74.Gabriel, A., M. Abdallah, C. S. Yost, B. D. Winegar, and C. H. Kindler. 2002. Localization of the tandem pore domain K+ channel KCNK5 (TASK-2) in the rat central nervous system. Brain Res. Mol. Brain Res. 98:153–163. [DOI] [PubMed] [Google Scholar]
- 75.Hablitz, J. J., U. Heinemann, and H. D. Lux. 1986. Step reductions in extracellular Ca2+ activate a transient inward current in chick dorsal root ganglion cells. Biophys. J. 50:753–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Xion, Z.-G., W.-Y. Lu, and J. F. McDonald. 1997. Extracellular calcium sensed by a novel cation channel in hippocampal neurons. Proc. Natl. Acad. Sci. USA. 94:7012–7017. [DOI] [PMC free article] [PubMed] [Google Scholar]