Optimal Specificity and Function for Flexible Biomolecular Recognition

Abstract

Biomolecular associations often accompanied by large conformational changes, sometimes folding and unfolding. By exploring an exactly solvable model, we constructed the free energy landscape and established a general framework for studying the biomolecular flexible binding process. We derived an optimal criterion for the specificity and function for flexible biomolecular binding where the binding and conformational folding are coupled.

The study of associations between two biomolecules (e.g., proteins, RNA, or DNA) is the key to understanding molecular recognition and function. A standard paradigm, which has been successfully applied for many enzyme proteins, is that molecular function (e.g., binding) is determined by molecular structure. The lock-and-key mechanism of binding assumes that biomolecules maintain rigid structures during association (1). The induced fit mechanism (2) suggests that biomolecules can adjust their conformations to a limited extent during the association. In nature, however, molecular binding often involves large conformational changes in various stages of cell function. It has been estimated that up to 30% of proteins, when isolated, are in their unfolded or partially disordered form (3–6). Because the final native binding state is usually well structured, this implies that binding toward the native state occurs concomitantly with large conformational changes (e.g., folding). The flexible or disordered form of the proteins in the cells can be targeted for rapid turnover, thus providing an additional lever of control. Here, flexibility rather than rigidity is crucial for binding as well as for biological function. However, flexible binding processes are not yet very well understood. An understanding of how flexibility might help molecular recognition and function is one of the most challenging tasks facing molecular biologists. Addressing this issue can lead to a new paradigm in molecular biology—one that will answer critical questions of how molecular function is determined by flexibility and dynamics, in addition to structure.

Some recent experiments have begun to investigate the mechanisms of flexible binding (7). However, there are so far limited theoretical investigations on this (4–6,8). Recently we carried out theoretical studies on biomolecular binding at the interface (9), which provided a basis for studying the more general case of flexible binding.

In this study, we will first construct a thermodynamic energy landscape for molecular recognition and address the roles of flexibility in determining the binding affinity and functional specificity. Affinity and specificity are the two key factors in molecular recognition. Affinity measures the stability resulting from the association of two molecules; specificity is the ability of one molecule to bind with another molecule while discriminating against others. For rigid binding, affinity, and specificity are often correlated. Yet, in flexible binding, flexibility can enable molecules to adjust their conformations to reach the best fit (e.g., high specificity). Quantifying the specificity as well as affinity in flexible binding is crucial in uncovering the mechanism of flexible binding.

Flexible binding involves both binding and conformational degrees of freedom. Thus we need at least three reaction coordinates to describe it: Q_b, fraction of native spatial contacts for interface binding; Q_f1 and Q_f2, fraction of native spatial contacts for flexible conformational change or folding (see Fig. 1). Based on this, we can construct an energy function and derive a free energy landscape

FIGURE 1.

Individual protein/interface landscapes and the resulting combined flexible binding landscape.

From the thermodynamic analysis, we expect that the requirement of stable binding against trapping would lead to a funneled binding landscape to guarantee both affinity and specificity (4–6,8,9). Only binding with landscape funneled against traps can survive natural evolution, be relatively stable, and perform specific biological functions. With this approach, the role of the interplay between binding and flexibility can be uncovered. Biomolecules need some affinity to be stable but they also need flexibility to adjust to achieve optimal fit and perform specific biological functions. The reality is a balance between the two. We will find an optimal criterion of binding specificity. It can be used for guiding further atomic detailed studies and flexible drug design.

It is known that the fundamental interactions of molecular binding are dominated by the hydrophobic interactions energetically, the electrostatic interactions often acting as the directional force guiding for the molecular binding (10). Binding is guided by the long-range electrostatic interaction. Binding is also controlled by hydrophobic interactions for the thermodynamic stability. The real binding process is the combination of the two. We will focus our attention on the latter process since the first process is studied by many researchers before (10).

We derived the thermodynamic free energy expression for the flexible binding (details in Supplementary Material):

where N₁ and N₂ are the numbers of the amino acid residues for protein 1 and 2. 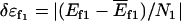is the energy gap or bias per contact toward the native folded state of protein 1, is the energy gap or bias per contact toward the native folded state of protein 2, is the energy gap or bias per contact toward the native binding state. T is temperature.

is the configurational entropy per contact. The are the variances or the roughness of the energy landscape per contact for the folding of protein 1, folding of protein 2, and the binding of protein 1 and 2, respectively.

There exists a characteristic temperature where the thermodynamic entropy of the system vanishes and below which the system is completely trapped:

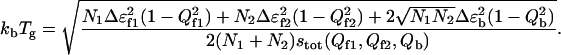This temperature signals the trapping into a low energy conformational state at We can clearly see

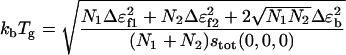when 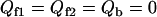(nonnative unfolding-unbinding states).

Fig. 2 shows the phase diagram in terms of the combined energy gap and roughness 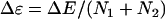relative to temperature for binding folding energy landscape. There are several phases, the native phase (both binding and folding), partially native phase (native binding but with unfolding phases, native binding but one folded and one unfolded phases, both native folded but unbinding phase, one native folded and one unfolded but unbinding phase), and completely unbinding and unfolded phase. In addition there might be a possible trapping phase for the whole complex.

FIGURE 2.

The phase diagram of binding: native, partially native, nonnative, and trapping phases with combined gap and roughness of the binding folding landscape.

The native transition temperature T_native can be determined by setting the free energy equal between native and nonnative phase

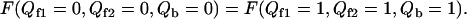To guarantee the thermodynamic stability and discriminate from the local traps, the binding transition temperature T_native needs to be higher than the local trapping temperature T_g, similar to protein folding (11). We can see the ratio between native phase transition temperature and glassy trapping temperature 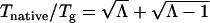monotonically depends on the ratio of gap to roughness ratio Λmodulated by entropy.

Λ can be translated to the structure parameter (representing the degree of biases toward native state relative to the roughness) of the underlying landscape. Thus the binding against trapping becomes the controlling factor determining the thermodynamics. In general we expect that the higher the binding transition temperature (or bias toward the native state) against the trapping temperature (or the roughness of the binding landscape), the more stable the system is. This can naturally lead to an optimization criterion for specificity of the binding-folding process. The real optimization scheme involves total biasing, which is the combination of folding gaps of biomolecules 1 and 2, and binding gap versus variances or traps of the underlying landscape, which is the combination of variances of the two nonnative biomolecules and the one for the binding interface. The Λ then should be significantly >1. This implies that the underlying combined energy landscape of folding and binding should be funneled toward the native state (Fig. 1).

Let us discuss the implications of the above specificity criteria. Protein folding stability is often determined by the hydrophobic core. Binding and function are often determined by the hydrophobic residues on the interface. In nature, there should be a funnel for stability of protein folding. But the landscape might not be maximally funneled, or having the maximal stability. This is clearly shown from the mutational experiments on folding (12). The native proteins are neither thermodynamically the most stable nor the kinetically fastest folders. This means that not all the hydrophobic residues are distributed inside the core of the proteins. There are certain distributions of the hydrophobic residues on the surface for functional purposes (binding). There are disadvantages from overstable and superfast protein folders, because they have less biological functions due to the decrease of surface hydrophobic residues. Furthermore, there is little flexibility to adapt for evolution. So the combined landscape is a delicate balance among folding and binding. The biomolecules should have enough thermodynamic stability and also maintain certain flexibilities for functions.

It is important to unravel the relationship between affinity and specificity. When biomolecules themselves are flexible, part of the affinity is used to adjust the conformations to best fit the binding partners. Therefore, flexibility through conformational change usually gives a good opportunity for realizing the specificity for molecular recognition, but often with the price of sacrificing certain amounts of affinity to adjust the conformations. The resulting lower affinity can give molecules the ability to both bind specifically and unbind easily, which is essential for cell signaling relay and gene regulation.

We believe specificity can be used as an important indicator in addition to affinity for drug screening and design (J. Wang, Y. Yang, D. Druekhammer, W. Yang, and G. M. Verkhivker, unpublished data).

The formalism here for the free energy of flexible binding can be extended to multiple binding complexes or to multidomain protein folding. This approach can also be extended to include multibody interactions among residues.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.