Abstract
We study a model system in which lipid bilayers are created using variable (precisely known) proportions of phosphatidylcholine and cholesterol. The model membranes exhibit cholesterol-enriched microdomains that are analogous to the so-called “lipid rafts” that form in living cells. After briefly presenting some experimental results, we formulate and solve a novel mathematical model based on the Smoluchowski equations for coagulation and fragmentation. We present a comparison between the distribution of lipid-raft areas observed in experimental lipid bilayers, and that distribution predicted by the theoretical model. Excellent agreement between the experiments and theory is obtained, with minimal parameter fitting.
INTRODUCTION
The term “raft” was first coined by Simons and Ikonen (1) in 1997 to describe lipid/protein microdomain structures that are observed within eukaryotic plasma membranes. Since then research interest in this area of cell biology has grown exponentially. The nature of these structures (and in fact even their experimental detection) has been debated vigorously (see, e.g., Lagerholm et al. (2)), as has their role in controlling processes such as membrane trafficking, signal transduction within the cell, endo/exocytosis (including virus entry into cells); and in many biochemical reactions occurring within the cell membrane.
Rafts may be characterized in various ways, but perhaps they are mainly defined by their property of detergent-insolubility in, for example, Triton X-100 or Brij98 (2). They may also be thought of as “viscous patches” on the cell membrane since, when the plasma membrane is viewed as a 2D fluid sheet, the raft phase is more viscous than the non-raft phase. Another characterization of rafts is, using the terminology of phase diagrams for multi-component membrane systems, as so-called “liquid-ordered” cholesterol- or sphingomyelin-enriched domains within cell membranes.
The phenomenology of the various kinds of biological processes in which rafts are involved has been discussed at length, and some consensus has emerged on their possible biological roles. As (essentially) phase-separated regions within the 2D membrane, it is thought that rafts can recruit certain reactants and prevent their interaction with other reactants in the “fluid-mosaic” membrane (3), or, conversely, bring desired reactants (particularly proteins) into close proximity, thus promoting certain reactions (4–6). In each case proteinaceous receptors and smaller ligands or protein-protein interactions may underlie the biological response, but both cases are conceptually analogous.
Thus rafts may play many very important roles in cell biology, although it must be conceded that some questions remain (2,7). Some of this uncertainty may well reside in the enormous complexity of real cell membranes, and the very small size of rafts in vivo (100–200 nm in diameter). Similarly, the basic principles that control the formation and function of rafts within cells remain poorly understood (8,9). To shed light on these fundamental issues we have embarked on a series of studies of simple in vitro model systems, generated in the laboratory in which larger “rafts” can be observed, and the key processes governing their dynamics identified. The hypotheses made as a result of the experimental observations can then be tested by formulating and solving a mathematical model of the experimental system.
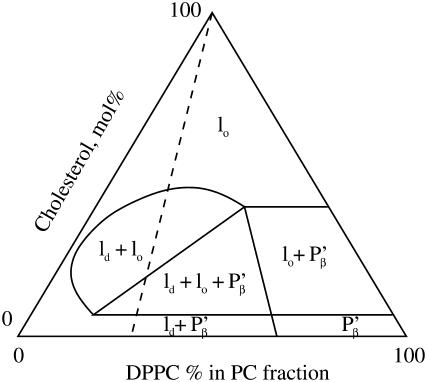
The model system we study is the simplest possible that gives rise to interesting and informative “raft” dynamics. (Although we utilize the term “raft” relatively indiscriminately in this article, we are aware that this terminology has certain meanings outside of the simple definition we take here, namely, that it represents a distinct microdomain within the membranes.) We work with planar lipid bilayers composed of precise ratios of phosphatidylcholine (PC; egg lecithin in our experiments) and cholesterol. This model of a cell membrane can then be successively elaborated until genuine “raft” behavior is identified. PC-cholesterol mixed composition bilayers have been studied in detail by many authors. Fig. 1 is adapted from Fig. 11 A of Silvius et al. (10) and shows the now well-known phase diagram for ternary PC-cholesterol mixtures, in which the PC contains variable proportions of dipalmitoyl phosphatidylcholine (DPPC) and a bromo-substituted derivative, 12BrPC (indicated along the bottom horizontal axis of the triangle). Although not strictly representative of the mixture of PC lipids in egg lecithin, the phase diagram provides valuable information on what might be happening in terms of phase in the PC-cholesterol membranes used in this study. The ratio of saturated and unsaturated PC lipids in egg lecithin is ∼45% saturated, 55% unsaturated. If we allow DPPC to represent the saturated PC lipid in the ternary phase diagram, then an indication of what the membrane phases are at certain cholesterol concentrations is given by the dashed line in Fig. 1.
FIGURE 1.
Ternary phase diagram for the 12BrPC/DPPC/cholesterol system at 25°C. The various phases found in this ternary system are liquid disordered, ld, liquid ordered, lo, and gel phase, P′β. Further details may be found in Silvius et al. (10).
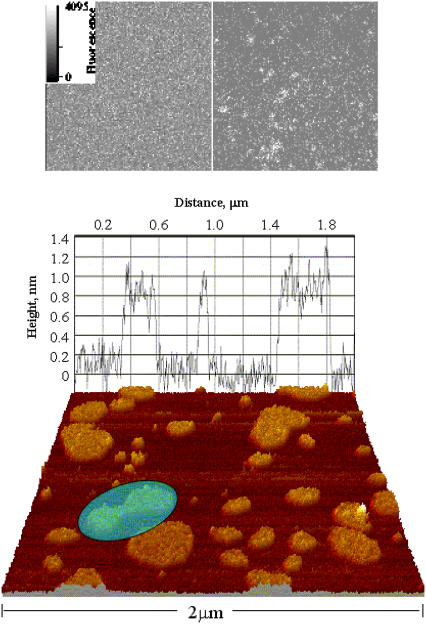
We observe cholesterol-rich microdomains (the rafts) forming spontaneously within the bilayer. In terms of the phase diagram of Fig. 1, we identify the raft phase with the liquid-ordered phase. The bilayer was left to equilibriate for 24 h, until a final (dynamic) equilibrium distribution of raft sizes (surface areas) was obtained. This raft size distribution was recorded, using fluorescence microscopy (in which fluorescent labeling molecules associate preferentially with the raft phase). We also carried out atomic force microscopy (AFM) studies, which detect the rafts by virtue of the different molecular chain lengths associated with the different lipid molecules. These results are described in separate publications (H. J. Harris, S. M. Rigby-Singleton, M. C. Davies, S. Allen, and P. O'Shea, unpublished, and (30)), but we have included a representative image in Fig. 2. We note here that related imaging studies have been carried out by other authors (12,13).
FIGURE 2.
(Upper) Fluorescent images of FPE-labeled PC100% (left), and PC67%/cholesterol33% (right). The images were obtained at room temperature with the bilayers submerged in Tris buffer (10 mM Tris, pH 7.4). (Lower) AFM image of the bilayer, illustrating cholesterol-enriched microdomains. The grape corresponds to the membrane topography at that location. Note the topology change (highlighted), where two microdomains are sintering together (or possibly splitting apart).
A mathematical model, based on the Smoluchowski theory of coagulation and fragmentation (14), was formulated to describe the interactions (binding and unbinding) of the cholesterol molecules. The expressions for the binding and dissociation rates of cholesterol molecules were derived using thermodynamic principles. The mathematical model was solved to predict the dynamics of raft formation and disassociation in the simple model system, and the results of numerical simulations compared with the experimental data. A number of key features that the model yields appear to be similar to what is observed experimentally, and thus may also feature in cellular membranes.
We also formulated the problem in terms of the Gibbs free energy, by making the usual assumptions about the entropy and enthalpy of a mixture of reacting molecules. However, the results of this calculation (the Gibbs free energy minimization) gave raft size distributions that were very heavily weighted in favor of very small cluster sizes, and did not agree at all with the experimental observations. We believe this is because the standard theory does not take account of the different dynamics of “molecules” (microdomains, in our system) of very disparate sizes.
One of the virtues of our approach (both experimental and theoretical) is that it lends itself to systematic further elaborations, such as the incorporation of additional lipid types and the inclusion of membrane proteins. These could be modeled in a similar manner to the cholesterol modeling, with averaged properties, to embody more realistic models of biological membranes. The obvious advantage of such a systematic approach is that it allows the effect of each new additional “complication” to be elucidated, as we build up the complexity from the very clean, simple system considered here.
The following sections detail the experimental methods and results, and also the assumptions underlying the mathematical model we use to describe the experiments. The results of the simulations versus experiments are then discussed, as well as the implications of our results for more complicated systems.
MATERIALS AND METHODS
PC was purchased from Lipid Products (Kent, UK). Polycarbonate filters (100-nm pore size) were purchased from Nucleopore Filtration Products (Pleasanton, CA). A pressure extruder bomb for model membrane preparation was obtained from Lipex BM Inc. (Vancouver, Canada). Fluorescein phosphatidylethanolamine (FPE) was synthesized from 1,2-dipalmyitoyl phosphatidylethanolamine and fluorescein purchased from Sigma Chemicals (Pool, Dorset, UK), as described by Wall et al. (15). Calcium chloride, cholesterol, dimethyl sulphoxide, DPPC, dioleoyl phosphatidylcholine, magnesium chloride, and Tris (hydroxymethyl) methylamine, were purchased from Sigma Chemicals.
Preparation of lipid vesicles
Phospholipids (13 mM), dissolved in chloroform and methanol, were mixed in a round-bottomed flask and dried under a stream of nitrogen until a thin lipid film was formed. The dried lipid film was rehydrated with Tris buffer (10 mM Tris, pH 7.4), which was quickly frozen in liquid nitrogen and thawed five times. Finally, the suspension was extruded 10 times through a 25-mm-diameter polycarbonate filter (100-nm-diameter pores). For all lipids to be in a fluid phase, the lipid suspensions were heated to 45°C before and during extrusion, resulting in a monodisperse, unilamellar suspension of 100-nm-diameter phospholipid vesicles (PLVs) (16).
PLVs were labeled exclusively in the outer lamella with FPE, as described in Cladera and O'Shea (17). The PLVs (13 mM lipid) were incubated in the dark with FPE (30 μM in ethanol) at 37°C for more than 1 h. The unincorporated FPE was removed by size exclusion chromatography using a Sephadex PD10 column, equilibrated with Tris buffer (10 mM Tris, pH 7.4). This procedure leads to the incorporation of 30–50% of the externally added FPE to the PLVs.
Bilayer preparation for laser scanning confocal microscopy imaging
Clean 22-mm Ø glass cover slips were treated with magnesium chloride (10 mM) at room temperature for 1 h. Fluorescently labeled liposomes (1.3 mM), heated to 45°C, were then added to the coverslip and left in the dark at room temperature for more than 5 h. The fusion of the liposomes, resulting in the unilamellar bilayer covering the glass slide, was pioneered by Watts et al. (18) and results in a bilayer forming on a layer of water on the solid support (the glass coverslip).
Single and two-photon microscopy
The single and two-photon fluorescence microscopy was carried out with a Leica (Wetzlar, Germany) SP2 MP, which utilizes a laser scanning confocal microscope (LSCM). The pinhole required for single-photon microscopy was set at one Airy unit. Alternatively, a Leica DMIRBE inverted fluorescence microscope equipped with a laser source and a mercury lamp/monochomator assembly with a LaVision (Goettingen, Germany) cooled charge-coupled device (CCD) camera was used. Both imaging systems were equipped with a thermostatted stage for temperature control. The optical slicing capability of the LSCM system was not necessary; we simply suggest that our experimental protocol can also be implemented with such a system if available instead of high-sensitivity (e.g., CCD-based) fluorescence microscopy. To prevent undersampling, and to increase the number of intensity levels of images, 512 × 512-pixel (12-bit) images were taken. Both single- and two-photon microscopy imaging were carried out with objectives with a magnification of 63 and a numerical aperture of 1.32, in illuminating wavelength of 488 or 490 nm. However, no differences were found between the image collection regimes. The laser power was kept at a minimum, and the offset and the photomultiplier voltage or CCD output were optimized at the beginning of each experiment and kept constant throughout to determine any contribution from photobleaching and for comparisons between experiments.
Data analysis
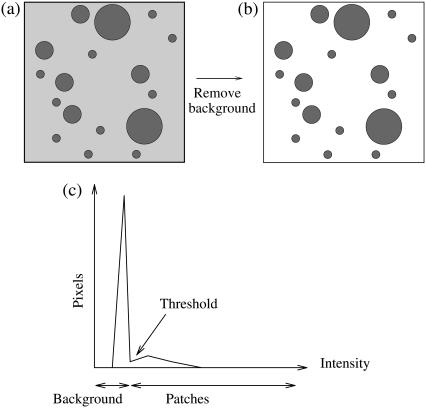
The images obtained from LSCM experiments (see Fig. 2 for an example) had a total of 10242 pixels and 0–4095 intensity levels (12-bit images). The images underwent particle analysis using the Scion Image software (Scioncorp, National Institutes of Health, Bethesda, MD) yielding the areas of the more fluorescent patches present in the membranes. The background “noise” was removed to avoid recording spurious microdomains; this process is illustrated schematically in Fig. 3. Patch areas were recorded for any connected set of at least five fluorescing pixels. The raw data was recorded as a column of figures: raft number versus its area.
FIGURE 3.
Method of image analysis. The intensity of the individual pixels in the fluorescent images (a) were plotted (c), and the background noise was removed, resulting in image b. A histogram of the various patch sizes was then plotted.
EXPERIMENTAL RESULTS
Mixed composition bilayers were left to equilibrate for 24 h at 20°C before fluorescence scanning images were obtained. Three different controlled compositions were used: 33% cholesterol/67% PC; 20% cholesterol/80% PC; and 5% cholesterol/95% PC. A typical fluorescence scanning picture is shown in Fig. 2, for a 33% cholesterol bilayer (this figure also shows one of our AFM images for the PC-cholesterol system, which gives a clearer idea of the raft structure).
The fluorescence images were analyzed as described above, and the data for microdomain areas thus obtained was represented in histogram form, with the bin size chosen as desired for comparison with the theoretical model. Histograms for each of the three data sets are presented later. The data is represented in the dimensionless form used for the theoretical model, which is explained in the following section.
THEORETICAL MODELING
We model the experimental system mathematically, applying the Smoluchowski theory of coagulation and fragmentation (14) to an idealized system in which a large number of cholesterol molecules in 2D clusters of differing sizes (the rafts, or patches) are diffusing around in an otherwise inert 2D fluid (the PC bilayer). Although this approach has been widely used to describe coagulation and fragmentation in a variety of systems (19–24,26,27), previous applications to the problem of lipid-raft formation, even in a very simple model system of the kind considered here, are almost nonexistent. The only previous such model we are aware of is by Turner et al. (28), who use such an approach to study the effect of membrane recycling on microdomain size distributions within living cells.
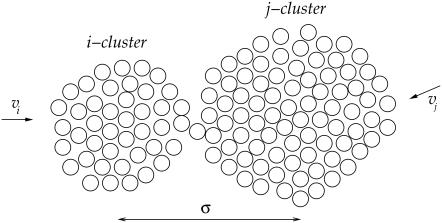
Consider first coagulation (or binding) events between groups or clusters of cholesterol molecules. We assume that these are rate-limited (slow) rather than diffusion-limited (fast), i.e., that relatively few of the collisions that occur between clusters of sizes i and j (clusters containing i and j cholesterol molecules, respectively) result in a coagulation event (a reaction). The concentration of clusters of any given size is thus fairly uniform throughout the bilayer. The reaction rate is proportional to the number of collisions, and hence to σ(vi + vj)[ci][cj], where vi and vj are the mean cluster velocities, [ci] and [cj] are the concentrations of i and j clusters, and the collision cross-section σ is taken as the sum of the cluster radii (proportional to (i½ + j½)). A schematic is shown in Fig. 4. Postulating that kinetic energies are proportional to thermal energies for the clusters gives vi ∝ (2kT/(mi))½, vj ∝ (2kT/(mj))½, where k is Boltzmann's constant, T is the system temperature, and m is the mass of an individual cholesterol molecule. Including an Arrhenius activation energy term to account for the fact that only a certain proportion of collisions result in coagulation gives the coagulation rate coefficients
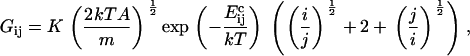 |
where K is a constant of proportionality, A is the area occupied by a cholesterol molecule within a cluster (since rafts are not composed solely of cholesterol, we expect that this will be greater than the cross-sectional area of a cholesterol molecule), and 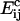 is the activation energy of coagulation between i and j clusters. A similar approach can be found in collision theory (see, e.g., Pilling and Seakins (25), Chapters 3 and 4). (We note that the standard Smoluchowski rate coefficient, for a diffusion controlled reaction, Gij ∝ (Di + Dj)(di + dj) (where Di is the diffusion coefficient of i-clusters and di their radius) also gives Gij ∝ ((i/j)½ + 2 + (j/i)½). However, there is some doubt about the correctness of this expression for such (diffusion-limited) reactions in two space dimensions, since the concentration of a reactant c about a reacting particle is, local to the particle, c = k log(r/r0), where r is the distance from the particle, r0 its radius, and k a constant. This is in contrast to the analogous case in three dimensions, for which c = k(1 – r/r0) and which tends to a finite limit as
is the activation energy of coagulation between i and j clusters. A similar approach can be found in collision theory (see, e.g., Pilling and Seakins (25), Chapters 3 and 4). (We note that the standard Smoluchowski rate coefficient, for a diffusion controlled reaction, Gij ∝ (Di + Dj)(di + dj) (where Di is the diffusion coefficient of i-clusters and di their radius) also gives Gij ∝ ((i/j)½ + 2 + (j/i)½). However, there is some doubt about the correctness of this expression for such (diffusion-limited) reactions in two space dimensions, since the concentration of a reactant c about a reacting particle is, local to the particle, c = k log(r/r0), where r is the distance from the particle, r0 its radius, and k a constant. This is in contrast to the analogous case in three dimensions, for which c = k(1 – r/r0) and which tends to a finite limit as 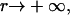 unlike in the 2D case.) We hypothesize that this coagulation takes place in stages, beginning with the formation of a single bond between an i and a j cluster (Fig. 4). With the clusters then held together, the slower formation of the subsequent bonds required to merge the clusters is facilitated. (See the AFM image in Fig. 2, illustrating such a coagulation process.) Where merging takes place in this kind of two-stage process, it suggests that
unlike in the 2D case.) We hypothesize that this coagulation takes place in stages, beginning with the formation of a single bond between an i and a j cluster (Fig. 4). With the clusters then held together, the slower formation of the subsequent bonds required to merge the clusters is facilitated. (See the AFM image in Fig. 2, illustrating such a coagulation process.) Where merging takes place in this kind of two-stage process, it suggests that 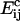 should be roughly constant (since the difficult step in the coagulation is formation of the initial bond), and we assume this from now on.
should be roughly constant (since the difficult step in the coagulation is formation of the initial bond), and we assume this from now on.
FIGURE 4.
Schematic illustrating collision of clusters of size i and j before coalescing. Cluster radii scale as i½ and j½.
For fragmentation of an (i + j) cluster into an i and a j cluster, we postulate that the rate should be proportional to the circumference of the fragmenting cluster, again with an Arrhenius term. Thus, we take fragmentation rate coefficients
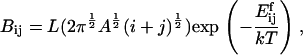 |
where L is a constant. The activation energy for fragmentation is proportional to the number of bonds that have to be broken, and we use a “surface tension” approximation, which says that 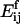 is proportional to the total length of boundaries after splitting minus the total boundary length before splitting:
is proportional to the total length of boundaries after splitting minus the total boundary length before splitting:
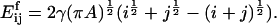 |
In terms of dimensionless variables ci*, t* (time) and the parameter M, defined by
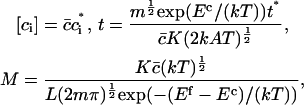 |
where 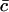 is the average number of cholesterol molecules per unit area in the bilayer and Ef is a typical fragmentation activation energy, the dimensionless Smoluchowski model is
is the average number of cholesterol molecules per unit area in the bilayer and Ef is a typical fragmentation activation energy, the dimensionless Smoluchowski model is
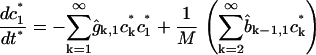 |
(1) |
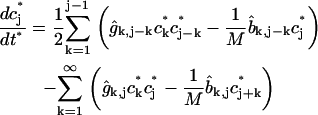 |
(2) |
where
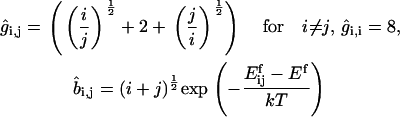 |
Note that for this system,
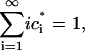 |
(3) |
that mass is conserved for all time.
The experimental observations have millions of molecules per raft, which corresponds to the parameter M being very large in the above model. Solving this discrete system numerically is prohibitively expensive in this regime, but if we introduce the scalings
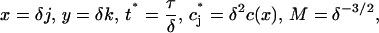 |
then, taking the limit δ → 0 in Eqs. 1 and 2 yields the integrodifferential equation
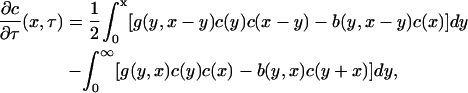 |
(4) |
where the coagulation and fragmentation kernels g(x,y) and b(x,y) are given by
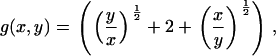 |
(5) |
and
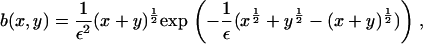 |
(6) |
with ε = δ½kT/(2γ(πA)½), and we have taken the arbitrary parameter of nondimensionalization Ef = kT(log(1/ε2) + log δ). Equation 4 preserves mass, so that the mass conservation condition (Eq. 3) becomes
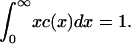 |
(7) |
This integrodifferential integral equation can be solved by discretization, on a mesh that requires far fewer points than the original discrete system in the regime of interest. This ensures that even where 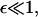 b(x,y) is order one in the sense that
b(x,y) is order one in the sense that 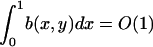 for y = O(1).
for y = O(1).
Note that the parameter ε characterizes the width of the dimensionless fragmentation kernel b(x,y), in the sense that for 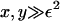 there is almost no fragmentation. Thus, in our model, the size of fragments that can break off is limited. Translating back into the dimensional variables, we find that almost no fragments of size
there is almost no fragmentation. Thus, in our model, the size of fragments that can break off is limited. Translating back into the dimensional variables, we find that almost no fragments of size
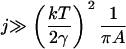 |
will break off from larger clusters.
RESULTS: COMPARISON OF EXPERIMENTAL DATA WITH MODEL
The experimental data gives the areas α of all rafts (above the microscopic resolution size αmin), in a given total area aT of the bilayer, when the system is judged to be in a steady state. A histogram is made of the numbers of rafts nm with areas in the range αm to αm+1 = αm + Δ, where Δ is some small area increment (the bin size). The mathematical model predicts that the number of rafts nm in the mth bin is
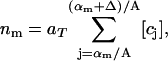 |
or, in terms of the continuum model (Eq. 4),
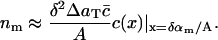 |
Thus, we should compare experimental plots of 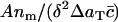 versus δαm/A (the histogrammed data, scaled appropriately), with theoretical plots from the model (Eq. 4) of c(x) versus x, taken at large enough times that the model solution has reached its steady state.
versus δαm/A (the histogrammed data, scaled appropriately), with theoretical plots from the model (Eq. 4) of c(x) versus x, taken at large enough times that the model solution has reached its steady state.
The dimensional constants Δ, aT and 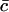 are known. The average area occupied by a cholesterol molecule in a raft, A, can then (in principle) be evaluated by considering the total area of all rafts measured experimentally, Ω(αmin) (where Ω(α) denotes the combined total area of all rafts with areas greater than α). We should have
are known. The average area occupied by a cholesterol molecule in a raft, A, can then (in principle) be evaluated by considering the total area of all rafts measured experimentally, Ω(αmin) (where Ω(α) denotes the combined total area of all rafts with areas greater than α). We should have
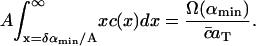 |
However, in addition to the experimental limitation of the fluorescence microscopy resolution size αmin, there is a numerical restriction due to the fact that the solution of Eq. 4 can only be evaluated on a finite domain 0 ≤ x ≤ xmax. When comparing the numerical solution to the experimental data it is crucial that the total raft area between x = δαmin/A and x = xmax (or equivalently α = αmin and α = xmaxA/δ) is the same in both numerical solution and experiment. This amounts to the condition
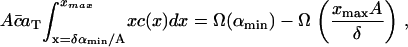 |
or, equivalently,
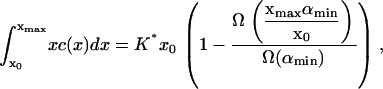 |
(8) |
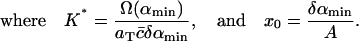 |
(9) |
Given δ, we can determine K* in terms of the experimental parameters αmin, Ω(αmin), aT, and 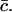 With xmax, αmin, and K* known, we can solve Eq. 8 to find x0, whence A can be determined from Eq. 9. We are then left with just two parameters we can adjust to fit the data: δ = M−2/3 and ε, which characterizes the width of the dimensionless fragmentation kernel b(x,y); once this fitting is done, the resulting value for A provides a further check on the reasonableness of the model.
With xmax, αmin, and K* known, we can solve Eq. 8 to find x0, whence A can be determined from Eq. 9. We are then left with just two parameters we can adjust to fit the data: δ = M−2/3 and ε, which characterizes the width of the dimensionless fragmentation kernel b(x,y); once this fitting is done, the resulting value for A provides a further check on the reasonableness of the model.
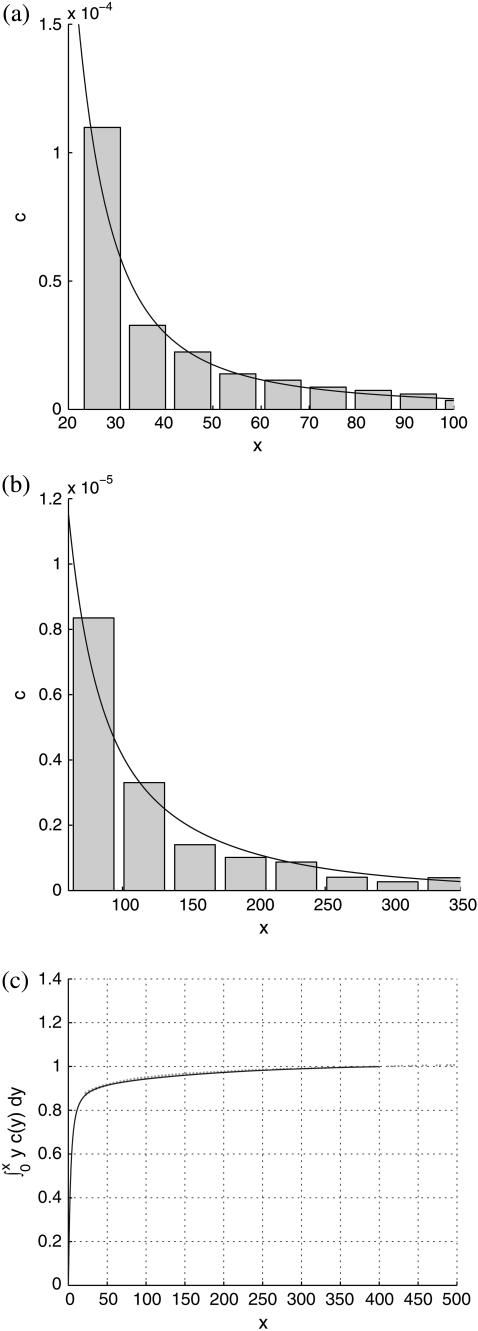
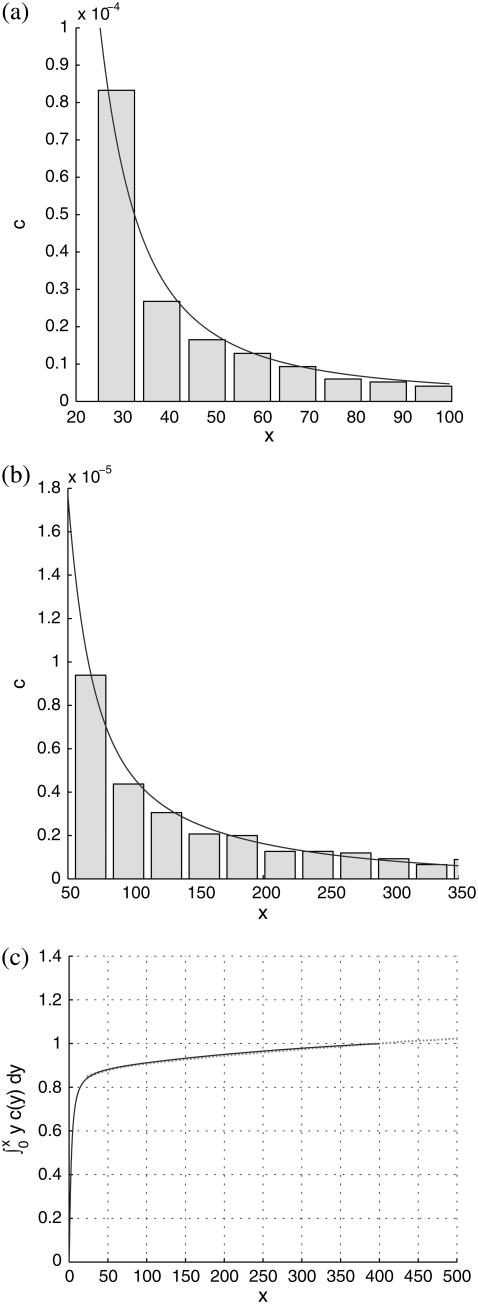
Best fits of the theoretical model to three sets of experimental data are shown in Figs. 5–7, corresponding to PC-cholesterol bilayers containing, respectively, 33%, 20%, and 5% cholesterol. In each case plots are shown of the experimental histogrammed data, scaled as explained above, compared directly with best-fit plots of c(x), both for rafts of small size (where most of the cholesterol mass in the system resides) and for larger raft sizes. We also plot the cumulative cholesterol mass for each case, that is, the proportion of the cholesterol in the system that resides in rafts of (dimensionless) size ≤x, versus x. From these cumulative mass plots it is clear that the model predicts that most cholesterol resides in rafts of dimensions that are less than diffraction-limited spots (i.e., rafts that are too small to measure). An alternative experimental approach that would have enabled us to measure the size of all rafts present would have been AFM; and indeed we did carry out a small number of AFM studies on model membranes (11). However, the disadvantage of this procedure is that the size of membrane that can be scanned is very limited. Thus, it is difficult (with current AFM technology) to obtain a statistically significant set of raft areas with which to compare the mathematical model.
FIGURE 5.
Comparison of theoretical predictions with experimental measurements for the 33% cholesterol membranes. Experimental measurements were made over a total membrane area of 40 μm × 40 μm. Best-fit parameter values for the theoretical model are δ = 1/8000, ε = 0.2375. (a and b) Experimental data shown as histograms of number of rafts versus number of cholesterol molecules per raft (both scaled as discussed in text), against the theoretical curve. Different bin sizes are used in the two histograms. (a) The focus is on smaller rafts, where most of the cholesterol mass in the system resides. (b) The whole range of raft sizes is represented. (c) Cumulative cholesterol mass in the system as a function of raft size, with the solid line representing the theoretical prediction and the dots the experimental data points.
FIGURE 6.
Same description as for Fig. 5, but for the 20% cholesterol membranes. Experimental measurements were made over a total membrane area of 240 μm × 240 μm. Best-fit parameter values for the theoretical model are δ = 1/60000, ε = 0.2375.
FIGURE 7.
Same description as for Fig. 5, but for the 5% cholesterol membranes. Experimental measurements were made over a total membrane area of 40 μm × 40 μm. Best-fit parameter values for the theoretical model are δ = 1/300, ε = 0.23375.
For the 33% cholesterol membrane (Fig. 5), the experimental measurements were made on a region of bilayer of size 40μm × 40μm, and the best fit to the experimental data was found to be δ = 1/2000, ε = 0.2375, giving a value A33% = 38 Å2 for the area occupied by a cholesterol molecule within the raft. In this case the theory predicts that the experimental measurements captured ∼25% of the total raft area present. This allows us to estimate the total proportion of membrane area occupied by rafts, P33%, from the experimental data as
 |
and so in this case the rafts are almost entirely composed of cholesterol (a figure of 0.33 would indicate pure cholesterol rafts). Hence the rafts for this data set contain a proportion D33% of cholesterol, where
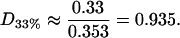 |
From this, we can use the model to estimate the actual cholesterol molecule area 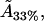 as
as
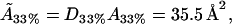 |
which provides a further check on the reasonableness of the mathematical model.
For the 20% cholesterol membrane, measurements were made over a larger region of membrane, 240μm × 240μm, and the best-fit parameter values were δ = 1/15000, ε = 0.2375, giving A20% = 80 Å2 for the area/cholesterol molecule. Here we estimate that the experimental measurements captured ∼15% of the total raft area present, from which we find the total proportion of membrane occupied by rafts, P20%, as
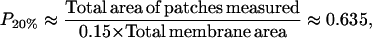 |
and so these rafts are much more dilute in cholesterol. The rafts for this data set contain a proportion D20% of cholesterol, where
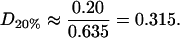 |
From this, we can again work out the actual cholesterol molecule area 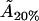 :
:
 |
Finally, for the 5% cholesterol case, measurements were made on a 40μm × 40μm membrane region, and values δ = 1/75, ε = 0.23375 gave the best fit to the data, giving A5% = 424Å2 for the area occupied by each cholesterol molecule within the raft, with ∼19% of the total raft area being measured by the experimental procedure. The total proportion of membrane occupied by rafts, P5%, is
 |
and these rafts are consequently very dilute in cholesterol. They contain a proportion D5% of cholesterol given by
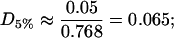 |
hence, the actual cholesterol molecule area 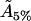 is estimated as
is estimated as
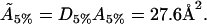 |
We note that the area/cholesterol molecule within the raft, A, increases as the cholesterol concentration in the bilayer mixture decreases. This is in line with the above results that show the rafts becoming much more dilute in cholesterol as the bilayer as a whole becomes more dilute. The actual molecular areas  show no definite trend, however. Our obtained values for
show no definite trend, however. Our obtained values for  may be compared with data from various sources summarized by Edholm and Nagle (29). This article reports values of cholesterol molecule areas in mixed DPPC/cholesterol bilayers with varying cholesterol concentrations. Using the above estimates for the cholesterol concentration within the rafts (93.5%, 31.5%, and 6.5%, respectively, for the three data sets), we take the figures that Edholm and Nagle report for bilayers that are very dense in cholesterol (27 Å2, to be compared with our value
may be compared with data from various sources summarized by Edholm and Nagle (29). This article reports values of cholesterol molecule areas in mixed DPPC/cholesterol bilayers with varying cholesterol concentrations. Using the above estimates for the cholesterol concentration within the rafts (93.5%, 31.5%, and 6.5%, respectively, for the three data sets), we take the figures that Edholm and Nagle report for bilayers that are very dense in cholesterol (27 Å2, to be compared with our value 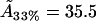 Å2), for bilayers that are 33% cholesterol (40.5 Å2, to be compared with our value
Å2), for bilayers that are 33% cholesterol (40.5 Å2, to be compared with our value 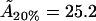 Å2), and for bilayers that are 6% cholesterol (51.8Å2, to be compared with our value
Å2), and for bilayers that are 6% cholesterol (51.8Å2, to be compared with our value 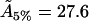 Å2), these being the results in Edholm and Nagle closest to those required.
Å2), these being the results in Edholm and Nagle closest to those required.
Thus, the molecular area 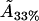 for the 33% cholesterol experiment is remarkably close to the desired result, whereas the other values are certainly qualitatively acceptable—remarkably so, given the simplicity of our model and the minimal fitting.
for the 33% cholesterol experiment is remarkably close to the desired result, whereas the other values are certainly qualitatively acceptable—remarkably so, given the simplicity of our model and the minimal fitting.
We observe also that the model is able to capture very closely the cumulative mass as a function of raft size in each case. This is particularly true of the results for the 33% cholesterol bilayers, where the experimental data is sufficiently good to demonstrate the sharp decay of the cumulative mass toward zero as the raft size decreases to zero (Fig. 5 c). The sharp decay of the data toward zero is almost perfectly captured by the numerical results.
An interesting peculiarity of our results is that, though the fitted value for the parameter δ varies widely between the three data sets, the best-fit value of ε is almost the same in all cases, ε = 0.2375, ε = 0.2375, and ε = 0.23375, for the 33%, 20%, and 5% cholesterol experiments, respectively. Further numerical calculations of the solution to Eq. 4 show that, for ε <∼ 0.23, the total mass within the computational domain 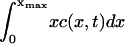 decreases with time as mass is lost to large values of x. It is not possible to tell from the computations whether this is as a result of a genuine bifurcation as ε passes some threshold value, in which mass is lost to infinity, or whether it is a consequence of the finite size of the computational domain. However, we show explicitly in the Appendix that a closely related (though simpler) toy model has a bifurcation in its steady-state solution. By comparing the small ε limit of the full model (Eq. 4) (in the steady case) with the toy model, we are able to argue that we believe such a bifurcation is highly likely in our system as ε decreases, and, moreover, that all the experiments lie rather close to this bifurcation point.
decreases with time as mass is lost to large values of x. It is not possible to tell from the computations whether this is as a result of a genuine bifurcation as ε passes some threshold value, in which mass is lost to infinity, or whether it is a consequence of the finite size of the computational domain. However, we show explicitly in the Appendix that a closely related (though simpler) toy model has a bifurcation in its steady-state solution. By comparing the small ε limit of the full model (Eq. 4) (in the steady case) with the toy model, we are able to argue that we believe such a bifurcation is highly likely in our system as ε decreases, and, moreover, that all the experiments lie rather close to this bifurcation point.
An equilibrium model based on thermodynamic arguments
Although we have good reasons for formulating a dynamic mathematical model (to compare theoretical results to future dynamic experimental measurements), it is of interest to consider whether a steady-state model based on thermodynamic considerations can be formulated to describe the experimental results presented here. To do this, we need to write down a Gibbs free-energy density for the system.
We postulate that the dimensionless internal energy of a cluster of size j is given by
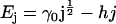 |
(10) |
for positive constants γ0 and h, the two contributions representing the surface energy and internal bond energy, respectively. The total enthalpy of the collection of clusters is then given by
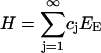 |
and the Gibbs free energy density of the system is
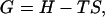 |
(11) |
where T is the system temperature and S is the entropy density, given, according to ideal mixture theory, by
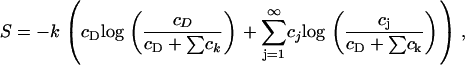 |
where cD is the concentration of DPPC in the membrane.
We have to minimize the Gibbs free energy, subject to the constraint that the total amount of cholesterol in the system is conserved. Nondimensionalizing as earlier, scaling concentrations with 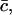 γ0, and h with kT, and G with
γ0, and h with kT, and G with 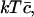 and working in the dimensionless variables henceforth, we must minimize
and working in the dimensionless variables henceforth, we must minimize
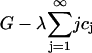 |
with respect to ci, where λ is a Lagrange multiplier for the mass conservation constraint. This leads to
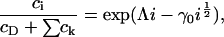 |
where Λ = h + λ is unknown as yet. However, if we assume that cholesterol is dilute in the membrane (a reasonable approximation for the membranes considered experimentally) then 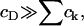 and thus
and thus
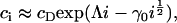 |
(12) |
and imposing mass conservation gives an equation to fix Λ,
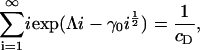 |
(13) |
which completes the solution for ci. It is clear that we require at least Λ ≤ 0 for the sum in Eq. 13 to converge. Consider the limiting case in which Λ = 0. In this case, Eq. 13 is an equation for γ0 only, and has a critical solution γ0* > 0 that is easily determined numerically (γ0* = 1.74515 for cD = 0.8). Consider what happens as γ0 passes through γ0*. From Eq. 13, we have
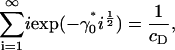 |
and, thus,
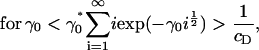 |
(14) |
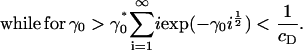 |
(15) |
Since we know Λ ≤ 0, exp(Λj) ∈ (0, 1) for all j, and it follows from Eq. 15, above, that Eq. 13 can never be satisfied for γ0 > γ0*. This demonstrates the existence of a bifurcation in the solution at a critical value of the surface energy parameter γ0*, in which mass is lost to a cluster of infinite size.
It is immediately obvious that the above approximate solution (Eq. 12) for ci can never be made to fit the experimental data, even approximately, since the decay in ci with i is always rapid unless the concentration of DPPC is absolutely tiny relative to that of cholesterol (corresponding to 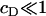 ). In this context, we note that there are various other scenarios in which it is inappropriate to apply equilibrium thermodynamics to determine equilibrium constants (e.g., diffusion-limited reactions).
). In this context, we note that there are various other scenarios in which it is inappropriate to apply equilibrium thermodynamics to determine equilibrium constants (e.g., diffusion-limited reactions).
Finally, we note that exactly the same solution for the ci can be derived by the alternative approach of using reaction coordinates ξij to parameterize the equilibrium in the reaction
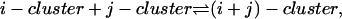 |
and minimizing the Gibbs free energy with respect to these reaction coordinates.
DISCUSSION AND CONCLUSIONS
We have presented three experimental data sets detailing microdomain (“raft”) formation in PC-cholesterol bilayers, and have derived a simple mathematical model based on plausible thermodynamic arguments that describes the experimental findings well for appropriate choices of two fitting parameters. A further check on the reasonableness of the theoretical results is provided by the predictions of the areas of cholesterol molecules within the rafts, which are qualitatively correct. Moreover, our results exhibit the right trend whereby rafts in more dilute cholesterol bilayers are themselves more dilute in cholesterol.
The mathematical model makes several simplifying assumptions, which may not be fully justified and which could be addressed by a more sophisticated model. One obvious point is that the phosphatidylcholine is assumed not to play a dominant role as far as the model is concerned. Although the PC may not play an important role in the simple experiments described here, we will in future consider more complex membrane systems that are more representative of real cell membranes. This will require development of theoretical models that can describe the simultaneous interaction of several bilayer components.
Our results may be discussed in light of the classical theory of phase transitions, referred to briefly in the Introduction. The phase diagram for PC-cholesterol mixed bilayers given in Silvius et al. (10) is reproduced in Fig. 1. The dashed line indicates where in the phase diagram we believe our experiments to lie, according to the fraction of DPPC in the PC component of the mixture. From this diagram we infer that, for the experiments with 33% cholesterol in the bilayer, our experimental results lie in the shaded region where liquid disordered and liquid ordered regions should coexist,. The 20% cholesterol experiments lie in the triangular region where, in addition to the liquid-ordered and disordered regions, we expect some gel phase. Finally, for the 5% cholesterol experiment, according to the phase diagram, there should only be liquid-disordered regions, together with some gel phase. The phase diagram suggests, then, that, at least for the 5% cholesterol experiment, the identification of the rafts with liquid-ordered regions may not be a perfect analogy, but that the experiments are also detecting and measuring gel phase, which may be enriched in cholesterol. This latter point has been examined, as it is simple to prepare FPE with various kinds of fatty acyl chains. In other words, we are able to prepare the FPE with unsaturated or saturated fatty acids, and this predisposes the FPE to “prefer” the raft regions of the fluid-mosaic membrane. In any event, however, this may not be a problem, as the mechanisms by which the gel phase becomes cholesterol-enriched are probably largely the same as those we postulate in our model. However, the difference in the physical structure of the cholesterol-enriched regions in the two cases may mean that trends in the data are obscured (see below).
It is interesting to note that although the value of the fitting parameter δ varies significantly from one set of experimental results to another, the best-fit value of ε is almost the same for all data sets. Recalling the definition of ε, this means that the quantity
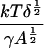 |
is more or less constant for all the experiments. Since (after fitting) the only unknown quantity here is the cluster “surface tension” γ, we can work out how γ varies from one experiment to the other. We find
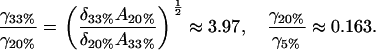 |
The trend for the 33% and 20% cholesterol bilayers is as we would expect. The clusters in the 33% bilayer are denser in cholesterol (as is reflected in the A-value); thus, the cholesterol molecules within the clusters are more strongly held together, leading to a higher effective surface tension for the cluster. The anomalous result for the 5% case (higher surface tension than the 20% case) we attribute to the fact, discussed above, that we are probably in a different region of the phase diagram, and so we are not really comparing like with like. The different nature of the molecular packing in the 5% cholesterol bilayer makes it difficult to draw direct comparisons between this experiment and the other two.
The last part of this article was concerned with attempts to formulate a steady-state model to describe the experiments, since all experimental measurements made were at steady state. We saw that the predictions of such thermodynamics-based models could not possibly explain the experimentally observed distributions, showing that the simple thermodynamic approach based on minimization of the Gibbs free energy for the system of clusters is not appropriate for our system, essentially because it does not take into account the different mobilities of the clusters of molecules, which have hugely varying sizes in our system.
In future, we intend to extend the experimental study 1), to measurements taken at different time points (to capture the dynamics of microdomain formation); and 2), to thermodynamically open systems (such as a real cell). In both respects, a formulation such as ours has considerable advantages over a purely equilibrium theory. To make it more biologically realistic, additional elaborations to the mathematical model that we plan include, in the first instance, modeling several lipid types (variations in headgroup identity/chemistry and fatty acyl saturation). We would also include the role of sphingomyelin. This would then put us in a position where we would be able to investigate the role of membrane proteins in modulating these interesting aspects of macroscopic membrane structure. We will also investigate the model for the diffusion-controlled limit (in which clusters react on collision, as opposed to the reaction-limited case considered here, in which the probability of coagulation on collision is relatively small) as an alternative hypothesis. The diffusion-limited problem is much more challenging, since one has to solve a local problem (Laplace's equation with appropriate boundary conditions) around each cluster to describe the “depletion zone” that surrounds it due to other clusters reacting with it. However, such local solutions in two space dimensions have logarithmic divergence in the far field, making construction of the full solution very delicate.
Acknowledgments
The authors are grateful to Kelly Vere for help with the experimental work, and to anonymous referees for helpful suggestions that led to improvements in the article.
G.W.R. thanks the Medical Research Council for financial support in the form of a Discipline-Hopping award. L.J.C. thanks the National Grid for financial support in the form of a sponsored Royal Society Dorothy Hodgkin Fellowship. H.H. thanks the Engineering and Physical Sciences Research Council for an EPSRC studentship.
APPENDIX: A BIFURCATION IN THE STEADY SOLUTION OF EQ. 4
Numerical calculations of the solution to Eq. 4 show that, for ε <∼ 0.23, the total mass within the computational domain 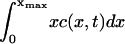 decreases with time as mass is lost to large values of x. It is impossible to tell from the computations whether this is as a result of a genuine bifurcation, in which mass is lost to infinity, or whether it is a consequence of the finite size of the computational domain. However, by considering the limit of the steady state equations for Eq. 4 as
decreases with time as mass is lost to large values of x. It is impossible to tell from the computations whether this is as a result of a genuine bifurcation, in which mass is lost to infinity, or whether it is a consequence of the finite size of the computational domain. However, by considering the limit of the steady state equations for Eq. 4 as 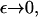 we can show that such a bifurcation is likely as ε decreases. We start by considering the toy model for which g(x, y) = 1,
we can show that such a bifurcation is likely as ε decreases. We start by considering the toy model for which g(x, y) = 1, 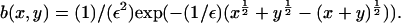 Here, there is an exact (detailed balance) steady solution to Eq. 4, obtained by setting both integrands in Eq. 4 to zero by writing
Here, there is an exact (detailed balance) steady solution to Eq. 4, obtained by setting both integrands in Eq. 4 to zero by writing
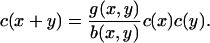 |
In turn, this gives the solution
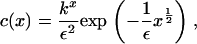 |
(16) |
where k is a constant that lies in the range 0 < k ≤ 1 (note that if k > 1, the integral diverges). The value of this constant is determined from the mass conservation condition
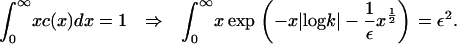 |
Furthermore, it is straightforward to show that 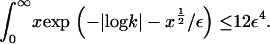 It follows that, for
It follows that, for 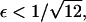 it is no longer possible for a solution of the form demonstrated in Eq. 16 to satisfy the mass conservation condition; in terms of the unsteady model, some of the mass is lost to infinity below the bifurcation point at
it is no longer possible for a solution of the form demonstrated in Eq. 16 to satisfy the mass conservation condition; in terms of the unsteady model, some of the mass is lost to infinity below the bifurcation point at 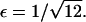
As 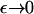 in the full model (Eqs. 4–6) the exponential term in the expression for b(x, y) becomes dominant. This suggests looking for a steady solution of the form
in the full model (Eqs. 4–6) the exponential term in the expression for b(x, y) becomes dominant. This suggests looking for a steady solution of the form
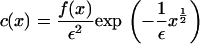 |
In our case, it proves convenient to introduce a further rescaling,
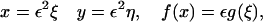 |
which leaves the steady equations for Eqs. 4–6 in the form
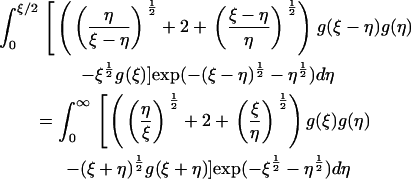 |
(17) |
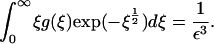 |
(18) |
It is obvious from Eq. 18 that g ≥ O(1/ε3) for mass conservation to be satisfied. If this is the case, the dominant terms in Eq. 17 are those that are quadratic in g, and it is fairly clear that, for sufficiently small E and ξ, no balance in which g ≥ O(1/ε3) is possible in Eq. 17. This suggests that the real model, like the toy one, exhibits a bifurcation as ε decreases through a critical value (our computations suggest ∼0.23) in which mass is lost to infinity.
H. J. Harris' present address is Division of Infection and Immunity, Institute of Biomedical Research, University of Birmingham, Birmingham, B15 2TT UK.
References
- 1.Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- 2.Lagerholm, B. C., G. E. Weinreb, K. Jacobson, and N. L. Thompson. 2005. Detecting microdomains in intact cell membranes. Annu. Rev. Phys. Chem. 56:309–336. [DOI] [PubMed] [Google Scholar]
- 3.Singer, S. J., and G. L. Nicolson. 1972. Fluid mosaic model of structure of cell membranes. Science 175:720–731. [DOI] [PubMed] [Google Scholar]
- 4.Bray, D. 1998. Signaling complexes: biophysical constraints on intracellular communication. Annu. Rev. Biophys. Biomol. Struct. 27:59–75. [DOI] [PubMed] [Google Scholar]
- 5.Harding, S. E., and P. O'Shea. 2003. Intermolecular associations in 2D and 3D. Biochem. Soc. Trans. 31:971–972. [Google Scholar]
- 6.Simons, K., and W. L. C. Vaz. 2004. Model systems, lipid rafts and cell membranes. Annu. Rev. Bioph. Biom. 33:269–295. [DOI] [PubMed] [Google Scholar]
- 7.Edidin, M. 2003. The state of lipid rafts: From model membranes to cells. Annu. Rev. Biophys. Biomol. Struct. 32:257–283. [DOI] [PubMed] [Google Scholar]
- 8.Mukherjee, S., and F. R. Maxfield. 2004. Membrane domains. Annu. Rev. Cell Dev. Bi. 20:839–866. [DOI] [PubMed] [Google Scholar]
- 9.London, E. 2002. Insights into lipid raft structure and formation from experiments in model membranes. Curr. Opin. Struct. Biol. 12:480–486. [DOI] [PubMed] [Google Scholar]
- 10.Silvius, J. R., D. delGiudice, and M. Lafleur. 1996. Cholesterol at different bilayer concentrations can promote or antagonize lateral segregation of phospholipids of differing acyl chain length. Biochemistry. 35:15198–15208. [DOI] [PubMed] [Google Scholar]
- 11.Reference deleted in proof.
- 12.de Almeida, R. F. M., L. M. S. Loura, A. Federov, and M. Prieto. 2005. Lipid rafts have different sizes depending on membrane composition: A time-resolved fluorescence resonance energy transfer study. J. Mol. Biol. 346:1109–1120. [DOI] [PubMed] [Google Scholar]
- 13.Tokumasu, F., A. J. Jin, G. W. Feigenson, and J. A. Dvorak. 2003. Nanoscopic lipid domain dynamics revealed by atomic force microscopy. Biophys. J. 84:2609–2618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.von Smoluchowski, M. 1917. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem. 92:129–168. [Google Scholar]
- 15.Wall, J., C. A. Golding, M. Van Veen, and P. O'Shea. 1995. The use of fluoresceinphosphatidylethanolamine (FPE) as a real-time probe for peptide-membrane interactions. Mol. Membr. Biol. 12:183–192. [DOI] [PubMed] [Google Scholar]
- 16.Mayer, L. D., M. J. Hope, and P. R. Cullis. 1986. Vesicles of variable sizes produced by a rapid extrusion procedure. Biochim. Biophys. Acta. 858:161–168. [DOI] [PubMed] [Google Scholar]
- 17.Cladera, J., and P. O'Shea. 2001. Generic techniques for fluorescence measurements of protein-ligand interaction; real-time kinetics and spatial imaging. In Protein-Ligand Interactions. S. E. Harding and B. Z. Chowdery, editors. Oxford University Press, Oxford, UK. 169–200.
- 18.Watts, T. H., A. A. Brian, J. W. Kappler, P. Marrack, and H. M. McConnell. 1984. Antigen presentation by supported planar membranes containing affinity-purified I-Ad. Proc. Natl. Acad. Sci. USA. 81:7564–7568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Davies, S. C., J. R. King, and J. A. D. Wattis. 1999. Self-similar behaviour in the coagulation equations. J. Eng. Math. 36:57–88. [Google Scholar]
- 20.Elminyawi, I. M., S. Gangopadhyay, and C. M. Sorensen. 1991. Numerical solution to the Smolochowski aggregation-fragmentation equation. J. Coll. Interface Sci. 144:315–323. [Google Scholar]
- 21.Family, F., P. Meakin, and J. M. Deutch. 1986. Kinetics of fragmentation with coagulation: scaling behaviour and fluctuations. Phys. Rev. Lett. 57:727–730. [DOI] [PubMed] [Google Scholar]
- 22.Meakin, P., and M. H. Ernst. 1988. Scaling in aggregation with breakup simulations and mean-field theory. Phys. Rev. Lett. 60:2503–2506. [DOI] [PubMed] [Google Scholar]
- 23.Odriozola, G., A. Schmitt, J. Callejas-Fernandez, R. Martinez-Garcia, R. Leone, and R. Hidalgo-Alvarez. 2003. Simulated reversible aggregation processes for different interparticle potentials: The cluster-aging phenomenon. J. Phys. Chem. B. 107:2180–2188. [Google Scholar]
- 24.Peled, C. R., G. Braun, and S. Nir. 1994. Time of equilibration in reversible aggregation of particles. J. Coll. Int. Sci. 169:204–213. [Google Scholar]
- 25.Pilling, M. J., and P. W. Seakins. 1995. Reaction Kinetics. Oxford University Press.
- 26.Sintes, T., R. Toral, and A. Chakrabarti. 1994. Reversible aggregation in self-associating polymer systems. Phys. Rev. E. 50:2967–2976. [DOI] [PubMed] [Google Scholar]
- 27.Sorensen, C. M., H. X. Zhang, and T. W. Taylor. 1987. Cluster size evolution in a coagulation-fragmentation system. Phys. Rev. Lett. 59:363–366. [DOI] [PubMed] [Google Scholar]
- 28.Turner, M. S., P. Sens, and N. D. Socci. 2005. Nonequilibrium raftlike membrane domains under continuous recycling. Phys. Rev. Lett. 95:168301. [DOI] [PubMed] [Google Scholar]
- 29.Edholm, O., and J. F. Nagle. 2005. Areas of molecules in membranes consisting of mixtures. Biophys. J. 89:1827–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rigby-Singleton, S. M., M. C. Davies, H. Harris, P. O'Shea, and S. Allen. 2006. Visualising the solubilization of supported lipid bilayers by an amphiphilic peptide. Langmuir. 22:6273–6279. [DOI] [PubMed] [Google Scholar]