Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2007 Mar 23;92(12):4196–4208. doi: 10.1529/biophysj.106.094995

Mechanisms of B-Cell Synapse Formation Predicted by Monte Carlo Simulation

Philippos K Tsourkas *, Nicole Baumgarth †, Scott I Simon *, Subhadip Raychaudhuri *
PMCID: PMC1877775  PMID: 17384077

Abstract

The clustering of B-cell receptor (BCR) molecules and the formation of the protein segregation structure known as the “immunological synapse” at the contact region between B cells and antigen presenting cells appears to precede antigen (Ag) uptake by B cells. The mature B-cell synapse is characterized by a central cluster of BCR/Ag molecular complexes surrounded by a ring of LFA-1/ICAM-1 complexes. In this study, we investigate the biophysical mechanisms that drive immunological synapse formation in B cells by means of Monte Carlo simulation. Our approach simulates individual reaction and diffusion events on cell surfaces in a probabilistic manner with a clearly defined mapping between our model's probabilistic parameters and their physical equivalents. Our model incorporates the bivalent nature of the BCR as well as changes in membrane shape due to receptor-ligand binding. We find that differences in affinity and bond stiffness between BCR/Ag and LFA-1/ICAM-1 are sufficient to drive synapse formation in the absence of membrane deformation. When significant membrane deformation occurs as a result of receptor-ligand binding, our model predicts the affinity-dependent mechanism needs to be complemented by a BCR signaling-driven shift in LFA-1 affinity from low to high in order for synapses to form.

INTRODUCTION

Specific recognition of foreign antigens by lymphocytes is central to the adaptive immune response. However, precisely how lymphocytes differentially respond to antigenic stimuli of varying type and strength remains unknown. Recent experimental evidence suggests antigen (or MHC-loaded peptides for the T-cell/APC system) presentation on the restricted geometry of a two-dimensional cell surface, together with recruitment of antigen into segregated clusters of receptor-ligand complexes, could be one possible mechanism by which lymphocytes recognize and respond to antigen (1–9).

The clustering of receptor molecules on the cell surface and the formation of segregated protein structures increasingly is seen as an efficient mechanism of cellular information exchange during cell-cell interactions (10). In the immune system, such clustering and segregation of membrane-bound proteins is observed at the intercellular junction between lymphocytes and antigen presenting cells (APC) as they become adherent and engage in antigen recognition. Because of the resemblance to neurological synapses, these structures have been collectively termed “immunological synapses” (2–4).

The mature B-cell synapse consists of a central cluster of B-cell receptor/antigen (BCR/Ag) molecular complexes (sometimes also referred to as the central supramolecular activation cluster, or c-SMAC), surrounded by a ring of lymphocyte function-associated antigen-1/intercellular adhesion molecule-1 (LFA-1/ICAM-1) complexes (also known as the peripheral SMAC, or p-SMAC). This is the much-studied canonical form of the immune synapse first observed at the intercellular junction between a T cell and an APC (1–4).

Although the mechanisms that drive synapse formation in T cells have extensively been modeled (11–18) since the pioneering work of Qi et al. (11), less is known about the mechanisms that govern synapse formation in B cells. Even though the structure of the B-cell synapse is similar to that of the canonical form of the T-cell synapse, factors such as receptor affinity, density, shape, and extracellular domain length vary significantly between T cells and B cells. B-cell receptors (BCRs) are bivalent antibody molecules (IgM and IgD for naïve B cells) whereas T-cell receptors are monovalent. Moreover, the affinity of BCR for antigen can vary between 105 M−1–1010 M−1, as compared to 104 M−1–107 M−1 in the case of T-cell receptors (TCRs) for MHCp. Furthermore, the typical density of BCR on B-cell surfaces (∼200 molecules/μm2) is an order of magnitude greater than the typical density of TCR on a T-cell surface (∼20 molecules/μm2). Importantly, the extracellular domain length of BCR/Ag complexes in B-cell synapse experiments (5–7) is close to that of LFA-1/ICAM-1 complexes (∼40 nm), which is markedly different from that of TCR/MHCp complexes (∼15 nm). The relatively short length of TCR/MHCp bonds is considered to be one of the major driving factors in T-cell synapse formation (11). For these reasons, it is thought that the mechanisms that drive synapse formation in B cells differ substantially from those in T cells (19).

B-cell synapse formation might be driven by signaling that results in changes in membrane shape as a result of affinity-dependent BCR/Ag binding (8). Alternatively, B-cell receptor clustering in B cells defective in signaling might be explained by the so-called “diffusion and binding” hypothesis (19). According to the latter model, the synapse forms mainly by undirected diffusion of receptors into the contact zone, whereupon they bind with high affinity and stay in place or are eventually expelled by crowding at the center of the contact zone. The experimental work (19) on which this model was based upon has crucial limitations, however, in that only a limited range of affinity (KA ∼ 108–1010 M−1) was considered, despite the fact that B cells can recognize antigen over KA ∼ 106–1010 M−1. In addition, the model does not consider the formation of the surrounding ring of LFA-1/ICAM-1 complexes observed in B-cell synapse experiments (5–7).

In this study, we investigate the molecular mechanisms of that drive B-cell synapse formation by systematically studying the effect of biophysical parameters. Our approach consists of a stochastic, agent-based computer model of B-cell/APC interaction in which individual molecular events such as diffusion and reaction are simulated using probabilistic rules. Individual parameter values can be varied in a controlled manner in successive in silico experiments to identify their contribution, or negate their importance, to the process of synapse formation. Interestingly, we are able to clearly define a mapping between the probabilistic parameters used in our simulation and their experimentally measured counterparts. Such a mapping scheme is crucial if we are to compare the results of in silico simulations to those of immunological experiments (20).

Our results show that differences in affinity and bond stiffness between BCR/Ag and LFA-1/ICAM-1 are sufficient to account for synapse formation when the affinity of BCR for antigen is less than that of LFA-1 for ICAM-1 and in the absence of membrane deformation (as is the case at the onset of synapse formation). For high-affinity BCR/Ag binding, our model predicts that it is necessary for BCR/Ag bonds to be stiffer than LFA-1/ICAM-1 bonds for a synapse to form. However, when significant membrane deformation is allowed in our model, active, signaling driven processes become necessary for synapse formation. One example of such a signaling-driven process is a shift in the affinity of LFA-1 from an initial low affinity state to a high-affinity state as a result of BCR signaling (6,7,9).

MODEL

Background

A Monte Carlo method was applied to model B-cell synapse formation. Thus, the molecular population is randomly sampled to undergo events such as diffusion and reaction, with its status updated at every time step. Monte Carlo methods have been successfully employed in the past to understand immune cell receptor-ligand binding, clustering, and signaling (13,18,20–24). Our model's distinguishing features are: i), the use of probabilistic rate constants instead of an energy-based Metropolis algorithm; ii), explicit spatial simulation of molecules; and iii), treatment of diffusion of receptor-ligand complexes. The explicit spatial simulation of molecules allows the modeling of crowding and exclusion effects that are potentially important in synapse formation but cannot easily be captured by differential equation-based models, particularly if more than one molecular species is present. The discrete nature of our model also eliminates the need to make assumptions about the continuity of molecular concentrations, which may not be valid at low antigen concentration. This is particularly relevant in light of the fact that antigen concentration is usually low at the onset of an immune response.

Model setup

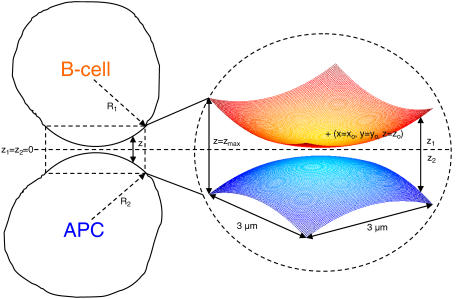
As shown in Fig. 1, the section of the B-cell/APC system we wish to model is the region of closest approach between the two cells, where the distance between the membranes is small enough to allow binding between molecules on opposite surfaces. The cell membranes are modeled as two Cartesian lattices, each discretized in an NXN grid of nodes. We assume the membranes initially have a spherical curvature, which, in the absence of external forces, both cells would tend toward to minimize surface energy. The total vertical separation distance z between the two surfaces at any given point (x, y) is given by z = z1 + z2, as in Fig. 1, with the half-heights z1 and z2 each given by:

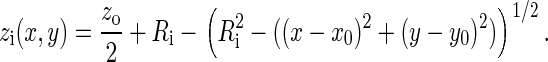graphic file with name M1.gif (1)

FIGURE 1.

FIGURE 1

Open in a new tab

Model of the B-cell/APC contact region. The cells are assumed to have a spherical shape, with the total vertical separation distance between the two surfaces at any point z = z1 + z2, with z1 and z2 given by Eq. 1. At the center of the contact zone (xo, yo), the vertical separation distance is at its minimum z = zo, whereas at the corners it is z = zmax. The 3 μm × 3 μm simulated area is large enough to include the entire zone where binding is possible.

At the center of the contact zone (x = xo, y = yo), the vertical separation between the two surfaces is at its minimum value, z = zo. We also can simulate a cell-bilayer system such as the one used in many synapse experiments (6–8) in the limit as R2→∞ and z2(x,y)→zo/2.

The size of the region we have chosen to simulate in our model is 3 μm × 3 μm, which is large enough to include the entire region over which binding can occur for spherical curvature (see Fig. 2), and also larger than typical experimentally observed synapse diameters of ∼2 μm (6,7). In addition, this area is believed to be sufficiently large such that a zero net flux condition exists at the boundaries, which in our agent-based simulator is simulated by means of fully reflecting boundaries. Only one molecule can occupy a node in our simulation, so we choose a nodal spacing equal to a membrane protein molecule's exclusion radius, ∼10 nm (resulting in 300 × 300 nodes). The exception are BCR molecules, which being bivalent, have a width of ∼25 nm (25,26), and thus occupy three nodes, with either a horizontal or vertical orientation on the lattice. The various parameters that relate to the spatial dimensions of our model are listed in Table 1.

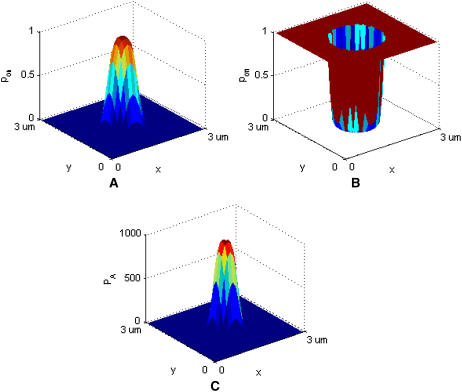
FIGURE 2.

FIGURE 2

Open in a new tab

Sample graphical representation of (A) pon, (B) poff, and (C) PA according to Eqs. 2–4. Receptor-ligand binding can only occur where pon > 0 and poff < 1. In this set of images, κ′ = 40 μN/m, κ = 2κ′, zeq = 42 nm, kB = 1.38 × 10−23 J/K, T = 300 K, pon = 1.0 and poff = 0.001.

TABLE 1.

Spatial dimensions of the model

Parameter Value
Size of contact region 3 μm × 3 μm
Number of nodes 300 × 300
Nodal spacing 10 nm
Cell radius (B Cell, APC) 6 μm
zmax from Eq. 1 (cell-bilayer case) 390 nm + zo
Open in a new tab

Simulation procedure: reaction and diffusion “moves”

At the start of a simulation run, molecules are uniformly distributed over the two surfaces at random. The molecular species represented are BCR and LFA-1 on the B-cell surface and antigen and ICAM-1 on the APC or bilayer surface. At every time step in the simulation, molecules from the population are individually sampled at random to attempt either diffusion or reaction events, determined by means of a coin toss with probability 0.5.

Reaction

If a molecule has been selected to undergo a reaction, the first step is to check the same node on the opposite surface for a complementary molecule. If that is the case, a random number trial with probability pon(i) is performed to determine if the two molecules will bind together and form a molecular complex. BCR molecules are modeled as being bivalent and occupy three nodes while being able to bind up to two antigen molecules, one on each end node (but not the middle node). If a free BCR molecule is selected for a reaction, a coin toss is additionally performed to pick one of the end nodes, and the APC surface opposite the chosen node is checked for a free antigen molecule. Sometimes a BCR molecule may have bound an antigen molecule on one Fab domain and have the other Fab domain free, forming a BCR/Ag complex. If the free Fab domain is selected, the reaction proceeds as described above, which may result in a second antigen molecule binding to the BCR/Ag complex (forming a BCR/Ag2 complex), while if the Fab domain with the bound antigen is selected, the BCR/Ag complex may dissociate into its component molecules with probability poff(i). If a BCR/Ag2 molecule is selected, one of the two Fab domains is selected at random to undergo dissociation as described above, resulting in the formation of a BCR/Ag complex and a free antigen molecule. Three reversible reactions are possible: LFA-1+ICAM-1↔LFA-1/ICAM-1, BCR+Ag↔BCR/Ag, and BCR/Ag+Ag↔BCR/Ag2. The binding and dissociation probabilities for the two reactions involving BCR are assumed to be the same and thus the subscript i refers to the BCR/Ag reactions when i = BA and the LFA-1/ICAM-1 reaction when i = LI.

We assume the probability of bond formation depends on the intermembrane distance z in accordance to the well-known linear spring model (27,28). Replacing the rate constant kon with the probability pon, we obtain the following probability density function:

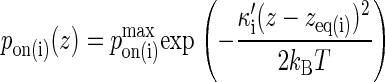graphic file with name M2.gif (2)

The bond is modeled as a mechanical spring with stiffness κ′ and equilibrium length zeq, whereas kB denotes the Boltzmann constant (1.38 × 10−23 J/K) and T the temperature (∼300 K). The probability of binding is greatest at the point z(x,y) = zeq, which will be the center of contact zone when zeq = zo, as in Fig. 2 A. In formulating our model, we assumed that as the two cells move closer to one another and zo decreases, the first binding event is likely to occur when zo approaches the value of zeq of one of the species, after which the cells stop moving toward each other. In our simulations we thus set zo equal to either zeq(BA) or zeq(LI), depending on the circumstances.

Similarly, the dissociation probability poff(i) is given by (27,28):

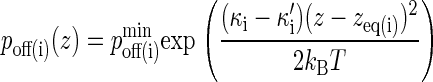graphic file with name M3.gif (3)

Without loss of generality, we can set κ(i) = 2κ′(i) so that the exponential in Eq. 3 is the same as that in Eq. 2 but with a positive sign in front. In contrast to pon, poff is a minimum at z = zeq, increasing away from this point, as in Fig. 2 B, where we also see that poff cannot exceed 1.0.

Since pon and poff are analogous to kon and koff, we can obtain the probabilistic analog to the association constant KA, denoted as PA, by dividing Eq. 2 by Eq. 3 and setting κ(i) = 2κ′(i):

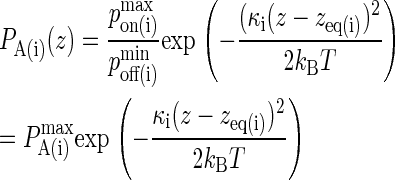graphic file with name M4.gif (4)

A typical plot of PA(i)(z) is shown in Fig. 2 C. The height of the peak is determined by the intrinsic affinity of the receptor-ligand pair, 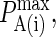Inline graphic whereas the bond stiffness κi determines how far from the optimum intermembrane spacing bonds can form, and hence the width of the peak in Fig. 2 C. The quantity PA(i)(z) defined in Eq. 4 thus denotes the overall receptor-ligand affinity, which consists of both the intrinsic affinity and the bond stiffness. 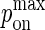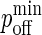Individually varying Inline graphic and Inline graphic while keeping the ratio 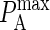Inline graphic constant changes the timescale of the simulation, but not the equilibrium behavior. It is important to note that PA(z) is not a probability but a probability ratio. 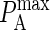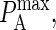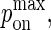The intrinsic affinity Inline graphic most closely corresponds to the quantity KA and the mapping between KA, kon, koff, and 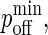Inline graphic Inline graphic Inline graphic respectively, is given in the Appendix.

Diffusion

On the other hand, if a molecule has been selected to undergo diffusion, a random number trial with probability pdiff(i) is used to determine if the diffusion move will occur successfully. If the trial is successful, the selected molecule will “hop” by a distance of one nodal spacing in one of four possible directions with equal probability. Because molecules are not allowed to occupy the same node, the diffusion hop will only occur if the appropriate nodes are unoccupied. For example, three nodes need to be free for a BCR molecule to diffuse the direction transverse to its length, whereas only one free node is needed in order for it to diffuse along its length. In the case of complexes, the appropriate nodes on both surfaces need to be free (two nodes for monomeric LFA-1/ICAM-1 complexes, two or four for BCR/Ag complexes, and three or five for BCR/Ag2 complexes). The mapping between pdiff(i) and the diffusion coefficient D is given in the Appendix.

Membrane free energy and deformation

Our simulation also allows the modeling of changes in the originally spherical membrane shape as a result of receptor-ligand binding. We use the membrane free energy used by Qi et al. (11) and Weikl and Lipowsky (18), which has the following form:

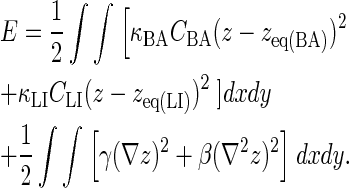graphic file with name M13.gif (5)

The first integral in the equation relates to the energy associated with receptor-ligand bond stretching, which is a function of the concentration of BCR/Ag and BCR/Ag2 complexes, CBA, and the concentration of LFA-1/ICAM-1 complexes, CLI, whereas the other two terms relate to the energy associated with membrane tension (γ) and bending rigidity (β), respectively. The change in the membrane separation distance z is modeled according to the well-known Landau-Ginzburg formulation in the manner of Qi et al. (11), which for the geometry used here has the form:

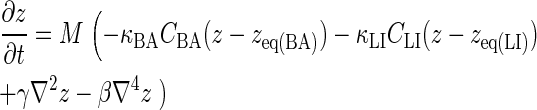graphic file with name M14.gif (6)

The constant M relates the timescale of membrane deformation relative to that of receptor-ligand binding, such that for small M, the membrane will essentially retain its shape for the duration of the simulation. Because the length scale of membrane deformation (set by (β/γ)1/2) is considerably larger than that of a protein's exclusion radius (∼100 nm instead of ∼10 nm), for the purpose of calculating z we coarse-grain the NXN membrane surface lattice into 10 × 10 node subdomains over which z is constant. The concentration of BCR/Ag, BCR/Ag2 and LFA-1/ICAM-1 complexes in each of these subdomains is then calculated and entered in the discrete form of Eq. 6.

Monte Carlo time step

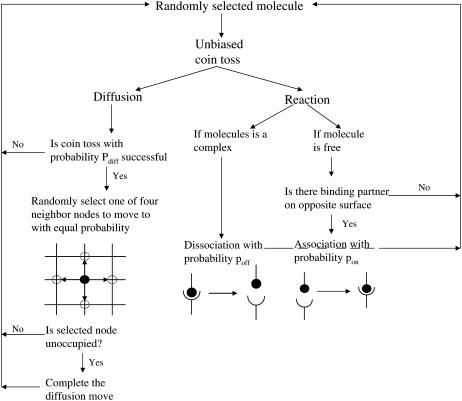
In our algorithm, a number S of diffusion/reaction trials is performed during every time step, at the end of which the membrane height is adjusted using Eq. 6 with Dirichlet boundary conditions obtained from Eq. 1. The number of trials S is set equal to the total number of molecules (free and complexes) present in the system at the beginning of each time step, and the simulation is run for a number of time steps T. Each Monte Carlo time step corresponds to 10−3 s, as shown in the Appendix. A summary of our Monte Carlo algorithm is shown in Fig. 3.

FIGURE 3.

FIGURE 3

Open in a new tab

Monte Carlo algorithm flow chart.

Model parameters

Our investigation strategy consists of successive virtual experiments in which individual parameter values are varied to determine the role of each parameter on synapse formation. Table 2 lists all biological parameters whose values can be varied in our simulations, excluding the spatial parameters listed in Table 1.

TABLE 2.

Parameters of the model

Parameter Description
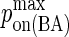Inline graphic Maximum BCR/Ag, BCR/Ag2 complex formation probability
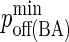Inline graphic Minimum BCR/Ag, BCR/Ag2 complex dissociation probability
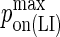Inline graphic Maximum LFA-1/ICAM-1 complex formation probability
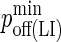Inline graphic Minimum LFA-1/ICAM-1 complex dissociation probability
B0 Initial number of free BCR molecules
A0 Initial number of free antigen molecules
L0 Initial number of free LFA-1 molecules
I0 Initial number of free ICAM-1 molecules
κBA Stiffness of BCR/Ag bond
κLI Stiffness of LFA-1/ICAM-1 bond
zeq(BA) Equilibrium extracellular length of BCR/Ag complex
zeq(LI) Equilibrium extracellular length of LFA-1/ICAM-1 complex
pdiff(B) Probability of diffusion of a free BCR molecule
pdiff(A) Probability of diffusion of a free antigen molecule
pdiff(L) Probability of diffusion of a free LFA-1 molecule
pdiff(I) Probability of diffusion of a free ICAM-1 molecule
pdiff(BA) Probability of diffusion of a BCR/Ag, BCR/Ag2 complex
pdiff(LI) Probability of diffusion of a LFA-1/ICAM-1 complex
M Timescale of membrane deformation
γ Membrane tension
β Membrane bending rigidity
Open in a new tab

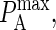
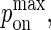
Many of the model parameters in Table 2 do not appear to vary significantly during physical experiments. Relevant experimentally obtained parameter values are listed in the two columns on the left-hand side of Table 3. In some cases, it is necessary to map the experimental value into the probabilistic analogs used by our model (see Appendix), as is the case with KA, kon, koff and 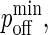Inline graphic Inline graphic Inline graphic respectively. Adapted forms of the experimentally-derived published parameter values used in our simulations are listed in the two columns on the right-hand side of Table 3.

TABLE 3.

Experimentally measured parameter values and their probabilistic counterparts

Experimental parameter Measured value Simulation parameter Mapped value
KA BCR/Ag 106–1010 M−1 (6,7) 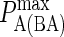Inline graphic 102–106
kon BCR/Ag 104–106 M−1s−1 (6,7) 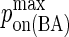Inline graphic 0.001–0.1
koff BCR/Ag 1–10−4 s−1 (6,7) 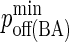Inline graphic 10−3–10−7
KA LFA-1/ICAM-1 3.3 μm2/molecules (29) 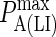Inline graphic 103
kon LFA-1/ICAM-1 0.33 μm2 s−1/molecules (29) 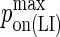Inline graphic 0.1
koff LFA-1/ICAM-1 0.1 s−1 (29) 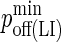Inline graphic 10−4
Antigen concentration 10–1000 molecules./μm2 (6) A0 100–10,000 molecules
ICAM-1 concentration 170 molecules/μm2 (6) I0 ∼2000 molecules
κLI 40 μN/m (12) κLI Same
zeq(LI) 42 nm (12) zeq(LI) Same
D free molecules ∼0.1 μm2/s (30) pdiff(F) 1.0
γ 24 μN/m (12) γ Same
β 5 × 10−20 J (12) β Same
Open in a new tab

Diffusion coefficients of free molecules in a biological membrane are in the range of ∼0.01–0.1 μm2/s (30), with little variation between species. We thus collectively group the individual diffusion probabilities of the free molecule species from Table 2 (pdiff(B), pdiff(A), pdiff(L), pdiff(I)) into a single parameter pdiff(F), and likewise group the individual diffusion probabilities of the complexes, pdiff(BA) and pdiff(LI), into a single parameter pdiff(C). A diffusion coefficient of the order of 0.1 μm2/s approximately corresponds to pdiff(F) = 1.0 (see Appendix), while pdiff(C) is assumed to be unknown and therefore variable.

The number of variable parameters can be further reduced by making assumptions regarding the number of free BCR and LFA-1 molecules initially present on the B-cell surface, B0 and L0. For instance, assuming a typical membrane protein molecule distribution of 105 molecules/cell (12,31), and using a typical lymphocyte radius of 6 μm (resultant area ∼450 μm2), the average molecular density is ∼220 molecules/μm2. For a contact area of 9 μm2, this means B0 = L0 = 2000. Because we are assuming a zero flux condition at the boundaries, the number of free molecules (B0, L0, A0, I0) cannot increase above this initial value. Binding and clustering at the center of the contact zone, however, will result in a concentration gradient that in real situations would cause a net flux of molecules into the contact zone. To address this, we compensate by setting the initial number of free molecule to a value higher than that given in experiments (6). From our simulations, we find that the number of complexes formed is not too large compared to B0, L0, A0, and I0 (of the order of hundreds) and we thus set B0 = L0 = 3000, which is sufficient to compensate for diffusion into the contact zone. A similar approach is used for I0 and A0.

It also is possible to estimate the equilibrium extracellular domain length of the BCR/Ag complex, even though an exact number is not available in the literature. In the in vitro experiments we are basing our model on, the antigen molecules are part of antigen-antibody immune complexes loaded onto Fc receptors (5–8), which would indicate a minimum extracellular domain length comparable to that of LFA-1/ICAM-1 complexes, i.e., ∼42 nm. However, it also is possible that in certain in vivo situations the antigens on the APC surface are fragments <1 nm in length, which would set the lower bound on the length of BCR/Ag complexes to the typical length of an antibody molecule, 22–23 nm (25,26). In our investigation we thus perform experiments where the length of the BCR/Ag complexes is set to either 22 or 42 nm.

When these assumptions and simplifications have been entered into our model, the list of variable parameters reduces to that shown in Table 4. These are the parameters for which defined values have not been reported, such as κBA and zeq(BA), (and which may well vary), or those that are varied in actual synapse experiments, such as antigen molecule number A0 and BCR affinity 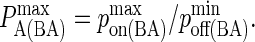Inline graphic These also are therefore the parameters we focused on as possible driving factors of B-cell synapse formation.

TABLE 4.

Unknown or variable parameters

Parameter Type
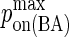Inline graphic Known, variable
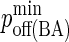Inline graphic Known, variable
A0 Known, variable
κBA Unknown, may vary
zeq(BA) May vary between ∼22 and 42 nm
M Unknown
pdiff(C) Unknown, may vary
Open in a new tab

RESULTS

No membrane deformation

Intrinsic affinity differences between BCR and LFA-1 can drive synapse formation at low BCR affinity

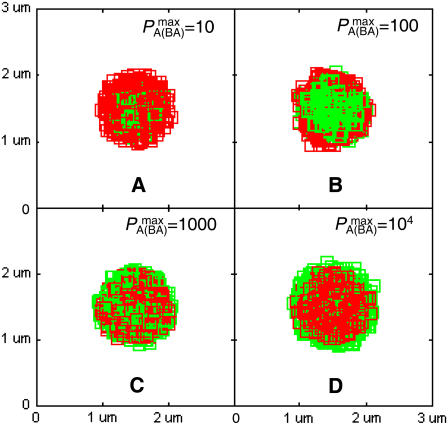
In nature, BCR affinity for antigen is critical in determining the strength of the B-cell response (32–36). In our simulations, we found that intrinsic BCR affinity can be a leading driver of synapse formation. In Fig. 4, the affinity of BCR for antigen is varied across four orders of magnitude, from KA = 105–108 M−1, whereas the affinity of LFA-1 for ICAM-1 is fixed at KA = 107 M−1. In Fig. 4 A (KA = 105 M−1), the affinity of BCR is clearly too low for a synapse to form, even though the traces of one are discernible. In Fig. 4 B (KA = 106 M−1), however, we can clearly see the difference in intrinsic affinity between BCR and LFA-1 is sufficient to produce patterns similar to experimentally observed B-cell synapses (6–8). No such pattern is observed when the affinities are equal (Fig. 4 C), whereas an inverted pattern forms when BCR affinity exceeds LFA-1 affinity (Fig. 4 D). The patterns generated in Fig. 4 are stable over a timescale of hours, although they do not represent the final equilibrium state of the system. The time evolution and final equilibrium behavior of the patterns in Fig. 4 are discussed in the Supplementary Material.

FIGURE 4.

FIGURE 4

Open in a new tab

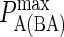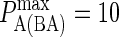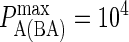Effect of varying BCR affinity (Inline graphic) on synapse formation. BCR/Ag complexes are shown in green, whereas LFA-1/ICAM-1 complexes are shown in red. The complexes are plotted in random order so as to simulate experimental intensity plots as closely as possible. In this set of figures the affinity of BCR was varied from Inline graphic to Inline graphic (KA ≈ 105–108 M−1). In panel A the affinity is too low for synapse formation but in B we see that the difference in affinity between BCR and LFA-1 is sufficient to produce a synapse. 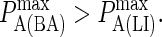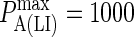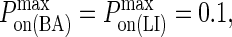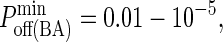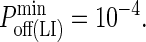This is no longer the case in panel C, where the affinities are equal, whereas an inverted pattern forms in D, where Inline graphic These images were taken after T = 105 time steps (100 s) with Inline graphic (KA ≈ 107 M−1), A0 = I0 = 2000 molecules, κBA = κLI = 40 μN/m, zeq(BA) = zeq(LI) = 42 nm, pdiff(F) = 1, pdiff(C) = 0.1, Inline graphic Inline graphic and Inline graphic

Our explanation for this behavior is as follows: Initially, the various molecules, all in the free state, are scattered uniformly over the cell surfaces. Because the region where binding is possible (defined by pon > 0 and poff < 1 in Fig. 2) is relatively small compared to the overall region of contact, at the start of our simulations most molecules are located outside the region of binding. The synapse pattern forms as free molecules from the periphery randomly drift into the zone of binding until they eventually find a binding partner and form a complex. If the complexes have relatively low diffusivity, as is the case in Fig. 4, a ring-like pattern results as the complexes tend to stay near where they formed, at the edge of the region of binding. Over time these complexes may break up, and some of the newly freed molecules are equally likely to drift further into the zone of binding. As the probability of binding is higher and that of dissociation lower in the interior of the contact zone due to the curvature of the membrane, the ring-like pattern becomes more cluster-like over time. In Fig. 4 B, BCR has a lower affinity and higher koff than LFA-1, so that it forms a cluster at a faster rate than LFA-1, thereby producing a synapse. The situation is reversed in Fig. 4 D, whereas a purely random pattern is produced in Fig. 4 C as the two species have the same affinity and off-rate. These results show that pattern formation is in large part driven by differences in intrinsic affinity between the BCR/Ag and LFA-1/ICAM-1 (and in particular koff).

BCR/Ag bond stiffness is crucial to synapse formation at high BCR affinity

It is clear from the above results that differences in intrinsic affinity between the two species are not sufficient to account for synapse formation across the entire physiological range of BCR affinity (KA = 106–1010 M−1). However, given there are several antibody molecules that serve as B-cell receptors, and that these receptors encounter a wide variety of antigens, it is reasonable to assume the stiffness of the BCR/Ag bond (κBA) will vary in addition to the intrinsic affinity. In our simulations we have discovered that increasing the stiffness of the BCR/Ag bond above that of the LFA-1/ICAM-1 bond can result in synapses forming over the entire physiological range of BCR affinity. For example, our simulations show that for BCR affinity 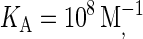Inline graphic a synapse such as the one in Fig. 4 B will form with a BCR/Ag bond stiffness value of κBA = 80 μN/m, whereas an inverted synapse pattern formed when the bond stiffness of the two species was equal (Fig. 4 D). At higher BCR affinity values, a greater increase in BCR/Ag bond stiffness is necessary to produce a synapse (κBA ≈ 160 μN/m at KA = 1010 M−1).

Our explanation for this mechanism of synapse formation is that increasing bond stiffness narrows the width of the graphs in Fig. 2 (without lowering their peak heights), thereby reducing the radius of the zone of binding for BCR and forcing the BCR/Ag complexes into a smaller area. BCR/Ag complexes thus form closer to the center than LFA-1/ICAM-1 complexes, resulting in a concentric pattern with BCR/Ag complexes on the inside and LFA-1/ICAM-1 complexes on the outside. If the bond stiffness is sufficiently high for a particular BCR affinity value, the ring of BCR/Ag complexes will compress into a cluster, resulting in a synapse. With increasing BCR affinity, it takes increasingly longer for the BCR/Ag complexes to collect into a cluster (since the dissociation probability decreases), and thus a stiffer bond is needed to produce a synapse.

Significant membrane deformation

Synapses cannot form due to affinity differences in the absence of a shift in LFA-1 affinity

No synapses are observed to form by the affinity-dependent mechanism when significant membrane deformation is allowed to take place. At low BCR affinity (KA = 106 M−1), the pattern formed is barely recognizable as a synapse, as can be seen in Fig. 5 A. The BCR/Ag are not arranged in a compact cluster and the center of the contact region moreover contains large gaps filled by LFA-1/ICAM-1 complexes. At high BCR affinity (KA ≥ 108 M−1) the BCR/Ag complexes are distributed in a ring at the outer edge of the region where binding is possible, even for relatively high BCR/Ag bond stiffness (κBA = 400 μN/m), as can be seen in Fig. 5 B.

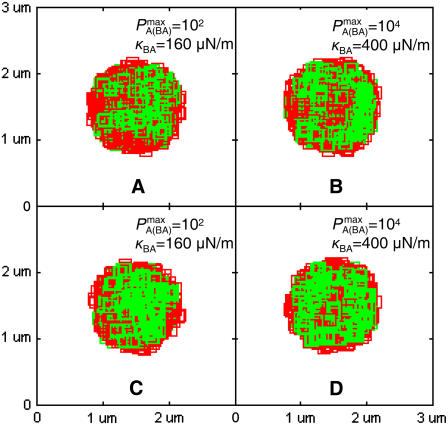
FIGURE 5.

FIGURE 5

Open in a new tab

Effect of membrane deformation on synapse formation. In panels A and B no synapse pattern is observed to form when LFA-1 is in a high-affinity state from the start, both for (A) low BCR affinity and (B) high BCR affinity and high BCR/Ag bond stiffness. In panel C, by contrast, we observe a synapse at low BCR affinity (KA ≈ 106 M−1) provided LFA-1 is initially in a low affinity state and switches to the high-affinity state after t ∼ 30 s (also provided κBA = 160 μN/m). In panel D we see that this mechanism no longer generates a canonical synapse at high BCR affinity (KA ≥ 108 M−1), even when BCR/Ag bond stiffness is 10-fold greater than that of LFA-1/ICAM-1 (κBA = 400 μN/m). These images were taken after T = 105 time steps (100 s) with 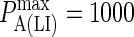Inline graphic (KA ≈ 107 M−1), A0 = I0 = 2000 molecules, κLI = 40 μN/m, zeq(BA) = zeq(LI) = 42 nm, pdiff(F) = 1 and pdiff(C) = 0.1, M ∼ 10−12 m4/Js, γ = 24 μN/m, and β = 5 × 10−20 J.

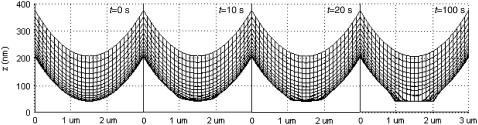
These results indicate that membrane deformation has a significant and detrimental effect on synapse formation. The explanation for this can be seen in Fig. 6, where we see that as a result of receptor-ligand binding, the membrane separation distance at the zone of binding achieves a uniform value approximately equal to the equilibrium bond length of BCR/Ag and LFA-1/ICAM-1 complexes (∼42 nm). The effect of membrane curvature, which previously was crucial to synapse formation by allowing the BCR/Ag complexes to collect into a cluster at a faster rate than LFA-1/ICAM-1 complexes (when BCR affinity was less than LFA-1 affinity) is now entirely negated. As the membrane separation distance in the contact region assumes this uniform value rather rapidly (t ∼ 2000 time steps; Fig. 6), the initial ring of BCR/Ag complexes never compresses into a compact central cluster, producing the pattern in Fig. 5 A. The uniform membrane separation distance in the contact region also negates the previously crucial effect of BCR/Ag bond stiffness at high affinity, as it makes differences in bond stiffness irrelevant. BCR/Ag complexes can thus form at the outer edge of the zone of binding, generating the image seen in Fig. 5 B.

FIGURE 6.

FIGURE 6

Open in a new tab

Cross-sectional view of the time evolution of membrane shape as a result of receptor-ligand binding. Already by t = 20 s, we can see that the membrane separation distance center of the contact zone has more or less attained a uniform value of z ∼ 40 nm. This image sequence was obtained with PA(BA) = 100 (KA ≈ 106 M−1), PA(LI) = 1000 (KA ≈ 107 M−1), A0 = I0 = 2000 molecules, κBA = κLI = 40 μN/m, zeq(BA) = zeq(LI) = 42 nm, pdiff(F) = 1, pdiff(C) = 0.1, M ∼ 10−12 m4/Js, γ = 24 μN/m, β = 5 × 10−20 J.

A shift in LFA-1 affinity can drive synapse formation

It recently has been hypothesized that LFA-1 on the B-cell surface is initially in a low affinity state before contact with the APC, and that it changes conformation to a high-affinity state after outside-in signaling following BCR activation upon antigen ligation (6,7,9). Our model shows it is possible for synapses to form when significant membrane deformation occurs only when the affinity and stiffness-dependent mechanism is combined with a shift in the affinity of LFA-1 from low to high as a result of BCR/Ag binding. To model the process, we initially set the affinity of LFA-1 to a low value of KA ≈ 104 M−1, and switch it to the high-affinity value of KA = 107 M−1 after 30 s have elapsed. A similar mechanism of LFA-1 affinity modulation has previously been observed in experimental systems involving immune cell activation (37). In Fig. 5 C we see that at low BCR affinity, the coupling of a shift in LFA-1 affinity with increased BCR/Ag bond stiffness can result in the formation of synapses where none formed previously (Fig. 5 A). Setting the time at which the LFA-1 affinity shift occurs to t > 30 s did not produce a significant change in results, whereas decreasing it below this threshold essentially negated its effect. At high BCR affinity (KA ≥ 108 M−1), however, no synapses are observed to form under any circumstances, regardless of BCR/Ag bond stiffness values or LFA-1 affinity shift (Fig. 5 D).

Our explanation for synapse formation due to a shift in LFA-1 affinity is as follows: When LFA-1 affinity is initially low, almost all complexes formed are BCR/Ag complexes. Because fewer complexes are formed, the central portion of the membrane deforms more slowly than when BCR/Ag and LFA-1/ICAM-1 complexes form simultaneously. This gives the initial ring of BCR/Ag complexes enough time to compress into a cluster before the membrane separation distance achieves a uniform value. By the time the affinity of LFA-1 is shifted, allowing rapid LFA-1/ICAM-1 binding, the center of the contact zone is already occupied by the BCR/Ag complexes, so that the LFA-1/ICAM-1 complexes cannot achieve numerical superiority in the center but do so at the periphery, generating a synapse pattern such as in Fig. 5 C. As BCR affinity increases above KA = 107 M−1, the faster rate of BCR/Ag complex formation results in faster membrane deformation and hence it becomes increasingly difficult for synapses to form (Fig. 5 D). This suggests that yet another mechanism must be responsible for synapse formation at high BCR affinity when significant membrane deformation occurs.

Importance of molecular size and diffusion on synapse formation

Though B-cell synapse formation experiments to date mostly consider antigen loaded onto immune complexes (5–7), which results in BCR/Ag complexes of length comparable to LFA-1/ICAM-1 complexes, the possibility that the equilibrium length of the BCR/Ag complexes can vary in vivo and can be equal to its minimum theoretical value (zeq(BA) = 22 nm) cannot be ruled out. In our simulations, we find that setting zeq(BA) = 22 nm enhances the affinity and signaling-mediated synapse formation mechanisms outlined above in all cases. At the low end of BCR affinity (KA < 108 M−1) in particular, the difference in length is sufficient to result in synapses without a difference in bond stiffness or a shift in LFA-1 affinity. Synapses formed with zeq(BA) = 22 nm are also larger than with zeq(BA) = 42 nm, ∼1.5 μm in diameter instead of ∼1 μm.

Throughout our investigations we also observed that synapses only formed when complex diffusivity was lower than free molecule diffusivity by at least an order of magnitude (i.e., pdiff(C) = 0.1 and pdiff(F) = 1). This applied regardless of the synapse formation mechanism (affinity and stiffness-dependent or LFA-1 affinity shift-dependent) or membrane deformation regime. Our explanation is that as the diffusivity of the molecular complexes increases, they become more likely to diffuse away from the zone of binding and eventually dissociate, resulting in less ordered and stable patterns. If the molecular complexes are as mobile as free molecules, the synapse will never form as entropic forces will win over free energy gain obtained from the ordered synapse pattern. Thus an order-of-magnitude difference between complex and free molecule diffusivity is needed for synapses to form in all cases. This is consistent with recent studies that show that the mobility of membrane proteins is strongly dependent on size (38–40), and in our simulations the difference in size between free monomeric molecules and BCR/Ag2 complexes is significant.

Effect of BCR bivalence

Throughout our simulations we have simulated BCR as a bivalent molecule, and it is of interest to compare these results with those obtained when BCR is simulated as a monovalent molecule. The most immediate difference is that fewer BCR/Ag complexes form with monovalent BCR, as the number of binding sites for antigen is essentially cut by half. This results in less dense BCR/Ag clusters and thus a lower probability of forming a synapse. For instance, the minimum BCR/Ag bond stiffness needed for synapse formation with monovalent BCR is roughly twice that needed with bivalent BCR.

Significantly, it is virtually impossible for synapses to form with monovalent BCR when membrane deformation is included in our model, no matter the BCR/Ag bond stiffness value or whether a shift in LFA-1 affinity occurs. At the low end of the BCR affinity range it is possible to obtain synapses only with both very stiff BCR/Ag bond values (at least an order of magnitude greater than LFA-1/ICAM-1) and a shift in LFA-1 affinity, whereas at the high end of the BCR affinity range no synapses form under any circumstances. Finally, an additional difference is that as a monovalent BCR molecule occupies only one node and can bind only a single antigen molecule, it is more mobile than a bivalent BCR molecule and hence synapse formation requires that pdiff(C) be at least two orders of magnitude lower than pdiff(F) in all cases.

DISCUSSION

Stochastic simulation of B-cell synapse formation reveals that an affinity-dependent mechanism appears sufficient to drive synapse formation in the absence of membrane deformation. When intrinsic BCR affinity is lower than LFA-1 affinity by an order of magnitude, synapses can form solely due to the difference in affinity. When intrinsic BCR affinity is higher than LFA-1 affinity, it is necessary for BCR/Ag bonds to be stiffer than LFA-1/ICAM-1 bonds in order for synapses to form. While we have not found literature values for BCR/Ag bond stiffness, our results indicate that the minimum necessary difference in bond stiffness between the two species is well within an order of magnitude (fourfold at most). Given the wide variety of antigens a B cell can encounter, we hypothesize that the requirement on BCR/Ag bond stiffness is not particularly severe and is likely to be met in many cases, particularly when considering that the intrinsic affinity of BCR for antigen ranges across five orders of magnitude. With the addition of significant membrane deformation, differences in affinity and bond stiffness are not sufficient to drive synapse formation and an additional mechanism, in the form of a signaling-driven shift in the affinity of LFA-1 is necessary. Even with a shift in LFA-1 affinity, however, synapses only form at the low end of BCR affinity, with no synapses observed above KA = 107 M−1.

Based on our model's results, we propose the following scenario as the most probable mechanism of synapse formation in B cells. As the B cell and APC approach each other, the LFA-1 is in a low affinity state, so that binding begins when the two cells are close enough for a BCR molecule to bind to an antigen molecule. BCR binding to antigen also initiates a signaling cascade directing LFA-1 to change conformation so that it can bind ICAM-1 with high affinity. BCR molecules from the periphery drift into the zone where binding is possible, whereupon they either bind to antigen and form a complex, or eventually drift back out to the periphery again. Because molecular complexes are considerably less mobile than free molecules, they tend to stay where they form, at the edges of the zone of binding, producing a ring-like pattern. This ring becomes more cluster-like over time as some complexes break up and their constituent molecules drift toward the center of the contact zone where they are more likely to bind another molecule. During this process the B-cell membrane deforms to accommodate the BCR/Ag complexes at their equilibrium bond length. After ∼30 s have passed, enough LFA-1 molecules have shifted to the high-affinity state so that LFA-1/ICAM-1 binding becomes significant, accelerating membrane deformation and resulting in uniform membrane separation distance at the center of the contact zone. The head start in binding of the BCR, combined with the potentially higher bond stiffness of the BCR/Ag bond, results in BCR/Ag complexes being numerically dominant at the center of the contact zone. The more flexible LFA-1/ICAM-1 bonds are more numerous at the outer part of the contact zone, producing the canonical immunological synapse pattern. At the high end of BCR affinity (KA ≥ 108 M−1), the rate of membrane deformation due to BCR/Ag complex formation is so high that the shift in LFA-1 affinity is not sufficient to produce synapses, leading us to speculate on the existence of additional synapse formation mechanisms for high BCR affinity and significant membrane deformation.

Although the B-cell synapse resembles the T-cell synapse in appearance, our model indicates that the mechanisms of synapse formation between T cells and B cells differ substantially. The primary mechanism of synapse formation in T cells is believed to be the active cytoskeletal drive of the TCR/MHCp complexes toward the center coupled with the difference in extracellular domain length between TCR/MHCp and LFA-1/ICAM-1 (11,12,14,18). Our results show that this is clearly not the case in B cells, where differences in extracellular domain length between the species are negligible (6,7,25,26) and synapses can form without cytoskeletal motion of receptors toward the center.

Comparison of our model's result with experimental data shows substantial agreement. With the mechanisms described above, our model predicts synapse formation over the entire range of physiological BCR affinity values (KA = 106–1010 M−1) (6,7). Furthermore, our model does not produce synapses below KA = 106 M−1, which is in line with experimental results (6,7). The minimum number of antigen molecules needed for a synapse is ∼1000 molecules, which corresponds to a concentration of ∼100 molecules/μm2, assuming a contact area of ∼9 μm2. The size of the synapses predicted by our model is ∼1–1.5 μm in diameter, which is comparable to the 1–2-μm diameter of real synapses. The timescale of synapse formation in our model is of the order of 105 time steps, which is mapped to physical time by matching the diffusion coefficients in our simulation to those reported in experiments (see Appendix). This yields a 1 ms per time step mapping, which means our model's timescale of synapse formation corresponds to the experimentally observed timescale of 1–2 min.

As it stands, our model possesses several attributes that make it particularly suitable for modeling B-cell synapse formation. The approach we are using is stochastic and discrete in nature, and hence is suitable for the modeling of situations of low antigen concentration, such as the onset of the immune response. Our model incorporates the bivalent nature of the BCR as well as changes in membrane shape due to receptor-ligand binding. In addition, we use a Monte Carlo scheme that is computationally efficient and can thus carry out an entire set of virtual experiments in a matter of minutes. Furthermore, we present a novel framework for mapping our model's probabilistic parameters into physical quantities and vice versa (see Appendix). Such a framework is notably absent from similar Monte Carlo models developed to study such systems in the past (20) and to the best of our knowledge is the first of its kind. Finally, our model can be easily modified to model a variety of similar cell-cell systems.

Future work will be aimed at making our model increasingly physiological, especially with regards to the modeling of signaling-induced processes. Most important is the investigation of the mechanisms of synapse formation at high BCR affinity when membrane deformation is significant. Another extension of our work could involve further exploration of the precise form of the LFA-1 affinity shift in B cells, about which little is currently known.

One of the main goals of this study is to make predictions about the process of B-cell synapse formation that may be experimentally tested. Accurate measurement of BCR/Ag bond stiffness, complex diffusivity, membrane deformation, and LFA-1 activation kinetics during synapse formation would go a long way toward establishing the validity of our model's predictions. It is our belief the combination of computational modeling and experimental investigations part of an iterative process can lead to a full understanding of the process of immunological synapse formation in B cells and further account for the physiological responses observed during B-cell immune function.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Acknowledgments

The authors thank Drs. Arup Chakraborty, Rajiv Singh, and Volkmar Heinrich for many insightful discussions over the course of this study. We also acknowledge Dr. Roger Zauel for his valuable help on random number generation.

N.B. acknowledges support from National Institutes of Health grant R01 AI051354. S.S. acknowledges National Institutes of Health grant AI27294.

APPENDIX

Because some of the parameters of our model are probabilistic in nature and therefore dimensionless, it is necessary to map them onto physical quantities to be able to physically interpret the results. Two such mappings are necessary: one that maps the probabilistic affinity 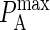Inline graphic to the association constant KA and one that maps the size of our model's time step to physical time by relating pdiff to the physical diffusion coefficient D.

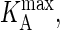We begin this section with the mapping between PA and the association constant KA. To map values of Inline graphic onto corresponding values of Inline graphic we make use of the fact that at kinetic equilibrium, the two-dimensional association constant, KA(2D), can be obtained from the following relation (12,28,31):

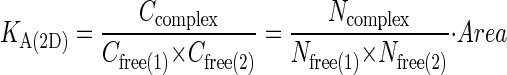graphic file with name M44.gif (A1)

Here C refers to the concentration (molecules/area), Ncomplex is the number of complexes formed at equilibrium, whereas Nfree(1) and Nfree(2) refer to the number of free molecules present at equilibrium. To map 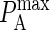Inline graphic to KA(2D), we run our simulation for a particular value of 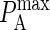Inline graphic to obtain Ncomplex, Nfree(1), and Nfree(2), and calculate KA(2D) from Eq. A1.

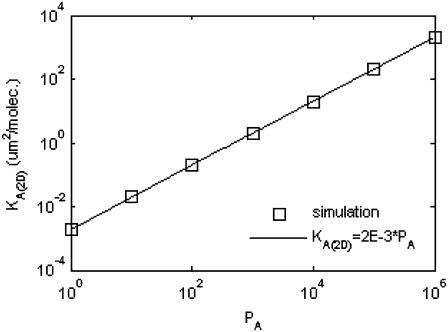
The results are shown in Fig. 7, where we see a linear relationship between KA(2D) and 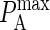Inline graphic of the form:

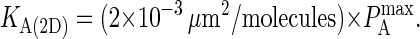graphic file with name M48.gif (A2)

FIGURE 7.

FIGURE 7

Open in a new tab

Mapping between simulated affinity PA and KA(2D). The relationship is perfectly linear, with order-of-magnitude increases in PA corresponding to order of magnitude increases in KA(2D).

Because the affinity of BCR in the experimental literature is usually given in units of three-dimensional KA, it also is necessary to convert values of KA(2D) to KA(3D). This is done by first multiplying by the effective confinement length in the manner of Bell (31), for which we use the thickness of cell membrane (∼10 nm). Because KA(3D) is usually given in units of M−1, the second step in the conversion consists of multiplying by the conversion factor 1L = (0.1 m)3 = 1015 μm3 and multiplying by Avogadro's number (1 mol = 6 × 1023 molecules). This results in the following relation between 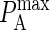Inline graphic and KA(3D):

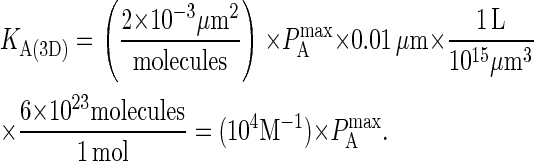graphic file with name M50.gif (A3)

Thus, for example, the reported value of LFA-1 affinity of 3.3 μm2/molecule (28) approximately maps to Inline graphic (using Eq. A2), which in turn corresponds to KA(3D) = 107 M−1 (using Eq. A3).

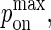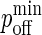Next, we establish the mapping of our model's timescale to physical time. There are two ways of doing this: One is to match the number of time steps it takes to obtain a synapse in our model to the timescale of synapse formation in experiments, and from there map pdiff, Inline graphic and Inline graphic to their physical counterparts. Another is to match the pdiff for which we obtain a synapse in our model to the diffusion D reported in physical experiments, and allow the timescale of our model to emerge naturally from this. Because it appears more sound, we use the latter approach.

As with affinity, we map the probability of diffusion pdiff to the diffusion coefficient D by means of direct simulation. In these simulations, we note the location and time of each molecule as it is created. For complexes, this is simply the time and location at which they form, whereas for free molecules this is either their initial location on the lattice and t = 0, or if they have been created as a result of a complex dissociating, the location and time at which the complex dissociated. At each time step, the square of the distance the molecule has traveled from its location of creation is divided by the number of time steps that molecule has been in existence. This is then averaged over all the molecules of that particular type to obtain the simulation diffusion coefficient, Dsim, at that particular time step. Thus we have:

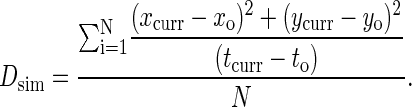graphic file with name M54.gif (A4)

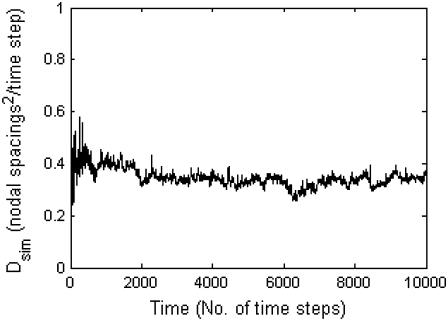
We then run the simulation for a particular value of pdiff to obtain a time plot of the value of Dsim in the manner of Fig. 8. From the figure, we see that a probability of diffusion pdiff = 1 corresponds to a value of Dsim in the range of 0.1–1 (nodal spacings)2/time step. We then multiply by the appropriate conversion factor to convert the length in nodes to physical length:

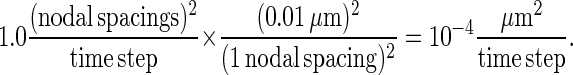graphic file with name M55.gif (A5)

FIGURE 8.

FIGURE 8

Open in a new tab

Plot of Dsim resulting from setting pdiff = 1.0.

We now match this value to that of diffusion coefficient in synapse experiments found in the literature to obtain the physical length of time of one of our model's time steps. The literature value of the diffusion coefficient in synapse experiments of ∼0.1 μm2/s indicates that a single time step in our model corresponds to 0.001 s, i.e., a 1 ms per time step mapping. The observed time of synapse formation of t = 105 time steps in our simulations thus corresponds to 100 s, which agrees rather well with the experimental time of synapse formation of 1–2 min. With this timescale mapping, the diffusion coefficient mapping now becomes:

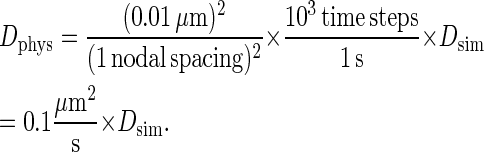graphic file with name M56.gif (A6)

Once we have obtained the timescale mapping, it is straightforward to map 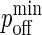Inline graphic to koff through the relation:

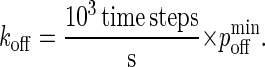graphic file with name M58.gif (A7)

Thus, the reported koff for LFA-1 in the literature of 0.1 s−1 (29) corresponds to 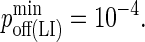Inline graphic Multiplying Eqs. A3 and A7, we obtain the mapping between 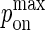Inline graphic and kon:

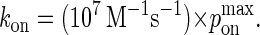graphic file with name M61.gif (A8)

From this, we estimate the measured value of kon = 2 × 106 M−1s−1 for the HEL line of antigens in Carrasco et al. (6,7) approximately corresponds to a 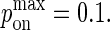Inline graphic Because 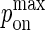Inline graphic cannot exceed 1, to simulate values of kon > 107 M−1s−1, the mapping between pdiff and D would have to be changed by matching pdiff = 1 to a higher D value.

References

  • 1.Wulfing, C., M. D. Sjaastad, and M. M. Davis. 1998. Visualizing the dynamics of T cell activation: intracellular adhesion molecule 1 migrates rapidly to the T cell/B cell interface and acts to sustain calcium levels. Proc. Natl. Acad. Sci. USA. 95:6302–6307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Monks, C. R., B. A. Freiberg, H. Kupfer, N. Sciaky, and A. Kupfer. 1998. Three-dimensional segregation of supramolecular activation clusters in T cells. Nature. 395:82–86. [DOI] [PubMed] [Google Scholar]
  • 3.Grakoui, A., S. K. Bromley, C. Sumen, M. M. Davis, A. S. Shaw, P. M. Allen, and M. L. Dustin. 1999. The immunological synapse: a molecular machine controlling T cell activation. Science. 285:221–227. [DOI] [PubMed] [Google Scholar]
  • 4.Krummel, M. F., M. D. Sjaastad, C. Wulfing, and M. M. Davis. 2000. Differential clustering of CD4 and CD3ζ during T cell recognition. Science. 289:1349–1352. [DOI] [PubMed] [Google Scholar]
  • 5.Batista, F. D., D. Iber, and M. S. Neuberger. 2001. B cells acquire antigen from target cells after synapse formation. Nature. 411:489–494. [DOI] [PubMed] [Google Scholar]
  • 6.Carrasco, Y. R., S. J. Fleire, T. Cameron, M. L. Dustin, and F. D. Batista. 2004. LFA-1/ICAM-1 interaction lowers the threshold of B cell activation by facilitating B cell adhesion and synapse formation. Immunity. 20:589–599. [DOI] [PubMed] [Google Scholar]
  • 7.Carrasco, Y., and F. D. Batista. 2006. B-cell activation by membrane-bound antigens is facilitated by the interaction of VLA-4 with VCAM-1. EMBO J. 25:889–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Fleire, S. J., J. P. Goldman, Y. R. Carrasco, M. Weber, D. Bray, and F. D. Batista. 2006. B cell ligand discrimination through a spreading and contracting response. Science. 312:738–741. [DOI] [PubMed] [Google Scholar]
  • 9.Carrasco, Y. R., and F. D. Batista. 2006. B cell recognition of membrane-bound antigen: an exquisite way of sensing ligands. Curr. Op. Immun. 18:286–291. [DOI] [PubMed] [Google Scholar]
  • 10.Bray, D., M. D. Levin, and C. J. Morton-Firth. 1998. Receptor clustering as a cellular mechanism to control sensitivity. Nature. 393:85–88. [DOI] [PubMed] [Google Scholar]
  • 11.Qi, S. Y., J. T. Groves, and A. K. Chakraborty. 2001. Synaptic pattern formation during cellular recognition. Proc. Natl. Acad. Sci. USA. 98:6548–6553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Burroughs, N. J., and C. Wülfing. 2002. Differential segregation in a cell-cell contact interface: The dynamics of the immunological synapse. Biophys. J. 83:1784–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Lee, K. H., A. R. Dinner, C. Tu, G. Campi, S. Raychaudhri, R. Varma, T. N. Sims, W. R. Burack, H. Wu, J. Wang, O. Kanagawa, M. Markiewicz, et al. 2003. The immunological synapse balances T cell receptor signaling and degradation. Science. 302:1218–1222. [DOI] [PubMed] [Google Scholar]
  • 14.Lee, S. J. E., Y. Hori, J. T. Groves, M. L. Dustin, and A. K. Chakraborty. 2002. Correlation of a dynamic model for immunological synapse formation with effector functions: two pathways to synapse formation. Trends Immunol. 23:492–502. [DOI] [PubMed] [Google Scholar]
  • 15.Lee, S. J. E., Y. Hori, and A. K. Chakraborty. 2003. Low T cell receptor expression and thermal fluctuations contribute to formation of dynamic multifocal synapses in thymocytes. Proc. Natl. Acad. Sci. USA. 100:4383–4388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Raychaudhuri, S., A. K. Chakraborty, and M. Kardar. 2003. Effective membrane model of the immunological synapse. Phys. Rev. Lett. 91:208101. [DOI] [PubMed] [Google Scholar]
  • 17.Coombs, D., M. Dembo, C. Wofsy, and B. Goldstein. 2004. Equilibrium thermodynamics of cell-cell adhesion mediated by multiple ligand-receptor pairs. Biophys. J. 86:1408–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Weikl, T. R., and R. Lipowsky. 2004. Pattern formation during T-cell adhesion. Biophys. J. 87:3665–3678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Iber, D. 2005. Formation of the B-cell synapse: retention or recruitment? Cell. Mol. Life Sci. 62:206–213. [DOI] [PubMed] [Google Scholar]
  • 20.Goldstein, B., J. R. Faeder, and W. S. Hlavacek. 2004. Mathematical and computational models of immune-receptor signaling. Nature Rev. Immunol. 4:445–456. [DOI] [PubMed] [Google Scholar]
  • 21.Hammer, D., and S. Apte. 1991. Simulation of cell rolling and adhesion of surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 63:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Mahama, P. A., and J. J. Linderman. 1995. Monte Carlo simulations of membrane signal transduction events: effect of receptor blockers on G-protein activation. Ann. Biomed. Eng. 23:299–307. [DOI] [PubMed] [Google Scholar]
  • 23.Van Kampen, N. G. 2001. Stochastic Processes in Physics and Chemistry. Elsevier, Amsterdam, The Netherlands.
  • 24.Chakraborty, A. K., M. L. Dustin, and A. S. Shaw. 2003. In silico models for cellular and molecular immunology: successes, promises, and challenges. Nat. Immunol. 4:933–936. [DOI] [PubMed] [Google Scholar]
  • 25.Alberts, B., A. Johnson, J. Lewis, M. Raff, D. Bray, K. Hopkin, K. Roberts, and P. Walters. 2003. Essential Cell Biology, 2nd ed. Garland Science, London.
  • 26.Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular Biology of the Cell, 4th Ed. Garland Science, London, UK.
  • 27.Dembo, M., T. C. Torney, K. Saxman, and D. Hammer. 1988. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 234:55–83. [DOI] [PubMed] [Google Scholar]
  • 28.Lauffenburger, D. A., and J. J. Linderman. 1993. Models for Binding, Trafficking and Signaling. Oxford University Press, Oxford, UK.
  • 29.Tominaga, Y., Y. Kita, A. Satoh, S. Asai, K. Kato, K. Ishikawa, T. Horiuchi, and T. Takashi. 1998. Expression of a soluble form of LFA-1 and demonstration of its binding activity with ICAM-1. J. Immunol. Meth. 212:61–68. [DOI] [PubMed] [Google Scholar]
  • 30.Favier, B., N. J. Burroughs, L. Weddeburn, and S. Valitutti. 2001. T cell antigen receptor dynamics on the surface of living cells. Int. Immunol. 13:1525–1532. [DOI] [PubMed] [Google Scholar]
  • 31.Bell, G. I. 1983. Cell-cell adhesion in the immune system. Immunol. Today. 4:237–240. [DOI] [PubMed] [Google Scholar]
  • 32.Lanzavecchia, A. 1985. Antigen-specific interaction between T and B cells. Nature. 314:537–539. [DOI] [PubMed] [Google Scholar]
  • 33.Batista, F. D., and M. S. Neuberger. 1998. Affinity dependence of the B-cell response to antigen: a threshold, a ceiling, and the importance of off-rate. Immunity. 8:751–759. [DOI] [PubMed] [Google Scholar]
  • 34.Kouskoff, V., S. Famiglietti, G. Lacaud, P. Lang, J. E. Rider, B. K. Kay, J. C. Cambier, and D. Nemazee. 1998. Antigens varying in affinity for the B cell receptor induce differential B lymphocyte responses. J. Exp. Med. 188:1453–1464. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Shih, T. A., E. Meffre, M. Roederer, and M. C. Nussenzweig. 2002. Role of antigen receptor affinity in T cell-independent antibody responses in vivo. Nat. Immunol. 3:399–406. [DOI] [PubMed] [Google Scholar]
  • 36.Shih, T. A., E. Meffre, M. Roederer, and M. C. Nussenzweig. 2002. Role of BCR affinity in T cell dependent responses in vivo. Nat. Immunol. 3:570–575. [DOI] [PubMed] [Google Scholar]
  • 37.Lum, A. F. H., C. E. Green, G. R. Lee, D. E. Staunton, and S. I. Simon. 2002. Dynamic regulation of LFA-1 activation and neutrophil arrest on intercellular adhesion molecule 1 (ICAM-1) in shear flow. J. Biol. Chem. 277:20660–20670. [DOI] [PubMed] [Google Scholar]
  • 38.Kahya, N., D. A. Wiersma, B. Poolman, and D. Hoekstra. 2002. Spatial reorganization of bacteriorhodopsin in model membranes: light induced changes. J. Biol. Chem. 277:39304–39311. [DOI] [PubMed] [Google Scholar]
  • 39.Lee, C. C., and O. N. Petersen. 2003. The lateral diffusion of selectively aggregated peptides in giant unilamellar vesicles. Biophys. J. 84:1756–1764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Gambin, Y., R. Lopez-Esparza, M. Reffay, E. Sierecki, N. S. Gov, M. Genest, R. S. Hodges, and W. Urbach. 2005. Lateral mobility of proteins in liquid membranes revisited. Proc. Natl. Acad. Sci. USA. 103:2098–2102. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES