Intrinsic Fluctuations, Robustness, and Tunability in Signaling Cycles

Abstract

Covalent modification cycles (e.g., phosphorylation-dephosphorylation) underlie most cellular signaling and control processes. Low molecular copy number, arising from compartmental segregation and slow diffusion between compartments, potentially renders these cycles vulnerable to intrinsic chemical fluctuations. How can a cell operate reliably in the presence of this inherent stochasticity? How do changes in extrinsic parameters lead to variability of response? Can cells exploit these parameters to tune cycles to different ranges of stimuli? We study the dynamics of an isolated phosphorylation cycle. Our model shows that the cycle transmits information reliably if it is tuned to an optimal parameter range, despite intrinsic fluctuations and even for small input signal amplitudes. At the same time, the cycle is sensitive to changes in the concentration and activity of kinases and phosphatases. This sensitivity can lead to significant cell-to-cell response variability. It also provides a mechanism to tune the cycle to transmit signals in various amplitude ranges. Our results show that signaling cycles possess a surprising combination of robustness and tunability. This combination makes them ubiquitous in eukaryotic signaling, optimizing signaling in the presence of fluctuations using their inherent flexibility. On the other hand, cycles tuned to suppress intrinsic fluctuations can be vulnerable to changes in the number and activity of kinases and phosphatases. Such trade-offs in robustness to intrinsic and extrinsic fluctuations can influence the evolution of signaling cascades, making them the weakest links in cellular circuits.

INTRODUCTION

Post-translational covalent modification cycles underlie a wide variety of cellular communication and control processes. Enzymes catalyzing these reactions make up a large part of an organism's genome. Humans have >500 protein kinases genes alone, 1.7% of the total genome (1). This emphasizes the importance of studying how cycles both signal reliably (robustness) and adjust to broad ranges of stimuli (tunability).

Covalent modification cycles consist of two reactions: one in which an enzyme catalyzes the addition of a prosthetic group to a substrate (for example phosphorylation by a kinase), and one where another enzyme undoes the modification (dephosphorylation by a phosphatase). Here we use protein phosphorylation terminology, though our results apply to covalent modification in general. Upstream biochemical signals modulate the number of active enzymes (kinases) in the cycle and serve as an input. The activation of kinases leads to change in the number of covalently-modified signaling molecules, which signal downstream and act as an output to the cycle. We assume that the function of the cycle is to generate an output that distinguishes signal from background for the duration of the signal.

This simple architecture has surprisingly rich behavior (2). Two natural limiting cases of the modification kinetics explain this behavior (Fig. 1). The first case (described as unsaturated, first-order or hyperbolic) occurs when catalyzing enzymes are unsaturated with respect to the substrate molecules. This system behaves in steady state as a weakly nonlinear amplifier, yielding graded responses to graded inputs (Fig. 1 C, green). The second case (saturated, zero-order, or ultrasensitive) occurs when substrate molecules saturate the enzymes. This system behaves like a thresholding digital amplifier in steady state (Fig. 1 C, blue). Intrinsic fluctuations, arising from stochastic chemical reactions, behave differently in the two cases. Unsaturated cycles are typically noisier, although ultrasensitive cycles have large fluctuations in the high gain region (Fig. 1 D and Eqs. 5 and 6) (3).

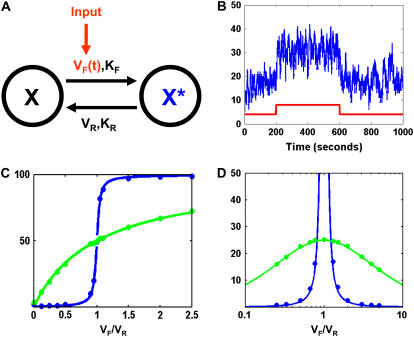
FIGURE 1.

Model description. (A) Schematic of our model. (B) The stimulation protocol used in our simulations. The red trace shows the kinase pulse V_F(t) (not to scale) against background activity. The blue trace shows the number of X* molecules in response to this kinase pulse. Phosphatase activity V_R is held constant. (C) Mean and (D) variance of the steady-state X* distribution as a function of the ratio V_F/V_R, in the hyperbolic (green) and ultrasensitive (blue) limits. Circles represent values from simulations (N = 100, hyperbolic K_M = 5000, ultrasensitive K_M = 1), curves are Eqs. 5 and 6.

Biochemical fluctuations may profoundly influence covalent modification cycles (4). The amount of signaling substrate in some systems may be rather low, and low molecular copy number increases the impact of fluctuations (5,6). Yeast, for example, have ∼10³ mitogen-activated protein kinase Kss1p and Fus3p molecules per cell (7), while large tissue culture cells have ∼10⁴ (8). Compartmental segregation and slow diffusion (5,6,9–12) potentially makes the effective number of reactants even smaller. For example, it takes >10 h for a protein to diffuse across a 0.5-mm Xenopus oocyte (assuming a diffusion coefficient of 5 μm²/s). Reliable signaling must therefore take place despite these fluctuations. Recent work has studied noise in genetic networks (13–17), but protein networks remain relatively unexplored. Fluctuations are both beneficial (causing phenotypic heterogeneity in clonal populations) (18,19) and detrimental (causing unreliable responses to signals).

Here we study a simple phosphorylation cycle subject to a time varying (square pulse) kinase stimulus. Most previous systems level studies focus on biochemical complexities (such as multisite phosphorylation (20,21)) and network properties (such as feedback and cascades (22–25)). We claim simple phosphorylation cycles alone have very rich behavior. We address the following:

1. How can a signaling cycle work reliably despite intrinsic fluctuations?

2. How do changes in extrinsic parameters lead to variability of response? Can cells use these parameters to tune the cycle to different ranges of stimuli?

3. Which of the two operational regimes (ultrasensitive or hyperbolic) is more beneficial from the point of view of robustness and tunability?

We therefore study the cycle's dynamic behavior and reliability/fidelity of signaling using basic techniques from statistical signal processing and information theory. We argue, in the spirit of Detwiler et al. (26), that cells may use the cycle's tunability to respond to different signaling contexts.

Our model shows that the cycle transmits information reliably in an optimal parameter range, despite intrinsic fluctuations and even for small input amplitudes. The cycle is sensitive to changes in some “soft” extrinsic parameters, such as concentration and activity of kinases and phosphatases. This sensitivity can lead to significant cell-to-cell response variability. It also allows cells to tune the cycle to transmit signals in a given amplitude range. Ultrasensitive cycles are superior to hyperbolic ones in both robustness and tunability. Cycles tuned to suppress intrinsic fluctuations, however, may be vulnerable to changes in the number and activity of kinases and phosphatases (27,28). Hyperbolic cycles, while noisier, require little tuning to transmit a broad range of input amplitudes. This motif's combination of robustness and flexibility makes it potentially suitable for a wide range of signaling tasks inside a cell.

MODEL AND METHODS

We consider N molecules of a signaling species X. Each molecule is either unmodified (X) or covalently modified (X*). We ignore effects such as degradation, sequestration, or dilution of the signaling species by enforcing a conservation relation X + X* = N. We assume the existence of two enzymes each present with fewer than N copies: E_F, which catalyzes the conversion of X to X* and E_R, which catalyzes the reverse conversion of X* to X. The molecules obey the following reactions:

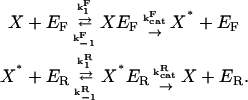The assumptions are consistent with minimal substrate sequestration and allow us to collapse the system to a pair of simplified reactions, X → X* and X* → X. The rate of creation, or birth, of X* from X is denoted by b(X). The rate of destruction, or death, of X* is denoted by d(X*). Under our assumptions, these rates follow the Michaelis-Menten approximation with maximal reaction rates 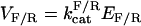and Michaelis constants 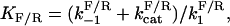for forward and reverse reactions, respectively. Reaction rates are in units of molecules per second and Michaelis constants are in units of molecules. The net rate of change of X* is the difference of the two leading to the dynamics:

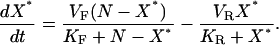(1)

To treat this problem stochastically, we analyze the probability distribution that there are n molecules of X* present at time t, namely p(n|t), for 0 ≤ n ≤ N. Under the assumption that chemical reactions are well mixed (29), this problem can then be recast into the form of a birth-death Markov process with the birth and death rates given above (30). The time evolution of the probability distribution obeys a master equation,

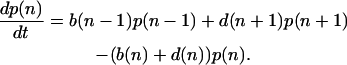(2)

In the limits of highly unsaturated enzymes (K_M ≫ N) and highly saturated enzymes (K_M ≪ 1), the steady-state distribution 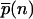can be found in closed form using recursion relations. They are

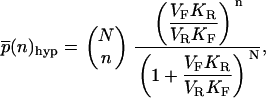(3)

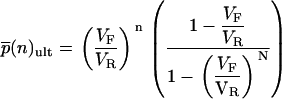(4)

The means and variances of these distributions are given below and are plotted in Fig. 1, C and D:

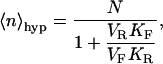(5a)

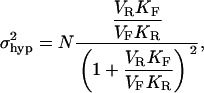(5b)

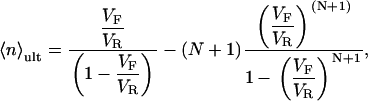(6a)

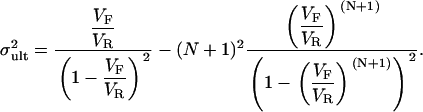(6b)

Simulations

We simulated our model using a Gillespie algorithm (29) that allows for time-varying input. Obtained distributions and time-series were resampled once per second to prevent oversampling of portions of the time series with faster kinetics.

Signal/noise ratio

The steady-state signal/noise ratio (SNR) of a signal with high and low values is defined as

(7)

The values μ_A and 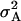are the mean and variance, respectively, of the steady-state X* distribution when V_F is at level A. Systems were allowed to relax to steady state for 20,000 s and the X* time series for 30,000 s after this was used as the steady-state distribution.

Mutual information

Mutual information, a relation between an input signal distribution X and an output signal distribution Y, quantifies how much one learns about one distribution by knowing the other (31). The mutual information between X and Y is given by the expression

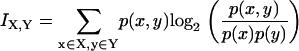(8)

We identify X(t) with the kinase input V_F(t) and Y(t) with the distribution of X*(t). By integrating over t, one can obtain the joint distribution p(X,Y). The kinase pulse, after an initial period in the low state allowing the system to relax to a steady state, takes on two values (high and then low) for equal amounts of time. From an information theoretic standpoint, this represents a fair coin containing one bit of information. The output distribution X*, taking possible values from 0 to N, was divided into 10 equally spaced bins to simulate discreteness of a biological detector. Different bin sizes and numbers did not change our qualitative results.

RESULTS

We model a population of signaling proteins being briefly phosphorylated by a kinase pulse above background activity and constant phosphatase activity (Fig. 1).

Can a cycle be tuned to minimize intrinsic fluctuations? The cycle possesses three readily adjustable parameters: forward phosphorylation velocity 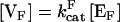; reverse dephosphorylation velocity 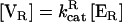; and substrate molecule number N. Cells can change the “soft” parameters [V_F] and [V_R] in real time by changing local enzyme concentrations [E]. The other two reaction parameters K_F and K_R represent less tunable (“hard”) binding parameters that may be changed by protein mutations on a much larger timescale. All parameters (k_cat, K_m, [E_R], [E_F], and N) can also be changed by covalent modification (32), making the cycle a highly tunable part of cellular circuitry.

Effects of intrinsic fluctuations

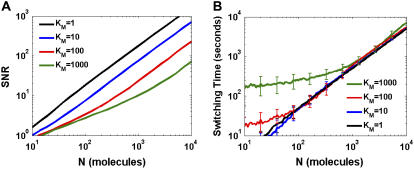
The first way to fight intrinsic fluctuations would be to increase the number of substrate molecules in the cycle. Signal/noise ratio (SNR, Eq. 7), the mean signal level divided by fluctuation magnitude, measures a noisy signal's fidelity. Random process steady-state SNRs typically grow with their size. As the number of substrate molecules increases, the system transitions from the hyperbolic to the ultrasensitive regime. The cycle's SNR increases as 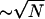in the hyperbolic regime and transitions smoothly to an ∼N increase in the ultrasensitive regime (Eqs. 5a, 5b, 6a, and 6b and Fig. 2 A). Thus, increasing N indeed seems to increase signaling fidelity.

FIGURE 2.

Noise rejection and switching time dependence on substrate amount, N. Colors represent different Michaelis constants; blue, K_M = 1; green, K_M = 10; and red, K_M = 100. (A) Steady-state SNR. Kinase and phosphatase rates (molecules/s) were V_F,Low = 4, V_F,High = 8, V_R = 6. (B) Mean switching time and standard deviation (error bars) in response to step input. The cycle was initialized at X* = 0 and given a step in kinase from V_F,Low = 0 to V_F,High = 8, with phosphatase values at V_R = 6. The system was allowed to relax to a numerically determined steady state and the first crossing point was chosen as the switching time. Panels A and B are plotted on the same abscissa scale for comparison. All curves are averaged over 100 trials.

This approach incurs a penalty in the cycle dynamics. Fig. 2 B plots the time for a cycle to reach steady state given a step input of kinase, starting with no substrate phosphorylated. The cycle's architecture causes switching time to increase slightly sublinearly with N in the unsaturated regime and linearly in the ultrasensitive regime. When unsaturated, catalytic velocities increase with the number of substrate molecules, compensating somewhat for the greater amount of substrate. When saturated, each substrate conversion takes constant time, and total switching time increases linearly with N.

Mutual information provides another way to quantify the performance of a signaling pathway. This information theoretic quantity (Eq. 8) measures how much a communication channel's output reduces uncertainty about the input. The input pulse with equal high and low times contains one bit of information. The mutual information transmitted by the channel thus takes a maximum value of one bit when the output allows the high and low states to be distinguished and a minimum value of zero bits when recognizing the original input signal in the distorted output is impossible. These maximal and minimal values are convenient for comparing signaling fidelity under different conditions. Mutual information reduced if the duration of the output pulse is shorter than duration of the activating input.

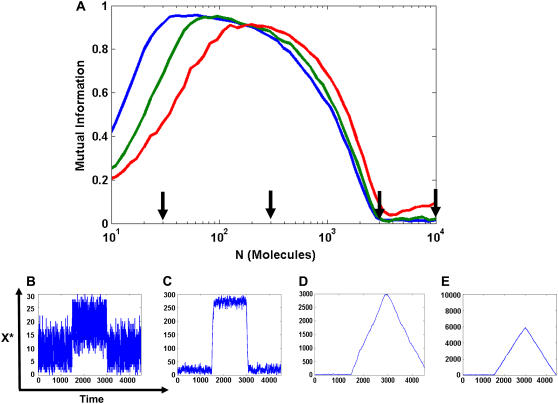
Fig. 3 A illustrates the impact of large N on signaling by plotting the mutual information transmitted by the cycle for the pulse input. Strikingly, the performance of the cycle as an information transmitting channel has a maximum at some optimal value of N, while dropping at smaller or larger number of substrate molecules. At low N, the cycle's intrinsic fluctuations distort pulse transmission by causing the high and low outputs to overlap and blur (Fig. 3 B). As N increases and we enter saturation, the mutual information approaches its maximal value of one, indicating a cleaner transmission of the pulse (Fig. 3 C). Finally, as N increases, further the mutual information decreases again due to slow response. This sluggish behavior at large N distorts the output leading to drop in information loss (Fig. 3, D and E). The system's optimal performance for a particular range of N is similar to system size resonance (33,34).

FIGURE 3.

Dynamic signaling quality as a function of substrate amount, N. Colors are as in Fig. 2. (A) Mutual information between the input and the output. The cycle was initially equilibrated for 1500 s at V_F,Low and then given a 1500 s V_F,High pulse before returning to V_F,Low for another 1500 s. Kinase and phosphatase parameters are identical to those in Fig. 2 a. Curves are averaged over 100 trials. (B–E) Representative time traces for N = 30 (B), N = 300 (C), N = 3000 (D), and N = 10,000 (E), shown by arrows in panel A.

Our model shows that a cycle works reliably when substrate amount lies in an optimal range, despite intrinsic fluctuations. A small number of substrate molecules leads to fluctuations. Excess substrate slows down the response, leading to a highly distorted or completely lost signal. The range of substrate that provides reliable signal transduction depends on the amplitude and duration of the pulse (C. Gomez-Uribe, G. Verghese, and L. A. Mirny, unpublished). The cycle probably tolerates substrate number fluctuations within the optimal range.

Effects of extrinsic parameters on the signaling performance

How sensitive is the signaling cycle to extrinsic variations in kinases and phosphatases? To study this we measure the information transmitted by the cycle as a function of the number of kinase molecules V_F and phosphatase molecules V_R, with an optimal N and balanced enzymatic saturations (K_M = K_F = K_R).The input pulse has background level V_F,Low and signal level V_F,High (Fig. 1). Fig. 4 shows information transmitted by a cycle as a function of V_R in response to two pulses with different background and signal levels.

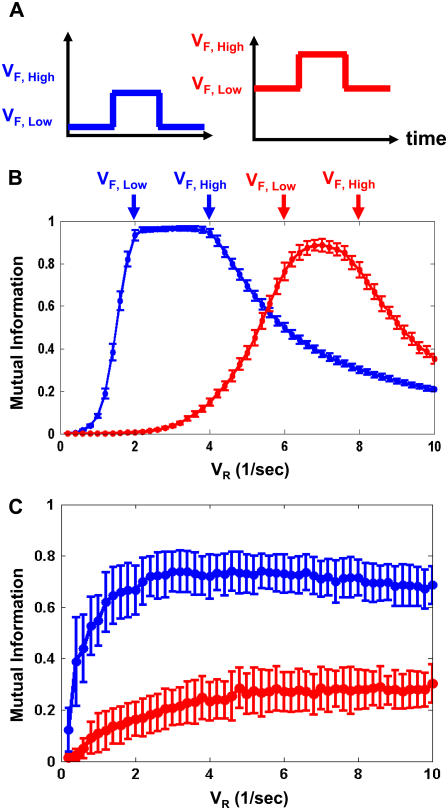
FIGURE 4.

Signaling quality dependence on kinase and phosphatase balance. (A) Two input stimuli with different background V_F,Low and V_F,High signal levels (molecules/s). Blue, V_F,Low = 2; V_F,High = 4. Red, V_F,Low = 6; V_F,High = 8 (shown by arrows on B). (B) Ultrasensitive cycle response to two stimuli as a function of V_R (for K_M = 5). (C) Hyperbolic cycle response as a function of V_R (K_M = 1000). Panels B and C plot mutual information between input and output. Pulse times are the same as in Fig. 3, and N = 100. Curves represent means, and error bars represent standard deviations, of mutual information over 100 trials.

An ultrasensitive cycle (Fig. 4 B) separates signal from background and transmits up to one bit of information. Cells must tune V_R to V_F,Low < V_R < V_F,High so high inputs produce high response and low inputs produce low response. As V_R leaves this range, signaling quality diminishes rapidly. The range of optimal V_R values is broader for signals strongly above background and narrower for weaker ones. Cycles tuned to one amplitude range respond poorly to signals far outside this range.

Hyperbolic cycles require less tuning and signal well in a broad range of V_R (Fig. 4 C). Signaling quality depends strongly on the background kinase activity V_F,Low. Signaling is somewhat erratic for signals on smaller background (Fig. 4 C, blue), but more so for signals on large backgrounds (Fig. 4 C, red).

Gradient sensing is an example of signaling on varying background levels (28,36–39). Here, cycles signal changes in a stimulant's concentration or gradient regardless of its background concentration. Hyperbolic cycles perform this task poorly, while ultrasensitive cycles need tuning.

This required tuning makes ultrasensitive cycles sensitive to extrinsic kinase and phosphatase fluctuations. Such fluctuations can be aggravated by compartmentalization and lead to cell-to-cell variation in response to external stimuli. The tuning requirement also makes signaling cycles vulnerable to mutations affecting the activity or concentration of kinases and phosphatases (27,28,40). Thus, ultrasensitive cycles minimize the effect of intrinsic fluctuations but remain sensitive to variations in extrinsic parameters.

Hyperbolic cycles are robust to extrinsic fluctuations but generate significant intrinsic noise and lose more information. The range of workable V_R levels increases as the cycle becomes less saturated.

Cycles are more robust to Michaelis constant changes. Fig. 5 A plots mutual information for varying saturation in forward and backward enzymes. The cycle functions optimally with both pathways similarly saturated. Precise matching is not necessary. This is fortunate since Michaelis parameters are not easily tuned, being set by enzyme-substrate binding affinity and changed by competitive inhibitors or mutations. This suggests that competitive inhibition of cycle enzymes is a poor way of controlling them. Noncompetitive or allosteric inhibition and covalent modification can alter V_F or V_R and have more profound effect on the signaling.

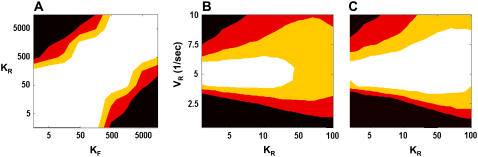
FIGURE 5.

Cycle phase space. (A) Effect of kinase (K_F) and phosphatase (K_R) Michaelis constants on mutual information. (B,C) Combined effect of varying K_M and V_R on the mutual information for N = 100 (B) and N = 200 (C). Contours highlight regimes of reliable signaling (black, I = 0–0.25; red, 0.25–0.50; yellow, 0.5–0.75; and white, 0.75–1.0).

How does a cycle respond to simultaneous changes in N, V_R, and K_m? Fig. 5, B and C, plots mutual information as a function of V_R and K_m for two different values of N. Increasing K_m causes a transition from the ultrasensitive to the hyperbolic regime. Low K_m cycles signal well in a tight V_R range (Fig. 4 B). As K_m increases, the cycle grows more robust to mistuned V_R while maximal mutual information decreases (Fig. 4 C). The fan-shaped phase space volume is typical for various values of N. Increasing N increases both the volume of workable phase space and the maximal mutual information of that volume (Fig. 5, B and C) until the system encounters the slowdown at high N explained before. An intermediate K_m regime is robust to intrinsic noise and has a broader working parameter range.

DISCUSSION

Despite their simplicity, covalent modification cycles exhibit rich behaviors with several implications for the functioning and evolution of signaling networks. Simple covalent cycles function well in a limited range of kinetic parameters. This range determines the cycle's inherent flexibilities, fragilities, and robustness.

The amount of signaling substrate, N, influences both the effect of fluctuations and the response speed. These competing constraints lead to an optimal number of substrate molecules to minimize noise effects in dynamic signaling, suggesting that cells control the amount of substrate. This optimal number of substrate molecules is reminiscent of system size resonance (33,34,41), although the optimum system size in covalent signaling arises from the tradeoff between noise and dynamics, not through enhancement of the signal by a critical value of intrinsic noise. A recent study of Morishita et al. (42) used a different measure of signal reliability, and came to the same conclusion of an optimal number of substrate molecules required for reliable signaling.

Substrate overexpression potentially mistunes a cycle, and this mistuning may propagate through an entire cascade. Increasing V_F and V_R would compensate for this effect, at a cost increasing the number of kinases and phosphatases. These in turn play the role of N for upstream steps of a cascade. In cases such as membrane receptors responding to a small number of external ligands, upregulating receptors would not increase V_F. Other mechanisms, such as allosteric interactions between receptors (43) or positive feedback, might increase V_F and speed up the cycle.

Experiments controlling the amount of signaling substrate (e.g., by inducible expression) can test our prediction of optimal concentration of substrates needed for reliable signaling. Spectroscopic studies of the spatial distribution of signaling substrates would also shed light on this phenomenon (44,45). On evolutionary timescales, changes in substrate gene dosage might mistune a cycle (46). Comparative genomics can help verify this prediction by correlating the frequency of gene duplications with the rate of evolution of kinases and phosphatases.

Cycles are also sensitive to the number of kinases and phosphatases, and to changes in their binding and rate constants. While the number of molecules can be regulated by the cell and is subject to random fluctuations (“soft” parameters), binding and rate constants of the enzymes cannot be easily tuned in real time but are subject to changes on the evolutionary timescales (“hard” parameters). This has three main implications.

First, extrinsic fluctuations in the number of enzymes may reduce the fidelity of signaling. Tuned ultrasensitive cycles with weak input are particularly sensitive, especially for weak signals on large backgrounds in situations like chemotaxis (36–38,47). Such fluctuations may lead to noise and cell-to-cell variability that, in turn, can be harmful, or may provide a diversity of responses and increase population-average survival and fitness (18,19). Sensitivity to exact tuning also leaves cycles vulnerable to kinase and phosphatase mutations. Numerous somatic mutations in kinases (28) and phosphatases have been detected in cancer cells (27) and pathogenic infections, like anthrax (40). These mutations often have moderate (less then a factor of two) effects on k_cat and K_m (27), while causing a profound physiological effect. These mutations may cause excessive signaling or lack of response to stimuli, especially in fragile parameter regimes. Our results predict that the physiological effects of changes in k_cat can be more profound than perturbations of K_m.

Second, sensitivity to extrinsic parameters provides an easy way to tune a signaling cycle to transmit signals of various amplitudes and background levels (see Fig. 4 A). This requires changing expression, degradation, modification or internalization of either kinases or phosphatases, possibly through feedback. This allows a cycle to adapt to a broad range of background amplitudes, similar to adaptation observed in bacterial chemotaxis (36,38). Although feedback is often associated with bistability (23,48–50) or noise suppression (22,51), we wish to highlight that feedback can keep signaling cycles tuned and adapt them to a range of stimuli amplitudes and background levels.

Third, easy tuning of signaling cycles to transmit signals of various amplitudes allows rapid evolution of signaling networks. Duplication and tuning of part of an existing cascade can produce a new pathway. Tuning a new cycle away from the optimal regime of the ancestral one may minimize the cross-talk between cascades. This remarkable tunability can make signaling cascades ubiquitous elements of cell circuitry.

Our model has several limitations and provides several directions for further research. We ignore multiple phosphorylation (20,21) and consider only the simplest signaling cycle undergoing a single phosphorylation event. Our model assumes Michaelis-Menten kinetics, a good approximation for systems like the phosphorylation of Fus3p by Ste7p in yeast, but unreasonable for systems like the phosphorylation of ERK2 MAP kinase by Mek-1 in Xenopus oocytes (8). We do not model spatial effects explicitly (52,53), although we consider them implicitly by studying sensitivity to the external parameters N, V_R, and V_F. Spatial heterogeneity (11), scaffolding (54,55), and compartmentalization (9,12,56,57) can lead to significant fluctuations in the number of active kinases, phosphatases, and their substrates. These fluctuations lead to mistuning and significant cell-to-cell variability in signaling predicted by our model and discussed above.

Here we studied the cycle's response to a square pulse of kinase activity. Three observations motivate our choice of a square pulse. First, response to a square pulse input is a sensitive engineering probe for both dynamic and steady-state behavior of the system. Second, single cell time-lapse microscopy has recently revealed pulselike and oscillatory dynamics inherent in major signaling networks such as the DNA damage response in both prokaryotes (58) and eukaryotes (59), and the NF-κB network (60). More examples will undoubtedly emerge as single cell techniques improve and expand. Third, extracellular inputs to signaling networks potentially take this form. For example, a receptor subject to spontaneous background activation may undergo rapid activation by a higher ligand concentration (or high affinity ligand), followed by a rapid inactivation (by internalization, or drop in the concentration of an activator).

We aim to understand the complexities, strengths, and weaknesses of this simple system, which provides a baseline for understanding the more complex networks often found in signaling pathways. More complex signaling networks probably evolved to improve performance of the simple cycle and to convey additional functionality. Cascades of moderate-gain phosphorylation cycles often appear, such as the canonical MAP kinase cascade, which shows net high gain (61). This topology has also been implicated in noise suppression (24). Feedback networks of kinase systems exhibit bistable behavior, as in Xenopus p42 MAPK/Cdc42 (23). Scaling up (62) our stochastic analysis to networks may prove challenging, although theoretical and experimental work in this spirit has begun in the context of gene expression networks. (14,17,56,63). We hope analyses of this type will produce a more systematic and quantitative understanding of biological signaling pathways.

In summary, we show that signaling cycles can reliably transmit information despite intrinsic fluctuations. An optimal number of substrate molecules balances speed of response with noise rejection. A trade-off exists between robustness to intrinsic and extrinsic fluctuations. In the ultrasensitive regime, the cycle is robust to intrinsic fluctuations but requires tuning of the kinase/phosphatase ratio. Fluctuations in this ratio lead to cell-to-cell variability of the signaling response. In contrast, a cycle in the hyperbolic (unsaturated) regime suffers from strong intrinsic fluctuations while being robust to changes in extrinsic parameters. Such a cycle requires no tuning but demonstrates poor performance. An intermediate regime shows the best of both worlds, being robust to both intrinsic noise and variations in extrinsic parameters. One can imagine that, depending on the spectrum of stimuli and requirements for more or less noisy response, an organism can choose to operate different signaling pathways in different regimes.