Robust coding of flow-field parameters by axo-axonal gap junctions between fly visual interneurons

Abstract

Complex flight maneuvers require a sophisticated system to exploit the optic flow resulting from moving images of the environment projected onto the retina. In the fly's visual course control center, the lobula plate, 10 so-called vertical system (VS) cells are thought to match, with their complex receptive fields, the optic flow resulting from rotation around different body axes. However, signals of single VS cells are unreliable indicators of such optic flow parameters in the context of their noisy, texture-dependent input from local motion measurements. Here we propose an alternative encoding scheme based on network simulations of biophysically realistic compartmental models of VS cells. The simulations incorporate recent data about the highly selective connectivity between VS cells consisting of an electrical axo-axonal coupling between adjacent cells and a reciprocal inhibition between the most distant cells. We find that this particular wiring performs a linear interpolation between the output signals of VS cells, leading to a robust representation of the axis of rotation even in the presence of textureless patches of the visual surround.

To guide a flying organism in three dimensions, flight control crucially relies on optic flow (1, 2). In the fly's brain, the lobula plate encodes visual motion information in a retinotopic manner and is thought to represent a neural control center for course corrections during flight (3). Here, large tangential cells form a set of ≈60 individually identifiable large-field motion-sensitive interneurons. With their large dendrites, these tangential cells integrate the output signals of retinotopically arranged local motion detectors (4) and connect via descending neurons (5) to the motor neurons in the thoracic ganglia. Among the tangential cells are 10 vertical system (VS) cells whose dendrites are positioned sequentially along the rostrocaudal axis jointly covering, with some degree of overlap, the entire lobula plate. In accordance with the retinotopic arrangement of the lobula plate, the locations of the tangential cells' dendrites correspond to adjacent vertical columns in the visual field. Surprisingly, however, the receptive fields of VS cells vastly exceed that predicted from the extent of their dendrites (6–9). Moreover, the local preferred direction of VS cells was found to vary in space such as to match the optic flow induced by self-rotation of the animal around various axes. Although this could correspond to an optimal linear estimator for rotation (10, 11), the reliability of such a system is severely compromised by nonlinearities such as synaptic saturation in the dendrite of individual cells (12) as well as the nonlinear dependency of the motion detector output as a function of velocity. Indeed, homogeneous large-field downward motion can effectively stimulate VS cells, and the postsynaptic V1 cell that integrates receptive fields of VS1–3 fails to respond significantly stronger to rotation than to translation (13). Moreover, it is not clear how such a system could deal with the pronounced pattern-dependence of motion signals (14) when confronted with natural image scenes containing patches of high and low contrast, or even areas without any texture. Consequently, mechanisms other than a simple matching of the rotational optic flow are most likely present at the readout level (11, 15).

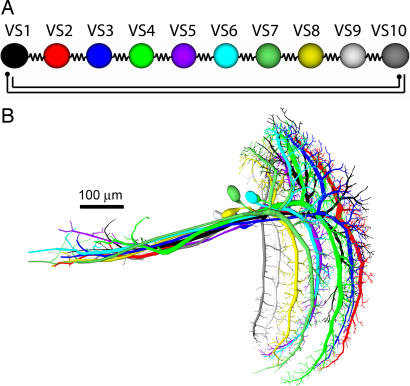
In a recent study on VS cells, double recordings from VS cell pairs were performed. Injecting current into one cell while measuring the response of another cell revealed a current spread throughout the VS cell network that decayed from one cell to its successive neighbors in a surprisingly linear way (16). The experiments suggested a particular connectivity scheme where neighboring VS cells are electrically coupled whereas distant cells inhibit each other bidirectionally (Fig. 1A). The proposed chain-like structure could be substantiated both by dye-coupling experiments (17) and laser ablation of individual VS cells (18). This type of coupling could explain the broad receptive fields of VS cells compared with the extent of their dendrites within the lobula plate. To validate the suggested connectivity between VS cells, we built a detailed model of the network. We reconstructed the neurons individually by using image stacks from two-photon microscopy (19) (F.F., H.C., J.H., and A.B., unpublished work). Passive models of all 10 reconstructed VS cells were aligned manually according to their locations in the lobula plate (Fig. 1B).

Fig. 1.

Overview of the VS cell network. (A) Suggested connectivity scheme from ref. 16. Adjacent cells are coupled electrically and distal cells inhibit each other (schematic filled circles). (B) Ten VS cells as obtained from two-photon image stacks for which detailed compartmental models were reconstructed. Cells were placed manually according to their position in the lobula plate with neighboring dendritic arborizations slightly overlapping.

Results

Electrical Coupling Is Located in the Axon Terminal Region.

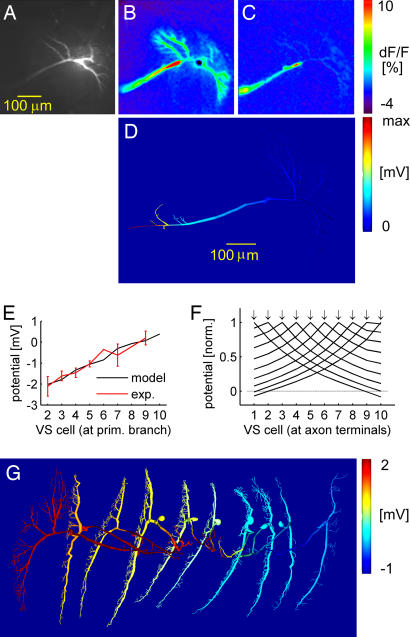
To determine, experimentally, the location of the connections between the cells, we recorded from a fly VS1 cell and filled it with a Ca²⁺-sensitive dye (Fig. 2A). Ca²⁺ concentration and membrane potential have previously been shown to depend linearly on one another in VS cells, except for a hot spot in the initial axonal region (20, 21). Although the response to current injection into VS1's primary dendrite could be seen throughout the cell (Fig. 2B), subsequent current injection into the neighboring VS2 cell resulted, apart from the hotspot, in a Ca²⁺ gradient with the strongest signal in the axon terminal (Fig. 2C). Similar data were obtained in five other experiments on various VS cell couples (data not shown). We therefore conclude that the VS cell coupling occurs in the axon terminals.

Fig. 2.

Connecting the VS network. (A–C) Ca²⁺ imaging in VS1. (A) Raw fluorescence image. (B) Relative change of fluorescence (ΔF/F) when injecting current in VS1 primary dendrite. (C) ΔF/F when injecting current in VS2 primary dendrite. (D) Potential distribution in the VS1 model when current is injected into the primary dendrite of VS2. (E) Potential responses at primary dendrite in VS2–10 after current injection of −10 nA in VS1 primary dendrite. Black line, model; red line, experimental counterpart. (F) Voltage transfer from all different VS cells at the location of the synapses in the axon terminal. Normalized amplitudes; dotted horizontal line represents 0 mV. Arrows indicate location of current injection for the different traces. (G) Potential response in a false-color spatial distribution throughout the VS network when injecting 10 nA in VS1 primary dendrite. The color scale saturates at 3 mV.

VS Connection Implements a Triangular Filter.

In accordance with the experimental results, we connected the model cells via their axon terminals. We adjusted the synaptic conductances in conjunction with the passive membrane parameters, which we allowed to vary for the different VS cell models. The parameters were then tuned to render a realistic voltage transfer within the VS network model while conserving the input resistances of all cells at ≈4 MΩ (22). With such a connectivity, injecting a current in one cell led to a potential gradient backward from the axon toward the dendrite in the adjacent cell (Fig. 2D). In further accordance with the experiments, the resulting network exhibited an approximately linear decay of the potential from one cell to the next (Fig. 2E) with the input resistance of each cell in a realistic range (3.7 ± 0.7 MΩ). Interestingly, simulations of current transfer from other VS cells revealed a symmetrical linear potential decay at the axonal synapses in all cases (Fig. 2F). The network thereby effectively implements a triangular filter. The linear potential decay is the result of a superposition of the potential decaying exponentially from VS1 to more distal VS cells and the inverse potential via the inhibition again decaying exponentially backward from the distal VS cell to the VS1 cell [supporting information (SI) Text, Simplified Model and Analytical Formulation of the Linear Relationship; SI Fig. 5; and SI Table 1]. The potential distribution throughout the network during current injection in the VS1 cell model is shown in Fig. 2G. In comparison with the parameters in unconnected VS cell models (22), the new cell models (for parameters, see SI Table 2) exhibited a higher axonal attenuation, as will be discussed below.

Pooled Axonal Visual Responses Do Not Invade the Dendrites.

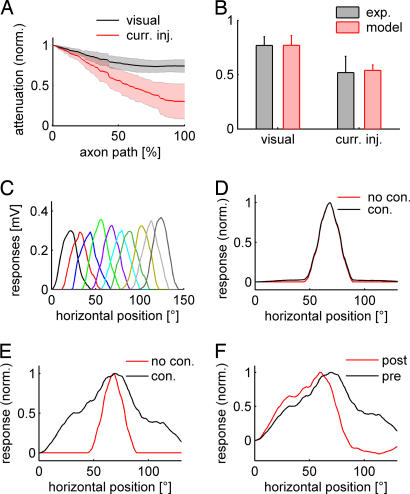
To simulate visual stimulation in the network model, we calibrated dendrite synaptic conductances. In each VS cell model, individually, synaptic conductances were set to result in the same potential response at the primary dendrite. Simultaneous activation in all VS cell models, as during whole field visual stimulation, increased the response in the primary dendrite by only ≈15%. Consequently, the signals of VS cells did not penetrate the dendrites of their neighboring cells. VS cells could therefore be considered to be efficiently compartmentalized into a dendritic and an axonal region. Because the contribution of neighboring VS cell models to the visual response in any one cell originated in the axon terminal, the attenuation of the visual response along the axon was smaller than during current injection into the dendrite (Fig. 3A). At the location in the axon where the voltage response to current injection in the main dendrite had attenuated to 50% (at ≈65% down the length of the axon), the visual response level was still at 77% of its counterpart in the primary dendrite branching (Fig. 3B).

Fig. 3.

Visual response in the VS network. (A) Attenuation along the axon of the visual response (black) and during current injection at the primary dendrite (red) in the model. Standard deviations among the different VS cells are represented by the shaded areas. (B) Potential attenuation halfway down the axon in the model (red) and from double recordings (black). (C) Dendritic responses of the individual VS cells along the horizontal axis of the visual field with the chosen distribution of dendritic synapses. Colors are as in Fig. 1. (D) Receptive field measured in the primary dendrite of a VS5 model in the connected (black) and unconnected (red) network. (E) Same as C, but measured in the axon terminal. (F) Receptive field measured in the axon terminal of a VS5 model in the connected network before (black) and after (red) simulated ablation of the neighboring VS6 cell.

To validate these quantitative model predictions, we performed double recordings at two locations within the axon of the same neuron in the fly. One electrode was located, as previously, in the primary branching point of the dendrite, and the second electrode was located approximately halfway down the axon. During current injection, the potential decayed to 54 ± 5% in the second electrode (n = 6; one VS2, two VS3s, two VS4s, one VS5). When whole-field visual stimulation was applied to four of the six VS cells (one VS2, one VS3, one VS4, one VS5), the dendritic potential decayed to only 77 ± 9%. Thus, in accordance with the model, much less attenuation was observed in the potential response during visual stimulation than during dendritic current injection (Fig. 3B). Consequently, the response further down in the axon indeed comprised a larger component originating from the visual response in the other VS cells, again confirming the coupling location in the axon terminal region (for corresponding receptive field measures, also see SI Fig. 6).

After assigning a visual angle to the horizontal coordinates of the dendritic inputs according to their relative location in the retinotopic arrangement within the lobula plate (Fig. 3C), receptive fields could be determined in the model, both with and without connections between neighboring cells. Whereas the receptive fields as computed in the primary dendrite were similar in the connected and unconnected model (Fig. 3D), the receptive fields in the axon terminal region were substantially widened when cells were connected (Fig. 3E). Corresponding to the linear decay of voltage between successive VS cells, the receptive field assumed a triangular shape at that location. When a neighboring cell model was blocked in such simulations, the receptive field width was impaired asymmetrically, reproducing experiments using laser ablation to eliminate individual cells from the circuit (Fig. 3F) (18).

Response to Natural Optic Flow.

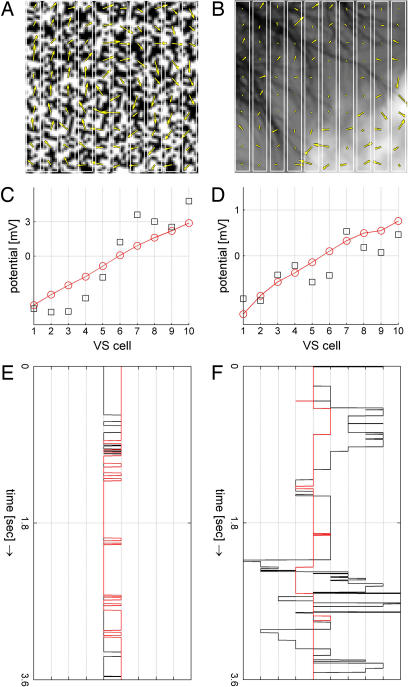
We have demonstrated here that VS cells are coupled to each other at their output region, leading to a strong broadening of their receptive field along the horizontal axis of the visual field. Without that coupling, i.e., when isolated from their neighbors, VS cells would only respond to downward motion within a rather narrow stripe of the visual field corresponding to the topographic location of their dendrites (23). To understand the functional significance of this type of postprocessing of visual motion information in the context of flight control, we returned to the original idea that the function of the VS cell network is to detect the axis of the fly's rotation from the visual flow-field. We used two different visual stimuli, one consisting of a random dot pattern (“artificial image”) and another one containing a natural scene characterized by its rather irregular texture and inhomogeneous contrast distribution (“natural image”). Technically speaking, the artificial image was characterized by a narrow autocovariance function (half-width ≈1.5° of visual angle), whereas the autocovariance function of the natural image had a rather broad half-width of >12° of visual angle (24). We rotated each image clockwise around its center at a speed of 1°/msec and fed this image sequence through a two-dimensional array of local motion detectors of the Reichardt type (25). Snapshots of the resulting flow-fields are shown superimposed on the original images in Fig. 4 A and B. According to its irregular contrast distribution, the flow-field resulting from rotation of the natural image exhibited irregular distribution of motion vectors compared with the rather regular rotational flow-field obtained from rotating the artificial image. The vertical vector components controlled synaptic conductances in the dendrites of each of the 10 VS cells. The values according to the directional selectivity in VS cells were negative in the left part of the image, indicating an upward direction, and positive in the right part, indicating a downward direction. Fig. 4 C and D represents the resulting membrane potential levels within the VS cell network at the primary dendrites and after processing in the output region at the axon terminal location. The pooled signals in the dendrites remained noisy in the case of the natural scene (black squares). However, the VS cell network output at the axon exhibited a filtered version, drawing a straight line corresponding to the axis of rotation (red line) performing like a visual gyroscope. In such an arrangement, the output of the VS cell that is closest to zero encodes the center of rotation. Accordingly, we followed the minimum absolute value along the time course of rotation of both images (Fig. 4 E and F; also see SI Movies 1 and 2). The center of rotation could be read out both at the dendrite and axon in the case of the regular texture (artificial image), indicating that the filtering through the VS cell network did not improve the signal there. In the case of the natural image, a slight offset in the frequency range of the rotation speed was present at first due to high-contrast patches that wandered around the visual field during rotation (see SI Fig. 7). This offset vanished, however, when the inhibitory input was set slightly stronger than the excitatory one, thereby normalizing for the irregularity of the distribution of the motion components. Then, during the rotation of the natural image, the zero-crossing of the dendritic signal still fluctuated throughout the entire range of VS cells (black line in Fig. 4F). Only the time course obtained from the signals at the axon showed a stable behavior at the position around which the image was rotated (red line in Fig. 4F).

Fig. 4.

Coupling improves detection of the center of rotation. (A) An artificial image rotating clockwise around its center. A snapshot of the visual flow-field as determined from a two-dimensional motion detector array is superimposed. The rotational structure is clearly visible. (B) Same as A, but using a natural image (taken from the natural image database, Hans van Hateren, http://hlab.phys.rug.nl/imlib/index.html). The flow-field structure is much less homogenous. (C and D) Visual response in the VS network model when the vertical vector components of the flow-field are fed into the respective VS dendrite synapses for both the artificial and the natural image. Black squares indicate unprocessed signals in the dendrites; red circles indicate axonal outputs. (E and F) VS cell with minimum absolute potential during the rotation of both images around 360°. Black line, potentials at the dendrites; red line, potentials at the axon.

Discussion

In summary, the simple connection scheme between VS cells as proposed in Fig. 1A turned out to be in agreement with a number of experimental findings obtained from VS cells in the fly. We showed evidence for an axonal location of the coupling leading to a pooling of the individual signals of VS cells there. The benefit of coupling the signals from neighboring VS cells after dendritic integration is to better represent rotational optic flow information in analogy to a gyroscope. This representation can be used, for example, to reliably and robustly extract the center of rotation in the activity distribution of the VS cell network. With this study, we assign a specific computational function to gap junctions different from its commonly known role of synchronizing activity in neuronal ensembles (26): by implementing a triangular filter through the coupling, the VS cell network is able to perform a linear interpolation between the signals from neighboring cells where local deviations due to low-contrast or textureless areas in natural image scenes disrupt the optic flow signal. The optimal slope of the triangular filter depends on the motion detector peak velocity. By changing the gain in each single cell, the inherent cellular adaptation mechanisms would automatically regulate this slope of linear decay from one cell to the next. The linear interpolation makes sense when put in the context of self-rotational optic flow in which amplitudes of motion vectors scale linearly with horizontal disparity (see SI Text, Significance of Triangular Filter, and SI Fig. 5 E–G).” With its connectivity scheme, the VS cell network incorporates prior knowledge about this linear relationship and ascribes to a cell without motion response the linearly interpolated value between its neighbors. Thereby, the true location of the center of rotation is represented by the zero-crossing of the VS cell network signal. The particular filter is therefore ideally suited to the extraction of rotational optic flow characteristics. The network model seemed quite robust to changes in the rotation velocity (set to 1°/ms in the above simulations). However, its specific sensitivity to rotation velocity could be investigated in further detail. Fast saccade-like movements could potentially be filtered out by the cellular time constants (27), but slower body rotations, which require compensatory motor actions, would be in the steady-state regime of the model and, therefore, would all be filtered in the same way. The necessity of such additional signal processing was not obvious when testing the system with artificial input images but became apparent only when natural images were used instead. This finding emphasizes the utility of natural images in understanding the functional significance of certain neural computations that otherwise would have remained elusive (28, 29). Our simulations lead to possible speculations about how the signals provided by the VS cell network can be read out and used for course control in cooperation with the mechanosensory input from the halteres (30). Whether the readout can indeed take advantage of this processed optic flow information, for example by locating the VS cell with the smallest deviation from rest, will need to be determined through experiments on descending neurons (31).

Materials and Methods

Electrophysiology and Imaging.

Fly preparation and electrophysiological investigation followed the procedure described in ref. 16. For the Ca²⁺ imaging experiment in Fig. 2 A–C, a VS cell was filled with the green fluorescent calcium-sensitive dye Calcium Green (Molecular Probes, Eugene, OR) by hyperpolarizing current pulses. Then, the electrode was discarded and replaced by another electrode containing the red fluorescent dye Alexa 568 (Molecular Probes), which was only used for later anatomical identification. Next, a neighboring VS cell was recorded from and depolarized by injection of a +10-nA current while the Ca²⁺ level in the first VS cell was monitored. For intracellular double recordings from the same cell (Fig. 3B and SI Fig. 6), one electrode was inserted into the primary dendritic branch point, and one was inserted into the axon at the border between the lobula plate and the protocerebrum, which corresponds to a distance of ≈50% of its total axonal length. In this constellation, the current transfer along the axon was measured, as was the attenuation of the visual response. For visual stimulation, a Tektronix monitor (Tektronix, Beaverton, OR) was used as described in ref. 16, covering a visual field of 48° along the horizontal axis and 54° vertically. Receptive field measurements were obtained by subdividing this visual field into six adjacent quadrants of 8° horizontal width.

Realistic Compartmental Models.

The models of all 10 VS cells were derived from two-photon microscope image stacks (19) (SI Fig. 8A) obtained from cells individually filled with Alexa 488 (Molecular Probes) by using custom-written software in MATLAB (MathWorks, Natick, MA). Simulations were done in MATLAB and validated with the NEURON software package (32). Cells were connected as described in VS Connection Implements a Triangular Filter. Electrical synapses were implemented as simple conductances. Because double recordings from VS cell pairs revealed a remarkable symmetry of the connection, rectifying properties of electrical synapses could be excluded. Additionally, values of input resistances and resting potentials in all VS cells could be considered to be similar. For distal VS cells, which are considerably smaller, the input resistances would be 2–3 times higher than in proximal VS cells if the same membrane parameters were used for all cells. This is not the case under experimental conditions. Also, because the VS1 and VS10 cells were electrically coupled each to only one neighboring VS cell in the model, their input resistances were affected in a different way than all other VS cells. As a consequence, we needed to consider membrane parameters of all VS cell models separately. The relationship between the membrane capacitance and membrane resistance was fixed by the time constant of the membrane τ = c_mr_m = 1.4 ms. Allowing a range for the capacitance of 0.6–1.6 μF/cm², the membrane resistance was therefore constrained between 700 and 2,500 Ωcm². The axial resistance was restricted to a range between 20 and 400 Ωcm. Setting the lower bound of axial resistance instead to the more realistic 50 Ωcm resulted in a slightly higher fitting error but did not qualitatively affect any of the results in this article. We chose here to display the results of the best fit. On the path down the axon toward the axon terminals, electrical synapses were positioned at locations matching best local input resistances of 8 MΩ and electrotonic distances of 0.6 length constants from the electrode locations (see SI Fig. 8B). Parameters were adjusted to best fit the voltage decay in the network (Fig. 2E) while keeping input resistances at ≈4 MΩ in all cells. Fitting of the parameters was done with the MATLAB fminsearch function, which uses the simplex algorithm. The respective values are given in SI Table 2. To simulate visual input, synapses were put in the dendrite branches with diameters of <3 μm (SI Fig. 8B), yielding between 227 and 767 synapses per cell. These chemical synapses were implemented as excitatory and inhibitory conductances for currents with reversal potentials of +40 mV above and −30 mV below rest, respectively. The effects presented here were robust far beyond the range of realistic synaptic conductance values (>100 nS), and replacing these synapses by simulated current injections did not alter the results. Angular coordinates were mapped on the dendrites of the VS cell models by attributing a horizontal position in the visual field to each dendritic synapse according to its location on the x axis. These were adjusted such as to result in ≈50% overlap of dendritic field between neighboring VS cells (23) (see Fig. 3C).

Motion Detection During Image Rotation.

As an artificial image, a 100 × 100 pixel random-dot pattern was created by assigning real values of either 0.0 or 1.0 to each pixel with equal probability. This image was then rebinned to a grid of 200 × 200 pixels. Alternatively, a natural image was taken from the image database (http://hlab.phys.rug.nl/imlib/index.html), rebinned to the 200 × 200 pixel size, and rescaled to real pixel values between 0.0 and 1.0. The half-width of the autocovariance function of the chosen natural image was typical for the images in the database (within one standard deviation distance from the mean). The images were rotated each ms by 1° in the clockwise direction around their centers and smoothed by a 2 × 2 box filter. To avoid edge effects, only the central part of the image was taken and subsequently fed to an array of 100 × 100 horizontal and vertical local-motion detectors of the Reichardt type (25). Within each detector, the pixel value was filtered by a first-order low-pass filter with a 30-ms time-constant and multiplied with the signal from the neighboring pixel (either in the horizontal or vertical direction) filtered by a first-order high-pass (75-ms time constant). This operation was done twice in a mirror-symmetrical way. The output signals resulting from both multiplications were assigned to excitatory and inhibitory synaptic conductances. The vector fields shown in Fig. 4 A and B were obtained by subtracting the output signals of the multipliers from the mirror-symmetrical units described above, to result in the local estimate of horizontal and vertical image-motion independently. Vertical-motion components were separately fed as conductance values in the excitatory and inhibitory dendritic synapses of the VS cell models according to their horizontal disparity in the visual field. A slight offset component at the frequency of rotation was present corresponding to the high-contrast parts in the image moving around the visual field. Weighting the inhibitory input more strongly than the excitatory input downscaled this offset. Note that in analogy to the preferred downward direction in VS cells, upward motion was represented by negative values. To avoid response transients, image rotation was performed around 410° in total, and the first 50 images were discarded.

Abbreviation

VS

vertical system.