Femtosecond studies of protein–ligand hydrophobic binding and dynamics: Human serum albumin

Abstract

In this contribution, we report studies of the nature of the dynamics and hydrophobic binding in protein–ligand complexes of human serum albumin with 2-(2′-hydroxyphenyl)-4-methyloxazole. With femtosecond time resolution, we examined the orientational motion of the ligand, its intrinsic nuclear motions, and the lifetime changes in the hydrophobic phase. For comparisons, with similar but chemical nanocavities, we also studied the same ligand in micelles and cyclodextrins. The hydrophobic interactions in the binding crevice are much stronger than those observed in cyclodextrins and micelles. The confined geometry restrains the nonradiative decay and significantly lengthens the excited-state lifetime. The observed dynamics over the femtosecond-to-nanosecond time scale indicate that the binding structure is rigid and the local motions of the ligand are nearly “frozen” in the protein. Another major finding is the elucidation of the directed dynamics by the protein. Proton transfer and intramolecular twisting of 2-(2′-hydroxyphenyl)-4-methyloxazole were observed to evolve along two routes: one involves the direct stretching motion in the molecular plane (≈200 fs) and is not sensitive to the environment; the second, less dominant, is related to the twisting motion (≈3 ps) of the two heterocyclic rings and drastically slows down in the protein hydrophobic pocket.

The understanding of molecular recognition in protein–ligand complexes on an atomic level is crucial to biological function and of significant, practical importance in the discovery of new drugs and in phototherapy (1, 2). The weak, noncovalent interactions (hydrophobic, electrostatic, van der Waals, and hydrogen bonding) govern the ligand-binding process during protein–ligand complexation. Elucidating the role of these interactions and the time scales involved provides insights into the mechanism of molecular recognition and the role of binding cooperativity in protein dynamics. Specific questions of interest here are the following. How rigid is the ligand binding to the protein? What is the time scale of the local motion of the ligand in the protein environment? How does the recognition by the protein influence the ligand dynamics in the hydrophobic cleft? Finally, what is the nature of the hydrophobic interactions in the internal nanocavity of the protein?

2-(2′-Hydroxyphenyl)-4-methyloxazole (HPMO), a proton-transfer fluorescent dye, was chosen as a probe ligand, and human serum albumin (HSA) was chosen as a prototype protein (Fig. 1). HSA recognizes a wide variety of agents and transports them in the blood stream (3). It comprises three homologous domains (denoted I, II, and III) determined from the recent x-ray crystal structure (4). Each domain is a product of two subdomains, A and B, with common structural motifs. The principal regions of ligand bindings to HSA are located in hydrophobic cavities in subdomains IIA (binding site I) and IIIA (binding site II).

Figure 1.

X-ray structure of the HSA protein and molecular structure of the probe ligand HPMO (Right), schematic representation of a micelle structure (Left Top), x-ray structure of β-cyclodextrin (Left Middle), and illustration of a protein–ligand recognition process (Left Bottom).

The crystal structure map of the binding region and extensive characterization of the drug bindings to HSA have identified that binding site I is dominated by the strong hydrophobic interactions with most neutral, bulky, heterocyclic compounds. On the other hand, with most aromatic carboxylic acids, binding site II mainly involves ion(dipole)–dipole, van der Waals, and/or hydrogen-bonding interactions in the polar cationic group of HSA (4–10). Thermodynamically, the recognition of the ligand by HSA at site I is an entropy-driven reaction with positive (or minimal negative) entropic contributions; at site II it is mainly an enthalpy-driven complexation with large, negative, entropic gains (9, 10). HPMO is hydrophobic and barely dissolves in water. As a neutral species, its binding to HSA by the strong hydrophobic interactions is at site I, as discussed above in x-ray studies and by observation of enhanced fluorescence intensity upon complexation (11). Fig. 1 illustrates this recognition process.

Upon electronic excitation in the UV region, HPMO undergoes an intramolecular proton transfer (12), which takes place in less than 300 fs (13). The process of intramolecular proton transfer results from an ultrafast electronic redistribution (14) initiated by the excitation and a vibrational coherence of the elementary modes modulating the hydrogen-bond coordinate(s) (see refs. 15–17). The transformation of the initial enol form to the keto form results in a Stokes shift, as large as ≈10,000 cm⁻¹, observed in the steady-state emission spectrum (11, 12).

By binding the ligand HPMO to the HSA protein in water (buffer) solution, we studied proton transfer dynamics and the orientational motions in the biological environment. The same processes in chemical caging structures, micelles and cyclodextrins (Fig. 1), were also studied. These confined geometries, ranging from “spheres” (micelles) and “cones” (cyclodextrins) to the more complex, three-dimensional networks of structures (proteins), provide a unique opportunity for studies of dynamics and binding. The dynamics of HPMO in the organic solvent p-dioxane were examined for comparison with a cavity-free environment. Liquid p-dioxane often is considered to be one of the best mimic environments of a protein environment; yet, the rigidity and compressibility are not liquid-type.

Methodology.

All experimental measurements use the femtosecond-resolved fluorescence up-conversion nonlinear technique. The experimental setup is described in detail elsewhere (18). The femtosecond pump pulse was set at 325 nm, with ≈250 nJ/pulse and the probe pulse at 790 nm. We also studied the ligand for 266-nm excitation; for the protein at this wavelength, both the tryptophan and ligand emission are observed. The 325-nm excitation is selective to the ligand even in the protein. The fluorescence was collected and focused into a nonlinear crystal to mix with the probe pulse by using two parabolic mirrors. The up-converted signal in the deep UV range (210–330 nm) was detected by a photomultiplier after dispersion through a double-grating monochromator. The pump polarization was adjusted to be parallel (I_∥) or perpendicular (I_⊥) to the fluorescence polarization, and the resulting anisotropy was measured carefully: r(t) = (I_∥ − I_⊥)/(I_∥ + 2I_⊥). Transients also were taken at the magic angle (54.7°) of the two polarizations.

Sample Preparation and Steady-State Studies.

The ligand HPMO was obtained as described (11). Heptakis-(2,6-di-O-methyl)-β-cyclodextrin (dm-β-CD), micelle of 1-O-octyl β-d-glucopyranoside (98%), HSA (99%), and all solvents (spectroscopy-grade) were purchased from Sigma and used as supplied.

HPMO was dissolved in DMSO and injected into the HSA solution of a 0.3-mM concentration in a 30 mM phosphate buffer at pH 7. The final HPMO concentration was ≈0.1 mM. The binding constant of HSA–HPMO complexes was measured from spectroscopic changes with concentration to be ≈47,000 ± 11,000 M⁻¹ at 300 K (I. Gracia-Ochoa, and A.D., unpublished results). Thus, about 70% of HPMO molecules were recognized by HSA to form complexes. Compared with the same concentration of HPMO dissolved in p-dioxane, the steady-state fluorescence intensity in the protein was enhanced by several hundred times, and the emission peak (455 nm) was blue-shifted by ≈10 nm. This observation indicates the change in the local environment of HPMO upon recognition by HSA and confirms the binding of HPMO to HSA.

For other complexes of dm-β-CD and micelle with HPMO, the guest concentration was 1–2 mM and the host concentrations were almost saturated. The association constant is 1,400 M⁻¹ (11) for dm-β-CD. More than 95% of HPMO molecules were entrapped in the confined geometry. The steady-state fluorescence emission of these complexes was more than 100 times stronger than in the free solvent, and the spectra also were blue-shifted by 5–10 nm. These findings are consistent with the inclusion of HPMO into the hydrophobic cavities of dm-β-CD and the micelle; for CD, part of the molecule could still be outside.

Results and Discussion

Molecular Binding and Structures.

Time-resolved anisotropy.

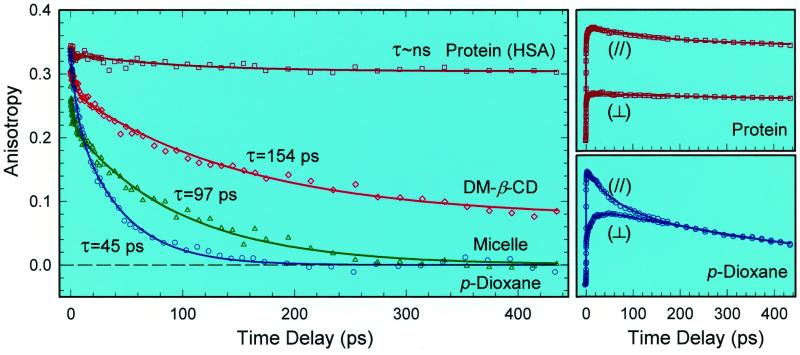
The femtosecond-resolved fluorescence anisotropy of HPMO at 470 nm, r(t), is given in Fig. 2 for the four studied systems, together with the corresponding femtosecond transients obtained at the parallel and perpendicular polarization for the HSA protein and for p-dioxane. In the nonpolar solvent, p-dioxane, the major part (74%) of the anisotropy decays to 0 with a time constant of 45 ps (Fig. 2); the minor component (26%) has a time constant of 5.3 ps. For HPMO in the micelle, these decay constants become 97 ps (83%) and 3.7 ps (17%); for dm-β-CD, they are 154 ps (84%) and 2.6 ps (16%). The anisotropy of HPMO in HSA protein is dramatically different from all others. It lacks a short-time behavior and has a slight drop (8%) with a lifetime of 93 ps, but the major component (92%) stays with no decay at a large constant value of 0.304. In the following, we first focus on the long-time dynamics of the dominant component to elucidate the binding interactions and the rotational motions of HPMO in the complexes. As discussed below, the minor short-decay component is due to structural relaxation.

Figure 2.

Femtosecond-resolved fluorescence anisotropy evolution in four typical environments at 470-nm emission. Note the striking contrast between the free solvent and protein dynamics. The corresponding polarization-analyzed (I_∥ and I_⊥) transients for the HSA protein and p-dioxane are shown on the right.

The persistence of the anisotropy in the HSA protein over 500 ps indicates that the observed diffusive orientational motion in solution essentially is absent in the protein. The rotational relaxation of HSA in water is on the time scale of tens of nanoseconds (11) and makes no contribution to the anisotropy of the ligand in the picosecond region. The high value of the initial anisotropy¶ and the lack of any initial ultrafast decay indicate the strong hydrophobic attraction by molecular recognition, the hindrance of molecular structure relaxation, and the rigidity of the local structure of the binding complex. The large and constant anisotropy on the longer time scale (up to 500 ps) verifies the total absence of the diffusive motion of the ligand in the hydrophobic pocket and, hence, its angular locking in the protein. Therefore, the binding is very tight and the protein–ligand complex is rigid. These results are consistent with recent x-ray structural studies (4), which indicate that at binding site I there are 16 hydrophobic residues, suggesting a strong hydrophobic interaction between the ligand's aromatic ring and the residues.

For the free ligand in p-dioxane, the observed 45-ps decay represents the complete orientational relaxation. Using the Stokes–Einstein–Debye hydrodynamics theory, we calculate the orientation relaxation times to be 64 and 23 ps for the stick- and slip-boundary condition limit, respectively. The molecular shape is taken to be a prolate ellipsoid, and τ_rot = fηV/kT (ref. 19; ref. 20 and references therein). Our experimental value of ≈45 ps lies in the middle.

In the micelle, the diffusive orientation relaxation of HPMO (97 ps) becomes two times longer than in p-dioxane (η = 1.18 cP), so the corresponding effective viscosity reaches 2.55 cP. There are two places in the micelle to host the HPMO molecule: a palisade layer and a hydrophobic core. The palisade layer is relatively rigid, hydrophilic, and composed of the glucopyranoside groups that form the hydrogen bonding with water molecules; the hydrophobic core is pliant and formed by flexible alkyl chains (Fig. 1). Because of this distinct polarity, the guest HPMO is buried in the hydrophobic core of the host. The ordered sizable alkyl chain (nonpolar) in the core hinders the HPMO rotation in comparison with a p-dioxane solution, so HPMO needs more time to change orientation. The observed anisotropy in the micelle indeed decays to zero, reflecting a complete orientation relaxation and indicating an “isotropic” environment in the core. The rotational relaxation of the whole guest–host complex occurs on a much longer time scale, and such motion does not influence the anisotropy of the guest in the picosecond range.

For the encapsulation of guest HPMO in dm-β-CD, the situation is different from micelles. The anisotropy decay (154 ps) is more than three times slower than in p-dioxane and the anisotropy does not decay to 0 up to 500 ps; it stays at 0.074. The deduced effective viscosity of the cavity environment is ≈4.0 cP because the orientational relaxation is much longer than in the bulk solvent. The persistence of the anisotropy at the value of 0.074 (not zero) indicates that the orientation relaxation is hindered as the system is not able to reach the isotropic [r(t) = 0] limit. This is consistent with the more rigid, confined geometry of dm-β-CD. From NMR studies (11), it was suggested that the oxazole component of the guest molecule insert into the cavity. Because the cavity inner diameter (6.2 Å) is smaller than the probe molecular length (≈9 Å long), the complete reorientation of the sequestered guest is hampered and the corresponding average change in direction of the transition moments from the initial anisotropy of 0.34 to the final value of 0.074 is about 30°. Compared with the core (>13 Å in diameter) of the micelle, the hydrophobic cavity of dm-β-CD (≈8 Å in inner large diameter; 6 Å in length) is smaller and more rigid. Thus, for HPMO, it takes longer to reorient in the CD cavity.

Wavelength-dependent lifetimes.

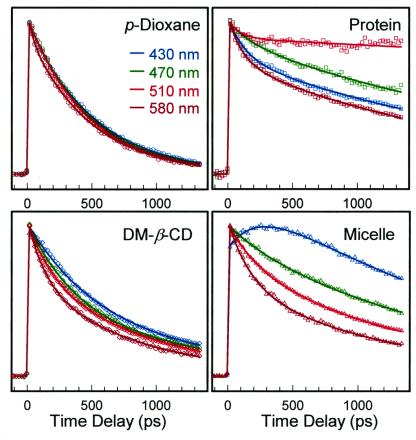
Fig. 3 shows a comparison of transients for different wavelengths at the magic angle (54.7°) and in the four environments studied; Table 1 lists the lifetimes and relative contributions. The contrast and trends for the decay over a 1-ns scale are very clear and suggest the following. First, the lifetimes in p-dioxane solution are similar, independent of wavelength of detection; the systematic, small changes with wavelength are a result of the population distribution after proton transfer, as discussed next. Second, the lifetimes change upon inclusion in CD or micelle, from a single-exponential decay in the free solvent to multiple-exponentials. This change in nonradiative decay reveals the heterogeneous local structure resulting from the anisotropic hydrophobic interactions between the probe and the surroundings (11, 21, 22). Third, the lifetimes in the HSA protein change differently from the blue side to the red side when compared with other environments studied (Fig. 3), showing the influence of the rigid binding on the population distribution and nonradiative decays. The lengthening of lifetime upon inclusion probably is from the suppression of the nonradiative channel induced by torsional motions.

Figure 3.

The wavelength-dependent (normalized) transients at long times for the four environments studied. Note the change upon complexation and in the protein; see text.

Table 1.

Lifetimes (ns) and relative contributions

λ (nm)	Dioxane	dm-β-CD	Micelle*	Protein
420		0.61 (0.88); 3.92	0.31 (rise); 2.47	0.10 (0.33); 6.20
430	0.52	0.58 (0.80); 2.73	0.25 (rise); 1.81	0.13 (0.25); 2.24
470	0.48	0.36 (0.56); 1.38	0.27 (0.08); 1.72	0.17 (0.12); 2.67
510	0.47	0.19 (0.35); 0.93	0.21 (0.24); 1.39	0.09 (0.12); ∼10
580	0.45	0.17 (0.35); 0.83	0.11 (0.28); 1.21	0.11 (0.28); 1.89

The relative contributions are listed in parentheses. 

^*The rise is probably from a relaxation process because of a unique weak coupling between HPMO and the alkyl chain of the hydrophobic core. 

Directed Dynamics in Confined Geometry: Intramolecular Proton Transfer.

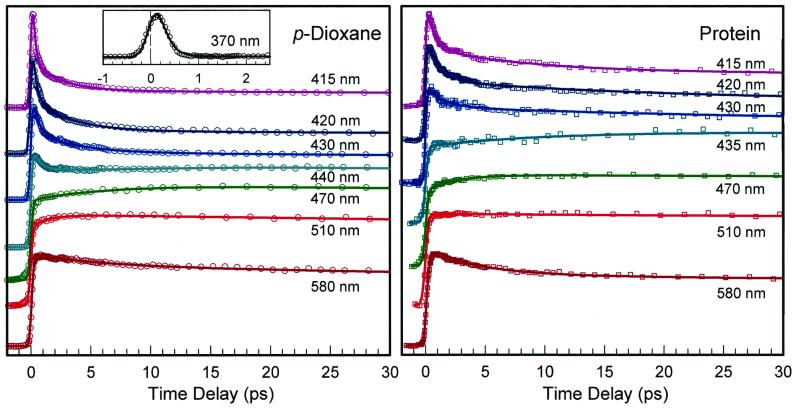
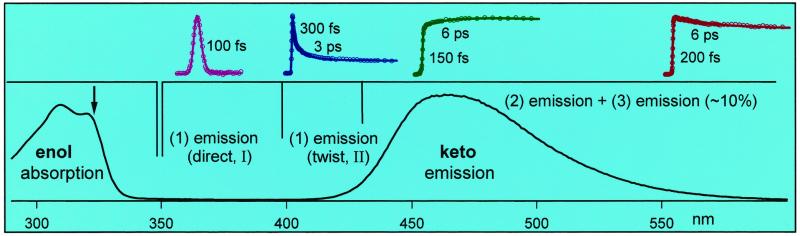
Fig. 4 shows the transient behavior for a series of emission detection in p-dioxane and HSA protein. Similar patterns also were observed in the guest–host complexes of cyclodextrin and micelle. Two groups of time-resolved fluorescence emission, which overlap around 430 nm, were observed. For the emission at wavelengths less than 430 nm, the transients have two initial decay components, for example, ≈300 fs and 3.1 ps at 420 nm in p-dioxane. These two time constants become much different in the protein and increase to ≈1.1 ps and 20 ps, respectively. However, nearly no changes were observed for the guest–host complexes of CD and micelle. The fluorescence intensity of this group of emission (≤430 nm) is very weak, and the emission at 420 nm is about 15% of the one at 470 nm. For the emission at longer than 430 nm, we also observed two short-time components: one that appears within ≈100–250 fs for all wavelengths and the other component (20–30%) that rises at the blue side and decays at the red side. The time constants change systematically, for example, from a decay of 6.3 ps at 580 nm to a rise of 6.5 ps at 470 nm in p-dioxane. No major change of time constants was observed for all complexes, including that with the protein.

Figure 4.

The normalized fluorescence transients for a systematic series of wavelength detections. Similar patterns were observed for dm-β-CD and for the micelle. The actual intensities at 420 and 580 nm are about ≈15% and ≈30% of that at 470 nm, respectively. Note the difference in time decays for p-dioxane and the protein at the short wavelengths shown (415–430 nm) and the similarity for both at longer wavelengths (470–580 nm); see text.

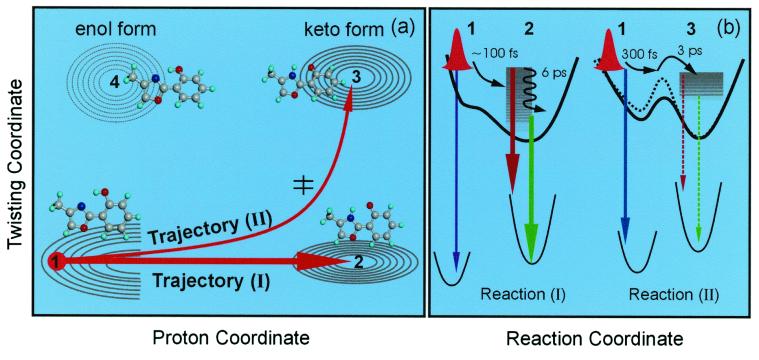
The two groups of emission are from two types of trajectories. A schematic potential energy contour is shown in Fig. 5a. In the ground state, the stable structure is planar in the enol form. The other isomers, such as the keto tautomer and the enol rotamers, lie at higher energy. After the initial ¹ππ^* excitation, the excited-state enol form suffers some loss of aromaticity in the six-member ring and the charge rapidly redistributes, which results in a steep potential surface and constitutes the driving force for the femtosecond proton transfer from N⋅⋅⋅H—O to N—H⋅⋅⋅O (14). Note that the charge redistribution barely changes the direction of transition moments because the observed initial anisotropy (≈0.34) is close to an ideal parallel transition (0.4).

Figure 5.

(a) The potential energy contour map for two of the nuclear coordinates involved: a schematic for two trajectories of the direct proton-transfer (I) and the one involving twisting (II). The initial wave packet (structure 1) bifurcates and evolves as shown. The dominant channel mainly involves the proton transfer coordinate (N⋅⋅⋅H—O) to form the keto form (structure 2). The minor channel initially follows the proton motion and finally proceeds along the twisting motion of the two heterocyclic rings reaching the keto rotamer minimum (structure 3). The corresponding molecular structures also are shown. (b) Potential energy curves along the reaction coordinate for the two trajectories with the observed emission indicated schematically. The black dashed line represents the potential energy in the protein environment, and the barrier is increased because of the rigid protein–ligand binding structure. Note that rotamers of nonplanar enol ground state (near structure 1) in this picture can undergo proton transfer on the upper surface after an initial twist toward planarity.

Because the minimum structure of the keto tautomer is also planar, the proton-transfer process mostly involves the stretch motion of the heavy atoms and is expected to be ultrafast. Experimentally, we observed a rising component (100–250 fs) for all transients recorded at longer than 430 nm. This observation indicates that vibrational energy redistribution also occurs simultaneously on a similar time scale. This prompt dynamic process evolves along the proton coordinate and is described as trajectory I in Fig. 5a. Clearly, the initial wave packet moves quickly along the repulsive potential toward the keto form (Fig. 5b), and the emission during the transformation is mainly around 360 nm (Fig. 6). We do observe a weak decay signal in that region with a time constant of ≈100 fs or less (Figs. 4 and 6). The time scale is similar to those found in other systems in the gas phase (14) or in solution (23–25). A barrierless mechanism (14) was proposed and supported by theoretical calculations (26, 27).

Figure 6.

A dissection of the fluorescence emission corresponding to the different dynamical regions described in Fig. 5. The corresponding transients are shown on the top. The arrow marks the excitation at 325 nm.

Besides the dominant, direct proton-transfer process (trajectory I), the launched wave packet can bifurcate (ref. 28 and references therein) and some family of trajectories evolve along a different route to a keto rotamer minimum, which lies in the same energy range, trajectory II in Fig. 5a. Such a trajectory involves two types of motions: one that is the proton motion at earlier times and the other that is the twisting motion of the two heterocyclic moieties at a later time. Because the potential energy in the rotamer ground state is higher than in the corresponding enol form, the rotamer emission during the twisting shifts to the long wavelength at around 410 nm (Fig. 6). This process involves a twisting motion of two rings and must slow down in the rigid protein–ligand complex. Along this twisting reaction coordinate, the tautomerization usually involves an energy barrier, as predicted by theoretical calculations (27).

In the rigid protein–ligand complex, this barrier increases and the reaction time lengthens significantly. Experimentally, we observed a fast decay component of 200 fs in p-dioxane but 640 fs in HSA protein at 415 nm. This component represents the initial motion of the wave packet out of the repulsive potential surface (Fig. 5b), and this time is longer than the 100 fs obtained for trajectory I because of the twisting motion. The second decay component of ≈3 ps in p-dioxane represents the barrier-crossing dynamics. This time constant increases to 8 ps at 415 nm, 20 ps at 420 nm, and 37 ps at 430 nm in the rigid protein–ligand complex. In contrast, the guest–host complexes of CD and micelle do not possess such protein rigidity, and in their cavities the twist angle may appear similar to that in p-dioxane. Indeed, we observe only a ≈10–20% change of time constants upon going from p-dioxane to the guest–host complexes.

For the dominant trajectory I, we observed that the resulting keto form decays (2–6 ps, depending on fluorescence wavelength) at longer than 520 nm and rises (2–6 ps) at shorter than 520 nm (Fig. 6); at 520 nm, we observe flattening of the transient. This observation reveals that the red-side emission is from the vibrationally hot structures after proton transfer, with transitions to the high vibrational states of the ground state (Fig. 5b). The time constant of 2–6 ps gives the rate at which these structures are relaxing to achieve the equilibrium configuration of the keto form. Because the process of proton transfer is barrierless (<100 fs) for this planar-type structure, the picosecond structural relaxation is expected to be the same as for solution or the protein environment, as observed experimentally.

As mentioned above, the anisotropy shows the decay by the time constant of this vibrational relaxation in addition to the major decay by the diffusive orientation process. Again, this observation supports the notion that after proton transfer on the femtosecond time scale the initial vibrational distribution decays in the keto form on the picosecond time scale, with a change in the structure (and its transition moment). Physically, this cooling helps the proton of trajectories I to achieve the minimum energy and the largest free energy change for a stable structure. For trajectory II, the vibrational relaxation of the keto rotamer (structure 3 in Fig. 5a) should be similar to the keto form (structure 2), with the final emission at longer than 430 nm (Fig. 5b). This weaker signal is buried in the strong emission from the keto form (Fig. 6).

Finally, for all systems studied here, we did not observe significant solvation kinetics. The lack of a solvent effect (decay in the blue and rise in the red because of stabilization of molecules in the excited-state potential by the solvent) is expected because HPMO is studied in solvent environments that are basically aprotic, nonpolar, or hydrophobic in nature. Although the dipole moment changes on the time scale of proton transfer, electronic redistribution occurs in less than 60 fs (14), shorter than the time scale of complete solvation. Even in methanol or acetonitrile (not shown), no apparent solvation dynamics were observed, consistent with this picture.

Conclusions

The reported studies with femtosecond time resolution of the ligand–protein binding (HPMO/HSA) in biological environments and those of guest–host binding (CD and micelle) elucidate the important role of dynamics in the recognition process and the interplay to structure. The protein exhibits the strongest binding in the hydrophobic phase of the structure with optimum rigidity; the persistence of the measured anisotropy of the ligand over hundreds of picoseconds indicates that the maximum motion is ≈3⁰, as measured by rotation of the dipoles. This crystalline (or dense fluid)-type environment of the protein is much more relaxed in the micelle or cyclodextrin; for them, we observed the loss of the anisotropy and measured the local viscosity (liquid-type environment). The unique rigidity of the protein has its roots in the chelating forces of the cavity.

The thermodynamics of recognition is clear: by measuring or inferring the overall rate of association and dissociation, one obtains the equilibrium constant, in this case on the order of ≈10⁴ M⁻¹, and the free energy change, ΔG = −RTlnK. However, such results do not provide a detailed picture of the mechanism of the molecular processes involved and their dynamical time scales, k_a, k_d, τ_TS, and τ_solv. For example, if the association is assumed to be diffusion-controlled (≈10⁸–10¹⁰ M⁻¹ s⁻¹), the dissociation rate constant becomes 10⁴–10⁶ s⁻¹. However, the true molecular time scale of recognition is masked by diffusion, which takes, at the concentration of 10⁻⁴ M, about 1–100 μs. The two rates critical for the final recognition are those describing the reorientation of the ligand (τ_r) in its solvent shell and the direct “reaction” in a single encounter (τ_e). In our case, τ_r ≈ 50 ps (taken to be similar to that of ground-state ligand in water), suggesting the regime in which τ_D > τ_r (τ_D is the average diffusion time) and, therefore, the recognition by the ligand is limited by τ_r/τ_e, which may reach a factor of 100. This same quantity is relevant to the degree of order in the solvent environment that controls the extent of hydrophobicity.

Studies of the nuclear motions of the ligand and its structural relaxation in the protein elucidate another point: the directed dynamics of motion imposed by the structural rigidity in the recognition process. The protein suppresses the “inefficient” picosecond proton transfer whereas the direct femtosecond channel of isolated systems (14, 29, 30) remains robust. Such rigidity of conformations and directed dynamics are less exhibited in the confined cavities of the guest–host complexes of micelles or CD sugars and may be a unique feature of the biological protein environment for the function (ref. 28 and references therein) and in this case for drug delivery.

Abbreviations

HSA

human serum albumin

HPMO

2-(2′-hydroxyphenyl)-4-methyloxazole

dm-β-CD

heptakis-(2,6-di-O-methyl)-β-cyclodextrin