The N-terminal transmembrane domain (TMD0) and a cytosolic linker (L0) of sulphonylurea receptor define the unique intrinsic gating of K_ATP channels

Abstract

ATP-sensitive potassium (K_ATP) channels comprise four pore-forming Kir6 and four regulatory sulphonylurea receptor (SUR) subunits. SUR, an ATP-binding cassette protein, associates with Kir6 through its N-terminal transmembrane domain (TMD0). TMD0 connects to the core domain of SUR through a cytosolic linker (L0). The intrinsic gating of Kir6.2 is greatly altered by SUR. It has been hypothesized that these changes are conferred by TMD0. Exploiting the fact that the pancreatic (SUR1/Kir6.2) and the cardiac (SUR2A/Kir6.2) K_ATP channels show different gating behaviours, we have tested this hypothesis by comparing the intrinsic gating of Kir6.2 with the last 26 residues deleted (Kir6.2Δ26) co-expressed with SUR1, S1-TMD0, SUR2A and S2-TMD0 at −40 and −100 mV (S is an abbreviation for SUR; TMD0/Kir6.2Δ26, but not TMD0/Kir6.2, can exit the endoplastic reticulum and reach the cell membrane). Single-channel kinetic analyses revealed that the mean burst and interburst durations are shorter for TMD0/Kir6.2Δ26 than for the corresponding SUR channels. No differences were found between the two TMD0 channels. We further demonstrated that in isolation even TMD0-L0 (SUR truncated after L0) cannot confer the wild-type intrinsic gating to Kir6.2Δ26 and that swapping L0 (SUR truncated after L0)between SUR1 and SUR2A only partially exchanges their different intrinsic gating. Therefore, in addition to TMD0, L0 and the core domain also participate in determining the intrinsic gating of Kir6.2. However, TMD0 and L0 are responsible for the different gating patterns of full-length SUR1 and SUR2A channels. A kinetic model with one open and four closed states is presented to explain our results in a mechanistic context.

The hallmark of ATP-sensitive potassium (K_ATP) channels is their regulation by intracellular nucleotides: inhibition by ATP but stimulation by MgADP (Ashcroft, 2005). K_ATP channels serve important functions such as insulin secretion, control of vascular tone and protection against ischaemia (Yamada et al. 2001; Miki et al. 2002; Gumina et al. 2003; Ashcroft, 2005). They are octameric complexes of four inwardly rectifying potassium (Kir) channel subunits (Kir6.1 or Kir6.2), and four regulatory sulphonylurea receptors (SUR1 or SUR2) (Fig. 1) (Aguilar-Bryan & Bryan, 1999). SUR1 associates with Kir6.2 (SUR1/Kir6.2) to form the pancreatic K_ATP channels whereas SUR2A/Kir6.2 channels are found in the heart (Inagaki et al. 1996). Mutations in K_ATP channels have been linked to persistent hyperinsulinaemic hypoglycaemia of infancy, permanent neonatal diabetes and dilated cardiomyopathy (Aguilar-Bryan & Bryan, 1999; Bienengraeber et al. 2004; Ashcroft, 2005). Most of these mutations alter gating and change the metabolic sensitivity of the channels. K_ATP channel-specific inhibitors (sulphonylureas, e.g. glibenclamide) and openers (e.g. diazoxide) are currently used to treat diabetes and hyperinsulinism. Understanding how K_ATP channels are gated is fundamental to our knowledge of how they function as metabolic sensors and how they are modulated by the clinically relevant drugs.

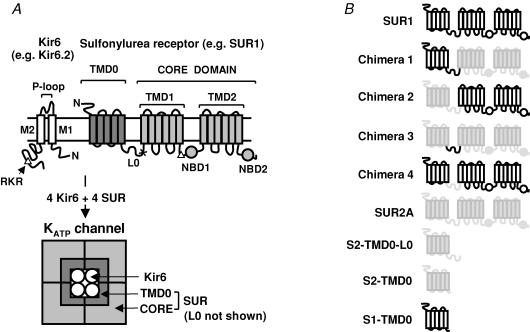
Figure 1. Topology of Kir6 and SUR and the octameric structure of the K_ATP channel complex.

A, K_ATP channels are octameric complexes of Kir6 and SUR. Kir6 comprises two transmembrane segments (M1 and M2) flanking the selectivity filter formed by the P-loop. Both its N- and C-termini are located intracellularly. SUR comprises TMD0, L0 and the core domain. The C-terminal part of L0 (denoted arbitrarily as the part after the ‘x’) and the core domain is homologous to a typical ABC protein made up of a cytosolic N-terminus, TMD1, NBD1, TMD2 and NBD2. SUR associates with Kir6 predominantly through TMD0. The ER-retention sequence, the RKR motif, is represented by the triangles. The schematic diagram at the bottom represents only the transmembrane domains of Kir6 and SUR. B, schematic representation of various SUR constructs used in this study.

Each channel subunit contains an RKR motif which causes endoplastic reticulum (ER) retention when either subunit is expressed alone (Fig. 1) (Zerangue et al. 1999). Removing this motif by deleting the last 26 amino acids in Kir6.2 (Kir6.2Δ26) results in its surface expression (Tucker et al. 1997; Zerangue et al. 1999). The Kir6.2Δ26 channels have low intrinsic open probability (P_o), are sensitive to ATP but not activated by MgADP. The SUR/Kir6.2Δ26 channels show > 5-fold higher intrinsic P_o with strikingly different single-channel kinetics and the sensitivity to MgADP is restored (Tucker et al. 1997; Drain et al. 1998; Chan et al. 2003).

SUR is an ATP-binding cassette (ABC) protein which contains the typical ABC protein domain-architecture (the core domain): two transmembrane domains (TMD1/2) and two nucleotide-binding domains (NBD1/2) (Fig. 1) (Croop, 1998; Dean et al. 2001). In addition, SUR contains an N-terminal transmembrane domain (TMD0). TMD0 is connected to the core domain through a cytosolic linker L0. We and others have shown that SUR1 associates with Kir6 predominantly through TMD0 (Chan et al. 2003; Babenko & Bryan, 2003). TMD0 can be independently expressed and associates with Kir6.2. However, the resulting complex reaches the cell membrane inefficiently unless the RKR motif in Kir6.2 is deleted. TMD0 can alter the gating of Kir6.2Δ26 (Chan et al. 2003; Babenko & Bryan, 2003).

In the absence of interacting ligands, K_ATP channels open spontaneously with intrinsic gating characterized by bursting kinetics and a high P_o (> 0.45 at −40 to −80 mV) (Babenko et al. 1998; Drain et al. 1998; Enkvetchakul et al. 2000; Chan et al. 2003; Proks et al. 2005). SUR2A/Kir6.2 has higher P_o and longer mean burst duration compared to SUR1/Kir6.2. These differences can be explained by the first ∼290 amino acids of SUR, which includes both TMD0 and L0 (Babenko et al. 1999). We previously showed that S1-TMD0/Kir6.2Δ26 (S is an abbreviation for SUR) and SUR1/Kir6.2Δ26 displayed very similar spontaneous bursting kinetics and suggested that L0 and the core domain do not contribute to intrinsic channel gating (Chan et al. 2003).

Here, we tested the hypothesis that TMD0 is sufficient to confer the wild-type (WT) intrinsic gating to Kir6.2. This hypothesis predicts that S2-TMD0/Kir6.2Δ26 should have a gating pattern identical to SUR2A/Kir6.2Δ26 but longer bursts and higher P_o compared to S1-TMD0/Kir6.2Δ26. We have performed detailed single-channel kinetic analyses on SUR1, S1-TMD0, SUR2A and S2-TMD0 channels under nucleotide-free conditions at −40 and −100 mV (hereafter we will refer to SUR/Kir6.2Δ26 and TMD0/Kir6.2Δ26 as SUR and TMD0 channels, respectively). Differences in the burst and interburst durations between TMD0 and the corresponding SUR channels were consistently found. No differences were found between S1- and S2-TMD0/Kir6.2Δ26. We further demonstrated that in isolation even TMD0-L0 cannot confer the WT intrinsic gating and that swapping L0 between SUR1 and SUR2A only partially exchanges the different burst durations between the two SUR channels. Finally, the rate constants for a minimal kinetic model with one open state and four closed states were determined and used to interpret our results in a mechanistic context.

Methods

Molecular biology and oocyte preparation

DNA coding for hamster SUR1, rat SUR2A, mouse Kir6.2Δ26, the TMD0 of SUR1 (comprising residues 1–195) and SUR2A (residues 1–193), and S2-TMD0-L0 (residues 1–290) were subcloned into pGEMHE (Liman et al. 1992). The compositions of chimeras 1–4 are SUR1_1–292SUR2A_291–1545, SUR2A_1–290SUR1_293–1582, SUR2A_1–193SUR1_196–292SUR2A_291–1545 and SUR1_1–195SUR2A_194–290SUR1_293–1582, respectively (Fig. 1B). Chimeras were made by PCR and linearized plasmids were used for in vitro transcription (Ambion). To reduce the chance of getting homomeric Kir6.2Δ26 channels, Kir6.2Δ26 RNA was mixed with 5- to 10-fold molar excess of RNA coding for various SUR constructs, and the mixtures were injected into Xenopus oocytes (stage V/VI) which were prepared as described before (Chan et al. 2000). Briefly, female Xenopus laevis were anaesthetized with 0.15% Tricaine (pH 7.5) for ∼15 min. A small incision was cut on one side of the abdomen and several ovarian sacs were removed. The incision was then sutured and the animal was allowed to recover. Each animal was used twice (once per side) and killed by an overdose of anaesthetic. All animal procedures were in accord with the Institutional Animal Care and Use Committe (IACUC). Oocytes were digested with 2 mg ml⁻¹ collagenase (Worthington) in OR2 solution containing (mM): NaCl 82.5, KCl 2, MgCl₂ 1 and Hepes 5 (pH 7.5) for ∼90 min at room temperature (25°C).

Electrophysiology, stability plots and kinetic analysis

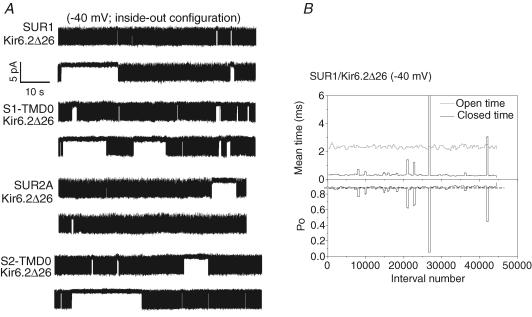
Axopatch 200B, Digidata 1322A and pCLAMP9 software (Axon) were used for patch clamping. Pipette solution contained (mM): KCl 96, MgCl₂ 1, CaCl₂ 1.8 and Hepes 10 (pH 7.35). Bath solution contained (mM): KCl 96, EGTA 1, EDTA 1 and Hepes 10 (pH 7.35). Inclusion of EDTA in the bath solution reduces channel rundown (Lin et al. 2003). Pipettes with resistances of ∼3–5 MΩ were pulled from Corning 0010 soft glasses (WPI). Inside-out patches were excised from de-vitellinized oocytes and single-channel currents recorded at −100 or −40 mV were filtered at 5 kHz and sampled at 25 kHz. Current records were re-filtered at 2 kHz and analysed primarily using custom-made software and partly by Clampfit 9. Single-channel currents were idealized by half-amplitude threshold crossing. To construct a stability plot, the observed mean open time, mean closed time and P_o were calculated for a moving window containing 500 contiguous openings with the window advancing 250 intervals per step (each opening is counted as an interval). The values of these parameters were plotted against the interval number corresponding to the centre of the window (Fig. 2B). The presence of a long closed time (also referred to as long gap) causes a large P_o drop in the stability plot. The dashed line shown in Fig. 2B roughly indicates the average P_o if there were no long gaps. Only stable continuous segments longer than 1 min with no obvious rundown (i.e. drop in the dashed line) were included in the kinetic analyses.

Figure 2. Long gaps are present in the single-channel recordings for SUR and TMD0/Kir6.2Δ26 channels.

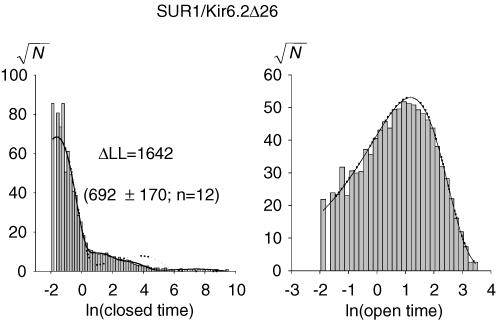
A, representative continuous recordings containing a single active channel measured for SUR1, S1-TMD0, SUR2A and S2-TMD0 co-expressed with Kir6.2Δ26. Downward deflections represent channel openings here and in all subsequent figures. Long gaps ranging from 1 to > 10 s are clearly present in these recordings. B, stability plot (see Methods) of a single-channel recording for SUR1/Kir6.2Δ26. The presence of a long gap is indicated by a much longer mean closed time (one peak in the closed time plot is out of scale) and results in a large drop in P_o in the stability plot.

The closed- and open-time distributions of each selected stable recording were fitted to mixtures of exponentials by unbinned maximum likelihood (ML; Colquhoun et al. 1995). Improvement by inclusion of an extra exponential component was judged significant if the increase in the log-likelihood (ΔLL) was > 3 (for our typical event numbers of 10⁴–10⁵, this ΔLL cutoff corresponds to a P value of ∼0.05; Csanády, 2006). Model fitting was done by simultaneous binned ML fitting of the closed- and the open-time distributions using an algorithm which accounts for the effect of missed events due to limited bandwidth (Csanády, 2000). For these fits, an artificial dead time of 0.14 ms was imposed retrospectively on the events lists.

Nomenclature and calculation of burst parameters

Single-channel recordings revealed characteristic bursting kinetics (Figs 2 and 3). Channel openings occur in bursts that are separated by interburst closures. A large number of bursts occur in clusters separated by infrequent long gaps. For most recordings and for all channel types the open- and closed-time distributions could be fitted by one and four exponentials (Table S1 of Supplemental Material); τ_ci and a_ci are the time constant and the fractional contribution of the i^th closed time component, respectively; τ_o,obs is the observed mean open time. Because the filter dead time (t_d≈ 0.09 ms) is comparable to the time constant of the shortest closed-time component (τ_c1 is ∼0.2 and 0.3 ms at −40 and −100 mV, respectively), and because the latter component typically contributes > 95% of all closed events, a large fraction (25–35%) of all channel closures remains undetected. Therefore, τ_o,obs is spuriously long. The true mean open time (τ_o), which would be observed if all closures were detected, is given by 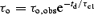(Davies et al. 1992; also see Supplemental Material). (Distortion of the closed-time distribution by omission of brief openings is neglected, as typically only 5–8% of all open events remains undetected.) The number of channel closures within a burst (N), the burst duration (τ_b) and the interburst duration (τ_ib) were calculated as follows.

(1)

(2)

(3)

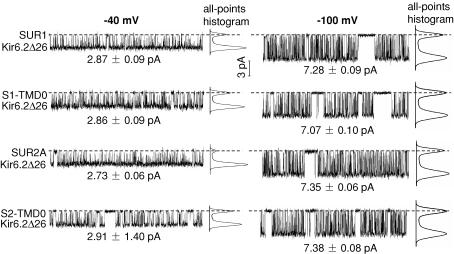
Figure 3. Representative segments of single-channel recordings where long gaps are absent.

Stable segments at −40 (shown on left) and −100 mV (right) are shown for each channel type. The total length of each displayed segment is 0.5 s. The single-channel current amplitudes were evaluated from all-points histograms and are indicated below each recorded segment. The single-channel chord conductance (γ) for each channel is ∼70 pS at either membrane potential.

Two alternative kinetic schemes with one open (O) state and several closed (C) states were explored (see Discussion). Scheme 1 is a model with one complex slow gate (represented by states C₂–C₄) and a separate fast gate (represented by state C₁), while Scheme 2 is a tetrameric model with four independent binary slow gates (with opening rate β and closing rate α), as well as a separate common fast gate (C₁).

(Scheme 1).

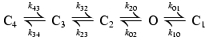
(Scheme 2).

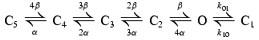
Results

Presence of long gaps in the TMD0 and SUR/Kir6.2Δ26 single-channel recordings

Figure 2A shows > 1 min of representative single-channel recordings for SUR1, S1-TMD0, SUR2A and S2-TMD0 channels obtained at −40 mV. SUR/Kir6.2Δ26 was inactive under cell-attached configuration (data not shown) and bursting activity appeared after the patches were excised into the ATP-free bath solution (Fig. 2A). On the other hand, on-cell patches containing TMD0/Kir6.2Δ26 were already active with low P_o (data not shown) which increased after patch excision. This difference reflects the higher ATP sensitivity of SUR/Kir6.2Δ26 (the half maximal inhibitory ATP concentration (IC_50(ATP))) for SUR1 and S1-TMD0 channels are ∼10 and 300 μm, respectively; Chan et al. 2003]). In each recording, channel openings appear in bursts which group to form clusters. Adjacent clusters are separated by a long gap during which the channel stays closed (mean long gaps are ∼1–2 s; see τ_c4 in Table 1). Although a long gap causes a sharp drop in P_o in the stability plot (Fig. 2B), the P_o usually recovers to its previous level afterwards, indicating that the long gap is not the result of rundown. Long gaps have also been reported for SUR1/Kir6.2 but were not analysed (Enkvetchakul et al. 2000). Here, they are considered as part of the intrinsic gating.

Table 1.

Single-channel parameters measured at −40 and −100 mV

	SUR1	S1-TMD0	SUR2A	S2-TMD0	S2-TMD0-L0
Po	0.77 ± 0.03	0.71 ± 0.03	0.87 ± 0.02	0.65 ± 0.03	0.72 ± 0.03
	(0.57 ± 0.02)	(0.52 ± 0.03)	(0.61 ± 0.03)	(0.49 ± 0.03)
τc1 (ms)	0.19 ± 0.004	0.20 ± 0.007	0.19 ± 0.010	0.20 ± 0.004	0.22 ± 0.003
	(0.33 ± 0.01)	(0.32 ± 0.01)	(0.30 ± 0.01)	(0.31 ± 0.01)
τc2 (ms)	2.34 ± 0.27	1.52 ± 0.08	1.80 ± 0.20	1.86 ± 0.18	1.80 ± 0.12
	(4.98 ± 0.34)	(1.93 ± 0.15)	(6.66 ± 0.67)	(2.04 ± 0.15)
τc3 (ms)	15.05 ± 3.38	9.64 ± 1.79	12.11 ± 2.75	8.67 ± 0.73	10.21 ± 0.87
	(21.39 ± 1.27)	(19.30 ± 0.98)	(19.92 ± 1.25)	(15.62 ± 1.02)
τc4 (ms)	1753 ± 602	1223 ± 196	1601 ± 630	1600 ± 360	1540 ± 372
	(2353 ± 650)	(1960 ± 411)	(4456 ± 1778)	(2743 ± 506)
ac1 (%)	97.66 ± 0.32	93.17 ± 0.70	99.51 ± 0.08	93.35 ± 0.47	95.87 ± 0.19
	(96.80 ± 0.31)	(93.88 ± 0.39)	(97.91 ± 0.20)	(94.04 ± 0.37)
ac2 (%)	1.56 ± 0.18	6.10 ± 0.62	0.35 ± 0.07	5.38 ± 0.43	3.51 ± 0.14
	(1.89 ± 0.19)	(4.24 ± 0.37)	(1.19 ± 0.08)	(3.91 ± 0.31)
ac3 (%)	0.76 ± 0.17	0.71 ± 0.11	0.14 ± 0.04	1.24 ± 0.16	0.59 ± 0.14
	(1.31 ± 0.18)	(1.86 ± 0.13)	(0.89 ± 0.16)	(2.04 ± 0.20)
ac4 (%)	0.026 ± 0.010	0.023 ± 0.005	0.006 ± 0.003	0.035 ± 0.007	0.033 ± 0.006
	(0.009 ± 0.003)	(0.019 ± 0.004)	(0.006 ± 0.002)	(0.019 ± 0.003)
τo (ms)	1.51 ± 0.05	1.33 ± 0.08	1.52 ± 0.09	1.44 ± 0.06	1.81 ± 0.03
	(0.98 ± 0.02)	(1.05 ± 0.04)	(0.93 ± 0.02)	(0.93 ± 0.03)
τib (ms)	5.30 ± 0.58	2.30 ± 0.17	3.96 ± 0.43	3.18 ± 0.33	2.97 ± 0.31
	(11.46 ± 0.77)	(7.47 ± 0.51)	(11.79 ± 0.55)	(6.95 ± 0.70)
N	48.49 ± 4.72	15.61 ± 2.03	230.04 ± 27.68	15.2 ± 1.4	23.9 ± 1.1
	(33.64 ± 3.23)	(16.23 ± 0.96)	(51.18 ± 3.71)	(16.73 ± 0.99)
τb (ms)	84.96 ± 8.90	25.13 ± 3.56	388.85 ± 45.02	26.62 ± 2.85	50.59 ± 2.46
	(45.39 ± 4.54)	(23.49 ± 1.71)	(64.92 ± 5.53)	(21.93 ± 1.47)
n	12 (13)	11 (16)	8 (13)	13 (17)	16

τ_ci and a_ci, the time constant and the fractional contribution of the i^th closed time component, respectively; τ_b, burst duration; τ_ib, interburst dutration; τ_o, true mean open time; N, number of channel closures within a burst; P_o, open probability; n, number of recordings used for the analyses; values are given as mean ± s.e.m. Values measured at −40 mV are not in parentheses; values measured at −100 mV are in parentheses.

TMD0 can confer most but not all of the intrinsic bursting kinetics to Kir6.2Δ26

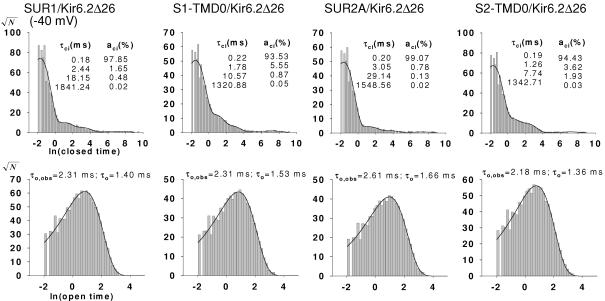
Figure 3 shows, on an expanded time scale, segments of single-channel recordings in which no long gaps occur. At −40 mV, the single-channel chord conductance (γ) of each channel type is ∼70 pS. The closed- and open-time distributions from each group were best fitted with four (τ_c1–τ_c4) and one (τ_o,obs) exponentials, respectively (Fig. 4; also see Methods for calculating τ_o from τ_o,obs). The time constants τ_c1 and τ_o for each group are similar (∼0.2 and ∼1.4 ms, respectively), reflecting similar intraburst kinetics (Table 1 and Fig. 1 of the Supplemental Material). To compare burst kinetics, N, τ_b and τ_ib were calculated according to eqns (1–3). τ_b was ∼3-fold smaller for S1-TMD0 channels compared to SUR1 channels, and ∼15-fold smaller for S2-TMD0 channels compared to SUR2A channels (Table 1). τ_ib was consistently shorter for TMD0/Kir6.2Δ26 compared to the corresponding SUR/Kir6.2Δ26. The fractional contribution of the intercluster closure (a_c4) was smaller and the P_o was larger for SUR2A than for S2-TMD0 channels (Table 1). Despite these differences, the intrinsic gating patterns of TMD0/Kir6.2Δ26 were still very similar to their corresponding SUR channels and visually different from the pattern of homomeric Kir6.2Δ26 channels (P_o for Kir6.2Δ26 is ∼0.1–0.15; Drain et al. 1998; Chan et al. 2003). Concerning the two TMD0 channels, we found no significant differences between their single-channel kinetics. On the other hand, SUR1/Kir6.2Δ26 clearly had shorter τ_b compared to SUR2A/Kir6.2Δ26, without a significant difference between their P_o. Taken together, these results indicate that the TMD0 from SUR1 and SUR2A are functionally equivalent and can confer most but not all the WT intrinsic gating pattern to Kir6.2Δ26.

Figure 4. Dwell-time histograms for SUR1, S1-TMD0, SUR2A and S2-TMD0 channels.

Histograms of closed times (A) and open times (B) were fitted with four and one exponentials, respectively. Data were obtained at −40 mV. The time constants for the exponential components are indicated in each plot.

Voltage dependence of intraburst and burst transitions

In order to study the effect of membrane potential on single-channel kinetics, we also performed single-channel recordings on all four channel types at −100 mV. The single-channel parameters are summarized in Table 1 and Fig. 2 of Supplemental Material. For each group, when the holding potential was changed from −40 to −100 mV, the current amplitude changed from ∼3 to ∼7 pA but the single-channel γ remained the same (∼70 pS) (Fig. 3). Although the closed- and open-time distributions were still best fitted with four and one exponentials, respectively, τ_c1–τ_c4 were all longer but τ_o was shorter at −100 mV, which resulted in a substantial decrease in the P_o (from 0.7–0.9 to 0.5–0.6). The voltage dependence of the intraburst kinetics, reflected by the changes in τ_c1 and τ_o, is one of the hallmarks of K_ATP channels (Alekseev et al. 1997; Benz et al. 1998; Babenko et al. 1998). It is interesting to note that we found that the burst kinetics also exhibit voltage dependence. For each group, τ_b was shorter, τ_ib was longer, and the mean intercluster closed time (τ_c4) was also longer at −100 mV.

The differences between TMD0 and the corresponding SUR channels, or between SUR1 and SUR2A channels, shown at −40 mV, were also observed at −100 mV. However, at −100 mV the differences in τ_b were noticeably smaller than at −40 mV. It is important to note that, as observed at −40 mV, no significant differences between the two TMD0 channels were found at −100 mV.

Both L0 and the core domain participate in determining the intrinsic gating of Kir6.2Δ26

As the TMD0-L0 domain is sufficient for determining the different gating patterns in channels containing full-length SUR1 or SUR2A (Babenko et al. 1999b), we tested whether the isolated TMD0-L0 domain can confer WT intrinsic channel gating. Therefore, we compared the intrinsic gating of S2-TMD0-L0/Kir6.2Δ26 to the S2-TMD0 and the SUR2A channels at −40 mV. Most single-channel parameters of S2-TMD0-L0 channels, including P_o, a_c1–a_c4, and τ_b were somewhat in between those of S2-TMD0 and SUR2A channels (Table 1). In particular, τ_b for S2-TMD0-L0 channels was significantly longer (∼2-fold) compared to that of S2-TMD0 channels but ∼8-fold shorter compared to that of the SUR2A channels. These data indicate that the presence of both L0 and the core domain are required for WT intrinsic channel gating.

Next, we tested whether transplanting just L0 from SUR2A to SUR1, or vice versa, can result in the acquisition of the intrinsic gating corresponding to the donor channel. We first made chimeras similar to those used in a previous study (Babenko et al. 1999) in which the entire TMD0-L0 domains were swapped between SUR1 and SUR2A (chimeras 1 and 2). We then made chimeras 3 and 4, in which only L0 was swapped between the two SUR (Fig. 1B). Each chimera was co-expressed with Kir6.2Δ26 and single-channel recordings were obtained at −40 mV. All the single-channel parameters are summarized in Table S2 in the Supplemental Material. As we did not observe differences in the P_o between the two SUR channels, we focused on comparing τ_b of the chimeras to those of the SUR1 and SUR2A channels. With the TMD0-L0 from SUR1 in a SUR2A background, τ_b of chimera 1 (+ Kir6.2Δ26; 140.37 ± 40.45 ms, n = 4) was not significantly different from that of SUR1/Kir6.2Δ26 (84.96 ± 8.90 ms, n = 12). Similarly, with the TMD0-L0 from SUR2A in a SUR1 background, τ_b of chimera 2 (307.56 ± 48.47 ms, n = 4) was very similar to that of SUR2A/Kir6.2Δ26 (388.85 ± 45.02 ms, n = 8). These data confirm that TMD0-L0 contains all the structural elements for determining the difference in τ_b between SUR1/Kir6.2Δ26 and SUR2A/Kir6.2Δ26. When only L0 from SUR1 was transplanted into a SUR2A background (chimera 3), τ_b (234.55 ± 37.34 ms, n = 4) became smaller than that of SUR2A/Kir6.2Δ26 but was still larger than that of SUR1/Kir6.2Δ26. Chimera 4, the reverse chimera, also had a τ_b value (251.32 ± 58.43 ms, n = 7) between those of the two SUR channels. These data indicate that transplanting L0 only partially transfers the burst duration characteristic of the donor channel.

Fits to a gating model provide mechanistic explanation of the observed gating patterns

Whereas fitting of the dwell-time histograms by sums of exponentials offers a detailed description which does not depend on any assumptions about a gating model, this approach yields limited mechanistic information. We therefore looked for a suitable model and identified Scheme 1 (see Methods) as the minimal model required for describing our data (see Discussion for choice of a gating model). Thus, we obtained ML fits to Scheme 1 to learn how the rate constants depend on channel structure and membrane potential. In Scheme 1, state C₁ accounts for the brief intraburst closure, C₂ and C₃ for interburst closures, and C₄ for the long gap. Accordingly, rates k_O1 and k_1O describe intraburst kinetics, whereas the other rates govern the slow gating process. Figure 5 summarizes the obtained rate estimates for all constructs and for both membrane potentials studied (see also Table S3 in the Supplemental Material).

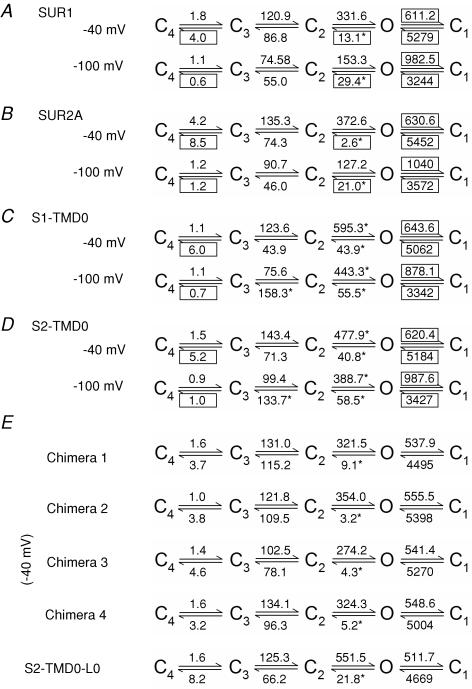
Figure 5. Summary of rate constants for kinetic Scheme 1.

Rate constants (in s⁻¹) were obtained for each channel construct by fitting our single-channel data to Scheme 1 (see Methods) at both −100 and −40 mV. Boxes mark rate constants that were found to be voltage dependent; asterisks identify rate constants that greatly differed for different SUR constructs.

Regarding voltage dependence, the following three observations can be made. (1) Slowing of k_O1 and acceleration of k_1O upon depolarization (Fig. 5A–D) explain the observed voltage dependence of τ_o and τ_c1, respectively (Table 1). The magnitude of these rates was identical for all nine channel constructs (Fig. 5A–E). (2) Depolarization strongly reduced k_O2 for SUR1/Kir6.2Δ26 (Fig. 5A), and even more so for SUR2A/Kir6.2Δ26 (Fig. 5B). Because N is equal to k_O1/k_O2, and burst duration is proportional to N, this voltage dependence of k_O2 accounts for much of the observed prolongation of τ_b upon depolarization for the SUR channels. The virtual absence of voltage dependence of k_O2 for the TMD0 channels explains the small effect of voltage on their τ_b. (3) k₃₄ increased by 5- to 8-fold upon depolarization for both SUR and TMD0 channels (Fig. 5A–D). As k₃₄ determines the frequency of access to C₄, the closed state accounting for the long gap, this observation predicts a larger fractional amplitude a_c4 at depolarized voltages. This prediction is mostly verified in Table 1, although statistical significance was not necessarily achieved because of the large variation in the fitted values of a_c4.

The characteristic differences between the bursting patterns of SUR1/Kir6.2Δ26 and SUR2A/Kir6.2Δ26 are explained by the striking difference of a single rate, k_O2, which was found to be much slower for the latter channel (Fig. 5A and B). This explains the differences in N and τ_b between the two SUR channels (Table 1). When comparing the two TMD0 channels to the SUR channels, two rates were found largely altered at both voltages: both k_O2 and k_2O were large in these constructs (Fig. 5C and D). The large value of k_O2 accounts for the smaller N and τ_b values, whereas the large k_2O explains the shorter τ_c2 of the TMD0 channels relative to WT (Table 1). Among the chimeric channels, k_O2 was the only rate that showed significant variation (Fig. 5E), rendering chimera 1 similar to SUR1/Kir6.2Δ26 (Fig. 5A, −40 mV) and chimera 2 similar to SUR2A/Kir6.2Δ26 (Fig. 5B, −40 mV). For chimeras 3 and 4, their k_O2 values were intermediate. The rate constants for S2-TMD0-L0 channels are almost identical to those of S2-TMD0 channels, except for k_O2 which is approximately halved thereby inreasing τ_b by ∼2-fold.

Discussion

SUR structure determines the pattern of gating

In agreement with previous studies, our data confirm that τ_b for SUR2A/Kir6.2 is larger than that of SUR1/Kir6.2. However, the difference we observed is smaller than the difference that has been reported previously (also at −40 mV), mainly because the τ_b for SUR1/Kir6.2Δ26 reported here is larger (∼85 ms versus < 30 ms) (Babenko et al. 1999b). This discrepancy cannot be explained by the different Kir6.2 constructs that were used (Kir6.2Δ26, in this study, versus Kir6.2), because we obtained similar τ_b values for SUR1/Kir6.2Δ26 and SUR1/Kir6.2 at −100 mV (Yang et al. 2005). In addition, we found no significant difference in the P_o of the SUR1 and SUR2A channels, unlike the reported P_o values (∼0.6 and 0.9 for SUR1 and SUR2A/Kir6.2, respectively) (Babenko et al. 1999b). The reasons for these differences may be attributed to the different expression systems (COSm6 cells versus Xenopus oocytes), different species-specific channel subunits (human SUR and Kir6.2 used by Babenko et al. (1999b)) and the different ways to analyse the data. Nevertheless, our data indicate that τ_b, rather than the P_o, is the most reliable parameter to distinguish between the recombinant pancreatic and cardiac K_ATP channels.

The two TMD0 channels were consistently found to have shorter τ_b and τ_ib values compared to the SUR channels. One possible reason for this is that the structure of TMD0 is slightly altered when it is detached from SUR. Even so, this cannot be the sole explanation because the two TMD0 channels have identical intrinsic gating at both −40 and −100 mV. Therefore, although in terms of gating pattern TMD0/Kir6.2Δ26 channels are much closer to the SUR/Kir6.2Δ26 channels than to Kir6.2Δ26 alone, TMD0 cannot completely confer the WT intrinsic gating to Kir6.2Δ26. We emphasize that the two TMD0 have identical gating effects on Kir6.2Δ26 only after they have been detached from the SUR molecules (see below). By characterizing the S2-TMD0-L0 channels, we further demonstrated that even TMD0-L0, when expressed in isolation, cannot confer the WT gating to Kir6.2Δ26. Our studies on chimera 1–4 channels indicate that whereas swapping TMD0-L0 between SUR1 and SUR2A can exchange their different gating patterns (τ_b), swapping L0 alone only results in partial exchange of τ_b. One possibility for this is that the gating effect of L0 on Kir6.2 depends on whether it is connected to S1- or S2-TMD0. Alternatively, the gating effect of TMD0 may depend on whether it is connected to S1- or S2-L0. In either case, interaction must exist between TMD0 and L0. Taken together, we conclude that in addition to TMD0 and L0, the presence of the core domain is also required for WT intrinsic channel gating. However, the unique gating patterns of SUR1/Kir6.2 versus SUR2A/Kir6.2 are defined co-operatively by TMD0 and L0, rather than by the identity of the core domain.

Voltage dependence of both intraburst and burst kinetics

The kinetic parameters obtained at −40 and −100 mV confirmed the previously demonstrated voltage dependence of the intraburst kinetics (τ₀ and τ_c1) (Alekseev et al. 1997; Benz et al. 1998; Babenko et al. 1998). It has not been reported whether the other time constants also show voltage dependence. Here, we found that depolarizing the membrane also led to a decrease in τ_c2–τ_c4. As a result, τ_b is longer but τ_ib and τ_c4 are shorter. It has been demonstrated that Kir channels have a fast gate close to the selectivity filter controlling the intraburst kinetics and a slow gate near the end of M2 controlling the burst kinetics (Loussouarn et al. 2000, 2002; Proks et al. 2001). Our data indicate that a decrease in the electrical field leads to the increase in the stability of both gates in the open conformations. As ATP inhibits K_ATP channels by acting on the slow gate (Loussouarn et al. 2002), we tested whether the voltage dependence of the slow gate affects the ATP sensitivity. We could not detect any significant difference between the IC_50(ATP) at −40 (29.2 ± 1.9 μm) and at −100 mV (32.5 ± 1.5 μm) for SUR2A/Kir6.2Δ26 (Fig. 2 of Supplemental Material). Further investigations are needed to elucidate the underlying molecular mechanisms for the voltage-dependence of both the fast and slow gates.

Choice of a gating model and its structural interpretation

Our choice of a gating scheme (Scheme 1) was based on the following considerations. As the fast and the slow gates are physically distinct, it is plausible to assign the intraburst flicker to a closed state (C₁) separated from the interburst closed state(s), with the two types of closure communicating only through the open state. Interburst closures revealed three distinct components requiring the presence of at least three such states (C₂–C₄). The simple linear arrangement of these three states is somewhat arbitrary, but can be rationalized considering the 4-fold structural symmetry of these channels. Thus, each subunit in the tetramer could possess a simple binary slow gate and the channel opens only if all four slow gates are in the active conformation. Then, C₂, C₃ and C₄ could correspond to channels with one, two and three slow gates in the inactive state, respectively. An additional state C₅, with all four slow gates inactive, might be accessed too infrequently to be observed in our recordings. Such a model, with four identical and independent subunits has been proposed (Scheme 2, see Methods) (Enkvetchakul et al. 2000). We initially fitted our data to Scheme 2 with rates α, β, k_O1 and k_1O left unconstrained. However, even the best fits provided visually bad descriptions of the closed-time distributions (Fig. 6). We then released the linear constraints between the parameters describing the slow gate in Scheme 2. ML fits to this new scheme (Scheme 1, state C₅ was neglected) consistently yielded much larger LL values (relative to Scheme 2, mean ΔLL = 960 ± 97 units; n = 139), indicating Scheme 1 is a better model for describing the intrinsic gating of K_ATP channels. Therefore, even if the overall structural interpretation of states C₂–C₅ in Scheme 2 is correct, the four slow gates are unlikely to be independent.

Figure 6. Model fits superimposed on the dwell-time histograms for a SUR1 channel.

Open- (shown on the right) and closed-time histograms (left) for a SUR1 channel, obtained at −40 mV. The solid and dotted lines were generated by fitting the data to Scheme 1 and Scheme 2, respectively (see Methods). ΔLL is the log-likelihood (LL) for fitting to Scheme 1 minus the LL for fitting to Scheme 2. The mean ΔLL ± s.e.m. and the number of experiments (n) are shown in parentheses. The two schemes produced very similar fits to the open-time histograms and the two fitted lines are indistinguishable from each other. Similar results were obtained for other channel types (data not shown).

Scheme 1 provided reasonable explanations for the effects on gating of SUR structure and membrane voltage. In particular, the different gating patterns of the various constructs resulted mainly from variations of rate k_O2, which governs the stability of the open burst state (Fig. 5). It is interesting that although k_O2 was increased by ∼3-fold for the TMD0 constructs at −100 mV, at this voltage the equilibrium constant K_2O was very similar for both TMD0 and both WT channels (0.19, 0.17, 0.13 and 0.15, for channels formed with SUR1, SUR2A, S1-TMD0 and S2-TMD0, respectively). Thus, in the TMD0 channels the relative stability (free energy) of state O relative to state C₂ is unaltered, but the height of the free energy barrier separating them is decreased by ∼1 kT.

Conclusion

SUR is the only ABC protein known to function as an accessory regulatory subunit of a potassium channel. However, it is not clear how SUR, with all the characteristics of an ABC protein, interacts with Kir6. The unique structural elements found in SUR but not found in most ABC proteins, which include TMD0 and part of L0, offer a glimpse of how SUR interacts with the Kir6 subunit. We have shown here that both these atypical ABC domains define the unique intrinsic gating of the SUR/Kir6.2 channels in a co-operative manner. It remains to be elucidated whether, and if so how, these unique structures relay the conformational changes initiated from the typical ABC domains to the channel gate.

Supplemental material

The online version of this paper can be accessed at:

DOI: 10.1113/jphysiol.2006.112748

http://jp.physoc.org/cgi/content/full/jphysiol.2006.112748/DC1 and contains supplemental material consisting of text entitled:

How to derive the relationship between τ_o and τ_o,obs? and the following figures and tables:

Figure S1

Bar charts comparing various selected single-channel parameters for the SUR and TMD0 channels obtained at −40 mV

Figure S2

Bar charts comparing various selected single-channel parameters for the SUR and TMD0 channels obtained at −100 mV

Figure S3

No detectable voltage dependence of ATP inhibition

Table S1

Number of SUR/Kir6.2▵26 recording whose closed times were best fitted with 3–5 exponentials

Table S2

Single channel parameters for chimera/Kir6.2▵26 measured at −40 mv

Table S3

Rate constants for studied channels (+ Kir6.2▵26)

This material can also be found as part of the full-text HTML version available from http://www.blackwell-synergy.com