Hyperpolarization-activated currents are differentially expressed in mice brainstem auditory nuclei

Abstract

The hyperpolarization-activated cation current (I_h) may influence precise auditory processing by modulating resting membrane potential and cell excitability. We used electrophysiology and immunohistochemistry to investigate the properties of I_h in three auditory brainstem nuclei in mice: the anteroventral cochlear nucleus (AVCN), the medial nucleus of the trapezoid body (MNTB) and the lateral superior olive (LSO). I_h amplitude varied considerably between these cell types, with the order of magnitude LSO > AVCN > MNTB. Kinetically, I_h is faster in LSO neurons, and more active at rest, compared with AVCN and MNTB cells. The half-activation voltage is −10 mV more hyperpolarized for AVCN and MNTB cells compared with LSO neurons. HCN1 immunoreactivity strongly labelled AVCN and LSO neurons, while HCN2 staining was more diffuse in all nuclei. The HCN4 subunit displayed robust membrane staining in AVCN and MNTB cells but weak labelling of the LSO. We used a dynamic clamp, after blocking I_h, to reinsert I_h to the different cell types. Our results indicate that the native I_h for each cell type influences the resting membrane potential and can delay the generation of action potentials in response to injected current. Native I_h increases rebound depolarizations following hyperpolarizations in all cell types, and increases the likelihood of rebound action potentials (particularly in multiple-firing LSO neurons). This systematic comparison shows that I_h characteristics vary considerably between different brainstem nuclei, and that these differences significantly affect the response properties of cells within these nuclei.

Auditory brainstem neurons process and compare binaural signals that are fundamental for sound localization. The superior olivary complex (SOC) is the first area within the auditory pathway where encoding of interaural time and level disparities (ITDs and ILDs, respectively) take place. The pathway that processes ILD cues is comprised of the anteroventral cochlear nucleus (AVCN), the medial nucleus of the trapezoid body (MNTB) and the lateral superior olive (LSO). Principal cells of the LSO receive ipsilateral excitation from AVCN spherical bushy cells and are inhibited by the MNTB principal cells that relay excitatory input from the contralateral globular bushy cells of the AVCN (Oertel, 1999). The medial superior olive (MSO) is thought to be involved in ITD computation, receiving binaural excitation from globular bushy cells of the AVCN and ipsilateral inhibition from the MNTB (Brand et al. 2002).

Since neurons at different levels of the circuit are required to process signals differently (e.g. AVCN and MNTB neurons phase lock to unilateral inputs while LSO neurons integrate bilateral excitation/inhibition), their respective properties are likely to be different to achieve this. A potentially important channel type expressed in these auditory brainstem neurons is the hyperpolarization-activated cyclic nucleotide-gated (HCN) channel family, which underlies the hyperpolarization-activated cation current, I_h (Chen, 1997; Bal & Oertel, 2000; Cuttle et al. 2001; Koch & Grothe, 2003; Santoro & Baram, 2003; Shaikh & Finlayson, 2003; Barnes-Davies et al. 2004). I_h is a mixed inward Na⁺–K⁺ current that influences the resting membrane potential and modulates excitability (Pape, 1996; Chen, 1997; Shaikh & Finlayson, 2003). Four HCN channel isoforms (HCN1–4) have been cloned (Santoro et al. 1997; Ludwig et al. 1998). These channel isoforms vary in their kinetics and modulation by cyclic-AMP (cAMP), which can alter the voltage sensitivity of HCN channels (Pape, 1996; Santoro et al. 2000; Yamada et al. 2005). Previous studies have shown that HCN1 channels activate more rapidly than HCN2 channels which are, in turn, faster than HCN4 channels. HCN2 and HCN4 channels are strongly modulated by cAMP while HCN1 channels are only weakly affected by cAMP (Santoro et al. 2000). All four channels are non-uniformly expressed throughout the mouse CNS (except for HCN3 channels which have a wide expression but at very low levels) (Ludwig et al. 1998; Moosmang et al. 1999; Santoro et al. 2000). It has been shown that AVCN, MNTB and LSO cells express I_h (Banks et al. 1993; Cuttle et al. 2001; Barnes-Davies et al. 2004; Koch et al. 2004; Leao et al. 2005b). However, a systematic comparison of I_h characteristics between these auditory nuclei has not been made.

In this study, using electrophysiology, including the dynamic clamp, and immunohistochemistry, we examined the differences in I_h properties and HCN channel expression between neurons of the AVCN, MNTB and LSO. Our data demonstrate that I_h has distinct features in different nuclei and these differences are associated with the heterogeneous expression of HCN subunits. The distinct I_h expression patterns result in differential modulation of firing properties of neurons in the auditory brainstem.

Methods

Slice preparation

Mice (CBA strain) at age 12–14 days postnatal were killed according to the Australian National University Animal Ethics Committee and Wright State University IACUC protocols. Following decapitation the brain was dissected in ice-cold standard artificial cerebral spinal fluid (ACSF) (mm: 130 NaCl, 3.0 KCl, 5.0 MgCl₂, 1.25 NaH₂PO₄, 26.2 NaHCO₃, 10 glucose, 218 sucrose equilibrated with 95% O₂, 5% CO₂). Transverse slices (180–200 μm) were made of the ventral cochlear nucleus (VCN), the medial nucleus of the trapezoid body (MNTB) and the lateral superior olive (LSO) using an oscillating tissue slicer (Integraslice 7550 PSDS, Campden Instruments, UK). Slices were incubated in normal ACSF (mm: 130 NaCl, 3.0 KCl, 1.3 Mg₂SO₄, 2.0 CaCl₂, 1.25 NaH₂PO₄, 26.2 NaHCO₃, 10 glucose, equilibrated with 95% O₂, 5% CO₂) at 35°C for 1 h and subsequently held at room temperature (22–24°C) or at physiological temperature (35–37°C), for electrophysiological recording.

Electrophysiological recordings

For whole-cell current- and voltage-clamp recordings one slice was transferred to a recording chamber of standard design and fixed to the glass bottom of the chamber with a nylon grid on a platinum frame. The slice chamber was constantly perfused with ACSF at a rate of 2 ml min⁻¹. Neurons in the AVCN, MNTB or LSO were visualized using an Olympus microscope fitted with a 5 × objective or a 60 × water-immersion objective combined with infrared videomicroscopy. Patch pipettes were made from borosilicate glass capillaries (tip Φ 2 μm, Vitrex, MODULOHMA/S, Denmark) using a patch-pipette puller (Narishige PP-83, Japan). The electrode resistance was typically 3–5 MΩ. The intracellular solution for current-clamp and voltage-clamp recordings was (mm): 130 KMeSO₄, 9.5 KCl, 3.0 MgCl₂, 10 TES, 3.0 Mg-ATP, 0.3 GTP-tris and 0.2 EGTA). The pH was adjusted to 7.3 using KOH. The cell was held at −60 mV and the access resistance was routinely compensated by > 80%. Current and voltage steps were applied and the corresponding neuronal responses recorded using an Axopatch 200B or an Axopatch 1D amplifier (Molecular Devices, Sunnyvale, CA, USA). Electrical signals were low-pass filtered at 5 kHz, digitized at 10 kHz using Axograph (Axon) and data were analysed with Matlab SV13 (Matworks, USA) software. Liquid junction potentials were not compensated for. The pipette offset was usually between 3.5 and 4.2 mV. In several experiments, 20 μm ZD7288 (Tocris Cookson Inc., UK) was added to the bath solution in order to block I_h (for 10–20 min before the recordings). Neurobiotin (0.5%) or Alexa-488 (Molecular Probes) was added to the internal solution in order to determine the spatial position of cells. We have previously demonstrated that there is a gradient of ionic currents, including I_h, in the MNTB. In this study, we have therefore used values obtained from the intermediate or central region of the MNTB as representative of an average value for the nucleus.

Dynamic clamp

We simulated I_h (and low-threshold K⁺ currents in some LSO cells) in neurons using a dynamic clamp. In order to assess the effect of I_h kinetics on cell function, we used two kinetically distinct I_h, a fastτI_h based on our LSO recordings and a slow τI_h based on our AVCN recordings in room temperature. Simulated I_h also varied in amplitude (A) (high-A I_h based on the LSO I_h amplitudes and low-A I_h based on AVCN I_h amplitudes). Our dynamic clamp method was implemented on a second computer running real-time Linux and custom-made software that read voltage and generates currents at 40 kHz. A description of the dynamic clamp technique can be found in our previous study (Leao et al. 2005b).

In order to add different macroscopic I_h to real neurons, we first blocked the ‘real’ I_h with 20 μm of ZD7288. Simulated I_h was calculated by 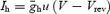where 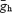is the maximal hyperpolarization-activated conductance, u is the evolution variable, V is the membrane voltage and V_rev is the I_h reversal voltage. Evolution variables were obtained by the following equation:

(1)

where x = u. Activation time constant versus voltage (τ_x(V)) and steady-state conductance versus voltage (x_∞ ‘Boltzmann’) functions for I_h slowτ and I_h fastτ were, respectively:

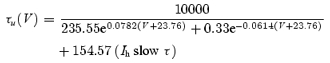(2)

(3)

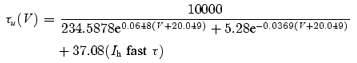(2)

(3)

These equations where obtained by fitting the time constants of I_h and the normalized I_h conductance across various voltages from I_h recordings of AVCN bushy cells (I_h slow τ) and LSO cells (I_h fastτ). Note, the Boltzmann relations shown here refer to steady-state conductance, not steady-state current. In order to account for the differences in amplitude found in different nuclei, we used different amplitudes of 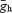(15 nS for low amplitude and 30 nS for high amplitude – low amplitudes in MNTB neurons had 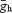= 7 nS). We have also simulated low-threshold voltage-dependent K⁺ currents, I_LT (Leao et al. 2005) using the dynamic clamp in some LSO cells.

Immunohistochemistry

Deeply anaesthetized mice were perfused intracardially with cold saline followed by fixative solution (4% paraformaldehyde in 0.1 m phosphate buffer (PBS), pH 7.4). The brainstem was dissected and post-fixed for up to 4 h before being transferred to PBS containing 15% sucrose. Transverse sections (30 μm thick) of the brainstem were obtained at the level of the AVCN and the LSO, using a cryostat. Brainstem slices were then incubated overnight in one of the following primary antibodies: anti-HCN1, anti-HCN2 or anti-HCN4 (Alamone Laboratories, rabbit, 1 : 100) followed by incubation (1–3 h) in the appropriate secondary antibody conjugated to FITC or Cy3 (Jackson, 1 : 50). Sections were mounted on glass slides and cover-slipped with fluorescent mounting medium (Vectashield, Vector labs).

Glutamatergic synaptic terminals were visualized with anti-VGlut1 (Chemicon, guinea pig, 1 : 1000). Fluorescent images were collected using a laser scanning confocal microscope (Olympus Fluoview) with 20 ×, 40 × or 60 × oil immersion objectives, at 1024 pixels by 1024 pixels resolution.

Image capture and quantity analysis

HCN1-immuno reactivity (IR) was examined with bright field illumination using a Nikon labophot-2 research microscope, equipped with a 20 × and a 60 × objective. Images were captured with a Spot CCD colour video camera; model RT Slider (Diagnostic Instruments, Sterling Heights, MI, USA). The resultant 8-bit monochrome image contained a greyscale of pixel intensities from 0 to 255, with 0 representing white and 255 representing black. Intensity analysis of immunoreactivity was performed in eight coronal sections throughout the rostrocaudal dimension of each nucleus. Optical density of HCN1-IR was measured by manually outline the staining surrounding cells using ImagePro Plus software (Media Cybernetics Inc.).

Data analysis

Results are presented as mean ± standard error of the mean (s.e.m.). Statistical calculations were preformed using Student's t tests, comparing samples with equal variance, or a single-factor ANOVA test, and significance (*) was noted if P < 0.05 and (**) for P < 0.01 (two-tailed), unless otherwise mentioned in the text.

Results

Whole-cell patch-clamp recordings were made from visualized neurons in the AVCN, MNTB and LSO in CBA mice age 12–14 days postnatal. Bushy cells in the AVCN were identified by their appearance under the microscope and onset-firing pattern in response to depolarizing current injections, and confirmed morphologically using a fluorescent dye in the internal solution (Alexa 488). Passive membrane properties of cells were measured before and after block of the hyperpolarization-activated channels with ZD7288, and are shown in Table 1. To gain additional insight into the consequences of different kinetics and amplitudes of I_h we have subsequently used the measured parameters of I_h in different combinations and applied them using the dynamic clamp to AVCN, MNTB and LSO cell types.

Table 1.

Passive membrane properties of auditory neurons before and after ZD7288

	AVCN	MNTB	LSO
Resting potential (mV)	−57.1 ± 0.8	−62.6 ± 0.8	−56.5 ± 0.6
+ ZD7288	−59.6 ± 2.9	−63.2 ± 0.7	−66.1 ± 3.3
Input resistance (MΩ)	120.8 ± 6.3	228.2 ± 14.0	70.1 ± 5.3
+ ZD7288	170.6 ± 15.6	257.2 ± 18.5	111.4 ± 13.0
Capacitance (pF)	22.3 ± 1.1	24.1 ± 1.1	22.2 ± 1.2
Control (n)	23	7	30
+ ZD7288 (n)	9	7	6

Neurons in the AVCN, MNTB and LSO differ in their I_h expression

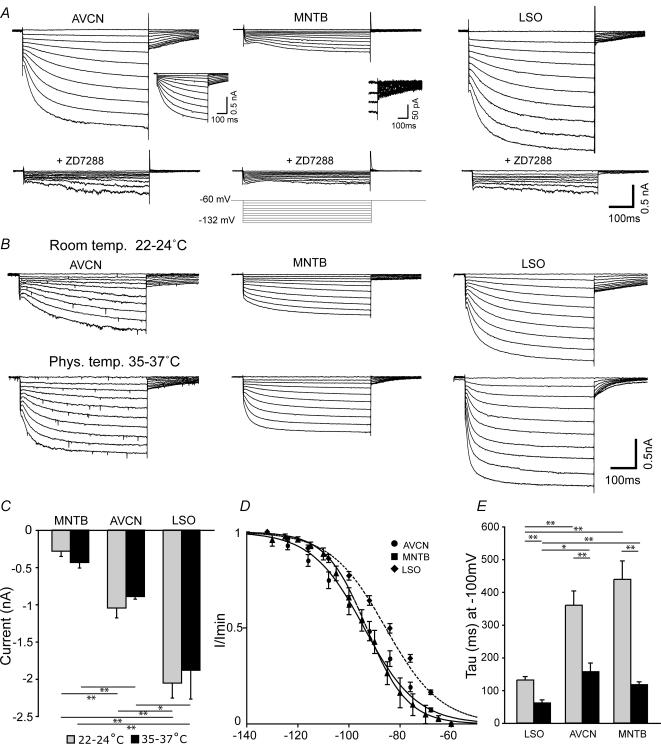
Activation of I_h was examined by injecting negative voltage steps (−60 to −132 mV, 8 mV increments) for 500 ms. I_h amplitudes were measured as the peak current amplitude subtracted by the peak current response following bath application of 20 μm ZD7288 (Fig. 1A and C). Longer voltage steps (1 or 3 s) did not significantly increase I_h amplitudes (data not shown), although these longer voltage steps were not used routinely because they caused electrophysiological recording instability. Both the amplitude and kinetics of I_h were quite variable in the AVCN, as emphasized by the inset in Fig. 1A which shows a second example trace with slower kinetics.

Figure 1. Neurons in the AVCN, MNTB and LSO exhibit diverse I_h expression.

A, upper panel shows example current traces from an AVCN bushy cell, a MNTB principal cell and a LSO principal cell. The cells represent the whole-cell current activated by negative voltage steps (10 steps from −60 to −132 mV in 8 mV increments, during 500 ms, see lower inset). Lower panel shows current traces from the same cells as above after application of 20 μm ZD7288 (same voltage steps as above) (scale bars: 0.5 nA, 100 ms, room temperature). The capacitance artefacts have been subtracted from the beginning of traces. Inset left: current trace showing an example with slower kinetics for an AVCN cell (scale bars: 0.5 nA, 100 ms). Inset centre: tail currents of the MNTB cells on a magnified scale (scale bars: 50 pA, 100 ms) B, upper panel show example current traces from an AVCN bushy cell, a MNTB principal cell and a LSO principal cell recorded in room temperature (22–24°C) after application of negative voltage steps (10 steps from −60 to −132 mV, during 500 ms). Lower panel shows current traces from the same cells, using the same voltage steps as above, after the bath temperature was heated to physiological temperature (35–37°C). The capacitance artefacts have been subtracted from the beginning of traces. (scale bars: 0.2 nA, 100 ms). C, summary of the ZD7288-sensitive I_h amplitude in room temperature (RT, grey bars) and physiological temperature (PT, black bars) (current activated by negative voltage steps subtracted by the current recorded after application of ZD7288, in response to a negative voltage step at −132 mV, 500 ms) in bushy cells of the AVCN (RT, n = 7; PT, n = 4) and principal neurons of the MNTB (RT, n = 12; PT, n = 3) and LSO (RT, n = 21; PT, n = 4). Error bars represent s.e.m. with P < 0.01 (**) or P < 0.05 (*). D, AVCN (•, line, n = 17), MNTB (▴, line, n = 13) and LSO (♦, dashed line, n = 17) tail currents were fitted to a Boltzmann equation to yield the I_h voltage dependency. Error bars show s.e.m.E, summary of the activation time constant (tau) at −100 mV, when a single exponential function fitted well to all the cells current response at room temperature (RT, grey bars) and physiological temperature (PT, black bars), of bushy cells of the AVCN (RT, n = 9; PT, n = 4) and principal neurons of the MNTB (RT, n = 12; PT, n = 3) and the LSO (RT, n = 15; PT, n = 4). Error bars show s.e.m., P < 0.01 (**) or P < 0.05 (*).

The ZD7288-sensitive current amplitudes activated by negative voltage steps (−60 to −132 mV) were 1.05 ± 0.13 nA in AVCN cells (n = 7), 0.28 ± 0.07 nA in MNTB cells (n = 12) and 2.06 ± 0.20 nA for LSO cells (n = 21) and were significantly different (P < 0.01, ANOVA). Since LSO principal cells can be single firing (SF, cells that fire single action potentials in response to sustained current injections) and multiple firing (MF, cells that fire multiple action potentials in response to sustained current injections) we compared I_h in single and multiple firing LSO neurons. There was no significant difference in ZD7288-sensitive current between SF cells (−1.98 ± 0.26 nA, n = 9) and MF cells (−2.17 ± 0.39 nA, n = 9) in response to negative voltage steps (−60 to −132 mV), in agreement with Barnes-Davies et al. (2004). Heating the slice chamber to 35–37°C gave a ZD7288-sensitive current of 0.89 ± 0.03 nA for AVCN bushy cells (n = 4), 0.43 ± 0.07 nA for MNTB cells (n = 3) and 1.88 ± 0.39 nA for LSO cells (n = 4). There was no difference in maximal I_h amplitude at room temperature and physiological recording temperature.

Tail currents elicited by the voltage protocol shown previously (−60 to −132 mV) in AVCN bushy cells (n = 17), MNTB principal cells (n = 9) and LSO principal cells (n = 17) were analysed by fitting a Boltzmann function (I/I_min = [1 + exp (V_1/2 − V)/k]⁻¹, where V_1/2 is the half-activation voltage and k is the slope factor) to the normalized current versus voltage relationships. There was a significant difference in V_1/2 (P = 0.002) between AVCN (V_1/2 = −94.0 ± 2.2 mV) and LSO cells (V_1/2 = −85.6 ± 1.2 mV), as well as a significant difference (P = 0.003) between LSO and MNTB cells (V_1/2 = −93.0 ± 2.2 mV). There was no difference in V_1/2 between AVCN and MNTB cells. Instead, the slope factor was different between AVCN (k = 10.3 ± 0.5) and MNTB (k = 8.0 ± 0.4) neurons (P = 0.01), and between MNTB and LSO (k = 10.8 ± 0.4) cells (P = 0.0001) (Fig. 1D).

The activation time constant (τ) was measured by fitting a single exponential function to the currents produced by hyperpolarizing voltage steps. At room temperature, the fit of a single exponential equation to the current trace after a −100 mV voltage step gave a τ for AVCN bushy cells of 360 ± 43.5 ms (n = 9), τ = 438.6 ± 56.3 ms for MNTB principal cells (n = 12) and τ = 131.1 ± 10.8 ms for LSO principal cells (n = 15) (Fig. 1E). These values were significantly different between AVCN, MNTB and LSO cells (P < 0.0001, ANOVA). At voltages to −100 mV, single exponential functions provided good fits to the currents in the three nuclei. In AVCN and LSO cells, τ was better fitted by double exponentials for more hyperpolarized potentials (< −100 mV). However, for comparisons between the three nuclei, we used data in which τ was fitted with single exponentials. Tau values were also significantly different between the nuclei at physiological temperature (P = 0.016, ANOVA). Tau decreased to 156.5 ± 26.7 ms for AVCN bushy cells (n = 4), 117.2 ± 8.5 ms for MNTB cells (n = 3) and 61.2 ± 9.6 ms for LSO cells (n = 4) after a single exponential fit, although a double exponential fit was better for LSO traces at physiological temperature at −100 mV (τ_fast = 22.2 ± 3.7 ms and τ_slow = 168.2 ± 38.5 ms). All cells had significantly smaller tau values at 35–37°C compared with at room temperature (P < 0.01 for all, see Fig. 1E).

HCN channel subunits are differently expressed in the three nuclei

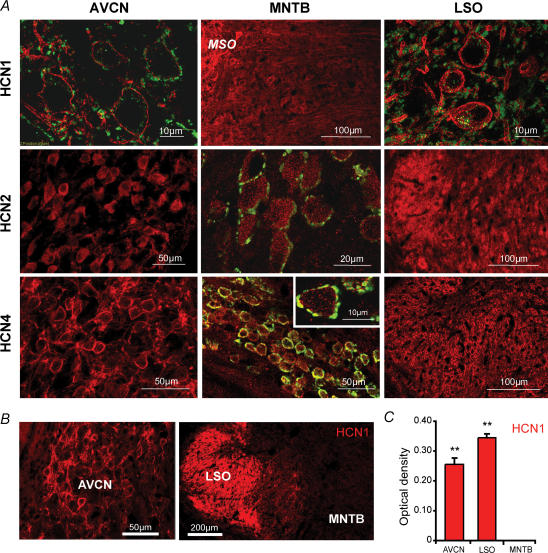
Immunohistochemistry using polyclonal antibodies against HCN1, HCN2 and HCN4 subunits revealed differential expression of these channels across the three brainstem nuclei (Fig. 2). Neuronal cell bodies in the LSO and AVCN exhibit strong membrane expression of HCN1 protein, whereas MNTB neurons express HCN1 at low levels. In the AVCN, membrane labelling appeared to be primarily in postsynaptic membranes of bushy cells, including some proximal processes. Most of the HCN1 labelling in the MNTB was co-localized with anti-VGlut1 labelling, which is a marker for glutamatergic presynaptic terminals, thus suggesting a presynaptic localization in calyceal terminals. HCN1 was highly expressed in LSO principal cells, with very strong somatic and dendritic membrane labelling. In the AVCN and LSO, the dense cell surface labelling was composed of fine, uniformly distributed punctae seen by high magnification (Fig. 2A, top row).

Figure 2. Composition of HCN family proteins in the AVCN, MNTB and LSO.

A, all red staining represents anti HCN1, -2 or -4 labelling (see row label for subunit). Green labelling, shown in high magnification images and MNTB nucleus outline, represents presynaptic terminals as stained with anti-vesicular glutamate transporter 1 (VGlut1). The HCN1 antibody showed strong membrane labelling of somata and processes in the AVCN and the LSO but only weak staining was observed in the MNTB (by comparison, some HCN1 staining of the MSO can be seen to the left of the MNTB). The HCN2 antibody labelled all nuclei diffusely, with some somatic and some surface labelling in the AVCN. The MNTB showed the highest levels of HCN2 expression of the three nuclei. The HCN4 antibody labelled membranes of neurons in the AVCN and LSO nicely. The MNTB also expressed some HCN4 labelling that was co-localized with VGlut1, showing a probable presynaptic labelling (see inset). B, fluorescent images of brainstem slices shows strong anti-HCN1 labelling (red) in the LSO, while the AVCN (magnification of the dorsal part) have robust staining compared with the MNTB showing very weak immunoreactivity (scale bars: 50 μm (left panel), 200 μm (right panel). C, optical density measurements of HCN1 immunoreactivity within neurons in the AVCN, LSO and MNTB. Significance (**) represents P < 0.01, paired Student's t test, error bars represent s.d.

AVCN cells displayed moderate cytoplasmic HCN2 staining with apparently little membrane labelling. There was also some indication of presynaptic HCN2 labelling in the AVCN. The MNTB showed moderate HCN2 labelling in the cytoplasm of principal neurons, and there was no evidence of presynaptic HCN2 staining in MNTB sections. LSO cells displayed a widespread but diffuse staining of HCN2 (Fig. 2A, middle row).

AVCN cells showed a significant expression of HCN4 in bushy cell surface membranes. The MNTB exhibits a tonotopic gradient of postsynaptic HCN4 expression in principal neurons, with higher HCN4 labelling in medial versus lateral regions (Leao et al. 2006); there appears to be minimal presynaptic expression of HCN4 in the MNTB. The LSO showed weak HCN4 expression in the membrane, although not in every cell (Fig. 2A, bottom row). A noticeable difference in strength of HCN1 expression was seen between the AVCN, LSO and MNTB nuclei (Fig. 2B). The mean optical density of immunoreactivity against HCN1 was significantly different (P < 0.01) between nuclei in the AVCN (0.255 ± 0.023), LSO (0.344 ± 0.013) and the MNTB, where staining was too weak to identify cell boundaries (Fig. 2C; Student's paired t test, errors represent standard deviation (s.d.)).

I_h modulates voltage responses to current injection

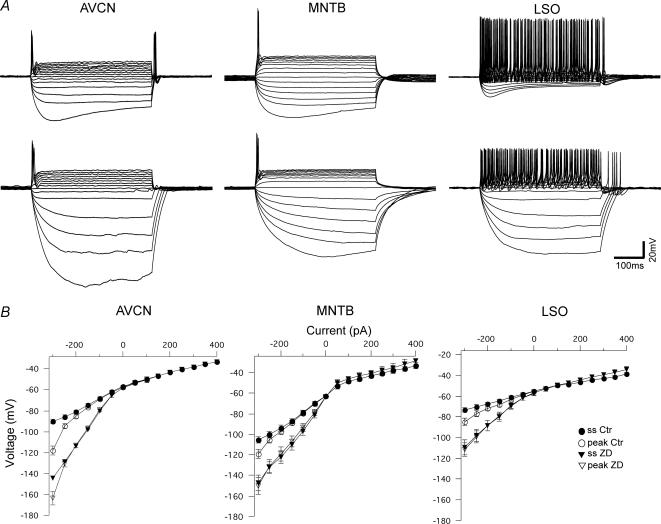
AVCN, MNTB and single firing LSO neurons responded to depolarizing current steps (50–400 pA, in 50 pA increments, 200 ms), with usually one or two action potentials (APs). The LSO principal cells also have a population of multiple firing neurons, probably due to a lower expression of low-threshold K⁺ currents (Barnes-Davies et al. 2004). Application of hyperpolarizing current steps (−50 to −300 pA, in 50 pA increments, 200 ms) caused a depolarizing sag (indicative of I_h activation) in neurons in all three nuclei (Fig. 3A). AVCN bushy cells showed prominent sags that slowly depolarized the membrane potential during hyperpolarization (Fig. 3A). MNTB principal cells usually showed weak depolarizing sags, also with slow depolarizations (Fig. 3A). Interestingly, LSO principal cells showed a small sag, quickly followed by depolarization (Fig. 3A). The negative peak voltage of the sag after negative current steps (−300 pA) was −118.3 ± 4.3 mV for AVCN (n = 18), −119.0 ± 4.3 mV for MNTB (n = 7) and −85.1 ± 3.9 mV for LSO cells (n = 26). Application of 20 μm ZD7288 decreased resting membrane potentials (see Table 1) and abolished depolarizing sags in all cell types (negative peak voltage after ZD7288 in AVCN: −163.6 ± 6.4 mV (n = 6), MNTB: −150.1 ± 8.3 mV (n = 7) and LSO: −111.3 ± 6.7 mV (n = 6)). Post-hyperpolarization action potentials (rebound APs) were also eliminated by ZD7288 (see AVCN traces in Fig. 3). However, in some cases when the hyperpolarizing currents caused the membrane voltage to descend below −150 mV (producing very unstable recordings) some multi-firing LSO cells showed action potentials after the termination of the negative current step (see LSO traces in Fig. 3A).

Figure 3. Voltage responses to depolarizing and hyperpolarizing 200 ms current step injections (−300 to +400 pA) of neurons in the AVCN, MNTB and LSO.

A, example of an onset response by an AVCN bushy cell (left), a MNTB principal neuron (middle) and a multiple firing LSO principal cell (right) before (upper panel) and after blocking of I_h with ZD7288 (lower panel). Scale bars: 100 ms and 20 mV. B, voltage–current relationships of the three neuron types measured at negative peak (peak Ctr, ^) and at the steady state (ss Ctr, •) of the voltage deflection under normal recording conditions and after application of ZD7288 (peak ZD, ◊, and ss ZD ▾). AVCN cells (n = 18) showed a wide sag and rebound action potential that was abolished by ZD7288. MNTB cells (n = 7) showed a small, wide sag and no rebound action potential. LSO cells (n = 26) showed a small, fast depolarizing sag and rebound spikes.

Current–voltage (I–V) relationships were also examined for the three cell types (Fig. 3B) by measuring peak voltages (measured at the most negative voltages) and steady-state currents (measured over the last 5 ms of the current step). All three brainstem neurons showed a flat but linear I–V relationship between depolarizing current injections (50–400 pA) and steady-state voltage, which did not change after application of ZD7288. MNTB and LSO cells showed a slight increase in voltage at positive current steps after blocking I_h. Voltage responses to negative current injections (−300 pA) showed a diversity in subtracted voltage (negative peak minus steady-state voltage) of 27.9 ± 3.5 mV, 13.3 ± 2.6 mV and 11.4 ± 2.4 mV for AVCN (n = 18), MNTB (n = 7) and LSO (n = 26) neurons (P < 0.001, ANOVA: single factor), respectively, that was not seen after ZD7288 application.

Effect of I_h on resting membrane potential and action potentials in AVCN, MNTB and LSO neurons

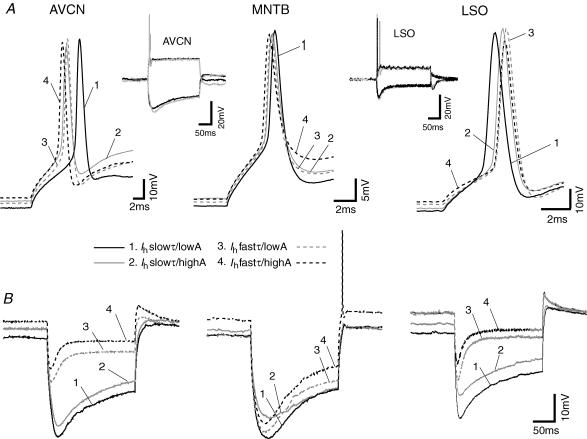
Using the dynamic clamp, we first altered I_h characteristics of AVCN, MNTB and LSO cells in order to assess the effect of I_h amplitude and kinetics on resting membrane potential. In order to assess whether I_h could be simulated by our dynamic clamp we compared control conditions before application of ZD7288 with the appropriate dynamic clamp simulation (I_h slowτ/lowA for AVCN and MNTB cells and I_h fastτ/highA for LSO cells – with maximal I_h conductance of 15 ± 1, 7 ± 1 and 30 ± 2 nS, for AVCN, MNTB and LSO, respectively). If a similar membrane potential was reached after I_h was blocked pharmacologically and subsequently reintroduced as the simulated I_h, the cell was accepted for further dynamic clamp experiments in which I_h was altered.

The resting membrane potential of AVCN bushy cells (n = 4) in control conditions, before application of ZD7288, was −58.8 ± 1.7 mV and after blocking I_h was −65.4 ± 5.0 mV. After reintroduction of an I_h appropriate for AVCN bushy cells (I_h slow τ/lowA) the membrane potential returned to −60.4 ± 0.4 mV. Increasing I_h amplitude (I_h slow τ/highA) caused the cell to depolarize approximately 1 mV (to −57.7 ± 1.7 mV, P = 0.04, paired t test). Adding a fast I_h to the membrane caused further depolarization (to −56.1 ± 1.7 mV for I_h fastτ/lowA and −53.7 ± 1.4 mV for I_h fastτ/highA, P < 0.01 for both cases, paired t test). In MNTB principal neurons (n = 4), altering only I_h amplitude (I_h slowτ/highA) caused the cell membrane to depolarize by 3 mV (from −65.3 ± 0.8 to −61.7 ± 0.2 mV, P = 0.01, paired t test). Addition of fast I_h also caused a significant change in cell membrane resting potential (to −63.5 ± 0.6 mV, I_h fastτ/lowA, P = 0.02, and to −61.4 ± 0.5 mV, I_h fastτ/highA, P < 0.01, paired t test). In LSO neurons (SF, n = 5), simulating I_h with different kinetics and amplitude dramatically altered the resting potential of the cells (from −61.3 ± 0.8 to −65.7 ± 0.4 mV, −64.6 ± 0.5 mV and −67.1 ± 0.2 mV for I_h slowτ/highA, I_h fastτ/lowA and I_h slowτ/lowA, respectively; P < 0.01 for all cases, n = 5; paired t test).

Action potential properties (amplitude and half-width) were also differently affected by changes in I_h in different nuclei. Using a 200 pA current step, control AP amplitude in AVCN cells was equal to 62.8 ± 5.3 mV and did not change significantly by altering I_h amplitude (I_h slowτ/highA). Changes in I_h kinetics significantly decreased the AP amplitude (58.7 ± 5.4 mV for I_h fastτ/lowA and 57.5 ± 5.9 mV for I_h fastτ/highA, P = 0.01 in both cases, n = 4, paired t test; Fig. 4A). AP amplitude in MNTB neurons was only affected by differences in I_h amplitude (control: 61.5 ± 4.1 mV; I_h slowτ/highA: 60.2 ± 3.9 mV; I_h fastτ/highA: 56.2 ± 3.1 mV; P = 0.03 and 0.01, respectively, n = 5, paired t test; Fig. 4A). In LSO neurons, ‘slowing’ I_h increased AP amplitude (control: 91.4 ± 5.7 mV; I_h slowτ/highA: 96.5 ± 3.4 mV; I_h slowτ/lowA: 99.8 ± 4.2 mV; P = 0.02 and 0.04, respectively, n = 5, paired t test; Fig. 4A). Action potential half-width in AVCN bushy cells was also affected by changes in I_h amplitude and kinetics (control: 1.30 ± 0.05 ms; I_h slowτ/highA: 1.13 ± 0.02 ms; I_h fastτ/lowA: 1.18 ± 0.01 ms; I_h fastτ/highA: 1.16 ± 0.02 ms; P < 0.01, P = 0.04, P = 0.03, respectively, n = 4, paired t test). In MNTB and LSO neurons, AP half-width was not affected by changes in I_h properties.

Figure 4. I_h differently affect membrane properties and AP characteristics in AVCN and SOC neurons.

A. examples of APs in response to a 200 pA current step using different I_h amplitudes and kinetics simulated by dynamic clamp in an AVCN bushy cell, a MNTB principal neuron and a LSO principal neuron. The continuous black traces show the neuron response with a slow τ and low-amplitude I_h (I_h slowτ/lowA is the control condition for AVCN bushy cells and MNTB neurons); continuous grey traces show the cell response when a slow τ and high-amplitude I_h was simulated (I_h slowτ/highA); dashed black traces represent cell responses to depolarizing current step when a fastτ and high-amplitude I_h was added to the membrane (I_h fastτ/highA is the control condition for LSO neurons) and the dashed grey trace show the cell response to a simulated fastτ and low-amplitude I_h (I_h fastτ/lowA). Insets, left, AVCN neuron response to a 200 pA and a −300 pA current step under control conditions (black traces) and with a simulated control conditions (I_h slowτ/lowA, grey traces); right, LSO neuron response to a 200 pA and a −300 pA current step under control conditions (black traces) and with a simulated control condition (I_h fastτ/highA, grey traces). B, AVCN, MNTB and LSO neuron responses to a −300 pA current step with different I_h properties as in A (all 3 panels have the same scale).

I_h is known to contribute to AP delay (time between 5% maximum AP amplitude and peak) in MNTB cells (Leao et al. 2005a); we thus investigated the effect of different I_h properties on AP delay. In AVCN bushy cells, neither I_h amplitude nor kinetics altered AP delay (for 200 pA current steps; Fig. 4A). MNTB neurons were as expected affected by changes in I_h (control: 3.1 ± 0.1 ms; I_h slowτ/highA: 2.7 ± 0.2 ms, P = 0.01; I_h fastτ/lowA: 2.6 ± 0.3 ms, P = 0.03; I_h fastτ/highA: 2.5 ± 0.2 ms, P < 0.01; n = 4, paired t test; Fig. 4A). Action potential delay in LSO neurons was not consistently altered by changing I_h properties (Fig. 4A).

We did not find action potentials to be delayed in the AVCN and the LSO due solely to alterations in I_h as previously reported for the MNTB (Leao et al. 2005a).

Rebound depolarizations

Hyperpolarizing current steps elicited rebound depolarizations in all three nuclei (Fig. 4B). Under control conditions, a −300 pA current step produced an average depolarization of 4.3 ± 0.9 mV in AVCN cells at the end of the step (Fig. 4B). Increasing the speed of I_h kinetics, with a V_1/2 10 mV more depolarized, increased the post-step depolarization (I_h fastτ/lowA: 5.4 ± 2.2 mV, P = 0.05; I_h fastτ/highA: 7.0 ± 0.8 mV, P < 0.01; n = 4, paired t test; Fig. 4B). These differences were more dramatic in MNTB cells; altering both I_h amplitude and kinetics caused significant increases in rebound depolarization, and addition of I_h fastτ/highA (Fig. 4B) triggered post-step APs (control: 3.8 ± 0.5 mV; I_h slowτ/highA: 6.3 ± 0.3 mV, P = 0.01; I_h fastτ/lowA: 7.7 ± 0.7 mV, P ≤ 0.01; n = 4, paired t test; Fig. 4B). Interestingly, I_h properties did not seem to affect rebound amplitude in LSO cells except when I_h slowτ/lowA was added to the membrane (control: 6.2 ± 0.2 mV versus I_h slowτ/lowA: 6.9 ± 0.2 mV; P < 0.01, n = 5, paired t test; Fig. 4B). This larger depolarization was probably due to the decreased resting membrane potential, causing the relative increase after hyperpolarization potential. If consideration was taken as to whether the LSO cell was multiple or single firing, changes in I_h properties similarly affected resting membrane potential and AP characteristics in MF and SF LSO cells. However, rebound depolarizations in MF cells were able to trigger APs (see following subsections). The dynamic clamp data are summarized in Table 2.

Table 2.

Effect of I_h on resting membrane potential, action potentials and rebound depolarization in the AVCN, MNTB and LSO

Vrest (mV)	AVCN	MNTB	LSO
Slowτ/lowA	−58.8 ± 1.7	−65.3 ± 0.8	−67.1 ± 0.2‡
Slowτ/highA	−57.7 ± 1.7†	−61.7 ± 0.2†	−65.7 ± 0.4‡
Fastτ/lowA	−56.1 ± 1.7‡	−63.5 ± 0.6‡	−64.6 ± 0.5‡
Fastτ/highA	−53.7 ± 1.4‡	−61.4 ± 0.5‡	−61.3 ± 0.8
AP amplitude (mV)
Slowτ/lowA	62.8 ± 5.3	61.5 ± 4.1	99.8 ± 4.2†
Slowτ/highA	62.5 ± 5.5	60.3 ± 4.0†	96.5 ± 3.4†
Fastτ/lowA	58.7 ± 5.5†	57.8 ± 2.9	91.2 ± 3.7
Fastτ/highA	57.5 ± 5.9†	56.3 ± 3.1†	91.4 ± 4.4
AP half-width (ms)
Slowτ/lowA	1.33 ± 0.04	1.05 ± 0.09	0.70 ± 0.06
Slowτ/highA	1.14 ± 0.02‡	1.20 ± 0.12	0.67 ± 0.07
Fastτ/lowA	1.17 ± 0.02†	1.21 ± 0.12	0.64 ± 0.07
Fastτ/highA	1.16 ± 0.01†	1.13 ± 0.10	0.59 ± 0.04
AP delay (ms)
Slowτ/lowA	5.5 ± 0.4	3.1 ± 0.1	3.1 ± 0.3
Slowτ/highA	4.6 ± 0.3	2.7 ± 0.2†	3.3 ± 0.5
Fastτ/lowA	4.6 ± 0.3	2.6 ± 0.3†	3.0 ± 0.1
Fastτ/highA	4.5 ± 0.3	2.5 ± 0.2‡	3.4 ± 0.2
Rebound dep (mV)
Slowτ/lowA	4.3 ± 0.9	3.8 ± 0.5	6.9 ± 0.2‡
Slowτ/highA	5.4 ± 2.2	6.3 ± 0.3†	7.0 ± 0.9
Fastτ/lowA	5.5 ± 1.3	7.7 ± 0.7‡	6.7 ± 0.2
Fastτ/highA	7.0 ± 0.8‡	NA	6.2 ± 0.2

Presented as mean ± S.E.M. Emboldened numbers represent control conditions. Significant difference from control condition

^†P < 0.05

^‡P < 0.01, Student's paired t test. Rebound dep, rebound depolarisations. NA, not available.

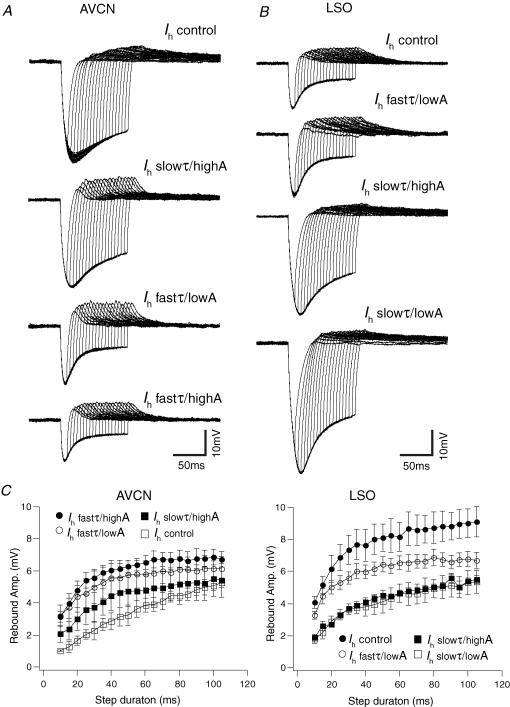
We did not observe any rebound APs in MNTB cells in a previous study (Leao et al. 2005), and I_h is unlikely to generate rebound APs in MNTB neurons under normal conditions. Therefore we further investigated the relationship between I_h properties and rebound depolarization in AVCN bushy cells and LSO principal neurons. In order to investigate the relationship between hyperpolarization duration, rebound depolarization amplitude, I_h properties and rebound firing, current steps (−300 pA) of various durations (10–110 ms, 5 ms steps; Koch & Grothe, 2003) were injected into AVCN and LSO cells as well as dynamic clamp I_h. AVCN neurons displayed a linear relationship between current-step duration and rebound depolarization under control conditions. In terms of depolarization amplitude, AVCN bushy cells did not show any difference between I_h control and slowτ/highA for any time step (Fig. 5A and C). Addition of a fast I_h, however, significantly increased rebound depolarization following steps from 45 to 55 ms for I_h fastτ/lowA (n = 4, P = 0.04 for all points) and after steps from 10 to 70 ms for I_h fastτ/highA (n = 4, P < 0.01 for all points). Also, under control conditions, the relationship between hyperpolarization step duration and depolarization potential could be well fitted with a linear function (e.g. y = ax+ b) while logarithmic functions (e.g. y = a log(x) + b) were more suited to fit this relationship if I_h amplitude was increased or its kinetics were changed (the goodness of fit was assessed by the magnitude of the residuals; data not shown).

Figure 5. Rebound depolarization shows different dependency on I_h in AVCN and LSO cells.

A, example of an AVCN bushy cell response to −300 pA hyperpolarizing current steps of various durations (10–105 ms, 5 ms increments) after different I_h properties had been applied by dynamic clamp to the same neuron. B, example of a SF LSO neuron voltage response to hyperpolarizing current steps (same as in A) with different I_h properties. C, summary of current step (−300 pA) duration versus rebound depolarization amplitude relationships for AVCN bushy cells and LSO principal neurons (data presented as mean ± s.e.m.) after different I_h properties had been applied by dynamic clamp.

Different I_h properties caused greater changes in the dependency of rebound depolarization on the hyperpolarizing current step duration in SF LSO cells (Fig. 5B and C). In general, rebound depolarizations were larger under control conditions (P < 0.05, when compared with I_h slowτ/lowA and I_h slowτ/highA for all steps, n = 5) except when compared with I_h fastτ /lowA (Fig. 5B and C). In contrast to AVCN neurons, all the hyperpolarizing step duration versus rebound amplitude relationships were better fitted with a logarithmic function. These results show that I_h fastτ/highA produces the largest rebound depolarization in AVCN cells and fastτ/lowA produce the largest depolarizations in LSO neurons, compared with control conditions.

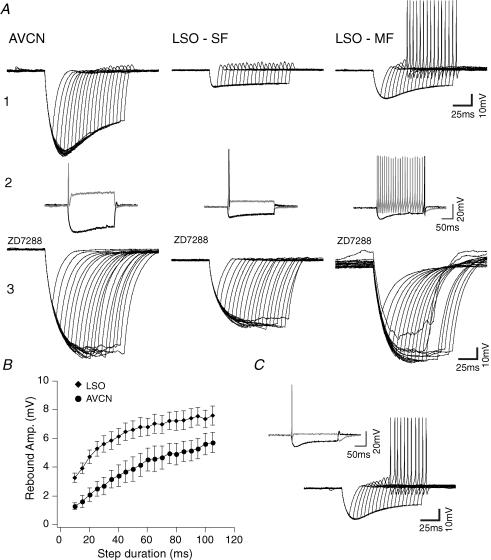
Rebound APs in response to hyperpolarizing current steps were observed in 29% of AVCN cells (n = 21) and in 35% of LSO cells (n = 20). Most of the LSO cells that fired rebound APs were MF cells (6 of 7 cells versus 1 of 13 SF cells). Rebound APs were eliminated by the addition of ZD7288 (Fig. 6A). Hyperpolarization durations necessary for rebound AP firing were significantly longer in AVCN cells when compared with LSO cells (58 ± 15 ms versus 26 ± 10 ms, P = 0.04, n = 10). AVCN bushy cells were invariably SF therefore the amount of I_LT was measured by applying depolarizing voltage steps. After a voltage step to −40 mV there was a significant difference (P < 0.05) in outward current between AVCN bushy cells that fired rebound action potentials (235 ± 16 pA, n = 21) compared with AVCN bushy cells that did not fire rebound action potentials (340 ± 33 pA, n = 21). Non-rebound spiking AVCN bushy cells also showed smaller rebound depolarizations when compared with non-rebound spiking LSO cells (for 55 ms long hyperpolarization: 4 ± 1 mV for AVCN cells versus 7 ± 1 mV for LSO cells, P = 0.01, n = 22; Fig. 6B). We also artificially injected I_LT using a dynamic clamp in four MF LSO cells in order to assess the effect of these currents on rebound spiking. Dynamic clamp K⁺ currents caused MF LSO cells to fire single spikes in response to depolarizing current steps and abolished rebound APs after −250 pA current steps (Fig. 6C, inset). However, these neurons still fired rebound APs after −300 pA current steps, but the hyperpolarization duration necessary for AP firing increased significantly (from 28 ± 18 to 62 ± 17 ms, P = 0.04, n = 4; Fig. 6C). We found that rebound depolarization magnitude depends jointly on I_h and I_LT, as these two currents appear to balance each other (I_h promoting rebound depolarization after hyperpolarizations and I_LT impeding rebound depolarizations to cause AP firing).

Figure 6. Rebound AP is dependent on I_h and low-threshold K⁺ current.

A1, example traces from an AVCN bushy cell, a LSO single-firing (SF) principal neuron and a LSO multiple-firing (MF) principal neuron after hyperpolarizing current injections of various durations (−300 pA, 10–105 ms, 5 ms increments). A2, AVCN, LSO SF and LSO MF membrane voltage response to a 200 pA and −300 pA current injection. A3, membrane voltage to different duration hyperpolarizing currents (as shown in A1) after addition of ZD7288. B, comparison of depolarization amplitudes after −300 pA current steps of different durations between non-rebound spiking AVCN and LSO cells (data presented as means ± s.e.m.). C, LSO MF cell (same as in A) response to the current protocol used in A after a low-threshold K⁺ current was artificially injected using dynamic clamp. Inset, LSO MF neuron (A2) voltage response to a 200 pA and −300 pA current injection after the addition of a simulated low-threshold K⁺ current.

Discussion

Our results show that the expression of the hyperpolarization-activated cation current, I_h, differs significantly between auditory brainstem nuclei. The magnitude of I_h is greater in LSO principal cells than AVCN bushy cells, which in turn exhibit an I_h significantly larger than in MNTB principal cells. The activation curve for I_h shows that the AVCN and MNTB cells have similar half-activation voltage, that is about −10 mV shifted towards hyperpolarized potentials compared with LSO principal cells. The activation kinetics of the LSO principal neurons were also significantly different to AVCN and the MNTB neurons. The activation kinetics of AVCN bushy cells were not significantly different to MNTB cells.

AVCN, MNTB and LSO cells express different combinations of HCN subunits

Neurons in the AVCN and SOC express more than one HCN channel subtype in combination. This HCN subunit composition, examined in the AVCN and the SOC using immunohistochemistry, agrees with our electrophysiological data measured in these nuclei. The slowly activating I_h in AVCN bushy cells is likely to be due to the expression of HCN4 channels, known to have slow kinetics. AVCN cells were also intensely labelled by anti-HCN1 antibodies, suggesting that HCN1 and HCN4 together account for the substantial I_h expressed by these cells. The observed variability in both amplitude and kinetics of I_h between AVCN neurons may therefore be due to differences in the proportion of HCN1 and HCN4 channels expressed in different neurons. MNTB cells appear to mostly express the slowly activating HCN2 and HCN4 channels, which may be reflected by the wide sag in response to negative current injections (Fig. 3). LSO cells strongly express HCN1 channels, in accordance with the fast activating I_h seen in these cells. This is in agreement with studies in rat displaying a strong labelling of HCN1 channels in LSO and AVCN and weak HCN1 staining in the MNTB, which instead had the strongest HCN2 staining of these three nuclei (Koch et al. 2004). Despite the fact that HCN1 is strongly expressed in both AVCN and LSO, I_h is substantially larger and faster in the latter. These differences might be related to heteromization of HCN channels. It has been shown elsewhere that I_h channel isoforms can exist as both homomers and heteromers (Moosmang et al. 1999; Santoro et al. 2000). Heteromers of the HCN1–HCN2 have been identified in mouse brain, indicating that heteromeric channels exist in vivo (Much et al. 2003). Some cells, such as basket and stellate cells of the cerebellum, exclusively express HCN1 but not HCN2, suggesting that HCN channels preferentially form homomeric complexes (Moosmang et al. 1999). Therefore, it is possible that HCN1 homomers are more ‘common’ in LSO neurons than AVCN bushy cells. Heteromeric HCN1–HCN4 channels have been studied in the rabbit heart, where neither HCN1 channel nor HCN4 channel activation could account for the native current seen in sino-atrial node cells alone, but a heteromeric expression of the two fitted activation kinetics and cAMP sensitivity (Altomare et al. 2003). This expression pattern might be applicable to AVCN bushy cells, accounting for an I_h magnitude that is between that of the largely HCN1-expressing LSO cells and the HCN4- and HCN2-expressing MNTB principal cells. This gradient of I_h magnitude was retained after heating the recording chamber to physiological temperature.

I_h kinetics are sensitive to temperature, with significantly decreased activation time constants for all cell types at physiological temperature compared with room temperature. Surprisingly, MNTB cells displayed faster I_h activation than the AVCN bushy cells in response to a −100 mV voltage step at 33–37°C. This could imply that the HCN4 channel subtype is more sensitive to temperature than the HCN1 channel, since the AVCN displays strong expression of both channel types. The activation constant for LSO cells was about twice as fast at physiological temperatures, compared with MNTB cells which displayed kinetics close to four times as fast.

In addition to different kinetics, there may also be differences in the modulation of I_h. I_h can be regulated by cAMP, which in its turn can be modified by neurotransmitters such as dopamine and adrenalin (Shepherd, 1994). However, this modulation is stronger in HCN2 and -4 subunits than for the HCN1 subunit. Our results demonstrate that HCN1 channels are the major carriers of I_h in LSO cells but not in the MNTB and AVCN, and therefore, catecholaminergic inputs could tonically alter the resting characteristics of MNTB (see Banks et al. 1993) and AVCN neurons but have little effect on LSO cells. Conversely, I_h in LSO neurons can be more ‘easily’ modulated by neural activity (e.g. APs and IPSPs) than I_h in AVCN and MNTB, as the kinetics of HCN1 are faster than the other subunits. This means that short bursts of APs are more likely to deactivate (and for IPSPs bursts, activate) I_h in the LSO than in the MNTB and AVCN.

Previous studies have shown that altered expression of single HCN channel subunits may have significant functional consequences. For example, knock-out of HCN1 in CA1 pyramidal neurons enhances performance of learning and memory tasks in mice (Nolan et al. 2004). It was proposed by Santoro & Baram (2003) that neuronal networks may regulate activity by up-regulating either the slow activating channels or the fast acting HCN1 channel. Slow kinetics of I_h has previously been suggested as a mechanism underlying neuronal tuning for sound duration (Casseday, 1994; Hooper, 2002). A recent study by Proenza & Yellen (2006) also focuses on distinct population of voltage-independent HCN channels. These channels could contribute to the instantaneous currents seen in current traces in response to negative voltage steps, which can accelerate both depolarization and repolarization.

I_h relationship to membrane potential and excitability

In this study we used a dynamic clamp to assess the effect of different types of I_h on cell excitability, by altering I_h amplitudes and kinetics. The results reveal effects on the resting membrane potential, with the membrane potential of AVCN bushy cells and LSO principal neurons more affected by changes in I_h compared with MNTB neurons. This difference suggests that in MNTB cells, other currents dominate around resting potential (e.g. twin-pore K⁺ channel currents) or that a strong I_LT prevents changes in I_h from affecting membrane potential. The observation of more positive resting potentials in AVCN neurons, compared with MNTB cells, could indicate that I_LT is less active in these cells, thus allowing changes in I_h to exert a greater influence on membrane potential. In LSO neurons, the strong hyperpolarization seen in resting conditions after I_h was decreased shows that I_h is a strong modulator of resting potential in these cells.

In vivo recordings have shown that blocking I_h leads to reduced excitability in the SOC (Shaikh & Finlayson, 2003). This effect is probably due to hyperpolarization of the resting membrane potential. Since the changes in membrane potential were greatest in LSO cells, this might indicate that I_h is more tonically active during rest in LSO neurons than in MNTB and AVCN neurons. This is also supported by the greater increase in input resistance after blocking I_h in LSO cells when compared with both MNTB and AVCN cells.

I_h and rebound depolarization

Another important aspect of this study was the assessment of the role of I_h in the generation of rebound over-threshold depolarizations. Activation of I_h by hyperpolarization is known to cause rebound APs in a variety of cells, including auditory neurons (Koch & Grothe, 2003; Ma et al. 2003). However, other ionic currents associated with I_h can prevent rebound APs (Ma et al. 2003). Here, we studied the effect of different I_h kinetics and amplitude on rebound firing in AVCN and LSO neurons, but not in the MNTB (because our previous study showed that it is unlikely that MNTB principal cells would fire rebound APs after prolonged activity; Leao et al. 2005). For both the AVCN and LSO, changing I_h characteristics did not cause rebound spikes in a previously non-rebound spiking neuron. Increasing amplitude or accelerating I_h kinetics altered the time dependency of hyperpolarization on rebound depolarization amplitudes in AVCN cells (from linear to logarithmic). This effect was probably due to larger rebound amplitudes activating low-threshold voltage-dependent K⁺ channels. Overall, rebound depolarizations were larger in LSO neurons when compared with AVCN cells, and more LSO neurons fired rebound APs compared with AVCN bushy cells. The strong correlation between small I_LT and rebound spiking in AVCN cells suggested that these currents prevent rebound depolarizations from reaching AP threshold. The same hypothesis is applicable to LSO cells, where multiple firing LSO cells, exhibiting less I_LT (Barnes-Davies et al. 2004), fired rebound APs with a greater frequency than single firing cells. By simulating I_LT, in LSO cells using the dynamic clamp, rebound APs could be strongly inhibited, supporting this theory. However, these dynamic clamp experiments failed to abolish rebound APs after application of long hyperpolarization protocols, probably because the activation of ‘real’ I_LT in LSO cells might be faster than the simulated current used in this work. We conclude that the rebound depolarization or rebound AP is modulated by the balance between I_h and I_LT activity.

In summary, this study highlights significant differences in I_h characteristics between different auditory brainstem nuclei, with each cell type expressing a distinct repertoire of I_h and HCN channel subtypes. Our results show I_h to be a key modulator of cell excitability that can be crucial for synaptic integration and coincidence detection.