Stochastic fluctuations in metabolic pathways

Abstract

Fluctuations in the abundance of molecules in the living cell may affect its growth and well being. For regulatory molecules (e.g., signaling proteins or transcription factors), fluctuations in their expression can affect the levels of downstream targets in a network. Here, we develop an analytic framework to investigate the phenomenon of noise correlation in molecular networks. Specifically, we focus on the metabolic network, which is highly interlinked, and noise properties may constrain its structure and function. Motivated by the analogy between the dynamics of a linear metabolic pathway and that of the exactly soluble linear queuing network or, alternatively, a mass transfer system, we derive a plethora of results concerning fluctuations in the abundance of intermediate metabolites in various common motifs of the metabolic network. For all but one case examined, we find the steady-state fluctuation in different nodes of the pathways to be effectively uncorrelated. Consequently, fluctuations in enzyme levels only affect local properties and do not propagate elsewhere into metabolic networks, and intermediate metabolites can be freely shared by different reactions. Our approach may be applicable to study metabolic networks with more complex topologies or protein signaling networks that are governed by similar biochemical reactions. Possible implications for bioinformatic analysis of metabolomic data are discussed.

Because of the limited number of molecules for typical molecular species in microbial cells, random fluctuations in molecular networks are common place and may play important roles in vital cellular processes. For example, noise in sensory signals can result in pattern formation and collective dynamics (1), and noise in signaling pathways can lead to cell-to-cell variability (2). Also, stochasticity in gene expression has implications on cellular regulation (3, 4) and may lead to phenotypic diversity (5, 6), whereas fluctuations in the levels of (toxic) metabolic intermediates may reduce metabolic efficiency (7) and impede cell growth.

In the past several years, a great deal of experimental and theoretical efforts have focused on the stochastic expression of individual genes, at both the translational and transcriptional levels (8–10, 26). The effect of stochasticity on networks has been studied in the context of small, ultra-sensitive genetic circuits, where noise at a circuit node (i.e., a gene) was shown to either attenuate or amplify output noise in the steady state (11, 12). This phenomenon, termed “noise propagation,” makes the steady-state fluctuations at one node of a gene network dependent in a complex manner on fluctuations at other nodes, making it difficult for the cell to control the noisiness of individual genes of interest (13). Several key questions that arise from these studies of genetic noise include (i) whether stochastic gene expression could further propagate into signaling and metabolic networks through fluctuations in the levels of key proteins controlling those circuits, and (ii) whether noise propagation also occurs in those circuits.

Recently, a number of approximate analytical methods have been applied to analyze small genetic and signaling circuits; these include the independent noise approximation (14–16), the linear noise approximation (14, 17), and the self-consistent field approximation (18). Perhaps due to the different approximation schemes used, conflicting conclusions have been obtained regarding the extent of noise propagation in various networks (see, e.g., ref. 17). Moreover, it is difficult to extend these studies to investigate the dependences of noise correlations on network properties, e.g., circuit topology, nature of feedback, catalytic properties of the nodes, and the parameter dependences. It is also difficult to elucidate these dependences by using numerical simulations alone, because of the large number of degrees of freedom involved even for a network with a modest number of nodes and links.

In this study, we describe an analytic approach to characterize the probability distribution for all nodes of a class of molecular networks in the steady state. Specifically, we apply the method to analyze fluctuations and their correlations in metabolite concentrations for various core motifs of the metabolic network. The metabolic network consists of nodes, which are the metabolites, linked to each other by enzymatic reactions that convert one metabolite to another. The predominant motif in the metabolic network is a linear array of nodes linked in a given direction (the directed pathway), which are connected to each other via converging pathways and diverging branch points (19). The activities of the key enzymes are regulated allosterically by metabolites from other parts of the network, whereas the levels of many enzymes are controlled transcriptionally and hence are subject to deterministic as well as stochastic variations in their expressions (20). To understand the control of metabolic network, it is important to know how changes in one node of the network affect properties elsewhere.

Applying our analysis to directed linear metabolic pathways, we predict that the distribution of molecule number of the metabolites at intermediate nodes is statistically independent in the steady state, i.e., the noise does not propagate. Moreover, given the properties of the enzymes in the pathway and the input flux, we provide a recipe that specifies the exact metabolite distribution function at each node. We then show that the method can be extended to linear pathways with reversible links, with feedback control, to cyclic and certain converging pathways, and even to pathways in which flux conservation is violated (e.g., when metabolites leak out of the cell). We find that in these cases correlations between nodes are negligible or vanish completely, although nontrivial fluctuation and correlation do dominate for a special type of converging pathways. Our results suggest that for vast parts of the metabolic network, different pathways can be coupled to each other without generating complex correlations, so that properties of one node (e.g., enzyme level) can be changed over a broad range without affecting behaviors at other nodes. We expect that the realization of this remarkable property will shape our understanding of the operation of the metabolic network, its control, as well as its evolution. For example, our results suggest that correlations between steady-state fluctuations in different metabolites bear no information on the network structure. In contrast, temporal propagation of the response to an external perturbation should capture, at least locally, the morphology of the network. Thus, the topology of the metabolic network should be studied during transient periods of relaxation, and not at steady-state.

Our method is motivated by the analogy between the dynamics of biochemical reactions in metabolic pathways and that of the exactly solvable queuing systems (21, 22) or, alternatively, as mass transfer systems (23, 24). Our approach may also be applicable to analyzing fluctuations in signaling networks, because of the close analogy between the molecular processes underlying the metabolic and signaling networks. To make our approach accessible to readers who may not be familiar with nonequilibrium statistical mechanics, we will present in the main text only the mathematical results supported by stochastic simulations and defer derivations and illustrative calculations to the supporting information (SI) Text. Although our analysis is general, all examples are taken from amino acid biosynthesis pathways in Escherichia coli (25).

Individual Nodes

A Molecular Michaelis–Menten (MM) Model.

To set up the grounds for analyzing a reaction pathway and to introduce our notation, we start by analyzing fluctuations in a single metabolic reaction.

Recent advances in experimental techniques have made it possible to track the enzymatic turnover of substrate to product at the single-molecule level (27, 28), and to study instantaneous metabolite concentration in the living cell (29). To describe this fluctuation mathematically, we model the cell as a reaction vessel of volume V, containing m substrate molecules (S) and N_E enzymes (E). A single molecule of S can bind to a single enzyme E with rate k₊ per volume, and form a complex, SE. This complex, in turn, can unbind (at rate k₋) or convert S into a product form, P, at rate k₂. This set of reactions is summarized by

Analyzing these reactions within a mass-action framework, keeping the substrate concentration fixed, and assuming fast equilibration between the substrate and the enzymes (k_± ≫ k₂), leads to the MM relation between the macroscopic flux c and the substrate concentration [S] = m/V:

where K_M = k₋/k₊ is the dissociation constant of the substrate and the enzyme, and v_max = k₂[E] is the maximal flux, with [E] = N_E/V being the total enzyme concentration.

Our main interest is in noise properties, resulting from the discreteness of molecules. We therefore need to track individual turnover events. These are described by the turnover rate w_m, defined as the inverse of the mean waiting time per volume between the (uncorrelated) synthesis of one product molecule to the next. Assuming again fast equilibration between the substrate and enzymes, the probability of having N_SE complexes given m substrate molecules and N_E enzyme is simply given by the Boltzmann distribution

for N_SE < N_E and m. Here K⁻¹ = Vk₊/k₋ is the Boltzmann factor associated with the formation of an SE complex, and the Z_{m, NE} takes care of normalization [i.e., chosen such that Σ_{N SE} p(N_SE|m, N_E) = 1]. Under this condition, the turnover rate w_m = k₂/V ΣN_SE · p(N_SE|m, N_E) is given approximately by

with v_max = k₂N_E/V (see SI Text). We note that for a single enzyme (N_E = 1), one has w_m = v_maxm/(m + K), which was derived and verified experimentally (28, 30).

Probability Distribution of a Single Node.

In a metabolic pathway, the number of substrate molecules is not kept fixed; rather, these molecules are synthesized or imported from the environment, and at the same time turned over into products. We consider the influx of substrate molecules to be a Poisson process with rate c. These molecules are turned into product molecules with rate w_m given by Eq. 4. The number of substrate molecules is now fluctuating, and one can ask what is the probability π(m) of finding m substrate molecules at the steady state. This probability can be found by solving the steady-state Master equation for this process (see SI Text), yielding

where z = c/v_max (32). The form of this distribution is plotted in SI Fig. 5 (solid black line). As expected, a steady state exists only when c ≤ v_max. Denoting the steady-state average by angular brackets, i.e., 〈x_m〉 ≡ Σ_mx_mπ(m), the condition that the incoming flux equals the outgoing flux is written (with s ≡ 〈m〉) as

Comparing this microscopically derived flux-density relation with the MM relation of Eq. 2 by using the obvious correspondence [S] = s/V, we see that the two are equivalent with K_M = (K + N_E)/V. Note that this microscopically derived form of MM constant is different by the amount [E] from the commonly used (but approximate form) K_M = K/V, derived from mass-action. However, for typical metabolic reactions, K_M ∼ 10–1,000 μM (24), whereas [E] is not more than 1,000 molecules in a bacterium cell (≈1 μM); thus, the values of the two expressions may not be very different.

We will characterize the variation of substrate concentration in the steady state by the noise index

where σ ₂^s is the variance of the distribution π(m). Because c ≤ v_max and increases with s toward 1 (see Eq. 6), η_s decreases with the average occupancy s as expected. It is bound from below by $1/\sqrt{K+N_E}$, which can easily be several percent. Generally, large noise is obtained when the reaction is catalyzed by a small number of high-affinity enzymes (i.e., for low K and N_E).

Linear Pathways

Directed Pathways.

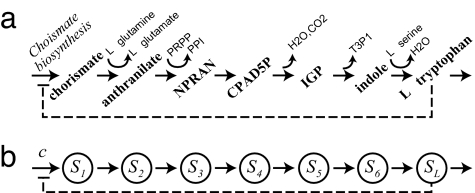
We now turn to a directed metabolic pathway, where an incoming flux of substrate molecules is converted, through a series of enzymatic reactions, into a product flux (19). Typically, such a pathway involves the order of 10 reactions. Each reaction takes as precursor the product of the preceding reaction, and frequently involves an additional side-reactant (such as a water molecule or ATP) that is abundant in the cell (and whose fluctuations can be neglected). As a concrete example, we show in Fig. 1a the tryptophan biosynthesis pathway of E. coli (25), where an incoming flux of chorismate is converted through six directed reactions into an outgoing flux of tryptophan, making use of several side-reactants. Our description of a linear pathway includes an incoming flux c of substrates of type S₁ along with a set of reactions that convert substrate type S_i to S_i+1 by enzyme E_i (see Fig. 1b) with rate w_mi⁽ⁱ⁾ = v_im_i/(m_i + K_i − 1), according to Eq. 4. We denote the number of molecules of intermediate S_i by m_i, with m₁ for the substrate and m_L for the end-product. The superscript (i) indicates explicitly that the parameters v_i = k₂(ⁱ) N_E(ⁱ)/V and K_i = (K⁽ⁱ⁾ + N_E(ⁱ⁾) describing the enzymatic reaction S_i → S_i+1 are expected to be different for different reactions.

Fig. 1.

Linear biosynthesis pathway. (a) Tryptophan biosynthesis pathway in E. coli. (b) Model for a directed pathway. Dashed lines depict end-product inhibition. CPAD5P, 1-O-carboxyphenylamino 1-deoxyribulose-5-phosphate; NPRAN, N-5-phosphoribosyl-anthranilate; IGP, indole glycerol phosphate; PPI, pyrophosphate; PRPP, 5-phosphoribosyl-1-pyrophosphate; T3P1, glyceraldehyde 3-phosphate.

The steady state of the pathway is fully described by the joint probability distribution π(m₁, m₂, …, m_L) of having m_i molecules of intermediate substrate type S_i. Surprisingly, this steady-state distribution is given exactly by a product measure,

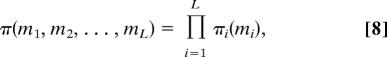where π_i(m) is as given in Eq. 5 (with K + N_E replaced by K_i and z by z_i = c/v_i), as shown in SI Text. This result indicates that in the steady state, the number of molecules of one intermediate is statistically independent of the number of molecules of any other substrate.^† The result has been derived previously in the context of queuing networks (21, 22) and of mass-transport systems (24). Either may serve as a useful analogy for a metabolic pathway.

Because the different metabolites in a pathway are statistically decoupled in the steady state, the mean s_i = 〈m_i〉 and the noise index η_si² = c⁻¹v_i/K_i can be determined by Eq. 7 individually for each node of the pathway. It is an interesting consequence of the decoupling property of this model that both the mean concentration of each substrate and the fluctuations depend only on the properties of the enzyme immediately downstream. Whereas the steady-state flux c is a constant throughout the pathway, the parameters v_i and K_i can be set separately for each reaction by the copy-number and kinetic properties of the enzymes (provided that c < v_i). Hence, for example, in a case where a specific intermediate may be toxic, tuning the enzyme properties may serve to decrease fluctuations in its concentration, at the price of a larger mean. To illustrate the decorrelation between different metabolites, we examine the response of steady-state fluctuations to a 5-fold increase in the enzyme level [E₁]. Typical time scale for changes in enzyme level much exceeds those of the enzymatic reactions. Hence, the enzyme level changes may be considered as quasi-steady state. In Fig. 2a we plot the noise indices of the different metabolites. Whereas noise in the first node is significantly reduced upon a 5-fold increase in [E₁] fluctuations at the other nodes are not affected at all.

Fig. 2.

Noise in metabolite molecular number (η_s = σ_s/s) for different pathways. Monte Carlo simulations (bars) are compared with the analytic prediction (symbols) obtained by assuming decorrelation for different nodes of the pathways. The structure of each pathway is shown under each image. Parameter values were chosen randomly such that 10³ < K_i < 10⁴ and c < v_i < 10c. Similar decorrelation was obtained for 100 different random choices of parameters and for 100 different sets with K_i 10-fold smaller (data not shown). The effect on the different metabolites of a change in the velocity of the first reaction, v₁ = 1.1c (dark gray) → 5c (light gray), is demonstrated. Similar results are obtained for changes in K₁ (data not shown). (a) Directed pathway. Here the decorrelation property is exact. (b) Directed pathway with two reversible reactions. For these reactions, v_3,4⁺ = 8.4, 6.9c; v_3,4⁻ = 1.6, 3.7c; K_3,4⁺ = 2500, 8000; and K_3,4⁻ = 7700, 3700. (c) Linear dilution of metabolites. Here β/c = 1/100. (d) End-product inhibition, where the influx rate is given by α = c₀[1 + (m_L/K_I)]⁻¹ with K_I = 1,000. (e) Diverging pathways. Here metabolite 4 is being processed by two enzymes (with different affinities, K^I = 810, K^II = 370) into metabolites 5 and 7, respectively. (f) Converging pathways. Here two independent three-reaction pathways, with fluxes c and c′ = c/2, produce the same product, S₄.

Reversible Reactions.

The simple form of the steady-state distribution 8 for the directed pathways may serve as a starting point to obtain additional results for metabolic networks with more elaborate features. We demonstrate such applications of the method by some examples below. In many pathways, some of the reactions are in fact reversible. Thus, a metabolite S_i may be converted to metabolite S_i+1 with rate v_max⁺m_i/(m_i + K_i⁺) or to substrate S_i−1 with rate v_max⁻m_i/(m_i + K_i⁻). One can show, in a way similar to ref. 24, that the decoupling property (Eq. 8) holds exactly only if the ratio of the two rates is a constant independent of m_i, i.e., when K_i⁺ = K_i⁻. In this case the steady state probability is still given by Eq. 5, with the local currents obeying

This is nothing but the simple fact that the overall flux is the difference between the local current in the direction of the pathway and that in the opposite direction.

In general, of course, K_i⁺ ≠ K_i⁻. However, we expect the distribution to be given approximately by the product measure in the following situations: (a) K_i⁺ ≃ K_i⁻; (b) the two reactions are in the zeroth-order regime, s ≫ K_i^±; and (c) the two reactions are in the linear regime, s ≪ K_i^±. In the latter case Eq. 9 is replaced by

Together, it is only for a narrow region (i.e., s_i ∼ K_i) where the product measure may not be applicable. This prediction is tested numerically, again by comparing two pathways (now containing reversible reactions) with 5-fold difference in the level of the first enzyme. From Fig. 2b, we see again that the difference in noise indices exist only in the first node, and the computed value of the noise index at each node is in excellent agreement with predictions based on the product measure (symbols). Similar decorrelation was obtained for 100 different random choices of parameters, and for 100 different sets with K_i 10-fold smaller (data not shown).

Dilution of Intermediates.

In the description so far, we have ignored possible catabolism of intermediates or dilution due to growth. This makes the flux a conserved quantity throughout the pathway and is the basis of the flux-balance analysis (33). One can generalize our framework for the case where flux is not conserved, by allowing particles to be degraded with rate u_m. Suppose, for example, that on top of the enzymatic reaction a substrate is subjected to an effective linear degradation, u_m = βm. This includes the effect of dilution due to growth, in which case β = ln(2)/(mean cell division time), and the effect of leakage out of the cell. As before, we first consider the dynamics at a single node, where the metabolite is randomly produced (or transported) at a rate c₀. It is straightforward to generalize the Master equation for the microscopic process to include u_m, and solve it in the same way. With w_m as before, the steady-state distribution of the substrate pool size is then found to be

where (a)_m ≡ a(a + 1)…(a + m − 1). This form of π(m) allows one to easily calculate moments of the molecule number from the partition function Z as in equilibrium statistical mechanics, e.g., s = 〈m〉 = c₀dZ/dc₀, and hence the outgoing flux, c = c₀ − βs. Using the fact that Z can be written explicitly in terms of hypergeometric functions, we find that the noise index grows with β as η_s² ≃ v/(Kc₀) + β/c₀. The distribution function is given in SI Fig. 5 for several values of β.

Generalizing the above to a directed pathway, we allow for β, as well as for v_max and K, to be i-dependent. The decoupling property of Eq. 8 does not generally hold in the nonconserving case (34). However, in this case the stationary distribution still seems to be well approximated by a product of the single-metabolite functions π_i(m) of the form of Eq. 10, with c₀/β → c_i−1/β_i. This is supported again by the excellent agreement between noise indices obtained by numerical simulations and analytic calculations using the product measure Ansatz (see Fig. 2c). In this case, change in the level of the first enzyme does “propagate” to the downstream nodes. But this is not a “noise propagation” effect, as the mean fluxes 〈c_i〉 at the different nodes are already affected. (To illustrate the effect of leakage, the simulation used parameters that corresponded to a huge leakage current, which is 20% of the flux. This is substantially larger than typical leakage encountered, say, due to growth-mediated dilution, and we do not expect propagation effects due to leakage to be significant in practice.)

Interacting Pathways

The metabolic network in a cell is composed of pathways of different topologies. Although linear pathways are abundant, one can also find circular pathways (such as the TCA cycle), converging pathways, and diverging ones. Many of these can be thought of as a composition of interacting linear pathways. Another layer of interaction is imposed on the system due to the allosteric regulation of enzyme activity by intermediate metabolites or end products. To what extent can our results for a linear pathway be applied to these more complex networks? Below we address this question for a few of the frequently encountered cases. To simplify the analysis, we will consider only directed pathways and suppress the dilution/leakage effect.

Cyclic Pathways.

We first address the cyclic pathway, in which the metabolite S_L is converted into S₁ by the enzyme E_L. Borrowing a celebrated result for queuing networks (35) and mass transfer models (36), we note that the decoupling property of Eq. 8 described above for the linear-directed pathway also holds exactly even for the cyclic pathways.^‡ This result is surprising mainly because the Poissonian nature of the “incoming” flux assumed in the analysis so far is lost.

In an isolated cycle the total concentration of the metabolites, s_tot, and not the flux, is predetermined. In this case, the flux c is given by the solution to the equation

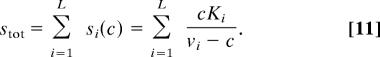Note that this equation can always be satisfied by some positive c that is smaller than all v_i values. In a cycle that is coupled to other branches of the network, flux may be governed by metabolites going into the cycle or taken from it. In this case, flux balance analysis will enable determination of the variables z_i, which specify the probability distribution.

End-Product Inhibition.

Many biosynthesis pathways couple between supply and demand by a negative feedback (19, 25), where the end-product inhibits the first reaction in the pathway or the transport of its precursor (see, e.g., the dashed lines in Fig. 1). In this way, flux is reduced when the end-product builds up. In branched pathways, this may be done by regulating an enzyme immediately downstream from the branch point, directing some of the flux toward another pathway.

To study the effect of end-product inhibition, we consider inhibition of the inflow into the pathway. Specifically, we model the probability at which substrate molecules arrive at the pathway by a stochastic process characterized by the rate α(m_L) = c₀[1 + (m_L/K_I)^h]⁻¹, where c₀ is the maximal influx (determined by availability of the substrate either in the medium or in the cytoplasm), m_L is the number of molecules of the end-product (S_L), K_i is the dissociation constant of the interaction between the first enzyme E₀ and S_L, and h is a Hill coefficient describing the cooperativity of interaction between E₀ and S_L. Because m_L is a stochastic variable itself, the incoming flux is described by a nontrivial stochastic process that is manifestly non-Poissonian.

The steady-state flux is now

This is an implicit equation for the flux c, which also appears in the right-hand side through the distribution π(m₁, …, m_L).

By drawing an analogy between feedback-regulated pathway and a cyclic pathway, we conjecture that metabolites in the former should be effectively uncorrelated. The quality of this approximation is expected to become better in cases where the ratio between the influx rate α(m_L) and the outflux rate w_mL is typically m_L independent. Under this assumption, we approximate the distribution function by the product measure of Eq. 8, with the form of the single node distributions given by Eq. 5. Note that the conserved flux then depends on the properties of the enzyme processing the last reaction and in general should be influenced by the fluctuations in the controlling metabolite. These fluctuations propagate throughout the pathway at the level of the mean flux, as expected from any node characterized by a high control coefficient (7).

Using this approximate form, Eq. 12 can be solved self-consistently to yield c(c₀), as is shown explicitly in SI Text for h = 1. The solution obtained is found to be in excellent agreement with numerical simulation (SI Fig. 6a). The quality of the product measure approximation is further scrutinized by comparing the noise index of each node upon increasing the enzyme level of the first node by 5-fold. Fig. 2c shows clearly that the effect of changing enzyme level does not propagate to other nodes. Although being able to accurately predict the flux and mean metabolite level at each node, the predictions based on the product measure are found to be underestimating the noise index by up to 10% (compare bars and symbols). We conclude that in this case correlations between metabolites do exist, but not dominate. Thus, analytic expressions derived from the decorrelation assumption can be useful even in this case (see SI Fig. 6b).

Diverging Pathways.

Many metabolites serve as substrates for several pathways. In such cases, different enzymes can bind to the substrate; each catabolizes a first reaction in a different pathway. Within our scheme, this can be modeled by allowing for a metabolite S_i to be converted to metabolite S₁^I with rate w_mi^I = v^Im_i/(m_i + K^I − 1) or to metabolite S₁^II with rate w_mi^I = v^IIm_i/(m_i + K^II − 1). The parameters v^I,II and K^I,II characterize the two different enzymes.

Similar to the case of reversible reactions, the steady-state distribution is given exactly by a product measure only if w_mi^I/w_i^II is a constant, independent of m_i (namely when K^I = K^II). Otherwise, we expect it to hold in a range of alternative scenarios, as described for reversible pathways.

Considering a directed pathway with a single branch point, the distribution 5 describes exactly all nodes upstream of that point. At the branch point, one replaces w_m by w_m = w_m^I + w_m^II, to obtain the distribution function

From this distribution one can obtain the fluxes going down each one of the two branching pathway, c^I,II = Σw_m^I,IIπ(m). Both fluxes depend on the properties of both enzymes, as can be seen from Eq. 13, and thus at the branch point the two pathways influence each other (37). Moreover, fluctuations at the branch point propagate into the branching pathways already at the level of the mean flux. This is consistent with the fact that the branch node is expected to be characterized by a high control coefficient (7).

Although different metabolite upstream and including the branch point are uncorrelated, this is not exactly true for metabolites of the two branches. Nevertheless, because these pathways are still directed, we further conjecture that metabolites in the two branching pathways can still be described, independently, by the probability distribution 5, with c given by the flux in the relevant branch, as calculated from Eq. 13. Indeed, the numerical results of Fig. 2e strongly support this conjecture. We find that changing the noise properties of a metabolite in the upstream pathway do not propagate to those of the branching pathways.

Converging Pathways: Combined Fluxes.

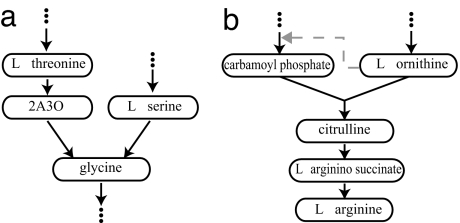
We next examine the case where two independent pathways result in synthesis of the same product, P. For example, the amino acid glycine is the product of two (very short) pathways, one using threonine and the other serine as precursors (Fig. 3a) (25). With only directed reactions, the different metabolites in the combined pathway, namely, the two pathways producing P and a pathway catabolizing P, remain decoupled. The simplest way to see this is to note that the process describing the synthesis of P, being the sum of two Poisson processes, is still a Poisson process. The pathway that catabolizes P is therefore statistically identical to an isolated pathway, with an incoming flux that is the sum of the fluxes of the two upstream pathways. More generally, the Poissonian nature of this process allows for different pathways to dump or take from common metabolite pools, without generating complex correlations.

Fig. 3.

Converging pathways. (a) Glycine is synthesized in two independent pathways. (b) Citrulline is synthesized from products of two pathways. 2A3O, 2-amino-3-oxobutanoate.

Converging Pathways: Reaction with Two Fluctuating Substrates.

As mentioned above, some reactions in a biosynthesis pathway involve side-reactants, which are assumed to be abundant (and hence at a constant level). Let us now discuss briefly a case where this approach fails. Suppose that the two products of two linear pathways serve as precursors for one reaction. This, for example, is the case in the arginine biosynthesis pathway, where l-ornithine is combined with carbamoyl-phosphate by ornithine-carbamoyltransferase to create citrulline (Fig. 3b) (25). Within a flux balance model, the net fluxes of both substrates must be equal to achieve steady state, in which case the macroscopic MM flux takes the form

Here [S_1,2] are the steady-state concentrations of the two substrates, and K_M1,2 the corresponding MM constants. However, flux balance provides only one constraint to a system with two degrees of freedom.

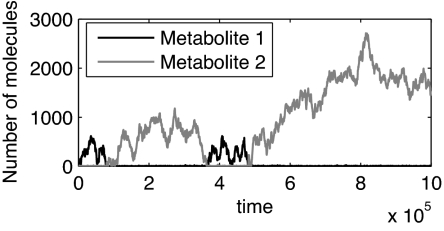
In fact, this reaction exhibits no steady state. To see why, consider a typical time evolution of the two substrate pools (Fig. 4). Suppose that at a certain time one of the two substrates, say S₁, is of high molecule-number compared with its equilibrium constant, m₁ ≫ K₁. In this case, the product synthesis rate is unaffected by the precise value of m₁, and is given approximately by v_maxm₂/(m₂ + K₂). Thus, the number m₂ of S₂ molecules can be described by the single-substrate reaction analyzed above, whereas m₁ performs a random walk (under the influence of a weak logarithmic potential), which is bound to return, after some time τ, to values comparable with K₁. Then, after a short transient, one of the two substrates will become unlimiting again, and the system will be back in the scenario described above, perhaps with the two substrates changing roles (depending on the ratio between K₁ and K₂).

Fig. 4.

Time course of a two-substrate enzymatic reaction, as obtained by a Gillespie simulation (31). Here c = 3t⁻¹, k₊ = 5t⁻¹, and k₋ = 2t⁻¹ for both substrates, with t being an arbitrary time unit.

Importantly, the probability for the time τ during which one of the substrates is at saturating concentration scales as τ^−3/2 for large τ. During this time the substrate pool may increase to the order $\sqrt{\tau }$. The fact that τ has no finite mean implies that this reaction has no steady state. Because accumulation of any substrate is most likely toxic, the cell must provide some other mechanism to limit these fluctuations. This may be one interpretation for the fact that within the arginine biosynthesis pathway, l-ornithine is an enhancer of carbamoyl-phosphate synthesis (dashed line in Fig. 3b).

In contrast, a steady state always exists if the two metabolites experience linear degradation, as this process prevents indefinite accumulation. However, in general one expects enzymatic reactions to dominate over futile degradation. In this case, equal influxes of the two substrates result in large fluctuations, similar to the ones described above (32).

Discussion

In this work we have characterized stochastic fluctuations of metabolites for dominant simple motifs of the metabolic network in the steady state. Motivated by the analogy between the directed biochemical pathway and the mass transfer model or, equivalently, as the queuing network, we show that the intermediate metabolites in a linear pathway, the key motif of the biochemical network, are statistically independent. We then extend this result to a wide range of pathway structures. Some of the results (e.g., the directed linear, diverging, and cyclic pathways) have been proven previously in other contexts. In other cases (e.g., for reversible reaction, diverging pathway, or with leakage/dilution), the product measure is not exact. Nevertheless, based on insights from the exactly solvable models, we conjecture that it still describes faithfully the statistics of the pathway. Using the product measure as an Ansatz, we obtained quantitative predictions, which turned out to be in excellent agreement with the numerics (Fig. 2). These results suggest that the product measure may be an effective starting point for quantitative, nonperturbative analysis of (the stochastic properties of) these circuit/networks. We hope this study will stimulate further analytical studies of the large variety of pathway topologies in metabolic networks, as well as in-depth mathematical analysis of the conjectured results. Moreover, it will be interesting to explore the applicability of the present approach to other cellular networks, in particular, stochasticity in protein signaling networks (2), whose basic mathematical structure is also a set of interlinked MM reactions.

Our main conclusion, that the steady-state fluctuations in each metabolite do not depend on the fluctuations in other upstream metabolites, is qualitatively different from conclusions obtained for gene networks in recent studies, e.g., the “noise addition rule” (14, 15) and its extension to cases where the signals and the processing units interact (17). Some cases that were found in ref. 17 to exhibit residual noise propagation generalize our results to the case of “bursty,” non-Poissonian, noise. While bursty noise is not expected for metabolic and signaling reactions, it is nevertheless important to address the extent to which the main finding of this work is robust to the nature of stochasticity. Our results, as well as generalized mass-transport models (38, 39), suggest that statistical independence goes well beyond the Poisson case.

The absence of noise propagation for a large part of the metabolic network allows intermediate metabolites to be shared freely by multiple reactions in multiple pathways, without the need of installing elaborate control mechanisms. In these systems, dynamic fluctuations (e.g., stochasticity in enzyme expression that occurs at a much longer time scale) stay local to the node and are shielded from triggering system-level failures (e.g., gridlocks). Conversely, this property allows convenient implementation of controls on specific nodes of pathways, e.g., to limit the pool of a specific toxic intermediate, without the concern of elevating fluctuations in other nodes. We expect this to make the evolution of metabolic network less constrained, so that the system can modify its local properties nearly freely to adapt to environmental or cellular changes. The optimized pathways then can be meshed smoothly into the overall metabolic network, except for junctions between pathways where complex fluctuations not constrained by flux conservation.

Recently, metabolomics, i.e., global metabolite profiling, has been suggested as a tool to decipher the structure of the metabolic network (40, 41). Our results suggest that in many cases, steady-state fluctuations do not bear information about the pathway structure. Rather, correlations between metabolite fluctuations may be, for example, the result of fluctuation of a common enzyme or coenzyme or reflect dynamical disorder (28). Indeed, a bioinformatic study found no straightforward connection between observed correlation and the underlying reaction network (42). Instead, the response to external perturbation (29, 40, 43) may be much more effective in shedding light on the underlying structure of the network and may be used to study the morphing of the network under different conditions. It must be noted that all results described here are applicable only to systems in the steady state; transient responses such as the establishment of the steady state and response to external perturbations will likely exhibit complex temporal as well as spatial correlations. Nevertheless, it is possible that some aspects of the response function may be attainable from the steady-state fluctuations through nontrivial fluctuation–dissipation relations as shown for other related nonequilibrium systems (23, 44).

Abbreviation

MM

Michaelis–Menten.