Abstract
Epistatic interactions among quantitative trait loci (QTL) contribute substantially to the variation in complex traits. The main objectives of this study were to (i) compare three- vs. four-step genome scans to identify three-way epistatic interactions among QTL belonging to a metabolic pathway, (ii) investigate by computer simulations the power and proportion of false positives (PFP) for detecting three-way interactions among QTL in recombinant inbred line (RIL) populations derived from a nested mating design, and (iii) compare these estimates to those obtained for detecting three-way interactions among QTL in RIL populations derived from diallel and different partial diallel mating designs. The single-nucleotide polymorphism haplotype data of B73 and 25 diverse maize inbreds were used to simulate the production of various RIL populations. Compared to the three-step genome scan, the power to detect three-way interactions was higher with the four-step genome scan. Higher power to detect three-way interactions was observed for RILs derived from optimally allocated distance-based designs than from nested designs or diallel designs. The power and PFP to detect three-way interactions using a nested design with 5000 RILs were for both the 4-QTL and the 12-QTL scenario of a magnitude that seems promising for their identification.
UNTIL now estimation of the positions of quantitative trait loci (QTL) in plant genetics was accomplished by classical linkage mapping (Lander and Botstein 1989). Recently, the adaption of association mapping in plant genetics has been proposed by several authors (e.g., Vuylsteke et al. 2000; Thornsberry et al. 2001). Both linkage and association mapping methods have merits and limitations for QTL mapping. While linkage mapping methods offer a high power to detect QTL in genomewide approaches, association mapping methods have the merit of a high resolution to detect QTL (Remington et al. 2001). Wu and Zeng (2001) studied a joint linkage and linkage disequilibrium (LD) mapping strategy for natural populations. Using data from a general complex pedigree of cattle, Blott et al. (2003) and Meuwissen et al. (2002) identified candidate-gene polymorphisms at previously mapped QTL by combining linkage and LD information.
In this study, we examine a genomewide QTL mapping strategy using genome sequence information of recombinant inbred lines (RILs) that were generated from several crosses of parental inbreds. This QTL mapping strategy is based on the idea that the genomes of RILs are mosaics of chromosomal segments of their parental genome. Consequently, within the chromosomal segments the LD information across the parental inbreds is maintained. Thus, if diverse parental inbreds are used as in this study, LD decays within the chromosomal segments over a short physical distance (Wilson et al. 2004). Therefore, the new mapping strategy will show not only a high power to detect QTL in genomewide approaches but also a high mapping resolution when both linkage and LD information are used.
Results from model organisms suggest that epistatic interactions among loci also contribute substantially to the variation in complex traits (Carlborg and Haley 2004; Marchini et al. 2005). While Rebai et al. (1997) applied classical linkage mapping to detect QTL with additive effects in connected mapping populations of maize, Blanc et al. (2006) used such populations to detect two-way epistatic interactions. The power to detect two-way interactions by using different mating designs was examined by Verhoeven et al. (2006). Furthermore, Ritchie et al. (2003) assessed the power of multifactor dimensionality reduction to detect two-way interactions. However, several studies described QTL × genetic background interactions (e.g., Doebley et al. 1995; Alonso-Blanco et al. 1998), which can be caused by higher-order epistatic interactions among QTL (Jannink and Jansen 2001). Furthermore, the metabolic pathways that presumably underlie quantitative traits involve multiple interacting gene products and regulatory loci that could generate higher-order epistatic interactions (McMullen et al. 1998). Information about the power for genomewide detection of epistatic interactions among more than two QTL is still lacking.
The objectives of our research were to (i) compare three- vs. four-step genome scans to identify three-way interactions among QTL involved in a metabolic pathway, (ii) investigate by computer simulations the power and proportion of false positives (PFP) for detecting three-way interactions among QTL in RIL populations derived from a nested mating design, and (iii) compare these estimates to those obtained for detecting three-way interactions among QTL using RIL populations derived from diallel and different partial diallel mating designs.
MATERIALS AND METHODS
Simulations:
Data underlying the simulations:
Our computer simulations were based on single-nucleotide polymorphism (SNP) haplotype data, comprising 653 loci of B73 and 25 diverse maize inbreds B97, CML52, CML69, CML103, CML228, CML247, CML277, CML322, CML333, Hp301, IL14H, Ki3, Ki11, Ky21, M37W, M162W, Mo18W, MS71, NC350, NC358, Oh7b, Oh43, P39, Tx303, and Tzi8. The 25 diverse inbreds were selected on the basis of 100 simple sequence repeat markers out of a worldwide sample of 260 inbreds to capture the maximum genetic diversity (Liu et al. 2003). The 26 inbreds were used to simulate the production of various RIL populations.
Examined mating designs:
The nested association mapping (NAM) data set was established in accordance with the crossing scheme applied in the project “molecular and functional diversity of the maize genome.” From each cross of the 25 diverse inbreds with B73, a segregating population with 200 RILs was developed. The diallel association mapping (DAM) data set DAM4875 was generated by deriving RIL populations with 15 RILs from each of the 325 crosses in the diallel (method 4; Griffing 1956) among all 26 inbreds.
The distance-based (DB) data sets DBc × r were created by selecting from the 325 crosses in a diallel the c combinations of parental inbreds that show, on the basis of all marker loci, the maximum genetic dissimilarity calculated according to Nei and Li (1979). For the c combinations of parental inbreds r RILs were derived from each combination. In our study the data sets DB75 × 65, DB125 × 39, and DB195 × 25 were examined. For single round robin (SRR) (Verhoeven et al. 2006), 188 RILs were derived from each of the 26 chain crosses, i.e., inbred 1 × inbred 2, inbred 2 × inbred 3, … , inbred 26 × inbred 1. The data sets DAM900, DB25 × 36, DB50 × 18, DB100 × 9, and DB150 × 6 were examined only in combination with the NAM data set and were therefore based on the 300 crosses in a diallel among the 25 diverse inbreds.
Definition of phenotypic values:
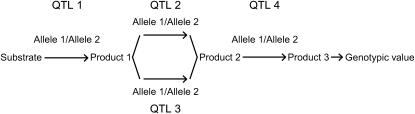
For each of the simulated 50 replications, four SNPs were sampled at random from the linkage map and defined as QTL of a four-locus pathway (Figure 1). The genotypic values assigned to the inbreds were based on their allelic states at the four QTL and chosen in such a way that a combination of complementary and duplicate molecular interactions existed among the QTL (Table 1) (Jayaram and Peterson 1990). On the basis of the F∞-metric model (Yang 2004) the corresponding additive effects of QTL1, QTL2, QTL3, and QTL4 were 1.375, 0.375, 0.500, and 0.250, respectively. Furthermore, the digenic additive × additive effects QTL1 × QTL2, QTL1 × QTL3, QTL1 × QTL4, QTL2 × QTL3, QTL2 × QTL4, and QTL3 × QTL4 were 0.375, 0.500, 0.250, 0.750, 0.250, and 0.125, respectively. Higher-order epistatic effects involving three and four QTL, QTL1 × QTL2 × QTL3, QTL1 × QTL2 × QTL4, QTL1 × QTL3 × QTL4, QTL2 × QTL3 × QTL4, and QTL1 × QTL2 × QTL3 × QTL4 were 0.750, 0.250, 0.125, 0.625, and 0.625, respectively. Under the assumption of allele frequencies of 0.5 and linkage equilibrium among the QTL, the assumed genotypic values correspond to variances 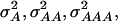 and
and 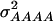 of 1.172, 0.273, 0.129, and 0.024, respectively (Wricke and Weber 1986). In the NAM data set,
of 1.172, 0.273, 0.129, and 0.024, respectively (Wricke and Weber 1986). In the NAM data set, 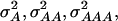 and
and 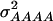 amounted 0.669, 0.087, 0.022, and 0.002, respectively, due to the deviations of allele frequencies from 0.5.
amounted 0.669, 0.087, 0.022, and 0.002, respectively, due to the deviations of allele frequencies from 0.5.
Figure 1.—
Metabolic pathway underlying the simulations.
TABLE 1.
Genotypic values for the four-locus genotypes underlying the simulations
| Genotype
|
||||
|---|---|---|---|---|
| QTL1 | QTL2 | QTL3 | QTL4 | Genotypic value |
| 1 | 1 | 1 | 1 | 4 |
| 1 | 1 | 1 | 2 | 4 |
| 1 | 1 | 2 | 1 | 4 |
| 1 | 1 | 2 | 2 | 4 |
| 1 | 2 | 1 | 1 | 4 |
| 1 | 2 | 1 | 2 | 4 |
| 1 | 2 | 2 | 1 | 4 |
| 1 | 2 | 2 | 2 | 4 |
| 2 | 1 | 1 | 1 | 10 |
| 2 | 1 | 1 | 2 | 6 |
| 2 | 1 | 2 | 1 | 7 |
| 2 | 1 | 2 | 2 | 7 |
| 2 | 2 | 1 | 1 | 2 |
| 2 | 2 | 1 | 2 | 5 |
| 2 | 2 | 2 | 1 | 10 |
| 2 | 2 | 2 | 2 | 7 |
In a second scenario, 12 QTL, organized in three four-locus pathways, were assumed. Genotypic values of the inbreds were determined by summing up the effects caused by the individual pathways. In this scenario 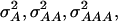 and
and 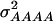 were 3.516, 0.820, 0.387, and 0.073, respectively, for a population with allele frequencies of 0.5, whereas for the NAM data set the corresponding variances were 2.034, 0.248, 0.064, and 0.007, respectively.
were 3.516, 0.820, 0.387, and 0.073, respectively, for a population with allele frequencies of 0.5, whereas for the NAM data set the corresponding variances were 2.034, 0.248, 0.064, and 0.007, respectively.
The phenotypic values of the RILs were generated by adding a normally distributed variable N(0, 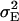 ) to the genotypic values. The error variance was calculated as
) to the genotypic values. The error variance was calculated as
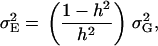 |
where 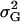 denotes the genetic variance and h2 denotes the heritability on an entry-mean basis. On the basis of previous empirical studies, we examined h2-values of 0.5 and 0.8 (Flint-Garcia et al. 2005). All simulations were performed with software Plabsoft (Maurer et al. 2004), which is implemented as an extension of the statistical software R (R Development Core Team 2004).
denotes the genetic variance and h2 denotes the heritability on an entry-mean basis. On the basis of previous empirical studies, we examined h2-values of 0.5 and 0.8 (Flint-Garcia et al. 2005). All simulations were performed with software Plabsoft (Maurer et al. 2004), which is implemented as an extension of the statistical software R (R Development Core Team 2004).
Statistical analyses:
Due to their vast number, it is intractable to detect three-way interactions using a three-dimensional genome scan. Therefore, we used two different model selection approaches for identifying three-way interactions that considerably reduce the number of models to be evaluated during the model selection process. For both approaches PROC GLMSELECT of the statistical software SAS (SAS Institute 2005) was used.
Several authors suggested the use of information criteria such as the Akaike information criterion or the Schwarz Bayesian criterion (Piepho and Gauch 2001) or modifications thereof (Bogdan et al. 2004; Baierl et al. 2006) to circumvent the problems connected with multiple likelihood-ratio tests for model selection. In preliminary simulations, however, we used the Schwarz Bayesian criterion and observed a high PFP (data not shown). Therefore, in our study we used the model selection criteria P-to-enter and P-to-stay (Miller 2002), which allows the use of a more conservative threshold.
All SNPs, and also those treated as QTL, were included in both approaches. Hence, QTL detection is not based on LD between QTL and adjacent molecular markers and, thus, the correlation structure among the RILs can be ignored.
Three-step genome scan:
The three-step genome scan applied in this study to identify three-way interactions was based on the one-dimensional genome scan described by Jannink and Jansen (2001). In the first step, stepwise multiple linear regression (Efroymson 1960) was performed on y, the phenotypic values of the RILs, as a dependent variable and w1, w2, … , w653, the SNP loci, and x, the affiliation of each RIL to a cross of parental inbreds, as independent variables. Independent variables showing P-to-enter or P-to-stay <1 × 10−8 were added or kept in the model.
In addition to the variables identified in the first step, the variables w1 × x, w2 × x, … , w653 × x were used as independent variables in the stepwise multiple linear regression of the second step, where variable selection was performed only on w1 × x, w2 × x, … , w653 × x. Variables showing a P-to-enter or P-to-stay <1 × 10−5 were added or kept in the model. The i variables w out of the i w × x interactions identified in the second step were used in the backward elimination procedure of the third step together with the 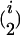 and
and 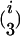 possible two- and three-locus interactions among them as independent variables. Variables showing a P-to-stay <1 × 10−5 were kept in the model. The model resulting from the third step was designated as the final model.
possible two- and three-locus interactions among them as independent variables. Variables showing a P-to-stay <1 × 10−5 were kept in the model. The model resulting from the third step was designated as the final model.
Four-step genome scan:
Stepwise multiple linear regression was also used for the four-step genome scan, where in the first step y was used as a dependent variable and w1, w2, … , w653, the SNP loci, as independent variables. The j loci identified in the first step were used together with the two-way interactions, which were constructed by combining the j loci with all loci, as independent variables in the stepwise multiple linear regression of the second step, where variable selection was performed only on the two-way interactions. The single loci and two-way interactions identified in the first and the second step, respectively, were used together with the three-way interactions, which were constructed by combining the two-way interactions with all loci, as independent variables in the stepwise multiple linear regression of the third step. Variable selection was performed only on the three-way interactions. Three two-way interactions are subordinated to each three-way interaction, whereas the significance of two of them was examined in the previous steps. To ensure the detection of three-way epistatic interactions and not the effect of three-way interactions confounded with that of the not examined, subordinated two-way interactions we applied in the fourth step backward elimination on all variables contained in the model resulting from the third step and the not examined, subordinated two-way interactions. In this step, variable selection was performed only on the three-way interactions and the not examined, subordinated two-way interactions. The model resulting from the fourth step was designated as the final model. In each of the four steps, variables showing a P-to-enter or P-to-stay <1 × 10−8 were added or kept in the model. This conservative threshold was chosen to warrant an acceptable PFP. To observe an acceptable PFP in studies based on empirical data we suggest using computer simulations to estimate the corresponding P-to-enter and P-to-stay.
The power 1 − β* to detect three-way interactions was calculated as the proportion of three-way interactions correctly identified in the final model out of the total number of three-way interactions simulated. We estimated the PFP (Fernando et al. 2004) as the proportion of three-way interactions for which at least one locus is not a QTL out of the total number of three-way interactions identified in the final model. Averages were calculated across the simulated 50 replications to determine 1 − β* and PFP.
RESULTS
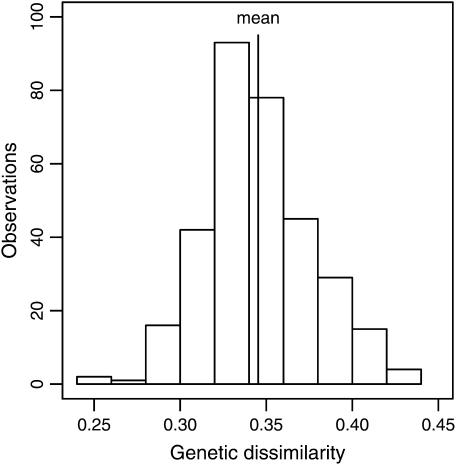
The average map distance between the 653 SNP markers was 2.6 cM. The pairwise genetic dissimilarity among the 26 inbreds ranged from 0.25 to 0.42 (Figure 2). The average frequency of the B73 allele was 0.81 in the RILs of the NAM data set and 0.64 in the RILs of data sets DAM4875 and SRR.
Figure 2.—
Distribution of pairwise genetic dissimilarities among the 26 parental inbreds based on 653 single-nucleotide polymorphism markers.
In the three-step genome scan, the power and PFP to detect three-way interactions were for the NAM data set 0.05 and 0.35 (4 QTL; h2 = 0.5), respectively (data not shown). For 12 QTL and h2 = 0.5, the power to detect three-way interactions using the NAM data set decreased to 0.00 and PFP increased to 1.00. A power 1 − β* of 0.08 (4 QTL; h2 = 0.5) was observed for data sets DAM4875 and DB125 × 39, whereas the PFP was 0.40 and 0.35, respectively.
Using the four-step genome scan, a power 1 − β* to detect three-way interactions of 0.28 (4 QTL; h2 = 0.5) was found for the NAM data set (Table 2). In the scenario with 12 QTL, the power 1 − β* was 0.18. Lower PFP was detected for the 12-QTL scenario (0.29) than for the 4-QTL scenario (0.54). Totals of 1.2 and 1.5 times higher power estimates were observed for the 4- and 12-QTL scenarios of the NAM data set, respectively, when increasing h2 from 0.5 to 0.8.
TABLE 2.
Power to detect three-way interactions (1 − β*) and proportion of false positives (PFP) using the four-step genome scan for different mating designs to establish recombinant inbred lines (RIL): nested (NAM), diallel (DAM), single round robin (SRR), and distance-based (DB) designs
| 4 QTL
|
12 QTL
|
|||||
|---|---|---|---|---|---|---|
| Mating design | No. RIL | Criterion | h2 = 0.5 | h2 = 0.8 | h2 = 0.5 | h2 = 0.8 |
| NAM | 5000 | 1 − β* | 0.28 | 0.33 | 0.18 | 0.29 |
| PFP | 0.54 | 0.64 | 0.29 | 0.41 | ||
| DAM4875 | 4875 | 1 − β* | 0.44 | 0.54 | 0.30 | 0.54 |
| PFP | 0.44 | 0.46 | 0.16 | 0.30 | ||
| SRR | 4888 | 1 − β* | 0.29 | 0.38 | 0.24 | 0.34 |
| PFP | 0.56 | 0.51 | 0.26 | 0.47 | ||
| DB75 × 65 | 4875 | 1 − β* | 0.38 | 0.41 | 0.29 | 0.49 |
| PFP | 0.47 | 0.63 | 0.19 | 0.37 | ||
| DB125 × 39 | 4875 | 1 − β* | 0.45 | 0.56 | 0.31 | 0.54 |
| PFP | 0.39 | 0.56 | 0.19 | 0.35 | ||
| DB195 × 25 | 4875 | 1 − β* | 0.45 | 0.58 | 0.32 | 0.57 |
| PFP | 0.45 | 0.64 | 0.17 | 0.34 | ||
| NAM and DAM900 | 5900 | 1 − β* | 0.40 | 0.60 | ||
| PFP | 0.47 | 0.51 | ||||
| NAM and DB25 × 36 | 5900 | 1 − β* | 0.27 | 0.33 | ||
| PFP | 0.52 | 0.64 | ||||
| NAM and DB50 × 18 | 5900 | 1 − β* | 0.38 | 0.53 | ||
| PFP | 0.46 | 0.58 | ||||
| NAM and DB100 × 9 | 5900 | 1 − β* | 0.42 | 0.60 | ||
| PFP | 0.46 | 0.51 | ||||
| NAM and DB150 × 6 | 5900 | 1 − β* | 0.39 | 0.57 | ||
| PFP | 0.46 | 0.59 | ||||
The power 1 − β* using DAM4875, SRR, or DB data sets ranged in the four-step genome scan from 0.29 to 0.45 (4 QTL; h2 = 0.5) and from 0.24 to 0.32 (12 QTL; h2 = 0.5). PFP varied for these data sets between 0.39 and 0.56 (4 QTL; h2 = 0.5). For the scenario with 12 QTL, lower PFP values were obtained.
For both levels of h2, ∼1.5 times higher power estimates were observed for the combined data set of NAM and DAM900 than for NAM. For the former, PFP was for both levels of h2 ∼0.50. The power 1 − β* for combined NAM and DB data sets ranged for 4 QTL and h2 = 0.5 from 0.27 to 0.42 and for h2 = 0.8 from 0.33 to 0.60. For these data sets PFP varied for 4 QTL and h2 = 0.5 between 0.46 and 0.52 and for h2 = 0.8 between 0.51 and 0.64.
DISCUSSION
The comparison of power 1 − β* of different statistical analyses requires an equal PFP. However, model selection procedures such as those applied in our study do not stringently adhere to a specified PFP (Miller 2002). Nevertheless, in our study similar PFP values were obtained for all mating designs of each simulation scenario under the four-step genome scan and, thus, power estimates can be compared.
Owing to technical reasons, we were not able to ascertain similar PFP values for the four-step genome scan as for the three-step genome scan. However, differences in 1 − β* between both approaches were of such size that the four-step genome scan seems more promising for detecting epistatic QTL in the assumed metabolic pathway than the three-step genome scan irrespective of the mating design. Therefore, the comparison between the examined mating designs was based only on results of the former.
Power to detect three-way interactions under different mating designs:
Despite a comparable number of RILs in the two data sets NAM and DAM4875, higher power estimates were found for the latter (Table 2). This observation is attributable to the average frequency of the B73 allele, which is closer to 0.5 for DAM4875 than for NAM. Crossing schemes resulting in RILs with an average allele frequency of 0.5 have a high power to detect QTL because the probability that some QTL haplotypes have only a very small class size is minimized (Verhoeven et al. 2006). For the detection of higher-order epistatic QTL this issue is even more important because the number of possible QTL haplotypes increases with an increasing number of QTL. But this reduces the probability that all QTL haplotypes are present in the data set.
The average frequency of the B73 allele was the same for the RILs of DAM4875 and SRR. Nevertheless, in our study a higher power to detect three-way interactions was found for the former. This is in contrast to a result of Verhoeven et al. (2006), who observed a considerably higher power to detect epistatic QTL for SRR than for the same number of RILs derived from a diallel. The different findings can be explained by the different assumptions underlying the simulations. Verhoeven et al. (2006) assumed a distinct allele for each parental inbred. In this case large numbers of small populations show, due to the increased probability that some QTL haplotypes have only very small class size, a lower power to detect epistatic QTL than do a small number of large populations. However, the assumption made by Verhoeven et al. (2006) ignores the consequences of genetic drift that for real data not all QTL segregate in every population (Xu 1996). In our study this fact was considered by using SNP haplotype data of 26 inbreds as a basis of the simulations. Consequently, the mating designs resulting in a large number of small populations have indeed the above-mentioned disadvantage but this is compensated by the large number of individuals within populations segregating for the QTL.
The probability that QTL are segregating is increased in individual line crosses by using parental inbreds that are phenotypically the opposite extremes for the trait of interest (Xu 1998). However, this may not be helpful for detecting QTL for other traits. Furthermore, results of Burkhamer et al. (1998) suggest that inbreds showing a large genetic distance on the basis of molecular markers also strongly differ in their alleles at QTL. Therefore, we examined the DB approach by using only those parental combinations of the diallel to establish RILs that show, on the basis of all marker loci, the maximum genetic dissimilarity. A higher power to detect three-way interactions was observed for DB125 × 39 and DB195 × 25 than was found for NAM, SRR, and DAM4875. This indicated that the DB design is promising for increasing the probability that QTL are segregating in populations.
Nevertheless, we observed a lower power to detect three-way interactions for DB75 × 65 than for DB125 × 39 and DB195 × 25. The opposite result was expected, on the basis of the average genetic dissimilarity among the parental inbreds and the higher number of RILs per segregating population (Xie et al. 1998). Presumably, the reason for our observation is the insufficient sampling of QTL alleles of the base population if the number of selected parental combinations is too low (Muranty 1996; Wu and Jannink 2004).
In summary, the results of our study indicated that for a genetic dissimilarity among the parental inbreds such as that observed in this study the crossing schemes underlying the data sets DB125 × 39 and DB195 × 25 are the most promising designs to detect three-way interactions. However, our results also suggest that only RILs derived from optimally allocated DB designs show an increased power to detect three-way interactions. Nevertheless, the project “molecular and functional diversity of the maize genome” applies the crossing scheme underlying the NAM data set to construct RIL populations. The reasons are: (i) The common reference parent B73 has been the subject of extensive genetic and genomic studies (e.g., Morgante et al. 2005), and (ii) crossing the 25 diverse inbreds to the well-adapted inbred B73 facilitates both the development and the phenotypic evaluation of RILs.
Factors influencing the power and PFP to detect higher-order epistatic QTL in NAM:
Genetic architecture of the trait:
A higher power 1 − β* of detecting three-way interactions was observed with a single pathway influencing the phenotypic trait than with three pathways influencing the phenotypic trait (Table 2). This is due to the increased proportion of variance explained by a single pathway. Thus, if pathways explain unequal proportions of the genotypic variance, the power to detect epistatic interactions is higher for pathways explaining a large proportion of the genotypic variance than for pathways explaining a small proportion of the genotypic variance. Higher PFP was observed for the one-pathway scenario than for the three-pathway scenario. This finding can be explained by the higher power to detect three-way interactions in the former than in the latter scenario.
In our study the genotypic values for the four-locus genotypes were arranged in such a way that they are interpretable as molecular interactions among genes (Figure 1) (Jayaram and Peterson 1990). Nevertheless, for each individual pathway genic effects of four single loci, six two-way interactions, four three-way interactions, and one four-way interaction can be estimated (Yang 2004). In addition, the variances 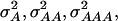 and
and 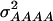 can be calculated. The variances
can be calculated. The variances 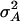 and
and 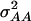 determined in our study under the assumption of allele frequencies of 0.5 agree well with those reported by Wolf et al. (2000) for various traits in an F2 maize population. Thus, we conclude that the assumptions underlying our simulations were realistic.
determined in our study under the assumption of allele frequencies of 0.5 agree well with those reported by Wolf et al. (2000) for various traits in an F2 maize population. Thus, we conclude that the assumptions underlying our simulations were realistic.
For pathways consisting of k QTL and showing mono-, di-, and trigenic effects similar to those of our study, a higher power to detect three-way interactions when k = 3 is expected. This is because a lower number of genic effects is influencing the genotypic value and, thus, each single genic effect is explaining a higher proportion of the genotypic variance. The opposite is expected for k > 4.
Detection method:
For the detection of three-way interactions, the four-step genome scan requires that the genic effects of at least one single locus and one two-way interaction are different from zero in addition to the genic effect of the three-way interaction. In contrast, using the three-step genome scan for the detection of three-way interactions the main effect of the QTL does not matter and only the interaction effect of all three QTL with the genetic background must be different from zero. Epistatic interactions among QTL cause QTL × genetic background interactions (Jannink and Jansen 2001) and, thus, the effect of the latter increases in our study with the size of the genic effects of two-, three-, and four-way interactions. Therefore, for both QTL detection approaches a higher power to detect three-way interactions is expected if genotypic values are assumed for the four-locus genotypes such that all genic effects have a higher absolute value than in our study. The opposite result is expected if all genic effects show a lower absolute value than in our study.
Different trends of the power to detect three-way interactions are expected for the two QTL detection approaches, if all genic effects of at least one of the steps, a single locus or two-way interactions, decrease. While a strong reduction in power to detect three-way interactions is expected by using the four-step genome scan, only a weak reduction is expected for the three-step genome scan. In the extreme, if all genic effects of one of these steps are zero, three-way interactions can be detected only by using the three-step genome scan. However, this case is very unlikely (Marchini et al. 2005). Further research is needed concerning the most promising detection method for epistatic interactions under different genetic architectures.
Probability of QTL segregation:
The probability of QTL segregation is influenced by (i) the average and (ii) the variance of the genetic dissimilarity among the parental inbreds of the RILs. The higher the average genetic dissimilarity among the parental inbreds, the higher the power is to detect three-way interactions for RILs derived from all mating designs. For a low average genetic dissimilarity the opposite result is expected. The optimal number of populations and RILs per population is not influenced by the average genetic dissimilarity among the parental inbreds. In contrast, the higher the variance of the genetic dissimilarity among the parental inbreds, the larger the difference in power 1 − β* is between mating designs considering genetic dissimilarities, like DB designs, and mating designs neglecting this information. For a low variance of the genetic dissimilarity the opposite result is expected.
Genetic map distance between marker loci and QTL:
In our study all SNPs, and also those treated as QTL, were included in the statistical analyses. This is because the proposed mapping strategy requires that markers are available for the QTL itself, which is true if the genome sequence of all RILs is known. Due to the fast progress of genome sequencing techniques (Churchill et al. 2004; Shendure et al. 2004) this is a realistic assumption in the foreseeable future, which maximizes the power to detect three-way interactions.
A decreased power to detect three-way interactions and an increased PFP are expected if RILs are genotyped for a lower number of SNPs. This is attributable to the decreased probability of substantial LD between QTL and marker loci (Marchini et al. 2005). Furthermore, the application of the proposed mapping strategy to true data sets for which the genome sequence of all individuals is not available requires major modifications, the most important one being that in this case QTL detection is based on LD between QTL and adjacent molecular markers and, thus, the correlation structure among the RILs must be considered. Furthermore, in some cases it might be necessary to (i) assume a certain QTL allele for each parental inbred or (ii) use multilocus haplotype data to infer parental allelic relationships at QTL (Jansen et al. 2003).
Heritability of the trait:
Increasing h2 from 0.5 to 0.8 resulted for all examined data sets and both numbers of QTL in a considerably higher power to detect three-way interactions. This is because for h2 = 0.8 the environmental influence on the phenotypic trait is reduced in comparison with h2 = 0.5. Hence, increasing h2 by conducting field experiments with several replications in several environments is a promising approach to increase the power to detect three-way interactions. However, in studies with a fixed budget this implies a reduction of the number of RILs to be tested in field experiments. Further research is needed concerning the optimal allocation of resources with respect to the number of RILs and the intensity of their phenotypic evaluation.
A higher PFP was observed for scenarios underlying a high heritability than for scenarios underlying a low heritability. This finding can be explained by the higher power to detect three-way interactions in the former than in the latter scenario.
Number of examined RILs:
Up to now, published QTL mapping experiments with replicated trials mostly employed between 100 and 200 progenies (Melchinger et al. 1998). Experiments of this size have a low power to detect epistatic QTL (Mihaljevic et al. 2005). However, in our study the power to detect three-way interactions with 5000 RILs derived from a nested design was relatively high for both the 4-QTL and the 12-QTL scenarios. Also the observed PFP of ∼0.54 (4 QTL) and 0.29 (12 QTL) was at an acceptable level considering the complex genetic architecture. Nevertheless, near-isogenic lines should be used to validate the identified epistatic interactions. For the validation of each identified three-way interaction, eight near-isogenic lines are required.
For detection of three-way interactions in pathways more complex than that of our study, the NAM data set must be complemented with additional RILs. Furthermore, our results suggest that the optimally allocated DB approach is more appropriate for complementing the NAM data set than deriving additional RILs from a diallel.
Acknowledgments
The authors thank the Cornell Institute for Social and Economic Research for use of their computer cluster. The authors thank the associate editor and two anonymous reviewers for their valuable suggestions. This work was supported by the National Science Foundation (DBI-9872631 and DBI-0321467) and the Department of Agriculture–Agricultural Research Service. Financial support for B.S. was provided by a grant from the German National Academic Foundation. Financial support for J.Y. was provided in part by a grant from the Department of Agriculture Cooperative State Research, Education, and Extension Service–National Research Initiative Plant Genome Program. Financial support for H.P.M. and H.F.U. was provided by grant 0313126B “GABI–BRAIN” within the framework “Genome Analysis of the Plant Biological System” supported by the German Federal Ministry of Education, Research and Technology.
References
- Alonso-Blanco, C., S. E.-D. El-Assal, G. Coupland and M. Kornneef, 1998. Analysis of natural allelic variation at flowering time loci in the Landsberg erecta and Cape Verde Islands ecotypes of Arabidopsis thaliana. Genetics 149: 749–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baierl, A., M. Bogdan, F. Frommlet and A. Futschik, 2006. On locating multiple interacting quantitative trait loci in intercross designs. Genetics 173: 1693–1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanc, G., A. Charcosset, B. Mangin, A. Gallais and L. Moreau, 2006. Connected populations for detecting quantitative trait loci and testing for epistasis: an application in maize. Theor. Appl. Genet. 113: 206–224. [DOI] [PubMed] [Google Scholar]
- Blott, S., J. J. Kim, S. Moisio, A. Schmidt-Kuntzel, A. Cornet et al., 2003. Molecular dissection of a quantitative trait locus: a phenylalanine-to-tyrosine substitution in the transmembrane domain of the bovine growth hormone receptor is associated with a major effect on milk yield and composition. Genetics 163: 253–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogdan, M., J. K. Ghosh and R. W. Doerge, 2004. Modifying the Schwarz Bayesian information criterion to locate multiple interacting quantitative trait loci. Genetics 167: 989–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkhamer, R. L., S. P. Lanning, R. J. Martens, J. M. Martin and L. E. Talbert, 1998. Predicting progeny variance from parental divergence in hard red spring wheat. Crop Sci. 38: 234–248. [Google Scholar]
- Carlborg, Ö., and C. S. Haley, 2004. Epistasis: Too often neglected in complex trait studies? Nat. Rev. Genet. 5: 618–625. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., D. C. Airey, H. Allayee, J. M. Nagel, A. D. Attie et al., 2004. The collaborative cross, a community resource for the genetic analysis of complex traits. Nat. Genet. 36: 1133–1137. [DOI] [PubMed] [Google Scholar]
- Doebley, J., A. Stec and C. Gustus, 1995. Teosinte branched1 and the origin of maize: evidence for epistasis and the evolution of dominance. Genetics 141: 333–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efroymson, M. A., 1960. Multiple regression analysis, pp. 191–203 in Mathematical Methods for Digital Computers, edited by A. Ralston and H. S. Wilf. Wiley, New York.
- Fernando, R. L., D. Nettleton, B. R. Southey, J. C. M. Dekkers, M. F. Rothschild et al., 2004. Controlling the proportion of false positives in multiple dependent tests. Genetics 166: 611–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint-Garcia, S. A., A. Thuillet, J. Yu, G. Pressoir, S. M. Romero et al., 2005. Maize association population: a high resolution platform for QTL dissection. Plant J. 44: 1054–1064. [DOI] [PubMed] [Google Scholar]
- Griffing, B., 1956. Concept of general and specific combining ability in relation to diallel crossing systems. Aust. J. Biol. Sci. 9: 463–493. [Google Scholar]
- Jannink, J.-L., and R. Jansen, 2001. Mapping epistatic quantitative trait loci with one-dimensional genome searches. Genetics 157: 445–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen, R. C., J.-L. Jannink and W. D. Beavis, 2003. Use of parental haplotype sharing. Crop Sci. 43: 829–834. [Google Scholar]
- Jayaram, C., and P. A. Peterson, 1990. Anthocyanin pigmentation and transposable elements in maize aleurone. Plant Breed. Rev. 8: 91–137. [Google Scholar]
- Lander, E. S., and D. Botstein, 1989. Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121: 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, K., M. Goodman, S. Muse, J. S. Smith, E. Buckler et al., 2003. Genetic structure and diversity among maize inbred lines as inferred from DNA microsatellites. Genetics 165: 2117–2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini, J., P. Donnelly and L. R. Cardon, 2005. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat. Genet. 4: 413–417. [DOI] [PubMed] [Google Scholar]
- Maurer, H. P., A. E. Melchinger and M. Frisch, 2004. Plabsoft: software for simulation and data analysis in plant breeding, pp. 359–362 in Genetic Variation for Plant Breeding. Proceedings of the 17th Meeting of the EUCARPIA General Congress, edited by J. Vollmann, H. Grausgruber and P. Ruckenbauer. September 8–11, 2004, Tulln, Austria.
- McMullen, M. D., P. F. Byrne, M. E. Snook, B. R. Wiseman, E. A. Lee et al., 1998. Quantitative trait loci and metabolic pathways. Proc. Natl. Acad. Sci. USA 95: 1996–2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchinger, A. E., H. F. Utz and C. C. Schön, 1998. Quantitative trait locus (QTL) mapping using different testers and independent population samples in maize reveals low power of QTL detection and large bias in estimates of QTL effects. Genetics 149: 383–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H., A. Karlsen, S. Lien, I. Olsaker and M. E. Goddard, 2002. Fine mapping of a quantitative trait locus for twinning rate using combined linkage and linkage disequilibrium mapping. Genetics 161: 373–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihaljevic, R., H. F. Utz and A. E. Melchinger, 2005. No evidence for epistasis in hybrid and per se performance of elite European flint maize inbreds from generation means and QTL analyses. Crop Sci. 45: 2605–2613. [Google Scholar]
- Miller, A. J., 2002. Subset Selection in Regression. Chapman & Hall, London.
- Morgante, M., S. Brunner, G. Pea, K. Fengler, A. Zuccolo et al., 2005. Gene duplication and exon shuffling by helitron-like transposons generate intraspecies diversity in maize. Nat. Genet. 37: 997–1002. [DOI] [PubMed] [Google Scholar]
- Muranty, H., 1996. Power of tests for quantitative trait loci detection using full-sib families in different schemes. Heredity 76: 156–165. [Google Scholar]
- Nei, M., and W. H. Li, 1979. Mathematical model for studying genetic variation in terms of restriction endonucleases. Proc. Natl. Acad. Sci. USA 76: 5269–5273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piepho, H.-P., and H. G. Gauch, Jr., 2001. Marker pair selection for mapping quantitative trait loci. Genetics 157: 433–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team, 2004. R: A Language and Environment for Statistical Computing. R Development Core Team, Vienna, Austria.
- Rebai, A., P. Blanchard, D. Perret and P. Vincourt, 1997. Mapping quantitative trait loci controlling silking date in a diallel cross among four lines of maize. Theor. Appl. Genet. 95: 451–459. [Google Scholar]
- Remington, D. L., J. M. Thornsberry, Y. Matsuoka, L. M. Wilson, S. R. Whitt et al., 2001. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc. Natl. Acad. Sci. USA 98: 11479–11484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie, M. D., L. W. Hahn and J. H. Moore, 2003. Power of multifactor dimensionality reduction for detecting gene-gene interactions in the presence of genotyping error, missing data, phenocopy, and genetic heterogeneity. Genet. Epidemiol. 24: 150–175. [DOI] [PubMed] [Google Scholar]
- SAS Institute, 2005. Documentation GLMSELECT. SAS Institute, Cary, NC.
- Shendure, J., R. D. Mitra, C. Varma and G. M. Church, 2004. Advanced sequencing technologies: methods and goals. Nat. Rev. Genet. 5: 335–344. [DOI] [PubMed] [Google Scholar]
- Thornsberry, J. M., M. M. Goodman, J. Doebley, S. Kresovich, D. Nielsen et al., 2001. Dwarf 8 polymorphisms associate with variation in flowering time. Nat. Genet. 28: 286–289. [DOI] [PubMed] [Google Scholar]
- Verhoeven, K. J. F., J.-L. Jannink and L. M. McIntyre, 2006. Using mating designs to uncover QTL and the genetic architecture of complex traits. Heredity 96: 139–149. [DOI] [PubMed] [Google Scholar]
- Vuylsteke, M., M. Kuiper and P. Stam, 2000. Chromosomal regions involved in hybrid performance and heterosis: their AFLP®-based identification and practical use in prediction models. Heredity 85: 208–218. [DOI] [PubMed] [Google Scholar]
- Wilson, L. M., S. R. Whitt, A. M Ibáñez, T. R. Rocheford, M. M. Goodman et al., 2004. Dissection of maize kernel composition and starch production by candidate gene association. Plant Cell 16: 2719–2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf, D. P., L. A. Peternelli and A. R. Hallauer, 2000. Estimates of genetic variance in an F2 population of maize. J. Hered. 91: 384–391. [DOI] [PubMed] [Google Scholar]
- Wricke, G., and W. E. Weber, 1986. Quantitative Genetics and Selection in Plant Breeding. De Gruyter, Berlin.
- Wu, R., and Z.-B. Zeng, 2001. Joint linkage and linkage disequilibrium mapping in natural populations. Genetics 157: 899–909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, X. L., and J. L. Jannink, 2004. Optimal sampling of a population to determine QTL location, variance, and allelic number. Theor. Appl. Genet. 108: 1434–1442. [DOI] [PubMed] [Google Scholar]
- Xie, C., D. D. Gessler and S. Xu, 1998. Combining different line crosses for mapping quantitative trait loci using the identical by descent-based variance component method. Genetics 149: 1139–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, S., 1996. Mapping quantitative trait loci using four-way crosses. Genet. Res. 68: 175–181. [Google Scholar]
- Xu, S., 1998. Mapping quantitative trait loci using multiple families of line crosses. Genetics 148: 517–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, R. C., 2004. Epistasis of quantitative trait loci under different gene action models. Genetics 167: 1493–1505. [DOI] [PMC free article] [PubMed] [Google Scholar]