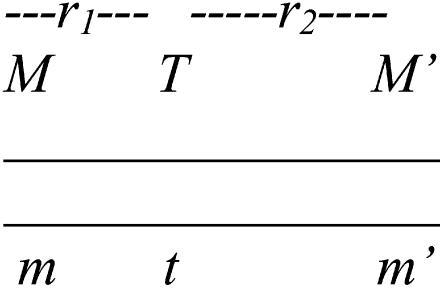Abstract
Cutaneous malignant melanoma in Sinclair swine is a hereditary disease that develops in utero or during the first 6 weeks of life. In many cases, the tumors regress and piglets survive the disease. Two different sets of gene(s) might be involved in the disease: tumor initiator (suppressor) locus or loci and loci affecting the aggressiveness of the disease (number and stage of tumors). We develop maximum-likelihood methods for interval mapping for both types of loci. The experimental design consisted of a boar mated to tumor-bearing sows with recording of tumor status and number of tumors in the 6 weeks of life of the offspring. The model to search for the tumor initiator locus (with alleles T and t) was tested by computer simulation. Estimates of penetrances (ΨTT and ΨTt for genotypes TT and Tt, respectively) were accurate even for small family sizes. Statistical power was >99% for a family size of 70 with ΨTT = 1 and ΨTt = 0. The models to test for number of tumors incorporated genotype information for the tumor initiator locus. All models were tested with data from a single boar family of 72 piglets over swine chromosomes 6 and 8 (SSC6 and SSC8). No tumor evidence for initiator loci was found associated with these chromosomes. However, association of a QTL affecting number of tumors at birth near microsatellite SW1953 on SSC8 was chromosomewise significant (P < 0.0124).
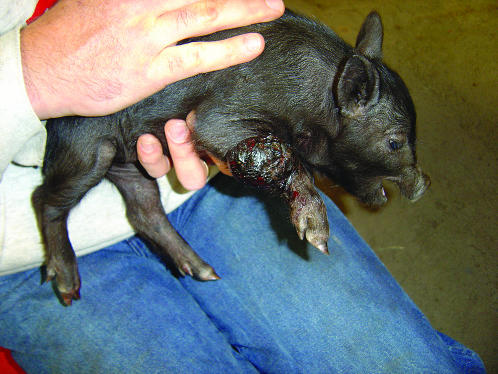
CUTANEOUS malignant melanoma of Sinclair swine (SSCM) (Figure 1) is a highly heritable (Hook et al. 1979; Tissot et al. 1987), histopathologically well-characterized metastatic disease (Das Gupta et al. 1989; Greene et al. 1994, 1997). Some animals die due to widespread disease but many develop a cell-mediated immune response that causes complete regression of the tumors (Greene et al. 1997).
Figure 1.—
Sinclair piglet with a malignant melanoma tumor in his right leg.
Malignant melanoma in Sinclair swine is a model to investigate familial malignant melanoma (FMM) in humans. FMM displays an apparent genetic heterogeneity, with four genes identified as susceptibility loci. Locus HSA p16/ARF on 9p21 (Cannon-Albright et al. 1992; Kamb et al. 1994; Hussussian et al. 1994) encodes two distinct melanoma predisposition genes, cyclin-dependent kinase inhibitor 2A (CDKN2A) (also called p16 or inhibitor of cyclin-dependent kinase 4A, INK4a) and ARF or p14 (Nobori et al. 1994; Quelle et al. 1995). Another high-penetrance melanoma predisposition gene is the cyclin-dependent kinase 4 (CDK4) located on HSA 12q13 (Zuo et al. 1996; Soufir et al. 1998). The fourth gene, the melanocortin receptor 1 (MC1R) gene, located on HSA 16q24.3, is a low-penetrance gene (Palmer et al. 2000). All four genes together account for half of FMM cases (Pho et al. 2006).
Research on the loci responsible for hereditary diseases in humans is limited by the small number of patients in human families. The limitation is much aggravated when there are several loci involved in susceptibility and penetrance of the disease and these loci interact in a nonadditive fashion. That is, knowing the effect of several individual loci on the disease does not help one to fully understand how all loci influence the disease jointly.
Studies that combined classical breeding (Tissot et al. 1987) and complex segregation analysis (Blangero et al. 1992) suggested that three major loci are involved in the inheritance and expression of SSCM. One locus contains a putative “tumor initiator (suppressor) gene” responsible for SSCM initiation. A second locus may lie within or close to the swine leukocytic antigen (SLA) complex on swine chromosome 7 (SSC7), and a third, as yet unidentified locus, affects the penetrance of the initiator locus. It has been hypothesized that the tumor initiator locus was a homozygous lethal in utero (Blangero et al. 1996) but this has not been verified. The complex inheritance of this disease, involving several loci with different penetrance and possibly different modes of gene action, makes resolving the mode of inheritance of this disease difficult just by phenotypic recording of crosses and tumor susceptibility in the offspring.
The availability of polymorphic DNA markers for the pig allowed their use to identify putative loci affecting melanoma susceptibility. A genome scan was carried out by Geffrotin et al. (2004), using the melanoblastoma-bearing Libechov minipig (MeLiM), which identified five chromosomal regions involved in predisposition to melanoma in SSC1, SSC2, SSC6, SSC7, and SSC8. The MeliM pig probably has a common ancestry with Sinclair swine via the Hormel strain of minipigs (Porter 1993). Geffrotin et al. (2004) used a backcross design and classified animals phenotypes I–IV according to their type of lesion. Phenotype I animals had the most severe lesions and phenotype IV animals were free of any lesions. Interval mapping with all four phenotypes was used to search for genes involved in melanoma susceptibility and penetrance. This approach does not consider that genes affecting initiation of melanoma might be different from genes affecting the severity of the lesions. In addition, they used a transmission disequilibrium test (Spielman et al. 1993) with only phenotypes I and IV to test the inheritance of marker alleles in susceptible offspring. However, this test does not use information on all offspring and does not test for tumor initiation genes within intervals bracketed by flanking markers.
Models that assume that the loci involved in initiation might be different from those loci contributing to the aggressiveness of the disease (represented by, e.g., the severity of the lesions or the number of tumors) could be constructed using maximum-likelihood methods. This approach would recognize the fact that individuals without tumors may be the result of either not being a carrier of tumor initiator alleles at the tumor initiator locus or being a carrier of tumor initiator alleles at the tumor initiator locus, but also a carrier of alleles at other loci related to low severity of the lesions or a low number of tumors.
We have approached this problem by: (1) developing a maximum-likelihood method to perform interval mapping of tumor initiator loci in Sinclair swine, (2) developing a maximum-likelihood method for interval mapping of a tumor suppressor locus with full mortality of homozygotes in utero, and (3) developing maximum-likelihood methods for interval mapping of loci affecting the aggressiveness of the disease (number of tumors), but accounting for the individual genotype of a tumor initiator locus located elsewhere in the genome. The models for interval mapping of the tumor initiator locus were tested by computer simulations. All interval mapping methods were used to search for the tumor initiator locus and for loci affecting the virulence of the disease in chromosomes 6 and 8 in a single boar family comprising 72 Sinclair piglets from 11 tumor-bearing dams.
THEORY
Experimental design and genetic model:
Assume that a boar is heterozygous at a tumor initiator locus and has a mixture of susceptible and nonsusceptible melanoma offspring. The boar is mated to a number of sows resulting in a total number of n offspring. The tumor initiator locus has alleles T and t, and among all gametes, the frequency of allele T coming from the dam population is fT. Offspring from this boar (with genotype Tt) will be TT, Tt, or tt with frequencies 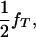
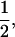 and
and 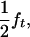 respectively. If ΨTT and ΨTt are the penetrances of the TT and Tt offspring, then the frequencies of susceptible and nonsusceptible offspring are
respectively. If ΨTT and ΨTt are the penetrances of the TT and Tt offspring, then the frequencies of susceptible and nonsusceptible offspring are 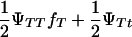 and 1 − (
and 1 − (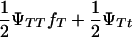 ), respectively. Penetrance is defined as the probability of initiating the disease given the genotype (ΨTT and ΨTt for TT and Tt individuals, respectively). It is not possible to estimate penetrances ΨTT and ΨTt together with allele frequency fT, since a given frequency of susceptible offspring may result from either a high penetrance or a high fT; i.e., penetrance and frequency of allele T are confounded. In the above formula, this is represented by the term
), respectively. Penetrance is defined as the probability of initiating the disease given the genotype (ΨTT and ΨTt for TT and Tt individuals, respectively). It is not possible to estimate penetrances ΨTT and ΨTt together with allele frequency fT, since a given frequency of susceptible offspring may result from either a high penetrance or a high fT; i.e., penetrance and frequency of allele T are confounded. In the above formula, this is represented by the term 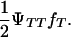 To ease this problem we propose an experimental setting including a boar mated only to susceptible gilts and evaluating the corresponding likelihoods at a given high fT. That is, the experiment is designed such that fT is forced to be high. Description of all variables in all models is given in Table 1.
To ease this problem we propose an experimental setting including a boar mated only to susceptible gilts and evaluating the corresponding likelihoods at a given high fT. That is, the experiment is designed such that fT is forced to be high. Description of all variables in all models is given in Table 1.
TABLE 1.
Variables used in the formulas for mapping a tumor initiator locus with a single DNA marker, interval mapping of a tumor initiator locus, and interval mapping of a locus affecting number of tumors
| ΨTT | Penetrance of homozygotes for allele T at the tumor initiator locus |
| ΨTt | Penetrance of heterozygotes for alleles T and t at the tumor initiator locus |
| fT | Frequency of the allele T among gametes contributed by the dams |
| cx | Recombination fraction between DNA marker and tumor initiator locus when mapping using a single DNA marker |
| tMs | No. of offspring with tumors and inheriting allele Ms initiator locus when mapping using a single DNA marker |
| t′Ms | No. of offspring without tumors and inheriting allele Ms initiator locus when mapping using a single DNA marker |
| tms | No. of offspring with tumors and inheriting allele ms initiator locus when mapping using a single DNA marker |
| t′ms | No. of offspring without tumors and inheriting allele ms initiator locus when mapping using a single DNA marker |
| r1 and r2 | Recombination fractions between each of the two DNA markers and the tumor initiator locus in interval mapping for the tumor initiator locus |
| c | Recombination fractions between the two DNA markers in interval mapping for the tumor initiator locus |
| tMM′ | No. of offspring with tumors and inheriting alleles MM′ at the tumor initiator locus in interval mapping |
| t′MM′ | No. of offspring without tumors and inheriting alleles MM′ at the tumor initiator locus in interval mapping |
| tMm′ | No. of offspring with tumors and inheriting alleles Mm′ at the tumor initiator locus in interval mapping |
| t′Mm′ | No. of offspring without tumors and inheriting alleles Mm′ at the tumor initiator locus in interval mapping |
| tmM′ | No. of offspring with tumors and inheriting alleles mM′ at the tumor initiator locus in interval mapping |
| t′mM′ | No. of offspring without tumors and inheriting alleles mM′ at the tumor initiator locus in interval mapping |
| tmm′ | No. of offspring with tumors and inheriting alleles Mm′ at the tumor initiator locus in interval mapping |
| t′mm′ | No. of offspring without tumors and inheriting alleles mm′ at the tumor initiator locus in interval mapping |
| PT | Probability of developing melanoma conditional on marker information in the full model |
| PNT | Probability of not developing melanoma conditional on marker information in the full model |
| PTNULL | Probability of developing melanoma conditional on marker information under the null hypothesis |
| PNTNULL | Probability of not developing melanoma conditional on marker information under the null hypothesis |
| PTBG | Probability of developing melanoma conditional on marker information in Blangero's model |
| PNTBG | Probability of not developing melanoma conditional on marker information in Blangero's model |
| s | Selection coefficient for Blangero's model, s = 1 implies full lethality of TT individuals, s = 0 implies full survival of TT individuals |
| r1 and rn | Recombination fractions between each of the two DNA markers and the locus affecting no. of tumors |
| r(n) | Recombination fractions between the two DNA markers bracketing the locus affecting no. of tumors |
| μQ and μq | Average no. of tumors among offspring inheriting Q and q alleles from the boar |
| TBIRTH | No. of tumors at birth |
| T6WK | No. of tumors at 6 wk |
| TB–6WK | Difference between no. of tumors at birth and at 6 wk |
| TMAX | Maximum no. of tumors during the first 6 wk of life |
Tumor initiator locus mapped with a single DNA marker:
Assume that the linkage phase in the boar is TMs/tms, where T and t are the alleles at the tumor initiator locus and Ms and ms are the alleles at the DNA marker. The recombination fraction between the two loci is cx. There are four types of offspring from this boar corresponding to piglets either susceptible or nonsusceptible to the disease and inheriting either allele T or allele t. Thus, four types of gametes will be produced by the boar: TMs, tMs, Tms, and tms. Using the frequencies (Table 2) and penetrances for each genotype in the offspring, the maximum-likelihood equation conditional on marker information is
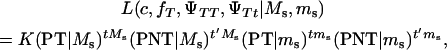 |
where
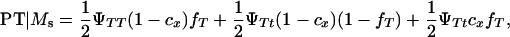 |
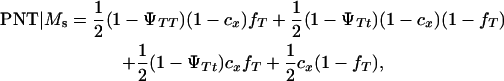 |
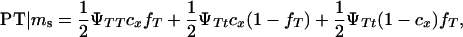 |
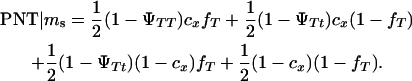 |
K is a constant, fT is the frequency of allele T in the dam population, PT | Ms and PNT | Ms are the conditional probabilities of initiating and not initiating the disease conditional to inheriting marker allele Ms from the boar, PT | ms and PNT | ms are the conditional probabilities of initiating and not initiating the disease conditional to inherit marker allele ms from the boar, tMs and t′Ms are the number of offspring with and without tumors inheriting allele Ms from the boar, and tms and t′ms are the number of offspring with and without tumors inheriting allele ms from the boar, respectively. The probabilities PT and PNT are computed using the expected frequencies of the different genotypes (Table 2).
TABLE 2.
Probabilities of offspring genotypes to construct the equations for mapping a single tumor initiator locus with a single DNA marker
| Dam allele and frequency
|
|||
|---|---|---|---|
| Sire | Frequency | TfT | t(1 − fT) |
| TMs |
 (1 − cx) (1 − cx) |
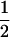 (1 − cx)fT (1 − cx)fT
|
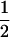 (1 − cx)(1− fT) (1 − cx)(1− fT) |
| Tms | 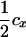 |
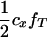 |
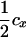 (1 − fT) (1 − fT) |
| tMs | 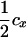 |
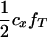 |
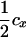 (1 − fT) (1 − fT) |
| tms |
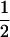 (1 − cx) (1 − cx) |
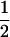 (1 − cx)fT (1 − cx)fT
|
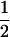 (1 − cx)(1 − fT) (1 − cx)(1 − fT) |
The linkage phase of the tumor initiator locus and DNA marker in the boar is TMs/tms, where T/t are the alleles at the tumor locus and Ms/ms are the alleles at the DNA marker. fT is the frequency of allele T among gametes produced by the sows.
Interval mapping for a tumor initiator locus:
A genome scan requires that DNA markers are evenly spaced at intervals of ≤20 cM to detect a chromosomal area segregating for a locus affecting the trait in question. We assumed that the recombination fraction between each pair of DNA markers and the linkage phase of the boar is known. In practice, both the recombination fraction and the linkage phase of the boar are estimated from the same data over which interval mapping is performed. For interval mapping, the inheritance of alternative alleles from the boar on tumor-bearing and not-tumor-bearing offspring is modeled using maximum likelihood. The assumed linkage phase of the boar for some DNA markers and the putative tumor initiator locus is depicted in Figure 2, with one of the homologous chromosomes being MM′ and the other mm′ for the two DNA markers. The recombination fractions between each of the two DNA markers and the tumor initiator locus are r1 and r2. The recombination fraction between the two DNA markers is c. The likelihood equation for interval mapping is
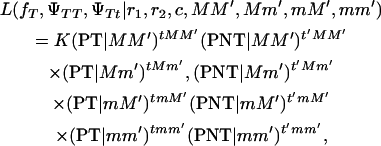 |
(1) |
where K is a constant, and PT | MM′, PT | Mm′, PT | mM′, and PT | mm′ are the probabilities of developing melanoma conditional to inheriting DNA marker alleles MM′, Mm′, mM′, and mm′ from the boar, respectively. The probabilities PNT | MM′, PNT | Mm′, PNT | mM′, and PNT | mm′ are the probabilities of not developing melanoma conditional to inheriting DNA markers MM′, Mm′, mM′, and mm′ from the boar, respectively. The probabilities PT and PNT can be derived using the equations presented in Table 3. Their values are shown in Table 4. The number of tumor-bearing offspring inheriting alleles MM′, Mm′, mM′, and mm′ from the boar are tMM′, tMm′, tmM′, and tmm′ from the boar, respectively. The number of offspring without tumors inheriting alleles MM′, Mm′, mM′, and mm′ from the boar are t′MM ′, t′Mm ′, t′mM ′, and t′mm ′ from the boar, respectively. Estimation of penetrances ΨTT and ΨTt are carried out assuming fT is known since fT is confounded with ΨTT and ΨTt. A statistical test was performed every 1 cM in the interval between each two DNA marker assuming a distance, r1, between the tumor initiator locus and the first DNA marker and with r2 = [c − r1]/[1 − 2r1] representing the distance between the tumor initiator locus and the second DNA marker (assuming no interference by the use of Trow's formula: c = r1 + r2 − 2r1r2).
Figure 2.—
Marker genotype configuration in the boar for interval mapping.
TABLE 3.
Offspring genotypes and their probabilities used in the equations for interval mapping of a tumor initiator locus in Equation 1
| Offspring genotype | Allele from boar | Allele from dam and frequency
|
||
|---|---|---|---|---|
| Frequency | T, fT | t, (1 − fT) | ||
| MM′ | T | [(1 − r1)(1 − r2)]/2 | TT | Tt |
| fT[(1 − r1)(1 − r2)]/2 | (1 − fT)[(1 − r1)(1 − r2)]/2 | |||
| t | [r1r2]/2 | Tt | tt | |
| fT [r1r2]/2 | (1 − fT)[r1r2]/2 | |||
| Mm′ | T | [(1 − r1)r2]/2 | TT | Tt |
| fT[(1 − r1)r2]/2 | (1 − fT)[(1 − r1)r2]/2 | |||
| t | [(1 − r2)r1]/2 | Tt | tt | |
| fT[(1 − r2)r1]/2 | (1 − fT)[(1 − r2)r1]/2 | |||
| mM′ | T | [(1 − r2)r1]/2 | TT | Tt |
| fT[(1 − r2)r1]/2 | (1 − fT)[(1 − r2)r1]/2 | |||
| t | [(1 − r1)r2]/2 | Tt | tt | |
| fT[(1 − r1)r2]/2 | (1 − fT)[(1 − r1)r2]/2 | |||
| mm′ | T | [r1r2]/2 | TT | Tt |
| fT[r1r2]/2 | (1 − fT)[r1r2]/2 | |||
| t | [(1 − r1)(1 − r2)]/2 | Tt | tt | |
| fT[(1 − r1)(1 − r2)]/2 | (1 − fT)[(1 − r1)(1 − r2)]/2 | |||
The linkage phase in the boar is MM′/mm′.
TABLE 4.
Probabilities of being tumor (PT) and not tumor (PNT) conditional on marker genotype information in the offspring (MM′, Mm′, mM′, and mm′)
| PT | MM′ | ΨTT fT[(1 − r1)(1 − r2)]/2 + ΨTt{(1 − fT)[(1 − r1)(1 − r2)]/2 + fT[(r1r2]/2} |
| PNT | MM′ | (1 − ΨTT)fT[(1 − r1)(1 − r2)]/2 + (1 − ΨTt){(1 − fT)[(1 − r1)(1 − r2)]/2 + fT[(r1r2]/2}+ (1 − fT)r1r2/2 |
| PT | Mm′ | ΨTTfT[(1 − r1)r2/2 ] + ΨTt{(1 − fT)[(1 − r1)r2]/2 + fT[(1 − r2)r1]/2} |
| PNT | Mm′ | (1 − ΨTT)fT[(1 − r1)r2/2] + (1 − ΨTt){(1 − fT)[(1 − r1)r2]/2 + fT[(1 − r2)r1]/2} + (1 − fT)(1 − r2)r1/2 |
| PT | mM′ | ΨTTfT[(1 − r2)r1]/2 + ΨTt{[(1 − fT) [(1 − r2)r1]/2 + fT[(1 − r1)r2]/2]} |
| PNT | mM′ | (1 − ΨTT)fT[(1 − r2)r1]/2 + (1 − ΨTt){[(1 − fT)[(1 − r2)r1]/2 + fT[(1 − r1)r2]/2]} + (1 − fT)[(1 − r1)r2]/2 |
| PT | mm′ | ΨTTfT[r1r2]/2 + ΨTt{(1 − fT)[r1r2]/2 + fT[(1 − r1)(1 − r2)]/2} |
| PNT | mm′ | (1 − ΨTT)fT[r1r2]/2 + (1 − ΨTt){(1 − fT)[r1r2]/2 + fT[(1 − r1)(1 − r2)]/2} + (1 − fT)[(1 − r1)(1 − r2)]/2 |
For the null hypothesis, we must assume that the locus contributing to the disease is located on another chromosome or in the same chromosome but far away from the point we are testing. This is a necessary assumption to account for the boar segregating offspring with and without melanoma. Another maximum-likelihood equation is developed for the null hypothesis,
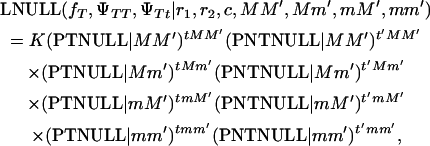 |
(2) |
where PTNULL | MM′ = 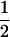 (ΨTT fT +ΨTt)(
(ΨTT fT +ΨTt)(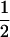 ((1 − r1)(1 − r2) + r1r2)), PNTNULL | MM′ = (1 −
((1 − r1)(1 − r2) + r1r2)), PNTNULL | MM′ = (1 − 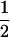 (ΨTT fT + ΨTt))(
(ΨTT fT + ΨTt))(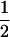 ((1 − r1)(1 − r2) + r1r2)), PTNULL | Mm′ =
((1 − r1)(1 − r2) + r1r2)), PTNULL | Mm′ = 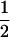 (ΨTT fT +ΨTt)(
(ΨTT fT +ΨTt)(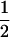 (1 − r2)(r1) + (
(1 − r2)(r1) + (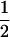 (1 − r1)(r2)), PNTNULL | Mm′ = (1 −
(1 − r1)(r2)), PNTNULL | Mm′ = (1 − 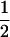 (ΨTT fT +ΨTt))(
(ΨTT fT +ΨTt))(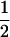 (1 − r2)(r1) + (
(1 − r2)(r1) + (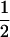 (1 − r1)(r2)), PTNULL | mM′ =
(1 − r1)(r2)), PTNULL | mM′ = 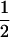 (ΨTT fT +ΨTt)(
(ΨTT fT +ΨTt)(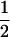 (1 − r2)(r1) + (
(1 − r2)(r1) + (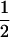 (1 − r1)(r2)), PNTNULL | mM′ = (1 −
(1 − r1)(r2)), PNTNULL | mM′ = (1 − 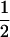 (ΨTT fT +ΨTt))(
(ΨTT fT +ΨTt))(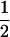 (1 − r2)(r1) + (
(1 − r2)(r1) + (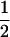 (1 − r1)(r2)), PTNULL | mm′ =
(1 − r1)(r2)), PTNULL | mm′ = 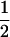 (ΨTT fT +ΨTt)(
(ΨTT fT +ΨTt)(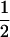 ((1 − r1)(1 − r2) + r1r2)), PNTNULL | mm′ = (1 −
((1 − r1)(1 − r2) + r1r2)), PNTNULL | mm′ = (1 − 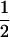 (ΨTT fT +ΨTt))(
(ΨTT fT +ΨTt))(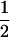 ((1 − r1)(1 − r2) + r1r2)). In these equations, the first factor represents the probability of being melanoma susceptible and the second factor the probability of inheriting DNA markers in that particular fragment. These two probabilities are independent of each other under the null hypothesis. Hypothesis testing can then be carried out by a lod score:
((1 − r1)(1 − r2) + r1r2)). In these equations, the first factor represents the probability of being melanoma susceptible and the second factor the probability of inheriting DNA markers in that particular fragment. These two probabilities are independent of each other under the null hypothesis. Hypothesis testing can then be carried out by a lod score:
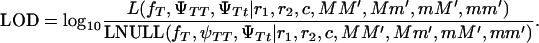 |
Note that because of the way the null hypothesis is constructed, the lod score can yield negative values; i.e., the null hypothesis (tumor locus located elsewhere in the genome) is more likely than the alternative hypothesis (tumor linked to the chromosomal fragment being tested). A likelihood-ratio test can also be constructed:
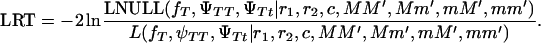 |
Interval mapping for a tumor initiator locus with full lethality of homozygotes:
To test the hypothesis of lethality in utero of homozygotes for the tumor initiator allele, T (Blangero et al. 1996), the above model of interval mapping can be generalized. Consider that selection coefficient S1 = (1 − s) is applied to homozygotes TT and selection coefficient S2 = 1 − s + [s/(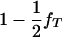 )] to any other genotype (Tt and tt). In these equations, s determines the fate of different genotypes in coefficients S1 and S2. If s = 1, then S1 = 0 and S2 = 1/(
)] to any other genotype (Tt and tt). In these equations, s determines the fate of different genotypes in coefficients S1 and S2. If s = 1, then S1 = 0 and S2 = 1/(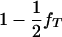 ). Therefore, for s = 1, offspring with genotype TT die before birth and the proportion of the remaining genotypes in the offspring is adjusted accordingly. Since the boar is heterozygous Tt the frequency of offspring dying in utero is
). Therefore, for s = 1, offspring with genotype TT die before birth and the proportion of the remaining genotypes in the offspring is adjusted accordingly. Since the boar is heterozygous Tt the frequency of offspring dying in utero is 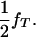 If s = 0, then S1 = 1 and S2 = 1. For s = 0, all offspring survive at birth and the model reduces to Equation 1. The maximum-likelihood equation, assuming the hypothesis of Blangero et al. (1996), is
If s = 0, then S1 = 1 and S2 = 1. For s = 0, all offspring survive at birth and the model reduces to Equation 1. The maximum-likelihood equation, assuming the hypothesis of Blangero et al. (1996), is
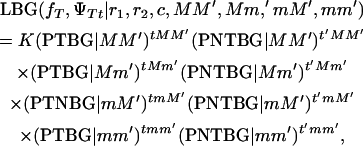 |
(3) |
where the values of the probabilities of offspring with tumors (PTBG) and offspring without tumors (PNTBG), conditional on the marker information, are given in Table 5.
TABLE 5.
Conditional probabilities from Equation 3 (Blangero model) allowing homozygotes for allele T to die before birth
| PTBG | MM′ | S1ΨTTfT[(1 − r1)(1 − r2)]/2 + S2ΨTt{(1 − fT)[(1 − r1)(1 − r2)]/2 + fT[(r1r2]/2} |
| PNTBG | MM′ | S1(1 − ΨTT)fT[(1 − r1)(1 − r2)]/2 + S2(1 − ΨTt){(1 − fT)[(1 − r1)(1 − r2)]/2 + fT[(r1r2]/2} + S2(1 − fT)r1r2/2 |
| PTBG | Mm′ | S1ΨTTfT[(1 − r1)r2/2 ] + S2ΨTt{(1 − fT)[(1 − r1)r2]/2 + fT[(1 − r2)r1]/2} |
| PNTBG | Mm′ | S1(1 − ΨTT)fT[(1 − r1)r2/2] + S2(1 − ΨTt){(1 − fT)[(1 − r1)r2]/2 + fT[(1 − r2)r1]/2} + S2(1 − fT)(1 − r2)r1/2 |
| PTBG | mM′ | S1ΨTTfT[(1 − r2)r1]/2 + S2ΨTt{[(1 − fT) [(1 − r2)r1]/2 + fT[(1 − r1)r2]/2]} |
| PNTBG | mM′ | S1(1 − ΨTT)fT[(1 − r2)r1]/2 + S2(1 − ΨTt){[(1 − fT)[(1 − r2)r1]/2 + fT[(1 − r1)r2]/2]} + S2(1 − fT)[(1 − r1)r2]/2 |
| PTBG | mm′ | S1ΨTTfT[r1r2]/2 + S2(ΨTt){(1 − fT)[r1r2]/2 + fT[(1 − r1)(1 − r2)]/2} |
| PNTBG | mm′ | S1(1 − ΨTT)fT[r1r2]/2 + S2(1 − ΨTt){(1 − fT)[r1r2]/2 + fT[(1 − r1)(1 − r2)]/2} + S2(1 − fT)[(1 − r1)(1 − r2)]/2 |
S1, S2, r1, r2, fT, ΨTT, and ΨTt are defined in the text.
The parameterization used with s = 1 for a full model and s = 0 for testing the hypothesis of Blangero et al. (1996) allows comparing the likelihoods using the logarithm of odds (LOD) of the likelihoods of the two models,
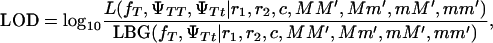 |
(4) |
where 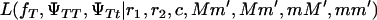 and
and 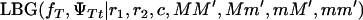 are the likelihoods for the full model (Equation 1) and the Blangero model (Equation 3), respectively.
are the likelihoods for the full model (Equation 1) and the Blangero model (Equation 3), respectively.
Interval mapping for number of tumors:
Once the tumor initiator locus or loci involved in susceptibility to malignant melanoma are mapped, the same loci or other loci may affect the aggressiveness of the disease. This can be represented by the number of tumors at birth (TBIRTH), the number of tumors at 6 weeks of age (T6WK), the number of tumors developed (or regressed) during the first 6 weeks of life (TB–6WK), and the maximum number of tumors developed during the first 6 weeks of life (TMAX). A maximum-likelihood approach testing the inheritance of alternative marker alleles from the boar can be used. For simplicity, normality is assumed. Assume that the linkage phase of the boar is M1M1′/m1m1′ and that n piglets are typed and scored for the trait. The likelihood equation is
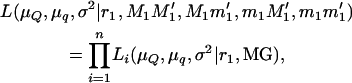 |
(5) |
where μQ and μq are the means of the offspring inheriting alternative alleles Q or q from the boar, σ2 is the variance of the trait, n is the number of piglets, and Li is the likelihood of the ith piglet inheriting × tumors conditional on the marker genotype inherited from the boar (MG = M1M1′, M1m1′, m1M1′, m1m1′), and
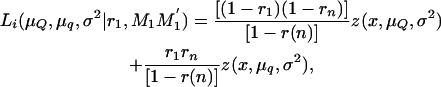 |
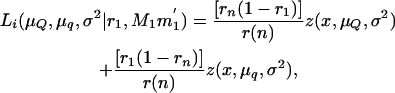 |
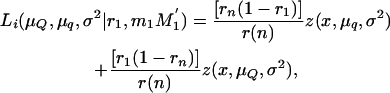 |
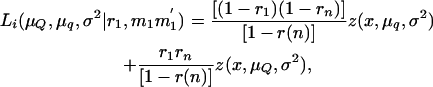 |
(6) |
where z(x, μQ, σ2) and z(x, μq, σ2) are the normal densities with common variance σ2 and means μQ and μq for piglets inheriting alleles Q and q from the boar, respectively. Here, r1 and rn are the recombination fractions between each of the two DNA markers flanking the QTL and the QTL itself and r(n) is the recombination fraction between the two DNA markers.
A more powerful method can be constructed using the information on the estimated genotype for the tumor initiator locus of each piglet. Thus, offspring that do not develop tumors within their first 6 weeks of life are considered TT or Tt with probabilities depending on marker information at the tumor initiator locus as given in the conditional probabilities in Table 4. For example, offspring with marker alleles MM′ will have a probability of being tumor susceptible at the tumor initiator locus with probability
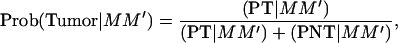 |
(7) |
where (PT | MM′) and (PNT = MM′) are as defined in Table 4. All other probabilities of being susceptible at the tumor initiator locus conditional on the marker information are computed in the same way.
When searching for QTL affecting the number of tumors, the information on tumor susceptibility, given the piglet's genotype at the tumor initiator locus, can be incorporated by including the probabilities estimated in Equation 7 into Equation 6. For example, the likelihood of an affected piglet with genotype information at the tumor initiator locus MM′ and inheriting marker alleles M1M1′ (in another chromosome fragment) when searching for a QTL at an interval becomes
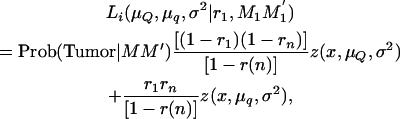 |
(8) |
where Prob(Tumor | MM′) is the conditional probability of being susceptible to malignant melanoma conditional on the marker information at the tumor initiator locus (Equation 7). This probability is 1 if the piglet develops melanoma in its first 6 weeks of life. If the piglet does not develop melanoma in its first 6 weeks of life, then account is taken for the genotype at the tumor initiator locus by giving less weight in the likelihood to piglets that eventually do not carry tumor initiator alleles.
Monte Carlo simulation for a single DNA-marker to map a tumor initiator locus:
A Monte Carlo simulation was carried out to test whether a single DNA marker can map a tumor initiator locus. The probabilities of developing tumors and inheriting marker alleles were computed by:
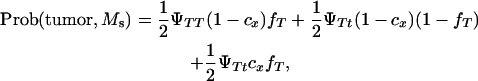 |
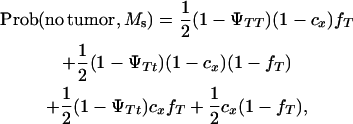 |
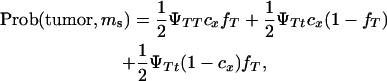 |
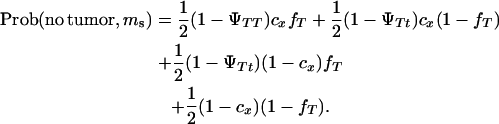 |
A random generator from the uniform distribution was used to generate the offspring. If the drawing of the uniform distribution was between 0 and 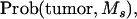 then the offspring developed tumors and had marker allele Ms inherited from the boar. If the drawing of the uniform distribution was between
then the offspring developed tumors and had marker allele Ms inherited from the boar. If the drawing of the uniform distribution was between 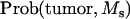 and
and 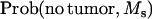 then the offspring did not develop tumors and had marker allele Ms inherited from the boar. Assigning offspring to the other marker allele ms was done following the same rule. The simulated situations were ΨTT = 0.5 and ΨTt = 0, family size = 200 and 2000, and recombination fraction (cx) = 0.05 and 0.15. Each simulation set was replicated 10,000 times.
then the offspring did not develop tumors and had marker allele Ms inherited from the boar. Assigning offspring to the other marker allele ms was done following the same rule. The simulated situations were ΨTT = 0.5 and ΨTt = 0, family size = 200 and 2000, and recombination fraction (cx) = 0.05 and 0.15. Each simulation set was replicated 10,000 times.
Monte Carlo simulation for interval mapping of a tumor initiator locus:
A computer simulation was carried out to test the proposed method for interval mapping of the tumor initiator locus and to compute statistical power for varying progeny size. A single boar, heterozygous at the tumor initiator locus, Tt, and its offspring were simulated assuming that the frequency of the allele T contributed by the dam was 0.5. A chromosomal fragment of 20 cM was simulated in the boar with two flanking markers. Two simulations were carried out for each set of parameters regarding the alternative hypothesis (tumor initiator locus within the bracket of DNA markers) and the null hypothesis (tumor initiator locus located elsewhere on the genome). For the first simulation, Equation 1 was used to simulate the tumor initiator locus half way between the two markers (i.e., ∼10 cM from each of the flanking markers). Equation 2 was also used to simulate the situation where the tumor initiator locus was located elsewhere in the genome (null hypothesis). A random generator from the uniform distribution was used to assign offspring with and without melanoma and to assign DNA-marker information according to their respective probabilities (Equations 1 and 2). The same principles were followed as those for simulating one single DNA marker as in the previous section. Progeny sizes were set at 70, 200, 500, and 2000 offspring. A progeny size of 70 was considered because DNA from a boar family with 72 piglets was available for genotyping and used for testing on SSC6 and SSC8. Other progeny sizes were chosen to investigate the boar family size required to detect a tumor initiator locus. Penetrance for homozygotes TT and heterozygotes Tt were ΨTT = 1 and ΨTt = 0, ΨTT = 1 and ΨTt = 0.5, ΨTT = 0.5 and ΨTt = 0, ΨTT = 0.25 and ΨTt = 0, and ΨTT = 0.10 and ΨTt = 0. A total of 10,000 replicates were carried out for each simulation set. The average and standard deviation over replicates for ΨTT and ΨTt were computed for each simulation set. Empirical power was computed by (1) sorting within each simulation set according to the likelihood-ratio estimate, when modeling the tumor initiator locus unlinked to the chromosomal fragment being tested (null hypothesis), (2) selecting the likelihood-ratio test threshold (THRES) value at significance level 0.05 or 0.01, (3) sorting the likelihood-ratio test of the simulation set for the alternative hypothesis (a true tumor initiator locus bracketed by two DNA markers, and (4) finding the percentage of replicates that gave a value higher than THRES. In addition, the location of the tumor locus was averaged over replicates. To know the number of progeny necessary for fine mapping (within 1 cM), the percentage of replicates that located the tumor within 1 cM of the simulated location was also computed.
Search for the tumor initiator locus and QTL affecting number of tumors in SSC6 and SSC8:
Boar 201134 is an intercross of Hanford with Sinclair and was mated to 11 tumor-bearing purebred Sinclair female sows producing 72 offspring. Since all dams were tumor bearing, the frequency of the tumor initiator locus in the gametes provided by the sows was assumed to be high. TBIRTH and T6WK were recorded. White blood cells and liver and tail samples from these progeny were stored at −80°. Total DNA was purified from white blood cells, tail, and liver following the manufacturer's instructions (QIAGEN, Valencia, CA). The DNA was diluted with AE buffer to 10 ng/μl and stored at −4° prior to genotyping.
Dinucletoide microsatellites were chosen to cover SSC6 (SW1353, SW2525, SW1038, SW492, SW1473, S0121, and SW1328) and SSC8 (SW2611, KS174, SW905, KS101, SW444, SW1953, and KS173). Primers for these chromosomes were selected on the basis of the allele variability and their location on a chromosome. Primers were diluted to 50 μm and stored at −4°. A primer mix was prepared containing 2 μl of each 50-μm primer set. Each PCR reaction contained a total volume of 15 μl consisting of 1.5 μl of each primer mix, 2 μl water, 4 μl DNA, and 7.5 μl PCR multiplex mix (QIAGEN). Gradients were performed to determine the optimal temperature for primer annealing. Amplification was carried out with a TC-512 thermal cycler. The initial denaturation step was performed at 95° for 15 min, followed by 35 cycles of 30 sec at 94°, 1 min and 30 sec at the optimum annealing temperature, and 1 min at 72° with a final extension of 30 min at 60°. Subsequently, 1 μl of PCR product was added to 199 μl water to make a 1:200 dilution. One microliter of this dilution was added to 10 μl of a formamide solution containing 1 ml formamide and 5 μl of ladder and denatured for 5 min at 95°. Genotyping was performed with the Applied Biosystems (Foster City, CA) (ABI) Prism 3730 DNA analyzer.
Interval mapping to search for a tumor initiator locus was performed on chromosomes 6 and 8 using Equation 1. These chromosomes were chosen because they were among the five chromosomes significant for melanoma susceptibility in the MeLiM swine model as reported by Geffrotin et al. (2004). The linkage phase in the boar and the genetic distance between each pair of consecutives markers were estimated from the same data using a computer program developed for that purpose by L. Gomez-Raya. Equation 4 was used to compute the LOD score, comparing the likelihoods of the full model (Equation 1) with a model with full homozygous lethality (Blangero et al. 1996). Interval mapping for loci affecting the aggressiveness of the disease was also carried out. Both models, accounting (Equation 8) and not accounting (Equation 6) for the piglet's genotype at the tumor initiator locus, were tested. The genotypic probabilities at the highest likelihood-ratio test on chromosome 8 were used when testing for number of tumors on SSC6. In the same way, the highest likelihood-ratio test on chromosome 6 describing the tumor initiator locus was used when searching for QTL affecting number of tumors on SSC8. The tested traits were TBIRTH, T6WK, TB–6WK, and TMAX. A permutation test was carried out on SSC8 and TBIRTH to account for multiple testing (Churchill and Doerge 1994) by shuffling the observations on TBIRTH 10,000 times and by randomly assigning those observations to piglets with given genotype information. The steps for computing chromosomewise P-values were (1) finding the maximum LRT among all tested points for each permuted chromosome, (2) ordering the maximum LRT for each permutation, (3) computing the number of times (ntimes) of 10,000 permutations that the LRT in the real data for SSC8 was higher than the value of the permuted data, and (4) computing the chromosomewise P-value as [1 − (ntimes/10,000)].
RESULTS
The inheritance of malignant melanoma in Sinclair swine was modeled with several methods. Our strategy was to attribute the susceptibility of the disease (i.e., to be born with or without melanoma) to one or few loci and the aggressiveness of the disease (i.e., TBIRTH and T6WK) to other loci. When testing for a tumor initiator locus, joint estimation of the penetrance of genotypes TT and Tt and the frequency of allele T is not possible because they are confounded. To overcome this problem, a mating design was developed in which a boar was mated to sows with malignant melanoma, resulting in offspring with and without tumors. In this way, the frequency or frequencies of the tumor initiator alleles among gametes from the dams are high. A maximum-likelihood method was developed to test if one single marker could be used to locate the tumor initiator locus. A Monte Carlo simulation was carried out for ΨTT = 0.5 and ΨTt = 0, for family sizes of 200 and 2000 offspring, and for recombination fractions between the tumor initiator locus and the DNA marker of 0, 0.05, and 0.15. The average of the estimates of c, ΨTT, and ΨTt among 10,000 replicates are given in Table 6. For example, a single DNA-marker can map the location of the tumor initiator locus only when the DNA marker and the tumor initiator locus are fully linked. If the DNA marker and the tumor initiator are not fully linked then the estimation of the location is biased (Table 6).
TABLE 6.
Average over replicates of the estimates of the recombination fraction between a DNA marker and a tumor initiator locus (c) and of estimates of penetrances for homozygotes for the tumor allele ΨTT and homozygotes ΨTt
|
n = 200
|
n = 2000
|
|||||
|---|---|---|---|---|---|---|
| c | ΨTT | ΨTt | c | ΨTT | ΨTt | |
| c = 0.00 | 0.000 | 0.501 | 0.000 | 0.000 | 0.500 | 0.000 |
| (0.000) | (0.087) | (0.000) | (0.000) | (0.027) | (0.000) | |
| c = 0.05 | 0.025 | 0.475 | 0.013 | 0.027 | 0.477 | 0.012 |
| (0.032) | (0.089) | (0.016) | (0.020) | (0.035) | (0.010) | |
| c = 0.15 | 0.080 | 0.421 | 0.040 | 0.079 | 0.422 | 0.039 |
| (0.065) | (0.100) | (0.034) | (0.050) | (0.057) | (0.026) | |
The standard deviations of the estimates are in parentheses. The simulated penetrances were ΨTT = 0.50, ΨTt = 0. Family sizes (n) were 200 and 2000.
A maximum-likelihood approach was developed to interval map the putative tumor initiator locus. A Monte Carlo simulation was carried out to test the method and to compute empirical power of detection in a chromosomal fragment of 20 cM bracketed by fully informative flanking DNA markers. The simulated distance of the tumor initiator locus to each of the DNA markers was 10 cM and the simulated allele frequency of the tumor initiator allele in the sows was 0.5. The estimates of the penetrance for homozygotes and heterozygotes were very close to the simulated parameters in most situations (Table 7), with the only exception of a simulated penetrance of ΨTT = 1 and low family sizes (70, 200), where the estimates were biased downward. Empirical power was also computed to be able to design experiments for interval mapping of malignant melanoma in Sinclair swine (Table 8). Power of detection increased with the penetrance of homozygotes ΨTT. A family size of 70 is sufficient to detect tumor initiator loci with ΨTT of ≥0.25. For a low penetrance (ΨTT = 0.10), a family size between 200 and 500 may be required.
TABLE 7.
Average over replicates of the estimates of penetrances, ΨTT and ΨTt, and their standard deviations (in parentheses) over 10,000 replicates for family sizes 70, 200, 500, and 2000
| Simulated penetrance | Family size
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
70
|
200
|
500
|
2000
|
||||
| ΨTT | ΨTt | ΨTT | ΨTt | ΨTT | ΨTt | ΨTT | ΨTt | ΨTT | ΨTt |
| 0.10 | 0.00 | 0.119 | 0.001 | 0.098 | 0.001 | 0.096 | 0.002 | 0.098 | 0.000 |
| (0.004) | (0.000) | (0.002) | (0.000) | (0.001) | (0.000) | (0.000) | (0.000) | ||
| 0.25 | 0.00 | 0.246 | 0.003 | 0.242 | 0.003 | 0.243 | 0.004 | 0.247 | 0.001 |
| (0.012) | (0.000) | (0.005) | (0.000) | (0.002) | (0.000) | (0.000) | (0.000) | ||
| 0.50 | 0.00 | 0.486 | 0.007 | 0.487 | 0.006 | 0.493 | 0.003 | 0.496 | 0.001 |
| (0.023) | (0.000) | (0.008) | (0.000) | (0.003) | (0.000) | (0.001) | (0.000) | ||
| 1.00 | 0.00 | 0.913 | 0.015 | 0.949 | 0.011 | 0.968 | 0.006 | 0.984 | 0.003 |
| (0.013) | (0.001) | (0.005) | (0.000) | (0.002) | (0.000) | (0.000) | (0.000) | ||
| 1.00 | 0.50 | 0.902 | 0.548 | 0.940 | 0.530 | 0.963 | 0.519 | 0.982 | 0.509 |
| (0.021) | (0.018) | (0.008) | (0.006) | (0.003) | (0.002) | (0.001) | (0.001) | ||
TABLE 8.
Empirical power to detect a tumor initiator for varying scenarios regarding the penetrances of homozygotes and heterozygotes
| Family size
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Penetrance
|
70
|
200
|
500
|
2000
|
|||||
| ΨTT | ΨTt | α = 0.01 | α = 0.05 | α = 0.01 | α = 0.05 | α = 0.01 | α = 0.05 | α = 0.01 | α = 0.05 |
| 0.10 | 0.00 | 10.18 | 28.63 | 37.12 | 76.64 | 91.71 | 98.81 | 100.00 | 100.00 |
| 0.25 | 0.00 | 31.30 | 64.98 | 93.76 | 99.09 | 100.00 | 100.00 | 100.00 | 100.00 |
| 0.50 | 0.00 | 82.75 | 95.73 | 99.98 | 99.99 | 100.00 | 100.00 | 100.00 | 100.00 |
| 1.00 | 0.00 | 99.62 | 99.97 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 1.00 | 0.50 | 89.97 | 97.68 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
The values are the percentage of replicates that were higher than thresholds at α = 0.01 and α = 0.05 in a computer simulation of the null hypothesis.
The average location and the percentage of replicates locating the tumor initiator locus within 1 cM of the simulated (true) locus are depicted in Table 9. The average over replicates of the estimates of the location (r1) was very close to the simulated (true) location (0.10) even for a small family size (70). The percentage of replicates that located the tumor initiator locus within 1 cM of the simulated (true) locus was small for family sizes between 70 and 500 (Table 9). However, with a family size of 2000 and full penetrance of the homozygotes (ΨTT = 1) there is a chance of 0.60 that the estimated location is within 1 cM of the tumor initiator locus. Therefore, a relative large family size in swine allows for fine mapping.
TABLE 9.
Average of the estimates of the location of the tumor initiator locus (r1) and percentage of replicates that located the tumor locus within 1 cM (PR1) for varying penetrances, ΨTT and ΨTt, over 10,000 replicates for family sizes 70, 200, 500, and 2000
| Simulated penetrance | Family size
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
70
|
200
|
500
|
2,000
|
||||
| ΨTT | ΨTt | r1 | PR1 | r1 | PR1 | r1 | PR1 | r1 | PR1 |
| 0.10 | 0.00 | 0.094 | 1.5 | 0.092 | 5.5 | 0.094 | 10.3 | 0.098 | 22.2 |
| 0.25 | 0.00 | 0.093 | 4.0 | 0.094 | 9.9 | 0.097 | 16.6 | 0.099 | 35.5 |
| 0.50 | 0.00 | 0.091 | 7.7 | 0.095 | 15.4 | 0.098 | 26.2 | 0.099 | 49.1 |
| 1.00 | 0.00 | 0.094 | 13.9 | 0.097 | 24.2 | 0.099 | 38.2 | 0.100 | 65.2 |
| 1.00 | 0.50 | 0.096 | 13.3 | 0.097 | 22.06 | 0.096 | 34.4 | 0.098 | 60.1 |
The simulated location was r1 = 0.10.
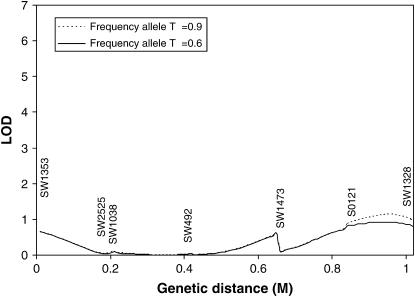
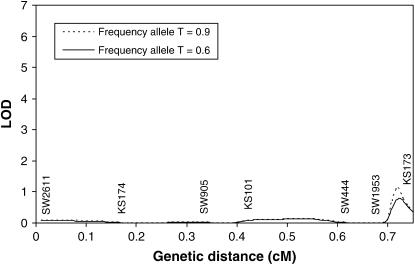
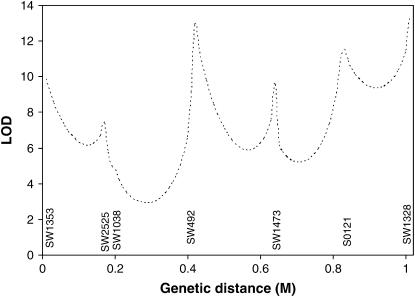
The methods developed in this article were used to search for a tumor initiator locus and number of tumors on SSC6 and SSC8 in a Sinclair boar family. The results for interval mapping for a tumor initiator locus are presented in Figures 3 and 4 for SSC6 and SSC8, respectively. The lod scores showed very small peaks in the distal parts of both chromosomes. At the location with the highest maximum likelihood, the likelihood of the model detecting a tumor initiator locus was ∼15 times more likely than the likelihood of a model under the null hypothesis. Examining the likelihoods at two different allele frequencies of gametes provided by the sows (0.6 and 0.9) revealed that they have only a very small influence at the observed peaks. A comparison of a full model (Equation 1) with a model with homozygous lethal (Blangero et al. 1996) at the tumor initiator allele (Equation 4) was carried out using the log of odds of the corresponding maximum likelihoods on SSC6. The full model is significantly more likely than the model with lethality of homozygotes throughout the entire chromosome (Figure 5).
Figure 3.—
Interval mapping searching for tumor initiator locus on SSC6 assuming a frequency of allele T of 0.9 and 0.6 in the gametes from the dams. Genetic distances are in morgans (M).
Figure 4.—
Interval mapping for tumor initiator locus on SSC8 assuming a frequency of allele T of 0.9 and 0.6 in the gametes from the dams. Genetic distances are in morgans (M).
Figure 5.—
Logarithm of odds comparing the maximum likelihood for a full model (allowing homozygotes to survive and to develop melanoma) vs. a model based on Blangero et al.'s (1996) hypothesis for SSC6.
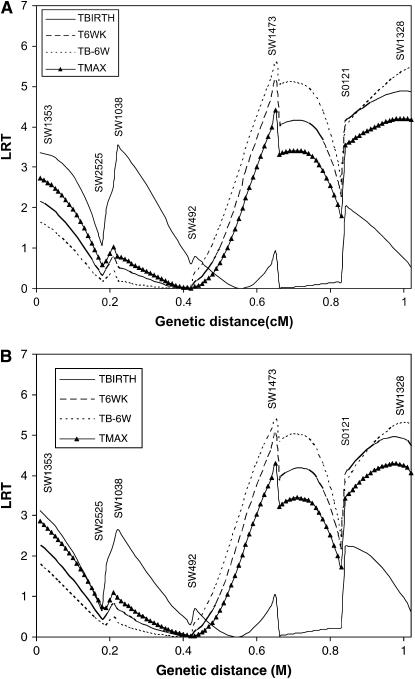
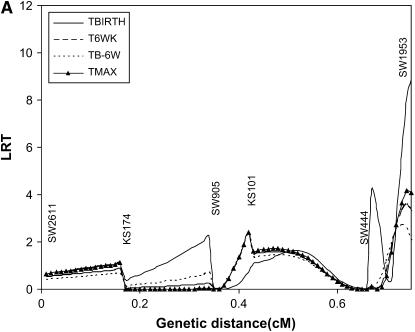
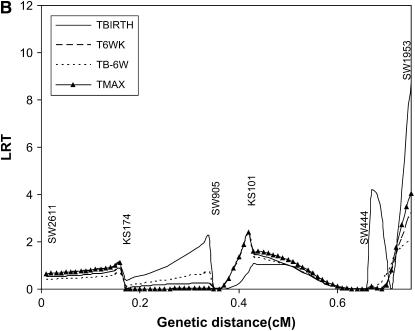
Results of interval mapping for TBIRTH, T6WK, TB–6W, and TMAX for SSC6 and SSC8 are depicted in Figures 6 and 7, respectively. Interval mapping for SSC6 was carried out with and without information on the tumor initiator locus at SSC8 (Equations 6 and 8). Similarly, interval mapping on SSC8 was carried out with and without the use of information on the tumor initiator locus on SSC6. There was very little impact of using the probability of carrying genes at the tumor initiator locus on the likelihood-ratio statistics for TBIRTH, T6WK, TB–6WK, and TMAX on either chromosome. The trait TBIRTH behaved differently from the other traits and showed a chromosomewise significant peak near SW1953 at the end of SSC8 (P < 0.0124).
Figure 6.—
Interval mapping for TBIRTH, T6WK, TB–6WK, and TMAX on SSC6 (A) not using information on the tumor initiator locus on SSC8 and (B) using information on the tumor initiator locus on SSC8.
Figure 7.—
Interval mapping for TBIRTH, T6WK, TB–6WK, and TMAX on SSC8 (A) not using information on the tumor initiator locus on SSC6 and (B) using information on the tumor initiator locus on SSC6.
DISCUSSION
Most hereditary diseases are complex with several genes involved in the susceptibility to the disease. Heritable cancers, such as familial malignant melanoma in humans, for which several predisposing genes have been reported, are among these (Cannon-Albright et al. 1992; Kamb et al. 1994; Hussussian et al. 1994; Quelle et al. 1995; Zuo et al. 1996; Soufir et al. 1998; Palmer et al. 2000). In humans, research for hereditary diseases has been focused on high-risk families, but the number of individuals per family in humans is low. This approach has proven useful in mapping genes involved in susceptibility to particular hereditary diseases but many questions remain unanswered (Carlson et al. 2004). Penetrance of the locus or loci is difficult to estimate. In addition, interactions among several loci involved in the susceptibility to the disease are difficult to evaluate because the frequencies of the alleles investigated change due to outbreeding of the family members with more or less genetically related individuals in different periods. One avenue to overcome these problems is to use an animal model such as malignant melanoma of Sinclair swine. The advantages of animal models are (1) penetrance of the disease can be more easily modeled since family sizes are large and (2) simultaneous testing of loci involved in susceptibility to a particular disease can be tested in the same individuals, which may lead to understanding interactions among different predisposing genes.
In this study, we modeled the inheritance of malignant melanoma using maximum-likelihood methods and a large half-sib family of affected and nonaffected offspring. Two different models were used: one for searching a tumor initiator locus (to develop or not to develop melanoma) and another for testing aggressiveness of the disease but accounting for animals being carriers of the tumor initiator alleles. The advantage of the methods proposed in this article over general mapping methods used in a standard genome scan is that the latter ignore that loci for initiation of the disease and for virulence of the disease might be different. Consequently, no information of the genes initiating the disease would be obtained in a standard genome scan.
The estimation of the location of a tumor initiator locus with one single DNA marker was biased, except when the DNA marker was very closely linked to the tumor initiator locus. However, maximum-likelihood methods for interval mapping were generally unbiased when tested by computer Monte Carlo simulations. Here, the only exception was when the simulated penetrance was 1 for homozygotes TT and the family size was relatively small (70). In that situation, the average over replicates of estimates of the penetrance was just over 0.90. This is due to the fact that maximum likelihood is asymptotically unbiased only for large sample sizes. Nevertheless, the method estimates the position of the tumor initiator locus very accurately. The average over replicates for any simulation set was always <1 cM far from the true simulated location.
The power results for detecting a tumor initiator locus suggest that even a family size of 70 is sufficient for the detection of loci with full penetrance. The inheritance of the chromosome fragment bracketed by DNA-marker alleles and carrying the tumor initiator allele is highly associated with the initiation of the disease in the offspring if the locus has a full penetrance (and with the exception of double recombinants). Thus, a tumor initiator locus requiring one or two copies of the allele to be necessarily present to initiate the disease can be easily mapped with DNA markers bracketing the tumor initiator locus. In terms of power, mapping loci with high penetrance of genotypes for a disease is equivalent to mapping QTL affecting quantitative traits having a very large effect (several phenotypic standard deviations). Therefore, the interval mapping methods proposed in this article are very powerful for diseases affected by loci with high penetrance. On the basis of previous knowledge (Blangero et al. 1992), we expect that the mode of inheritance of malignant melanoma in Sinclair swine is attributable to very few loci each with a high penetrance and therefore even experiments with a relatively small family size are sufficient to identify the mode of inheritance of SSCM. However, for fine mapping, at least 2000 offspring are required to locate the marker within 1 cM of its true location, even with a high penetrance of the tumor initiator locus.
The maximum-likelihood methods assumed that the allele frequency in the gametes provided by the dams is known. This is a necessary assumption since the penetrance and allele frequencies from the dams are confounded. By mating a boar to dams that develop melanoma we assure that the frequency of the tumor initiator allele (T) is high. Using real data on SSC6 and SSC8 revealed that the impact of this assumption is small when the method does not detect a tumor initiator locus in the area. However, the likelihood-ratio statistics slightly increased with increasing allele frequency of the dams (0.6 vs. 0.9) in the distal areas of SSC6 and SSC8.
The results for interval mapping for T6WK, TB–6WK, and TMAX were very similar among themselves for SSC6 and for SSC8. TBIRTH behaved differently from the other traits. When genotype information at the tumor initiator locus was accounted for, it had a small impact on either SSC6 or SSC8 when testing for TBIRTH. This is attributable to the fact that the loci detected in the distal part of SSC6 and SSC8 were not significant for the tumor initiator locus.
It has been argued that the tumor initiator locus might be lethal in utero in homozygotes (Blangero et al. 1996). We developed methods to compare this model with a model allowing full survival of the homozygotes. The results from SSC6 suggest that if a tumor initiator locus was present, then the full survival model is significantly more likely.
The only published literature for testing susceptibility to melanoma with DNA markers and a similar swine model of heritable melanoma was carried out by Geffrotin et al. (2004). They located a susceptibility locus near the MC1R locus. Our closer marker (SW1353) was 20 cM apart from the location of their susceptibility locus. They also identified markers significantly associated with susceptibility on SSC8 in the same area where we detected a QTL significant for TBIRTH. The detected QTL on SSC8 illustrates that genes involved in the initiation of the disease (no tumor initiator locus was detected) may be different from genes involved in the progression and aggressiveness of the disease.
Our experimental design consisted of one large boar family with affected and nonaffected offspring for the disease. It is possible that other boar families would be segregating other tumor loci and therefore the experiments must be replicated to fully understand the mode of inheritance of malignant melanoma in Sinclair swine.
The statistical methods derived in this article can be applied to find the mode of inheritance of human or farm animal diseases using farm animals with a half-sib structure, such as cattle or sheep. Farms usually keep records of pedigree and phenotypes. Over 1000 diseases in domesticated animals have a human counterpart as currently reported in the Online Mendelian Inheritance in Animals (http://omia.angis.org.au/). Human diseases could be investigated in swine and dairy and beef cattle with very large progeny groups. For example, malignant melanoma has also been described in Duroc and Iberian pigs that are commercial swine breeds (Hordinsky et al. 1985; Perez et al. 2002). The simulation results for interval mapping suggest that fine mapping might be possible in those populations since progeny groups can be rather large (from 60 to several thousand).
The methods developed in this article can also be extended to multiple loci involved in the initiation of the disease. The interaction between loci could be modeled in a similar way to what we have reported for the tumor initiator locus and the locus affecting number of tumors.
The conclusion of this article is that powerful methods are possible to uncover the mode of inheritance of human diseases in animals by taking advantage of the large progeny groups feasible in large animal models.
Acknowledgments
We are very grateful to Max Amoss for providing the tissue samples for boar family 201134. We are grateful to O. Ash, B. Kindred, H. Mobley, and A. Lipka for sampling, trait recording, and animal care of the Sinclair swine herd. We are also thankful to Veronica Kirchoff for technical assistance in the genotyping of microsatellites. Genotyping was carried out at the Nevada Genomics Center.
This article is dedicated to J. M. Malpica with admiration and respect.
References
- Blangero, J., S. Williams-Blangero, C. M. Kammerer, B. Towne and L. W. Konigsberg, 1992. Multivariate genetic analysis of nevus measurements and melanoma. Cytogenet. Cell Genet. 59: 170–181. [DOI] [PubMed] [Google Scholar]
- Blangero, J., R. G. Tissot, C. W. Beattie and M. S. Amoss Jr., 1996. Genetic determinants of cutaneous malignant melanoma in Sinclair swine. Br. J. Cancer 73: 667–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannon-Albright, L. A., D. E. Goldgar, L. J. Meyer, C. M. Lewis, D. E. Anderson et al., 1992. Assignment of a locus for familial melanoma, MLM, to chromosome 9p13-p22. Science 258: 1148–1152. [DOI] [PubMed] [Google Scholar]
- Carlson, C. S., M. A. Eberle, L. A. Kruglyak and D. A. Nickerson, 2004. Mapping complex disease loci in whole-genome association studies. Nature 429: 446–452. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., and R. W. Doerge, 1994. Empirical threshold values for quantitative trait mapping. Genetics 138: 963–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das Gupta, T. K., S. G. Ronan, C. W. Beattie, A. Shilkaitis and M. S. Amoss Jr., 1989. Comparative histopathology of porcine and human cutaneous melanoma. Pediatr. Dermatol. 6: 289–299. [DOI] [PubMed] [Google Scholar]
- Geffrotin, C., F. Crechet, P. Le Roy, C. Le Chalony, J. J. Leplat et al., 2004. Identification of five chromosomal regions involved in predisposition to melanoma by genome-wide scan in the MeLiM swine model. Int. J. Cancer 110: 39–50. [DOI] [PubMed] [Google Scholar]
- Greene, J. F., J. S. Townsend and M. Amoss Jr., 1994. Histopathology of regression in Sinclair swine model of melanoma. Lab. Invest. 71: 17–24. [PubMed] [Google Scholar]
- Greene, J. F., C. D Morgan, A. Rao, J. R. Amoss and F. Arguello, 1997. Regression by differentiation in the Sinclair swine model of cutaneous melanoma. Melanoma Res. 7: 471–477. [DOI] [PubMed] [Google Scholar]
- Hook, R. R., Jr., M. D. Aultman, E. H. Adelstein, R. W. Oxenhandler, L. E. Millikan et al., 1979. Influence of selective breeding on the incidence of melanoma in Sinclair miniature swine. Int. J. Cancer 24: 668–672. [DOI] [PubMed] [Google Scholar]
- Hordinsky, M. K., G. Ruth and R. King, 1985. Inheritance of melanocytic tumors in Duroc swine. J. Hered. 76: 385–386. [PubMed] [Google Scholar]
- Hussussian, C. J., J. P. Struewing, A. M. Goldstein, P. Higgins, D. S. Ally et al., 1994. Germline p16 mutations in familial melanoma. Nat. Genet. 8: 15–21. [DOI] [PubMed] [Google Scholar]
- Kamb, A., D. Shattuck-Eidens, R. Eeles, Q. Liu, N. A. Gruis et al., 1994. Analysis of the p16 gene (CDKN2) as a candidate for the chromosome 9p melanoma susceptibility locus. Nat. Genet. 8: 22–26. [DOI] [PubMed] [Google Scholar]
- Nobori, T., K. Miura, D. J. Wu, A. Lois, K. Takabayashi et al., 1994. Deletions of the cyclin-dependent kinase-4 inhibitor gene in multiple human cancers. Nature 368: 753–756. [DOI] [PubMed] [Google Scholar]
- Palmer, J. S., D. L. Duffy, N. F. Box, J. F. Aitken, L. E. O'Gorman et al., 2000. Melanocortin-1 receptor polymorphisms and risk of melanoma: Is the association explained solely by pigmentation phenotype? Am. J. Hum. Genet. 66: 176–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez, J., P. M. Garcia, M. J. Bautista, Y. Millan, J. Ordas et al., 2002. Immunohistochemical characterization of tumor cells and inflammatory infiltrate associated with cutaneous melanocytic tumors of Duroc and Iberian swine. Vet. Pathol. 39: 445–451. [DOI] [PubMed] [Google Scholar]
- Pho, L., D. Grossman and S. A. Leachmana, 2006. Melanoma genetics: a review of genetic factors and clinical phenotypes in familial melanoma. Curr. Opin. Oncol. 18: 173–179. [DOI] [PubMed] [Google Scholar]
- Porter, V., 1993. Pigs: A Handbook to the Breeds of the World. Helm Information, Mountfield, UK, pp. 151–226.
- Quelle, D. E., F. Zindy, R. A. Ashmun and C. J. Sherr, 1995. Alternative reading frames of the INK4a tumor suppressor gene encode two unrelated proteins capable of inducing cell cycle arrest. Cell 83: 993–1000. [DOI] [PubMed] [Google Scholar]
- Soufir, N., M. F. Avril, A. Chompret, F. Demenais, J. Bombled et al., 1998. Prevalence of p16 and CDK4 germline mutations in 48 melanoma-prone families in France: the French Familial Melanoma Study Group. Hum. Mol. Genet. 7: 209–216. [DOI] [PubMed] [Google Scholar]
- Spielman, R. S., R. E. Mcginnis and W. Ewens, 1993. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am. J. Hum. Genet. 52: 506–516. [PMC free article] [PubMed] [Google Scholar]
- Tissot, R. G., C. W. Beattie and M. S. Amoss Jr., 1987. Inheritance of Sinclair swine cutaneous malignant melanoma. Cancer Res. 47: 5542–5545. [PubMed] [Google Scholar]
- Zuo, L., J. Weger, Q. Yang, A. M. Goldstein, M. A. Tucker et al., 1996. Germline mutations in the p16/INK4a binding domain of CDK4 in familial melanoma. Nat. Genet. 12: 97–99. [DOI] [PubMed] [Google Scholar]