Abstract
Horizontal plasmid transfer plays a key role in bacterial adaptation. In harsh environments, bacterial populations adapt by sampling genetic material from a horizontal gene pool through self-transmissible plasmids, and that allows persistence of these mobile genetic elements. In the absence of selection for plasmid-encoded traits it is not well understood if and how plasmids persist in bacterial communities. Here we present three models of the dynamics of plasmid persistence in the absence of selection. The models consider plasmid loss (segregation), plasmid cost, conjugative plasmid transfer, and observation error. Also, we present a stochastic model in which the relative fitness of the plasmid-free cells was modeled as a random variable affected by an environmental process using a hidden Markov model (HMM). Extensive simulations showed that the estimates from the proposed model are nearly unbiased. Likelihood-ratio tests showed that the dynamics of plasmid persistence are strongly dependent on the host type. Accounting for stochasticity was necessary to explain four of seven time-series data sets, thus confirming that plasmid persistence needs to be understood as a stochastic process. This work can be viewed as a conceptual starting point under which new plasmid persistence hypotheses can be tested.
COMPARATIVE molecular phylogenies (Gogarten and Townsend 2005; Sørensen et al. 2005) and prospective, mathematical models coupled with experimental data sets have shown that horizontal gene transfer (HGT), and in particular conjugative plasmid transfer (Stewart and Levin 1977; Levin 1980; Simonsen 1991), is an important mechanism for bacterial adaptation. The search for adaptive traits within a large horizontal gene pool is often facilitated by plasmids, since these mobile genetic elements often carry genes that are advantageous to their hosts (e.g., genes required to exploit new carbon sources, antibiotic resistance genes, etc.). As these genetic functional units allow their host to occupy new ecological niches, then the persistence of plasmids in bacterial populations under local selective pressures can be understood (Gogarten and Townsend 2005; Sørensen et al. 2005). Perhaps most difficult to understand is the persistence of plasmids under nonselective conditions, that is, when the plasmid's genetic material does not confer any advantage to its hosts. This scenario is the focus of our research. Understanding this scenario has many important applications. For example, the loss or persistence of plasmids carrying antibiotic resistance genes, when the selective pressure of the antibiotic is removed from the population, has major human health implications.
In the absence of selection, a plasmid may be maintained if a certain balance exists between three key factors (Stewart and Levin 1977; Simonsen 1991; Freter et al. 1983; Lenski and Bouma 1994). These factors are (i) plasmid loss by segregation during bacterial replication, (ii) the burden or fitness cost associated with carrying and/or expressing the extra piece of genetic material, and (iii) plasmid transmission via conjugation. In other words, for a plasmid to persist, horizontal transmission must compensate for segregational loss and fitness cost of the plasmid. The framework under which most of this knowledge about plasmids persistence has been built is deterministic differential equation modeling. Yet, the main biological mechanisms and principles under which evolution and adaptation are theoretically understood are essentially stochastic (Novozhilov et al. 2005).
Adequately connecting deterministic and stochastic population models to real time-series data via statistical time-series methods is an important yet difficult task (Cushing et al. 2002; Dennis et al. 2006). The statistical framework under which these analyses are performed while considering both, process and observation uncertainty is well formalized and known as state-space modeling (SSM) (Carlin et al. 1992; Meyer and Millar 1999; Dennis et al. 2006). One important class of SSMs is the HMM. Much work remains to be done to assess the reliability and accuracy of maximum-likelihood parameter estimates from population dynamics hidden Markov models and the inferences made from them. A recent study in theoretical population dynamics (Dennis et al. 2006) has shown that even in the simple case of a linear and Gaussian SSM, the likelihood function is highly multimodal and that the finite samples ML estimates do not enjoy good statistical properties. These statistical deficiencies would be expected to vanish when either multiple replicated samples are taken or true process replicates are observed, something that is rarely feasible in macroecological studies, but relatively easy to accomplish in microbial experiments. Finally, we expect that a careful time-series analysis might lead to a better understanding of plasmid persistence in bacterial populations.
The objective of our current work is twofold: first, we formulate, fit, and later compare deterministic and stochastic models to time-series data on plasmid persistence in seven bacterial strains. In doing so we consider taking into account both process and observation uncertainty using analytical methods for SSM. Second, we show via extensive simulations that the statistical procedures implemented here provide the means to reliably make biological inferences from plasmid instability time-series data (De Gelder et al. 2007). We briefly explain the stability experiment methods used to obtain time-series data on plasmid instability and refer to De Gelder et al. (2007) for technical details on the experimental procedures. We also present a mathematical modeling section in which we state and develop each one of the deterministic and stochastic models that include segregation, selection, and horizontal transfer processes used throughout the article. In a supplemental data file (at http://www.genetics.org/supplemental/), the statistical methodology used to confront the models with the time-series data and evaluate their performance is explained in detail. Finally, we discuss the implications, significance, and weaknesses of our findings in light of the current studies in the area.
THEORETICAL BACKGROUND
Segregation and selection model:
Our simplest dynamic model summarizing the growth dynamics of the fraction of plasmid-free cells in the experiments described below (see materials and methods) is a simple system of difference equations where it is assumed that at any generation, the abundance of the plasmid-free cells (m) increases due to (1) plasmid segregation from the wild-type cells (n) at a frequency λ and (2) growth of segregants at a rate 21+σ, where σ represents the selection coefficient
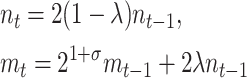 |
(1) |
and the fraction of plasmid-free cells xt is given by
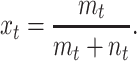 |
(2) |
This deterministic model was developed by De Gelder et al. (2004) and assumes that there is no conjugational transfer from plasmid-carrying cells to segregants.
Throughout this article, the segregation and selection (SS) model serves as our null hypothesis against which more complex models and growth behaviors were tested. The solution to the SS model is presented in De Gelder
et al. (2004, appendix a). This fraction of plasmid-free cells grows logistically starting very close to 0 and approaching 1 as 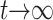 . We note that Joyce
et al. (2005) also showed that it can be assumed that the deterministic growth of plasmid-free cells is basically unaffected by the daily bottlenecks described below (materials
and
methods).
. We note that Joyce
et al. (2005) also showed that it can be assumed that the deterministic growth of plasmid-free cells is basically unaffected by the daily bottlenecks described below (materials
and
methods).
Horizontal transfer model:
A horizontal transfer (HT) model can be generated from Equation 1 by incorporating a term that accounts for the fraction of plasmid-free cells that reacquire the plasmid through conjugative transfer. The typical approach to model conjugation (Levin 1980; Simonsen 1991; Stewart and Levin 1977) is to use the mass-action principle, where the rate at which conjugation occurs depends linearly on the concentration of plasmid-free and plasmid-carrying cells. Using the mass-action principle, the horizontal transfer model where γ represents a constant conjugative transfer frequency would be written as follows:
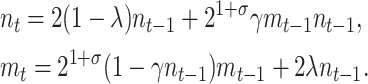 |
(3) |
Here we model conjugation by relaxing the mass-action principle with the following system of equations,
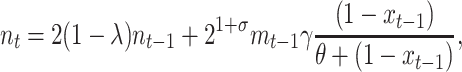 |
(4) |
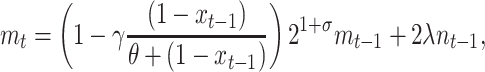 |
(5) |
where xt is the fraction of segregants at time t (2), γ is an asymptotic maximum conjugation frequency during a time interval, and θ represents the fraction of the plasmid-carrying cells at which the frequency of conjugations is half its maximum. The second term in Equation 4 assumes that the transfer process works as in an enzymatic reaction, where enzyme and substrate are the plasmid-carrying and plasmid-free cells, respectively (Andrup and Andersen 1999).
The system of Equations 4 and 5 can be readily reduced to a single model equation for the fraction xt of plasmid-free cells at time t:
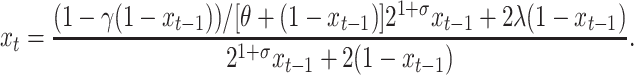 |
(6) |
A local stability analysis (Kot 2001) shows that this model has three equilibrium solutions, the simplest of which is 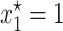 . The other two solutions
. The other two solutions 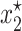 and
and 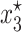 are
are 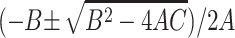 , where
, where 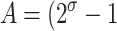 ,
, 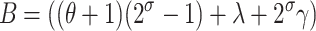 , and C = −λ(θ + 1). The equilibrium solution
, and C = −λ(θ + 1). The equilibrium solution 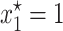 is stable as long as the plasmid burden σ is big enough to satisfy
is stable as long as the plasmid burden σ is big enough to satisfy
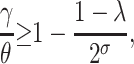 |
(7) |
provided θ > γ . As it is illustrated in Figure 1, when the solution 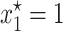 is stable, the plasmid-carrying cells are guaranteed to be lost from the population. When σ is too small so that inequality 7 is not satisfied, the equilibrium solution
is stable, the plasmid-carrying cells are guaranteed to be lost from the population. When σ is too small so that inequality 7 is not satisfied, the equilibrium solution 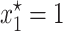 becomes unstable and one of the other two solutions of the model, the one inside the interval (0, 1), (
becomes unstable and one of the other two solutions of the model, the one inside the interval (0, 1), (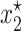 ), becomes stable. This new equilibrium solution basically predicts that plasmids will never be lost from the population.
), becomes stable. This new equilibrium solution basically predicts that plasmids will never be lost from the population.
Figure 1.—
Sample deterministic trajectories (left) and growth rates (right) of the horizontal transfer (HT) model. These plots illustrate that for certain parameter values, the HT model predicts that a long-term coexistence of plasmid-free and plasmid-carrying cells will occur. When coexistence is predicted, the growth rate of the segregants fraction as a function of the fraction of plasmid-free cells adopts a cubic-like form reminiscent of an Allee effect model. Here, however, the interior equilibrium is stable and not unstable as in typical Allee effect models. The different curves correspond to different plasmid cost σ values. The other parameters remained fixed. The parameter values used were close to the ML estimates for the strain P21: λ = 6.851044 × 10−05, θ = 0.25, γ = 2.443239 × 10−02.
Note that inequality 7 is readily interpretable: Since the fraction γ/θ is a measure of the intensity of the transfer frequency, this formula basically states that a high loss of plasmids due to segregation must be balanced by a high transfer frequency for the plasmids to persist in the population. Likewise, a high cost would decrease the fraction (1 − λ)/2σ and hence increase the size of the transfer-frequency threshold needed to guarantee the persistence of plasmids in the population. This property of the HT model is analogous to the results of Stewart and Levin (1977), who found that in a chemostat, plasmids can be maintained only when the cell density and conjugational transfer rate constant are large enough for the transmission of the plasmid to overcome its loss through segregation and the selection against plasmid-carrying bacteria. However, we note that the HT model also shows that, when the frequency dependence in transfer is strong, i.e., at higher values of θ, the persistence threshold γ/θ becomes smaller and the loss of plasmids through segregation and selection can be more easily overcome. If the loss by segregation and the frequency of frequency-dependent transfer are kept fixed, a reduction in the size of the cost σ down to a critical value (see inequality 14) allows the invasion of plasmids in the population. This behavior is visualized by plotting both solution trajectories and the growth rate of the fraction of plasmid-free cells at different values of σ (see Figure 1). As the plasmid burden σ decreases, the growth rate ceases to be parabolic in shape (as in a typical logistic growth curve) and adopts a cubic-like form with a root inside the interval (0, 1), which is a stable equilibrium. That is, it is the point where the long-term fraction of plasmid-free bacteria stagnates, thus predicting a long-run coexistence between plasmid-free and plasmid-carrying bacteria.
The variable selection model:
The dynamic equations explained so far assume that during an entire plasmid stability experiment the growth of the fraction of plasmid-free cells follows essentially a deterministic pattern. That is, all the deviations from the deterministic smooth growth Equations 1, 2, 4, and 5 that appear in the data are assumed to be pure random sampling error. However, theory and experiments (De Visser and Rozen 2005) suggest that during a 600-generations experiment, the occurrence of compensatory mutations and/or a variable host-dependent plasmid burden would dramatically alter the plasmid loss dynamics. Periods of overall heavy plasmid loss would be followed by periods in which the relative frequency of segregants remains almost unchanged. Therefore, as an alternative hypothesis, we propose a stochastic formulation of the segregants growth dynamics that assumes that at each time step, the burden is a value drawn from a continuous probability distribution. By doing so, the fraction of plasmid-free cells grows stochastically. This variable selection (VS) model is then recognized as a model with environmental stochasticity (Lewontin and Cohen 1969; Keiding 1975; Cushing et al. 2002). Hence, to specify our variable selection model we let the selection coefficient be drawn at each time step from a Normal distribution (Lewontin and Cohen 1969; Keiding 1975) St with mean μ and variance τ2. Then, the VS model can be written as
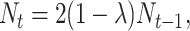 |
(8) |
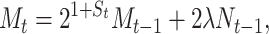 |
(9) |
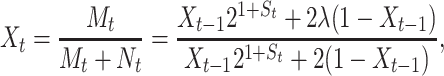 |
(10) |
where uppercase letters denote random variables and lowercase letters hereafter are used to denote realizations of the random variables involved. Then Xt becomes a Markov process whose transition probability density function (pdf) is found to be (appendix):
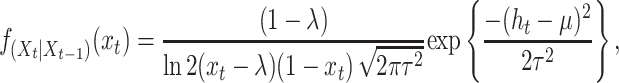 |
(11) |
where
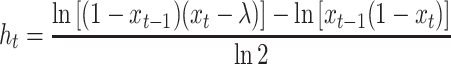 |
and xt > λ. The transition pdf (Equation 11) provides us the means to characterize the behavior of Xt via analytical and simulation results. Also, this pdf provides the proper link between parameter estimation and the hypothesized biological process.
MATERIALS AND METHODS
Stability experiments and time-series data:
To investigate whether the ability of a broad-host-range plasmid to be stably maintained in a bacterial population varies between different hosts, plasmid stability experiments were performed with different bacterial strains carrying the same plasmid pB10, as described by De Gelder et al. (2005, 2007). The experimental approach is briefly summarized below. The 64.5-kb plasmid pB10 (Schlüter et al. 2003), isolated from the bacterial community of a wastewater treatment plant (Dröge et al. 2000), is a self-transmissible, BHR IncP-1β plasmid that mediates resistance to the antibiotics tetracycline (Tc), streptomycin (Sm), amoxicillin, and sulfonamide and to HgCl2. For each strain, stability experiments were performed in triplicate, starting from three separate colonies, which were each inoculated in 5 ml LB with the appropriate concentrations of Tc and Sm to select for pB10. After incubation for 24 hr, these cultures were washed to remove the antibiotics by spinning down 1 ml culture and resuspending the pellet in 1 ml saline. From these cell suspensions, 4.88 μl was transferred to 5 ml of LB such that the cells went through 10 generations of growth during each 24-hr growth cycle. These freshly inoculated cultures constituted time point zero. After they were plated on LB plates and an aliquot was archived at −80°, they were incubated on a rotary shaker for 24 hr. Then, 4.88 μl of the full-grown cultures was transferred each 24 hr to fresh 5 ml LB. These were the daily bottlenecks mentioned in the theoretical background section. At various time points, the cultures were diluted and plated on LB plates. The fraction of plasmid-free cells in the population was determined by replica picking 50 colonies per culture at random from the LB plates onto LB–Tc, LB–Sm, and LB plates and scoring Tc−Sm− colonies. Random Tc−Sm− isolates of each strain were confirmed as true segregants through comparison of their genomic fingerprints (BOX PCR) (Rademaker et al. 1997) with those of the original strains from which they were derived and through gel electrophoresis of plasmid extracts (Kado and Liu 1981; Top et al. 1990). The time-series data thus obtained were analyzed using three population dynamics models.
Statistical analysis:
Deterministic modeling (sampling error with no environmental noise):
A sample of size dtj colonies was taken at random from a replicated culture j, j = 1, 2, … , r, at day t. Each individual has a probability xt of being a segregant and (1 − xt) of being a wild type, where xt is the model-predicted fraction of segregants at generation t. This defines a binomial sampling process with dtj trials and the fraction of segregants xt changes deterministically in time according to the dynamic Equations 1, 2, 4, and 5. Then, the number of plasmid-free cells observed in culture j at day t, denoted Ytj, is a binomial random variable, and
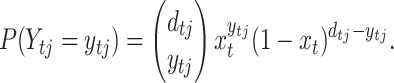 |
(12) |
The two deterministic models, SS (Equations 1 and 2) and HT (Equations 4 and 5), with the sampling process defined by Equation 12, account for the deviations of the observations from the predicted growth pattern. Therefore, the next step in the model-building process was to rigorously connect the data with the model using the above binomial sampling process. This was done using the method of maximum likelihood (Rice 1995) in the case of the SS and HT models, as in De Gelder
et al. (2004). For these two models, a likelihood-ratio test (LRT) was carried out, where under the null hypothesis the data were binomially distributed according to Equation 12, and under the alternative hypothesis the data were still binomially distributed but with a different mean ptj unrelated to the model. Under the null hypothesis, the estimated mean trend is 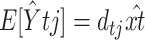 , where
, where 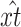 is the model-predicted fraction of segregants at generation t using the ML estimates for the parameters σ, λ, γ, θ, and x0. Under the alternative hypothesis, the estimated mean trend is
is the model-predicted fraction of segregants at generation t using the ML estimates for the parameters σ, λ, γ, θ, and x0. Under the alternative hypothesis, the estimated mean trend is 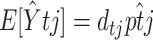 , where
, where 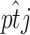 is just the empirical estimate of the segregants' proportion at replicate j and generation t. After taking the natural logarithm and multiplying by −2, the LRT Λ reduces to
is just the empirical estimate of the segregants' proportion at replicate j and generation t. After taking the natural logarithm and multiplying by −2, the LRT Λ reduces to
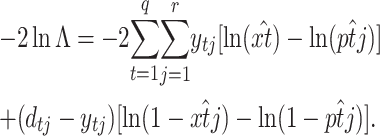 |
(13) |
To approximate the distribution of −2 ln Λ we used parametric bootstrap likelihood-ratio tests (Efron and Tibshirani 1993) and proceeded as in De Gelder et al. (2004). While the chi-square distribution is often used to approximate the distribution of −2 ln Λ, it is valid only if the sample sizes are large enough. The asymptotic theory is known to be unreliable for small sample sizes, which is exactly the case in our data during the early time periods. Our approach has the advantage that it does not rely on asymptotic theory and the accuracy of the approximation is determined by the number of simulations, which we can completely control. A more extensive discussion of this issue appears in De Gelder et al. (2004, p. 1137).
Stochastic modeling (sampling error plus environmental noise):
To carry out parameter estimation for the stochastic model in Equations 8–10, we reformulate it as a SSM or HMM. For each replicated time series of the process, we denote its realizations as Xt,j, t = 1, 2, … , q, and j = 1, 2, 3. The stochastic growth equation that governs each of the unobserved Xt,j random realizations is therefore given by (see Equation 10)
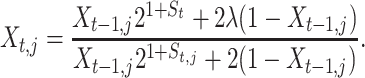 |
(14) |
Given an (unobservable, or “hidden”) replicated random path Xj = [X1,j, X2,j, … ,Xq,j]′ that starts from a fixed (unknown) proportion of plasmid-free cells x0,j, each observation in the vector of recorded plasmid-free colonies counts Yj = [Y0,j, Y1,j, Y2,j, … ,Yq,j]′ is assumed to be drawn from a binomial probability distribution with samples sizes dj = [d0,j, d1,j, … ,dq,j]′ and probabilities vector
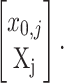 |
That is,
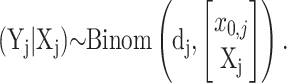 |
(15) |
Note that Equation 15 differs from Equation 12 in an important way: In Equation 15, except for x0,j, the probabilities used to evaluate the binomial sampling distribution are themselves random variables and not fixed quantities as in Equation 12. Equation 14 is called the “state equation” and Equation 15 is called the “observation equation.” Together, Equations 14 and 15 constitute the state-space model formulation (Dennis et al. 2006) of the segregation-selection problem.
We used a Monte Carlo technique to retrieve the maximized likelihood scores and carry out model selection. The maximized likelihood scores were computed by evaluating the likelihood function of the observed time series at the ML estimates. Let ϕ = [λ, μ, τ2, x0, 1, x0, 2, … , x0,r]′ be the model parameters of interest for r replicated time series of the process. Then, the likelihood function of the observed time series for these r replicates, denoted by L(ϕ), is
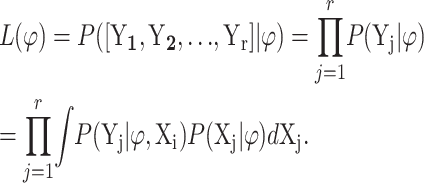 |
(16) |
The integral in Equation 16 cannot be computed directly and was approximated using importance sampling as in George and Thompson (2002). Before doing so, the ML estimates of the model parameters were computed using Gibbs sampling Carlin et al. (1992). However, we note that the methods used here generalize their approach, as Carlin et al. (1992) treat only the case in which the state and observation equations have additive state and observation errors into their nonlinear and non-Gaussian models. Carlin et al. (1992) formulated their methods using the Bayesian paradigm of statistical estimation. In De Gelder et al. (2007), however, we adopted the frequentist perspective to find the SS and HT model parameter estimates. So, to make the results of the SS model comparable to those of De Gelder et al. (2004, 2007), we adopted the strategy of George and Thompson (2002) and used the Bayesian methodology of Carlin et al. (1992) just as a numerical device to compute the ML estimates of the VS model parameters: By adopting uniform priors for all the parameters, the posterior modes of the parameters of interest are equivalent to the ML estimates.
In the supplemental data (at http://www.genetics.org/supplemental/), we present first the Gibbs sampling algorithm for a single time series of plasmid stability, with no replicas. Then we extend this procedure to the case in which a number r of replicated time series are recorded. We also present there the details of an extensive simulation experiment performed to evaluate the performance of the parameter estimation method, using the concept of bootstrap (Efron and Tibshirani 1993). Also, in the supplemental data we explain in detail the calculation of the likelihood Equation 16. For a very good description of the Gibbs sampling algorithm, and why it works, we refer the reader to Casella and George (1992).
RESULTS
Results of fitting the models to the plasmid stability data via LRTs:
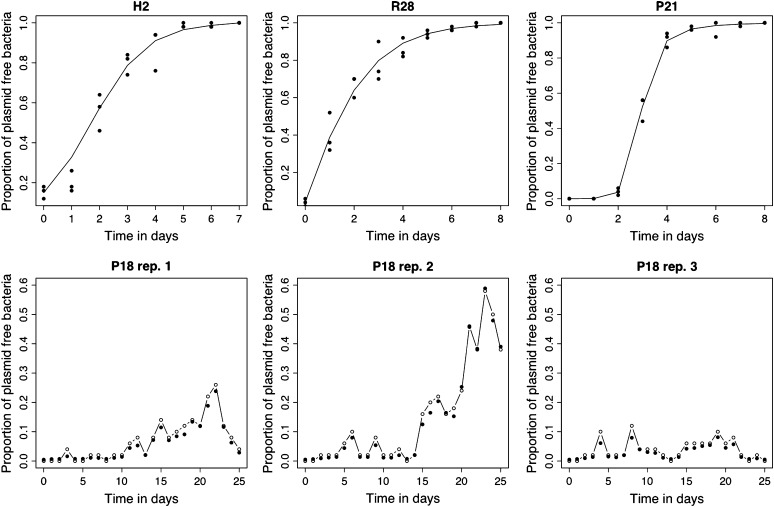
The different mathematical models were fitted to time-course data that represent the stability of plasmid pB10 in seven different hosts (2). In Figure 2, top, we plotted the model predicted fraction of segregants' growth along with the replicated data, for strains H2 and R28 under the SS model and for strain P21 under the HT model. The results of the SS model fitting to the plasmid stability time series (Table 1 and Figure 2, top) showed that for the strains Pseudomonas putida H2 and P. koreensis R28 only two simple factors, plasmid cost and the segregation frequency, were necessary to explain the segregant fraction time series and most of the variation in the data, as confirmed by the absolute goodness-of-fit P-values. For Stenotrophomonas malthophilia P21, fitting the SS model was not sufficient and it was necessary (Figure 2) to include frequency-dependent plasmid transfer in the deterministic model equations. For the strains P. plecoglossicida P18, P. veronii S34, Ochrobactrum tritici S55, and Ensifer adhaerens S96, both deterministic models failed to fit the data as they showed more variability than what could have arisen from simple random sampling off the deterministic trajectories (Figure 2, Equations 1, 4, and 5). For these strains the VS model provided an adequate explanation of the data. Finally, note that if two models are nested, the ML score of the more complex model has to be the biggest. In Table 1, for the strains H2 and R28, after rounding, the ML score of models HT and SS are the same. Recall that in the HT model, when γ = 0, the HT model is identical to the SS model. As we show in De Gelder et al. (2007), the ML estimates of γ for these two strains are 2.11E − 09 and 1.99E − 30 respectively. Thus, the ML estimate under the HT model for these strains basically says that γ ≈ 0. Therefore, the HT model estimates converge to the SS model and hence their maximum-likelihood scores must be nearly identical. For the S55 strain the estimate of γ is 1.348896E-05, and, although this number is also close to 0, we note that neither the SS nor the HT model fits the data and that these models were rejected according to the absolute goodness-of-fit test.
Figure 2.—
For each of four bacterial strains (H2, R28, P21, and P18) the data (solid circles) and the estimated model trajectories (lines) are plotted. (Top) Maximum-likelihood observation error fit of the dynamic Equation 1 for H2 and R28 and Equations 4 and 5 for P21. There, it is assumed that the underlying trajectories obey a deterministic dynamic equation (solid line) and that any deviation from that trajectory seen in the data (solid circles) is attributed to sampling error. (Bottom) A process noise plus observation error fit for each of the three replicates of strain P18. The model parameters were estimated using the three replicates simultaneously and are presented separately with a different vertical scale for clarity. In each case, the open circles joined by a solid line show the observations and the solid circles represent the location of the underlying estimated trajectory (the Xt process) from which the observations were assumed to be drawn.
TABLE 1.
Likelihood-ratio tests and model selection results
|
P-values for likelihood-ratio test of: |
||||||
|---|---|---|---|---|---|---|
| Strain |
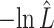 SS (P-value absolute g.o.f.) SS (P-value absolute g.o.f.) |
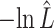 HT (P-value absolute g.o.f.) HT (P-value absolute g.o.f.) |
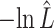 VS VS |
SS vs. HT | SS vs. VS | HT vs. VS |
| H2 | NA | 1 | NA | NA | ||
| R28 | 49.77485 (0.1304) | 49.77485 (0.2457) | NA | 1 | NA | NA |
| P21 | 45.738 (0.00052) | 30.24335 (0.5313) | NA | 1.86534E-07 | NA | NA |
| P18 | 246.0254 (0) | 245.2713 (0) | 104.4029 | NA | 4.20413 × 10−61 | 3.14139 × 10−63 |
| S34 | 189.7365 (0) | 175.8767 (0) | 64.91768 | NA | 7.8379 × 10−54 | 3.45158 × 10−50 |
| S96 | 644.6472 (0) | 520.86 (0) | 59.69714 | NA | 2.4877 × 10−253 | 1.3758 × 10−202 |
| S55 | 227.3623 (0) | 227.3623 (0) | 83.82895 | NA | 6.26173 × 10−62 | 2.16624 × 10−64 |
The estimated negative log-likelihood score 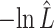 for each model (SS, segregation selection; HT, horizontal transfer; VS, variable selection) and strain combination is given under the first three columns. The better the model fit, the lower its computed
for each model (SS, segregation selection; HT, horizontal transfer; VS, variable selection) and strain combination is given under the first three columns. The better the model fit, the lower its computed 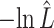 value. For the SS and HT model columns, the absolute goodness-of-fit (g.o.f.) P-values in parentheses indicate whether the model describes adequately (P-value > 0.05) or not (P-value < 0.05) the data at hand. Finally, the last three columns present the P-values for the likelihood-ratio tests to evaluate which model was the best for describing the data.
value. For the SS and HT model columns, the absolute goodness-of-fit (g.o.f.) P-values in parentheses indicate whether the model describes adequately (P-value > 0.05) or not (P-value < 0.05) the data at hand. Finally, the last three columns present the P-values for the likelihood-ratio tests to evaluate which model was the best for describing the data.
Results of predicted growth patterns:
The SS and HT models predict a smooth trajectory and the deviations of the data from those trajectories were assumed to be due to sampling noise (see Figure 2). The SS and HT model have the advantage of providing a very simple explanation of the data, yet they explain only a small number of growth patterns. In Figure 2, bottom, we plotted the recorded data for each replicated stability experiment of the strain P18, along with the posterior mode of the estimated trajectory under the VS model. Following the HMM assumptions, the process of growth is itself stochastic, so that the recorded data set would not deviate from a smooth unknown trajectory, but instead from a variable growth pattern. Thus, Figure 2, bottom, should not be interpreted as a typical “observed vs. predicted” plot. A major advantage of the VS model is that it can explain much more complex growth patterns. Its one disadvantage is that it does not provide a precise explanation as to what might cause the variation in selection over time. How well the VS model approximates a more mechanistic model is a topic for further research.
Results of the stability analysis under the HT model:
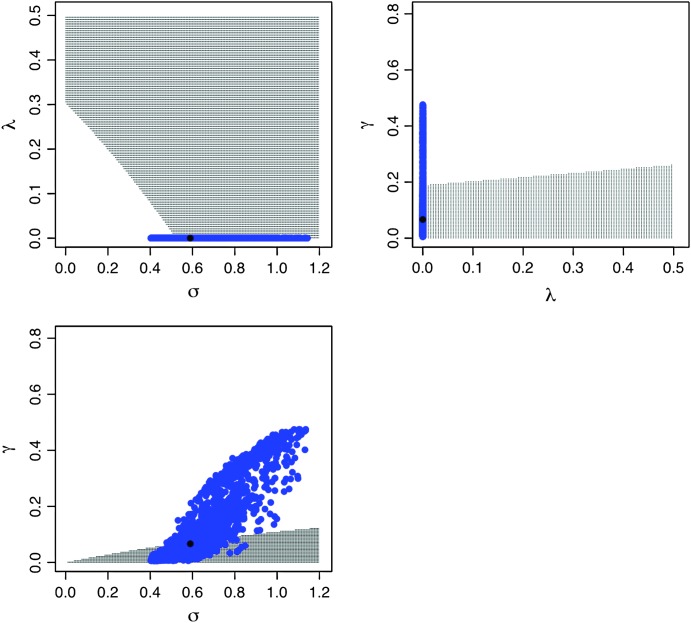
As explained before, the plots in Figure 1 reveal that there exist particular combinations of parameter values for which a long-term coexistence of plasmid-free and plasmid-carrying bacteria is predicted. Figure 3 depicts explicitly the regions of the parameter space for which this coexistence occurs. Take for instance the first subplot in Figure 3, where the plasmid burden σ is located in the abscissa and the segregation frequency λ is in the ordinate. The picture inside these axes was produced as follows: First, note that solving for σ in inequality 7, it follows that for fixed (biologically meaningful) values of θ, λ, and γ, 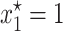 is stable (i.e., the plasmid will always go extinct) whenever
is stable (i.e., the plasmid will always go extinct) whenever
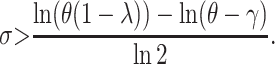 |
Figure 3.—
Stability boundaries for the horizontal transfer (HT) model, location of the estimated model parameters for the P21 strain and their joint approximate 95% confidence region. In each subplot, the HT model stability boundaries are plotted as a function of each parameter combination. The shaded area corresponds to the set of parameter values for which the plasmid-carrying cells eventually disappear (i.e., where the point x = 1 is stable) and the unshaded area denotes the parameter space for which the point x = 1 ceases to be a stable equilibrium and a new stable equilibrium x ∈ (0, 1) appears. In the unshaded area, a long-run coexistence between plasmid-free cells and plasmid-carrying cells is predicted. In each case, the solid dot locates the maximum-likelihood estimated parameter values and the cloud of blue points around them is their approximate joint 95% confidence cloud.
Then, for each combination of σ and λ the right-hand side of the above inequality was evaluated using the ML estimates of θ and γ. Then, a dot was simply plotted if the above inequality was satisfied. By repeating the same procedure for many combinations of σ and λ in the quadrant, a shaded area enclosing the parameter region where the point 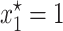 is stable appeared. The unshaded area denotes the set of parameter values for which
is stable appeared. The unshaded area denotes the set of parameter values for which 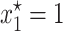 is an unstable equilibrium. As mentioned before, when this occurs, a new stable equilibrium
is an unstable equilibrium. As mentioned before, when this occurs, a new stable equilibrium 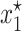 appears and the fraction of plasmid-free bacteria never converges to 1, but to a point in (0, 1). In other words, the plasmid-carrying bacteria remain in the population at a certain fraction.
appears and the fraction of plasmid-free bacteria never converges to 1, but to a point in (0, 1). In other words, the plasmid-carrying bacteria remain in the population at a certain fraction.
The ML estimates for the data set of the strain P21 were superimposed on these stability boundaries plots and fell inside the region where no long-run coexistence between plasmid-free bacteria and plasmid-carrying bacteria is predicted. To account for sampling uncertainty we added the approximate 95% parametric bootstrap confidence cloud around the ML estimates (Dennis et al. 1995; Hilborn and Mangel 1997; De Gelder et al. 2004). The joint confidence interval can be interpreted as an inverted likelihood-ratio test (Rice 1995): The points inside that interval denote the plausible parameter values under which the data at hand could have arisen, given the specified model. The (blue) cloud of points in Figure 3 lies within both the shaded and unshaded areas. Therefore, due to this observation it cannot be concluded that the plasmids will always be completely lost in the population in repeated experiments, using the strain P21.
Assessing the reliability and accuracy of the variable-selection (VS) model via simulations:
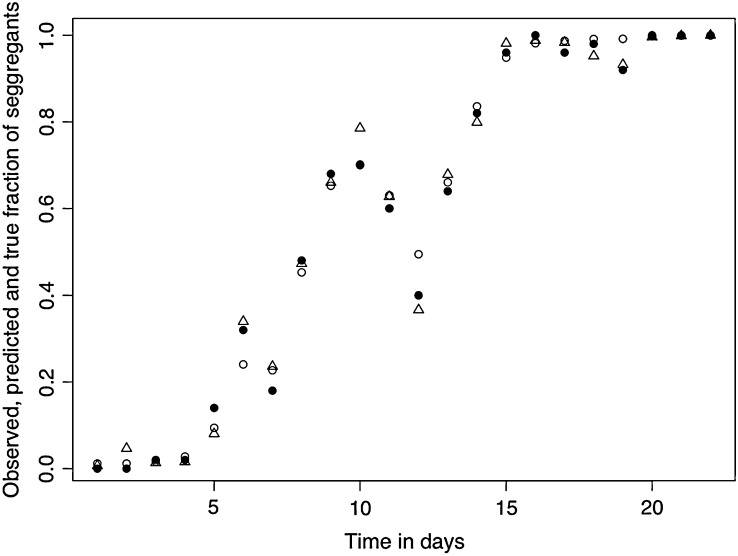
To assess the performance of the HMM formulation of the VS model, an extensive simulation study was performed. Data were simulated under the assumptions of the VS model using the parameter values x0 = 0.0066, μ = 0.01166667 per generation, τ2 = 0.1583333 per generation, and λ = 1.533333 × 10−05 per generation. Figures 4–6 were all based on simulated data sets.
Figure 4.—
Example of a simulated trajectory under the variable selection (VS) model (triangles), sampled observations from the trajectory according to a binomial sampling process (open circles) and the HMM estimates of the true simulated trajectory (solid circles) using only the observations (open circles). The parameter values used for the simulations are x0 = 0.0066, μ = 0.01166667 per generation, τ2 = 0.1583333 per generation, and λ = 1.533333 × 10−05 per generation.
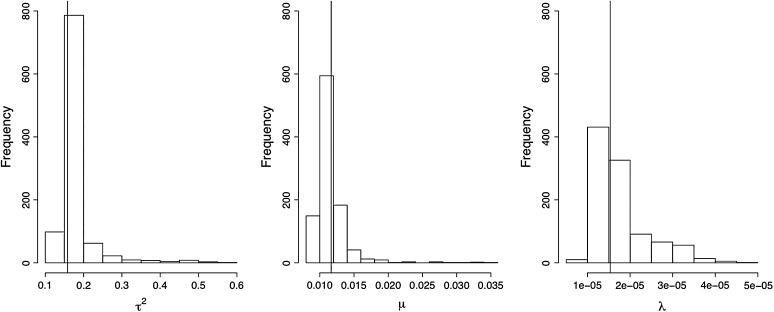
Figure 5.—
Evaluation of the performance of the HMM parameter estimation methods. One thousand data sets containing three replicated time series of plasmid loss each were simulated using the VS model plus binomial sampling error. For each data set, the posterior modes of the model parameters were found and the thus-obtained set of 1000 posterior modes for each parameter was plotted in a histogram and compared against the true values used to simulate (vertical lines).
Figure 6.—
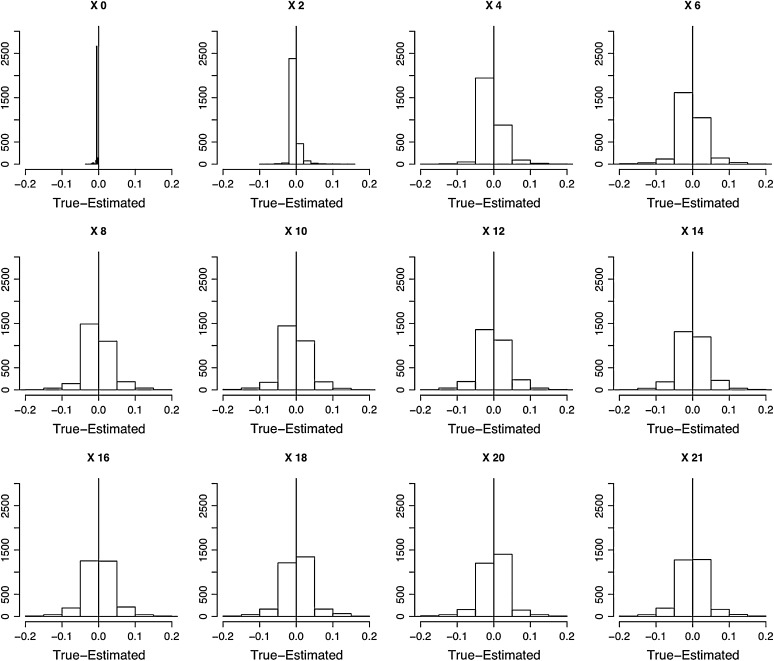
Evaluation of the performance of the HMM parameter estimation methods. One thousand data sets containing three replicated time series of plasmid loss each where simulated using the VS model plus binomial sampling error. For each data set, the posterior modes of the underlying (unseen) trajectory were estimated and their difference against the true simulated trajectory was computed. The 1000 sets of differences between the posterior mode of the X process trajectories and the true simulated value of the X process are shown as histograms, from day 0 to day 21.
Assessing how well the HMM formulation of the VS model predicted the underlying frequency dynamics was done as follows: A single simulated trajectory of the growth of the frequency of segregants over time under the VS model was produced and plotted in Figure 4 with triangles. Then, a random sample under the binomial model Equations 14 and 15 with 50 trials and probability equal to the size of the segregants fraction at each time step was taken. Those samples were then treated as an observed data set and plotted with open circles in Figure 4. The samples were then analyzed using the Gibbs sampling algorithm (see the supplemental data file at http://www.genetics.org/supplemental/). The results were plotted with solid circles in Figure 4. As Figure 4 suggests, the VS model does well at predicting the underlying frequency dynamics.
The parameter estimation method (see the supplemental data file at http://www.genetics.org/supplemental/) for the HMM formulation of the segregants' population dynamics provides reliable estimates of the plasmid cost and plasmid segregation frequency. One thousand data sets containing each three replicated time series of length 22 were simulated using the VS model. For each replicated realization of the process within each one of the “true” 1000 data sets, one random sample using the binomial observation error model was generated, thus obtaining 3000 simulated “observed” time series. The simulated observed time series were used to estimate (1) the posterior distributions of the model parameters and (2) the posterior distributions of the true simulated trajectories. Thus, 1000 posterior distributions were obtained for each of the model parameters μ, τ2, and λ.
The posterior modes of the model parameters posterior distributions were retrieved each time and were plotted in a histogram and compared to the true values used to generate the simulations in Figure 5. Because uniform priors were used throughout, the posterior modes of the model parameters are identical to the ML estimates of the model. Therefore, the variability around the mode of the posterior modes histograms is an estimate of the variance of the ML estimates. In these histograms, the 3 modes of the ML estimates of the model parameters μ, τ2, and λ lay very close to the true values, thus showing that the HMM parameter estimation framework provides nearly unbiased estimates of the model parameters. Also, the posterior distributions of the estimates of each point in the simulated true trajectories were computed (thus obtaining a total of 3000 × 22 posterior distributions). The posterior mode of each of those 3000 × 22 posterior distributions was computed and the difference between those modes and the true unknown trajectory point values was computed and plotted as histograms in Figure 6. The mode of those histograms lies in general right above 0, implying that the mode of the ML estimates is usually an unbiased estimate. The mode of the ML estimate of x0 was ∼0.050 and thus conveyed a biased estimate of the true original value x0 = 0.0066. A closer inspection of the Monte Carlo Markov chains generated using Gibbs sampling and simulations not presented here showed that the Gibbs algorithm had trouble converging for x0.
DISCUSSION
The patterns generated by the dynamics of plasmid loss in seven bacterial strains were effectively explained by our deterministic and stochastic population dynamics models. The segregation selection and horizontal transfer models with added observation noise together explained three of seven data sets. Nonneglegible plasmid transfer was a necessary component in our models to explain the data set for the P21 strain. The need of including process noise was evidenced by the rejection of the pure deterministic observation error models in four of the seven data sets in favor of the VS model. Hence, our analysis shows clearly that different strains presented different plasmid-loss dynamics. Moreover, the parameter estimates helped to explain which of the three underlying mechanisms was most responsible for the observed rapid plasmid loss. In the case of hosts H2 and P21, segregation rate was estimated to be respectively very low to low, but the plasmid cost was high to very high, suggesting that few segregants were formed but swept through the population once they appeared. In contrast, the very high segregation frequency estimate for host R28 with a low cost suggest that the major cause of rapid plasmid loss is a high segregational loss rate and not so much the growth advantage of plasmid-free segregants. Importantly, in the case of σ, the plasmid cost, which was also measured empirically, the model-based estimates were very similar to the experimental estimates obtained by De Gelder et al. (2007) for the same strains.
Although the HT model predicts that there exist certain parameter combinations for which the plasmid-carrying and plasmid-free bacteria coexist in the long-term, the ML parameter estimates for the strain P21 data indicated that the amount of transfer was not high enough to compensate for the loss via segregation and the selection against the plasmid-carrying cells. However, sampling variability can blur the certainty that over time, the plasmids will disappear from a bacterial population. Even if the ML parameter estimates predict the eventual loss of the plasmids, the joint confidence interval of the model parameters may encompass values that are both consistent with the loss of plasmid-carrying cells and their long-term presence, as shown by our results (Figure 3).
The VS model is a major departure from other modeling approaches (Stewart and Levin 1977; Levin et al. 1979; Levin 1980; Levin and Stewart 1980; Seneta and Tavaré 1982, 1983; Freter et al. 1983; Cooper et al. 1987; Simonsen 1991; Proctor 1994; Tolker-Nielsen and Boe 1994; Boe 1996; Boe and Rasmussen 1996; Bergstrom et al. 2000; Gasunov and Brilkov 2002; Wahl et al. 2002; Tanaka et al. 2003; Novozhilov et al. 2005). The process noise included in the VS model represents the variability due to the environment, where the environment may be understood as the host itself and the host's growth environment (De Gelder et al. 2007). Our model suggests that the plasmid cost changes from one day to the other. The growth rate of fraction of plasmid-free bacteria, a function of the plasmid cost, then becomes a random variable. Modeling plasmid cost as random effect substantially improves our ability to adequately explain much of the data. These stochastic changes in the plasmid cost may be due to the effect of beneficial or deleterious mutations in the host chromosome and/or the plasmid. Plasmid-carrying bacteria can acquire, for instance, compensatory mutations that allow them to grow as fast as or faster than the plasmid-free bacteria. These processes are not, however, explicitly modeled in the VS model equations and further work is required to unravel the underlying biological mechanisms behind this variable plasmid cost. How well the VS approximates a more mechanistic model is a topic for further research.
The fact that the VS model provided a substantially better fit to most of the data sets makes the use of SSMs an important tool for understanding plasmid-growth dynamics. However, a careful analysis, followed by extensive simulations, is required when using SSMs. As mentioned before, a recent study in population dynamics (Dennis et al. 2006) has shown that in the simple case of a linear and Gaussian SSM, the likelihood function is highly multimodal and ML estimation is not a trivial task. In fact, in some cases, the globally highest peak in the likelihood produces parameter estimates that are quite biased compared with estimates based on other modes. However, Jensen and Petersen (1999) showed that the maximum-likelihood estimates for SSMs are indeed asymptotically normal, which implies consistency. This does not contradict the simulation results of Dennis et al. (2006), since the multimodality eventually disappears and in the limit as the samples sizes goes to infinity, the maximum-likelihood estimate will converge to the true parameter. Yet, for finite amounts of data, the maximum-likelihood estimate may not be the best. Stochastic methods such as the Gibbs sampler used in this article can often fail to sample all the modes. For this reason, if multimodality of the likelihood surface is suspected, then extensive validation of the statistical methodology is required. Fortunately, the SSMs presented in this article did not exhibit any of the exotic behavior found in Dennis et al. (2006).
Stochastic population dynamics modeling in microbial systems is a subject that is still in its infancy and we stress that much remains to be done in the experimental, mathematical, and statistical areas. One of the final comments of Novozhilov et al. (2005, p. 1727) was that “unfortunately, quantitative estimates (of the different process rates) are lacking, which precludes us from supplementing the mathematical analysis of the model with empirical estimates….” Our study is an attempt to answer the plea of Novozhilov et al. (2005).
Acknowledgments
We thank Larry J. Forney and Zaid Abdo for their comments and help during the preparation of the manuscript and research. This work was supported by grants from the National Institutes of Health (P20 RR16448, NIH-R01 GM076040-01, NIH 1 R01 GM73821-02) and the National Science Foundation (NSF-DEB-0515738).
APPENDIX: DERIVATION OF THE VS MODEL TRANSITION PDF
Recall that in the right-hand side (RHS) of Equation 8, xt−1 is the realized value of the process Xt at time t − 1. Also, St comes from a normal distribution with mean μ and variance τ2. Provided that 0 ≤ λ < Xt | Xt−1 = xt−1 < 1, it follows from Equation 10 that
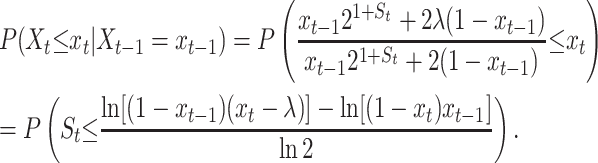 |
After differentiation and setting 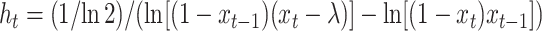 we get
we get
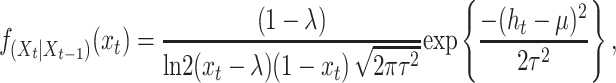 |
which is the transition pdf shown in Equation 11.
References
- Andrup, L., and K. Andersen, 1999. A comparison of the kinetics of plasmid transfer in the conjugation systems encoded by the F plasmid from Escherichia coli and plasmid pCF10 from Enterococcus faecalis. Microbiology 145 2001–2009. [DOI] [PubMed] [Google Scholar]
- Bergstrom, C. T., M. Lipsitch and B. R. Levin, 2000. Natural selection, infectious transfer and the existence conditions for bacterial plasmids. Genetics 155 1505–1519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boe, L., 1996. Estimation of plasmid loss rates in bacterial populations with a reference to the reproducibility of stability systems. Plasmid 36 161–167. [DOI] [PubMed] [Google Scholar]
- Boe, L., and K. V. Rasmussen, 1996. Suggestions as to quantitative measurements of plasmid loss. Plasmid 36 153–159. [DOI] [PubMed] [Google Scholar]
- Carlin, B. P., N. G. Polson and D. S. Stoffer, 1992. A Monte-Carlo approach to nonnormal and nonlinear state-space modeling. J. Am. Stat. Assoc. 87 493–500. [Google Scholar]
- Casella, G., and E. I. George, 1992. Explaining the Gibbs sampler. Am. Statist. 46 167–174. [Google Scholar]
- Cooper, N. S., M. E. Brown and C. A. Caulcott, 1987. A mathematical method for analysing plasmid instability in micro-organisms. J. Gen. Microbiol. 133 1871–1880. [DOI] [PubMed] [Google Scholar]
- Cushing, J., R. Costantino, B. Dennis, R. Desharnais and S. Henson, 2002. Chaos in Ecology. Academic Press, San Diego.
- De Gelder, L., J. M. Ponciano, Z. Abdo, P. Joyce, L. J. Forney et al., 2004. Combining mathematical models and statistical methods to understand and predict the dynamics of antibiotic sensitive mutants in a population of resistant bacteria during experimental evolution. Genetics 168 1131–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Gelder, L., F. Vandecasteele, C. Brown, L. J. Forney and E. M. Top, 2005. Plasmid donor affects host range of the promiscuous IncP-1β plasmid pB10 in a sewage sludge microbial community. Appl. Environ. Microbiol. 71 5309–5317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Gelder, L., J. M. Ponciano, P. Joyce and E. M. Top, 2007. Stability of a promiscuous plasmid in different hosts: no guarantee for a long-term association. Microbiology 153 452–463. [DOI] [PubMed] [Google Scholar]
- Dennis, B., R. Desharnais, J. Cushing and R. Costantino, 1995. Nonlinear demographic dynamics: mathematical models, statistical methods, and biological experiments. Ecol. Monogr. 65 261–281. [Google Scholar]
- Dennis, B., J. M. Ponciano, S. Lele, M. Taper and D. Staples, 2006. Estimating density dependence, process noise and observation error. Ecol. Monogr. 76(3): 323–341. [Google Scholar]
- De Visser, J., and D. Rozen, 2005. Limits to adaptation in asexual populations. J. Evol. Biol. 18 779–788. [DOI] [PubMed] [Google Scholar]
- Dröge, M., A. Pühler and W. Selbitschka, 2000. Phenotypic and molecular characterization of conjugative antibiotic resistance plasmids isolated from bacterial communities of activated sludge. Mol. Gen. Genet. 263 471–482. [DOI] [PubMed] [Google Scholar]
- Efron, B., and R. Tibshirani, 1993. An Introduction to the Bootstrap. Chapman & Hall, New York.
- Freter, R., R. Freter and H. Brickner, 1983. Experimental and mathematical models of Escherichia coli plasmid transfer in vitro and in vivo. Infect. Immun. 39 60–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasunov, V. V., and A. V. Brilkov, 2002. Estimating the instability parameters of plasmid-bearing cell. I. Chemostat culture. J. Theor. Biol. 219 193–205. [DOI] [PubMed] [Google Scholar]
- George, A., and E. Thompson, 2002. Multipoint linkage analyses for disease mapping in extended pedigrees: a Markov chain Monte Carlo approach. Technical Report 405, Department of Statistics, University of Washington, Seattle.
- Gogarten, J., and J. Townsend, 2005. Horizontal gene transfer, genome innovation and evolution. Nat. Rev. Microbiol. 3 679–687. [DOI] [PubMed] [Google Scholar]
- Hilborn, R., and M. Mangel, 1997. The Ecological Detective: Confronting Models With Data. Princeton University Press, Princeton, NJ.
- Jensen, J. L., and N. V. Petersen, 1999. Assymptotic normality of the maximum likelihood estimator in state space models. Ann. Statist. 27 514–535. [Google Scholar]
- Joyce, P., Z. Abdo, J. Ponciano, L. De Gelder, L. Forney et al., 2005. Modeling the impact of periodic bottlenecks, unidirectional mutation and observational error in experimental evolution. J. Math. Biol. 50 645–662. [DOI] [PubMed] [Google Scholar]
- Kado, C. I., and S. T. Liu, 1981. Rapid procedure for detection and isloation of small and large plasmids. J. Bacteriol. 145 1365–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiding, N., 1975. Extinction and exponential growth in a random environment. Theor. Popul. Biol. 8 49–63. [DOI] [PubMed] [Google Scholar]
- Kot, M., 2001. Elements of Mathematical Ecology. Cambridge University Press, Cambridge, UK.
- Lenski, R. E., and J. E. Bouma, 1994. Effects of segregation and selection on instability of plasmid pACYC184 in Escherichia coli B. J. Bacteriol. 169 5314–5316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin, B., 1980. Conditions for the existence of R-plasmids in bacterial populations, pp. 197–202 in Fourth International Symposium on Antibiotic Resistance, edited by S. Mitsuhashi, L. Rosival and V. Krcmery. Springer-Verlag, Berlin.
- Levin, B. R., and F. M. Stewart, 1980. The population biology of bacterial plasmids: a priori conditions for the existence of mobilizable nonconjugative factors. Genetics 94 425–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin, B. R., F. M. Stewart and V. A. Rice, 1979. Kinetics of conjugative plasmid transmission: fit of a simple mass-action model. Plasmid 2 247–260. [DOI] [PubMed] [Google Scholar]
- Lewontin, R., and D. Cohen, 1969. On population growth in a randomly varying environment. Proc. Natl. Acad. Sci. USA 62 1056–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer, R., and R. B. Millar, 1999. Bayesian stock assessment using a state-space implementation of the delay difference model. Can. J. Fish. Aquat. Sci. 56 37–52. [Google Scholar]
- Novozhilov, A. S., G. P. Karev and E. V. Koonin, 2005. Mathematical modeling of evolution of horizontally transferred genes. Mol. Biol. Evol. 22 1721–1732. [DOI] [PubMed] [Google Scholar]
- Proctor, G. N., 1994. Mathematics of microbial plasmid instability and subsequent differential growth of plasmid-free and plasmid-containing cells, relevant to the analysis of experimental colony number data. Plasmid 32 101–130. [DOI] [PubMed] [Google Scholar]
- Rademaker, J. L. W., F. J. Louws and F. J. de Bruijn, 1997. Characterization of the diversity of ecologically important microbes by REP-PCR genomic fingerprinting, pp. 1–26 in Molecular Microbial Ecology Manual, Supplement 3, edited by A. D. L. Akkermans, J. D. van Elsas and F. J. de Bruijn. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- Rice, J., 1995. Mathematical Statistics and Data Analysis, Ed. 2. Duxbury Press, Belmont, CA.
- Schlüter, A., H. Heuer, R. Szczepanowski, L. J. Forney, C. M. Thomas et al., 2003. The 64,508 bp IncP-1β antibiotic multiresistance plasmid pB10 isolated from a wastewater treatment plant provides evidence for recombination between members of different branches of the IncP-1β group. Microbiology 149 3139–3153. [DOI] [PubMed] [Google Scholar]
- Seneta, E., and S. Tavaré, 1982. Stochastic models for plasmid copy number, pp. 27–33 in First Rocky Mountain Regional Conference on Medical Applications of Statistics. University of Colorado Health Sciences Center, Denver.
- Seneta, E., and S. Tavaré, 1983. Some stochastic models for plasmid copy number. Theor. Popul. Biol. 23 241–256. [DOI] [PubMed] [Google Scholar]
- Simonsen, L., 1991. The existence conditions for bacterial plasmids: theory and reality. Microb. Ecol. 22 187–205. [DOI] [PubMed] [Google Scholar]
- Sørensen, S., M. Bailey, L. Hansen, N. Krower and S. Wuertz, 2005. Studying plasmid horizontal transfer in situ: a critical review. Nat. Rev. Microbiol. 3 700–710. [DOI] [PubMed] [Google Scholar]
- Stewart, F., and B. Levin, 1977. The population biology of bacterial plasmids: a priori conditions for the existence of conjugationally transmitted factors. Genetics 87 209–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka, M. M., C. T. Bergstrom and B. Levin, 2003. The evolution of mutator genes in bacterial populations: the roles of environmental change and timing. Genetics 164 843–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolker-Nielsen, T., and L. Boe, 1994. A statistical analysis of the formation of plasmid-free cells in populations of Escherichia coli. J. Bacteriol. 176 4306–4310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Top, E. M., M. Mergeay, D. Springael and W. Verstraete, 1990. Gene escape model: transfer of heavy metal resistance genes from Escherichia coli to Alcaligenes eutrophus on agar plates and in soil samples. Appl. Environ. Microbiol. 56 2471–2479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wahl, L., P. Gerrish and I. Saika-Voivod, 2002. Evaluating the impact of population bottlenecks in experimental evolution. Genetics 162 961–971. [DOI] [PMC free article] [PubMed] [Google Scholar]